SUMMARY
Neumann et al. [1] developed a widely used model for the analysis of hepatitis C virus (HCV) dynamics after the initiation of interferon therapy that assumes the effectiveness of therapy in blocking virion production, ε, is constant. However, with pegylated interferon α-2b (PEG-IFN) given weekly, there are significant changes in drug concentration between doses, leading to changes in drug effectiveness and viral rebounds. To investigate the appropriateness of the constant effectiveness (CE) model [1] for studies involving PEG-IFN, we simulated PEG-IFN treatment, using 294 sets of pharmacokinetic/pharmacodynamic (PK/PD) parameters that span observed ranges and fit the simulated data to the CE model. For most combinations of PK/PD parameters, the fits resulted in an infected cell loss rate, δ, that underestimates the true value used in the simulations and yielded over-estimates of the average effectiveness of PEG-IFN. In the setting of PEG-IFN therapy, the use of the CE model of HCV kinetics has to be reevaluated and the validity of its use depends on the amount of HCV RNA rebound observed between doses.
Keywords: hepatitis C virus, modelling, pegylated interferon α-2b, pharmacodynamics, pharmacokinetics, viral kinetics
INTRODUCTION
Neumann et al. [1] developed what has become a standard model for the analysis of hepatitis C virus (HCV) dynamics after the initiation of antiviral therapy. The model is similar in many respects to models developed to analyse the response to therapy of human immunodeficiency virus (HIV) [2] and hepatitis B virus (HBV)-infected patients [3,4]. One common feature of almost all published viral dynamic models is that they assume that the effect of drug therapy can be summarized by single constant parameter, ε, the drug efficacy or effectiveness in blocking virion production. However, recent work has suggested that for therapy using pegylated interferon (PEG-IFN) given once weekly, the assumption of constant effectiveness (CE) may be rather poor [5-9]. Here, we show that the Neumann et al. [1] model, which we shall call the CE model to emphasize this key assumption, when used to analyse data from studies involving PEG-IFN α-2b can lead to systematic errors in the estimation of drug effectiveness and viral kinetic parameters.
The CE model was developed to interpret the changes in HCV RNA measured after the initiation of daily interferon (IFN) therapy in HCV-infected patients. Lam et al. [10] had previously showed that HCV RNA, after an initial delay, declines during the first 24 h following IFN administration and then partially rebounds by the 48-hour post-treatment. Thus, a clinical trial using three different daily doses of IFN was conducted and interpreted with viral kinetic modelling. The work showed that IFN acted mainly by partially blocking the production of HCV from infected cells and the degree of blockage, termed the drug effectiveness in blocking production, ε, was estimated to be 81, 95 and 96% for drug doses of 5, 10 and 15 mIU [1]. The initial delay, t0, before HCV RNA begins declining was also estimated, as were the rate of virion clearance from the serum, c and the rate of loss of infected cells, δ. The success of the CE model in summarizing viral load data led to its being used more widely. For example, Torriani et al. [11] and Sherman et al. [12] used the method to estimate drug effectiveness and viral kinetic parameters in HIV/HCV coinfected patients treated with PEG-IFN α-2a given weekly once. Powers et al. [8] and Talal et al. [9], studying HIV/HCV infected patients treated with PEG-IFN α-2b showed that viral loads initially decreased after IFN administration but then began to rebound towards the end of the dosing interval. They also measured serum PEG-IFN concentration and showed that the viral rebound occurred as drug concentration waned, an observation also made by Formann et al. [6] for HCV-monoinfected patients treated with PEG-IFN α-2b. Buti et al. [5] also reported rebounds in HCV RNA levels by 72 h after PEG-IFN α-2b administration in HCV genotype 1-monoinfected patients. In order to analyse the viral kinetic data, Powers et al. [8] and Talal et al. [9] modified the CE model by assuming that the drug effectiveness, ε, rather than being constant varied with the measured drug concentration and thus successfully accounted for both the viral decline and rebounds observed during the first two weeks of therapy.
In most studies, serum drug concentrations are not measured and the only information available for modelling is the sequential changes in serum HCV RNA with time on treatment. Because drug concentration changes with time, drug effectiveness also changes. Here we ask, if we assume a CE that reflects the weekly average effectiveness, is it possible to model the patterns of HCV RNA changes seen during once weekly dosing with PEG-IFN? To answer this question, we have used the viral kinetic model of Powers et al. [8] and Talal et al. [9] in which PEG-IFN effectiveness depends on drug concentration, to generate artificial data sets of HCV RNA changes. The data sets we generate are based on parameters characterizing the pharmacokinetics (PK) and pharmacodynamics (PD) of PEG-IFN in a manner that reflects the patient-to-patient variation observed by Talal et al. [9]. We then assumed no knowledge of drug concentration or variation in effectiveness and fitted the datasets to the CE model. We estimated a constant effectiveness, ε, which we hoped will reflect the average effectiveness of PEG-IFN, as well the viral kinetic parameters c, δ and t0. As the actual values of the parameters that were used to generate the viral load data sets were known, we could then compare the estimated values that we obtained using the CE model with the true values. We could thus obtain information on the circumstances under which the CE model gives reasonably accurate estimates and those under which this procedure may give rather poor parameter estimates.
MODEL AND METHODS
In the CE model, the change in the number of infected cells, I(t) and in free virus, V(t), are given by
| (1a) |
| (1b) |
Here T is the number of uninfected cells that are targets for infection, β is the infection rate, δ is the death rate of infected cells, c is the rate constant characterizing clearance of free virus and p is the viral production rate per infected cell. The drug effectiveness in blocking virion production is ε, with ε = 1 being a 100% effective drug and ε = 0 being 0% effective.
We assumed that at t = 0, the time of therapy initiation, the patient's HCV infection is in steady state with target cell, infected cell and virus levels (T0, I0, V0) = (cδ/(βp), cV0/p, V0), where V0 is the baseline viral load, a parameter that can be easily estimated from patient data.
The change in viral load with time on therapy was derived by Neumann et al. [1] from equations (1a,b) under the assumption that the number of target cells T is constant (at T0), and that the effectiveness of the drug, ε(t) = ε, is constant after some time delay, t0. The solution is
| (2) |
where and A = (εc–λ2)/(λ1–λ2).
When PEG-IFN is given weekly, drug concentration and hence, drug effectiveness is not constant. A model that has been found to summarize the observed serum drug concentration variation of PEG-IFN α-2b is a standard ‘absorption and elimination’ PK model [9]. The model considers an absorption site and blood. After the drug injection, drug is localized in an absorption site from which it enters the blood at rate ka and is subsequently eliminated from the blood at rate ke. The rates of change of the amount of bioavailable drug at the absorption site, X and in the blood, A, are given by
| (3a) |
| (3b) |
We focused on the case when PEG-IFN is injected once at t = 0. The initial conditions for equations (3a,b) are X0 = FD and A0 = 0, where F is the bioavailability (0 ≤ F ≤ 1) and D is the total amount of drug administered. The drug concentration is C(t) = A(t)/Vd, where Vd is the drug's volume of distribution. We modelled the effectiveness of the drug in blocking virion production by a PD model [13] that assumes
| (4) |
where EC50 is the drug concentration in blood at which the drug is 50% effective and n is the Hill coefficient, a parameter that determines how steeply the effectiveness changes with variations in drug concentration.
To generate surrogate viral load data sets we solved equations (1a,b), (3a,b) and (4) with the initial conditions (T0, I0, V0, X0, A0) and parameter values as specified in Table 1. The values of c, d, V0, D and F/Vd were chosen based on results from a previous study using PEG-IFN α-2b [8,9]. The values of β and p need not be specified. Notice that if both sides of equation (1a) are multiplied by p, then with T0 = cδ/(βp), the equation becomes, dy/dt = δ(cV-y), with y = pI and with initial condition y0 = cV0. Equation (1b) now becomes, dV/dt = (1–ε)y–cV, and β and p no longer appear. The remaining parameters related to PK and PD, i.e. ka, ke, EC50 and n, were varied, using ranges obtained in a study in which both HCV RNA and the PEG-IFN α-2b concentration in serum were measured [9]. In that study, the mean values estimated were ka = 2.43 day−1, ke = 0.46 - day−1, EC50 = 0.30 μg/L and n = 2.7. Further, we could not detect a significant correlation among the values of ka, ke and EC50 estimated for each patient [9] (partial correlation coefficients, t-test, P > 0.05) [14]. Thus, we assumed that values of ka, ke and EC50 could be chosen independently in generating the surrogate data sets. For ka, we chose the minimum (0.19 day−1), approximately the average (2.0 day−1) and the maximum value (7.0 day−1) estimated previously [9]. For ke, we chose seven values distributed uniformly between the estimated [9] minimum (0.2 day−1) and maximum (0.8 day−1), i.e. 0.2, 0.3... 0.8 day−1. For EC50, we chose six values uniformly from 0.1 to 0.6 μg/L, i.e. 0.1, 0.2, ... 0.6 μg/L, based on the fact that previous estimates [9] of EC50 ranged up to 0.64 μg/L. In addition, we also chose a small EC50, 0.01 μg/L, representative of a few patients who showed sustained virological response [9]. Further, for the Hill coefficient (n), Talal et al. [9] considered integer values between 1 and 4, so here we chose as representative: n = 1, which implies ε increases gradually with PEG-IFN concentration, C(t) and n = 3, which gives a more abrupt increase in ε as C(t) approaches EC50. Thus, we studied a total of 294 (=3×7×7×2) surrogate data sets for different PK/PD parameters. Note that in this study we are interested in the effects of different PK/PD in estimates of the viral kinetic parameters (c, δ and ε), thus to simplify matters we kept these parameters constant when generating the surrogate data sets. Another approach would be to also vary these parameters together with the PK/PD parameters. However, this would require many more datasets/simulations and we opted for the simplest scenario, which also allows a more direct observation of the effects of the PD without confounding variation in viral kinetic parameters.
Table 1.
Parameters used to generate the surrogate data
| Parameters for which we used different values in simulations | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Description | Notation | Units | Values used in simulations | ||||||
| Absorption rate of drug into blood | ka | day−1 | 0.19 | 2 | 7 | ||||
| Drug concentration that leads to 50% effectiveness | EC50 | μg/L | 0.01 | 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 |
| Elimination rate of drug from blood. | ke | day−1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 |
| Hill coefficient | n | 1 | 3 | ||||||
Parameter values used in all the simulations: Virion clearance rate; c = 9.9 day−1: Infected cell loss rate; δ = 0.32 day−1: Initial viral load; V0 = 5.0 × 106 IU/mL: Total drug dose; D = 129.6 μg: Production rate of virus per infected cell; P = 10 virions day−1: Bioavailability of drug/volume of distribution; F/Vd = 0.01 L−1: Initial number of infected cells; I0 = cV0/p = 4.95 × 106: Number of target cells; T0 = 1.53 × 106 cell/mL: Infection rate constant; β = cδ/(T0p) = 1.0 × 10−7 IU−1 ml day−1: Initial concentration of drug at injection site; X0 = FD = 1.296 Vd μg/L: Initial concentration of drug in blood; A0 = 0 μg/L.
Using the surrogate data as if it were real experimental data, we then estimated the parameters c, δ, V0, t0 and ε of the CE model by performing nonlinear least squares fitting of the logarithm of V(t) in equation (2) to the logarithm of the data. We used the viral load data from time 0 to day 7 for the parameter estimation procedure. We assumed that V(t) was measured every 8 h, generating 22 viral load measurements. This is more than typically measured in practice and thus we are biasing our analysis towards a situation in which errors are not being made as a result of poor viral load sampling.
The CE model (equation 2) has five parameters c,δ, V0, t0 and ε. Below we report the difference between the values of c and δ which were used to generate the surrogate data and those which were estimated with equation (2). In the surrogate data, there was no explicit delay, t0, but rather the PK and PD determined when enough drug was first present to have a noticeable effect. Thus, although we estimated t0, we only compared it with the time at which the PEG-IFN concentration reached its maximum. Lastly, we report the difference between the estimated CE and the average drug effectiveness, εa, calculated from the PK/PD model . Here, we report direct comparisons between our simulations with known parameters and the patient-by-patient estimates obtained with the CE model, because we are specifically interested in the results for each surrogate dataset (‘patient’). However, in clinical practice, it is often more desirable to use a population approach (based on mixed-effects models) [15], where one is not interested in the specific parameter values for each patient, but rather is attempting to estimate population averages [16,17].
In principle, if the drug enters the blood with infinite speed (ka = ∞) and if the drug in blood does not decay (ke = 0), then the average effectiveness and the estimated effectiveness should be the same and t0 should be equal 0. As a check of our procedure, we confirmed this limiting case (data not shown), before proceeding to the more realistic study, using the PK and PD parameters described above.
RESULTS
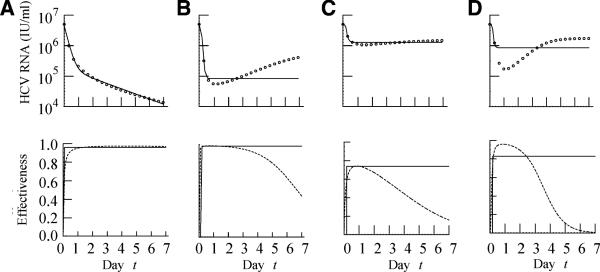
We generated by numerical simulation surrogate viral load data sets and then fitted the CE model to this data. Figure 1 shows a number of examples of both the viral loads and the ‘actual’ drug effectiveness profile used to generate the viral load changes. When the actual effectiveness increases to a high level immediately after the initiation of therapy and this level is sustained until day 7, the viral load shows a biphasic decline and the CE model fits the viral load data well (Fig. 1a). On the other hand, when the actual effectiveness rapidly increases to a high level but then decreases towards day 7, the viral load initially declines but then rebounds (Fig. 1b). As the CE model does not allow for a decline in drug effectiveness, it cannot model viral load rebounds. Hence, the best fit of the CE model to the data is poor and shows a flat second phase instead of a rebound (Fig. 1b).
Fig. 1.
Surrogate viral load data generated assuming PEG-IFN α-2b therapy starting at t = 0. Open circles are the data obtained by numerical simulation of equations (1a,b), (3a,b) and (4) with a 4th-order Runge-Kutta method. Solid lines are the best-fit of the CE model (equation 2) to the data. Note the CE model always predicts a monotonic decrease of HCV RNA. The parameters used to generate the surrogate data in the figure are: (A) ka = 0.19 day−1, EC50 = 0.01 μg/L, ke = 0.3 day−1, n = 1, (B) ka = 2 day−1, EC50 = 0.01 μg/L, ke = 0.8 day−1, n = 1 and (C–D) ka = 2.32 day−1, EC50 = 0.30 μg/L, ke = 0.48 day−1, n = 1 and n = 3, respectively. The other parameters are given in Table 1. The PK parameters used to generate panels (C) and (D) represent average values, while the parameters used to generate panels (A) and (B) represent plausible but less frequently observed values.
In the patient data presented by Talal et al. [9], the viral load patterns presented in Figs 1a,b might be considered the extremes and are not seen very often. Thus, to explore more realistic examples, we show in Fig. 1 results using the average values of the PK/PD parameters (ka, ke and EC50) estimated by Talal et al. [9], as well as n = 1 or 3. When the Hill coefficient was n = 1, the actual effectiveness increased gradually with time reaching a maximum of about 0.75, and the viral load declined by 0.5-log and then rebounded slowly (Fig. 1c). Even though the CE model does not capture the rebound, the fit obtained with a flat second phase is reasonable. When the Hill coefficient was n = 3, the actual effectiveness increased to a higher level after the initiation of therapy and the high level was sustained for a few days followed by a rapid decrease (Fig. 1d). As one might expect from this drug effectiveness pattern, the viral load declined rapidly (by 1.5 log) and then rebounded (Fig. 1d). As in the previous case of a viral rebound, the CE model could not fit the rebound and instead generated a flat second phase (Fig. 1d).
Relationship between actual effectiveness and estimated effectiveness
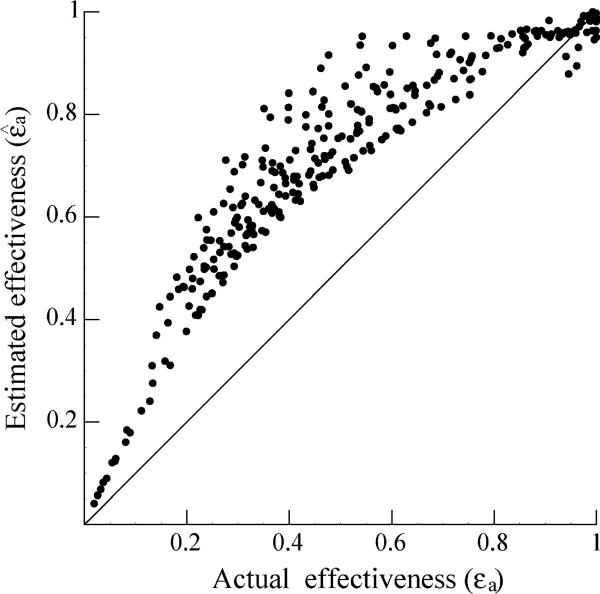
In the surrogate data, the value of the drug effectiveness changes during the week, as the drug concentration first increases and then wanes. We calculated its average, εa, obtained from equations (3) and (4), and compared it with the average of the estimated effectiveness, , where the estimated effectiveness is obtained by fitting the CE model to the surrogate data. Figure 2 shows the relationship between the actual average effectiveness and the estimated effectiveness. Most of the estimates (277/294) of the average effectiveness obtained with the CE model are above the line , i.e. the estimated effectiveness is larger than the true average effectiveness, εa. Further, Fig. 2 shows that for higher values of the actual effectiveness, the estimates obtained with the CE model improved, i.e. the estimates approached the line . However, because of the PK of PEG-IFN, it is unlikely that enough drug will be available toward the end of the weekly dosing interval to generate a very high average effectiveness. For example, in Talal et al. [9], the average effectiveness during the first week of therapy was 0.64.
Fig. 2.
The average of estimated effectiveness, , obtained by fitting the CE model to the surrogate data plotted against the average of actual effectiveness, εa, used to generate the data. Each point corresponds to the estimate obtained from analyzing one data set. Solid line indicates the ideal situation . Data points above the line indicate that the average estimates are larger than the actual average effectiveness.
Estimate of the viral clearance rate and the infected cell loss rate
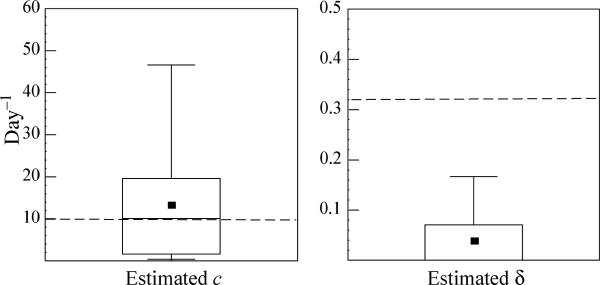
When we generated the surrogate data sets we fixed the value of the virion clearance rate c at 9.9 day−1 and the infected cell loss rate δ at 0.32 day−1, the averages estimated by Talal et al. [9]. The values of c and δ estimated from the data fitting using the CE model are denoted and . The estimated and are shown in Fig. 3. If both ka and ke are large, the viral load rebounds towards the end of the week, the CE fit is poor and the true value of c is overestimated (148/294 cases). However, in the remaining cases (146/294), c was underestimated. Averaging over all cases, we found while the median was 10.1, close to the true value of c. In contrast, the true value of δ was underestimated in most of the cases (288/294 cases), and very often (204/294) the estimated infected cell loss rate was less than 0.01, i.e. a flat second phase was generated. In conclusion, the CE model produces inaccurate estimates of both c and δ.
Fig. 3.
Estimates of the viral clearance rate, and the infected cell loss rate, , obtained using the CE model. Dashed lines indicate the true values of c (9.9 day−1) and δ (0.32 day−1). The horizontal lines within the boxes denote the medians (c = 10.1 day−1 and δ = 0 day−1, which for δ is the same as the minimal value), while the lines at the bottom and top of the boxes show 25 and 75% quartiles, respectively. The whiskers show the 10 and 90% percentiles. Squares in the boxes denote the estimated averages (c = 13.2 day−1 and δ = 0.04 day−1).
DISCUSSION
Using the CE model to fit simulated data in which HCV RNA is assumed to change because of therapy with PEG-IFN α-2b given once weekly resulted in estimates of the infected cell loss rate δ (Fig. 3) that underestimated the true value, while the average effectiveness of PEG-IFN over the 7-day-dosing interval was overestimated (Fig. 2). In addition, in 293 of 294 cases, the estimated value of the delay (t0) until a drug effect is observed was smaller than the time to the peak drug concentration in blood (not shown). The underestimate of δ occurs in part, because for many PK/PD parameter sets (e.g. when ka and ke are large) the second phase is essentially flat or rebounds, and in the CE model, this pattern can only be accommodated with a negligible loss rate of infected cells [18].
Our analysis, which relied on surrogate data, was restricted to the case in which the viral load data included no testing and/or sampling error, which is not true of real data. In addition, in clinical studies, blood samples are taken less frequently than the 8-hour sampling interval assumed here. The effects of less than ‘perfect’ sampling on parameter estimation still remain to be examined, but the major conclusion from this study is that, even under the best of circumstances, accurate parameter estimation cannot be performed using only HCV RNA data collected frequently at the beginning of PEG-IFN α-2b therapy. While we expect the same to be true for studies using PEG-IFN α-2a (40 kD), because viral load rebounds have also been observed between doses [7], we have not directly analysed this situation.
What is one to do in a clinical viral kinetics study now that the standard of care involves use of PEG-IFN plus ribavirin? An approach, as in the work of Powers et al. [8] and Talal et al. [9], is to simultaneously measure the HCV RNA and PEG-IFN concentrations, and then use a combined PK/PD viral dynamic analysis. This remains to be done in the context of HCV-monoinfected patients. A second approach is to do a brief (2−4 week) viral dynamic study using daily high-dose IFN, as was performed by Neumann et al. [1], and then switch the patients to PEG-IFN standard of care. It would be of interest to learn whether the estimates of the parameters, ε (which is treatment related) and δ (which is host related), made during the period that daily IFN was given, are predictive or even correlative of the long-term response on PEG-IFN based therapy [19]. We note that before PEG-IFN therapy was the standard of care, kinetic studies during 4 weeks of intense daily therapy with IFN were predictive of clinical outcome, even when the patients were switched to the standard regime of IFN given three times per week for the remaining 44 weeks of treatment [20,21]. Another possibility is to use a heuristic model with a time-varying efficacy, such as was done before [22]. We are studying different versions of such models to determine which form for the efficacy leads to the best estimates of the kinetic parameters. Lastly, it may be possible to obtain better estimates of δ, the loss rate of infected cells, by collecting data over longer periods of time even if the CE model is used to analyse the viral load data (A. Neumann, personal communication). In a similar study using simulated data for 4 weeks of therapy, we have now shown that δ is still inaccurately estimated with the CE model [23].
In conclusion, we have shown that the use of the CE model to interpret viral kinetic data obtained with PEG-IFN is fraught with difficulties and can generate inaccurate parameter estimates.
ACKNOWLEDGEMENTS
This work was performed under the auspices of the US Department of Energy under contract DE-AC52-06NA25396 and supported by NIH grants RR06555 and AI065256 (A.S.P), P20-RR18754 (R.M.R.), and JSPS grant 16-06631 (E.S.) which she received as a research fellow in Kyushu University, Japan (2004−2006).
Abbreviations
- HCV
hepatitis C virus
- HBV
hepatitis B virus
- CE
constant effectiveness
- PK
pharmacokinetic
- PD
pharmacodynamic
- PEG-IFN
pegylated interferon
REFERENCES
- 1.Neumann AU, Lam NP, Dahari H, et al. Hepatitis C viral dynamics in vivo and the antiviral efficacy of interferon-alpha therapy. Science. 1998;282(5386):103–107. doi: 10.1126/science.282.5386.103. [DOI] [PubMed] [Google Scholar]
- 2.Perelson AS, Neumann AU, Markowitz M, Leonard JM, Ho DD. HIV-1 dynamics in vivo: virion clearance rate, infected cell life-span, and viral generation time. Science. 1996;271(5255):1582–1586. doi: 10.1126/science.271.5255.1582. [DOI] [PubMed] [Google Scholar]
- 3.Nowak MA, Bonhoeffer S, Hill AM, Boehme R, Thomas HC, McDade H. Viral dynamics in hepatitis B virus infection. Proc Natl Acad Sci USA. 1996;93(9):4398–4402. doi: 10.1073/pnas.93.9.4398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Tsiang M, Rooney JF, Toole JJ, Gibbs CS. Biphasic clearance kinetics of hepatitis B virus from patients during adefovir dipivoxil therapy. Hepatology. 1999;29(6):1863–1869. doi: 10.1002/hep.510290626. [DOI] [PubMed] [Google Scholar]
- 5.Buti M, Sanchez-Avila F, Lurie Y, et al. Viral kinetics in genotype 1 chronic hepatitis C patients during therapy with 2 different doses of peginterferon alfa-2b plus ribavirin. Hepatology. 2002;35(4):930–936. doi: 10.1053/jhep.2002.32150. [DOI] [PubMed] [Google Scholar]
- 6.Formann E, Jessner W, Bennett L, Ferenci P. Twice-weekly administration of peginterferon-alpha-2b improves viral kinetics in patients with chronic hepatitis C genotype 1. J Viral Hepat. 2003;10(4):271–276. doi: 10.1046/j.1365-2893.2003.00446.x. [DOI] [PubMed] [Google Scholar]
- 7.Levy-Drummer R, Haagmans B, Soulier A, et al. Pharmacodynamic modeling of HCV kinetics during peg-interferon-alfa-2A (40KD) and Ribavirin treatment of chronic hepatitis C genotype 1 patients in the DITTO–HCV study. Hepatology. 2004;40(S4):390A. [Google Scholar]
- 8.Powers KA, Dixit NM, Ribeiro RM, Golia P, Talal AH, Perelson AS. Modeling viral and drug kinetics: hepatitis C virus treatment with pegylated interferon alfa-2b. Semin Liver Dis. 2003;23(Suppl 1):13–18. doi: 10.1055/s-2003-41630. [DOI] [PubMed] [Google Scholar]
- 9.Talal AH, Ribeiro RM, Powers KA, et al. Pharmacodynamics of PEG-IFN α differentiate HIV/HCV coinfected sustained virological responders from nonresponders. Hepatology. 2006;43(5):943–953. doi: 10.1002/hep.21136. [DOI] [PubMed] [Google Scholar]
- 10.Lam NP, Neumann AU, Gretch DR, Wiley TE, Perelson AS, Layden TJ. Dose-dependent acute clearance of hepatitis C genotype 1 virus with interferon alfa. Hepatology. 1997;26(1):226–231. doi: 10.1002/hep.510260130. [DOI] [PubMed] [Google Scholar]
- 11.Torriani FJ, Ribeiro RM, Gilbert TL, et al. Hepatitis C virus (HCV) and human immunodeficiency virus (HIV) dynamics during HCV treatment in HCV/HIV coinfection. J Infect Dis. 2003;188(10):1498–1507. doi: 10.1086/379255. [DOI] [PubMed] [Google Scholar]
- 12.Sherman KE, Shire NJ, Rouster SD, et al. Viral kinetics in hepatitis C or hepatitis C/human immunodeficiency virus-infected patients. Gastroenterology. 2005;128(2):313–327. doi: 10.1053/j.gastro.2004.11.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Gabrielsson J, Weiner D. Pharmacokinetic/Pharmacodynamic Data Analysis: Concepts and Applications. 3rd edn. Apotekarsocieteten; Stockholm, Sweden: 2000. rev. and expanded edn. [Google Scholar]
- 14.Sokal RR, Rohlf FJ. Biometry: The Principles and Practice of Statistics in Biological Research. 3rd edn W.H. Freeman; New York: 1995. [Google Scholar]
- 15.Pinheiro JC, Bates DM, ebrary I. Mixed-effects Models in S and S-PLUS. Springer; New York: 2000. [Google Scholar]
- 16.Neumann AU, Lam NP, Dahari H, et al. Differences in viral dynamics between genotypes 1 and 2 of hepatitis C virus. J Infect Dis. 2000;182(1):28–35. doi: 10.1086/315661. [DOI] [PubMed] [Google Scholar]
- 17.Thiebaut R, Guedj J, Jacqmin-Gadda H, et al. Estimation of dynamical model parameters taking into account undetectable marker values. BMC Med Res Methodol. 2006;6:38. doi: 10.1186/1471-2288-6-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Dahari H, Lo A, Ribeiro RM, Perelson AS. Modeling hepatitis C virus dynamics: liver regeneration and critical drug efficacy. J Theoret Biol. 2007;247(2):371–381. doi: 10.1016/j.jtbi.2007.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Dixit NM, Layden-Almer JE, Layden TJ, Perelson AS. Modelling how ribavirin improves interferon response rates in hepatitis C virus infection. Nature. 2004;432(7019):922–924. doi: 10.1038/nature03153. [DOI] [PubMed] [Google Scholar]
- 20.Layden-Almer JE, Layden TJ, Reddy KR, Levy-Drummer RS, Poulakos J, Neumann AU. First phase viral kinetic parameters as predictors of treatment response and their influence on the second phase viral decline. J Viral Hepat. 2002;9:340–345. doi: 10.1046/j.1365-2893.2002.00377.x. [DOI] [PubMed] [Google Scholar]
- 21.Layden-Almer JE, Ribeiro RM, Wiley T, Perelson AS, Layden TJ. Viral dynamics and response differences in HCV-infected African American and white patients treated with IFN and ribavirin. Hepatology. 2003;37(6):1343–1350. doi: 10.1053/jhep.2003.50217. [DOI] [PubMed] [Google Scholar]
- 22.Bekkering FC, Neumann AU, Brouwer JT, Levi-Drummer RS, Schalm SW. Changes in anti-viral effectiveness of interferon after dose reduction in chronic hepatitis C patients: a case control study. BMC Gastroenterol. 2001;1:14. doi: 10.1186/1471-230X-1-14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Shudo E, Ribeiro RM, Pelelson AS. Modeling the Kinetics of hepatitis C virus RNA decline over four weeks of treatment with pegylated interferon α-2b. J Viral Hepat. doi: 10.1111/j.1365-2893.2008.00977.x. (in press) [DOI] [PMC free article] [PubMed] [Google Scholar]