Skip to main content
PMC home page
BioMedical Engineering OnLine logoLink to BioMedical Engineering OnLine
. 2003 Oct 14;2:17. doi: 10.1186/1475-925X-2-17

Exotendons for assistance of human locomotion

Antonie J van den Bogert 1,2,✉
PMCID: PMC270067  PMID: 14613503

Abstract

Background

Powered robotic exoskeletons for assistance of human locomotion are currently under development for military and medical applications. The energy requirements for such devices are excessive, and this has become a major obstacle for practical applications. Legged locomotion in many animals, however, is very energy efficient. We propose that poly-articular elastic mechanisms are a major contributor to the economy of locomotion in such specialized animals. Consequently, it should be possible to design unpowered assistive devices that make effective use of similar mechanisms.

Methods

A passive assistive technology is presented, based on long elastic cords attached to an exoskeleton and guided by pulleys placed at the joints. A general optimization procedure is described for finding the best geometrical arrangement of such "exotendons" for assisting a specific movement. Optimality is defined either as minimal residual joint moment or as minimal residual joint power. Four specific exotendon systems with increasing complexity are considered. Representative human gait data were used to optimize each of these four systems to achieve maximal assistance for normal walking.

Results

The most complex exotendon system, with twelve pulleys per limb, was able to reduce the joint moments required for normal walking by 71% and joint power by 74%. A simpler system, with only three pulleys per limb, could reduce joint moments by 46% and joint power by 47%.

Conclusion

It is concluded that unpowered passive elastic devices can substantially reduce the muscle forces and the metabolic energy needed for walking, without requiring a change in movement. When optimally designed, such devices may allow independent locomotion in patients with large deficits in muscle function.

Background

Powered robotic exoskeletons are currently under development for enhancement of human locomotor performance in the military [1], in industry [2], and for patients with mobility impairments [3]. When compared to wheeled vehicles and wheelchairs, exoskeleton-based assistive devices have several advantages. They allow the user to go outside of paved surfaces, and there is the possibility of an intuitive haptic user interface, which senses the user's intended movement and assists it automatically [2]. Energy efficiency is, however, a major problem for such technology. Wheeled vehicles, once at constant speed, only require power to overcome small amounts of energy lost due to rolling friction and air resistance. Legged systems, on the other hand, require considerable additional energy to accelerate and decelerate the limbs and to dynamically support the body mass against gravity [4]. Inverse dynamic analysis of human movement has shown that, when driven by hypothetical motors at each joint, walking would require about 60 W of steady state power [5]. Powered exoskeletons for military applications are estimated to require 600 W of steady state power at running speeds when carrying a maximum payload [6]. Supplying power to such devices for several hours is well beyond the capabilities of current battery technology. Only an internal combustion engine can provide sufficient energy while still being small enough to be carried, with sufficient fuel, in a backpack [2].

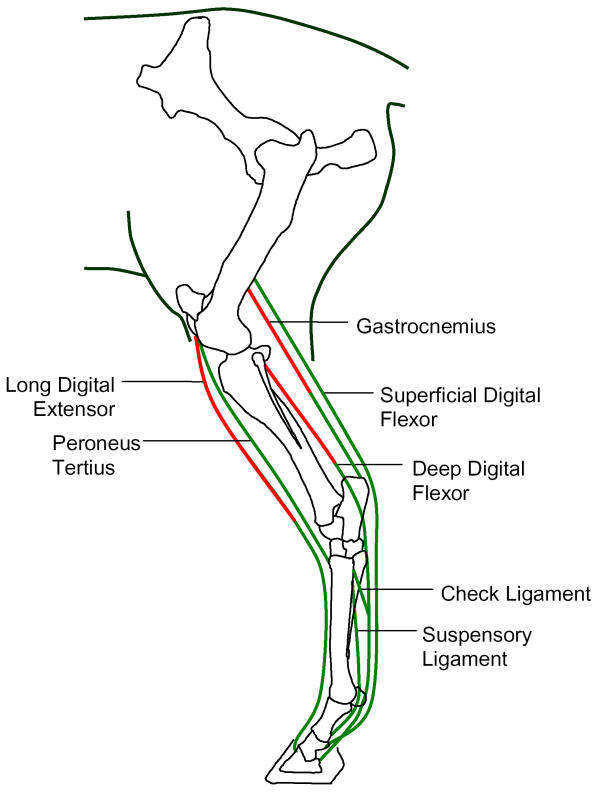
Efficient legged locomotion systems can be found in nature. Large terrestrial animals typically do not power their movements with a motor at each joint. Muscles often span multiple joints, which results in energy-saving power transfers when a movement simultaneously requires negative power at one joint and positive power at another joint [7]. Furthermore, it is often possible to make effective use of passive elastic properties to generate part of the required force or power without metabolic cost, especially when muscle-tendon units span multiple joints [8,9]. These mechanisms are highly developed in horses. Of the seven musculotendinous structures in the distal part of the equine hindlimb, four have become almost completely tendinous and the others have short muscle fibers with strong parallel elastic tissue and a long series elastic component spanning up to four major joints [10-12] (Figure 1). Measurements of bone kinematics and tendon strain have shown that forces in the digital flexors and in the Peroneus Tertius are consistent with passive elastic mechanisms for force generation [13-15]. This limb design results in various "pogo-stick" and "catapult" mechanisms that contribute to efficient locomotion [15-17]. Consequently, horses consume 50% less metabolic energy for running than humans, per kg of body weight [10]. In contrast to these efficient natural systems, current designs for powered exoskeletons use a traditional robotics approach where movement is generated by stiff servomotors, each moving a single joint. This approach is thought to be responsible for poor efficiency and stiff-legged gait in legged robots [18].

Figure 1.

Figure 1

Open in a new tab

Schematic representation of the complete below-knee musculature in the equine distal limb, showing the relative arrangement of muscles (red) and tendons (green).

In this paper we explore the potential utility of passive elastic devices for assisting human movement, attached external and in parallel to the body. Such "exotendons" would span multiple joints as in the design of equine limbs. Artificial exotendons offer some additional possibilities that are not found in natural systems. For example, they can cross over from the posterior side to the anterior side of a limb, and can even originate in one limb and insert into another limb. We will first present a general procedure to find an optimal geometrical arrangement of exotendons for assistance of any given movement. Subsequently, we will show an application of this method, resulting in specific assistive devices for normal human walking.

Methods

General procedure

We consider exotendons guided by one to six pulleys, each attached at one of the joints in the lower extremities: left and right hip, knee, and ankle. The analysis considers motion in the sagittal plane only, i.e. flexion and extension. In such a system, exotendon length L is a linear function of six joint angles φ (in radians):

graphic file with name 1475-925X-2-17-i1.gif

where L0 is exotendon length when all joint angles are zero and ri is the moment arm at joint i. We use the convention that joint angles increase during an anterior swing of the distal segment of the joint [13]. Hence, a positive moment arm ri in equation (1) indicates that the exotendon runs anterior to the joint i. Conversely, a negative sign indicates that the exotendon runs posteriorly.

The exotendon is assumed to be made of a rubber-like material, with zero force below slack length and a constant stiffness k at larger length. Exotendon force F is thus given by:

graphic file with name 1475-925X-2-17-i2.gif

This exotendon force F generates a moment F·ri at joint i. Assuming that the total joint moments, Mi, required for the movement are known from an inverse dynamic analysis, e.g. [19], the residual joint moment Ri required from the muscles crossing joint i, after accounting for contributions from N exotendons, can be calculated as:

graphic file with name 1475-925X-2-17-i3.gif

For design optimization, we may assume without loss of generality that L0 is zero, since only the difference between L0 and slack length is of importance. Similarly, it can be seen that stiffness k is not an independent design parameter, since only products of the type krirj will affect performance. An exotendon system with N exotendons, each crossing J joints, therefore has Np = N(J + 1) design parameters, J moment arms (pulley radii) and one slack length for each exotendon. Stiffness was given an arbitrary value (k = 100 kN m-1), which can be realized using rubber material, and was found to result in pulley radii of a convenient size.

Two optimization criteria are proposed to find optimal design parameters. The first criterion is based on minimization of the residual joint moments, averaged over all joints and over the duration of the gait cycle:

graphic file with name 1475-925X-2-17-i4.gif

where T is the duration of the gait cycle. This cost function is proportional to the muscle forces that contribute to the joint moments. Minimization of Cmom would be suitable for patients with deficits in muscle strength. For military applications, the objective would be to reduce the metabolic energy required for movement, or to reduce muscle fatigue. Cmom is qualitatively related both of these objectives [4]. In order to explore alternative energy-based objectives, we also minimized a cost function that represents the average mechanical power generated by the residual joint moments:

graphic file with name 1475-925X-2-17-i5.gif

Application to human walking

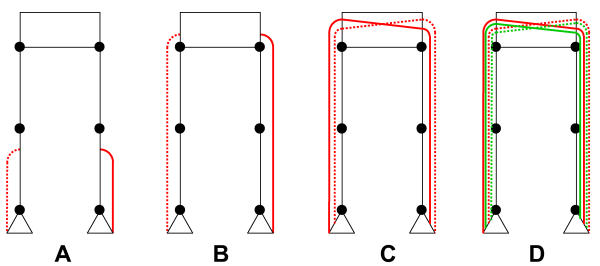
We considered four possible exotendon systems with increasing design complexity: (A) a one-joint exotendon in each leg, (B) a three-joint exotendon in each leg, crossing the hip, knee, and ankle, (C) a six-joint exotendon spanning all of the joints in the two legs, and (D) two six-joint exotendons, each spanning all joints in the two legs (Figure 2). Bilateral symmetry was achieved by giving each exotendon a twin with equal, but left-right reversed design parameters. System (D) thus had a total of four exotendons, each spanning six joints, while all others consisted of two exotendons, each spanning one, three, or six joints. Each of these four systems was optimized and evaluated for its potential to assist normal human walking.

Figure 2.

Figure 2

Open in a new tab

Frontal view showing the topologies of the four exotendon systems that were considered. The exotendons only assist flexion and extension of the hip, knee, and ankle joints in the sagittal plane. Continuous and dashed lines of the same color indicate symmetric twins with identical design parameters.

Time histories of sagittal plane joint angles and joint moments for the hip, knee, and ankle joints during normal walking were obtained from the literature [19] and scaled to obtain representative data for a hypothetical 70 kg subject with 0.9 m leg length at a walking speed of 1.2 m s-1 [20]. Data for the contralateral limb were obtained by a half-cycle phase shift. Joint angular velocities 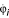Inline graphic were obtained from the joint angle data by numerical differentiation with a 3-point central difference method. The complete set of gait data is included in Sheet 1 of the additional data file exotendons.xls, which also evaluates cost functions (4) and (5).

Global optimization of the design parameters for each of the four systems was performed using simulated annealing [21], using the moment-based criterion (4) as well as the power-based optimization criterion (5). Exotendon moment arms were optimized within the range -0.1 to 0.1 m, and slack lengths were allowed to vary between -0.3 and 0.3 m. The temperature reduction rate for the annealing algorithm was set to 1% for each 1000 Np cost function evaluations, and optimizations were terminated after 30 million function evaluations. To verify that a global optimum was found, each optimization was performed five times, with different random number sequences used in the annealing process. The simulated annealing procedure consistently found the same optimal design parameters in all five optimization runs, except for the design D where multiple solutions were found that had almost identical cost function values. For design D, the cost function was then augmented with 10-5 times the peak exotendon force, in order to find the solution with lowest exotendon force. This resulted in a unique global optimum that was consistently found by the simulated annealing algorithm.

Results

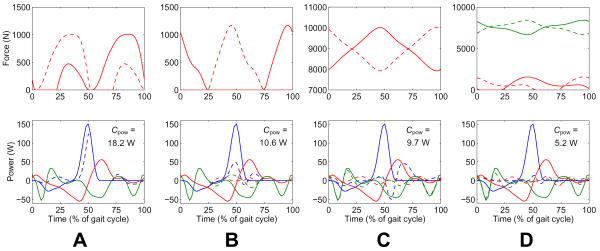
When the exotendon designs were optimized to minimize the mean residual joint moment (Cmom), considerable reductions in residual joint moments were achieved (Figure 3). The optimal single-joint design (type A) had a single exotendon on the posterior side of each ankle joint. This system was able to produce most of the required ankle plantarflexor moment in the middle of the stance phase, resulting in a 21% reduction in overall joint moments. The optimal three-joint design (type B) had exotendons running posterior to the ankle and anterior to the hip, and a very small moment arm at the knee. This system was able to produce most of the ankle and hip moment for the final two-thirds of the stance phase, with an overall savings of 46% in joint moment. The optimal six-joint exotendon system (type C) performed marginally better, but a system with two different six-joint exotendons (type D) was able to produce almost all of the required ankle and hip joint moments, leaving only the knee extensor moment in the first third of stance to be produced by muscles, an overall savings of 71%.

Figure 3.

Figure 3

Open in a new tab

Results obtained from the moment-based optimization of the four exotendon designs, arranged from left to right in order of increasing complexity. Exotendon forces are shown on the top row, with the contralateral (phase shifted) twin represented by a dashed line. Note the different scale of vertical axes. The second row shows the total joint moments in one leg (red: hip, green: knee, blue: ankle) with the residual moments as dashed lines. Moments are defined positive when causing an anterior acceleration of the distal body segment. Horizontal axes represent one full gait cycle from heel strike to the next heel strike. The cost function without exotendon assistance was Cmom = 14.09 N m. The bottom row displays the optimized designs, with exotendons in red and green, pulleys and exoskeleton in blue. The optimized design parameters for all exotendon systems can be found in Table 1, and also in Sheet 2 of the additional data file exotendons.xls.

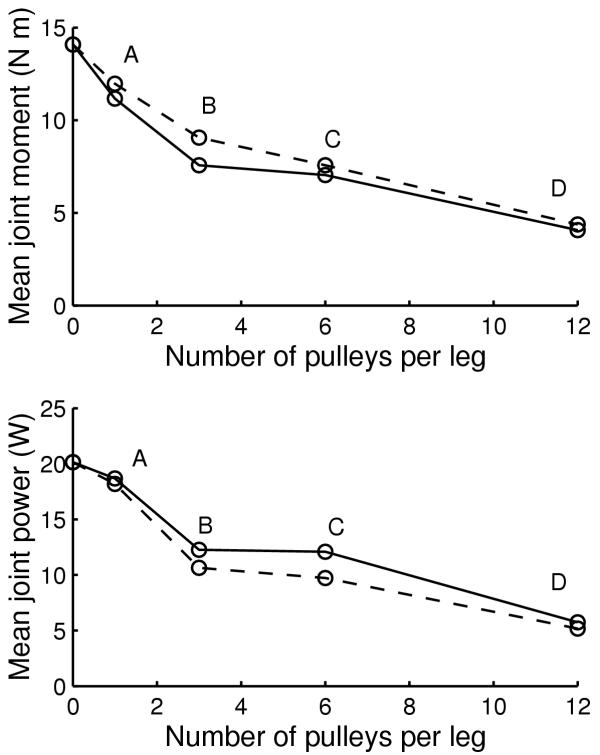
Without assistance, the average joint power Cpow was 20.12 W per joint. With exotendon systems optimized to minimize residual joint power, reductions of 10% to 74% were obtained (Figure 4). The results of all optimizations are summarized in Figure 5 and Table 1. Figure 5 shows that residual joint moments and residual joint powers tended to be reduced similarly, independent of which of the two was used as the design criterion.

Figure 4.

Figure 4

Open in a new tab

Results obtained from the power-based optimization of the four exotendon designs. The cost function without exotendon assistance was Cpow = 20.14 W. See Figure 3 for details.

Figure 5.

Figure 5

Open in a new tab

Summary of cost functions obtained from all design optimizations. Results from minimization of joint moments are shown as continuous lines, results from minimization of joint power are shown as dashed lines. For the most complex system (D), it does not seem to matter which cost function is optimized in order to find the optimal design.

Table 1.

Design parameters for all optimized exotendon systems. Designs A, B, and C consist of a single exotendon and a symmetric twin, each spanning one, three, or six joints respectively. Design D consists of two exotendons, each spanning six joints, plus their symmetric twins. Each exotendon has up to six moment arms r and a slack length (Lslack). The cost function values are shown in the two rightmost columns. The cost function values without exotendon assistance were Cmom = 14.09 N m and Cpow = 20.14 W.

Moment optimized RIGHT LEFT
rhip (mm) rknee (mm) rankle (mm) rhip (mm) rknee (mm) rankle (mm) Lslack (mm) Cmom (N m) Cpow (W)
A N/A N/A -60.20 N/A N/A N/A 6.54 11.17 18.68
B 21.18 0.23 -34.63 N/A N/A N/A -7.77 7.56 12.26
C 21.23 -0.61 -34.31 -8.08 -5.63 0.00 -4.04 7.04 12.09
D 7.77 4.25 -23.45 -5.24 0.65 21.91 -24.34 4.08 5.66
D -7.60 -11.92 -15.68 10.70 -4.37 -5.88 -11.53 4.08 5.66
Power optimized RIGHT LEFT
rhip (mm) rknee (mm) rankle (mm) rhip (mm) rknee (mm) rankle (mm) Lslack (mm) Cmom (N m) Cpow (W)
A N/A N/A N/A -49.83 N/A N/A 1.04 11.97 18.18
B 33.06 12.76 -32.85 N/A N/A N/A -1.55 9.06 10.64
C -10.05 -2.74 13.79 10.87 3.22 -16.12 -89.62 7.57 9.73
D -4.69 -9.77 -19.04 10.89 -5.67 -0.17 -12.30 4.37 5.18
D 7.47 3.98 -25.11 -6.82 -2.18 24.18 -75.33 4.37 5.18
Open in a new tab

The complete results, including all gait data, are included in the additional file exotendons.xls.

Discussion

It was found that exotendons could significantly reduce the muscle forces required for locomotion. For practical relevance, it is important to show that these results are robust and not dependent on particular details of the model and data that were used in the present analysis.

The gait data that were used for the analysis were obtained from a gait analysis laboratory [19] which uses a well-established and validated methodology (C.G. Kirtley, personal communication). These data, included in the additional data file, are consistent with other commonly cited sources, e.g. [5]. However, these data are an average of many subjects and therefore lack subject-specific details that may be important. Therefore, the analyses were repeated with gait data collected in our own laboratory from an adult female subject. The optimized designs and cost function values were virtually the same as those obtained with the normative gait data, suggesting that the design optimization only needs to consider the movement task that is to be assisted (e.g., walking), and not the detailed differences in movement execution between individuals.

All analyses were also repeated with a nonlinear (quadratic) force-length relationship for the exotendons, which is closer to the properties of biological soft tissue. Again the results were identical for all practical purposes, indicating that nonlinear material properties are probably unimportant for energetics. However, nonlinear exotendon material would have the advantage that the user would not feel a sudden change in stiffness when the exotendon goes from slack to taut.

It should be noted that we used two simple cost functions that are related to muscle forces and the metabolic cost of locomotion. Other expressions could have been used to better represent muscle energetics, such as a reduced weighting of negative joint power to account for the lower energy cost of eccentric muscle contractions. Although we have not explored this, the fact that both cost functions (residual moment and residual power) were reduced simultaneously (Figure 5) suggests that these results are robust with respect to the choice of cost function for optimization.

Most of the benefit of exotendons derived from the fact that the ankle plantarflexor and hip flexor moments in walking both reach their peak at the end of the stance phase (Figure 3). The rotational movements in the ankle and hip joints during normal walking happen to be such that a properly placed exotendon can produce both joint moments passively and automatically at the right time. However, none of the exotendon systems were able to assist the knee extensors significantly during the first part of the stance phase. Further analysis showed that, within the class of systems examined, no exotendon with an extensor moment arm at the knee could be designed to switch automatically from slack (during swing) to stiff (during stance) through length changes caused by movements at other joints. An active control system may be required to provide this function. Surprisingly, solutions that resemble the action of the bi-articular human Gastrocnemius muscle were not found. Optimization of the three-joint system (B) resulted in a design that exploits the ankle-hip synergy rather than the ankle-knee synergy. Optimization of an additional two-joint (ankle-knee) exotendon system was also done, and was found to reduce joint moments and power by 23% and 11% respectively, only marginally better than the one-joint system (A). It is possible that the ankle-knee synergy is more useful in movements such as running and jumping (7). Overall, a good compromise between performance and design complexity seems to be the three-joint exotendon design (B), which requires only one pulley on each joint and reduces joint moments and powers by about 50%.

This analysis has been entirely theoretical, based on the assumption that human muscles can produce the residual joint moments that are required to maintain a normal gait in the presence of exotendons. Because the residual moments are low, this is certainly within the force generating capacity of even very weak muscles. A more challenging concern is that of controllability. When more than half of the muscle force is replaced by passive elastic mechanisms, neural feedback mechanisms that operate during locomotion may become less effective and this could make the user less stable. However, exotendons have force-length properties, which contribute to short-term (within the gait cycle) gait stability [22], probably enough so that the residual neuromuscular function can actively maintain long-term stability over multiple gait cycles. This is supported by the observation that bipedal animals with passive elastic mechanisms, such as kangaroos and ostriches, are stable even at low levels of muscle recruitment. Furthermore, the human motor control system has a remarkable ability to adapt to unusual force fields such as those presented by exotendons [23]. In fact, it is likely that humans will benefit more from exotendons than the present analysis has predicted, because they could self-optimize their movements to gain additional advantages. The potential benefits of exoskeletons can therefore only be fully determined with human experiments, including metabolic measurements. Theoretical design optimization of exotendon systems will still be required, since it is impossible to sufficiently explore the space of possible designs in human subject experiments. Such optimizations will necessarily involve forward dynamic simulations to optimize muscle activation patterns and device design parameters simultaneously [22,24].

The design optimization procedure presented here will result in optimal performance for one specific movement task: walking on level ground at a single speed. Tasks other than that for which the system has been optimized will benefit less, or could even become energetically costly. This issue becomes important when considering exotendons as an alternative for wheelchairs, with the advantage of access to uneven terrain where limb movements necessarily will deviate from the nomimal patterns used in the present analysis. Further analysis with experimental data is needed to quantify these effects. We do expect, however, that an exotendon system will have sufficient elasticity to accomodate moderate changes in limb movements without affecting its assistive function. When considering a range of speeds, from walking to running, larger changes in movement will be needed. It is straightforward to include other movements in the design optimization process, and arrive at design that is best for the total of all movement patterns under consideration. However, such designs would always be a compromise and therefore suboptimal. A better approach may be to find a set of new movement patterns, analogous to the gaits of horses, that can all make effective use of the same passive exotendon system. This would, again, require forward dynamic modeling to find those new movements.

Exotendons are attached in parallel to the human body, and therefore are essentially different from series elastic mechanisms such as compliant running surfaces [25], pogo-stick-like devices [26] and energy-storing prosthetic feet [27]. Series devices do not directly assist muscles, but rather alter the human movement such that muscles can operate under more favorable conditions. The energy savings from such devices are much smaller than what is possible with exotendons, especially if drastic alterations in movement must be avoided. Parallel elastic devices have only been described previously for single joints, such as an elastic shoe to assist flexors of the metatarso-phalangeal joint [28] and a spring with controlled release to assist knee extension in the swing phase of gait [29]. We have shown here that elastic devices can be much more effective if they span multiple joints.

Conclusion

Control complexity and energy requirements are two major obstacles for the design of robotic devices for locomotion assistance for military applications and for persons with disabilities. We have shown here that a properly designed passive exotendon system can replace most of the muscle forces in human walking without requiring a control system or an energy supply. Such a reduction in muscle forces will significantly increase endurance time and reduce fatigue in healthy individuals. More importantly, this may allow independent locomotion in individuals with large deficits in muscle function. These benefits are obtained without altering the normal gait pattern. Anthropomorphic legged robots could benefit similarly from these mechanisms, resulting in a dramatic increase in battery life.

Supplementary Material

Additional File 1

The file contains two spreadsheets. Sheet 1 contains formulas and data to perform the analysis of an exotendon system as described in the article. The cells in the spreadsheet are color coded. Pink cells represent design parameters of the exotendon system, green cells are the gait data that were used as input for the design optimization, and blue cells are results. The reader is encouraged to alter the design parameters, or copy the parameters from previously optimized designs (Sheet 2). When design parameters are modified, all results will be recalculated immediately, and results displayed as the two cost function values (cells J1 and J2) and the graphs in row 8. Sheet 2 contains the design parameters for all eight optimized exotendon systems: designs A, B, C, and D, each optimized for minimal residual joint moment and for minimal residual joint power. The tables in Sheet 2 have been formatted to that they can be directly pasted into the corresponding part of Sheet1 (cells B6-H6 and B7-H7) to evaluate the performance of each of the eight optimized exotendon designs

Click here for file (85KB, xls)

Acknowledgments

Acknowledgement

The author thanks Dr. Chris Kirtley (Catholic University of America, Washington DC) for providing the gait data and scaling algorithms.

References

  1. Lemley B. Future Tech: Really Special Forces. Discover. http://www.discover.com/issues/feb_02/departments/featteach 2002, 23, February.
  2. Kazerooni H. The human power amplifier technology at the University of California, Berkeley. Rob Autonom Syst. 1996;19:179–187. doi: 10.1016/S0921-8890(96)00045-0. [DOI] [PubMed] [Google Scholar]
  3. Belforte G, Gastaldi L, Sorli M. Pneumatic active gait orthosis. Mechatronics. 2001;11:301–323. doi: 10.1016/S0957-4158(00)00017-9. [DOI] [Google Scholar]
  4. Kram R, Taylor CR. Energetics of running: a new perspective. Nature. 1990;346:265–267. doi: 10.1038/346265a0. [DOI] [PubMed] [Google Scholar]
  5. Winter DA. Energy generation and absorption at the ankle and knee during fast, natural, and slow cadences. Clin Orthop. 1983;175:147–154. [PubMed] [Google Scholar]
  6. Jansen J, Richardson B, Pin F, Lind R, Birdwell J. Technical Report TM-2000/256. Oak Ridge National Laboratory; 2000. Exoskeleton for soldier enhancement systems feasibility study.http://www.ornl.gov/~webworks/cpr/rpt/108469_.pdf [Google Scholar]
  7. van Ingen Schenau GJ, Bobbert MF, Rozendal RH. The unique action of bi-articular muscles in complex movements. J Anat. 1987;155:1–5. [PMC free article] [PubMed] [Google Scholar]
  8. Alexander RM, Bennet-Clark HC. Storage of elastic strain energy in muscle and other tissues. Nature. 1977;265:114–117. doi: 10.1038/265114a0. [DOI] [PubMed] [Google Scholar]
  9. Dickinson MH, Farley CT, Full RJ, Koehl MA, Kram R. How animals move: an integrative view. Science. 2000;288:100–106. doi: 10.1126/science.288.5463.100. [DOI] [PubMed] [Google Scholar]
  10. Biewener AA. Muscle-tendon stresses and elastic energy storage during locomotion in the horse. Comp Biochem Physiol B Biochem Mol Biol. 1998;120:73–87. doi: 10.1016/S0305-0491(98)00024-8. [DOI] [PubMed] [Google Scholar]
  11. Minetti AE, Ardigo LP, Reinach E, Saibene F. The relationship between mechanical work and energy expenditure of locomotion in horses. J Exp Biol. 1999;202:2329–2338. doi: 10.1242/jeb.202.17.2329. [DOI] [PubMed] [Google Scholar]
  12. Biewener AA, Roberts TJ. Muscle and tendon contributions to force, work, and elastic energy savings: a comparative perspective. Exerc Sport Sci Rev. 2000;28:99–107. [PubMed] [Google Scholar]
  13. Riemersma DJ, van den Bogert AJ, Schamhardt HC, Hartman W. Kinetics and kinematics of the equine hind limb: in vivo tendon strain and joint kinematics. Am J Vet Res. 1988;49:1353–1359. [PubMed] [Google Scholar]
  14. van den Bogert AJ, Hartman W, Schamhardt HC, Sauren AAHJ. In vivo relationship between force, EMG, and length change in the deep digital flexor muscle in the horse. In: de Groot G, Hollander AP, Huijing PA, van Ingen Schenau GJ, editor. In Biomechanics XI-A. Champaign, Illinois: Human Kinetics Publishers; 1989. pp. 68–74. [Google Scholar]
  15. van Weeren PR, Jansen MO, van den Bogert AJ, Barneveld A. A kinematic and strain gauge study of the reciprocal apparatus in the equine hind limb. J Biomech. 1992;25:1291–1301. doi: 10.1016/0021-9290(92)90284-8. [DOI] [PubMed] [Google Scholar]
  16. Wilson AM, McGuigan MP, Su A, van den Bogert AJ. Horses damp the spring in their step. Nature. 2001;414:895–899. doi: 10.1038/414895a. [DOI] [PubMed] [Google Scholar]
  17. Wilson AM, Watson JC, Lichtwark GA. A catapult action for rapid limb protraction. Nature. 2003;421:35–36. doi: 10.1038/421035a. [DOI] [PubMed] [Google Scholar]
  18. Pratt GA, Williamson MW, Dillworth P, Pratt J, Ulland K, Wright A. Stiffness isn't everything. In Proceedings of the Fourth International Symposium on Experimental Robotics (ISER '95): Stanford, California. June 30–July 2 1995.
  19. Stansfield BW, Hillman SJ, Hazlewood ME, Lawson AM, Mann AM, Loudon IR, Robb JE. Normalisation of gait data in children. Gait Posture. 2003;17:81–87. doi: 10.1016/S0966-6362(02)00062-0. [DOI] [PubMed] [Google Scholar]
  20. Kirtley C, Cisper J, Sukal T, Wall A. Normalization for autointerpretation of gait analysis data. In Proceedings of the Gait and Clinical Movement Analysis Society (GCMAS): Chattanooga, Tennessee. 2002.
  21. Goffe WL, Ferrier GD, Rogers J. Global optimization of statistical functions with simulated annealing. J Econometrics. 1994;60:65–99. doi: 10.1016/0304-4076(94)90038-8. [DOI] [Google Scholar]
  22. Gerritsen KG, van den Bogert AJ, Hulliger M, Zernicke RF. Intrinsic muscle properties facilitate locomotor control – a computer simulation study. Motor Control. 1998;2:206–220. doi: 10.1123/mcj.2.3.206. [DOI] [PubMed] [Google Scholar]
  23. Bhushan N, Shadmehr R. Computational nature of human adaptive control during learning of reaching movements in force fields. Biol Cybern. 1999;81:39–60. doi: 10.1007/s004220050543. [DOI] [PubMed] [Google Scholar]
  24. van den Bogert AJ. Optimization of the human engine. In Proceedings of the 8th Conference of the Canadian Society for Biomechanics: 1994; Calgary, Canada. 1994. pp. 160–161.
  25. McMahon TA, Greene PR. The influence of track compliance on running. J Biomech. 1979;12:893–904. doi: 10.1016/0021-9290(79)90057-5. [DOI] [PubMed] [Google Scholar]
  26. Dick GJ, Edwards EA. Human bipedal locomotion device. US Patent 5,016,869. 1990.
  27. Prince F, Winter DA, Sjonnensen G, Powell C, Wheeldon RK. Mechanical efficiency during gait of adults with transtibial amputation: a pilot study comparing the SACH, Seattle, and Golden-Ankle prosthetic feet. J Rehabil Res Dev. 1998;35:177–185. [PubMed] [Google Scholar]
  28. Stefanyshyn DJ, Nigg BM. Influence of midsole bending stiffness on joint energy and jump height performance. Med Sci Sports Exerc. 2000;32:471–476. doi: 10.1097/00005768-200002000-00032. [DOI] [PubMed] [Google Scholar]
  29. Gharooni S, Heller B, Tokhi MO. A new hybrid spring brake orthosis for controlling hip and knee flexion in the swing phase. IEEE Trans Neural Syst Rehabil Eng. 2001;9:106–107. doi: 10.1109/7333.918283. [DOI] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Additional File 1

The file contains two spreadsheets. Sheet 1 contains formulas and data to perform the analysis of an exotendon system as described in the article. The cells in the spreadsheet are color coded. Pink cells represent design parameters of the exotendon system, green cells are the gait data that were used as input for the design optimization, and blue cells are results. The reader is encouraged to alter the design parameters, or copy the parameters from previously optimized designs (Sheet 2). When design parameters are modified, all results will be recalculated immediately, and results displayed as the two cost function values (cells J1 and J2) and the graphs in row 8. Sheet 2 contains the design parameters for all eight optimized exotendon systems: designs A, B, C, and D, each optimized for minimal residual joint moment and for minimal residual joint power. The tables in Sheet 2 have been formatted to that they can be directly pasted into the corresponding part of Sheet1 (cells B6-H6 and B7-H7) to evaluate the performance of each of the eight optimized exotendon designs

Click here for file (85KB, xls)

Articles from BioMedical Engineering OnLine are provided here courtesy of BMC

RESOURCES