Abstract
Genetic association studies achieve an unprecedented level of resolution in mapping disease genes by genotyping dense SNPs in a gene region. Meanwhile, these studies require new powerful statistical tools that can optimally handle a large amount of information provided by genotype data. A question that arises is how to model interactions between two genes. Simply modeling all possible interactions between the SNPs in two gene regions is not desirable because a greatly increased number of degrees of freedom can be involved in the test statistic. We introduce an approach to reduce the genotype dimension in modeling interactions. The genotype compression of this approach is built upon the information on both the trait and the cross-locus gametic disequilibrium between SNPs in two interacting genes, in such a way as to parsimoniously model the interactions without loss of useful information in the process of dimension reduction. As a result, it improves power to detect association in the presence of gene-gene interactions. This approach can be similarly applied for modeling gene-environment interactions. We compare this method with other approaches: the corresponding test without modeling any interaction, that based on a saturated interaction model, that based on principal component analysis, and that based on Tukey’s 1-df model. Our simulations suggest that this new approach has superior power to that of the other methods. In an application to endometrial cancer case-control data from the Women’s Health Initiative (WHI), this approach detected AKT1 and AKT2 as being significantly associated with endometrial cancer susceptibility by taking into account their interactions with BMI.
Keywords: Genetic association analysis, Interaction, Gene, Environment, Endometrial cancer
Introduction
Large scale genetic association studies offer an unprecedented opportunity to find genes underlying human diseases [Hirschhorn and Daly, 2005;Risch and Merikangas, 1996]. With the availability of SNP chip techniques, multiple SNPs are often typed in a gene region. To the extent that these markers, especially tagSNPs that are selected based on the linkage disequilibrium (LD) pattern, are able to capture most of the genetic variance in a population, genetic association studies should achieve a satisfactory coverage of the genomic region, offering new hope to identify important genes underlying complex diseases [Conrad et al., 2006; de Bakker et al., 2006]. Nevertheless, they also pose new challenges. The immediate question is how to handle a large amount of genotype data in the analysis. Another more profound question is related to the consistency of results [Hirschhorn et al., 2002]. It has been suggested that inconsistent results in mapping genes reflect the fact that the influence of a specific gene on the trait usually relies on the genetic and environmental background, including, but not limited to, gene-gene and gene-environment interactions.
Although the potential importance of gene-gene and gene-environment interactions in the etiology of complex diseases has been widely recognized, how to optimally model these interactions when multiple correlated SNP markers are available is not clear. A common approach used in practice simply ignores any interaction, which could result in missing important genes with no, or small, marginal effects. An alternative method models all pair-wise interactions. One concern about this approach relates to the large number of degrees of freedom involved in the test statistic, which could result in a severe penalty on the efficiency of detecting association. For example, for two candidate genes with k1 and k2 SNPs typed, respectively, there are potentially k1 × k2 possible pair-wise interactions. Furthermore, a SNP by SNP approach to model interaction discards the LD information among SNPs. When the disease variant itself is directly genotyped, this approach may lead to a powerful test. Otherwise, it could be less efficient than an approach that simultaneously takes into account the multiple correlated SNPs.
An ideal approach for modeling gene-gene and gene-environment interactions should be able to make use of all the useful information from multiple SNPs and yet avoid the penalty due to a large number of degrees of freedom. Recently, a procedure based on Tukey’s 1-df model for non-additivity was proposed to improve the power of detecting association in the presence of gene-gene and gene-environment interactions [Chatterjee et al., 2006]. This procedure assumes that the SNP marker data,S, are a surrogate for an underlying quantitative biological phenotype and that the mean of this quantitative phenotype can be described by a linear function of S. As a result, a parsimonious model is built up with only one parameter involved in modeling the interactions. This interaction parameter is estimated by searching in a pre-specified region to maximize the association between the gene and the trait. Essentially, this method extracts the genotypic information of multiple SNPs of a gene region as a single component, i.e. the biological phenotype, and this compression process is made possible by using the correlations between the SNPs and the trait values. Because of its parsimony, this procedure has been shown to greatly improve the power to detect association in the presence of interactions. However, SNPs around the causal variant may have no, or small, marginal effects in certain genetic models and therefore the correlations between these SNPs and the trait tend to be small and uninformative for reducing the genotype data. Nevertheless, in this case the gametic disequilibrim (GD) between the two genes (or the association between a gene and an environmental factor) could still be useful. So, a generally powerful approach may be obtained by simultaneously exploiting both the trait-SNP correlations and the GD between the two gene regions or the association between a gene and an environmental factor. (In this paper, for the sake of clarity, we use the general term GD – more fully, gametic phase disequilibrium – for cross-locus associations and reserve the term LD for associations within a gene).
This motivates us to develop a new method for modeling gene-gene and gene-environment interactions. We consider a regression model in which the interaction is modeled by latent components. To extract an informative latent component, multiple SNP data are compressed by simultaneously exploiting both the GD between two gene regions (or the association between a gene and environmental factor) and the trait information. The latent component is defined to have maximal correlation with both the trait and the SNPs in another gene or environmental factor, and it is obtained by the partial least square (PLS) algorithm. We simulate case-control data to evaluate the type I error rate and power of this new method. The results demonstrate the superior power of this new method to other approaches, namely the corresponding test without modeling any interaction, that based on a saturated interaction model, that based on a principal component analysis of the SNP data, and that based on Tukey’s 1-df model. Finally, we apply this method to the endometrial cancer case-control data from the Women’s Health Initiative (WHI)(1998).
Methods
Consider a case-control design in which a sample of cases (D = 1) and controls (D = 0) is selected from a population. We first consider modeling gene-gene interaction. We assume the disease status depends on two underlying genetic variants, u1and u2, in two gene regions through a linear model with interaction as given by equation 1.
| (1) |
We assume two sets of SNP markers are genotyped in the two gene regions with genotype values S1 = (s11, s12,…, s1k1) and S2 = (s21, s22,…, s2k2). The underlying causal genetic variants are not necessarily included in the two sets of observed SNPs. We consider an additive coding scheme in which the genotype value of each SNP can be 0, 1 or 2, corresponding to genotypes aa, Aa and AA. We are interested in modeling the interaction between the two underlying variants with the aim of improving the power to detect association.
To take the interaction between two underlying genetic variants into account in detecting association, a conventional method exhaustively models all pair-wise interactions between the two genes by fitting a logistic regression model of the form
| (2) |
We can see that a large number of parameters are used in modeling the interaction between the two genes in this way and therefore the statistic to detect association involves a large number of degrees of freedom. Moreover, although different pairs of SNPs may have quite different information to predict the pair of underlying disease variants, in this method each pair of SNPs is treated equally with one degree of freedom.
The test based on Tukey’s model
To avoid the severe penalty on power from having a large number of degrees of freedom, an efficient approach to model interaction should remove non-informative SNPs or weight each SNP based on its information regarding the interaction effect. One approach relies on the trait information. Given a genetic interaction model with non-negligible marginal effects, it is often assumed that a SNP marker with a larger marginal effect should have a larger interaction effect. In this way, Tukey’s 1-df interaction model can be constructed so that the interaction effect is proportional to the product of two main effects; these are each described by a weighted sum of all SNPs in a region, with the weights being determined according to the SNP’s correlation with the trait [Chatterjee et al., 2006]. This model can be described by the logistic regression model
| (3) |
Fixing the effects of the SNPs in one gene region, the interaction parameter in this model, θ, can be looked upon as a transformation parameter to remove any removable non-additive effect of the tested gene.
Because of the parsimony of the above model, in the presence of interaction it has major advantages over both the test that does not model any interaction and the test based on model (2). But the gain in power of this approach depends on the assumption that a SNP’s interaction effect on the trait is approximately proportional to its marginal effect on the trait. Hence, we should not expect this approach to be optimal in power when there exist no, or only small, marginal effects.
The test based on principal component analysis
In contrast to the approach based on model (3), the genotype dimension reduction could also rely solely on the genotype data themselves. One common approach is to use principal component analysis (PCA). Consider p SNPs in a gene region evaluated on each member of a sample of n persons, so that the multiple genotype values make up a p × n matrix S. The singular value decomposition of S is S=UDVT, where D is a diagonal matrix containing the singular values, and the elements of the column vector U are the principal components U1, U2,…, Um (in which m≤p is the rank of S). For the sake of simplicity, here we only consider the first principal component, but the method can be easily extended to include more components. Then, a parsimonious interaction model between the two genes can be described by
| (4) |
This model also uses only one parameter,βg1g2 , in modeling the interaction between two genes. Because this principal component analysis depends solely on the genotype data S, it can also be used to reduce the dimension for modeling main effects without introducing bias in the subsequent tests [Gauderman et al., 2007]. Here, we focus on modeling the interaction between two genes. The rationale for the test based on principal component analysis is that, if the first few principal components are able to capture most of the variation in the genotype data in the two regions, it may be reasonable to assume that the genotypic variation introduced by the genetic interaction effects is likely to be included in the first few components.
Because the PCA approach characterizes the pair-wise LD pattern of genotype data, though not the correlations of SNPs with the trait, it may be able to detect interactions within a gene that the approach based on the marginal effect of each SNP could otherwise miss. Nevertheless, the principal components are computed solely from the distribution of genotype data and, consequently, the first components may have little necessary relation with the trait. So, the logistic regression based on the first few components, such as model (4), might not always work well in certain LD structures.
We can illustrate this problem with the extreme LD pattern shown in Figure 1. The genotype values for each SNP in a gene region are displayed by a row and the genotype values for an individual are given by a column in Figure 1a. The three genotype values are coded white (2), gray (1) and black (0). It can be seen that the subset of SNPs labeled “A” have higher genotype values in the first and second blocks of subjects and have lower values in the third and fourth blocks of subjects, whereas the subset labeled “B” have higher values in the first and third blocks and lower values in the second and fourth blocks. PCA is able to uncover the structure of these genotype data. The first two eigenvalues are 21.82 and 5.09. The set of SNPs (A) that shows the largest variation contributes most to the first principal component (Figure 1b). However, in this example the set of SNPs (A) is in fact not informative for detecting association with the trait. So it is necessary to include more than one principal component to detect the association. From this fictitious example, we can see that the first principal component may explain the genotype data rather than the trait, and nothing guarantees that the first principal component is consistently informative relative to the disease in the various possible LD patterns.
Figure 1.
A: A heat plot of genotype type values in a fictitious gene region. B: distribution of the first two principal components of the fictitious data.
The test based on PLS
It is unlikely that the above genotype dimension reduction methods, either the approach based on the marginal effects of SNPs or the approach based only on the local pair-wise LD structure, are uniformly powerful in different situations. One approach may be highly powerful in certain situations, but it may also have no power at all in other situations. Unfortunately, it is unclear which one should be used in a real dataset, because the power of these methods depends on the unknown genetic model.
It is therefore useful to develop a new approach to model gene-gene and gene-environment interaction effects that can generally perform well in different situations. The idea of our approach is that, rather than directly exploit the LD structure of SNP markers in a gene region as PCA does, we shrink multiple SNP genotypes into one component by using information from both the marginal effects of the SNPs and the joint effects on the trait of all pairs of SNPs in the two genes.
The marginal effect of a SNP can be characterized by the correlation between its genotype value and the trait value. Several methods have successfully used this correlation to reduce the dimension for modeling gene-gene interactions. For example, in the scenario of genomewide association studies, Machini et al. consider a two-stage approach in which a subset of selected SNPs is further modeled for interaction [Marchini et al., 2005]. The criterion to remove uninformative SNPs relies on this trait-genotype correlation. In certain genetic models with no or small marginal effects, it is also useful to explore the joint effect of SNPs in order to reduce the genotype data for modeling gene-gene and gene-environment interactions.
To investigate the joint effect of SNPs for a case-control sample, we assume there are two independent underlying disease variants,u1 and u2, one in each gene region. Let A1and a1be the two alleles of a SNP marker that is in LD with u1 and A1 and a2 be the two alleles of a SNP marker that is in LD with u2. Let fi1j2 = P(D|i1j2)be the marginal penetrance of haplotype i1j2, where i and j can each be one of the alleles A or a. In the case group,
GD is expected between two causal loci in cases and is given by
From this equation, we can see that the joint effect of two causal variants will lead to cross-locus GD between alleles of the variants in cases as long as fa1a2 fA1A2 − fa1A2 fA1a2 ≠ 0. Furthermore, the correlation between two markers that are in LD with the two causal variants can be observed, and its expectation is given by
| (5) |
where Δ1and Δ2are the LD coefficients between the two markers and the two variants, respectively [Zhao et al., 2006]. Similarly, the joint effect of two disease variants introduces cross-locus GD between alleles of the two causal variants and the markers in the controls, but this has an opposite sign, and is given by
| (6) |
From equations (5) and (6), we can see that, even when the marginal effects of the causal variants are small, for example in a cross-over model (fa1a2 and fA1A2 > fa1A2 and fA1a2), the cross-locus GD between SNPs in two genes can be large. In a case-control study, especially for rarer diseases, cases are usually over-sampled and the cross-locus GD in controls tends to be closer to the population level and smaller in magnitude. Hence, although cases and controls have opposite signs, we can still expect GD between SNP markers in two gene regions for the whole pooled sample of cases and controls whenever two causal variants have a joint effect on the disease. This suggests that this cross-locus GD between two genes can be a useful alternative source of information to reduce the genotype data for modeling interactions when marginal effects are small. We note that, because this genotype reduction does not make use of disease status information, under the null hypothesis the reduced genotype data are independent of disease status and therefore the subsequent test is still valid [Millstein et al., 2006].
The joint effect of two SNPs may be directly characterized by the LD coefficient. However, the LD coefficients cannot be estimated directly, because the haplotype phase of two SNPs in two genes is unknown. Although the haplotype phase may be inferred, e.g. by the expectation-maximization (EM) algorithm with the assumption that the two SNPs are in Hardy-Weinberg equilibrium (HWE), the sample HWE is likely to be distorted in the regions with causal variants. To avoid such an assumption, the composite LD measures are useful alternatives. The composite LD is estimated simply as half the usual sample covariance of the genotype values and the composite LD correlation is estimaed by the sample correlation [Zaykin et al., 2006].
To incorporate information from the SNP-trait correlation and the cross-locus GD between SNPs of two gene regions in modeling interactions, we here describe a new procedure. Let be S1 be an N × k1 genotypic matrix of N cases and controls and k1 SNPs in the gene region g1 and let Y denote the N × 1 vector indicating disease status. We are interested in detecting association between the gene g1 and disease status. Also, let S2 be the genotypic matrix for another gene region g2. In PCA, the principal components may be defined sequentially by:
where var indicates the variance of the N sample values that comprise the elements of S1v and arg refers to v, a vector of weights. The first component is the linear combination that has the maximum variance. As discussed before, PCA maximizes the variance of the linear combination of multiple genotype values and may not necessarily yield a component that is informative for modeling interaction because it ignores the information from Y and S2. For this reason, a different criterion is necessary for extracting a component that is informative for modeling interactions. How well this genetic component represents u1 depends on: (1) the magnitude of its correlation with the trait, if there exists a marginal effect of the underlying variant u1; and (2) the magnitude of its correlation with the SNPs in the other region g2, if there exists a joint effect of the two causal variants. In other words, a useful component has to be defined on the basis of information from the cross-locus GD between the SNPs in regions g1and g2 and the all the marginal correlations between the SNPs and the trait.
Based on the above criteria, we consider another linear combination, S1w, to represent u1. Letting Z = (Y,S2), which combines the vector Y and the matrix S2, the weight vector w can be analogously defined by
The weights and c can be found by a Partial Least Square (PLS) algorithm [Helland, 1988;Helland, 1990]. PLS is now provided by commonly used statistical packages, such as SAS and R. Although PLS can sequentially find more orthogonal components, in our application we use only the first component to estimate the underlying interaction component of u1 with u2. Like PCA, the PLS component is a linear combination of genotype values of SNPs in a local region, but we can see that the PLS and PCA yield different weights for the SNPs, based on the different criteria of PCA and PLS, namely maximizing var(S1v) and cov2(S1W, Zc) respectively.
It is useful to understand the PLS component given by different genetic models. If u1 has no marginal effect, the component is obtained by giving more weight to SNPs that have stronger correlations with the SNPs in g2. If a larger marginal effect exists, the component is defined by giving more weights to SNPs having larger absolute correlations with the trait. So the PLS component is more likely to capture information from multiple SNPs than a PCA component for the aim of modeling interactions. Based on this informative component, we can apply conventional logistic regression by replacing the principal component(s) with the PLS component(s) in model (4) to efficiently test the interaction effect and the overall association. In model (4), the null hypothesis of no association of disease with u1 can be statistically stated as H0 : both βg1g2 and β1i = 0 for all i = 1, …, k1. The test examines the overall association, including main and interaction effects and a similar joint hypothesis was proposed before in the context of testing gene-environment interaction [Kraft et al. 2007].
This procedure can also be used to model gene-environment interaction by simply replacing the matrix of genotype values with the observed values S2 of environmental factors. In summary, our procedure for detecting association of a gene region with multiple SNPs genotyped is as follows: (1) Standardize the genotypes and traits to have zero mean and unit norm; (2) Find ; (3) Obtain the latent variable for the other gene or environmental factors. For our simulations, we estimated this by the fitted values of a standard logistic-regression model involving the main effects of the SNPs in the other gene; (4) Detect association by a likelihood ratio test based on a regression model of the form (4) to test H0 : both βg1g2 and β1i = 0 for all i = 1, …, k1..
Simulation Study
Simulation Design
We now evaluate the performance of the proposed method and several other approaches by simulations. In our simulations, all approaches are used to jointly test the interaction and main effects, except the standard main effect logistic regression without taking interactions into account. We simulate two candidate gene regions, g1 and g2, with seven SNPs in each. In each region one of the simulated SNPs is assumed to be the causal variant and the others are the SNP markers. We assume the causal variant and other SNP markers are in LD. The haplotypes of correlated SNP markers and the causal variant are simulated based on a multivariate normal distribution with pair-wise correlations ρij, where i and j are the position indices. The absolute value of ρij is set to be 0.95|I−j| and the sign of ρij is randomly assigned. We assume that the trait variant is located at the first position. Each allele of a haplotype is generated by dichotomizing the marginal normal distribution and the cutoff is determined by the allele frequency. The allele frequency of a SNP is randomly sampled from a uniform distribution between 0.1 and 0.5. This simulation yields correlations between SNPs with absolute values roughly in a range of 0.1 to 0.75.
The disease status of each subject is simulated based on a dominant inheritance model,
where Iu1and Iu2 are indicator variables for the disease alleles at the two causal loci. We fix the intercept parameter θ0, which corresponds to the probability of disease for a group of subjects who do not carry any disease alleles, to be 0.018. For each replicate, we generate a homogenous study population and then randomly sample a balanced dataset with 400 cases and 400 controls.
To evaluate the type I error rate of the different approaches to detect association between and the disease, we first assume the two genes are independent. We consider two situations: (1) neither nor is associated with the disease (θ1 = θ2 = θ12 = 0) and (2) only u2 is related to the disease (θ2 =2, θ1 = θ12 = 0). Because the derivation of the proposed PLS is based on the assumption of independence of the two genes, we further evaluate the type I error rate of PLS in the presence of various levels of correlation between the two gene regions. To do this we simulate a large set of correlated SNPs as before, in which the two genes are assumed to have a distance between the last SNP of gene 1 and the first SNP of gene 2, i.e. |j−i|, of 2, 4, 6 and 8. Because in this case the two genes are closely correlated, both genes have to be simulated to be not associated with the disease (θ1 = θ2 = θ12 = 0). For each scenario we use 10,000 replicates to evaluate the type I error rate.
To compare the power of the different methods, we consider three different genetic models. In a multiplicative model, the joint effect of two factors,u1 and u2, is simulated to be the product of their main effects (θ12 = 0, θ1 and θ2 > 0) In a purely epistatic model, the main effects of u1 and u2 are simulated to be 0 (θ1 = θ2 = 0)and the joint effect of the two factors is solely determined by the interaction effect (θ12 > 0). In a cross-over model, we assume u1 has opposite effects depending on the genotype u2. We fix θ1 = −0.5 and θ12 > 0. We consider two scenarios: (1) the causal variants u1 and u2 are not genotyped, i.e. the first SNP is removed from the analysis; and (2) the causal variants are gentoyped, in which case the last SNP is removed from the analysis, so that in each case there are consistently six SNPs (per gene) in the analysis.
Simulation Results: Type I error rate
Simulations show that the proposed test has good control of the 1% and 5% error rates when the markers in the two genes are independent (Table 1). However, we find evidence that the statistic based on a full regression model is anticonservative. Because the number of parameters involved in this method is large, the poor control of the type I error rate of the statistic is likely the result of small sample violations of asymptotic theory. Therefore, we increased the sample size and then found the type I error of the statistic tended to be close to the nominal level.
Table 1.
The empirical type I error rates of various methods to detect association of gene 1 at the significance levels 0.05 and 0.01 when two genes are independent
| α=0.05 | α=0.01 | |||
|---|---|---|---|---|
| θ2 = 0 | θ2 = 2 | θ2 = 0 | θ2 = 2 | |
| Main | 0.051 | 0.052 | 0.011 | 0.011 |
| Full | 0.094 | 0.102 | 0.023 | 0.027 |
| PCA | 0.052 | 0.048 | 0.013 | 0.009 |
| Tukey | 0.049 | 0.047 | 0.010 | 0.010 |
| PLS | 0.051 | 0.049 | 0.011 | 0.011 |
We further evaluated the validity of PLS when markers in two genes are correlated. This showed that PLS can keep good control of type I error rate even when correlations exists between the two regions. The empirical type I error rates were 0.053, 0.049, 0.048, 0.050 for the distances (|j−i|) 2, 4, 6 and 8, respectively, at a significance level of 0.05; and 0.011, 0.010, 0.010 and 0.010 at a significance level of 0.01.
Simulation Results: Power
Figures 2–4 show the empirical power of different methods for testing association of the disease and the underlying causal variant u1 at a significance level of α = 0.05 when the causal variant is not genotyped. Because the test based on a full logistic regression does not have good control of the type I error rate and is generally much less powerful than the other approaches, the results of this approach are not shown.
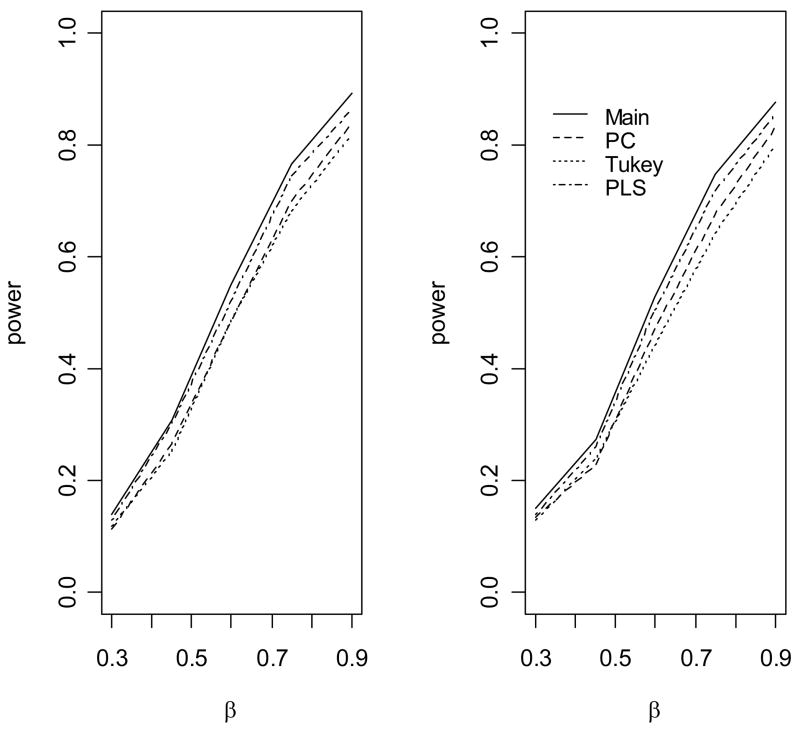
Figure 2.
The empirical power to detect association of the disease with gene 1 under a multiplicative model. The causal variants are not gentoyped. (1) The allele frequency of u2 is 0.1; (2) The allele frequency of u2 is 0.2.
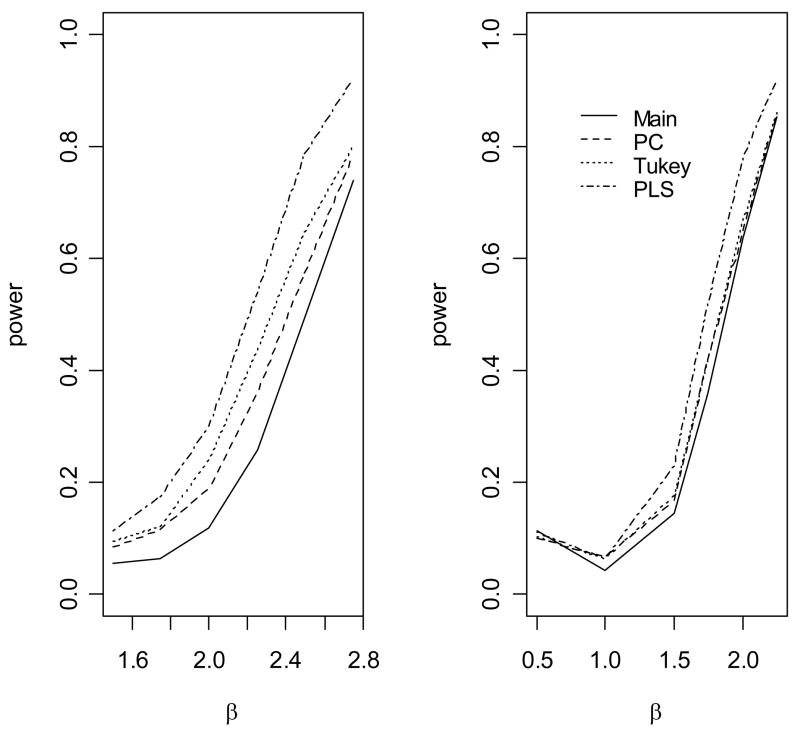
Figure 4.
The empirical power to detect association of the disease with gene 1 under an crossover model. The causal variants are not gentoyped. (1)The allele frequency of u2 is 0.1; (2) The allele frequency of u2 is 0.2
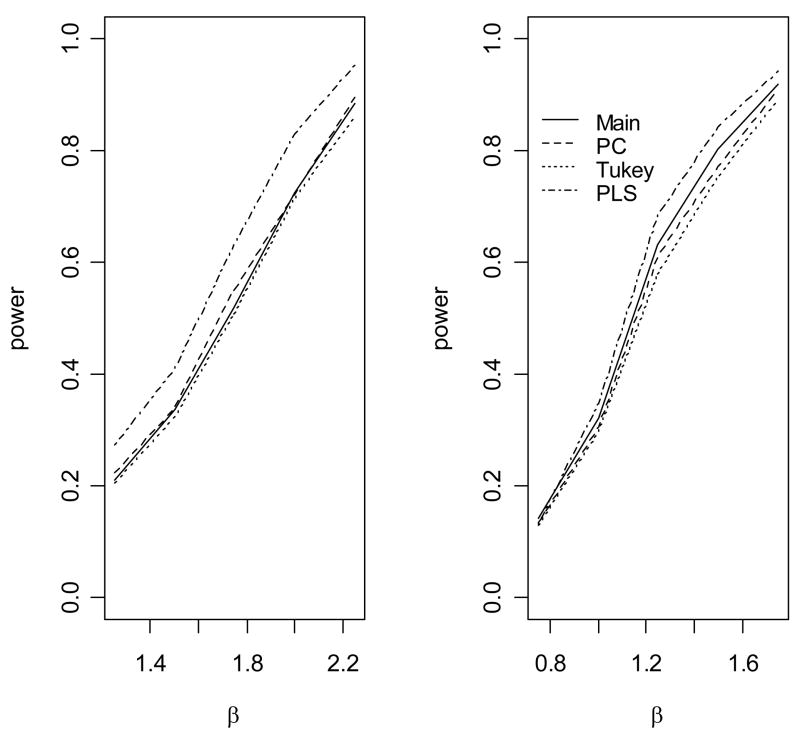
When the genetic model is multiplicative (Figure 2), the standard main effect logistic regression (Main) is most powerful, as expected. However, the proposed approach (PLS), the score test based on the first principal component (PC) and the score test based on Tukey’s 1 degree of freedom model (Tukey) have only slightly less power than the main effect logistic regression model, because only one degree of freedom is unnecessarily used for modeling interaction. In contrast, the logistic regression model with full pair-wise interactions between two SNPs in two genes significantly loses power because of the penalty on the power owing to the large number of degrees of freedom for modeling interactions (data not shown). We can also see that, because we use a likelihood ratio test rather than a score test, there are a minor differences in power among PLS, PC and Tukey’s method. When the underlying genetic model is purely epistatic (Figure 3), the new approach clearly has the best performance among all approaches. The full logistic regression again has the worst performance. Interestingly, we can see that the PC and Tukey approaches have power very similar to that of the main effect logistic regression model. The power of a test statistic that models interactions depends on a trade-off between the number of degrees of freedom and the interaction effects of the SNP markers. As the correlations between the underlying disease variants and the genotyped SNPs are moderate in this simulation, the interaction effects of the SNPs are small and so the PC and Tukey approaches do not outperform the main effect logistic regression. However, the new PLS approach outperforms the other approaches by taking advantage of information from both the phenotype and the genotypic correlation structure. We can see that the gain in power of PLS depends on the allele frequency of u2 When the allele u2 is rarer, the gain in power is larger, which was also observed by Chatterjee et al in examining the power of Tukey’s approach [Chatterjee et al., 2006]. Figure 4 shows the empirical power of the various methods as a function of θ12 when the underlying genetic model is a crossover model (θ1 = −0.5). We can see that, because of the modest marginal effects, the main effect logistic regression has much lower power than the PLS, PC and Tukey methods, among which the PLS has the best power performance.
Figure 3.
The empirical power to detect association of the disease with gene 1 under an epistatic model. The causal variants are not gentoyped. (1) The allele frequency of u2 is 0.1; (2) The allele frequency of u2 is 0.2.
We also evaluated the empirical power of the different approaches under the same genetic models when the underlying disease variants are gentoyped. Because the interaction effects are more significant, the power advantage of the PLS approach is further increased in this case (data not shown).
Application: A study of AKT1, AKT2 and Risk of endometrial cancer
Cancer of the endometrium is the most common gynecologic malignancy and accounts for 6% of all cancers in women. Estimated new cases and deaths from endometrial cancer in the United States in 2007 are 39,080 and 7,400, respectively. Estrogen replacement therapy (ERT) in menopause and obesity are the principal risk factors for endometrial cancer [Kaaks et al., 2002; Pike and Ross, 2000]. Although only a small proportion of women using ERT or with obesity will develop endometrial cancer, little is known about genetic susceptibility to the disease.
We have conducted a genetic study of endometrial cancer within the Women’s Health Initiative (WHI), a prospective study of over 90,000 postmenopausal women. This study has investigated several candidate genes, including AKT1 (MIM164730) and AKT2 (MIM164731), in 246 endometrial cancer cases and 688 controls. AKT1 and AKT2 are members of the AKT family, which is relevant to tumorigenesis because of its effect on anti-apoptosis and cell proliferation [Altomare and Testa, 2005]. The AKT1 and AKT2 genes have been localized to human chromosome 14, band q32, and chromosome 19, band q13, respectively. Also available is body mass index (BMI) for each participant in the study.
To illustrate the method proposed here, we applied different approaches to detect the association of the AKT1 and AKT2 genes with endometrial cancer by taking gene-environment interaction (interaction between these two genes and BMI) into account. In this study, seven and six tag-SNPs are genotyped for AKT1 and AKT2, respectively. The frequencies of the minor SNP alleles range from 0.04 to 0.45. Table 2 presents the p-values and number of degrees of freedom for the different multi-locus analysis approaches to detect association of the these two candidate genes with endometrial cancer. From this table, we can see that the main-effect test and other approaches fail to detect association between AKT1 and endometrial cancer, suggesting that the marginal effects of SNPs in AKT1 may be small. The PLS approach suggests that AKT1 is associated with endometrial cancer susceptibility at the significance level 0.05, although the interaction effect itself between the latent variable of the AKT1 gene and BMI is not significant (the estimated regression coefficient of the interaction term between the latent variable of the AKT1 gene and BMI is −0.08376; p = 0.075). All tests, except PC, show significant association between AKT2 and cancer, for which the new PLS method tends to show slightly stronger evidence of association than the other approaches. The estimated regression coefficient of the interaction term between the latent variable of the AKT2 gene and BMI in the PLS model is 0.167 (p = 0.007). These results provide an example of how we can improve the power of detecting association by appropriately modeling an interaction, even when the interaction term itself is not statistically significant. The results also suggest that the proposed method may outperform other approaches in certain circumstances, which is consistent with what we observed in the simulation studies.
Table 2.
The p-values of different approach in testing AKT1 and AKT2 associated with endometrial cancer by taking their interactions with BMI into account.
| AKT1 | AKT2 | |||
|---|---|---|---|---|
| d.f, | p-value | d.f, | p-value | |
| Main | 7 | 0.083 | 6 | 0.026 |
| PC | 8 | 0.097 | 7 | 0.102 |
| Tukey | 8 | 0.058 | 7 | 0.006 |
| PLS | 8 | 0.042 | 7 | 0.002 |
Discussion
Modeling gene-gene and gene-environment interactions can not only improve the power for detecting association of genetic markers with diseases, but also be useful for understanding the underlying mechanisms of diseases. However, the prevailing analysis strategy for genetic association studies still follows a locus-by-locus strategy. One major reason for this is the lack of powerful approaches. Although a conventional logistic regression can be readily applied, a large number of parameters have to be used in modeling all possible pairs of SNPs, even for only candidate genes and, as shown in our simulations, this could lead to an unsuccessful test.
In this paper, we have proposed a new approach to model gene-gene and gene-environment interactions when multiple SNPs are genotyped in a gene. This approach is similar to the procedure based on Tukey’s 1 df model in that we shrink multiple SNPs into a single latent variable to capture the useful information. Because only one degree of freedom is involved in modeling the interaction, this approach has least cost in power when the true genetic model is purely multiplicative. When the underlying genetic model is an interaction model in which the effect of a causal variant depends on the genotypes of another variant, this approach potentially has a major power advantage over a procedure that does not take interactions into account, because, although the marginal effect of the causal variant can be small, there may be large effects within each genotype group of the other variant.
An alternative approach to shrink SNPs in modeling gene-gene or gene-environment interactions follows a two-stage procedure in which SNPs that meet some threshold in a test at the first analysis phase are subsequently followed up for modeling interactions. The selection of SNPs may be simply based on a test to examine the correlation between SNPs and the phenotype, which relies on the existence of non-negligible marginal effects [Evans et al., 2006;Marchini et al., 2005]. Millstein et al. have described another alternative method: first select SNPs based on a test for the significance of correlations in pair-wise SNPs [Millstein et al., 2006]. However, the correlation test is usually less efficient than the marginal effect test when non-negligible marginal effects exist. The usefulness of these two approaches may vary for different underlying genetic models. Moreover, it is not clear how to choose the threshold for selection in this two-stage procedure. The method proposed here and the procedure based on Tukey’s 1-df model take a “soft” shrinkage approach in which SNPs are given different weights, so that the threshold does not need to be specified in advance.
Our approach is different from the procedure based on Tukey’s 1-df model in that in our ‘procedure the shrinkage of multiple SNPs relies on both the marginal effects of SNPs and the association between the two genes, or between the gene and the environment factor, in the sample. Because of the use of both sources of information, our method is likely to be more powerful, as shown by our simulations. In an extreme gene-gene interaction example, in which a causal variant has opposite effects according to different genotypes of the other variants, so that marginal effects of neither variant exist, the proposed approach can work well because the cross-locus GD is still useful to obtain an informative latent component. However, the non-additive effect of the causal variant introduced by the gene-gene interaction in this case is non-removable in Tukey’s model, so that the procedure based on Tukey’s model would not have good power to detect such association. Another advantage of our procedure is that the interaction between two genes can be directly tested by applying a standard logistic regression, but how to test the non-additive effect is not obvious in the procedure based on Tukey’s model.
The major assumption of our approach is that the two genes are independent in the population. When this assumption is true, we have shown that the interaction effect can introduce GD between SNPs in the two genes and, more importantly, the magnitude of the association depends on the LD between the SNPs and the causal variants (equation 5). So it is reasonable to give larger weights to SNPs that have stronger association with SNPs in another gene (or environmental factors) to improve power. However, when background association due to various other genetic effects exists, it can mask the association introduced by the interaction effects and therefore the magnitude of the association does not reflect the LD between the SNP marker and the causal variant. In this case, these weights might not be optimal in terms of power, although the test based on this approach can still keep good control of the type I error rate. It may be useful to estimate shrinkage by means of the genotype values to remove the “background” association [Wang et al., 2007]. Another limitation of our approach, as with all other approaches to model interactions, is that the efficiency to detect interactions decreases rapidly with decreasing LD between the marker and the causal variants. Without a satisfactory coverage of SNPs, the gain in power of the proposed method tends to be small, even in a purely epistatic model, although it does not lead to a significant decrease in power. To successfully detect association of genes that have no, or small, marginal effects, denser markers are desirable than for a design to detect marginal effects.
Our approach can handle any number of SNPs in a gene, but it may not be wise to blindly apply this approach to a large number of SNPs because accumulated noise from unrelated SNPs could mask any real association. Before applying this method, it is useful to first examine the LD pattern of the gene. When SNPs tend to be in different LD blocks, one component may not be enough to capture all the information. One may consider applying this approach to each block, or using more than one component in modeling interactions.
In summary, we have proposed an approach to improve the power of detecting association by taking gene-gene and gene-environment interaction into account. We demonstrated that this approach has more power than several other approaches, in both our simulations and an application study. The proposed approach focuses on pair-wise interactions. However, multiple genes and environmental factors can be involved in the pathways of complex diseases. Further work is necessary to extend our current approach to efficiently model interactions among several genes.
Acknowledgments
This work was partially supported by a Pilot and Feasibility Award from the diabetes research and training center at AECOM. GYFH was supported by National Institute of Health grants R01 CA102691and R01 CA108841. RCE was supported in part by a U.S. Public Health Service Resource Grant from the National Center for Research Resources (RR03655), a Research Grant from the National Institute of General Medical Sciences (GM28356) and a Cancer Center Support Grant from the National Cancer Institute (P30CAD43703).
The WHI program is funded by the National Heart, Lung and Blood Institute, U.S. Department of Health and Human Services. The WHI participating investigators are listed as follows:
Program Office: (National Heart, Lung, and Blood Institute, Bethesda, Maryland) Elizabeth Nabel, Jacques Rossouw, Shari Ludlam, Linda Pottern, Joan McGowan, Leslie Ford, and Nancy Geller.
Clinical Coordinating Center: (Fred Hutchinson Cancer Research Center, Seattle, WA) Ross Prentice, Garnet Anderson, Andrea LaCroix, Charles L. Kooperberg, Ruth E. Patterson, Anne McTiernan; (Wake Forest University School of Medicine, Winston-Salem, NC) Sally Shumaker; (Medical Research Labs, Highland Heights, KY) Evan Stein; (University of California at San Francisco, San Francisco, CA) Steven Cummings.
Clinical Centers: (Albert Einstein College of Medicine, Bronx, NY) Sylvia Wassertheil-Smoller; (Baylor College of Medicine, Houston, TX) Jennifer Hays; (Brigham and Women’s Hospital, Harvard Medical School, Boston, MA) JoAnn Manson; (Brown University, Providence, RI) Annlouise R. Assaf; (Emory University, Atlanta, GA) Lawrence Phillips; (Fred Hutchinson Cancer Research Center, Seattle, WA) Shirley Beresford; (George Washington University Medical Center, Washington, DC) Judith Hsia; (Los Angeles Biomedical Research Institute at Harbor- UCLA Medical Center, Torrance, CA) Rowan Chlebowski; (Kaiser Permanente Center for Health Research, Portland, OR) Evelyn Whitlock; (Kaiser Permanente Division of Research, Oakland, CA) Bette Caan; (Medical College of Wisconsin, Milwaukee, WI) Jane Morley Kotchen; (MedStar Research Institute/Howard University, Washington, DC) Barbara V. Howard; (Northwestern University, Chicago/Evanston, IL) Linda Van Horn; (Rush Medical Center, Chicago, IL) Henry Black; (Stanford Prevention Research Center, Stanford, CA) Marcia L. Stefanick; (State University of New York at Stony Brook, Stony Brook, NY) Dorothy Lane; (The Ohio State University, Columbus, OH) Rebecca Jackson; (University of Alabama at Birmingham, Birmingham, AL) Cora E. Lewis; (University of Arizona, Tucson/Phoenix, AZ) Tamsen Bassford; (University at Buffalo, Buffalo, NY) Jean Wactawski-Wende; (University of California at Davis, Sacramento, CA) John Robbins; (University of California at Irvine, CA) F. Allan Hubbell; (University of California at Los Angeles, Los Angeles, CA) Howard Judd; (University of California at San Diego, LaJolla/Chula Vista, CA) Robert D. Langer; (University of Cincinnati, Cincinnati, OH) Margery Gass; (University of Florida, Gainesville/Jacksonville, FL) Marian Limacher; (University of Hawaii, Honolulu, HI) David Curb; (University of Iowa, Iowa City/Davenport, IA) Robert Wallace; (University of Massachusetts/Fallon Clinic, Worcester, MA) Judith Ockene; (University of Medicine and Dentistry of New Jersey, Newark, NJ) Norman Lasser; (University of Miami, Miami, FL) Mary Jo O’Sullivan; (University of Minnesota, Minneapolis, MN) Karen Margolis; (University of Nevada, Reno, NV) Robert Brunner; (University of North Carolina, Chapel Hill, NC) Gerardo Heiss; (University of Pittsburgh, Pittsburgh, PA) Lewis Kuller; (University of Tennessee, Memphis, TN) Karen C. Johnson; (University of Texas Health Science Center, San Antonio, TX) Robert Brzyski; (University of Wisconsin, Madison, WI) Gloria E. Sarto; (Wake Forest University School of Medicine, Winston-Salem, NC) Mara Vitolins; (Wayne State University School of Medicine/Hutzel Hospital, Detroit, MI) Susan Hendrix.
Footnotes
Web Resources
The URL for data presented here is as follows: HapMap, http://www.hapmap.org/http://www.ncbi.nlm.nih.gov/Omim.
References
- Design of the Women’s Health Initiative clinical trial and observational study. The Women’s Health Initiative Study Group. Control Clin Trials. 1998;19:61–109. doi: 10.1016/s0197-2456(97)00078-0. [DOI] [PubMed] [Google Scholar]
- Altomare DA, Testa JR. Perturbations of the AKT signaling pathway in human cancer. Oncogene. 2005;24:7455–7464. doi: 10.1038/sj.onc.1209085. [DOI] [PubMed] [Google Scholar]
- Conrad DF, Jakobsson M, Coop G, Wen X, Wall JD, Rosenberg NA, Pritchard JK. A worldwide survey of haplotype variation and linkage disequilibrium in the human genome. Nat Genet. 2006;38:1251–1260. doi: 10.1038/ng1911. [DOI] [PubMed] [Google Scholar]
- de Bakker PI, Burtt NP, Graham RR, Guiducci C, Yelensky R, Drake JA, Bersaglieri T, Penney KL, Butler J, Young S, Onofrio RC, Lyon HN, Stram DO, Haiman CA, Freedman ML, Zhu X, Cooper R, Groop L, Kolonel LN, Henderson BE, Daly MJ, Hirschhorn JN, Altshuler D. Transferability of tag SNPs in genetic association studies in multiple populations. Nat Genet. 2006;38:1298–1303. doi: 10.1038/ng1899. [DOI] [PubMed] [Google Scholar]
- Evans DM, Marchini J, Morris AP, Cardon LR. Two-stage two-locus models in genome-wide association. PLoS Genet. 2006;2:e157. doi: 10.1371/journal.pgen.0020157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gauderman WJ, Murcray C, Gilliland F, Conti DV. Testing association between disease and multiple SNPs in a candidate gene. Genet Epidemiol. 2007;31:383–395. doi: 10.1002/gepi.20219. [DOI] [PubMed] [Google Scholar]
- Helland IS. Partial Least-Squares Regression and Statistical-Models. Scandinavian Journal of Statistics. 1990;17:97–114. [Google Scholar]
- Helland IS. On the Structure of Partial Least-Squares Regression. Communications in Statistics-Simulation and Computation. 1988;17:581–607. [Google Scholar]
- Hirschhorn JN, Daly MJ. Genome-wide association studies for common diseases and complex traits. Nature Reviews Genetics. 2005;6:95–108. doi: 10.1038/nrg1521. [DOI] [PubMed] [Google Scholar]
- Hirschhorn JN, Lohmueller K, Byrne E, Hirschhorn K. A comprehensive review of genetic association studies. Genet Med. 2002;4:45–61. doi: 10.1097/00125817-200203000-00002. [DOI] [PubMed] [Google Scholar]
- Kaaks R, Lukanova A, Kurzer MS. Obesity, endogenous hormones, and endometrial cancer risk: a synthetic review. Cancer Epidemiol Biomarkers Prev. 2002;11:1531–1543. [PubMed] [Google Scholar]
- Kraft P, Yen Y, Stram DO, Morrison J, Gauderman WJ. Exploiting gene-environment interaction to detect genetic associations. Hum Hered. 2007;63:111–119. doi: 10.1159/000099183. [DOI] [PubMed] [Google Scholar]
- Marchini J, Donnelly P, Cardon LR. Genome-wide strategies for detecting multiple loci that influence complex diseases. Nat Genet. 2005;37:413–417. doi: 10.1038/ng1537. [DOI] [PubMed] [Google Scholar]
- Millstein J, Conti DV, Gilliland FD, Gauderman WJ. A testing framework for identifying susceptibility genes in the presence of epistasis. Am J Hum Genet. 2006;78:15–27. doi: 10.1086/498850. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pike MC, Ross RK. Progestins and menopause: epidemiological studies of risks of endometrial and breast cancer. Steroids. 2000;65:659–664. doi: 10.1016/s0039-128x(00)00122-7. [DOI] [PubMed] [Google Scholar]
- Risch N, Merikangas K. The future of genetic studies of complex human diseases. Science. 1996;273:1516–1517. doi: 10.1126/science.273.5281.1516. [DOI] [PubMed] [Google Scholar]
- Wang T, Zhu X, Elston RC. Improving power in contrasting linkage-disequilibrium patterns between cases and controls. Am J Hum Genet. 2007;80:911–920. doi: 10.1086/516794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zaykin DV, Meng Z, Ehm MG. Contrasting linkage-disequilibrium patterns between cases and controls as a novel association-mapping method. Am J Hum Genet. 2006;78:737–746. doi: 10.1086/503710. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao JY, Jin L, Xiong MM. Test for interaction between two unlinked loci. American Journal of Human Genetics. 2006;79:831–845. doi: 10.1086/508571. [DOI] [PMC free article] [PubMed] [Google Scholar]