Newborn infants perceive abstract numbers

Abstract

Although infants and animals respond to the approximate number of elements in visual, auditory, and tactile arrays, only human children and adults have been shown to possess abstract numerical representations that apply to entities of all kinds (e.g., 7 samurai, seas, or sins). Do abstract numerical concepts depend on language or culture, or do they form a part of humans' innate, core knowledge? Here we show that newborn infants spontaneously associate stationary, visual-spatial arrays of 4–18 objects with auditory sequences of events on the basis of number. Their performance provides evidence for abstract numerical representations at the start of postnatal experience.

Are humans endowed with abstract representations of the surrounding world? In the domain of number, animals and preverbal infants have been shown to react to the cardinal values of sets presented in a variety of different stimulus formats, and this core number sense is thought to guide learning of numeric symbols and arithmetic in human children and adults (1–5). For example, by the age of 4.5 to 6 months, infants are able to discriminate between numbers differing in a 1:2 ratio (e.g., 16 vs. 32, 8 vs. 16, 4 vs. 8), when presented with arrays of dots (6, 7), sequences of sounds (8), or sequences of actions (9). In each of these experiments, however, infants were tested with only 1 type of stimulus, raising the question of the level of abstraction of these numeric representations.

From the early 1980s to present, several investigations have tested for numeric cross-modal matching in infants with mixed results. Although infants initially were reported to look longer at a set of objects that matched a sequence of sounds played simultaneously (10, 11), subsequent experiments yielded either no such preference (12) or a reversed preference (13). Failures to match sounds and objects on the basis of number have been documented until 3–4 years of age, eventually resolving as children start to master verbal counting (14). By using more natural stimuli, later research showed unequivocally that infants and animals could detect the numerical correspondence between 2 or 3 items in different modalities (15–18). In all of these studies, however, matching was elicited either by drawing on cross-modal correspondences that were familiar [faces and voices (15, 16) or objects with similar features presented across the visual and tactile modalities (18)], or by presenting a familiarization phase in which events in different modalities occurred in synchrony (17). In these situations, cross-modal matching might be achieved by calling on amodal representations of objects rather than amodal representations of abstract, cardinal values. For example, presentation of a voice may elicit an image of a face; when 3 distinct voices are played, therefore, infants may represent 3 correspondingly distinct faces that then can be quantified and compared to a matching or nonmatching visual stimulus. Indeed, the numbers tested in these studies were small enough to allow for simultaneous object representations (3 objects at most); infants failed to respond to amodal correspondences when tested with larger numbers (18). In sum, infants appear able to construct amodal representations of faces and other objects, but they may not match sets of unrelated objects and events on the basis of their common abstract, cardinal value.

Still, some lines of evidence suggest that infants might possess abstract number representations. First, infants discriminate numbers with the same precision in all modalities (19). Second, in monkeys, children and adults, the representation of numerical information involves an area in the intraparietal sulcus that responds to numbers presented in a variety of formats (20–25); a precursor of this intraparietal activation has been found in infants as young as 3 months of age (26). Third, presentation of redundant information in the auditory and visual modalities increases the precision of infants' numerical discriminations (27), although it is not clear whether the convergence of information occurs at the level of numerical representation or at a later processing step (e.g., response selection). Moreover, auditory and visual events were presented in synchrony, and therefore, here again, numerical matching may have been grounded in amodal representations of individual events, not in an abstract representation of the cardinal values of the sets.

Clear evidence for abstract numerical representations comes from studies of trained animals and of human children and adults who are presented with sets where cardinal values exceed the limits of object-based attention (beyond 3). For example, monkeys trained to match numerical values (2, 3, 5, 8) across auditory and visual formats were able to generalize this competence to all numbers up to 9 (28). However, the animals developed this ability only after thousands of training trials involving sequences of visual and auditory events presented in synchrony, that could have induced the formation of abstract representations by association of modality-specific number representations. Evidence for generalization of numerical quantities across modalities has also been reported in rats (29, 30). After learning to associate 2 response levers to auditory sequences differing in number, rats generalized the trained responses to new sequences mixing auditory and tactile stimuli, even though they were never reinforced on such compound sequences (29). Moreover, rats showed a cost for learning new associations between response levers and visual sequences if the mapping did not match the associations learned in the auditory modality (30). In both these conditions, however, the initial training may have induced the animals to form abstract representations of relative quantity (less/more), rather than number (31), leaving open the question of whether animals spontaneously form abstract number representations.

In contrast, human adults and 5-year-old children show evidence for spontaneous, abstract concepts of number. For example, they can compare numerical quantities presented in different formats and modalities as easily as they compare numbers within 1 modality and format (32, 33), with no specific training at matching formats. Nevertheless, these adults and children have already mastered symbols that refer to abstract numbers, therefore, raising the possibility that abstract representations of number arise only with the acquisition of numeric symbols. In sum, no experiments yet reveal whether abstract numerical representations are spontaneously available to any species.

The absence of a spontaneous generalization of number across modalities and formats could be explained in 2 ways. First, infants and animals may possess neural mechanisms for representing numbers of objects and numbers of events, but the 2 types of numerical representations may be functionally distinct. In the absence of language, there may exist no truly abstract numerical representations. Second, animals and infants may possess abstract numerical representations, but those representations may be overshadowed by the salient differences between objects and events. On the former view, abstract numerical representations are a product of language and culture; on the latter view, language and culture make more prominent a preexisting representational capacity.

The present experiments sought direct evidence for the detection of numerical correspondences across modalities in newborn human infants. In contrast to older infants, newborn infants have sharply diminished sensitivity to the visual and auditory features that characterize specific objects and events (34). Nevertheless, they are sensitive to abstract geometric properties of objects (35) and actions (36). Perceptual development has been proposed to begin with sensitivity to these abstract distinctions and proceed to an analysis of more concrete ones (37). If humans and animals are endowed with abstract numerical representations, therefore, these representations may be more prominent to newborn infants than to older children.

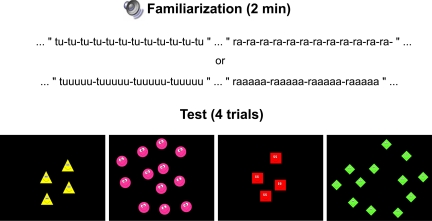
Accordingly, we conducted 3 experiments assessing newborn infants' cross-modal discrimination among large numbers of objects. Each infant was familiarized with sequences of syllables repeated a fixed number of times in a continuous auditory stream. After 2 min of familiarization, looking time was tested with 4 visual images containing either the same number of objects as the auditory sequences (congruent number), or a different number (incongruent number). To prevent matching of visual and auditory stimuli on a non-numerical stimulus dimension, the familiarization and test stimuli varied using procedures that controlled for a host of quantitative variables including intensity, duration, and spatial or temporal frequency (see Methods and Fig. 1). In each experiment, infants were tested with a pair of numbers in a design that counterbalanced both the numerical value of the familiar and novel numbers and the order of the congruent and incongruent tests.

Fig. 1.

Newborn infants were familiarized with auditory sequences containing a fixed number of syllables, and were then tested with images of the same or a different number of items (here 4 or 12). Auditory sequences were equated across numbers on extensive parameters (total duration), and visual arrays where equated on intensive parameters (size of each item, density of the array).

Results

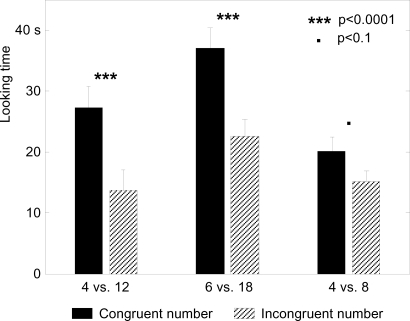
In the first experiment, infants were familiarized with sequences of either 4 or 12 sounds, accompanied by visual arrays of either 4 or 12 objects. Newborn infants in both familiarization conditions looked longer at the visual image with the matching number of objects (15 out of 16 infants showed this preference; T₍₁₅₎ = 5.3, P < 0.0001, see Fig. 2). To examine the generality of this finding, a new group of infants were tested in a second experiment with auditory sequences and visual arrays of either 6 or 18 sounds and objects. Again, the infants looked longer at the matching visual array (15 out of 16 infants; T₍₁₅₎ = 6.0, P < 0.0001). The preference for the numerically matching image was equivalent in the 2 experiments, showing no effect of numerical size on the infants' performance (F_(1,30) < 1). Accordingly, the last experiment tested for an effect of ratio on the infants' performance by presenting auditory sequences and visual arrays of 4 vs. 8 elements. In contrast to the previous experiments, infants showed only a weak preference for the numerically matching display (11 out of 16 infants looked more at the congruent image; T₍₁₅₎ = 1.9, P = 0.071). A comparison across experiments revealed a reliable effect of numerical ratio on the infants' performance (3:1 vs. 2:1 ratio; F_(1,46) = 8.7, P = 0.0050). Newborn infants, therefore, show the ratio-dependent numerical processing that is characteristic of older children and adults*.

Fig. 2.

Newborns looked consistently longer at the displays that were congruent in number with the auditory sequences presented during familiarization, when the numbers to discriminate were separated by a ratio of 3:1 (4 vs. 12, 6 vs. 18), but not for a smaller ratio (4 vs. 8; ratio 2:1). Error bars represent standard errors.

Discussion

In the present experiments, human newborns responded to abstract numerical quantities across different modalities and formats (sequential vs. simultaneous). In previous research, older infants had shown evidence for intermodal numerical matching, but only under conditions in which matching could be based on multimodal representations of objects, rather than on representations of cardinal values (10, 11, 15, 17, 18). In contrast, the present research presented visible objects that were too numerous for infants to track, and sounds that were not time-locked with the images in a way that could have specified multimodal events or objects. The current results, therefore, provide evidence for abstract numerical representations at the start of human life.

Newborn infants' sense of numbers presents the characteristic ratio dependence that is observed later in life and in other species, indicating continuity over development and speciation. Nevertheless, their performance contrasts with that of adult animals and of older infants in 2 respects. First, although a wealth of research shows that older infants and untrained adult monkeys discriminate reliably between numbers within each modality (6, 8, 9, 38), no direct evidence for spontaneous cross-modal matching has been reported in either population. The question whether older infants and adult animals are able to generalize numbers across different modalities deserves further investigation, but this absence of reports suggests that abstract numerical representations may be easier to elicit very early in development, perhaps because very young infants have lower sensitivity to modality-specific aspects of visual and auditory displays (37).

Second, our findings provide further evidence that numerical representations increase in precision over the course of human development. Although the participants in the present study discriminated numbers robustly only when they differed by a ratio of 3:1, infants show reliable discrimination at ratios of 2:1 by 6 months of age, and 3:2 by 9 months of age (6, 19, 39), and older children and adults discriminate numbers at progressively smaller ratios (40). A refinement of numerical representation thus occurs progressively from human infancy, before experience with symbolic numeric labels. Abstract numerical representations likely are progressively enriched through both the maturation of brain systems and the accumulation of experience, a process that extends through childhood.

Our findings may have practical applications. Impairments to the system of approximate numerical representations have been related to the occurrence of dyscalculia (41), a specific deficit for learning mathematics with a prevalence of 3–6% in school-aged children. Since the test reported here evoked a consistent response in almost all infants, it could inspire the development of new diagnostic tools to detect early deficits in the processing of quantities.

Methods

Participants.

Sixteen infants were included in each of the 3 experiments (mean age 49 h, range 7–100 h; 26 females). Fifty additional infants were excluded from the final sample, 35 for fussiness, 10 for falling asleep, and 5 for experimenter intervention.

Displays.

Example stimuli can be viewed in Movie S1. Infants were first familiarized with a continuous auditory stream, which consisted of sequences of syllables each repeated a fixed number of times. During familiarization, all of the sequences had the same numerical value for any given infant; the number used for familiarization varied both between participants and across experiments. Infants then were tested with visual images presenting the same number and a different number (larger for half the participants and smaller for the others). Eight different syllables of variable duration were used to construct the sequences. Within each number pair condition, sequences were equated in duration across numbers. In consequence, each syllable was shorter for the larger number than for the smaller number. The average duration of syllable sequences was 2.9 s, 4.4 s, and 2.9 s, respectively, for the pairs 4 vs. 12, 6 vs. 18, and 4 vs. 8. Successive sequences were separated by a variable silent interval of 1–3 s duration.

Test images were prepared with a variant of a program used in previous publications (26), available at http://www.unicog.org/main/pages.php?page = Documentation. Each image presented a set of brightly colored, simple geometrical shapes with facial features (eyes and mouth). All of the objects were identical within each image, but 4 different shapes and colors were used across the 4 test images. The order of appearance of the different shapes, and their pairing with the different numbers (congruent or incongruent, small or large) were randomized across participants. To maintain the infants' interest, the test images were animated with a stroboscopic movement each 1.0 s, unsynchronized with the onset of auditory sequences. The full images were ≈14–25 cm in size, and depending on the condition, the size of each individual object varied from 2.8–4.8 cm.

In contrast to the auditory stream in the test images, the intensive parameters (item size, density) were equated across numbers, such that the extensive parameters (summed luminance, total surface occupied by the array) increased with number. As a consequence, if infants attended to intensive parameters and were able to generalize these parameters across modalities, they would respond equally to all of the test images. Moreover, if infants attended to extensive parameters and showed cross-modal generalization of those parameters, they should exhibit the same test preference regardless of the familiarization conditions.

Procedure.

Participants were tested in a separate room in the maternity hospital where they were born. The infants were seated in an infant seat, ≈60 cm from a 22-inch monitor, and an experimenter stood behind the infant to monitor for potential signs of discomfort. The experimenter did not usually need to intervene in the course of the experiment, and data were excluded if the experimenter touched the infant (5 infants). During the familiarization phase, the screen stayed black and sounds were played through 2 speakers that were located just behind the infant seat on each side. After 2 min of familiarization with auditory sequences, the infants were presented with test images while the auditory stimulus continued to play in background. Four test images were presented, alternating between the congruent number and an incongruent number. The images stayed on the screen until the infant looked away for >2 seconds, or after 60 s of looking.

Looking times were recorded online by a trained observer who was blind to the image presented. A second measurement of looking times was performed offline by a different observer, also blind to the experimental condition [correlation between the 2 measurements: R² = 0.86, with a slope of 0.95, nondifferent from 1 (P = 0.097)]. Because newborns tend to not open their eyes as wide as older infants, their looks are harder to assess, therefore, an additional offline measurement was performed when the assessments differed by >5 s (13% of the trials). This procedure reduced the variance due to uncertainty from the coders, and resulted in a 95% confidence interval of ±1.6 s for the variance due to coding, which ensures enough statistical power to detect effects of 2.2 s and more (all of the effects reported exceed this range). The analyses reported above are based on averages of the 2 closest measurements for each trial (all of the results remain the same when looking times are based on an average of the 2 first measurements instead). Since the presentation of each image was limited to 60 s, all looking times fall within 2.5 standard deviations of the mean, and therefore no outlier was excluded from the analyses.