Toolbox model of evolution of prokaryotic metabolic networks and their regulation

Abstract

It has been reported that the number of transcription factors encoded in prokaryotic genomes scales approximately quadratically with their total number of genes. We propose a conceptual explanation of this finding and illustrate it using a simple model in which metabolic and regulatory networks of prokaryotes are shaped by horizontal gene transfer of coregulated metabolic pathways. Adapting to a new environmental condition monitored by a new transcription factor (e.g., learning to use another nutrient) involves both acquiring new enzymes and reusing some of the enzymes already encoded in the genome. As the repertoire of enzymes of an organism (its toolbox) grows larger, it can reuse its enzyme tools more often and thus needs to get fewer new ones to master each new task. From this observation, it logically follows that the number of functional tasks and their regulators increases faster than linearly with the total number of genes encoding enzymes. Genomes can also shrink, e.g., because of a loss of a nutrient from the environment, followed by deletion of its regulator and all enzymes that become redundant. We propose several simple models of network evolution elaborating on this toolbox argument and reproducing the empirically observed quadratic scaling. The distribution of lengths of pathway branches in our model agrees with that of the real-life metabolic network of Escherichia coli. Thus, our model provides a qualitative explanation for broad distributions of regulon sizes in prokaryotes.

Biological functioning of a living cell involves coordinated activity of its metabolic and regulatory networks. Although the metabolic network specifies which biochemical reactions the cell is, in principle, able to carry out, its actual operation in a given environment is orchestrated by the transcription regulatory network through up- or down-regulation of enzyme levels. A large size of the interface between these 2 networks in prokaryotes is indicated by the fact that nearly half of transcription factors in Escherichia coli have a binding site for a small molecule (1), which implicates them (2) as potential regulators of metabolic pathways. This interface is further increased when one takes into account two component systems whose sensors bind to small molecules and only then activate a dedicated transcription factor. Thus, at least in prokaryotes, regulation of metabolism occupies the majority of all transcription factors.

Two recent empirical observations shed additional light on evolutionary processes shaping these 2 networks:

• The number of transcriptional regulators is shown to grow faster than linearly (3–6) [approximately quadratically (4)] with the total number of proteins encoded in a prokaryotic genome.

• The distribution of sizes of coregulated pathways (regulons), which in network language correspond to out-degrees of transcription factors in the regulatory network, has long tail (7). As a result, the set of transcription factors of each organism includes few global (“hub”) regulators controlling hundreds of genes, many local regulators controlling several targets each, and all regulon sizes in-between these 2 extremes.

A simple evolutionary model explains both these empirical observations in a unified framework based on modular functional design of prokaryotic metabolic networks and their regulation.

Toolbox View of Metabolic Networks

Metabolic networks are composed of many semiautonomous functional modules corresponding to traditional metabolic pathways (8) or their subunits (9). Constituent genes of such evolutionary modules tend to cooccur (be either all present or all absent) in genomes (9, 10). These pathways overlap with each other to form branched, interconnected metabolic networks. Many of these pathways/branches include a dedicated transcription factor turning them on under appropriate environmental conditions. In prokaryotic organisms there is a strong positive correlation between the number of protein-coding genes in their genomes, the number of metabolic pathways formed by these genes, the number of transcription factors regulating these pathways, and, finally, the number of environments or conditions that organism is adapted to live in.

We propose to view the repertoire of metabolic enzymes of an organism as its toolbox. Each metabolic pathway is then a collection of tools (enzymes), which enables the organism to use a particular metabolite by progressively breaking it down to simpler components, or, alternatively, to synthesize a more complex metabolite from simpler ingredients. Adapting to a new environmental condition e.g., learning to metabolize a new nutrient, involves acquiring some new tools as well as reusing some of the tools/enzymes that are already encoded in the genome. From this analogy it is clear that as the genome of an organism grows larger, on average, it needs to acquire fewer and fewer new tools to master each new metabolic task. This is because the larger is the toolbox the more likely it is to already contain some of the tools necessary for the new function. Therefore, the number of proteins encoded in organism's genome is expected to increase slower than linearly with the number of metabolic tasks it can accomplish. Or, conversely, the number of nutrients an organism can use via distinct metabolic pathways is expected to scale faster than linearly with its number of enzymes or reactions in its metabolic network. This last prediction is empirically confirmed by the data in the KEGG database (8): as shown in supporting information (SI) Fig. S1, the best power-law fit to the number of metabolic pathways vs. the number of metabolic reactions in prokaryotic genomes has the exponent 2.2 ± 0.2. This is in agreement with quadratic scaling of the number of transcription factors (4) if one assumes that most of these pathways are regulated by a dedicated transcription factor.

Results

Evolution of Networks by Random Removal and Addition of Pathways.

We propose a simple model of evolution of metabolic and regulatory networks based on this toolbox viewpoint. The metabolic network of a given organism constitutes a subset of the “universal biochemistry” network, formed by the union of all metabolites and metabolic reactions taking place in any organism. An approximation to this universal biochemistry can be obtained by combining all currently known metabolic reactions in the KEGG database (8). The universal network used in our study formed by the union of all reactions listed in the KEGG database is shown in Fig. S2. For prokaryotes, entire metabolic pathways from this universal network could be added by the virtue of horizontal gene transfer (HGT), which according to ref 11 is the dominant form of evolution of bacterial metabolic networks. Recent studies (12) reported a number of HGT “highways” or preferential directions of horizontal gene transfer between major divisions of prokaryotes. As a result of these and other constraints the effective size of the universal network from which an organism gets most new pathways is likely to deviate from the simple union of reactions in all organisms. Metabolic networks can also shrink because of removal of pathways. This often happens when a nutrient disappears from the environment of an organism over an evolutionary significant time interval [see “use it or lose it” principle by Savageau (13)]. A massive elimination of pathways occurs, e.g., when an organism becomes an obligate parasite fully relying on its host for “preprocessing” of most nutrients.

The state-of-the-art information on metabolic networks is not adequate for a fully realistic modeling of their evolution. Fortunately, faster-than-linear scaling of the number of pathways and their regulators with the number of genes is the robust outcome of the toolbox evolution scenario, and as such, it is not particularly sensitive to topological structure of the universal biochemistry network. In particular, we found (see Fig. S3) essentially identical scaling in 2 models using 2 very different variants of the universal biochemistry network:

• the union of KEGG reactions (8) in all organisms (see Dataset S1). A similarly sized universal network was used in ref. 29. The part of this network connected to the biomass production consists of N_univ ≃ 1,800 metabolites;

• a random spanning tree on the fully connected graph of N_univ metabolites. Although certainly not realistic, this version is mathematically tractable.

Furthermore, it turned out that many other details of pathway acquisition process do not change scaling exponents of our model (see Fig. S4). In the rest of this study we use the first universal network (union of all KEGG reactions) in our numerical simulations of the model and the second network in our mathematical analysis.

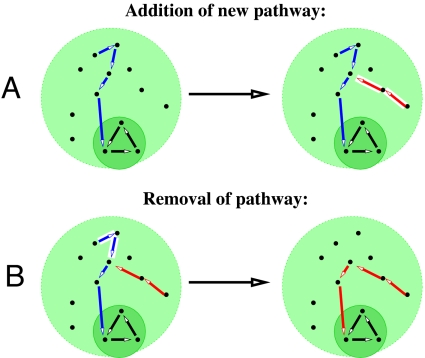
Although the toolbox view of evolution is equally applicable to catabolic (breakdown of nutrients) and anabolic (synthesis of complex metabolites) pathways, for simplicity we will simulate only addition and removal of catabolic branches. Given the repertoire of enzymes of an organism each of the N_univ universal metabolites can be categorized as either “metabolizable” (connected to biomass production), or “nonmetabolizable” (currently outside of the metabolic network). To add a new branch to the network in our model, we first randomly choose a nonmetabolizable molecule as a new nutrient (leaf). A pathway/branch that begins at the leaf and connects it to the set of metabolizable molecules is then added to the network. This connecting pathway consists of a linear chain of reactions randomly selected from the universal network until it first intersects with the already existing metabolic network of the organism. The leaf plus all of the intermediate metabolites of this branch thereby become metabolizable. This process is illustrated in Fig. 1A.

Fig. 1.

“Toolbox” rules for evolving metabolic networks in our model. (A) Addition of a new metabolic pathway (red) that is long enough to connect the red nutrient to a previously existing pathway (blue) that further converts it to the central metabolic core (dark green). (B) Removal of a part of the blue pathway after loss of the blue nutrient. The upstream portion of the blue pathway that is no longer required is removed down to the point where it merges with another pathway (red). The light green circle denotes all metabolites in the universal biochemistry network from which new pathways are drawn.

In our model, pathway additions and removals are treated in a symmetric fashion. The steps leading to pathway deletion are illustrated in Fig. 1B. First, 1 of the leaves of the network corresponding to a vanished nutrient is chosen randomly. The branch starting at this nutrient/leaf is followed downstream to the point where it first intersects another branch of the network. This entire path, starting from the leaf down to the merging point with another pathway is then removed from the network. The selected nutrient along with all intermediate metabolites thereby become nonmetabolizable.

The network in our model evolves by a random sequence of pathway additions and removals (see Methods for more details). Because our goal is to understand how properties of metabolic and regulatory networks scale with the genome size of an organism, we take multiple snapshots of the evolving network with different values of N_met—the current number of nodes in the metabolic network, which in our model is equal to the number of reactions or metabolic enzymes.

Assigning Transcriptional Regulators to Metabolic Pathways.

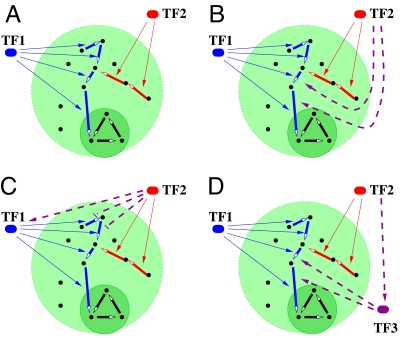
Operation of metabolic networks involves regulating production of enzymes in response to nutrient availability. In prokaryotes, most of this regulation is achieved at the transcriptional level. To investigate the interface between metabolic and regulatory networks, we extend our model to include transcription factors (TFs) that are activated by nutrient availability to turn on or off the enzymes in individual metabolic pathways. In the basic version of our model shown in Fig. 2A, we chose the following simple method to assign TFs to reactions: One randomly picks a leaf/nutrient and follows its reactions downstream until this branch either reaches the metabolic core or merges with a pathway regulated by a previously assigned TF. A new TF is then assigned to regulate all reactions in this part of the nutrient utilization pathway. This process is repeated until all enzymes/reactions have been assigned a (unique) transcriptional regulator. Each TF is activated by the presence of the corresponding nutrient in the environment. Note that this method results in exactly 1 TF per nutrient, and that the out-degree distribution of TFs in the regulatory network is identical to the distribution of branch lengths in the metabolic network.

Fig. 2.

Schematic diagrams illustrating several possible regulatory network architectures for control of metabolic enzymes/pathways. Four panels correspond to different versions of our model discussed in the article. (A) In the basic model there is no coordination of activity between red and blue metabolic pathways. (B–D) More realistic models include extra regulatory interactions (purple dashed lines) and transcription factors (purple TF3 in D), ensuring that only the part of the blue pathway necessary for utilization of the red nutrient is turned on by the corresponding transcription factor (red TF2).

In addition to this simple regulatory network architecture, we have tried several others illustrated in Fig. 2 B–D. The advantage of these more complicated schemes is that they ensure that on/off states of connected metabolic pathways are properly coordinated with each other. For example, unlike in Fig. 2A, in Fig. 2 B–D, the transcription factor of the red pathway (TF2) turns on the downstream (and only the downstream) part of the blue pathway necessary for utilization of the red nutrient. We will further compare network topologies generated by these rules in Discussion.

Comparison of the Model with Empirical Data.

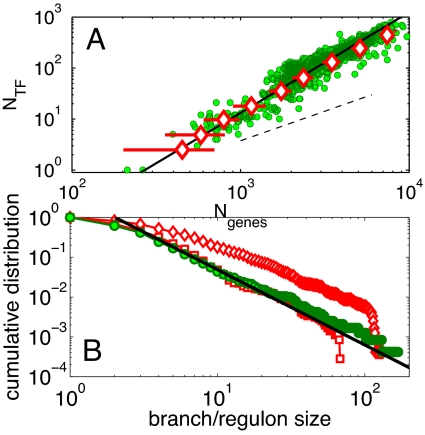
In agreement with the toolbox argument outlined in the Introduction, we found (see Fig. 4A) that the number of transcriptional regulators of an organism scales steeper than linearly with the total number of metabolites in its metabolic network, which in our model is equal to its number of reactions or enzymes:

The best fit has α = 1.8 ± 0.2. In Fig. 4A we directly compare numerical simulations of the toolbox model (red diamonds) to the empirical scaling of the number of transcription factors with the number of genes in all currently sequenced prokaryotic genomes (green circles). To approximate the total number of genes N_genes in our model genome, we multiplied the number of metabolites/reactions N_met by a constant factor. The empirical value of the ratio N_met/N_genes ≈0.2 was estimated as follows: Metabolic enzymes constitute approximately a quarter of all genes in a prokaryotic genome independent of its size (see blue line in figure 1A of ref. 4). Because of the presence of isoenzymes, the number of different reactions catalyzed by these enzymes (equal to the number of metabolites N_met in our model) is somewhat smaller and its average value all currently sequenced prokaryotic genomes (14) is 20%. The model results in Fig. 4 were simulated on the universal network formed by the union of KEGG reactions in all organisms. However, a model simulated on a random universal network of the same size N_univ ≃ 1,800 produced essentially identical results (black crosses in Fig. S3). This agreement indicates that the scaling between N_TF and N_met for the most part is determined by just the number of universal metabolites—N_univ and is not particularly sensitive to the topology of connections between them. On the other hand, we believe that nearly precise agreement of the actual number of regulators in real prokaryotic genomes and in the model is coincidental. Indeed, even in prokaryotes, not all transcription factors are dedicated to regulation of metabolic enzymes. This means that to represent all TFs in the whole genome the number of metabolic TFs in our model has to be multiplied by a currently unknown number. Furthermore, as discussed in the beginning of the Results section the effective size of the universal network for real-life horizontal transfer of metabolic pathways is likely to be different from the union of all reactions currently listed in KEGG. We still believe that the KEGG-based universal network provides a correct order-of-magnitude estimate of N_univ. Hence, the approximate agreement between N_TF vs. N_genes plots in our model and real prokaryotic genomes is an encouraging sign.

Fig. 4.

Scaling plots in real and model networks. (A) The number of transcription factors scales approximately quadratically with the total number of genes in real prokaryotic genomes (8, 27) (green) and our model (red) simulated on the KEGG universal network with N_univ = 1,800. The number of metabolic reactions in the model was rescaled to approximate the total number of genes in a genome (see Results for more details). Error bars correspond to data scatter in multiple simulations of the model. The solid line with slope 2 is the best power-law fit to the scaling in real prokaryotic genomes (the best fit to our model is 1.8 ± 0.2), whereas the dashed line with slope 1 is shown for comparison to emphasize deviations from linearity. (B) Cumulative distributions of pathway/branch lengths in the E. coli metabolic network (green circles) and our model of comparable size (red symbols) have similar tail exponents. The negative slope of the best power-law fit γ − 1 = 1.9 ± 0.2 (solid line) is consistent with our analytical result γ = 3 (see text for details). The toolbox model with N_met = 400 was simulated on universal networks of KEGG reactions with N_univ = 1,800 (red diamonds) and N_univ = 900 (red squares) nodes.

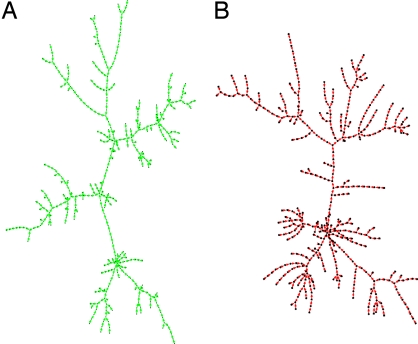
In addition to providing an explanation to the quadratic scaling between numbers of leaves and all nodes, our model nicely reproduces the large-scale topological structure of real-life metabolic networks. An example of a metabolic network generated by the toolbox model is shown in Fig. 3B. Its tree-like topology reflects our simplification that each reaction converts a single substrate to a single product. The network is hierarchical in the sense that smaller linear pathways tend to be attached to progressively longer and longer pathways until they finally reach the metabolic core. This architecture is reminiscent of drainage networks in which many short tributaries merge to give rise to larger rivers. For comparison, in Fig. 3A we show a tree-like backbone (to match linear pathways in our model) of the E. coli metabolic network (8, 14) of approximately the same size as the model network in Fig. 3B. The details of generating this backbone are described in Methods. The overall topological structure of real and model networks clearly resemble each other.

Fig. 3.

Visual comparison of a real-life metabolic network with that generated by our model. (A) The backbone of the metabolic network in E. coli (8) located upstream of the central metabolism (green). (B) A similarly sized model network (red). Note the hierarchy of branch lengths in both images in which shorter pathways tend to be attached to progressively longer pathways. The branch length distributions in real and model networks are shown as green circles and red squares in Fig. 4B.

To better quantify this visual comparison in Fig. 4B, we compare cumulative branch length distributions P (K_out ≥ K) in our model with N_met = 400 (red diamonds for N_univ = 1,800 and red squares for N_univ = 900) and in real metabolic network in E. coli of comparable size (green circles). All 3 distributions are characterized by a long power-law tail: P (K_out) ≈ K_out^−γ. The best-fit value of the exponent γ = 2.9 ± 0.2 is similar in model and real-life networks and agrees with our analytical result γ = 3 derived in the next section. Furthermore, the data in our model simulated on a truncated universal network with N_univ = 900 (red squares in Fig. 4B calculated for the network shown in Fig. 3B) are in excellent agreement with their real-life counterpart in E. coli (green circles in Fig. 4B calculated for the green network in Fig. 3A) throughout the whole range.

In Fig. S5 we compare distributions of regulon sizes (branch lengths) in our model (red diamonds in Fig. 4B) and in the Regulon database (15) including all presently known transcriptional regulations in E. coli. One can immediately see that the tail of the distribution in the Regulon database has the exponent ≃ 2 and, therefore, considerably broader than γ = 3 in our model. There are several possible explanations of this discrepancy: (i) coordination of activity of different metabolic pathways with each other as shown in Fig. 2 B–D inevitably increases out-degree of transcription factors and gives rise to larger regulatory hubs; (ii) regulation of proteins other than metabolic enzymes in the same regulon; (iii) an anthropogenic effect in which better studied transcription factors included in the Regulon database have larger-than-average out-degrees. In Discussion, we return to comparison between real-life and model regulatory networks in more detail.

Mathematical Derivation of Scaling Behavior in Toolbox Model.

When a new nutrient (leaf) is added to a network of size N_met, the length of the metabolic pathway required for its utilization is (on average) inversely proportional to N_met. This result is easy to show for a mean-field version of the model on a randomly generated universal network. In this case, each reaction in the new pathway has the same probability p = N_met/N_univ to end in one of the N_met currently metabolizable molecules. The minimal pathway required for utilization of the new nutrient involves only the reactions until the first intersection with the already existing metabolic network. The average length of such pathway is just the inverse of this probability: 1/p = N_univ/N_met. When this pathway is added, the number of metabolizable molecules increases by ΔN_met = N_univ/N_met and the number of regulators increases by 1: ΔN_TF = 1. In the steady state of the model, removal of a branch produces the opposite result: ΔN_met = −N_univ/N_met, ΔN_TF = −1. In both cases one has:

the integration of which gives

Therefore, the quadratic scaling between N_TF and N_met naturally emerges from our toolbox model.

Similar calculations allow one to derive the scale-free distribution of branch lengths (regulon sizes) in our model:

with γ = 3. Indeed, the expected length of a newly added metabolic pathway (or the out-degree of its regulator in transcription regulatory network shown in Fig. 2A) is K_out = N_univ/N_met. As the size of the metabolic network increases, the length of each newly added pathway progressively shrinks. If the network was monotonically growing, longer pathways of length K_out ≥ K were added at the time when the number of metabolites was smaller than N_univ/K or equivalently the number of transcription factors was <N_univ/(2K²). Therefore, P (K_out ≥ K) = N_univ/(2K²)/N_TF or P (K_out = K) ≈ N_univ/(N_TFK³) so that γ = 3 in Eq. 4. As evident from Fig. 4B, random cycling through addition and removal of pathways in the steady state of our model does not significantly change this exponent with best fit value of γ = 2.9 ± 0.2 shown as solid line in Fig. 4B.

Discussion

Trends of Average in- and out-Degrees in the Regulatory Network as a Function of Genome Size.

As was pointed out by van Nimwegen (4, 16, 17) faster-than-linear scaling of the number of transcription factors generates systematic differences in topology of transcriptional regulatory networks as a function of genome size. Indeed, the total number of regulatory interactions (edges between TFs and their target genes) in a given organism can be written either as N_genes〈K_in〉 if one counts the incoming regulatory inputs of all genes, or as N_TF〈K_out〉 if one counts the regulatory outputs of all transcription factors. Here, the brackets denote the average over a given genome. Therefore, one always has

The empirical data (3, 4) indicate that the left-hand side of this equation monotonically grows with genome size and is approximately proportional to N_genes. Therefore, an increase in the number of genes in larger genomes must be accompanied either by an increase in average in-degree 〈K_in〉 of all genes or by a decrease in average out-degree 〈K_out〉 of transcriptional regulators. The latter trend is indirectly supported by the empirical observation (16) that the average operon size (a lower bound on regulon size) is negatively correlated with N_genes. This trend also exists in our basic model (Fig. 2A) in which K_out of transcription factors regulating newly added metabolic pathways progressively decreases with N_met ≈ N_genes. Furthermore, another recent study (17) found no systematic correlation between 〈K_in〉 and N_genes. This is the case in our model in Fig. 2A where all enzymes representing the vast majority of all proteins in our model have the same K_in = 1 independently of genome size. However, such complete lack of coordination between different metabolic pathways is not realistic. To correct this we explored several other regulatory network architectures illustrated in Fig. 2 B–D. In all these models enzymes are regulated by more than 1 transcription factor. Transcription factors in the model in Fig. 2B ensure complete top-to-bottom regulation of the entire pathway for utilization of each nutrient. In this case centrally positioned metabolites have unrealistically large in-degrees. Opposite to the basic model in Fig. 2A, the average in-degree 〈K_in〉 in Fig. 2B increases with N_genes, whereas 〈K_out〉 remains constant. Real-life regulatory networks are likely to be somewhere in-between these 2 extreme scenarios illustrated in Fig. 2 A and B.

Coordination of Activity of Upstream and Downstream Metabolic Pathways.

Converting a nutrient into biomass of an organism often involves several successive pathways each regulated by its own transcription factor. States of activity of such pathways have to be coordinated with each other. Our basic model illustrated in Fig. 2A does not involve such coordination. In this model:

• Transcription factors do not regulate other transcription factors. This results in “shallow” transcriptional regulatory networks consisting of only 2 hierarchical layers: the upper level including all regulators, and the lower level including all workhorse proteins (metabolic enzymes). Although this assumption in its pure form is certainly unrealistic, it approximates the hierarchical structure of real prokaryotic regulatory networks, which were shown to be relatively shallow (7, 18, 19). That is to say, the number of hierarchical layers in these networks was shown to be smaller than expected by pure chance (19).

• In the regulatory network shown in Fig. 2A every enzyme is regulated by precisely 1 transcription factor. Once again this feature, although obviously unrealistic, approximates topological properties of real-life regulatory networks, e.g., one in E. coli. In ref. 7, it was shown that in this network the in-degree distribution peaks at 1 regulatory input per protein beyond which it rapidly (exponentially) decays. This should be contrasted with a broad out-degree (regulon size) distribution (7) that has a long power-law tail reaching as high as hundreds of targets.

Several possible regulatory network architectures ensuring necessary coordination of activity of upstream and downstream pathways are shown in Fig. 2 B–D. Models shown in Fig. 2 C and D solve the coordination problem by adding regulatory interactions among transcription factors. The positive regulation TF2 → TF1 in Fig. 2C ensures that the nutrient processed by the red pathway would be converted to the central metabolism (dark green area) by the downstream part of the blue pathway.*One problem with adding the TF2 → TF1 regulation is that it stimulates some unnecessary enzyme production. Indeed, the presence of the red nutrient triggers the production of enzymes of the entire blue pathway including those located upstream of the merging point with the red pathway that are not required for red nutrient utilization. To eliminate this waste of resources, we added negative regulations of these upstream enzymes by TF2 (see Fig. 2C). Other architectures shown in Fig. 2 B and D instead of suppressing the upstream enzymes of the blue pathway exclusively activate its downstream enzymes. In Fig. 2B TFs regulate the entire length of the long path from every leaf (nutrient) all of the way down to central metabolism. Another option illustrated in Fig. 2D is to add a new TF (TF3) activated by the TF2 to regulate only the downstream part of the blue pathway. Even though the number of TFs in Fig. 2D is up to 2 times larger than the number of leaves in the metabolic network, we have verified that their quadratic scaling remains unchanged.

Transcription regulatory networks are also characterized by a large number of feed-forward loops (18). It has been also conjectured (18) that some of them serve as low-pass filters buffering against transient fluctuations in nutrient availability. Such loops could be easily incorporated in our models. One possibility would be to add regulatory interaction between TF2 and TF1 in Fig. 2B. For the model in Fig. 2D one might extend the range of TF2 to include at least part of the targets of TF3 and/or add a regulatory interaction between TF1 and TF2. Our simulations of models in Fig. 2 B–D indicate that they all give rise to very long regulons. The distribution of regulon sizes of these models shown in Fig. S6 has a tail significantly broader than the one empirically observed in E. coli (15). A detailed study of regulatory network architectures used by real-life prokaryotes to ensure coordination of activity of their metabolic pathways goes beyond the scope of this study and will be addressed in our future research.

Prokaryotic Genomes Are Shaped by Horizontal Gene Transfer and Prompt Removal of Redundant Genes.

The horizontal gene transfer (HGT) of whole modules of functionally related genes from other organisms is the likely mechanism by which new pathways are added to the metabolic network in our model. Indeed, the rules of our model imply that an organism acquires all of the enzymes necessary to use a new nutrient not one by one but in one step. Indeed, a pathway converting a nutrient to a downstream product that is disconnected from the rest of the metabolic network does not contribute to biomass production and thus confers no evolutionary advantage to the organism. The dominant role of HGT in shaping contents of prokaryotic genomes in general and their metabolic networks in particular is well documented (21). For example, a recent empirical study (11) reports that horizontally transferred enzymes

• Outnumber duplicated enzymes during the last 100 million years in evolution of E. coli.

• Frequently confer condition-specific advantages, facilitating adaptation to new environments. As a consequence, horizontally transferred pathways tend to be located at the periphery of the metabolic network rather than near its core.

• tend to come in functionally coupled groups (see also ref. 9 for a genome-wide analysis of this trend).

These empirical observations make the central assumptions of our model all the more plausible. Another feature the evolution of prokaryotic genomes used in our model is their tendency to promptly remove redundant genes. Indeed, in our model we implicitly assume that if a set of horizontally transferred genes contains some enzymes that are already encoded in the genome, these redundant copies are promptly removed. Terminating the added metabolic branch precisely at the intersection point with the existing metabolic network corresponds to the instantaneous removal of these redundant genes. We verified that this simplification could be relaxed without changing scaling exponents of the model. This is demonstrated in Fig. S4, where we simulated a version of our model assuming more realistic finite rate of removal of extra copies of genes.

Both these features (massive horizontal gene transfers and prompt removal of redundant genes) are not characteristic of eukaryotic genomes in general, and those of multicellular organisms in particular. That is consistent with our finding of approximately linear scaling of N_TF with N_genes in genomes of animals (see Fig. S7 where the best-fit exponent 1.15 ± 0.2). The best-fit exponent for all eukaryotic genomes [1.3 ± 0.2 (4)] is marginally higher and is still much lower than its value in prokaryotes (2.0 ± 0.2).

Several earlier modeling efforts (4, 22, 23) explained the quadratic scaling in terms of gene duplications followed by divergence of the resulting paralogs. Models of this type assume that additions and deletions of individual genes are, to a large degree, decoupled from their biological function. Conversely, our model is, to the best of our knowledge, the first attempt to explain this scaling relation in purely functional terms. Instead of single genes we add and delete larger functional units (metabolic pathways) and assume that they are retained by evolution only if they positively contribute to the functioning of the organism, that is to say if they get connected to its biomass production through the existing metabolic network. Also, contrary to earlier explanations (4, 22, 23), our toolbox model relies on a different evolutionary mechanism (HGT vs. gene duplications) that is predominant in prokaryotes.

How Quickly Do New Pathways Acquire Transcriptional Regulators?

In our model we assume that the regulatory network closely follows changes in the metabolic toolbox of the organism. For the sake of convenience in our simulations, we choose to assign regulators de novo to each new state of the metabolic network. To verify that this simplification does not distort our final results, we studied a variant of our model in which the transcriptional regulatory network dynamically follows changes in the metabolic network. The regulon size distribution in this model was essentially unchanged from the case where regulators were assigned de novo.

Such nearly immediate assignment of regulators to newly acquired pathways is supported by the empirical study of Price and collaborators (24) reporting that horizontally transferred peripheral metabolic pathways frequently include their own transcriptional regulators. This should come as no surprise, given many well known cases where metabolic enzymes and their regulators either belong to the same operon or are located very close to each other on the chromosome (as, e.g., the Lac repressor and the Lac operon). Our model is also full consistent with the selfish operon theory (25) stating that genomic proximity of functionally related genes is favored by evolution because it increases the likelihood of a successful horizontal transfer of a fully functional pathway.

Overall, the emerging consensus (26) is that regulatory networks in prokaryotic genomes are flexible, quickly adaptable, and rapidly divergent even between closely related strains. Thus, even in cases when a horizontally transferred pathway does not include a dedicated transcriptional regulator it could nevertheless be quickly acquired in a separate HGT event or created by gene duplication of another TF in the genome.

Materials and Methods

Numerical Simulations of the Model.

The metabolic network in our model is shaped by randomly repeating pathway addition and pathway removal steps. The boundary conditions for this stochastic process do not allow the number of metabolites to fall below 40 or exceed ≈1,600. Networks with different values of N_met are then sampled and analyzed. The universal network used in our study consists of the union of all reactions listed in the KEGG database (8). The directionality of reactions and connected pairs of metabolites are inferred from the map version of the reaction formula: ftp.genome.jp/pub/kegg/ligand/reaction/reaction_mapformula.lst. Because our goal is to model the conversion of nutrients to organism's biomass, we kept the metabolites located upstream of the central metabolism (reachable by a directed path from Pyruvate). This left us with 1,813 metabolites connected by 2,745 edges. The exact size and topological structure of the universal network is not known. To test our model on a universal network of a different size (red squares in Fig. 4B) we pruned the KEGG network down to ≈900 metabolites. This pruning was achieved by randomly removing nodes along with branches that got disconnected from the central metabolism. In yet another version shown in Fig. S3, the universal network linear branches were formed by random walks on the fully connected graph of N_univ = 1,800 metabolites. The metabolic network of an organism changes by:

1) Pathway addition. A new leaf (nutrient) is randomly chosen among all currently nonmetabolizable nodes and a self-avoiding random walk on the universal network. This directed walk is started at the leaf and extended until it first intersects the subset of N_met presently metabolizable molecules. The leaf plus all of the intermediate metabolites of this new branch thereby become metabolizable.

2) Pathway deletion. One of the N_TF network leaves (nutrients) is chosen randomly. The links downstream from this leaf are followed until the first merging point of 2 metabolic branches. All of the metabolites down to this merging point are removed from the network, thereby becoming nonmetabolizable.

We typically choose to begin all simulations with 20 nodes in the “metabolic core” (the dark green central circle in Figs. 1 and 2) that are already metabolizable. This core could be thought of as the “universal central metabolism” present in most organisms. The number of these core metabolites, N_core, is the second parameter of our model. However, in practice, as long as N_core ≪ N_univ, the network topological structure in the steady state does not depend on the value of N_core. In our simulations we also tried different starting sets of metabolizable molecules connected by linear branches to the core but inevitably arrived to the statistically identical steady-state networks.

Sources of Empirical Datasets.

The distribution of branch lengths in Fig. 2A was calculated as follows: First a leaf was randomly chosen and followed to the metabolic core. Subsequent branches were followed until the merging point with another branch that was previously selected. In the metabolic network of the K-12 strain of E. coli leaves were defined as either (i) having zero in-degree (no production within the organism) or (ii) having an undirected degree of 1 (end points of linear branches formed by reversible reactions). The backbone of the E. coli network was defined by following random linear paths starting at these leaves and ending at the intersection with each other or at the metabolic core. This left us with the network in Fig. 3A of ≈420 metabolite nodes (including 112 leaves) located upstream of the central metabolism (8).

To estimate the number of transcription factors in different genomes shown in Fig. 4A (green symbols), we used the DBD database (27) (www.transcriptionfactor.org) with its manually curated list of 147 Pfam families of transcription factors. The resulting values of N_TF are in good agreement with those obtained in earlier studies (3–6).