Methods for Equivalence and Noninferiority Testing

Abstract

Classical hypothesis testing focuses on testing whether treatments have differential effects on outcome. However, sometimes clinicians may be more interested in determining whether treatments are equivalent or whether one has noninferior outcomes. We review the hypotheses for these noninferiority and equivalence research questions, consider power and sample size issues, and discuss how to perform such a test for both binary and survival outcomes. The methods are illustrated on 2 recent studies in hematopoietic cell transplantation.

INTRODUCTION

Most studies of factors affecting outcome in hematopoietic stem cell transplantation (HSCT) are based on a classical hypothesis testing formulation. In this formulation the investigator poses the question “do these factors have differential effects on outcome”? The tests are designed to protect the null hypothesis that the factors have no influence on survival or whatever outcome is of primary interest. The tests are designed to make decisions about a difference in outcome which is indicated by a small P-value. When the P-value is large in many cases investigators conclude incorrectly that the factor has no effect on outcomes. No evidence of a difference in such studies may be a result of inadequate sample sizes, small treatment differences or simply chance.

As an example of this problem, consider the recent study of the effects of HLA matching on unrelated donor transplants [1]. Here, classical hypothesis testing asks questions like “does a patient with a 7/8 donor transplant have different survival then one with an 8/8 donor?” or “Is the survival different for a patient if they had a 7/8 A mismatched donor than if they had a 7/8 B mismatched donor?” What may be of more clinical interest is whether a 7/8 donor can be substituted for an 8/8 donor, so that the primary question is either “Do patients with a 7/8 and 8/8 donor have equivalent survival” or “Do patients with 7/8 donors have survival which is not inferior to an 8/8 donor.” We could ask similar questions about the choice of which loci a 7/8 donor was mismatched at.

Another example is a study to compare peripheral blood stem cells (PBSC) versus bone marrow (BM) as a cell source for unrelated donor transplants for patients with leukemia undergoing myeloablative transplants [2]. The advantage of peripheral blood over BM is that the collection is easier for the donor, because no anesthesia, hospitalization, and potential exposure to blood products is needed. Studies in related donors have indicated faster engraftment for PBSC, along with potentially greater graft-versus-host disease (GVHD) burden and lower relapse risk. Given the GVHD burden of PBSC, clinicians may be interested in learning whether BM is not inferior to PBSC in terms of survival.

Clinical trials are often conducted with new experimental treatments or therapies that may reduce side effects, costs, or have another advantage over the usual standard treatment. In these situations, the new treatment is often compared to the standard with the aim of showing it is therapeutically equivalent or not inferior. A new treatment is called equivalent if its outcome does not differ from that of the standard therapy by more than a prespecified clinically significant amount, although it is called noninferior if its outcome is no worse than that of the standard by a prespecified amount. These types of studies require that we reformulate hypotheses and that we look at testing in a different light.

Noninferiority and Equivalence Hypotheses for a Binary Endpoint

For simplicity, we will discuss tests that have a single binary outcome (success or failure). This outcome could be engraftment, GVHD, or death at some time. If we are interested in a specific time (eg, survival at 1 year or engraftment at 100 days), the outcome for each patient is his/her status (dead/alive or engraftment/no engraftment), so that we have a binary endpoint. We assume that there is no censoring, so that the status for each patient is known at the time of interest. Formulation of the hypotheses depends on whether we focus on the probability of a good outcome (survival, engraftment) or the probability of a bad outcome (GVHD, death). First we focus on the former, where p_T and p_C are probabilities of a good outcome (eg, survival, engraftment) in the treatment group and control group, respectively.

The hypotheses for noninferiority and equivalence can be stated in terms of a number of different measures of relative efficacy. The most commonly used ones are the difference in proportions D = p_T − p_C or the odds ratio

$$OR=\frac{p_T}{(1-p_T)}\frac{(1-p_C)}{p_C}.$$

We shall first consider the difference of proportions D. Recall that the classical hypothesis testing framework tests the null and alternative hypotheses

$$\begin{array}{l}{\text{H}}_0:D=p_T-p_C=0\\ {\text{H}}_A:D=p_T-p_C\ne 0.\end{array}$$ (1)

The null hypothesis says that there is no difference between the treatment and the control, and we are trying to show that there really is a difference (the alternative hypothesis). Here we control the probability of a type I error (often at 5%), which is the chance that we incorrectly reject the null hypothesis, or conclude that there is a difference when, in fact, there really is no difference in outcomes. This control of the type I error rate protects us against incorrectly identifying a difference between the 2 treatments when they are the same. However, note that when we are testing the hypothesis given by (1) and if we fail to reject the null hypothesis, we cannot conclude that the treatments are equivalent, we only can say that there is not enough evidence to show a difference between the treatments. Formal establishment of noninferiority or equivalence requires testing of a different set of hypotheses as well as prespecification of an equivalency threshold as described below.

The hypotheses for noninferiority are reversed somewhat from this classical formulation. The hypotheses for noninferiority in this situation are

$$\begin{array}{l}{\text{H}}_0:D=p_T-p_C\le -\delta \\ {\text{H}}_A:D=p_T-p_C>-\delta ,\end{array}$$ (2)

where δ > 0 is the noninferiority margin of clinical interest. Here, the null hypothesis is stating that the treatment success rate is at least an amount δ worse than the control success rate, whereas the alternative hypothesis that we want to prove is stating that the treatment is noninferior. Noninferiority here means that the treatment rate can be no worse than δ lower than the control rate. For example, if the treatment is cells from a 7/8 donor and the control is cells from a 8/8 donor, p the probability of 1-year survival and δ = 0.1, we would say that the 7/8 donor transplant was noninferior to an 8/8 donor if the 1-year survival probability is no more than 10% lower with the 7/8 donor than with an 8/8 donor.

The type I error rate for these tests is now the likelihood that we conclude the treatment group is not inferior to the control, when in fact it really is inferior. When we control the type I error for these noninferiority hypotheses, we are protecting against incorrectly concluding noninferiority for the treatment group compared to the control group.

Note that these noninferiority hypotheses require that one define a noninferiority margin. This noninferiority margin should be based on clinical judgment and it has the interpretation of how close the new treatment must be to the control to be considered equivalent (or noninferior). The choice of the margin δ is a critical issue and a difficult task [3–5]. As pointed out by Rousson et al. [5], when the hypotheses are stated in terms of the difference D, the value of δ may depend on the value of the control group probability of success p_C. The margin δ should be smaller than p_C because it makes no sense to test if p_T is greater or smaller than a negative number. This may be viewed as a disadvantage over stating the hypotheses in terms of the odds ratio. We explore the relationship between the noninferiority margin and the scale of the treatment effect in a later section.

The noninferiority hypotheses above apply when we define the probabilities p_T and p_C as probabilities of a good outcome. However, if p_T and p_C refer to probabilities of a bad outcome (GVHD or death), then the directions of the inequalities need to be switched around. This reflects the fact that noninferiority now means that the treatment outcome probability is not much higher than the control outcome. The correct specification of the noninferiority hypothesis would be

$$\begin{array}{l}{\text{H}}_0:D^{\ast }=p_T^{\ast }-p_c^{\ast }\ge {\delta }^{\ast }\\ {\text{H}}_A:D^{\ast }=p_T^{\ast }-p_c^{\ast }<{\delta }^{\ast }.\end{array}$$

In many situations, an equivalence test is more appropriate than a noninferiority test. For such tests we want to show that the treatment and control outcomes are within a specified amount of one another in either direction. The equivalence hypotheses are

$$\begin{array}{l}{\text{H}}_0:D=\mid p_T-p_C\mid \ge \delta \\ {\text{H}}_A:D=\mid p_T-p_C\mid <\delta ,\end{array}$$ (3)

where δ > 0 is the margin of clinically accepted difference. Here, the null hypothesis states that the treatment success proportion is different from the control proportion by at least an amount δ, whereas the alternative hypothesis states that it is equivalent (within δ of the control proportion). The type I error rate is the likelihood that we conclude the treatments are equivalent when in fact they are not.

Noninferiority and Equivalence Tests and Confidence Intervals for a Binary Endpoint

Assume initially that we are interested in testing the noninferiority hypothesis (2). Following Laster et al. [6], the test statistic used for this test is very similar to the usual test for proportions; the only difference is that we need to add the non inferiority margin δ in the numerator. The test statistic for testing (2) is then given by

$$z=\frac{({\widehat{p}}_T-{\widehat{p}}_C+\delta )}{\sqrt{\frac{{\widehat{p}}_T(1-{\widehat{p}}_T)}{n_T}+\frac{{\widehat{p}}_C(1-{\widehat{p}}_C)}{n_C}}},$$ (4)

where p̂_T and p̂_C are the observed proportions of success in the treatment and control groups, respectively, n_T and n_C are the sample sizes of the corresponding groups. For large enough sample sizes, this test statistic has a standard normal distribution under the null hypothesis. Thus, noninferiority is concluded at the level α if z > z_1−α, where z_1−α is the (1−α)-percentile of a standard normal distribution. The noninferiority P-value is given by P_NI = 1 − Φ(z), where Φ (z) is the probability that a standard normal random variable is less than z.

An equivalent way of verifying noninferiority is by computing a 1-sided confidence interval for the difference in proportions and rejecting the null hypothesis if −δ is below the confidence bound. More precisely, following Phillips [7], the 1-sided lower confidence bound for the difference is given by

$$LB={\widehat{p}}_T-{\widehat{p}}_C-z_{1-\alpha }\sqrt{\frac{{\widehat{p}}_T(1-{\widehat{p}}_T)}{n_T}+\frac{{\widehat{p}}_C(1-{\widehat{p}}_C)}{n_C}}$$

and the null hypothesis is rejected if LB > −δ. Note that LB is the lower limit of the usual 2-sided interval where we use a confidence coefficient of (1 − 2α) × 100% (ie, we use z_1−α) rather than the usual (1 − α) × 100% (ie, z_1−α/2) confidence interval. For example, if we are testing for noninferiority with a 5% significance level, we would construct a 90% 2-sided confidence interval and use the lower bound to determine noninferiority.

Two-sided confidence intervals are usually useful in equivalence testing, where one is interested in the composite hypothesis (3). The equivalence hypothesis is often tested by comparing the (1 − 2α) × 100% confidence limits of the difference in proportions with the limits (−δ;δ) and the null hypothesis is rejected (ie, equivalence is claimed) if the entire interval falls within (−δ;δ).

This confidence interval approach is operationally the same as conducting 2 tests with hypothesis given by

$$\begin{array}{l}{\text{H}}_{0L}:D=p_T-p_C\le -\delta \\ {\text{H}}_{AL}:D=p_T-p_C>-\delta \end{array}$$ (5a)

and

$$\begin{array}{l}{\text{H}}_{0U}:D=p_T-p_C\ge \delta \\ H_{AU}:D=p_T-p_C<\delta .\end{array}$$ (5b)

The test statistic for (5a) is the same as that given in (2); however, the test statistic for (5b) is:

$$z=\frac{({\widehat{p}}_T-{\widehat{p}}_C-\delta )}{\sqrt{\frac{{\widehat{p}}_T(1-{\widehat{p}}_T)}{n_T}+\frac{{\widehat{p}}_C(1-{\widehat{p}}_C)}{n_C}}}$$ (6)

and we reject that null hypothesis if z < z_α. In order to be equivalent to the confidence interval method, the critical region for both 1-sided tests must be constructed based on a significance level equal to α (Lewis [8]).

Power and Sample Size Considerations for Binary Outcomes

Power has a different interpretation when we are doing noninferiority testing than when we are performing a traditional hypothesis test. In the classical hypothesis testing framework, power refers to the likelihood that we correctly conclude the treatments are different. In the noninferiority setting, power refers to the likelihood that we correctly conclude the treatment is noninferior, when it really is noninferior. Power depends both on the noninferiority margin δ and the true difference in proportions ε, between the treatment and control arms. To evaluate power when the treatment is considered noninferior, we usually assume that the treatment and standard have the same outcomes, so that ε = 0. In the balanced case with n_T = n_c = n, the sample size required to have a prespecified power 1 − β is given by

$$n=\frac{2{(z_{1-\alpha }+z_{1-\beta })}^2{p}_C(1-p_C)}{{\delta }^2}$$

where z_β is the value such that Φ(z_1−β) = 1 − β. For the common values of α = 0.05 and β = 0.2, this reduces to

$$n=\frac{12.35p_C(1-p_C)}{{\delta }^2}.$$

Note that this formula looks similar to the sample size formula for the usual testing problem, except that the true difference, ε used in the usual formulation, is replaced by the noninferiority margin δ. This is an important difference. Often researchers plan a study to detect a 20% difference in success rates with 80% power, for example, so that ε = 0.2. However, a margin for considering a treatment noninferior might be much smaller, say δ = 5% or 10%. This narrower margin results in the generally larger sample sizes often associated with noninferiority testing.

For equivalence testing, the formula for computing the sample size is similar, but an adjustment must be made because we are actually performing two 1-sided tests (see Farrington [9]):

$$n_{eq}=\frac{2{(z_{1-\alpha }+z_{1-\beta /2})}^2{p}_C(1-p_C)}{{\delta }^2}.$$

Notice that the adjustment is made on the normal percentile corresponding to the power: we use now z_1−β/2 instead of z_1−β.

Table 1 illustrates examples of sample sizes per treatment arm required to determine noninferiority and equivalence for a variety of settings, using p_C = 0.5. (Note that p_C is a worst case scenario because p_C (1 − p_C) has its largest values when p_C = 0.5). In Table 2 we show the minimum δ that should be used in order to have an 80% or 90% power to detect noninferiority for 2 different values of p_C (0.5 and 0.9). Note that the value of δ is smaller when p_C is farther from 1/2. It is also interesting to see that to use the very liberal ±10% cutoff for equivalence we need over 856 patients (428 per arm) to have just an 80% chance of showing equivalence. The usual test of the hypothesis (1), on the other hand needs only a sample size of 776 (388), a savings of 80 patients to have 80% power to detect a 10% difference in probability when p_C = 1/2 and p_T = 0.6.

Table 1.

Sample Sizes per Treatment Arm for Different Powers and α = 5%

Power	δ	Sample Size Noninferiority	Sample Size Equivalence
80%	0.010	30,876	42,778
	0.025	4940	6844
	0.050	1235	1711
	0.075	549	761
	0.100	309	428
	0.150	137	190
90%	0.010	42,778	54,120
	0.025	6844	8659
	0.050	1711	2165
	0.075	761	962
	0.100	428	541
	0.150	190	241

Table 2.

Minimum δ needed to be Used in Order to Have an 80% or 90% Power, for Different Sample Sizes per Treatment Arm

	Noninferiority				Equivalence
	pC = 0.5		pC = 0.9		pC = 0.5		pC = 0.9
Sample Size	80% Power	90% Power	80% Power	90% Power	80% Power	90% Power	80% Power	90% Power
50	0.249	0.293	0.149	0.176	0.293	0.329	0.176	0.197
100	0.176	0.207	0.105	0.124	0.207	0.233	0.124	0.140
150	0.144	0.169	0.086	0.101	0.169	0.190	0.101	0.114
200	0.124	0.146	0.075	0.088	0.146	0.164	0.088	0.099
300	0.102	0.119	0.061	0.072	0.119	0.134	0.072	0.081
500	0.079	0.093	0.047	0.056	0.093	0.104	0.056	0.062
800	0.062	0.073	0.037	0.044	0.073	0.082	0.044	0.049
1200	0.051	0.060	0.030	0.036	0.060	0.067	0.036	0.040
1500	0.045	0.053	0.027	0.032	0.053	0.060	0.032	0.036
2000	0.039	0.046	0.024	0.028	0.046	0.052	0.028	0.031
3000	0.032	0.038	0.019	0.023	0.038	0.042	0.023	0.025

Noninferiority and Equivalence Hypotheses in Terms of Odds Ratio

The hypothesis may be stated in terms of the odds ratio instead of the difference D. The use of the odds ratio has some advantages over the difference D: it takes values between zero and infinity for any value of p_C, so that the choice of the margin does not depend on p_C; it is symmetric when success and failure are interchanged. The hypotheses for noninferiority in terms of the odds ratio are given by

$$\begin{array}{l}{\text{H}}_0:OR\le {\delta }_{OR}\\ {\text{H}}_A:OR>{\delta }_{OR},\end{array}$$ (7)

where 0 < δ_OR < 1 is the clinically significant odds ratio margin, and assuming that we are focusing on the odds of a good outcome such as survival or engraftment. For equivalence testing we consider the hypotheses (for δ_OR < 1)

$$\begin{array}{l}{\text{H}}_0:OR\le {\delta }_{OR}\text{or}OR\ge 1/{\delta }_{OR}\\ {\text{H}}_A:{\delta }_{OR}<OR<(1/{\delta }_{OR}).\end{array}$$ (8)

Several authors have suggested values for δ_OR. For example, the suggestion made by Senn [10] is δ_OR = 0.55, so that the maximum possible noninferiority difference between the 2 proportions of success is 0.15. Note that a particular noninferiority margin on the odds ratio scale will have different corresponding noninferiority margins on the difference in proportions scale, depending on the success proportion in the control arm. This relationship between the noninferiority margins on different scales is shown in Figure 1. For each of several noninferiority margins on the difference scale, δ, the corresponding odds ratio noninferiority margin δ_OR is plotted against the control proportion p_C. For example, if we considered 10% an appropriate difference noninferiority margin, the corresponding odds ratio noninferiority margin would range from approximately 0.45 when p_C is 0.2 to approximately 0.65 when p_C = 0.5. Therefore, one must be very careful in selecting an appropriate noninferiority margin on the odds ratio scale, to ensure that it is clinically appropriate.

Figure 1.

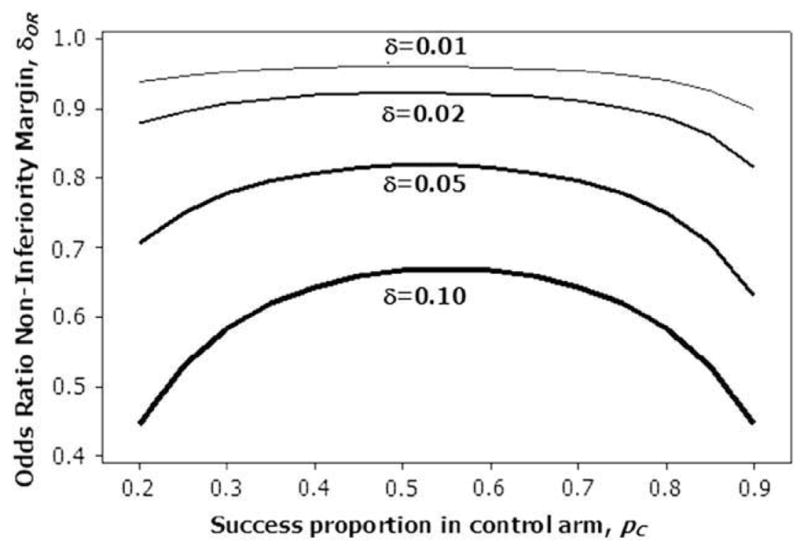
Relationship between noninferiority margin on the odds ratio scale, δ_OR, and the margin on the difference scale, δ.

Noninferiority or equivalence testing can be easily adapted to the odds ratio scale using the confidence intervals approach described previously. First construct a (1 − 2α) level confidence interval for the odds ratio. Then if the confidence interval is entirely above δ_OR one could conclude noninferiority at the α significance level. Similarly, if the confidence interval is entirely between δ_OR and 1/δ_OR, one could conclude equivalence at the α significance level.

Noninferiority and Equivalence for Survival Outcomes

In many situations, it is of interest to show noninferiority or equivalence of treatments in terms of survival probabilities. Frequently, the assessment of noninferiority for survival time data is reduced to a comparison of survival probabilities at a single time point τ. If data is not censored, then methods for binary outcomes can be applied. However, usually survival data is right censored and the methods for testing noninferiority must account for censoring.

For censored data, noninferiority can be tested using the Kaplan-Meier estimator of the survivor functions of the 2 groups at a single fixed time point τ, as suggested by Com-Nougue [11]. Let S_T(t) denote the survival function of the new treatment group and S_C(t) the survival function of the control group. The hypotheses for testing noninferiority are exactly as in (1) with p = S(τ)

$$\begin{array}{l}{\text{H}}_0:d(\tau )=S_T(\tau )-S_C(\tau )\le -\mathrm{\Delta }\\ {\text{H}}_A:d(\tau )=S_T(\tau )-S_C(\tau )>-\mathrm{\Delta }.\end{array}$$ (9)

Confidence intervals for the difference in survival proportions to test either noninferiority or equivalence are constructed using standard survival analysis techniques [12] with modified confidence levels as discussed above for binary endpoints. Test statistics for noninferiority and equivalence hypotheses are similar to the ones presented for binary outcomes, only using the Kaplan-Meier estimator of the survival proportion and replacing the variance estimator in the denominator by the Greenwood’s variance estimator of the survival function. If one is interested in adjusting for covariates, one can model the odds ratio for survival at time τ using a pseudovalue regression technique [13–15] with a logit link function, and use the confidence interval techniques described previously for odds ratios to test noninferiority or equivalence. The same caveats about the choice of noninferiority threshold on the odds ratio scale hold here as well.

The noninferiority or equivalence hypothesis can also be stated in terms of the relative risk. This can be a useful way of testing for noninferiority when adjusting for covariates that may be different between the treatment group and control group. Let h_T(t) and h_C(t) be the hazard rates at time t for the groups to be compared. The relative risk of failure is given by r(t) = h_T(t)/h_C(t). Testing noninferiority or equivalence using a relative risk threshold is appropriate when a proportional hazards assumption holds, in which r(t) = h_T(t)/h_C(t) = r for all t. Then the hypothesis of noninferiority can be stated as

$$\begin{array}{l}{\text{H}}_0:r\ge {\gamma }_0\\ H_A:r<{\gamma }_0,\end{array}$$ (10)

where γ₀ > 1 is the acceptable upper limit for noninferiority. This is an upper bound rather than a lower bound because higher r corresponds to worse outcomes. Notice that in this case we are not comparing survival probabilities at 1 time point only, but are comparing the entire survival curves for evidence of noninferiority. The Cox proportional hazards [16] model can be used to estimate and construct confidence intervals for the relative risk. One could conclude noninferiority if the (1 − 2α) level confidence interval for the relative risk is entirely below γ₀. Similarly, one could conclude equivalence if the (1 − 2α) level confidence interval is entirely between 1/γ₀ and γ₀. If one is interested in noninferiority or equivalence at a single point in time, τ, an appropriate confidence interval for r can be constructed using the pseudo-observation approach [13] with a complimentary log-log link.

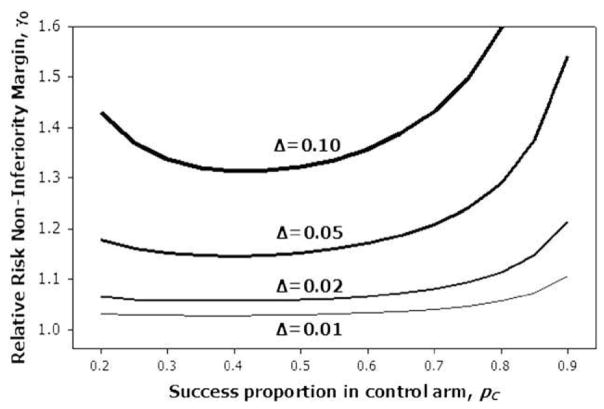
An important issue in noninferiority testing in survival outcomes is the determination of acceptable values for noninferiority thresholds Δ and γ₀. Although Δ has a direct clinical interpretation in terms of the difference in survival probabilities, the hazard ratio threshold γ₀ is not so clear. One approach is to use the relationship between the hazard ratio and the survival probabilities to determine an appropriate γ₀. When the proportional hazards model holds, the following relation is valid:

$$S_T(t)={(S_C(t))}^{\gamma }\text{or}\gamma =\frac{log(S_T(t))}{log(S_C(t))}.$$

Therefore, for a particular choice of noninferiority threshold γ₀, the equivalent noninferiority threshold on the survival probability scale depends on the survival probability for the control group. Figure 2 shows the relative risk noninferiority margins γ₀ for select survival difference noninferiority margins Δ, plotted as a function of S_C(t). For example, if we considered 10% an appropriate survival difference noninferiority margin, the corresponding relative risk noninferiority margin would range from approximately 1.3 when S_C(t) = 0.4 to approximately 1.6 when S_C(t) = 0.8. Therefore, one must be especially careful when picking noninferiority thresholds on the relative risk scale to be aware of how those noninferiority thresholds translate to the survival probability scale. These calculations assume that S_T and S_C do not depend on other covariates. If these are denoted by Z and they are modeled in the Cox model or pseudo-observation regression model assuming proportional hazards effects then the difference in survival functions at time t is

Figure 2.

Relationship between noninferiority margin on the relative risk scale, γ₀, and the margin on the survival difference scale, Δ.

$$\mathrm{\Delta }=S_o{(t)}^{exp\left\{\beta \mathbf{Z}\right\}}-{\left[S_o{(t)}^{exp\left\{\beta \mathbf{Z}\right\}}\right]}^{\gamma }.$$

EXAMPLES

Example 1: PBSC versus BM for Unrelated Donor Allogeneic Transplants

In this example, we examine whether BM is noninferior to PBSC in myeloablative unrelated donor transplantation, using the data from Eapen et al. [2]. If this is the case, the greater GVHD burden of PBSC might make clinicians less likely to use PBSC in this setting. We use a noninferiority margin of 10%, and examine treatment-related mortality (TRM), relapse, leukemia-free survival (LFS), and overall survival (OS). We first select a time point of 6 months to illustrate the procedures in a binary outcome framework, because there is no censoring prior to 6 months. We also show results for 3 years using the Kaplan-Meier probabilities. The number of patients experiencing each outcome by 6 months are shown in Table 3. The Z test statistics for LFS and OS are from equation (4); the statistics for TRM and Relapse are from equation (6). Note that the P-values for TRM, relapse, and LFS are all significant at the 5% level, indicating that BM is not inferior to PBSC on these outcomes at the 5% significance level. For OS, the P-value is 0.052, so we cannot conclude noninferiority. The 90% confidence intervals for TRM and relapse are both below 10%, indicating that these incidences for patients receiving BM are < 10% higher than for patients receiving PBSC. The 90% confidence interval for LFS is above −10%, indicating that the LFS for patients receiving BM is no more than 10% worse than the LFS for patients receiving PBSC. Analysis of longer term outcomes, such as LFS at 3 years, would require use of the Kaplan-Meier estimates. In this case, the estimates (SE) of LFS at 3 years are 32% (2%) and 31% (3%) for the BM and PBSC arms, yielding a 90% confidence interval for the difference of (−5%, 7%). This interval is entirely above −10%, indicating that BM is no more than 10% worse than PBSC in terms of 3-year LFS. Note that this comparison does not adjust for risk factors; we illustrate such techniques in the next example.

Table 3.

Results of Noninferiority Analysis for PBSC versus BM Study at 6 Months

		Number of Patients Having Each Outcome at 6 Months
	n	TRM	Relapse	LFS	OS
BM	583	187 (32%)	93 (16%)	303 (52%)	331 (57%)
PB	328	95 (29%)	58 (18%)	175 (53%)	201 (61%)
z		−2.18	−4.52	2.50	1.62
P		0.015	0.000	0.006	0.052
90% CI		(−2.1%,8.3%)	(−6.0%,2.5%)	(−7.0%,4.3%)	(−10.1%,1.1%)

TRM indicates treatment-related mortality; CI, confidence interval; LFS, leukemia-free survival; OS, overall survival.

Example 2: Choice of a 7/8 Unrelated Donor

In this example we consider the choice of a 7/8 allele matched unrelated donor for use in a transplant for leukemia. The data is from the study by Lee et al. [1] of unrelated donors who received cells from BM. In the study there were 274 cases where the donor was mismatched at the A loci only, 116 at B only, 478 at C only, and 117 mismatched at DRB1 only. Of interest is testing the equivalence of the 4 donor types in terms of 1-year survival. For illustration we will perform 6 pairwise equivalence tests with no adjustment for multiple testing.

We first look at unadjusted tests. Here we will perform the tests using a δ of 0.10 and a 5% type I error. We see in Table 4 using this rather liberal definition of equivalence that the survival of the A and C, and that of the B and C locus mismatched patients is equivalent because the corresponding 90% confidence intervals are contained in the interval (−0.1, .1). However, we cannot conclude that the A and B locus mismatched patients are equivalent, and there is no evidence of equivalence between any of the Class I mismatches and the DRB1 mismatch.

Table 4.

Unadjusted Equivalence Testing for 7/8 Matched Unrelated Donor Transplants Donor

			90% CI for Difference with
Location of Mismatch	S(1)	SE of S(1)	A	B	C
A	0.4088	0.0297
B	0.4397	0.0461	(−0.06, 0.12)
C	0.4448	0.0228	(−0.03, 0.10)	(−0.08,0.09)
DRB1	0.3846	0.045	(−0.11, 0.06)	(−0.16,0.05)	(−0.14,0.02)

We next look at the equivalence test adjusted for some covariates that influence survival. We will adjust the comparison for recipient age (0–9 n = 188; 10–19 n = 152, 20–29 n = 174, 30–39 n = 222, 40–49 n = 229, ≥ 50 n = 88), Disease stage at transplant (early n = 378, intermediate n = 410, and advanced n = 195) and recipient race (White n = 857, Black (50), Hispanic (52), or other (24)). We will fit a relative mortality model for 1-year survival based on the pseudo-observation approach and a complimentary log-log link. The model, when examining equivalence of A mismatched transplants to the other types of transplants includes a set of binary covariates describing HLA matching like X_B = {1 if donor was B mismatched only, 0 otherwise}, X_C, X_DRB1, and the usual covariates for age, race, and disease status. We will define equivalence in terms of a relative risk of the 1-year mortality being between 0.75 and 1.33 and test this hypothesis at a 5% level using a 90% confidence interval as discussed above. Here the value of .75 corresponds to about a 10% difference in 1-year survival between the donor groups when the true survival in the A group is 50%. Based on the data and the fitted model the actual maximal difference between the 1-year survival in the A arm(Treatment) as compared to the other donor choices is, for example, 0.092 for a 0–9-year-old White patient with early disease: A mismatched survival estimated at S_A(1) = 0.69, 0.105 for a 30–39-yea-old White patient with early disease, S_A(1) = 0.49, or 0.101 for a 40–49-year-old patient with advanced disease, S_A(1) = 0.21.

Table 5 shows the 90% confidence intervals for the relative risk of death at 1 year. Here we can conclude that C and B mismatches have equivalent 1-year survival.

Table 5.

Tests for Equivalence of 1-Year Survival by Donor Type Adjusted for Patient Age, Race, and Disease Status

“Control”	“Treatment”	90% Confidence Interval
A Mismatched	B Mismatched	(0.66,1.11)
	C Mismatched	(0.71,1.02)
	DRB1 Mismatched	(0.81,1.36)
B Mismatched	C Mismatched	(0.79,1.27)
	DRB1 Mismatched	(0.91,1.67)
C Mismatched	DRB1 Mismatched	(0.97,1.57)

CONCLUSION

We have shown that tests for the equivalence or noninferiority of treatments are possible in HSCT studies. In many cases these may be of greater interest than the usual hypothesis tests that simply ask if there is a difference. They may be particularly useful in deciding on alternative donors, sources of stem cells or other transplant therapies.

The simplest approach to noninferiority or equivalence is based on a modified confidence interval approach. These confidence intervals can be based on any meaningful parameter comparing the treatment and control group. Although the tests are simple in concept they are complicated by the need for larger than usual sample sizes. An additional major difficulty in applying these techniques is in defining for the parameter meaningful clinical bounds on what it means to be noninferior.