Locating the transition from periodic oscillations to spatiotemporal chaos in the wake of invasion

Abstract

In systems with cyclic dynamics, invasions often generate periodic spatiotemporal oscillations, which undergo a subsequent transition to chaos. The periodic oscillations have the form of a wavetrain and occur in a band of constant width. In applications, a key question is whether one expects spatiotemporal data to be dominated by regular or irregular oscillations or to involve a significant proportion of both. This depends on the width of the wavetrain band. Here, we present mathematical theory that enables the direct calculation of this width. Our method synthesizes recent developments in stability theory and computation. It is developed for only 1 equation system, but because this is a normal form close to a Hopf bifurcation, the results can be applied directly to a wide range of models. We illustrate this by considering a classic example from ecology: wavetrains in the wake of the invasion of a prey population by predators.

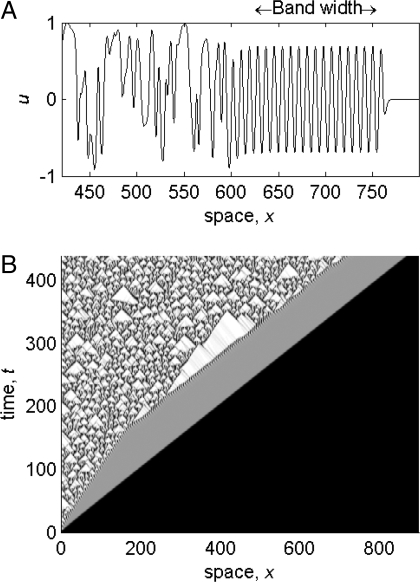
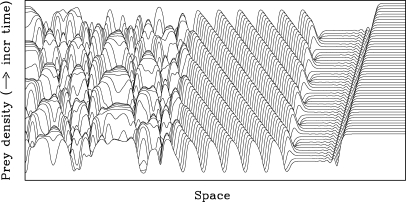
Wavetrains are a fundamental solution type in spatially extended oscillatory systems. They were observed in the Belousov–Zhabotinskii reaction >30 years ago (1), and experimental and theoretical demonstrations of their importance are now widespread, in applications including hydrodynamics (2–4), solar cycles (5), chemical reactions (6, 7), cell biology (8), and ecology (9, 10). Moreover, wavetrains provide the background state for many more complicated behaviors, including spatiotemporal chaos. A striking illustration of this is provided by the invasion of an unstable equilibrium, where a band of wavetrains can occur between the invasion front and a region of spatiotemporal chaos (Fig. 1 A). This behavior is associated with the wavetrain being unstable. Intuitively, the wavetrain is generated by the invasion process, but at the same time, unstable linear modes are excited. Immediately behind the front, the amplitude of these modes is negligible, and the wavetrain is visible; further back, the instabilities have grown larger, eventually dominating the solution at some distance behind the invasion front. Behavior of this type occurs in a range of model types including reaction–diffusion equations (11–13), the complex Ginzburg–Landau equation and generalizations (14, 15), integrodifferential equations (16), integrodifference equations (17), and cellular automata (18). The best-studied application is the invasion of a prey population by predators (9, 19). Here, the wavetrain would correspond to spatially organised multiyear population cycles, which have been observed in a number of field studies (10, 19). Simulations such as Fig. 1 B show that after an initial increase, the width of the wavetrain band remains constant as the invasion progresses. The key issue of whether wavetrains will be observed in applications depends on the value of the band width, which we calculate. We focus on 1 particular equation system, but its generic nature enables our results to be applied directly to a wide range of models spanning many application areas.

Fig. 1.

A numerical simulation of invasion in Eqs. 1, for ω₀ = 3.1, ω₁ = 3.0. At time t = 0, a small perturbation is applied near x = 0 to the unstable steady state u = v = 0. An invasive wave front spreads across the domain (at speed c _inv = 2), behind which is a wavetrain band of constant width, followed by spatiotemporal disorder. (A) u vs x at t = 385. (B) A space–time plot of amplitude r (darker shading indicates smaller r, 0 < r < 1). The boundary conditions are u _x = v _x = 0 at x = 0,900. Our numerical method is semiimplicit finite difference, with grid spacing of 0.18 and a time step of 10⁻³.

Wavetrains Behind Invasion in a Prototype Model

We develop our method for equations of “λ – ω” reaction–diffusion form:

This is the complex Ginzburg–Landau equation with a real diffusion coefficient (20). Its kinetics are the normal form of any oscillatory system of differential equations close to a standard supercritical Hopf bifurcation, making our calculations directly relevant to many models with low-amplitude cycles. Eqs. 1 are most conveniently studied in terms of amplitude r = (u ² + v ²)^1/2 and phase θ = tan⁻¹(v/u); wavetrain solutions have r = R, a constant, and θ = (ω₀ − ω₁ R ²)t ± (1 − R ²)^1/2 x, and exist for 0 ≤ R ≤ 1. The scenario we consider is local perturbation (near the left-hand boundary) of u = v = 0, on a large finite domain with zero Neumann boundary conditions. The resulting dynamics depend only on the parameter ω₁; ω₀ simply determines the rotation rate of the phase, and does not affect r or θ_x. For suitable values of ω₁ (detailed below), the solution has the form of an invasive transition wave in r, with spatiotemporal irregularities further back (Fig. 1 B). Careful numerical studies suggest that these irregular oscillations are a genuine example of spatiotemporal chaos (21). Substitution of the travelling wave ansatz $r(x,t)=\tilde{r}(x-c_{\text{inv}}t)$, $\theta (x,t)=\tilde{\theta }(x-c_{\text{inv}}t)+{\omega }_{0}t$ shows that the constant values of wave amplitude $\tilde{r}$ and phase gradient $\tilde{\theta }\text{'}$ behind the front are uniquely determined, with the wavetrain amplitude R* = [((4ω₁ ²/c _inv ² + 1)^1/2 − 1)c _inv ²/(2ω₁ ²)]^1/2 (4, 14, 22, 23). When Eq. 1 is linearized about u = v = 0, r decouples from θ to give r _t = r _xx + r, and standard theory suggests that a localized initial perturbation of u = v = 0 leads to the invasion speed c _inv = 2 (4, 22, 24); this is confirmed by numerical simulations. Our objective is to calculate the width of the region in which r ≈ R*. Numerical simulations indicate that once the solution form is established, this width remains constant as the invasion progresses (Fig. 1). Some previous studies on the complex Ginzburg–Landau equation have reported solutions in which a propagating front is followed by a wavetrain band whose width increases over time (4, 14). However, this is in fact a transient phenomenon, and longer-term simulations reveal that once the band width reaches a certain size, it then remains constant, as for Eqs. 1. Note that we restrict attention to solution times that are short enough that the invasion front remains far from the right-hand boundary (for details of longer term behavior, see ref. 25).

Stability in Moving Frames of Reference

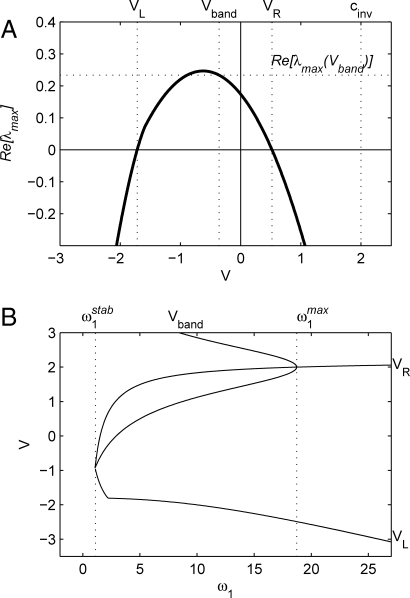
The key to understanding the width of the wavetrain band is to consider absolute stability (26) when viewed in a frame of reference moving with a fixed, arbitrary velocity V. That is, we consider whether perturbations to the wavetrain grow or decay over time when viewed at a fixed point traveling with velocity V. Perturbations that grow but simultaneously propagate at other velocities may contribute to convective instability in this frame of reference, but these are not relevant to our calculation. We denote by λ_max(V) the growth rate λ of the most unstable linear mode, with ν_max(V) being the corresponding spatial eigenvalue. Using general theory of absolute stability (26, 27), we reduce the calculation of these quantities to the numerical tracking of solutions of a quartic polynomial as parameters in the coefficients vary (see Methods). Fig. 2 A illustrates the typical form of λ_max(V). There is a range of velocities (V _L,V _R) for which λ_max > 0; all perturbations decay in frames of reference moving with velocities below V _L or above V _R. Note that in this figure, V _R < c _inv, so that all growing perturbations move away from the invasion front, resulting in a nonzero band width. One advantage of our method of calculation is that it is straightforward to monitor V _L and V _R while varying ω₁ (Fig. 2 B). V _L = V _R at the onset of wave instability, which can be shown analytically to occur at ω₁ = ω₁ ^stab = 1.0714 (for c _inv = 2) (23, 28). As ω₁ increases through ω₁ ^stab, the behavior behind invasion changes from an uninterrupted expanse of wavetrain, to spatiotemporal irregularity behind a wavetrain band. The change in sign of V _R corresponds to the onset of absolute instability in a stationary frame of reference; we compute this point as ω₁ = 1.512658 (for c _inv = 2).

Fig. 2.

(A) A typical plot of Re[λ_max(V)], the maximum growth rate of perturbations to the wavetrain in a frame of reference moving with velocity V (ω₁ = 2,c _inv = 2). (B) Plots of V _L, V _R, and V _band vs ω₁. The wavetrain becomes unstable at ω₁ = ω₁ ^stab; here V _L = V _R = V _band. As ω₁ is increased, the range of frame velocities for which the wavetrain is unstable grows, and V _band increases. At ω₁ = ω₁ ^max, the V _band curve folds, at V _band = V _R = 2, which is the invasion speed c _inv. The “kink” that is visible in the V _L curve at ω₁ = 2.20 corresponds to a triple point (see Methods). For ω₁ > 2.2, ν_max(V _L) has a nonzero imaginary part, whereas for ω₁ < 2.2 it is real.

A Formula for the Band Width

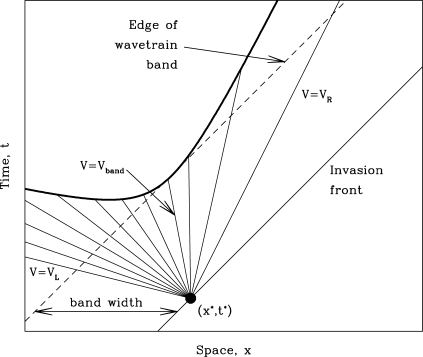
Having calculated λ_max(V), we can address the width of the wavetrain band. For this, we require a precise definition of its left-hand edge, which we take as the first point at which the perturbations to the wavetrain that are present immediately behind the invasion front become amplified by a factor ℱ. The value of ℱ is arbitrary, but we will show that the dependence of the wavetrain band width on ℱ and ω₁ decouples, having the form log(ℱ)𝒲(ω₁). We refer to 𝒲(ω₁) as the “band width coefficient.” Let (x*,t*) be a point on the invasion front. We make the generic assumption that the most unstable linear modes are present in the perturbation given to the wavetrain at such a point. As t increases above t*, these perturbations will spread out in space and time, growing along all rays x = x* + (t − t*)V with V ∈ (V _L,V _R) (a selection of such rays is sketched in Fig. 3). On any such ray, the initial perturbation becomes amplified by the factor ℱ at time t _crit(V) = t* + log(ℱ)/Re[λ_max(V)], at location x _crit(V) = x* + V log(ℱ)/Re[λ_max(V)]. The curve (x _crit(V),t _crit(V)) (V _L < V < V _R) is indicated by the thick solid line in Fig. 3. The left-hand edge of the wavetrain band occurs at the point on this curve that is closest to the invasion front x = x* + (t − t*)c _inv, which occurs at V = V _band, where

The width itself is given by

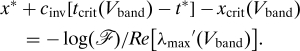We show in Methods that λ_max′(V) = ν_max(V), so that Eq. 2 is

with the band width coefficient 𝒲 = 1/Re[ν_max(V _band)].

Fig. 3.

A schematic illustration of the argument underlying our calculation of the width of the wavetrain band. The band width is defined by the point at which (x _crit(V),t _crit(V)) is closest to the invasion front, which occurs when V = V _band.

It is of course entirely expected that 𝒲 is the reciprocal of the real part of the spatial eigenvalue; our key result is Eq. 3 for the frame velocity V _band at which this eigenvalue should be calculated. The form of V _band(ω₁) is plotted in Fig. 2 B, and the corresponding width coefficient 𝒲 is shown in Fig. 4 A for a limited range of ω₁. At the onset of instability (ω₁ = 1.0714), V _band = V _L = V _R and 𝒲 = ∞. The width decreases with ω₁, through the onset of absolute stability (ω₁ = 1.512658). This transition has no particular implications for the width of the wavetrain band, though it does alter the behavior behind the band, from a pattern of sources and sinks to more comprehensive spatiotemporal disorder (29, 30). Finally, at ω₁ = ω₁ ^max = 18.72751, V _band reaches the invasion speed c _inv = 2. At this point, V _R = 2 also, and the V _band(ω₁) curve folds; there is another branch of solutions of Eq. 3 with values greater than V _R, which has no practical relevance. For ω₁ > ω₁ ^max, perturbations to the wavetrain can actually outrun the invasion, so that there is no wavetrain band.

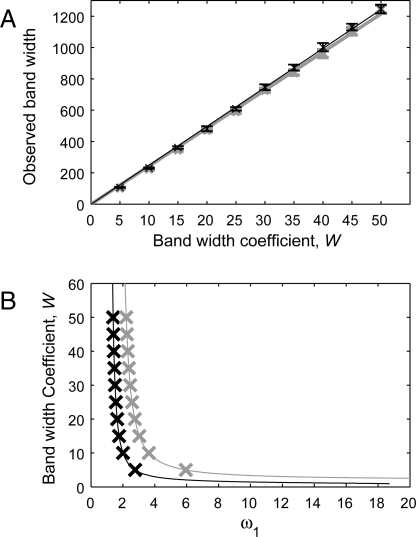
Fig. 4.

Comparison of the band width coefficient 𝒲 with the width of the wavetrain band in numerical simulations of invasion in Eqs. 1, as ω₁ varies. (A) The crosses and error bars show the mean and standard deviation of the observed band width at 100 solution times, spaced 1 time unit apart. Black: initial conditions as in Fig. 1, which give an invasion speed c _inv = 2. Grey: $u(x,0)=v(x,0)=exp[-(2-\sqrt{3})x]$, which gives c _inv = 4. We superimpose the best-fit regression lines, which are 25.55 𝒲 – 24.08 (c _inv = 2) and 25.18 𝒲 – 31.20 (c _inv = 4), with regression coefficients 0.9999 and 0.9994, respectively (n = 1,000). We expect the slopes of the regression lines to be independent of c _inv, and indeed the error bars show that the slight difference is within the variation intrinsic to our method of measuring the band width. This method measures the width of a central region of the wavetrain band but excludes regions at the edges of the band, giving rise to the nonzero intercepts in the regression lines. In both cases the values of ω₁ are chosen to give (approximately) equally spaced band widths: c _inv = 2 : 1.39 ≤ ω₁ ≤ 2.77; c _inv = 4 : 2.21 ≤ ω₁ ≤ 5.94. These ranges of ω₁ provide an effective coverage of the variation in band width, as illustrated in B, where lines show the predicted band width coefficients, and crosses show the mean band widths observed in simulations, rescaled to give equivalent band width coefficients using the slopes of the regression lines in A. In simulations ω₀ = 3, and we define the observed band width via the condition |∂r/∂x| < 5 × 10⁻⁷. This condition gives a robust measure of band width; the small size of the threshold means that the resulting values are significantly smaller than (but directly correlated with) estimates suggested by visual inspection of space–time plots such as Fig. 1 B. We estimated the derivative numerically after applying a smoothing algorithm followed by a polynomial fit over a moving window of 9 grid points. The equations were solved by using a semiimplicit finite difference method, with a grid spacing of 0.2 and a time step of 10⁻³. The domain length and run time were set to ensure that our measured band width data showed no temporal trends (the initial growth phase of the wavetrain band was omitted from the band width measurements).

To test our predictions, we performed numerical simulations of Eqs. 1, defining the wavetrain band by the condition that |∂r/∂x| is below a small, arbitrary threshold. The comparison with our theoretical prediction 𝒲 is extremely good (Fig. 4). Moreover, the slope of the regression line in this figure is a suitable value for log(ℱ), which can be used to convert predictions of band width coefficient to actual band widths in applications. As a further test, we repeated this comparison using initial conditions in which u and v decay slowly to zero, rather than being exactly zero away from the left-hand boundary. This can generate a “pushed” rather than “pulled” invasive wave (4) with speed c _inv > 2, which changes both the wavetrain amplitude and the band width. Fig. 4 shows that for c _inv = 4 the comparison between theory and simulations is again extremely good.

Example of Application: Predator–Prey Invasion

The wider significance of our results hinges on the fact that the kinetics of the λ – ω system (Eqs. 1) are not only the standard prototype oscillator but also the normal form of any oscillatory system near a standard supercritical Hopf bifurcation. This makes our results applicable to a wide range of models with low-amplitude cycles across many disciplines. To illustrate this, we consider a classic ecological example: the invasion of a prey population by predators, using the standard Rosenzweig–MacArthur model (see Methods). We do not attempt a detailed ecological investigation—rather, our objective is to illustrate the ease with which our method can be applied. To simulate invasion, we use initial conditions in which a small, localized predator density is introduced into a prey population at its carrying capacity. This generates an advancing front of predators, and a corresponding receding front of prey. A large body of theoretical work has shown that in the case of cyclic population dynamics, the behavior behind the invasion front consists of spatiotemporal oscillations (13, 31, 32). In some cases, these are a stable wavetrain; when the appropriate wavetrain is unstable, more complicated dynamics occur, with a typical example shown in Fig. 5. Immediately behind the invasion front, the population densities are almost constant, at their (unstable) coexistence steady state. Behind this, there is a wavetrain band whose width remains constant as the invasion progresses, and which is followed by spatiotemporal chaos (31, 32).

Fig. 5.

Wavetrain generation in a simulated invasion of a prey population by predators. We plot prey density as a function of space and time. There is a receding invasive wave front, behind which the solution settles at the (unstable) coexistence steady state. A wavetrain band then develops; the wavetrain is unstable, and destabilises to give irregular spatiotemporal oscillations. As for the λ – ω Eqs. 1, careful numerical studies suggest that these oscillations are a genuine example of spatiotemporal chaos (12, 32). The predator dynamics are directly analogous, with the oscillations of the 2 populations being out of phase. The initial conditions correspond to a prey-only state everywhere, except for a small nonzero predator density at the left hand boundary. By appropriate rescaling (35), Eqs. 4 can be specified by 3 dimensionless parameter ratios, which for this simulation are a/b = 1.3, r/a = 1.2, kh ₀ = 10.0. The domain length for the dimensionless spatial coordinate x(r/δ)^1/2 is 1,000, and the solution is plotted for dimensionless times rt between 1,186 and 1,318. The equations were solved using a semiimplicit finite difference method, with a grid spacing of 0.5 and a time step of 3 × 10⁻⁵.

The predator–prey invasion process is different from that studied for the λ – ω equations; in particular, the prey-only state has no analogue in Eqs. 1, with u = v = 0 corresponding to a constant coexistence of predators and prey. However, detailed calculations show that the behavior behind the initial invasion front corresponds exactly to the λ – ω invasion scenario (33). This is a general result, not restricted to the particular case of Eqs. 4; effectively, the leading invasion front leaves the system at the coexistence steady state and also initiates an invasion of that state in the opposite direction. This means that close to Hopf bifurcation in the kinetics, the width of the wavetrain band is given by our calculations for the λ – ω system (Eqs. 1).

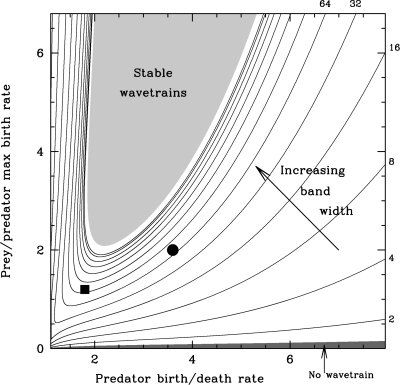
The key step in applying our results, both to predator–prey invasion and more generally, is thus to determine ω₁ as a function of the model parameters. This is done by the standard method of reduction to normal form (34); detailed presentations of this calculation for the Rosenzweig–MacArthur equations are given in refs. 35 and 36. By combining this with our previous calculation of the band width coefficient as a function of ω₁, we can calculate the dependency of the width of the wavetrain band on the underlying ecological parameters. For example, Fig. 6 shows contours of band width (with exponential spacing) in a key parameter plane. Note that because they are based on a normal form reduction, predictions such as those in Fig. 6 are valid only as approximations close to Hopf bifurcation in the local dynamics.

Fig. 6.

A contour plot of wavetrain band width as a function of parameters for the Rosenzweig–MacArthur predator–prey model (Eqs. 4). The contour levels have a power law spacing, with band width coefficient 𝒲 = 2,4,6,16,…,8192. The light shaded region corresponds to stable wavetrains behind invasion, and there is no wavetrain band for parameters in the shaded region immediately above the horizontal axis; in such cases, irregular oscillations develop immediately behind the invasion front. Two specific predator–prey systems are discussed in Example of Application: Predator–Prey Invasion, and the corresponding parameters are indicated in the figure by the square [weasels/field voles: a/b = 1.8, r/a = 1.2 (35)] and circle [zooplankton/phytoplankton: a/b = 3.6, r/a = 2.0 (43)]. The band width coefficients are calculated for c _inv = 2, because it is the “pulled” invasive front that is relevant in applications such as this (4, 33).

One natural population in which wavetrains have been widely reported is the field vole (Microtus agrestis) (10, 37, 38). Possible causes of the cyclic dynamics of this population include their predation by weasels (Mustela nivalis) (39, 40). The Rosenzweig–MacArthur model omits a number of factors that are likely to influence the behavior of any real weasel/field vole interaction, but nevertheless it represents a useful caricature model, and typical parameter estimates (35) yield a band width coefficient of 156. It is convenient to express this as the number of wavelengths in the wavetrain band, which is given by multiplying by our estimate for log(ℱ) and dividing by the wavelength = 2π/(1 − R*)^1/2. This predicts 295 wavelengths in the band, which is much longer than any practical ecological habitat, suggesting that even though the appropriate wavetrain is unstable, spatiotemporal disorder will not be observed after invasion. This conclusion is valid even after the whole domain has been invaded, for typical (zero flux) boundary conditions, because wavetrain solutions then undergo a gradual transition to spatially uniform oscillations. In contrast, systems in which the prey birth rate is smaller relative to that of the predator would have a smaller band width, or in extreme cases, no wavetrain band at all (Fig. 6). Irregular oscillations would then develop more quickly after invasion, and would persist after the whole domain had been invaded (25). This illustrates one important practical benefit of band width calculations for conducting experiments and surveys: estimating whether or not the domain is sufficiently large for irregular spatiotemporal dynamics to be observed. It is important to note that our results only apply to the behavior after the invasion of prey by predators. Other scenarios may generate different behaviors, including spatiotemporal disorder, in the model Eqs. 4—for instance, landscape obstacles can also generate chaos via unstable wavetrains (41). Moreover, some alternative predator–prey models predict an even wider range of spatiotemporal phenomena, including “patchy invasion” in which the invasion process and the transition to chaos are simultaneous (9, 42). For the specific case of field voles, field data reveal a variety of population dynamics, including both regular cycles and quasichaos (40). A natural extension to our study is to apply the methods to more realistic models, potentially including the stochasticity that is implicit in both the underlying biology and the process of data collection.

An important implication of the contours in Fig. 6 is that the width of the wavetrain band is much more sensitive to variations in some parameters than others. For instance, in the field vole–weasel case, a 5% increase in predator mortality reduces the band width by just 0.5%, whereas a corresponding increase in prey birth rate increases the band width by 22%. An even more striking example of this nonlinearity is provided by the interaction between the zooplankton Daphnia pulex and the phytoplankton Chlamydomonas reinhardii. To the best of our knowledge, there are no spatiotemporal data from which wavetrains could be inferred in this case. However, using estimates of the relevant parameters (43), we predict that the width of a wavetrain band behind invasion would be extremely sensitive to the estimate of zooplankton birth rate, with a reduction of only 5.2% sufficient to double the band width. Such sensitivity has an important general implication: Major differences in spatiotemporal dynamics may result from even slight changes in parameter values. For example, a large body of evidence now indicates that as well as increasing the frequency of ecological invasions (44), climate change is having a significant effect on the demographic parameters underlying oscillatory ecological systems (45, 46). Our results suggest that the consequent changes in some spatiotemporal behaviors may be even more dramatic.

Methods

Calculation of λ_max(V).

The key quantity in our calculation of wavetrain band width is λ_max(V), the maximum growth rate of a linear mode in a frame of reference moving with velocity V. To determine this, we replace x by the moving coordinate x − Vt, and then compute “branch points” in the absolute spectrum (26). We do this via the numerical continuation approach of Rademacher et al. (27). Briefly, we linearize the equations satisfied by r(x,t) and θ(x,t) about the wavetrain, and denote by 𝒟(λ,ν;V) = 0 the dispersion relation for linear modes with temporal and spatial eigenvalues λ and ν, respectively. For given λ, 𝒟 is a quartic polynomial in ν, and we label the roots ν₁,…,ν₄ so that Reν_i ≥ Reν_i+1. The absolute spectrum defined in ref. 26 is the set of λ for which Reν₂ = Reν₃, and the branch points are the 4 values of λ for which 𝒟 has repeated roots for ν. Note that for a branch point, the condition ν₂ = ν₃ corresponds to the “pinching condition” of refs. 47, 48, and its instability implies pointwise growth of perturbations in the comoving frame. In the language of ref. 4, absolute instability corresponds to a positive value of the linear spreading speed.

More generally, the absolute spectrum is the accumulation set of eigenvalues in the limit of large domain length under generic separated boundary conditions. Branch points typically form endpoints of curves of the absolute spectrum, which can therefore contain λs with a larger real part than any branch point in the absolute spectrum. However, these would lead to “remnant instabilities,” associated with perturbations reflecting repeatedly off the domain boundaries (26). Hence, we expect that such an instability would be irrelevant in the present context. In fact, computations of the full absolute spectrum (via continuation from branch points, as in ref. 27), for a wide range of ω₁ and V, indicate that for our system, the most unstable point in the absolute spectrum is always a branch point.

Therefore λ_max(V) can be found simply by calculating the four branch points, which are the solutions of 𝒟(λ,ν;V) = 𝒟 _ν(λ,ν;V) = 0, and identifying which of these are in the absolute spectrum. We numerically continue these solutions in V, giving λ_max and the corresponding spatial eigenvalue ν_max as functions of V. A complication is that the appropriate branch point can change at “triple points,” when 3 roots of 𝒟(λ,ν) have equal real parts; therefore, and to check Reν₂ = Reν₃, it is necessary to continue all 4 branch points and monitor their ν values. We calculate V _band simply by monitoring the 2 sides of Eq. 3 during the continuation. Moreover, having found V _band for one value of ω₁, continuation in ω₁ is straightforward, enabling the plot in Fig. 2 B.

The above procedure is significantly simpler, and more portable, than that used in the few previous articles we are aware of that compute λ_max(V) for other systems (49–51); these studies involve continuation of a saddle point of λ(ν) − Vν in the complex ν plane.

Calculation of λ_max′(V).

The derivative λ_max′(V) is required for calculation of the band width, and this can be found very easily. We have 𝒟(λ_max,ν_max;V) = 0 for all V, so that at λ = λ_max and ν = ν_max

(subscripts denote partial derivatives). But since λ_max and ν_max occur at a branch point, 𝒟 _ν = 0. Therefore λ_max′(V) = −𝒟 _V/𝒟 _λ. For any reaction–diffusion system, the dispersion relation satisfies

Therefore λ_max′(V) = ν_max(V),

Predator–Prey Example.

The application of our results to predator–prey invasion uses the Rosenzweig–MacArthur model

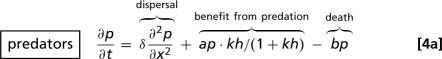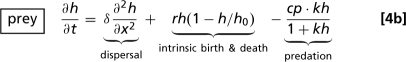(52–54). Here p and h denote predator and prey densities, which depend on space x and time t. The populations are assumed to have the same dispersal coefficient, δ; however, we have shown previously that the “band width phenomenon” also occurs in this model when the dispersal coefficients are different (41) or even density-dependent (55). The local population dynamics depend on the positive parameters a, b, c, r, h ₀, and k. The prey consumption rate per predator is an increasing saturating function of the prey density: c represents the maximal consumption rate, and k reflects how quickly the consumption rate saturates as prey density increases. Parameters a and r denote maximal per-capita predator and prey birth rates; for predators, this is the birth rate when the prey density is very high, whereas for prey it is the birth rate at very low prey density. The per-capita predator death rate is denoted by b, and h ₀ is the prey-carrying capacity. For suitable parameter values, the local dynamics of Eqs. 4 are oscillatory: specifically, there is a standard supercritical Hopf bifurcation as kh ₀(a − b) − a − b increases through zero.