Modeling morphological instabilities in lipid membranes with anchored amphiphilic polymers

Abstract

Anchoring molecules, like amphiphilic polymers, are able to dynamically regulate membrane morphology. Such molecules insert their hydrophobic groups into the bilayer, generating a local membrane curvature. In order to minimize the elastic energy penalty, a dynamic shape instability may occur, as in the case of the curvature-driven pearling instability or the polymer-induced tubulation of lipid vesicles. We review recent works on modeling of such instabilities by means of a mesoscopic dynamic model of the phase-field kind, which take into account the bending energy of lipid bilayers.

Introduction

Lipid bilayers are the common framework that guarantee a stable but flexible surrounding for cells and cell organelles [2]. However, it is biologically necessary to provide every one of these membrane-enclosed entities with very specific structural and functional properties. For that reason, the biochemical composition of eukaryotic cell membranes has to be rather complex [107] and differs from membrane to membrane. The basic components of a cell membrane include several kinds of lipids, some of which form the lipid bilayer, and some others control its fluid behavior, and membrane proteins, usually involved in both functional and structural membrane features. The typical thickness of a lipid bilayer is ~4 nm, while cell sizes are three to four orders of magnitude larger.

Lipid bilayers are the most simple models of biological membranes. By reconstituting model membranes from a small number of lipids and proteins, a molecular-level understanding of specific membrane properties can be achieved. However, the complexity of biological membranes also involves the possible existence of phase-separated domains with different elastic properties [3, 7, 13, 16, 32, 61, 103], or the shaping effect of membrane proteins [4, 21, 28, 36, 42, 44, 45, 51, 59, 68, 75, 76, 84, 89, 102, 115, 121].

Here, we deal with a specific minimal system to study the basic morphological properties of biological membranes. Such a system consists of a fluid monocomponent lipid bilayer with anchored amphiphilic polymers, mimicking the bending capability of some membrane proteins [21, 76, 121]. It has been experimentally used [29, 43, 92, 93, 105, 112–114] to understand and characterize the effect of amphiphilic polymers on the shape of lipid vesicles. We review recent theoretical results on these shape instabilities. In addition, these morphological instabilities may have a counterpart in cell biology, being involved, for instance, in intracellular transport phenomena [2]. A deep understanding of a simple system as the one we review here should be the starting point to further address more complex biological systems.

Mechanics of lipid bilayers and vesicles

Understanding the key mechanical aspects of lipid bilayers has been the subject of many studies [22, 35, 50, 70, 73, 98, 99]. The shape of lipid vesicles—that is, of closed lipid bilayers—is due to the curvature of the membrane considered as a regular two-dimensional surface embedded in the Euclidean three-dimensional space. The elastic free energy, f, of an infinitesimal piece of membrane is expressed in terms of the two curvature invariants: the total curvature and the Gaussian curvature (see the Appendix). The free energy is expressed as an expansion up to second order in curvatures,

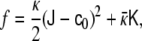1

where κ and 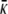, named as the bending modulus and the Gaussian rigidity, respectively, are two elastic parameters that depend, for instance, on the lipid composition of the bilayer and on the temperature. In addition, 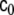is the so-called spontaneous curvature, which takes into account possible asymmetries between the two leaflets of the bilayer. The total bending energy of a lipid vesicle can be found by integrating the energy density Eq. 1 over the entire vesicle surface area, Ω, as .

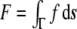The Gauss–Bonnet theorem [23, 58] states that the integral of the Gaussian curvature of a regular surface over its whole area is a topological invariant, that is, it takes a given value for a given topology regardless of the surface shape. This theorem implies that, for homogeneous vesicles, the Gaussian part of the membrane bending energy is a constant as long as topological changes are not considered. Under such assumptions, the bending energy of a lipid vesicle can be written as

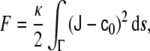2

which is usually referred to as the spontaneous curvature model of bending energy [99]. For the situation where symmetric bilayers are considered, such that the spontaneous curvature vanishes, the resulting energy model is normally referred to as the minimal model.

Understanding the shape of lipid vesicles is then related to the specific election of an energy model. In addition, one has to take into account some geometric constraints for the vesicle shapes [99]. The surface area of the vesicle remains constant if one assumes that there is no exchange of lipids and that the lipid bilayer is an incompressible fluid. Also, the inner volume of the vesicle has to be kept fixed by osmotic regulation. The stationary shapes of lipid vesicles have been found according to different energy models by means of different minimization techniques. The first approach, which goes back to Helfrich’s seminal paper [50], uses variational calculus to work out the Euler–Lagrange equation for the shape of rotationally symmetric bilayers. Shape equations such as Euler–Lagrange equations for the energy functional under consideration have been widely studied since then [31, 50, 56, 57, 62, 77, 100, 119, 120]. Although a general shape equation can be found without assuming any symmetry of the resulting shapes, it is usually of a practical reason to get an axisymmetric parametrization of the vesicle shape. Such a simplification results in a nonlinear ordinary differential equation whose solution, under certain boundary conditions, leads to the stationary shapes of vesicles. In addition to this method, numerical minimization on triangulated surfaces has been implemented to find nonaxisymmetric shapes [118], and also in order to find red blood cell shape transformations coupling the curvature model with the cytoskeleton elasticity [72, 78]. Mesoscopic simulations using dissipative particle dynamics have been performed by Noguchi and Gompper [81–83] to study hydrodynamic effects on lipid vesicles. Lattice Boltzmann methods [71, 106] have also been used to study vesicle shapes. Different phase-field models have been implemented to study the stationary shapes of vesicles [8, 17, 33].

In this review, we present a derivation of a bending phase-field model, a dynamic model to study different morphological instabilities on membranes. We start in the section “Bending phase-field model” by introducing the main aspects of phase-field models and by giving a derivation of a phase-field model for dealing with the bending energy of lipid bilayers. Next, we review some of the dynamic instabilities that have been observed in a system consisting of a lipid vesicle and a certain concentration of amphiphilic molecules anchored on it. In particular, in the section “Pearling instability”, we review the theoretical results on the curvature-induced pearling instability and, in the section “Tubulation instability”, on the tubulation instability. Finally, in the section “Outlook and future perspectives”, we briefly summarize the main aspects of the topic and point out some of the questions that remain to be answered.

Bending phase-field model

Phase-field models

Phase-field models are dynamic models of the Ginzburg–Landau type [53] that have been broadly used to study different interfacial problems in physics [1, 14, 25, 37–40, 48, 52, 64–66, 87, 88, 104]. Generally, one of the points making interfacial problems complex is that it is necessary to track the interface during the dynamic evolution. Phase-field models do not consider only the interface as a sharp boundary between two bulk phases but considers them as a single volume.

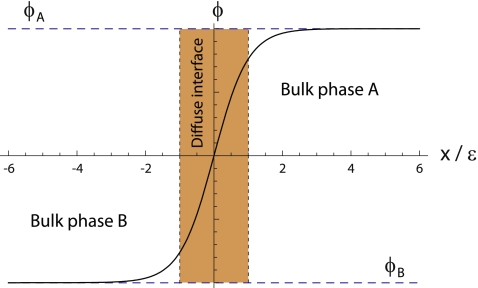
Which characteristics should one require to a phase field? For a two-dimensional, two-phase problem, the phase field, ϕ, has to be a smooth, well-behaved function that takes real values in the whole two-dimensional domain, Ω. Besides, we require the constituent dynamic equations to be such that the solution for the phase field acquires two different plateaux, ϕ_A and ϕ_B, one for each phase (see Fig. 1). Therefore, it will be possible to know in which physical phase a given point belongs by checking the value of the phase field at that point. The values of these two plateaux are arbitrary, but in the literature, they are mainly chosen to be ±1, or 0 and 1. In the diffuse interface region, the phase field cannot have any of these two bulk values, but it has to change abruptly, albeit continuously, from one to the other (Fig. 1). The width of this region is characterized by a small parameter of the model, ε. The abrupt interface can be recalled at any time by finding the level-set 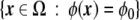, where, again, ϕ₀ is an arbitrary position between the two bulk phases, but it is normally taken to be ϕ₀ = (ϕ_A + ϕ_B)/2.

Fig. 1.

Qualitative profile of a one-dimensional phase field, ϕ(x). The values of the two plateaux, ϕ_A and ϕ_B, correspond to each of the two stable phases, A and B, and the phase field continuously interpolates from one to the other in a thin but finite region, the diffuse interface (dark region)

Using a phase-field method, it is possible to substitute a moving boundary condition by a partial differential equation for this auxiliary field. This new equation has to be constructed in such a way that the interfacial dynamics was as similar as possible to the free boundary problem’s. Therefore, one asks that, in the so-called sharp interface limit [34], i.e., the limit when the width of the diffuse interface goes to zero, the resulting physics will be the same as in the original problem.

This makes to whole thing simpler, but usually more time-consuming, from a computational point of view. In addition, phase-field models naturally allow for topological changes. On the contrary, a new length-scale, the width of the diffuse interface, is introduced on the model. Although the sharp-interface limit guarantees equivalence between the free boundary problem and the phase-field problem, in practice, one has to choose a finite value for this small parameter, ε. This parameter has to be smaller than all the other length scales in the system, but it still needs to be resolved by the lattice, in case the partial differential equations were discretized.

A lipid vesicle can be mathematically interpreted as a boundary separating two media, the inner volume and the outer volume. The shape of this surface changes dynamically according to the hydrodynamics of the aqueous solutions surrounding it, and also according to its own energetics. Besides, additional destabilizing effects can be included in the system, as, for instance, proteins or polymers changing the morphology and/or the properties of the membrane, and so on and so forth. This problem is a free boundary problem. In this case, the boundary is not a separation layer between two different phases as in the oil–water example, but a physically differentiated region, the membrane, separating two regions of the same phase. In the simplest case, where no destabilizing effects are added to the system, and hydrodynamics is not relevant, a phase-field model can be used to study the morphology of vesicles given a bending energy model [8, 17, 33, 74].

Phase-field implementation of the bilayer bending energy

Here, we review the mathematical bases of a curvature phase-field model [17, 19, 33]. We decided to give a detailed derivation of the model in order to assemble the different published parts in a logical order. The membrane is considered to be a two-dimensional surface embedded in the Euclidean three-dimensional space. In order to build a phase-field model that takes into account the bending energy of fluid vesicles, the surface geometric properties (the ones involved in the bending energy) are expressed as a function of the phase field. Also, as part of the physical constraints needed to be taken into account, the vesicle surface area and enclosed volume have to be included in the phase-field description.

Let us assume the existence of a field, 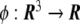, in all the points of the Euclidean three-dimensional space 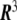. This field is the so-called phase field. Since phase fields are regular functions, they can, in general, be written in terms of any smooth function of the coordinates. In particular, the phase field can be written as a function of the signed distance to the interface, ,

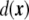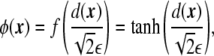3

where a tanh-like profile for the phase field was assumed, and ε is the mesoscopic parameter of the phase field, related to the finite width of the diffuse interface. This parametrization is chosen because it involves the signed distance to the interface, whose first derivative is a unit normal vector to the interface,

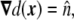4

and whose second derivative is the curvature tensor [23]

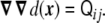5

The derivatives of the phase field with respect its argument are

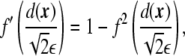6

and

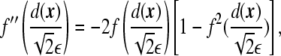7

where primes precisely denote the derivatives with respect to the argument, in this case, with respect to 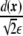. Considering the derivatives of the phase field with respect to the x_i coordinates,

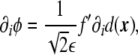8

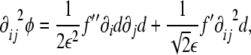9

where we used the notation 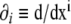for the partial derivatives with respect to the coordinates. From Eqs. 8 and 9, it is possible to express the second derivatives of the signed distance as a function of the phase field and its derivatives, as

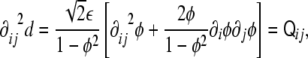10

which is the three-dimensional tensor of curvature 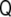(see Appendix).

This tensor has remarkable properties. First of all, it is a symmetric tensor, 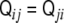. Second, since the gradient of the signed distance is a unitary vector (see Eq. 4), the curvature tensor has a zero eigenvalue, with 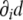being the corresponding eigenvector:

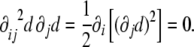11

Therefore, its determinant is zero.

An n×n tensor has, at most, n independent invariant quantities under changes of coordinates [63]. These invariants can be expressed by the coefficients of the characteristic polynomial. In the case of a 3×3 tensor, these coefficients correspond to the determinant, the trace, and the sum of the principal minors of the tensor matrix. Since the determinant of the curvature tensor is always zero, there are only two nonvanishing invariants. These two invariants are related to the total and Gaussian curvatures of the surface [97]. The total curvature reads as

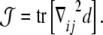12

From the expression of the curvature tensor as a function of the phase field, Eq. 10, we can thus write it as a function of the phase field and its derivatives as

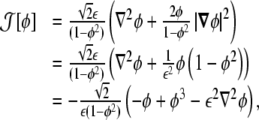13

where we used Eq. 6.

Minimal model It is now possible to express the minimal model for the bending energy as a function of the phase field. There is a fundamental difference between the Canham–Helfrich version of the free energy and the one we seek in terms of the phase field: the former is a surface integral, and the latter should be a volume integral, since one does not want to track the interface position (the membrane location in our case) during the time evolution. Therefore, one seeks for something of the form

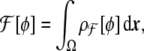14

where Ω is the three-dimensional domain of the phase field, and is the three-dimensional volume element.One way to express a surface integral as a volume integral is by using distributions [91]. In our case, an obvious manner is by implementing a Dirac delta function on the interface, where the signed distance vanishes,

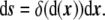15

It is necessary to find a representation of the Dirac delta in terms of the phase field. Phase-field functions are continuous functions that only change substantially in a neighborhood of size ~ε around the interface. In the sharp-interface limit, a phase-field function becomes a step function. For this reason, a first candidate for a delta function would be the derivative of the phase field. Rewriting Eq. 6, using the tanh-like profile for the phase field Eq. 3,

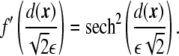16

Using the fact that

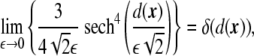17

one can write that

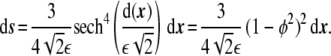18

Now, using Eqs. 13 and 18, it is possible to explicitly write the minimal model as a function of the phase field

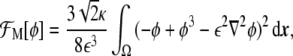19

or, in other words,

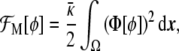20

where

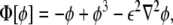21

and

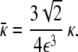22

Note that the free energy density functional in Eq. 20, Φ², is nothing other than the square of the chemical potential (the functional derivative of the free energy) associated with the Cahn–Hilliard problem [15].The minimum of the free energy Eq. 20 is ideally obtained by setting Eq. 21 equal to 0. In one dimension, this leads to the tanh-like solution 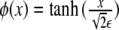, given the usual boundary conditions ϕ(± ∞ ) = ±1. Therefore, we recover our original assumption on the profile of the phase field Eq. 3.

Spontaneous curvature With the phase-field expressions of the local geometric properties of the membrane above, one can generalize the minimal model by letting the membrane adopt a nonvanishing preferred curvature. This model, first proposed by Helfrich [50], is normally referred to in the literature as the spontaneous curvature model, Eq. 2. Proceeding as before, we can write the spontaneous curvature free energy as a function of the phase field [17]

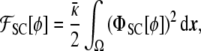23

where

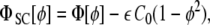24

where 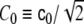may, in general, be position-dependent, or even ϕ-dependent.

Geometrical constraints

Lipid vesicle shapes are generally subject to the constraints that their enclosed volume and surface area remain constant. There are different ways to impose these constraints, some of which we review here.

Surface area To implement the constraint of constant vesicle surface area, one can choose to add a penalty to the energy to keep the vesicle surface from deviating from a constant value [33]. This is, in a sense, similar to choosing a Lagrange multiplier, being local or global [17], ensuring the area conservation. To use a Lagrangian method, it is needed to define an effective free-energy functional

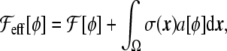25

where 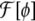is any bending free energy, σ is a Lagrange multiplier (interpreted as a surface tension in this case), and a[ϕ] is the local surface area functional,

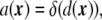26

which is expressed in terms of the parameter ε using the representation of the delta, Eq. 17, as

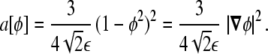27

Using Eq. 26, i.e., Eq. 27 in the sharp-interface limit, the last expression integrated over the whole domain Ω is equivalent to the surface area of the vesicle,

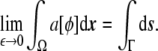28

In addition, there is another way of dealing with the area conservation, which requires the inclusion of the hydrodynamics of the system [9, 55]. Then, imposing the fact that the membrane has to be an incompressible fluid, the local area conservation is guaranteed.

Enclosed volume An obvious way to implement the condition of fixed inner vesicle volume in the free energy would be, as explained before for the surface area constraint, to introduce another Lagrange multiplier coupled to the volume term or a penalty in the free energy, ensuring its conservation [33]. However, there is a straightforward manner to implement this constraint without the need of a Lagrange multiplier. This is to introduce it through a dynamic equation. A dynamic equation such as (see the section “Dynamic equation” below)

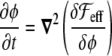29

ensures that 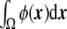is constant in time, since it is nothing other than the divergence of a flux. This integral is equal to the difference of the inner and outer volumes (ϕ takes its stable values + 1 and − 1 inside and outside the vesicle, respectively), as ε→0. As the sum of the inner and outer volumes is the volume of the integration domain Ω (which is constant), then we can write the inner volume as

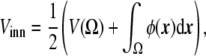30

which is conserved during the dynamic evolution.

Dynamic equation

Once a free-energy functional in terms of the phase field has been obtained, and there is a way of dealing with the geometrical constraints, the next step is to find a minimization technique to find the stationary shapes of vesicles. Here, we show a method based on the derivation of a dynamic equation for the phase field, in such a way that the time evolution follows a conserved relaxational dynamics, Eq. 29 [17, 19]. Relaxational dynamics [41] have been used before, for instance, to study phase-separation dynamics of two-component vesicles [109]. In this phase-field approach, the functional derivative in Eq. 29 has to be computed. This calculation leads to the following dynamic equation for the phase field ϕ(x) of the minimal model [17],

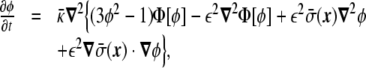31

where 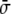is defined as

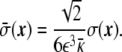32

The term proportional to 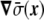in the dynamic equation (the last term in Eq. 31) is shown numerically to be small, and the Lagrange multiplier, 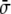, can be considered homogeneous [17].

Similarly, the dynamic equation for the spontaneous curvature model is [19],

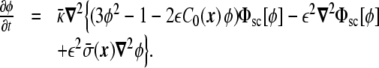33

Pearling instability

In this section, we review the curvature-driven pearling instability in lipid vesicles induced by the anchorage of amphiphilic polymers on the membrane [114] and how it can be theoretically modelled [18]. Such amphiphilic polymers insert hydrophobic anchor groups on the outer part of the bilayer, generating membrane curvature. The phase-field model of the bilayer bending energy reviewed in the section “Bending phase-field model,” Eq. 23, is used [17] to understand the instability, in which the formation of a homogeneous pearled structure is achieved by consequent pearling of an initial cylindrical tube from the tip [114]. Both homogeneous and inhomogeneous size distributions of pearls are found depending on the polymer concentration. Theoretical and experimental results are compared. It is important to remark that the pearling instability we report here is driven by curvature, and not by tension, as the classical Rayleigh–Plateau instability of liquid jets [24].

Pearling instabilities in physics

The formation of pearled structures is ubiquitous in nature [110]. For instance, the classical Rayleigh–Plateau instability [85, 90], which explains how a falling stream of fluid breaks up into smaller packets with the same volume but less surface area, is responsible for the pearling observed when water is dripping from a faucet. When the free surface of a liquid cylinder undulates with a wavelength λ, its area decreases [24], provided that λ is larger than the circumference of the cylinder (in the case of a liquid jet of radius R, larger than 2π R).

Besides this, pearling instabilities in lipid vesicles have been reported due to different mechanisms. Pearling was induced while perturbing cylindrical vesicles with optical tweezers. This produced tension in the membrane [5, 6]. Such an instability is also understood in the framework of the Rayleigh–Plateau instability [47, 79], in the sense that it is a capillary instability in which there exists a competition between creating droplets that minimize the surface energy and the kinetic cost of moving such quantities of water over large distances. It has also been studied in charged membrane tubes [80].

Pearled geometries are also found in Golgi tubules [117]. Both pearling and prefission neck narrowing are explained theoretically by lateral partitioning of diacylglycerol, a membrane lipid with a large negative spontaneous curvature, using a fourth-order elastic energy [101].

Experimental background

Experiments by Ringsdorf and collaborators [29, 92, 93] revealed a pearling instability in tubular vesicles incubated in a solution of amphiphilic polymers having a certain number of hydrophobic anchors in a polysaccharide hydrophilic backbone. This instability started when the polymer concentration was high enough. This critical concentration, above which the instability was seen, decreased for increasing numbers of anchors per backbone. The instability was nonexistent when the polymers contained only the hydrophilic backbone, suggesting that the curvature generated by the anchorage of the hydrophobic anchors was a possible mechanism for the pearling of the vesicle.

Further experimental evidence for this claim was brought by the group of Joel Stavans. They experimentally studied the morphological changes of lipid vesicles upon interaction with amphiphilic polymers [111]. In particular, they observed pearling of tubular vesicles [114]. The system they studied consisted of monocomponent membranes made of stearoyloleoylphosphatdylcholine with C₁₈ alkyl chains in a liquid disordered state. Similar to Ringsdorf and collaborators, hydrophilic dextran was used as the polymer backbone. This polymer, consisting of multiple glucose units, was functionalized with dodecanoic nitrobenzoxadiazole chains as fluorescent markers, and palmitoyl alkyl chains acting as hydrophobic anchor groups (see [114] for further details).

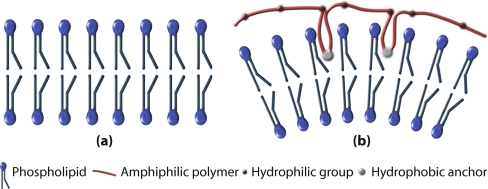
By fluorescence imaging, they demonstrated first the association of polymer with the membrane. They also showed that there is a coupling between the polymer concentration on the membrane and the local curvature. The polymer hydrophobic backbones anchor to the outer leaflet of the bilayer in order to minimize its hydrophobic interaction [108], acting, thus, as a wedge locally changing the curvature of the bilayer (see Fig. 2).

Fig. 2.

Polymer wedge effect inducing a spontaneous curvature in a bilayer. A bilayer formed by one kind of lipid with zero spontaneous curvature tends to be flat (a). When a certain number of anchor groups of an amphiphilic polymer get stuck in the outer leaflet of the bilayer, a spontaneous curvature is induced (b)

Curvature-driven pearling instability

To incorporate the effect of curvature generation by the anchored polymers, a linear coupling between the spontaneous curvature and the polymer concentration [21, 69] was assumed to model the pearling instability [18],

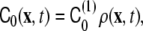34

where 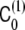is the polymer-induced spontaneous curvature, ρ(x,t) is the local density of polymer, and no bare spontaneous curvature of the bilayer was assumed. Under these conditions, the spontaneous curvature phase-field model, Eq. 23, was numerically solved in order to find the dynamics of the instability [18].

In the experiments by Tsafrir et al. [114], amphiphilic polymers were introduced in the bulk outside the vesicle, both globally and locally close to the tip of the tube. Polymer molecules diffuse in the bulk until they come across the membrane, where they get stuck in such a way that their hydrophobic parts anchor in the bilayer in order to satisfy the hydrophobic interaction. Once a polymer is anchored, it diffuses superficially along the membrane.

In [18], the situation of global application of the polymer was considered, assuming that the polymer concentration almost immediately reaches a homogeneous profile along the membrane. Under such assumptions, the dynamic evolution is, thus, fully understood from the shape dynamics, so there is no need for a dynamic equation for the density field. In an alternate analysis, Góźdź [49] studied how nonuniform distributions of anchored molecules—causing a nonhomogeneous spontaneous curvature profile on the vesicle—influence and get influenced by the diffusion process.

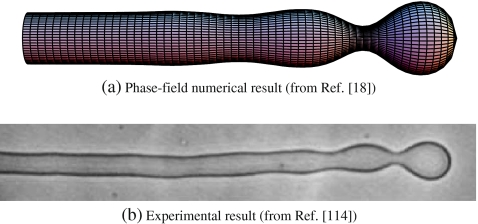
Curvature-driven pearling instability theoretically studied by means of a bending phase-field model reported that, for small enough polymer concentration, the onset of the instability was observed (see Fig. 3a), in agreement with the experimental results (see Fig. 3b) [18].

Fig. 3.

Onset of the pearling instability. Comparison of the phase-field numerical result from [18] (a) and the experimental result from [114] (b). Such a situation corresponds to a relatively small concentration of anchoring molecules globally applied to the tubular liposome. In the numerical results, there is no fitting parameter in the numerical integration and the spontaneous curvature is taken to be homogeneous and equal to 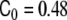, below the pearling instability limit

For intermediate values of the spontaneous curvatures, between 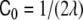and 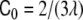—where λ = V/A is the volume-to-area ratio of the vesicle—, Deuling and Helfrich [31] showed that there exist minimal surfaces, called Delaunay surfaces, that are global minima of the bending energy Eq. 2, for axial symmetrical shapes. These shapes range from a cylinder to a set of spheres connected by infinitesimal necks, through a whole range of unduloids. However, the dynamics of the pearling instability does not occur following a set of Delaunay shapes, but, as seen both experimentally [114] and theoretically [18], through a subsequent formation of spheres beginning from the tip of the tube. Eventually, for large enough polymer concentrations, beyond a certain critical concentration, tubes formed by a set of pearls of different sizes are the energetically favorable shapes.

Tubulation instability

In this section, we review the formation of long membrane tubes and short buds out of oblate vesicles, due to the existence of a concentration profile of amphiphilic polymer molecules [112]. The formation and extrusion of lipid membrane tubes has been extensively studied both experimentally and theoretically. Here, we focus on the mechanism by which tubes are extruded not by applying a directed force, but due to the existence of a polymer concentration profile outside the mother vesicle. As in the case of the curvature-driven pearling instability, anchor groups of the amphiphilic polymers insert on the outer part of the lipid bilayer, inducing curvature. Assuming a linear coupling between the polymer concentration and the capability of inducing spontaneous curvature to the membrane, it is possible to explain [20] the formation of long tubes and short buds as reported experimentally [112].

Experimental background

As part of cellular dynamic processes, membranes adopt different shapes in order to exchange matter with their surroundings. Many possibilities appear here, from budding and eventual fission of small transport vesicles [36] to formation of large tethers connecting distant organelles, as in the Golgi apparatus and the endoplasmic reticulum (ER) [115, 116], or even between different cells [96]. Actually, the ER is a huge network of interconnected tubules, vesicles, and cisternae, which act as transport carriers for proteins and other functional entities to be transported to other parts of the cell [2].

The formation of these tethers can be driven by the application of a point-like force to the membrane [30, 86]. Understanding the nature of this force is of major importance, and we will review the main theoretical aspects of such a mechanism in the section “Tubulation by applying a directed force.”

There are different mechanisms leading to such a tubulation phenomenon in cells as, for instance, the growing of microtubules pushing the membrane from inside [46] and the extrusion from vesicles due to a hydrodynamic shear flow [11, 12, 94]. Other works have experimentally studied the force generated by molecular motors pulling membrane tubes in vitro [67, 95] and by optical tweezers [26, 27, 60].

Besides this, Tsafrir et al. studied the tubulation induced in highly oblate vesicles by the anchoring of amphiphilic polymers without any directed force [112]. In those experiments, macromolecules containing hydrophobic groups were administered in the surroundings of a giant oblate vesicle. Those molecules diffused in the bulk and eventually anchored the membrane inducing a local spontaneous curvature by the mechanism of hydrophobic insertion [21, 121], leading to the formation of one or several buds. Under certain circumstances, buds may grow into long tubular structures.

Tubulation by applying a directed force

When a force is applied on a small spot of a vesicle, deformation occurs. Depending on the conditions of this force, a membrane tube can be extruded from a mother vesicle. There are many works in the literature, both experimental and theoretical, about the physics of membrane tube extraction by a directed force. Here, we review a theoretical explanation of tube extraction by a localized force, based on [30, 86].

Given a fluid vesicle with fixed tension, σ, and pressure, p, on which a force, f, is locally applied normally outwards the vesicle, the energy can be written, according to the minimal model (Eq. 2 with vanishing spontaneous curvature),

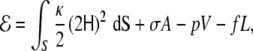35

where A and V are, respectively, the area and volume of the vesicle and L is the end-to-end distance in the direction defined by the force vector. For a cylindrical tube of length L, radius R, at vanishing osmotic pressure, since the pressure effects are misleading (see [86] for a discussion on this issue), the energy reads

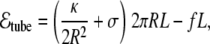36

from where one can see that the bending term favors the radial growth of the tube (since it decreases the bending energy), and the tension term favors the tube shrinkage. Therefore, the competition between these two terms leads to an equilibrium intermediate solution that can be easily found by minimizing Eq. 36 with respect to the radius and length of the tube,

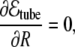37

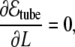38

from where one obtains

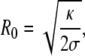39

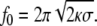40

This has been done for the minimal model. However, a membrane bare spontaneous curvature can also be straightforwardly introduced and proceed analogously (see [121]).

Typical values for the force and the optimal radius are f₀~10 pN and R₀~20 nm, respectively. Actually, the value of the force needed to extract a membrane tube is of the order of the force generated by a few molecular motors [54, 121], meaning that these motors are plausible candidates to extract and form intracellular carriers.

Polymer-induced tubulation

Here, we review a mechanism of tube extraction not caused by the application of a directed force [20]. This mechanism is based on the assumption that a gradient in the polymer concentration profile in the extravesicular medium can cause a free energy profile favoring tubulation. This assumption was studied in the framework of the Canham–Helfrich curvature model, initially in a simplified geometry allowing for an analytical treatment. Under such conditions, and depending on the length of an initially preformed tube (or bud) and on a parameter linked to the slope of polymer concentration profile (assumed to be linear in that approximation), tubes of a finite length can be steadily formed.

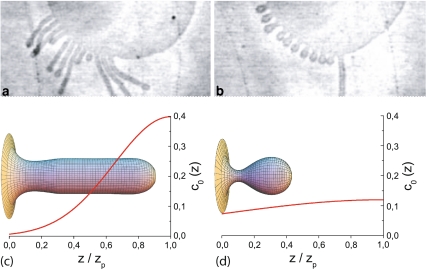
To study the complete situation, no assumption is made on the tube geometry during the dynamics, and a more general profile (a Gaussian decay) for the polymer concentration gradient is assumed. In that case, there is no possibility to analytically solve the problem, due to the nonlinearities of the shape equations [62]. Therefore, a bending phase-field model was used. Then, numerically solving the corresponding phase-field dynamic equation for different parameters, two kinds of shapes were found [20]: long tubes and shorter bud-like shapes (Fig. 4). These results are in very good qualitative agreement with the experimental results [112], showing that the tubulation mechanism due to the existence of a nonhomogeneous concentration profile of amphiphilic molecules is a plausible mechanism.

Fig. 4.

Tubes extruded from a vesicle by a nonhomogeneous polymer profile. Comparison between the experimental results from [112] (a, b) and the phase-field integrations from [20] (c, d). For short time periods, long tubes are obtained (a, c), and for long time periods, buds appear (b, d). The resulting profile for the spontaneous curvature is shown for the phase-field integrations

Outlook and future perspectives

Biological membranes are complex entities formed by several kinds of biochemical molecules. Their basic structure is that of a lipid bilayer that can, however, consist of dozens of different kinds of lipid molecules. In addition, such a purely lipidic membrane can have phase-separated domains, some of them being liquid-disordered, some of them being in the more condensed liquid-order phase, and some others being in a solid-like gel phase. Biological membranes are believed to present such a richness, albeit a liquid-disordered state is known to be the predominant phase. Moreover, biomembranes include different kinds of associated proteins. These proteins are not only functional in order to communicate with other cells or cell organelles, but they are also involved in membrane shaping.

In this review, we studied a simple model membrane, consisting of monocomponent fluid lipid bilayers, closed to form vesicles. These are, perhaps, the most simple models for biological membranes. Obviously, they cannot include all the phenomenology of actual membranes, but they indeed grasp some essence of their behavior. Such lipid bilayers are mathematically described as two-dimensional surfaces embedded in a three-dimensional space. From a purely geometric description, they can be characterized by giving, at each point, the value of the radii of curvature in two perpendicular directions. From there, and using symmetry considerations, it is possible to describe the bilayer energy in terms of those curvatures, in the so-called Canham–Helfrich model [22, 50].

The aim of this paper was to review the theoretical approaches to study the membrane dynamics in different circumstances due to the anchoring of amphiphilic polymers on the membrane surface. We focused on the explanation of a class of dynamic models for interfaces, the phase-field models, which have been used to study membrane dynamics. Further, such a model has been used to explain both the curvature-driven pearling instability and the polymer-induced tubulation of lipid vesicles.

As far as we are concerned, hydrodynamic effects have not been introduced to study these instabilities, although it would be interesting to study the whole model coupling the phase-field model (or any other dynamic model) for the membrane shape to the proper hydrodynamics of both the membrane and the aqueous media surrounding it.

The systems where morphological transitions occur, due to the insertion of amphiphilic polymers in monocomponent lipid membranes that are studied, are simple models to unravel some of the physical phenomena underlying other more complex biological systems. Thus, intracellular transport mechanisms in the ER or the Golgi are due to the generation of large-curvature intermediates by proteins anchored on their membranes [76]. In this review, we presented results that can shed some light on these mechanisms, from a physical point of view and by taking the minimal essential ingredients.

Appendix

Differential geometry of surfaces

A two-dimensional, well-behaved surface embedded in Euclidean three-dimensional space, 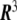, is mathematically defined univocally by a vector field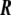

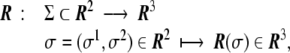41

which maps a two-dimensional coordinate system, 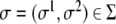, onto a surface embedded in the three-dimensional space. This way of defining a surface is called the parametric form, since one needs a two-dimensional coordinate system to parametrize the surface. A surface can also be described by the so-called implicit form, i.e., by all the points in 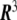that satisfy the surface equation F(x,y,z) = 0 [10].

Parametric form

Assume a surface defined in the parametric form. At each point P of this surface, a tangent plane is defined by two tangent vectors (see Fig. 5) as

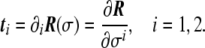42

The scalar product of these tangent vectors defines the covariant metric tensor,

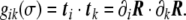43

The contravariant metric tensor is defined as

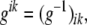44

which implies that

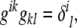45

where δ is the Kronecker delta, and the Einstein summation convention, 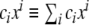, is used. From the metric tensor, the Euclidean distance between two infinitesimally close points on the surface, d s, can be calculated as

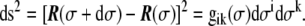46

Also, the infinitesimal area element can be found

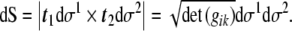47

At any point P on the surface, a unit normal vector perpendicular to the tangent plane can be defined (Fig. 5). Due to the properties of the cross product, it is given by

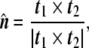48

where the sign is arbitrarily chosen; so is the election of which coordinate is named σ¹ and which σ². The unit normal vector has remarkable properties in our context, since its changes along the surface define the so-called curvature tensor, K,

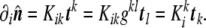49

The sign of the curvature tensor is, again, arbitrary. In this thesis, we choose it in such a way that sphere-like curvatures are positive, as it is a normal convention in physics. In mathematical literature, the sign is most often taken in the opposite way.

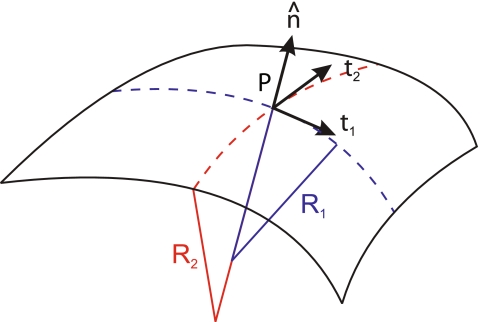
Fig. 5.

Differential geometry of a surface. In the point P, two tangent vectors, and 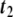, are defined. From them, a unit normal vector 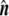is constructed, pointing outwards. Also, two radii of curvature, R₁ and R₂, are geometrically traced at each point

The curvature tensor is symmetric and diagonalizable. The two eigenvalues are the so-called principal curvatures, c₁ = 1/R₁ and c₂ = 1/R₂ (see Fig. 5). These curvatures correspond to the inverse of the two principal radii of curvature of the surface at the given point. The two invariants of the curvature tensor, K, are its trace, 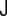, and its determinant, 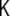. The trace is called total curvature of the surface, 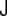, and is represented by

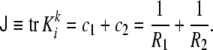50

Usually, the so-called mean curvature, is also used to refer to this invariant, and is defined as the arithmetic mean of the principal curvatures, corresponding to half the total curvature,

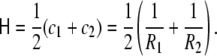51

The other invariant, the determinant, is called the Gaussian curvature of the surface, 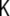, and is given by the product of the principal curvatures,

52

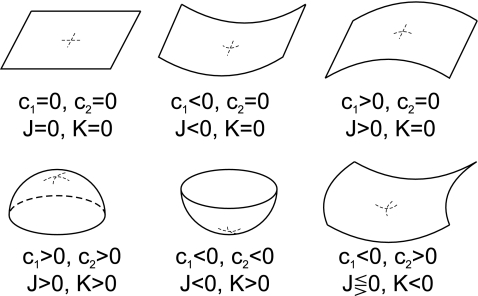
For a discussion on the signs of the curvatures depending on the different kinds of shapes, see Fig. 6.

Fig. 6.

Different kinds of surfaces classified by their curvatures. Depending on the sign of the two principal curvatures, different kinds of surfaces have positive–zero–negative combinations of the total and Gaussian curvatures, as written in the figure

Monge parametrization All the definitions in the previous section are general for any surface defined by a parametric form. A simple but useful example of a parametrization is one where the coordinates are nothing other than the x,y Cartesian coordinates, and the vector field describing the surface is

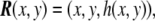53

where the third Cartesian coordinate, the height, is z = h(x,y). This is called the Monge parametrization, named after the French mathematician Gaspard Monge. Under this parametrization, which is definitely valid for almost planar surfaces (the height function h(x,y) has to be univaluated), the tangent vectors Eq. 42 are

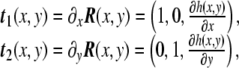54

and the covariant metric tensor

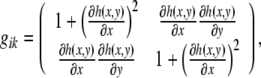55

with determinant

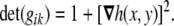56

The normal vector Eq. 48 is

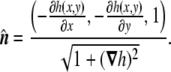57

Wherefrom the total and Gaussian curvatures can be calculated:

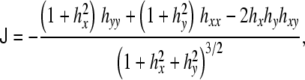58

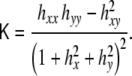59

In the limit of nearly flat surface, where h_x ≪ 1, and h_y ≪ 1, the curvature invariants read

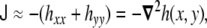60

and

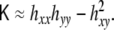61

Implicit form

In the case where a two-dimensional surface is implicitly defined by a function F such as

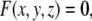62

we can also find the curvature tensor and all the geometric properties of such a surface. First, we have to note that, since the surface is defined by the level-set of a function, this function is constant on the surface; therefore,

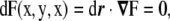63

where 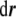is a vector that connects any two points in this surface, being tangent to a certain direction in the surface. Because of this fact, from Eq. 63, we infer that the vector 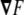is normal to the surface at the point (x,y,z). The unit normal vector is found by normalizing it,

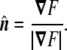64

Once the normal vector is known, the curvature tensor, 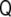, can be defined by the changes of this vector along the tangent directions, namely,

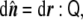65

where the colon symbolizes tensor contraction. By differentiating Eq. 64, we can write the curvature tensor as a function of the derivatives of the implicit function as

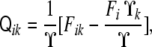66

where 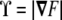and 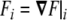. Note that this curvature tensor 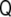differs from the curvature tensor K_ik (Eq. 49) we used in the previous section, the former being represented by a 3×3 matrix and the latter by a 2×2 matrix. Here, the tensor has three invariants, although one of them is a trivial one (the determinant of the tensor is zero [97]). The other two, the trace and the sum of the principal minors, define the total and Gaussian curvatures, respectively. They read as

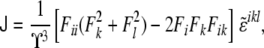67

where 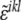is a modified Levi-Civita symbol, such as 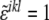for all even permutations of the indices, and zero otherwise. The Gaussian curvature is, similarly, given by

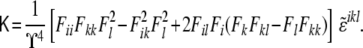68

The Monge representation can also be implemented by using an implicit form of the surface, by defining the function

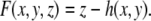69