Decision Making in Fuzzy Discrete Event Systems

Abstract

The primary goal of the study presented in this paper is to develop a novel and comprehensive approach to decision making using fuzzy discrete event systems (FDES) and to apply such an approach to real-world problems. At the theoretical front, we develop a new control architecture of FDES as a way of decision making, which includes a FDES decision model, a fuzzy objective generator for generating optimal control objectives, and a control scheme using both disablement and enforcement. We develop an online approach to dealing with the optimal control problem efficiently. As an application, we apply the approach to HIV/AIDS treatment planning, a technical challenge since AIDS is one of the most complex diseases to treat. We build a FDES decision model for HIV/AIDS treatment based on expert’s knowledge, treatment guidelines, clinic trials, patient database statistics, and other available information. Our preliminary retrospective evaluation shows that the approach is capable of generating optimal control objectives for real patients in our AIDS clinic database and is able to apply our online approach to deciding an optimal treatment regimen for each patient. In the process, we have developed methods to resolve the following two new theoretical issues that have not been addressed in the literature: (1) the optimal control problem has state dependent performance index and hence it is not monotonic, (2) the state space of a FDES is infinite.

1. Introduction

The supervisory control theory of discrete event systems (DES) (see, for example, [12, 7, 1]) has been applied to many engineering fields. In most of engineering applications, the states of a DES are crisp. However, this is not the case in many other applications in complex systems such as biomedical systems and economic systems. For instance, it is vague when a company’s financial situation is said to be “good”. Furthermore, the transition from one state to another is also vague. It is hard to say at what point exactly a company’s condition has changed from “good” to “bad”. For such applications, we need to introduce fuzzy logic to DES.

In a conference paper [8] and then a journal paper [9], we first proposed a new method for control of fuzzy discrete event systems (FDES). [8] also introduces observability of FDES, which extends the observability theory of crisp DES [7]. [9] further extends the results of [8] to control of FDES by considering an optimal control problem.

Since the publication of [8, 9], other researchers have continued the work in FDES. For example, [11] studies the controllability theorem and nonblocking controllability theorem for FDES and derives the conditions for the existence of supervisors for FDES. More recent works include [21,22].

Meanwhile, our focus has been on applying the FDES theory to clinical treatment planning, in particular, to HIV/AIDS treatment, because it is one of the most challenging treatment decision processes in medicine. We study real patients’ data and drug regimens, using the most up-to-date treatment practices. Our results have been presented in two conference papers [10, 18]. In [10], an online approach is proposed to solve an optimal control problem of FDES, which is at the heart of our application. The optimal control problem is nontrivial because its performance index is state dependent and hence not monotonic. Furthermore, the state space of a FDES is infinite in general. We show that an online approach can solve this problem efficiently. In [18], we apply FDES theory to design a treatment planning system for HIV/AIDS patients who have never received highly active antiretroviral therapy (HAART). We also statistically evaluate the preliminary results produced by the system in comparison with two HIV/AIDS specialists on our team. The results indicate strong agreement between the physicians and the FDES.

Despite the progress made in [10, 18], we realized that the existing control architectures needed to be improved for our application and other applications in complex systems. This is because, in particular, optimization objectives depend on each particular case and the corresponding input data, and are not as obvious and easy to obtain as in engineering applications. Therefore, we propose a new control architecture in this paper.

In the architecture, two major modeling parts are FDES decision model and fuzzy objective generator. Both parts are built from expert’s knowledge, statistics of relevant database, and other information available in the literature [5, 10, 13, 20, 23, 28, 29]. We will outline how these two parts were built using the example of HIV/AIDS treatment, but we will omit some details for the sake of brevity.

The fuzzy objective generator that produces optimization objectives on a case-by-case basis for any given patient’s conditions is a new feature in this architecture. For example, for HIV/AIDS treatment, this generator takes a patient’s conditions (e.g., plasma HIV RNA levels and CD4+ counts–two most important measures of the extent of the disease) as inputs and determines the objectives for optimization in terms of a performance index.

The optimization is done using online optimal control. We extend the results in [10] to accommodate the performance index obtained by the fuzzy objective generator. For the applications that we have in mind, the performance index is often state dependent rather than event dependent, as it is in most optimal control problems in crisp DES. Therefore, the performance index is not monotonic, which makes the problem much more difficult. The online approach investigated in this paper can solve such optimal control problems efficiently. Online approaches for controlling crisp DES were first proposed in [2, 3, 4]. Our control mechanism includes both disablement and enforcement, which is similar to a generalized framework proposed in [6].

The published results on using fuzzy discrete event systems to clinical treatments are very limited. We are only aware of [14], where fuzzy automata are used in clinical monitoring (see also [15]). Knowledge-based records for HIV patient are discussed in [13]. More generally, fuzzy logic is often used to deal with uncertainties [17]. Other methods to deal with uncertainties in discrete event systems include reinforcement learning [16, 19].

This paper is divided into two main parts. We first present the control architecture and theoretical issues related to the architecture. We then illustrate the theoretical results with the example of our application for HIV/AIDS treatment.

2. Control Architecture

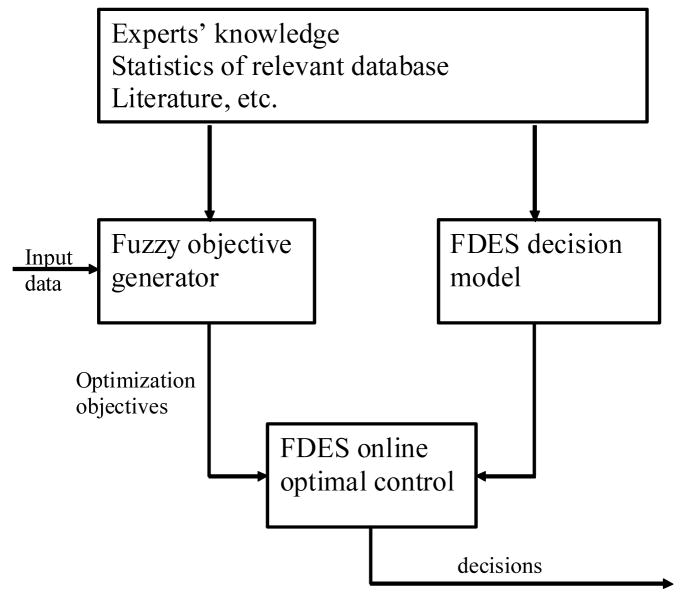
Our proposed control architecture is shown in Figure 1. It consists of three blocks: (1) Fuzzy objective generator, (2) FDES decision model, and (3) FDES optimal control. We discuss these blocks in this section.

Figure 1.

Control architecture of FDES.

2.1. FDES Decision Model

The FDES decision model describes various decisions available and their expected results. We have proposed that the best way to build such a model is to use a fuzzy automaton [8, 9], denoted as

$$G=(Q,\mathrm{\sum },\delta ,q_o).$$

In G, Q = [0,1]ⁿ is the fuzzy state space, with n being the number of states. A state vector q ∈ Q is a vector q = [v₁,v₂,…, v_n], where v_i ∈ [0,1] is the possibility (membership function) that the system is in state i. Σ= {σ¹,σ²,…,σ^m} is the set of events. Each event σ^k is represented by a matrix ${\sigma }^k={[{\sigma }_{ij}^k]}_{n\times n}$, where ${\sigma }_{ij}^k$ is the possibility that if σ^k occurs, the system will move from state i to state j. δ describes the state (vector) transition: If the current state vector is q and event σ^k occurs, then the next state vector is q′ = q ○σ^k, where ○ is some fuzzy operation specified by δ. q_o ∈Q is the initial state vector. Note that unlike a crisp DES, whose state space is usually finite, the state space of a fuzzy DES is usually infinite.

In general, the FDES decision model may consists of N components for different aspects of the decision making, modeled by N fuzzy automata

$$\begin{array}{llll}{G}_1\hfill & G_2\hfill & \dots \hfill & G_N.\hfill \end{array}$$

Their state vectors are denoted by q₁ q₂… q_N respectively. Their event sets are denoted by Σ₁ Σ₂ … Σ_N respectively, which may or may not be disjoint. Σ = Σ₁∪Σ₂∪… ∪Σ_N is the set of all events in the system.

In the HIV/AIDS treatment planning example to be discussed below, the FDES decision model consists of four fuzzy automata, one for each of the following four aspects (factors) considered by doctors when deciding which drug regimen to use: potency of the regimen, adherence to the regimen, adverse events caused by the regimen, and future drug options if the current regimen fails. Each fuzzy automaton has 3 or 4 states. For example, the fuzzy automaton for potency has the following three states: Initial (pre-treatment), High, and Medium (referring to the expected potency of the regimens). The events describe the use of a particular regimen. For potency, the events are represented by 3×3 matrices. These fuzzy automata (including event matrices) are obtained from expert’s knowledge, treatment guidelines, clinic trials, patient database statistics, and other information available in the medical literature [18, 10].

2.2. Optimization Objectives

The FDES decision model describes the anticipated results of various decisions. Which result is expected to be optimal for a particular case depends on its circumstances as specified by the input data and may change from case to case. In the proposed architecture, this is formalized as how to determine optimization objectives for a particular case.

More specifically, the optimization objectives are determined by (1) a fuzzy function (or mapping) from the input data to fuzzy discrete states describing the desired outcomes, and (2) a mapping from the fuzzy discrete states to weight vectors. The weight vector of a particular case describes the optimization objectives for that case. Formally, this can be modeled as follows:

• Let P be a set of input data.

• Let S = S₁×S₂×… ×S_N be a set of fuzzy discrete states. Here s_i ∈ S_i = [0,1]^li describes the ith aspect of the desired outcomes and l_i is the number of states in S_i.

• Let W = W₁×W₂×… ×W_N be a set of weight vectors. Here w_j ∈ W_j = R^nj is the weight vector corresponding to the jth automaton G_j in the FDES decision model and n_j is the number of states in G_j.

The optimization objectives can be formally determined by two mappings f and e:

$$P\stackrel{f}{\to }S\stackrel{e}{\to }W.$$ (1)

To specify f in Equation 1, we often consider f = f₁×f₂×… ×f_L, where f_i: P→S_i can be obtained by a set of fuzzy rules combined with various fuzzy operations. For example, doctors may use the following rule to determine the desired treatment outcome for potency: “If a patient’s CD4+ cell count (a measure of the degree of immunosuppression or immunodeficiency) is less that 50 cells/μL (profound immunodeficiency), then use a regimen with high expected potency”.

In our example of HIV/AIDS treatment, various rules have been obtained by extensive interviews with HIV/AIDS specialists in our team. This process is very time-consuming and often requires several iterations. Fuzzy operations can also be used to combine some of these rules and different weights can be used for different rules. The final output of f is the desired treatment choices represented by fuzzy discrete states. For example, for a particular patient, the desired treatment choice might be an anticipated membership of 0.65 for “medium potency” with a corresponding membership of 0.35 for “high potency”.

A weight vector for optimization is then determined from the fuzzy discrete states obtained from f. This relationship is described by the mapping e in Equation 1. In our example of HIV/AIDS treatment, the mapping e is determined as follows. We first determine the weight vectors for the “extreme” states, for example, the state of medium potency (medium potency with membership 1 and high potency with membership 0). This is done by asking doctors’ choices of treatment under various states and trying to match their choices as closely as possible. Since doctors often disagree with each other on the best treatment, this process can be complicated, but we have developed some effective procedures for doing this using generic algorithms [18]. After determining the weight vectors for the extreme states, we use linear interpolation to determine the weight vectors for other states.

We use the following notation for the weight vectors: If the fuzzy state of the FDES decision model is q₁ q₂ … q_N, then the corresponding weight vector is denoted by w₁ w₂ … w_N. The performance index for state q = [q₁, q₂,…, q_N] is then given by

$$J(q)=w_1^T{q}_1+w_2^T{q}_2+\dots +w_N^T{q}_N.$$ (2)

2.3. Online Optimization

Online optimization is achieved by applying optimal control of FDES. To this end, we assume that some of the events can be disabled or enforced. The events that can be disabled are called controllable events. The events that can be enforced are called enforceable events. The set of controllable events is denoted by Σ_c (Σ_c ⊆ Σ). The set of enforceable events is denoted by Σ_f (Σ_f ⊆Σ). This control mechanism is similar to a generalized framework for crisp DES proposed in [6].

Control is achieved by disabling some controllable events and/or enforcing some enforceable events. Note that the control mechanisms are crisp in that if an event is disabled, then its occurrence can be prevented with certainty. Similarly, if an event is enforced, then it will definitely occur.

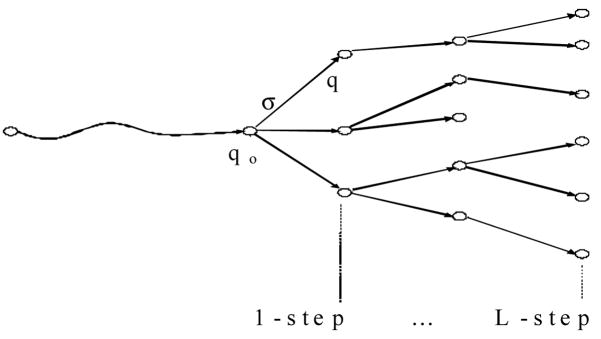
Our goal is to maximize the performance index J(q). We do this using an online approach. Online (optimal) control for crisp DES has been studied in the literature. For crisp DES, to design a control online, we do the following [2]: After each occurrence of events, the controller will evaluate the possible future execution of the system and determine which events to disable and which events to enforce. Therefore, we will construct a forward-looking tree as shown in Figure 2.

Figure 2.

Forward-looking tree for online control synthesis.

For a fuzzy DES, the construction of this tree is different than for the tree construction for a crisp DES. Each node in the tree no longer represents a crisp state, but rather a fuzzy state with vector q = [q₁,q₂,…,q_N], where q_i is the state vector of component G_i. If an event σ occurs in the system, the next state vector is q′ = [q′₁,q′₂,…,q′_N], where q′_i is calculated as follows. If σ is an event in G_i, then q′_i = q_i ○ σ. If σ is not an event in G_i, then q′_i = q_i. In this way, each node is represented by the corresponding state vector q. The root of the tree represents the current state vector. How big the tree is depends on the number of forward-looking steps, denoted by L. Looking ahead further will produce better results, but also requires more computation. Also, a variable look-ahead policy may be used by specifying some intelligent terminating conditions [3]. The main difference between a crisp DES tree and the fuzzy DES tree is that there are more branches in the fuzzy DES tree, because the system can now be partially in more than one state and, therefore, more events are possible at each node in the fuzzy DES tree. We denote the forward-looking tree by T(q_o). For a node q in T(q_o), the next node after executing an event σ is denoted by child(q,σ).

In our example of HIV/AIDS treatment, a one-step tree corresponds to first round treatments and two-step tree corresponds to both first round and second round treatments. Each branch of the tree represents the use of a particular regimen.

After constructing the forward-looking tree, we use the output of fuzzy objective generator to compute the performance index J (q) for each node using Equation 2.

Our goal is to design a control (using disablement and enforcement) so that the above performance index can be maximized at the Lth step of the forward-looking tree, that is,

$$\underset{\gamma }{max}J(q_L),$$

where γ is the control (disablement and enforcement) and q_L is the nodes at the Lth step of the forward looking tree.

The control is specified by events to be disabled or enforced at each node in T(q_o), which is given by two control maps:

$$\begin{array}{l}{C}_d^{\ast }:T(q_o)\to 2^{{\mathrm{\sum }}_c}\\ C_f^{\ast }:T(q_o)\to {\mathrm{\sum }}_f\cup \{\epsilon \}\end{array}$$

where $C_d^{\ast }(q)$ is the set of events to be disabled at node q and $C_f^{\ast }(q)$ is the event to be enforced at node q. If $C_f^{\ast }(q)=\epsilon$, then no event is enforced. We assume that enforcement has priority over disablement. That is, if $C_f^{\ast }(q)=\sigma$, then the only event that will occur in q is σ, even if it is disabled ( $\sigma \in C_d^{\ast }(q)$).

To compute $C_d^{\ast }(q)$ and $C_f^{\ast }(q)$, we first calculate the performance achievable at each node q in T(q_o) under control, called controlled performance and denoted by J_c(q), by recursively backtracking from L-step nodes at the boundary of T(q_o) as follows.

For a L-step node q, the controlled performance is equal to its performance, because no control is given at q

$$J_c(q)=J(q).$$

If the controlled performance for all (i+1)-step nodes is calculated, then the controlled performance of an i-step node can be calculated by considering the following two cases.

1. No event is enforced. In this case, the system will either stay in q or one of the enabled events σ will occur, taking the system to child(q,σ). Since we do not know which will actually occur, the controlled performance is the minimum of all possibilities:

   $$\underset{\sigma \notin C_d^{\ast }(q)}{min}\{J(q),J_c(\mathit{child}(q,\sigma ))\}.$$ (3)

   Obviously, to maximize the above minimum, the controller needs to disable as many events as possible (Note that enforcement will overwrite disablement). Therefore $C_d^{\ast }(q)={\mathrm{\sum }}_c$ for all q∈T(q_o).

2. Event σ′∈Σ_f is enforced. In this case, the controlled performance is

   $$J_c(\mathit{child}(q,{\sigma }^{\prime })).$$ (4)

   Since both (1) and (2) are valid control. The optimal control will be the one that maximizes the expressions in Equations 3 and 4:

   $$J_c(q)=\underset{{\sigma }^{\prime }\in {\mathrm{\sum }}_f\cup \{\epsilon \}}{max}\{J_c(\mathit{child}(q,{\sigma }^{\prime })),\underset{\sigma \notin {\mathrm{\sum }}_c}{min}\{J(q),J_c(\mathit{child}(q,\sigma ))\}\}$$

2.4. Extended Optimization Problem

The above optimization problem with one performance index is sufficient for our HIV/AIDS treatment planning application. However, for other applications, we may want to use two performance indexes, one for effectiveness and one for cost. We therefore define the effectiveness M(q) and cost C(q) for each node. Both are functions of q = [q₁,q₂,…,q_N]:

$$M(q)=f_M(q_1,q_2,\dots ,q_N),C(q)=f_C(q_1,q_2,\dots ,q_N)$$

They can be obtained using the fuzzy objective generator in a way similar to that for J(q) in Equation 2.

The extended optimization problem is to maximize the effectiveness for a given cost. In other words,

$$maxM(q),\mathit{such}\mathit{that}C(q)<C_{max}$$ (5)

where C_max is a (given) constant restricting the maximum cost.

Our goal is to design a control so that the optimization in Equation 5 can be achieved. The design will be done in two steps: (1) to design a safety controller to ensure that the maximum cost will never be exceeded; and (2) to design an optimal controller to maximize the effectiveness.

To design a safety controller, let us first identify all nodes in the forward-looking tree T(q_o) whose cost is greater than C_max and denote these “undesired nodes” as

$$UN(q_o)=\{q\in T(q_o):C(q)\ge C_{max}\}.$$

Obviously, a safety controller must ensure that the system will never enter these undesired nodes. This is similar to the safety problem in the supervisory control theory [12, 7], with additional control mechanism of enforcement that is not available in the supervisory control (see [6]). The safety controller is specified by events to be disabled or enforced at each node in T(q_o), which is given by two control maps:

$$\begin{array}{l}{C}_d^s:T(q_o)\to 2^{{\mathrm{\sum }}_c}\\ C_f^s:T(q_o)\to 2^{{\mathrm{\sum }}_f}\end{array}$$

where $C_d^s(q)$ is the set of events needed to be disabled at node q and $C_f^s(q)$ is the set of events needed to be enforced at node q (which one of $C_f^s(q)$ will be actually enforced will be determined by the optimal controller). To compute $C_d^s$ and $C_f^s$, we will calculate the set of nodes that have the potential of becoming undesirable. This set is denoted by BN and is calculated recursively as follows. Initially, we have BN = UN(q_o). We then consider all the “neighbors” of BN:

$$\pi (BN)=\{q\in T(q_o):(\exists \sigma \in \mathrm{\sum })\mathit{child}(q,\sigma )\in BN\}.$$

A node q∈π(BN) shall be added to BN if there exists an uncontrollable event that leads to BN and there exists no enforceable event that can prevent it from leading to BN. The set is denoted by

$$\mu (BN)=\{q\in \pi (NB):(\exists \sigma \notin {\mathrm{\sum }}_c)\mathit{child}(q,\sigma )\in BN\wedge (\forall \sigma \in {\mathrm{\sum }}_f)\mathit{child}(q,\sigma )\in BN\}.$$

In this way, we can calculate BN. If the root of the tree q_o ∉ BN, then a safety controller exists and is given as follows. For q∈T(q_o) −BN,

$$\begin{array}{l}{C}_d^s(q)=\{\sigma \in {\mathrm{\sum }}_c:\mathit{child}(q,\sigma )\in BN\},\\ C_f^s(q)=\{\begin{array}{ll}\{\sigma \in {\mathrm{\sum }}_f:\mathit{child}(q,\sigma )\notin BN\}\hfill & if(\exists {\sigma }^{\prime }\notin {\mathrm{\sum }}_c)\mathit{child}(q,{\sigma }^{\prime })\in BN\hfill \\ \epsilon \hfill & \mathit{otherwise}\hfill \end{array}\end{array}$$

For q ∈ BN, $C_d^s(q)$ and $C_f^s(q)$ is undefined because the system shall never get into these nodes.

When the safety controller is in place, we can then design an optimal controller, which is given by

$$\begin{array}{l}{C}_d^o:T(q_o)\to 2^{{\mathrm{\sum }}_c}\\ C_f^o:T(q_o)\to {\mathrm{\sum }}_f\cup \{\epsilon \}\end{array}$$

where $C_d^o(q)$ is the set of events to be disabled at node q and $C_f^o(q)$ is the event to be enforced at node q. The computation of $C_d^o(q)$ and $C_f^o(q)$ is similar to that of $C_d^{\ast }(q)$ and $C_f^{\ast }(q)$ discussed in Section 2.3, with the forward-looking tree T(q_o) replaced by T(q_o) − BN.

3. Example of HIV/AIDS Treatment

3.1. Problem Description

In this section, we illustrate our new architecture by applying it to HIV/AIDS treatment. We selected HIV/AIDS treatment as our application area because it arguably involves some of the most complex therapeutic decision processes in medical science. This complexity is partly due to the fact that there is no cure for HIV/AIDS. Therefore, the current treatments can only suppress the HIV virus (by reducing the plasma HIV RNA levels) and boost the immune system (by increasing the CD4+ cell counts). This is done by using a combination of two or more classes of drugs to create a drug regimen. Since the number of drug classes available is rather limited (4 total) and it is easy for the virus to develop resistance if a patient does not adhere to the medication, it is not a trivial task to decide which regimen to use for a particular patient. If a wrong decision is made, the patient may run out of options on available drugs much sooner than otherwise.

In deciding which regimen to use, doctors consider mainly the following four factors:

1. Potency: This may be counterintuitive, but unlike treatments of many other diseases, it is not always desirable to use the most potent regimen for HIV/AIDS treatment. In fact, at the initial stage after HIV infection, it is probably best not to use any regimen at all, because initiating antiretroviral therapy when the immune system is reasonably intact does not prolong survival any more than delaying therapy until a more substantial degree of immunosuppression exists. As one can see, this factor alone makes HIV/AIDS treatment more complex than treatments of many other diseases.

2. Adherence: Again, unlike treatments of most other diseases, adherence is critical to the future success of any HIV/AIDS regimen. Missing more than 5% of doses dramatically reduces the probability that a patient will enjoy the maximum benefits of antiretroviral therapy and also increases the risk of the virus eventually developing resistance to the drugs or the classes of drugs in the regimen. Once HAART resistance has developed within a patient, the use of these drugs or drug classes may be lost forever for that patient. Since there are only very limited number of drugs, such loss of drugs will significantly shorten the life of a patient. Studies of HIV/AIDS and other chronic diseases demonstrate that without efforts to increase a patient’s adherence, patients may take only 50–70% of prescribed doses of long-term medications; so achieving ideal levels of adherence with antiretroviral medications is very challenging.

3. Adverse events: Adverse events include side effects (mild to severe) and toxicity (including potentially severe interactions with other concurrently-used medications). Side effects are common in HIV/AIDS treatment, especially during the early stages of therapy. Typical mild-moderate symptoms include abdominal discomfort, loss of appetite, diarrhea, nausea and vomiting. Toxicity may cause liver problems (hepatitis), osteopenia/osteoporosis, leukopenia, pancreatitis, hyperglycemia, etc. and in some instances can be fatal.

4. Future drug options: Perfect adherence with complex regimens is difficult for patients to maintain over long periods of time. Development of drug resistance frequently occurs. Therefore, before deciding on a regimen, it is important to consider the future drug options after the resistance occurs. In other words, available regimens must be sequenced appropriately to preserve maximal availability of the drugs.

The above four factors are interrelated. For example, adverse events may cause non-adherence, which in turn will reduce the potency of a regimen.

Based on patient’s conditions, as observed by the doctor and reflected in the test data, the doctor must decide which regimen to use. Typically, the decision process of a doctor can be conceptualized into two steps. In the first step, the doctor decides patient’s desired treatment outcomes. For example, is it best to treat the patient with a regimen that has a medium potency, easy adherence, low adverse events, and high future drug options or a regimen that has a high potency, moderate adherence, medium adverse events, and high future drug options? After this is decided, the doctor then selects a regimen that can best achieve the desired treatment outcomes in the second step.

Our FDES methodology and architecture follow the same line of reasoning as used by the doctors. We first decide a patient’s desired treatment outcomes using fuzzy sets and associated methods. We then use an (online) optimization to determine which regimen to use. Both processes depend on the FDES decision model that we must first establish.

In this paper, we consider only treatment-naïve patients, that is, those patients who have never been treated by HAART. We consider first one or two rounds of treatment of these patients. We also limit the regimens to those that are commonly used at the time when our data were collected. These regimens are combinations of drugs in the following three classes: (1) Protease inhibitors (PIs); (2) Nucleoside reverse transcriptase inhibitors (NRTIs); and (3) Non-nucleoside reverse transcriptase inhibitors (NNRTIs).

3.2. Determine FDES Treatment Model

Our FDES decision model consists of four components for the four factors considered in the treatment, modeled by four fuzzy automata

$$\begin{array}{llll}{G}_1\hfill & G_2\hfill & G_3\hfill & G_4\hfill \end{array}.$$

G₁ models potency. It has three states: Initial, Medium, and High. Before treatment, G₁ is at the Initial state. After treatment using a particular regimen, G₁ moves to the Medium (potency) state or High (potency) state. Using a particular regimen is modeled as an event. For the first round of treatment, we consider three commonly used regimens. Therefore, we define the following three events (CBV etc. are acronyms for drug names).

• α₁: Using regimen CBV+EFV;

• α₂: Using regimen CBV+NVP;

• α₃: Using regimen CBV+ABC.

The matrices describing these events in G₁ are obtained from the characteristics of these regimens shown in Table 1. The table represents the consensus reached by experts on the four factors discussed above. The table shall be interpreted as follows. Potency: the percentage of patients who achieve plasma HIV RNA less than 400 copies/mL after 48 weeks of treatment; Adherence: the percentage of prescribed doses taken weekly for each regimen; Adverse events: the percentage of patients who experience undesirable side effects (Grades 1 to 2) and toxicities (Grades 3 and 4); and Future drug options: the percentage of drugs remaining that have efficacy in the presence of detected or expected mutations already selected.

Table 1.

Characteristics of the three regimens.

	Potency	Adherence	Adverse events	Future drug options
Regimen 1: CBV+EFV	90%	80%	20%	60%
Regimen 2: CBV+NVP	85%	85%	20%	60%
Regimen 3: ABC+CBV	80%	90%	10%	85%

Based on Table 1, the transition matrices for events can be computed using fuzzy logic. The detailed procedure to compute these matrices is long and omitted here but can be found in [18]. For example the matrix for α₁ is given by

$${\alpha }_1=\left[\begin{array}{ccc}0& 0.1652& 0.8348\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]$$

For the second round of treatment, we consider six regimens, which are grouped into three classes. Therefore, we define the following three events.

• β₁: Using NNRTI regimens EFV+ABC+d4T or EFV +TDF+ddI;

• β₂: Using PI regimens ATV+ABC+d4T or Fos-Amp +TDF+ddI;

• β₃: Using a ritonavir-boosted PI regimen ATV/r+ABC+ddI or LPV/r+ABC+d4T;

Based on a table (not shown here) similar to Table 1 for the second round regimens, we can determine the matrices describing these events in G₁.

• G₂ models adherence. It has four states: Initial, Challenging, Moderate, and Easy. Therefore, the matrices describing events α_i and β_j in G₂ have dimension 4×4.

• G₃ models adverse events. It has four states: Initial, Medium, Low, and Very Low. Therefore, the matrices describing events α_i and β_j in G₃ have dimension 4×4.

• G₄ models future drug options. It has three states: Initial, Medium, and High. Therefore, the matrices describing events α_i and β_j in G₄ have dimension 3×3.

After obtaining G_i, i = 1,2,3,4, we can construct the forward-looking tree for one or two rounds of treatment as shown in Figure 3². In the figure, the dotted lines stand for the second round regimens that are most likely to be unavailable because of the drug resistance. Therefore, we will not consider these regimens. The initial node q = 0 in the figure is represented by the four initial state vectors as follows.

Figure 3.

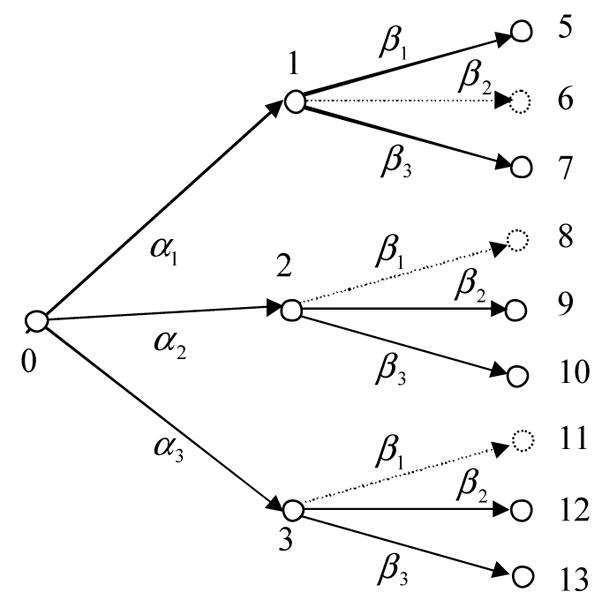
Forward-looking tree for two rounds of HIV/AIDS treatment.

$$q_1=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right],q_2=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right],q_3=\left[\begin{array}{c}1\\ 0\\ 0\\ 0\end{array}\right],q_4=\left[\begin{array}{c}1\\ 0\\ 0\end{array}\right].$$

The vectors for other nodes are calculated from the initial state vector and the corresponding event matrices as described in Section 2.1. For example, the state vectors for node q = 7 is

$$q_1=\left[\begin{array}{c}0\\ 0.2313\\ 0.7687\end{array}\right],q_2=\left[\begin{array}{c}0\\ 0.2098\\ 0.4442\\ 0.3460\end{array}\right],q_3=\left[\begin{array}{c}0\\ 0.1561\\ 0.3630\\ 0.4809\end{array}\right],q_4=\left[\begin{array}{c}0\\ 0.1996\\ 0.8004\end{array}\right].$$

3.3. Determine Weight Vectors

After we obtain the FDES decision model and construct the forward-looking tree, the next step is to calculate the performance index J(q) for each node in the tree:

$$J(q)=w_1^T{q}_1+w_2^T{q}_2+w_3^T{q}_3+w_4^T{q}_4.$$

To this end, we need to determine the weight vectors w_i, i = 1,2,3,4, which vary from patient to patient.

The weight vectors for a particular patient are obtained from two mappings $P\stackrel{f}{\to }S\stackrel{e}{\to }W$ as in Equation 1. Let us discuss the second mapping from fuzzy discrete states describing patient’s desired treatment outcomes S to the weight vectors W first. The mapping is obtained by asking experts about their ranking of regimens for different “extreme cases” of patients’ desired treatment outcomes. For desired potency, there are two extreme cases: High and Medium. For desired adherence, there are three extreme cases: Easy, Moderate, and Challenging. For desired adverse events, there are three extreme cases: Medium, Low, and Very Low. For desired future drug options, there are two extreme cases: High and Medium. Therefore, there are 2 × 3× 3 ×2 = 36 combinations of extreme cases (some of these combinations may not be sensible clinically). The experts are asked to rank the three regimens (for the first round) for these combinations. Table 2 shows a part of the ranking of one expert. For example, if it is most desirable to treat the patient with a regimen that has a high potency, easy adherence, medium adverse events, and high future drug options, then Regimen 3 is the 1^st choice, Regimen 1 is the 2^nd choice, and Regimen 2 is the 3^rd choice (the first row).

Table 2.

A part of an expert’s ranking of the three regimens.

Potency	Adherence	Adverse events	Future drug options	1st choice	2nd choice	3rd choice
High	Easy	Medium	High	3	1	2
High	Easy	Medium	Medium	1	2	3
High	Moderate	Very Low	Medium	1	3	2

Based on these rankings, we can determine the ten weight vectors for the extreme cases using generic algorithms. The detailed procedure of generic algorithms is not the focus of this paper and is omitted here. The resulting weight vectors are:

$$\begin{array}{l}{W}_{HP}^1=[\begin{array}{lll}0\hfill & 0\hfill & 1\hfill \end{array}]\text{for}\text{high}\text{potency};\\ W_{MP}^1=[\begin{array}{lll}0\hfill & 0.4388\hfill & 0.5612\hfill \end{array}]\text{for}\text{medium}\text{potency};\\ W_{EA}^1=[\begin{array}{llll}0\hfill & 0.0556\hfill & 0.5000\hfill & 0.4444\hfill \end{array}]\text{for}\text{easy}\text{adherence};\\ W_{MA}^1=[\begin{array}{llll}0\hfill & 0.5189\hfill & 0.4623\hfill & 0.0189\hfill \end{array}]\text{for}\text{moderate}\text{adherence};\\ W_{CA}^1=[\begin{array}{llll}0\hfill & 0.2069\hfill & 0.5402\hfill & 0.2529\hfill \end{array}]\text{for}\text{challenging}\text{adherence};\\ W_{ME}^1=[\begin{array}{llll}0\hfill & 0.1250\hfill & 0.3304\hfill & 0.5446\hfill \end{array}]\text{for}\text{medium}\text{adverse}\text{events};\\ W_{LE}^1=[\begin{array}{llll}0\hfill & 0.3557\hfill & 0.3154\hfill & 0.3289\hfill \end{array}]\text{for}\text{low}\text{adverse}\text{events};\\ W_{VE}^1=[\begin{array}{llll}0\hfill & 0.3374\hfill & 0.3129\hfill & 0.3497\hfill \end{array}]\text{for}\text{very}\text{low}\text{adverse}\text{events};\\ W_{HF}^1=[\begin{array}{lll}0\hfill & 0.1455\hfill & 0.8545\hfill \end{array}]\text{for}\text{high}\text{future}\text{drug}\text{options};\\ W_{MF}^1=[\begin{array}{lll}0\hfill & 0.4767\hfill & 0.5233\hfill \end{array}]\text{for}\text{medium}\text{future}\text{drug}\text{options}.\end{array}$$

These ten weight vectors are for the first round treatment and will be used to calculate w_i, i = 1,2,3,4 as to be shown below. In a similar way, we can determine another ten weight vectors for the second round treatment. They are denoted by $W_{HP}^2,W_{MP}^2,W_{EA}^2,W_{MA}^2,W_{CA}^2,W_{ME}^2,W_{LE}^2,W_{VE}^2,W_{HF}^2,W_{MF}^2$ respectively.

The first mapping in $P\stackrel{f}{\to }S\stackrel{e}{\to }W$ is the mapping from patient’s conditions and clinical test data P to fuzzy discrete states describing patient’s desired treatment outcomes S. This mapping is implemented as a set of fuzzy rules. These fuzzy rules are based on experts’ opinion on what are the patient’s desired treatment outcomes given patient’s conditions and clinical test data. There are total 17 fuzzy rules in the current system. For example, for potency, the experts’ opinion is as follows.

1. If a patient’s CD4+ cell count is less than 50 cells/μL or the CD4+ cell count is less than 200 cells/μL and HIV RNA is greater than 100,000 copies/ml, then a regimen with high expected potency must be used;

2. If a patient’s CD4+ cell count is greater than 200 cells/μL and HIV RNA is less than 100,000 copies/ml, then a regimen with medium expected potency must be used.

3. Otherwise, a regimen with either medium or high expected potency may be used. We build a fuzzy potency system to formalize the above experts’ opinion. The system has two input variables, CD4+ and HIV RNA; and two output variables H_p and M_p, denoting the memberships of desired potency being high and medium respectively.

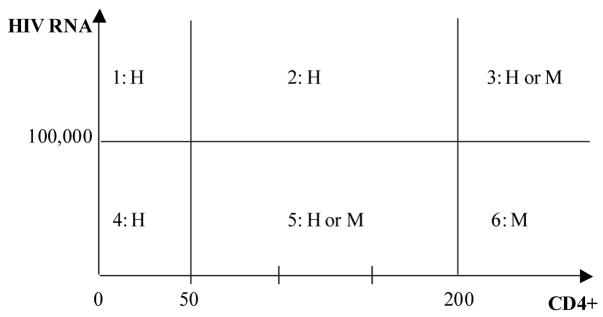
To this end, we first note that the experts’ opinions divide the two-dimensional space of CD4+ and HIV RNA into six regions as shown in Figure 4.

Figure 4.

Six regions in the space of CD4+ and HIV RNA.

In Regions 1, 2, 3, 4, and 5, a regimen with high (H) expected potency may be used; while in Regions 3, 5, and 6, a regimen with medium (M) expected potency may be used. To specify this mathematically, we can define an “indicator” function H̄_P to indicate if a regimen with high expected potency may be used (H̄_P = 1) or not (H̄_P = 0) as follows.

$${\overline{H}}_P=\{\begin{array}{ll}1\hfill & \text{if}\text{CD}4+,\text{HIV}\text{RNA}\in \text{Regions}1-5\hfill \\ 0\hfill & \text{otherwise}\hfill \end{array}.$$

Similarly, we can define an “indicator” function M̄_P to indicate if a regimen with medium expected potency may be used or not.

However, there are two problems with the above “crisp” approach: (1) If CD4+ (or HIV RNA) is near the boundary of two regions, a slight change in CD4+ (say, from 49 to 51) will results in two very different outputs. (2) The decision is not unique (in Regions 3 and 5).

To overcome the above problems and to add a learning capability to the system, we use fuzzy sets as follows. Define two fuzzy membership functions:

$$\begin{array}{l}{\mu }_{HP}(\text{CD}4+,\text{HIV}\text{RNA})=1-(\frac{1}{1+e^{-0.05\times (\text{CD}4+-200)}})\times (1-\frac{1}{1+e^{-0.05\times (\text{HIV}\text{RNA}/1000-100)}}),\\ {\mu }_{MP}(\text{CD}4+,\text{HIV}\text{RNA})=\frac{1}{1+e^{-0.05\times (\text{CD}4+-50)}}+(\frac{1}{1+e^{-0.05\times (\text{CD}4+-200)}}-\\ \frac{1}{1+e^{-0.05\times (\text{CD}4+-50)}})\times \frac{1}{1+e^{-0.05\times (\text{HIV}\text{RNA}/1000-100)}}\end{array}$$

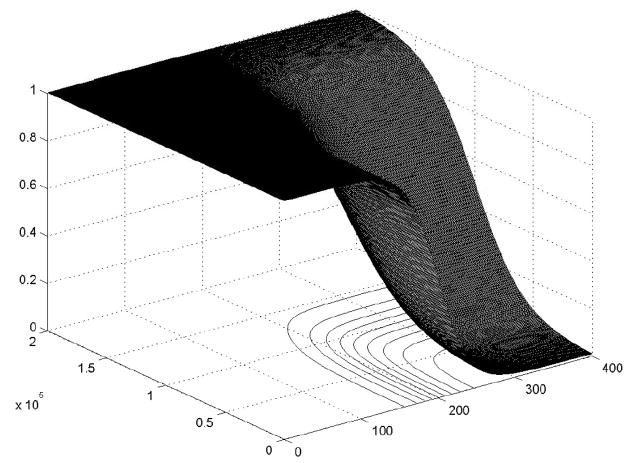
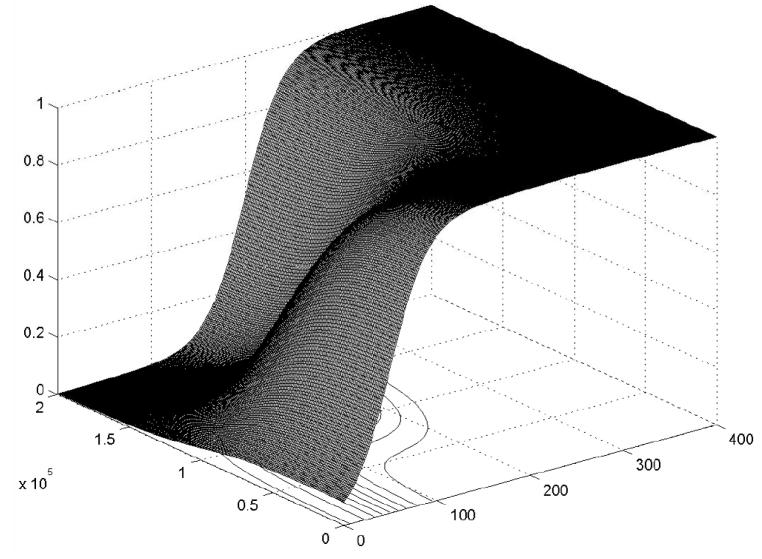
μ_HP(CD4 +, HIV RNA) (μ_MP(CD4 +, HIV RNA)) can be viewed as a fuzzified version of H̄_P (M̄_P). The membership surfaces of μ_HP(CD4 +, HIV RNA) and μ_MP (CD4,+ HIV RNA) are shown in Figures 5 and 6 respectively.

Figure 5.

Membership function of μ_HP(CD4+, HIV RNA).

Figure 6.

Membership function of μ_MP(CD4+, HIV RNA).

The outputs of the system, H_p and M_p, will be the weighted average of μ_HP (CD4 +, HIV RNA), μ_MP(CD4 +, HIV RNA) and their complements:

$$\begin{array}{l}{H}_P={WP}_{\mathit{Rule}1}\times {\mu }_{HP}(\text{CD}4+,\text{HIV}\text{RNA})+{WP}_{\mathit{Rule}2}\times (1-{\mu }_{MP}(\text{CD}4+,\text{HIV}\text{RNA}))\\ M_P={WP}_{\mathit{Rule}1}\times (1-{\mu }_{HP}(\text{CD}4+,\text{HIV}\text{RNA}))+{WP}_{\mathit{Rule}2}\times {\mu }_{MP}(\text{CD}4+,\text{HIV}\text{RNA})\end{array}$$

The weights WP_Rule1 and WP_Rule2 can be either fixed or learned. We use the generic algorithm to learn WP_Rule1 and WP_Rule2 (the detailed learning procedure is omitted here).

Similarly, we can determine the other fuzzy memberships for adherence, adverse events, and future drug options:

• E_A is the membership of desired adherence being easy;

• M_A is the membership of desired adherence being moderate;

• C_A is the membership of desired adherence being challenging;

• M_E is the membership of desired adverse events being medium;

• L_E is the membership of desired adverse events being low;

• V_E is the membership of desired adverse events being very low;

• H_F is the membership of future drug options being high;

• M_F is the membership of future drug options being medium.

From these memberships and the ten weight vectors for the extreme cases determined early, we can calculate the weight vectors for a particular patient by linear interpolation. For the first round treatment,

$$\begin{array}{l}{w}_1=H_P{W}_{HP}^1+M_P{W}_{MP}^1\text{for}\text{the}\text{weight}\text{on}\text{potency}\text{vector};\\ w_2=E_A{W}_{EA}^1+M_A{W}_{MA}^1+C_A{W}_{CA}^1\text{for}\text{the}\text{weight}\text{on}\text{adherence}\text{vector};\\ w_3=M_E{W}_{ME}^1+L_E{W}_{LE}^1+V_E{W}_{VE}^1\text{for}\text{the}\text{weight}\text{on}\text{adverse}\text{events}\text{vector};\\ w_4=H_F{W}_{HF}^1+M_F{W}_{MF}^1\text{for}\text{the}\text{weight}\text{on}\text{future}\text{drug}\text{options}\text{vector}.\end{array}$$

For the second round treatment, w₁ w₂ w₃ w₄ are calculated similarly with $W_{HP}^2,W_{MP}^2,W_{EA}^2,W_{MA}^2,W_{CA}^2,W_{ME}^2,W_{LE}^2,W_{VE}^2,W_{HF}^2,W_{MF}^2$. Finally, the performance index is given by

$$J(q)=w_1^T{q}_1+w_2^T{q}_2+w_3^T{q}_3+w_4^T{q}_4.$$

J(q) is calculated for all the nodes in the forward-looking tree. We take, as an example, a particular patient in our database with the profile.

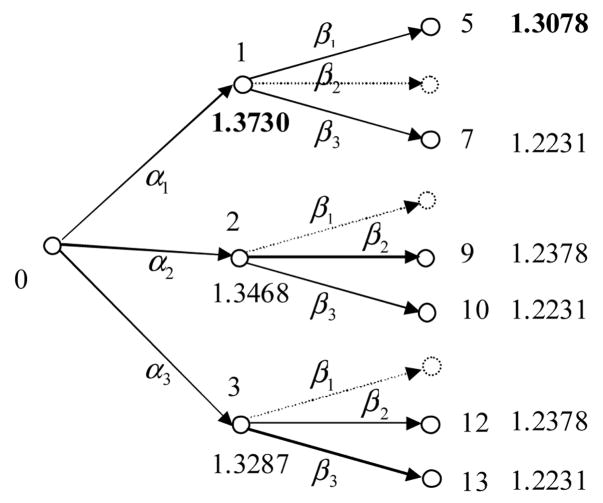
For this patient, we calculate J (q) for all nodes in the tree, which are shown in Figure 7.

Figure 7.

Results for a particular patient in our database.

From Figure 7, we can conclude that for the first round, Regimen CBV+EFV shall be used (event α₁) and for the second round, NNRTI regimen EFV+ABC+d4T or EFV +TDF+ddI shall be used (event β₁).

We compare our computer results with the actual prescriptions given by 13 doctors for 35 patients in our database who were treated in 2001. Our computer results exactly matched the actual prescriptions for 28 (80%) of the patients for the first round of treatment. This is a very encouraging preliminary result, given that the system was set up using the expert advice of only two of the 13 prescribing physicians in the test data set and the fact that expert opinion can be quite divergent for treatment planning decisions of such complexity

4. Conclusions

In this paper, we viewed a complex decision making problem as an optimal control problem in the framework of fuzzy discrete event systems. We proposed a new control architecture for FDES decision making models along with an online fuzzy objective generator and an online optimal control scheme. We demonstrated the architecture by applying it to HIV/AIDS treatment and testing our approach retrospectively on real patient data. Our preliminary results show that the approach is promising.

Our proposed approach and architecture are not limited to HIV/AIDS treatment. In addition to biomedical applications, they are also suitable for decision making in other complex systems such as economical systems.

Table 3.

Profile of a patient in our database.

CD4	24 cells/μL	Substance Abuse	No	Hepatitis B	Negative
HIV RNA	150,000 copies/ml	Active Psych	No	Hepatitis C	Negative
Age	42	Smoker	No	Cholesterol	192mg/dL
Gender	Male	Missing Clinic Visit	0	HDL	32mg/dL
Homeless	No	Diabetic	No	Systolic Blood Pressure	115mm