Segmentation of Textures Defined on Flat vs. Layered Surfaces using Neural Networks: Comparison of 2D vs. 3D Representations

Abstract

Texture boundary detection (or segmentation) is an important capability in human vision. Usually, texture segmentation is viewed as a 2D problem, as the definition of the problem itself assumes a 2D substrate. However, an interesting hypothesis emerges when we ask a question regarding the nature of textures: What are textures, and why did the ability to discriminate texture evolve or develop? A possible answer to this question is that textures naturally define physically distinct (i.e., occluded) surfaces. Hence, we can hypothesize that 2D texture segmentation may be an outgrowth of the ability to discriminate surfaces in 3D. In this paper, we conducted computational experiments with artificial neural networks to investigate the relative difficulty of learning to segment textures defined on flat 2D surfaces vs. those in 3D configurations where the boundaries are defined by occluding surfaces and their change over time due to the observer’s motion. It turns out that learning is faster and more accurate in 3D, very much in line with our expectation. Furthermore, our results showed that the neural network’s learned ability to segment texture in 3D transfers well into 2D texture segmentation, bolstering our initial hypothesis, and providing insights on the possible developmental origin of 2D texture segmentation function in human vision.

1 Introduction

Detection of a tiger in the shrub is a perceptual task that carries a life or death consequence for preys trying to survive in the jungle [1]. Here, figure-ground separation becomes an important perceptual capability. Figure-ground separation is based on many different cues such as luminance, color, texture, etc. In case of the tiger in the jungle, texture plays a critical role. What are the visual processes that enable perceptual agents to separate figure from ground using texture cues? This intriguing question led many researchers in vision to investigate the mechanisms of texture perception.

Beck [2][3] and Julesz [4] conducted psychological experiments investigating the features that enable humans to discriminate one texture from another. These studies suggested that texture segmentation occurs based on the distribution of simple properties of “texture elements,” such as brightness, color, size, and the orientation of contours, or other elemental descriptors [5]. Julesz also proposed the texton theory, in which textures are discriminated if they differ in the density of simple, local textural features, called textons [6]. Most models based on these observations lead to a feature-based theory in which segmentation occurs when feature differences (such as difference in orientation) exist. On the other hand, psychophysical and neurophysiological experiments have shown that texture processing may be based on the detection of boundaries between textures using contextual influences via intra-cortical interactions in the visual cortex [7][8][9] (for computational models, see [10][11]).

In the current studies of texture segmentation and boundary detection, texture is usually defined in 2D. However, an interesting hypothesis arises when we ask an important question regarding the nature of textures: What are textures, and why did the ability to discriminate textures evolve or develop? One possible answer to the question is that texture is that which defines physically distinct (i.e., occluded or occluding) surfaces belonging to different objects, and that texture segmentation function may have evolved out of the necessity to distinguish between different surfaces. Human visual experience with textures can be, therefore, in most cases to use them as cues for surface perception, depth perception, and 3D structure perception. In fact, psychological experiments by Nakayama and He [12][13] showed that the visual system cannot ignore information regarding surface layout in texture discrimination and proposed that surface representation must actually precede perceptual functions such as texture perception (see the discussion section for more on this point).

From the discussion above, we can reasonably infer that texture processing may be closely related to surface discrimination. Surface discrimination is fundamentally a 3D task, and 3D cues such as stereopsis and motion parallax may provide unambiguous information about the surface. Thus, we can hypothesize that 3D surface perception could have contributed in the formation of early texture segmentation capabilities in human vision. In this paper, through computational experiments using artificial neural networks, we investigated the relative difficulty of learning to discriminate texture boundaries in 2D vs. 3D arrangements of texture. In the 2D arrangement, textures are shown on a flat 2D surface, whereas in the 3D counterpart they are shown as patterns on two surfaces, one occluding the other which also appears to slide due to the motion of the observer. We will also evaluate whether the learned ability to segment texture in 3D can transfer into 2D. In the following, we will first describe in detail the methods we used to prepare the 2D and the 3D texture inputs (Section 2.1), and the procedure we followed to train multilayer perceptrons to discriminate texture boundaries (Section 2.2). Next, we will present our main results and interpretations (Section 3), followed by discussion (Section 4) and conclusion (Section 5).

2 Methods

To test our hypothesis proposed in the introduction, we need to conduct texture discrimination experiments with 2D and 3D arrangements of texture. In this section, we will describe in detail how we prepared the two different arrangements (Section 2.1), and explain how we trained two standard multilayer perceptrons to discriminate these texture arrangements (Section 2.2). We trained two separate networks that are identical in architecture, one with input prepared in a 2D arrangement (we will refer to this network as the 2D-net), and the other with inputs in a 3D arrangement (the 3D-net).

2.1 Input preparation

We used three sets of texture stimuli S₁, S₂, and S₃ for our experiments (Figure 1). Textures in S₁ were simple artificial texture images (oriented bars of orientation 0, $\frac{\pi }{4},\frac{\pi }{2}$, or $\frac{3\pi }{4}$ at two different spatial frequencies); those in S₂ were more complex texture images such as crosses and circles, adapted from Krose [14] and Julesz [15]; and those in S₃ were real texture images from the widely used Brodatz texture collection [16]. For the training of the 2D-net and the 3D-net, the eight simple texture stimuli in S₁ were used. For testing the performance of the 2D-net and the 3D-net, all sets of texture stimuli (S₁, S₂ and S₃) were used.

Fig. 1.

Texture stimuli. Three texture sets S₁, S₂, and S₃ are shown from the top to the bottom row.

In order to extract the primitive features in a given texture, we used Gabor filters. Previous results have shown that Gabor filters closely resemble experimentally measured receptive fields in the visual cortex [17] and they have been widely used to model the response of visual cortical neurons. A number of texture analysis studies also used oriented Gabor filters or difference of Gaussian (DOG) filters to extract local edge features [18][19][20].

We used a bank of oriented Gabor filters to approximate the responses of simple cells in the primary visual cortex. (Figure 2 shows a summary of the process outlined below.) The Gabor filter is defined as follows [21] (the formula below closely follows [22]):

$$G_{\theta ,\phi ,\sigma ,\omega }(x,y)={exp}^{-\frac{{x^{\prime }}^2+{y^{\prime }}^2}{{\sigma }^2}}cos(2\pi \omega x^{\prime }+\phi ),$$ (1)

where θ is the orientation, φ the phase, σ the standard deviation (width) of the Gaussian envelope, ω the spatial frequency, (x, y) the pixel location, and x′ and y′ defined as:

$$x^{\prime }=xcos(\theta )+ysin(\theta ),$$ (2)

$$y^{\prime }=-xsin(\theta )+ycos(\theta ).$$ (3)

Fig. 2.

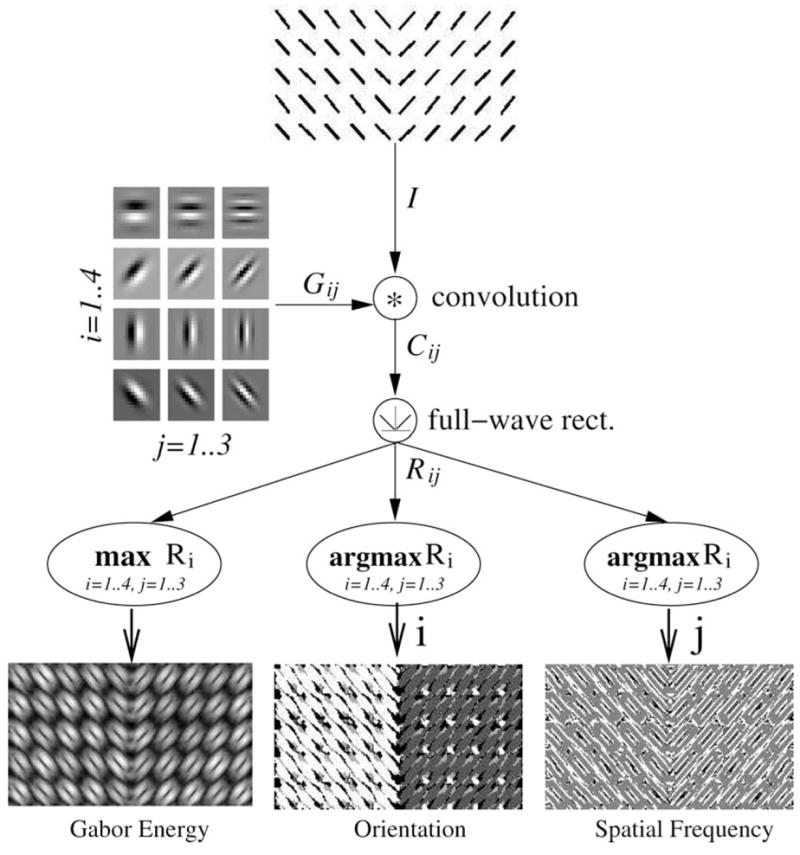
Gabor filter bank. The process used to generate feature matrices is shown. The texture I is first convolved with the Gabor filters G_ij (for I = 1..4, j = 1..3), and the resulting responses are passed through a full-wave rectifier resulting in R_ij. Finally, we obtain the Gabor energy matrix E_ij, orientation index matrix O_ij, and frequency index matrix F_ij.

The size of the filter was 16 × 16 (n × n where n = 16). For simplicity, only four different orientations, 0, $\frac{\pi }{4},\frac{\pi }{2}$, and $\frac{3\pi }{4}$, were used for θ. (Below, we will refer to G _θ,φ,σ,ω as simply G.) The phase of the cosine was $\phi =\frac{\pi }{2}$, and the Gaussian envelope width was $\sigma =\frac{n}{2}$. To adequately sample the spatial-frequency features of the input stimuli, three frequencies, $\frac{1}{n},\frac{2}{n}$, and $\frac{3}{n}$, were used for ω. This resulted in 12 filters G_ij, where the index over orientations was $i=\mathrm{1..4}\left(\theta =\frac{(i-1)\pi }{4}\right)$, and that over spatial frequencies $j=\mathrm{1..3}\left(\omega =\frac{j}{n}\right)$. To get the Gabor response matrix C_ij for orientation index i and spatial frequency index j, a gray-level intensity matrix I was obtained from the images randomly selected from S₁ and convolved with the filter bank G_ij:

$$C_{ij}=I\ast G_{ij},$$ (4)

where i = 1..4 and j = 1..3 denote the orientation and spatial frequency indices of the filters in the filter bank, and * represents the convolution operator. The Gabor filtering stage is linear, but models purely based on linear mechanisms are not able to reproduce experimental data [23]. Thus, half-wave rectification is commonly used to provide a nonlinear response characteristic following linear filtering. However, in our experiments, full-wave rectification was used as in [24], which is similar to half-wave rectification, but is simpler to implement. Full-wave rectification is equivalent to summing the outputs of the two corresponding half-wave rectification channels (see, e.g. Bergen and Adelson [25] [23]). The final full-wave rectified Gabor feature response matrix is calculated as

$$R_{ij}=\mid C_{ij}\mid ,$$ (5)

for i = 1..4 and j = 1..3, where |·| represents the element-wise absolute value of the matrix.

For each sample texture pair, we acquired three response matrices: the Gabor energy matrix E, the orientation index matrix O, and the frequency index matrix F. The E matrix simply indicates the “edgyness” at each point, which is analogous to the orientation selectivity in primary visual cortical (V1) neurons [26]. On the other hand, O indicates which orientation is most prominent at each point, which again has an analog in neurophysiology: the orientation preference in V1 neurons [26]. Finally, F represents how fine the spatial feature is at each point, for which its neural mechanism is also known [27]. Thus, the selection of these three features are consistent with known neurophysiology of V1.

The Gabor energy response matrix E was defined as follows:

$$E(x,y)=\underset{i=\mathrm{1..4},j=\mathrm{1..3}}{max}{R}_{ij}(x,y),$$ (6)

where (x, y) is the location in each matrix, and i and j are the orientation and spatial frequency indices, and R_ij the response matrix (Equation 5). The orientation index matrix O and the frequency index matrix F were calculated as

$$(O(x,y),F(x,y))=\underset{i=\mathrm{1..4},j=\mathrm{1..3}}{argmax}{R}_{ij}(x,y),$$ (7)

where arg max(·) is a vector valued function which returns two indices i and j where R_ij (x, y) is the maximum, one for orientation and one for spatial frequency, which are subsequently assigned to O(x, y) and F (x, y), respectively. Finally, each matrix was independently normalized by dividing with its maximum value. Figure 2 shows the Gabor filter bank and the three matrices E, O, and F of the given texture pair.

To get the 2D training samples for the 2D-net, two randomly selected textures from S₁ were paired side-by-side and convolved with the Gabor filter bank (Figure 2). The E, O, and F matrices were then obtained using Equations 6 and 7, and then normalized as explained above.

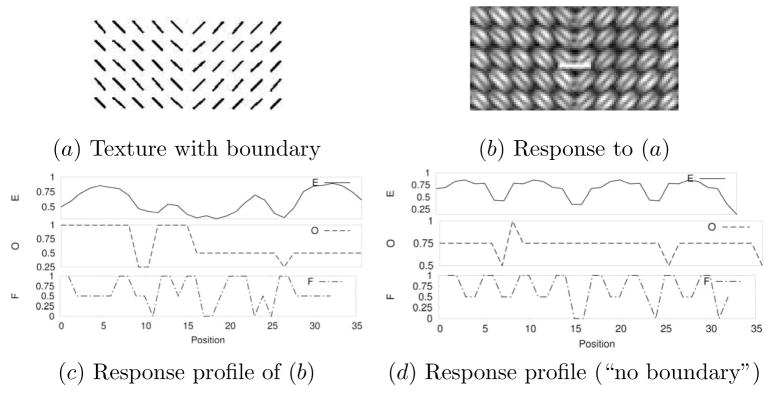
Each training input in the 2D training set consisted of three 32-element vectors taken from a horizontal strip from the E, O, and F matrices (Figure 3b, showing E, marked white). Each horizontal strip had a width of 32, and was taken from the center of the matrix where the two textures meet, with a varying y location randomly chosen where the E sum in that row exceeded the mean row sum of E for that particular texture (Figure 3b). The three vectors were pasted to form a 96-element vector ${\xi }_k^{2\text{D}}$, where k represents the training sample index, and the superscript 2D denotes that this vector is in the 2D set. Finally, the target ${\zeta }_k^{2\text{D}}$ was set either to 0 (for “no border” condition) or to 1 (for “border” condition), thus giving an input-target pair ( ${\xi }_k^{2\text{D}},{\zeta }_k^{2\text{D}}$) for the 2D case. Examples of these three 32-element vectors are shown in Figure 3c (texture with boundary), and in Figure 3d (texture without boundary).

Fig. 3.

Generating the 2D input set. The procedure used to generate the 2D training data is shown. (a) Input with a texture boundary. (b) Orientation response calculated from (a). Only the E matrix is shown. The 32-pixel wide line marked in white indicates where an input vector was sampled. (c) The response profile from the 32-pixel wide area marked with a white rectangle in (b). The three curves represent the profiles in the E, O, and F matrices. (d) A similarly calculated response profile in a different input texture, for an area without a texture boundary (note the identical periodic peaks, unlike in (c)).

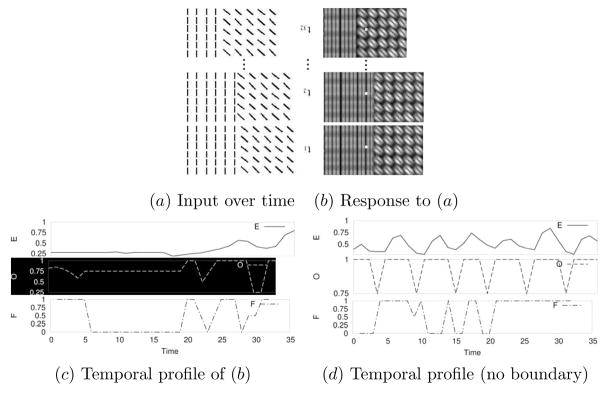
In order to generate samples for the 3D-net, occlusion cue generated from self-motion was used as shown in Figure 4. One texture from a pair of textures occluded the other where the texture above was allowed to slide over the other, which resulted in successive further occlusion of the texture below. The occluding texture above was moved by one pixel at a time 32 times and each time the resulting 2D image ( $I_t^{\prime }$, for t = t₁…t₃₂; Figure 5a) was convolved with the oriented Gabor filter bank followed by full-wave rectification as in the 2D case (Figure 5b). To generate a single training input-target pair ( ${\xi }_k^{3\text{D}},{\zeta }_k^{3\text{D}}$) for the 3D-net, at each time step the Gabor energy response value E(x_c, y_c), orientation response value O(x_c, y_c) and frequency response value F (x_c, y_c) were separately collected into three 32-element vectors, where x_c was 16 pixels away to the right from the initial texture boundary in the middle, and y_c was selected randomly as in the 2D case (the white squares in Figure 5b). Finally, the three 32-element vectors were pasted to form a 96-element vector ${\xi }_k^{3\text{D}}$. Figure 5c shows examples of ${\xi }_k^{3\text{D}}$ (note that the x-axis represents time, unlike in the 2D case where it is spatial position: see the discussion section for more on this point) for a case containing a texture boundary, and Figure 5d for a case without a boundary. The target value ${\zeta }_k^{3\text{D}}$ of the input-target pair ( ${\xi }_k^{3\text{D}},{\zeta }_k^{3\text{D}}$) was set in a similar manner as in the 2D case, either to 0 (no boundary) or to 1 (boundary). When collecting the training samples for the 3D-net where there was a texture boundary, the above procedure was performed with two different 3D configurations. In the first configuration, the texture on the left side was on top of the texture on the right side with self-motion of observer from right to left. In the second configuration, the texture on the right was on top of the texture on the left side with self-motion of observer from left to right. For an unbiased training set, the same number of samples were collected for each 3D configuration. The “no boundary” condition was identical to the 2D case without a boundary, since no texture boundary in 3D means one uniform texture over a single surface.

Fig. 4.

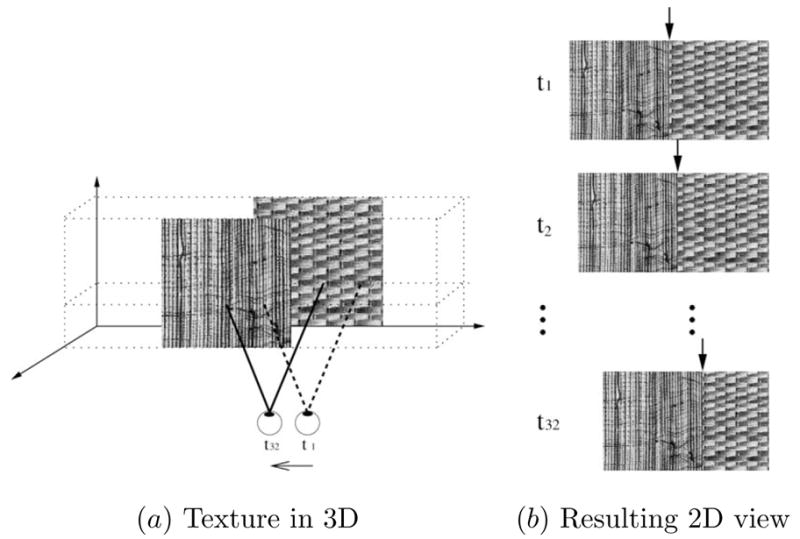
Generating the 3D input set. (a) A 3D configuration of textures and (b) the resulting 2D views before, during, and after the movement are shown. As the viewpoint is moved from the right to the left (t₁ to t₃₂) in 32 steps, the 2D texture boundaries in (b) (marked by black arrows) show a subtle variation.

Fig. 5.

Generating 3D input set through motion. (a) Texture pair images resulting from simulated motion: $I_t^{\prime }$ for each t = t₁..t₃₂. (b) The response matrix of the texture pair: $R_{ij}^{3D}$. The location sampled for the input vector construction is marked as a white square in each frame. (c) Response profile obtained over time near the boundary of two different texture images (marked by the small white squares in b). Take note of the flatness of the profile on the left half of the plots, which is quite different from the 2D case. (d) A similarly measured response profile collected over time, using a different input texture, near a location without a texture boundary (note the periodic peaks).

For both the 2D and the 3D arrangements, texture patches were uniformly randomly sampled to form a texture pair, and 2,400 “boundary” and 2,400 “no boundary” cases were generated for each arrangement. This resulted in 4,800 input-target samples for each training set.

2.2 Training the texture segmentation networks

We used standard multilayered perceptrons (MLPs) to perform texture boundary detection. The networks (2D-net and 3D-net), which consisted of two layers including 96 input units, 16 hidden units and, 2 output units, were trained for 2,000 epochs each using standard backpropagation (see e.g., [28]) ^2. The target outputs were set to (1, 0) for the “boundary” case, and (0, 1) for the “no boundary” case. The goal of this study was to compare the relative learnability of the 2D vs. the 3D texture arrangements, thus a backpropagation network was good enough for our purpose. The hyperbolic tangent function (f (v) = tanh(v)) was used as the activation function of the hidden layer. For the activation function of the output layer, radial basis function (RBF) was used (φ(v) = exp(−v²)). The use of the radial basis function in standard MLP is not common: It is usually used as an activation function of the hidden layer in radial basis function networks, which has additional data-independent input to the output layer. In the experiment, as shown in the previous section, an input vector to the MLP is symmetric about the center when there is no boundary. On the other hand, an input vector to the MLP is quite asymmetric when there is a boundary, but the mirror image of that vector should result in the same class. This observation led us to use the radial basis function, which has a Gaussian profile. Several preliminary training trials showed that the use of the RBF as the activation function enabled both the 2D-net and the 3D-net to converge faster (data not shown here). For the training, the input vectors were generated from the texture set S₁. Backpropagation with momentum and adaptive learning rate was applied to train the weights.

To determine the best learning parameters, several preliminary training runs were done with combinations of learning rate parameters η ∈ {0.01, 0.1, 0.5} and momentum constants α ∈ {0.0, 0.5, 0.9}. MLPs with each combination were trained with the same set of inputs so that the results of the experiment can be directly compared. Each training set consisted of 280 examples, drawn from S₁ and processed by the input preparation procedure. The training process continued for 1,000 epochs. The MLPs with other combination of parameters failed to converge. Based on these preliminary training tests, we chose the learning parameters as follows: learning rate η = 0.01, and momentum constant α = 0.5.

We also applied standard heuristics to speed up and stabilize the convergence of the networks. First, each input vector was further normalized so that its vector mean, averaged over the entire training set, is zero. Secondly, adaptive learning rate was applied. For each epoch, if the mean squared error (MSE) decreased toward the goal (10⁻⁴), then the learning rate (η) was increased by the factor of η_inc:

$${\eta }_n={\eta }_{n-1}{\eta }_{\text{inc}},$$ (8)

where n is the epoch. If MSE increased by more than a factor of 1.04, the learning rate was adjusted by the factor of η_dec:

$${\eta }_n={\eta }_{n-1}{\eta }_{\text{dec}}.$$ (9)

The learning constants selected above (η = 0.01, α = 0.5) were used for the second test training to choose the optimal adaptive learning rate factors (η_inc and η_dec). Combinations of the factors η_inc ∈ {1.01, 1.05, 1.09} and η_dec ∈ {0.5, 0.7, 0.9} were used during the test training to observe their effects on convergence. The combination of factors η_inc = 1.01 and η_dec = 0.5 were chosen based on these results.

After the training of the two networks, the speed of convergence and the classification accuracy were compared. To test generalization and transfer potentials, test stimuli drawn from the texture sets S₁, S₂, and S₃ were processed using both 2D- and 3D input preparation methods to obtain six test input sets (each with 4,800 inputs). These input samples were then presented to the 2D-net and the 3D-net to compare the performances of the two networks on these six test input sets. The results from these experiments will be presented in the following section.

3 Experiments and Results

We compared the performance of the two trained networks (2D-net and 3D-net), and also compared the performance of the two networks over novel texture images that were not used in training the networks.

3.1 Speed of convergence and accuracy on the training set

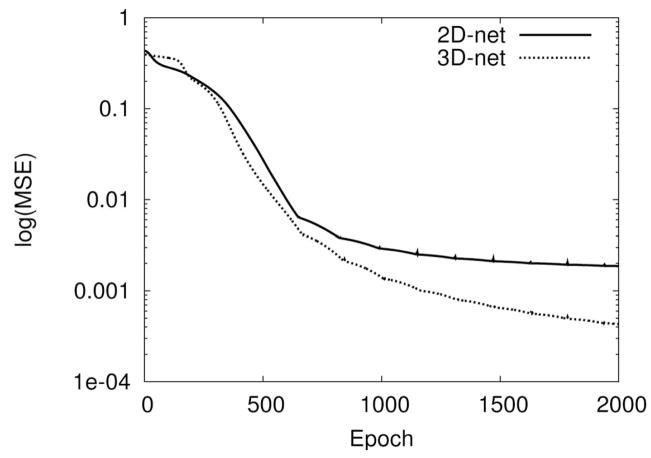
Figure 6 shows the learning curves of the networks during training. The learning processes continued for 2,000 epochs. After 2,000 epochs, the average mean squared error (MSE) of the 2D-net was 0.0006 and that of the 3D-net was 0.0003. The learning curve also shows that the 3D-net converges faster than the 2D-net. The class response of the network was determined by finding which output node (among the two) had the higher value. If the first output neuron had a greater response than the second, the classification was deemed to be “boundary,” and otherwise “no boundary.” The misclassification rate was computed based on the comparison of this classification response against the target value (ζ). The misclassification rate for the 2D-net was 0.3%, and for the 3D-net, 0.02%. In summary, the network learned texture arrangements represented in 3D faster and more accurately than those in 2D.

Fig. 6.

Learning curves of the networks. The learning curves of the 2D-net and the 3D-net up to 2,000 epochs of training on texture set S₁ are shown. The 3D-net is more accurate and converges faster than the 2D-net (the 3D-net reaches the asymptotic value of the 2D-net near 750 epochs), suggesting that the 3D-processed training set is easier to learn than the 2D set.

3.2 Generalization and transfer (I)

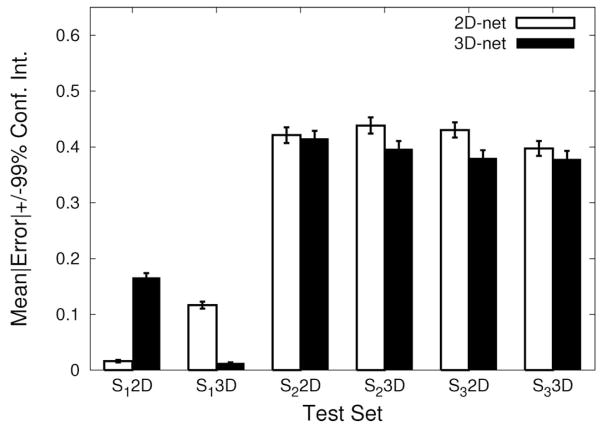
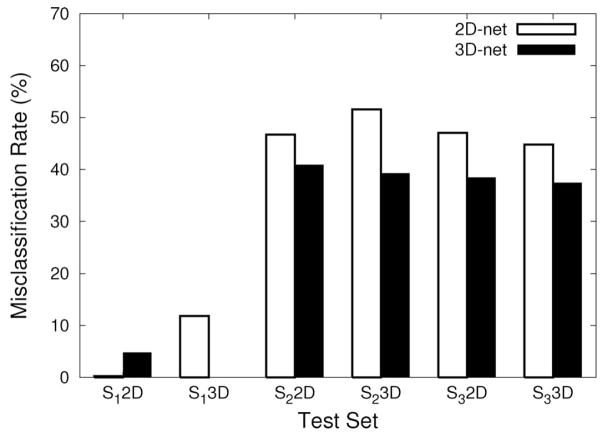
The 2D-net and the 3D-net trained with the texture set S₁ were tested on texture pairs from S₁, S₂ and S₃. (Note that for the texture set S₁, input samples different from those in the training set were used.) The input sets were prepared in the same manner as the training samples (Section 2.1). All 6 sample sets (= 3 texture sets × 2 representations) were presented to the 2D-net and the 3D-net. Two methods to compare the performance of the networks were used. First, we compared the misclassification rate, which is the percentage of misclassification. Misclassification rates were calculated for all 12 cases (= 6 sample sets × 2 networks): Figure 7 shows the result. The 3D-net outperformed the 2D-net in all cases, except for the sample set from S₁ with 2D input processing, which was similar to those used for training the 2D-net. The result in the S₁ 2D experiment may suggest that transfer from 3D to 2D may have been weak. However, what is more notable is that the 3D-net outperformed the 2D-net on the sample sets from realistic textures in S₂ and S₃ prepared with 2D input processing (third and the fifth pair in Figure 7; these are basically a 2D texture segmentation problem), where one would normally expect the 2D-net to perform better because of the manner in which the input was prepared. Here, the performance is not too high (near 40% misclassification), which is due to the fact that S₂ and S₃ were not used in the training runs, but in our view, what is more important is the fact that the 3D-net outperformed the 2D-net. (Using a larger, richer, realistic training set is part of our planned future work.) These results suggest that the 3D representation can help 2D texture segmentation under novel conditions.

Fig. 7.

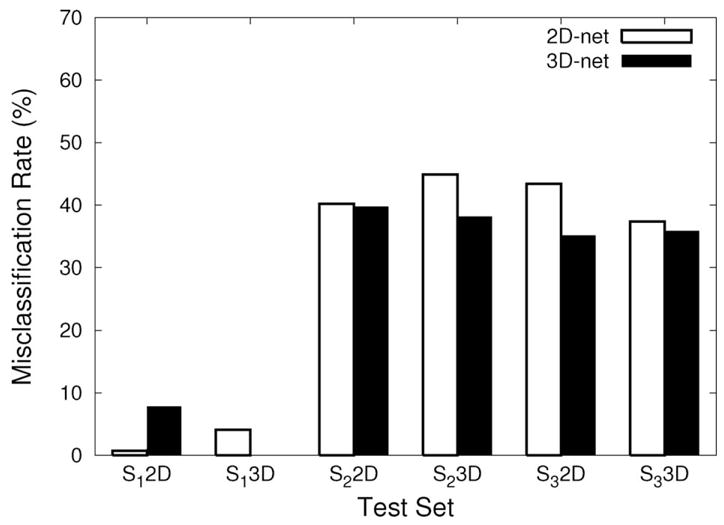
Comparison of misclassification rates. The misclassification rates of the different test conditions are shown. Six sets of experiments are shown (indicated under the x axis), each conducted on test examples generated from one of the data sets S₁, S₂, or S₃, using either a 2D- or a 3D representation (3 × 2 = 6 test input sets). For example, “S₁ 2D” means the 2D representation for the S₁ data set. Each test input set was used to evaluate the 2D-net (white bars) and the 3D-net (black bars) trained on S₁. In all cases, the 3D-net shows a lower misclassification rate compared to that of the 2D-net, except for the 2D representation of S₁ (S₁ 2D). (See the text for the interpretation of the results.)

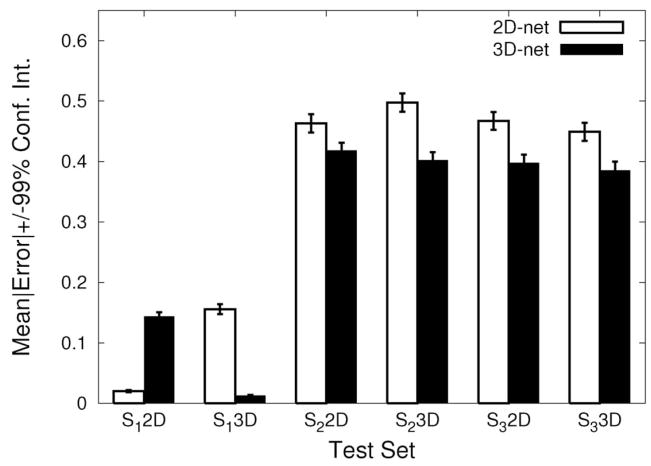
As another measure of performance, we compared the absolute error (= |target − output|) for each test case for the two networks. The results are shown in Figure 8. The plot shows the mean absolute errors and their 99% confidence intervals. The results are comparable to the misclassification rate results reported above. The 3D-net consistently outperformed the 2D-net for the sample sets from S₂ and S₃, and the differences were found to be statistically significant (t-test: n = 4, 800, p < 0.02) except for S₂ 2D (p = 0.47) where it was found to be no worse than the 2D-net. However, the 2D-net outperformed the 3D-net for the sample set from S₁ (Figure 8 first pair from the left). Again, since S₁ processed in 2D was used for training the 2D-net (although the samples were different), this was expected from the beginning.

Fig. 8.

Comparison of output errors. The mean error in the output vs. the target value in each trial and its 99% confidence interval (error bar) are shown for all test cases (the plotting convention is the same as Figure 7). In all cases, the differences between the 3D-net and the 2D-net were significant (t-test: n = 4, 800, p < 0.02), except for S₂ 2D (p = 0.47) where the performance was comparable. Note that for the 2D representation of S₁, 2D-net < 3D-net.

3.3 Generalization and transfer (II)

The main goal of our work was to understand the nature of textures, and from that emerged the importance of 3D cues in understanding the texture detection mechanism in human visual processing. To emulate 3D depth, we employed motion cues to provide depth. This imposes potential limitations on our work, which is that additional information in 3D input may have become available to the 3D-net; some form of temporal information that 2D inputs does not have. For example, in the 3D case, sliding of one texture over another produces richer local textures near the boundary than in the 2D case, where the boundary has a fixed local texture. This can be seen as an unfair advantage for the 3D-net. One way of addressing this issue may be to normalize (or equalize) the information content in the 2D vs. the 3D input preparation, which may allow us to more fairly assess the differences between the two modes of texture processing. This can be done by generating 2D textures by altering their overlap location rather than always putting them together in the center.

We conducted an identical set of experiments described in the previous sections with the only difference being the difference in the 2D input set preparation. We used the same procedure prescribed in Section 2.1, except that the 2D texture boundary in the middle was made by allowing the texture boundary to be defined not only by abutting the two input patches side-by-side, but also by slightly overlapping one over the other as in Figure 4b (but on the same flat plane). The amount of overlap was randomly varied from 0 to 32 in the horizontal direction.

The misclassification rate and MSE results are shown in Figures 9 and 10. The results are consistent with (or, even stronger than) the previous results. An interesting observation is that the performance of the 2D-net became worse, which is somewhat counter to our expectations given our rational for conducting this experiment provided earlier in this section. Our observation is that the added variety of the possible combination of texture features near the boundary resulted in the increase in the number of representative patterns to classify as “boundary,” thus the network had a harder time learning all these different characteristic patterns (i.e., there were too many equivalence classes to learn). In summary, the results presented here and in the previous section support our main hypothesis.

Fig. 9.

Comparison of misclassification rates. The misclassification rates of the different test conditions are shown (the plotting convention is the same as Figure 7). In all cases, the 3D-net shows a lower misclassification rate compared to that of the 2D-net, except for the 2D representation of S₁.

Fig. 10.

Comparison of output errors. The mean error in the output vs. the target value in each trial and its 99% confidence interval (error bars) are shown for all test cases. The same plotting convention was used as in Figure 7. In all cases, the differences between the 3D-net and the 2D-net were significant (t-test: n = 4800, p < 10⁻⁸). Note that for the 2D representation of S₁, 2D-net < 3D-net.

3.4 Separability of 2D vs. 3D representations

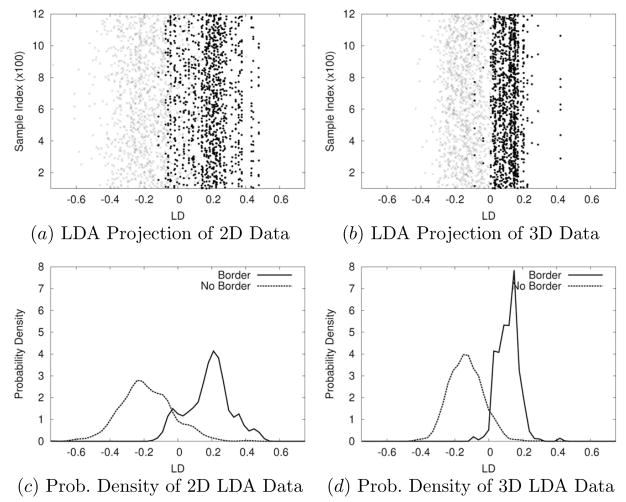
In order to better understand the reason why the 3D representation is superior to its 2D counterpart, we analyzed the two representations using Linear Discriminant Analysis (LDA; see e.g., [29]). Figure 11 shows the results on representations drawn from input data set S₁.

Fig. 11.

Comparison of Linear Discriminant Analysis (LDA) Projection of 2D- and 3D-processed Data. The LDA projections for the 2D- and the 3D-processed data are shown. (Only half the dataset, 1,200 in each class for each representation, is shown to avoid clutter.) (a) LDA projection of the 2D training set is shown. The x and the y axes represent the linear discriminant axis and the input sample index. Each input sample is plotted either as “•” (for “border”) or “×” (for “no border”). The two classes overlap over a large region in the middle. (b) The same, as in (a), for the 3D training set is shown. The overlap region is much smaller than in (a). (c) The probability density along the linear discriminant eigenvector projection (projection onto the x-axis in a) is shown for the 2D training set. The “border” case is plotted as a solid curve, and the “no border” case as a dotted curve. There is a large overlap near 0. (d) The same, as in (c), for the 3D training set is shown. The overlapping area in the middle is much smaller than in (c).

The training sets with 2D and 3D input processing were projected onto their linear discriminant eigenvectors. In each case, samples from the “no boundary” case and the “boundary” case are shown as two separate classes. It is clear from the plots that the the 3D-processed training set is easier to separate than the 2D one since it has less overlap near the class boundary.

It seems that the flatness of Gabor filter bank responses (especially that of E: see Figure 4c, for example) in one half of each response profile (either the left side or the right side) in the 3D case with texture boundary gives more separability than different textural responses in the 2D case. The 3D representations were generated from motion and occlusion cues, thus, the analysis above suggests that motion and 3D arrangement of textures can allow us to separate two texture surfaces more easily than with spatial features limited to 2D, and this may be one of the causes underlying the higher performance on the 3D set shown in the results sections.

4 Discussion

Since the early works of Julesz [4] and Beck [2] on texture perception, many studies have been conducted to understand the mechanisms of the human visual system underlying texture segmentation and boundary detection in both psychophysical research and in pattern recognition research. In most cases their main concerns have been about the texture perception ability of human in 2D. The work presented in this paper suggests an alternative approach to the problem of texture perception, with a focus on boundary detection. First, we demonstrated that texture boundary detection in 3D is easier than in 2D. We also showed that the learned ability to find texture boundary in 3D can easily be transferred to texture boundary detection in 2D. Based on these results, our careful observation is that the outstanding ability of 2D texture boundary detection of the human visual system may have been derived from an analogous ability in 3D.

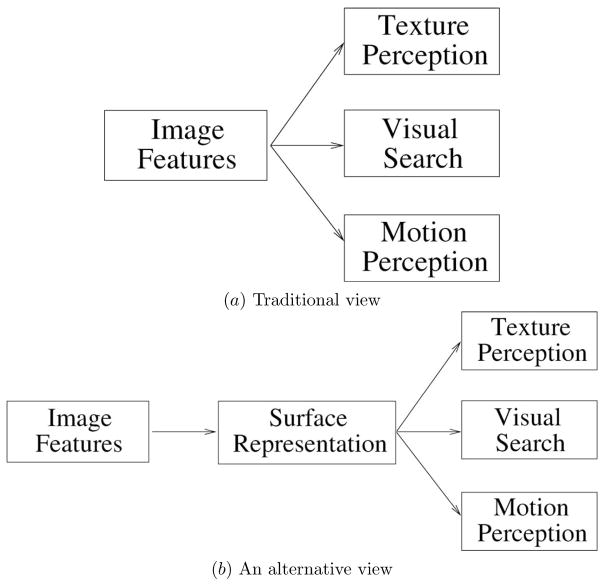
Our results allow us to challenge one common notion that many other texture boundary detection studies share. In that view, intermediate visual processing such as texture perception, visual search and motion process do not require object (in our context, “3D”) knowledge, and thus perform rapidly; and texture perception is understood in terms of features and filtering, so the performance is determined by differences in the response profiles of receptive fields in low-level visual processing. A similar point as ours was advanced by Nakayama and his colleagues [12][13]. In Nakayama’s alternative view on intermediate visual processing, visual surface representation is necessary before other visual tasks such as texture perception, visual search, and motion perception can be accomplished (Figure 12). Such an observation is in line with our results indicating that 3D performance can easily transfer into a 2D task. (Note that there is yet another possibility, where all of these visual tasks are processed concurrently at the same stage, but we do not have enough evidence to either accept or reject such a proposal.)

Fig. 12.

Two views of intermediate visual processing. (a) In the traditional view, texture perception, visual search, motion perception depend on feature processing in early cortical areas. (b) In an alternative view, surface representation must precede intermediate visual tasks [13]. (Adapted from [13].)

Even though we briefly discussed why we think the 3D representation turned out to be better than 2D (in Section 3.4), further analysis may be helpful in determining exactly what aspect of the 3D representation contributed to the results. The basis of the difference between the 3D and the 2D representations in this paper was the occlusion cue due to self-motion of the observer. (Note that the cue only provided the “rank” in depth, and not the “magnitude.”) However, self-motion induces a more complex effect known as motion parallax, which not only gives occlusion cues but also relative difference in displacement (or relative speed) of the objects in the scene as a function of the distance of the observer from those objects [30]. We would like to clarify that our results, even though they are based on self-motion, do not account for (or utilize) the relative speed cue present in motion parallax. An important point here is that there is a much richer set of information in 3D than the simplistic occlusion cue used in our model, and that the use of such extra information (also including stereo cues) may further assist in texture segmentation. These 3D cues carry the most important piece of information, that “these two patches of patterns are different,” thus providing the initial basis of discriminability (i.e., a supervisor signal) in texture segmentation.

Also, as pointed out in the text (Section 2.1), the 3D representations we generated (the 96-element vectors) is defined over time, as opposed to the 2D ones defined over space. How is it possible that generalization can happen across such seemingly incompatible representations? One clue can be found in spatiotemporal receptive fields in the visual pathway (e.g., in the lateral geniculate nucleus: [31]). These LGN neurons not only respond to spatial patterns but also to patterns defined over time which have temporal profiles similar to the spatial profiles. It is tempting to speculate that these spatiotemporal receptive fields may hold key to relating the transfer effect exhibited by our neural network model to texture segmentation in humans. Also, this line of reasoning suggests that it may be productive to investigate the role of motion centers in the visual pathway (such as MT) in texture segmentation.

Finally, one potential criticism may be that we only used S₁ for training. Would a contradictory result emerge if S₂ or S₃ was used to train the networks? We are currently investigating this issue as well, but we are confident that our main conclusion in this paper will hold even in such different training scenarios.

5 Conclusion

We began with the simple question regarding the nature of textures. The tentative answer was that textures naturally define distinct physical surfaces, and thus the ability to segment texture in 2D may have grown out of the ability to distinguish surfaces in 3D. To test our insight, we compared texture boundary detection performance of two neural networks trained on textures arranged in 2D or in 3D. Our results revealed that texture boundary detection in 3D is easier to learn than in 2D, and that the network trained in 3D solved the 2D problem better than the other way around. Based on these results, we carefully conclude that the human ability to segment texture in 2D may have originated from a module evolved to handle 3D tasks. One immediate future direction is to extend our current approach to utilize stereo cues and full motion parallax cues as well as monocular occlusion cues used in this paper.