Partial wave microscopic spectroscopy detects sub-wavelength refractive index fluctuations: an application to cancer diagnosis

Abstract

Existing optical imaging techniques offer us powerful tools to directly visualize the cellular structure at the microscale; however, their capability of nanoscale sensitivity is restricted by the diffraction-limited resolution. We show that mesoscopic light transport theory analysis of the spectra of partial waves propagating within a weakly disordered medium such as biological cells (i.e. partialwave spectroscopy, PWS) quantifies refractive index fluctuations at subdiffractional length scales. We validate this nanoscale sensitivity of PWS using rigorous Finitedifference time-domain (FDTD) simulations and experiments with nanostructured models. We also demonstrate the potential of this technique to detect nanoscale alterations in cells from patients with pancreatic cancer who are otherwise classified as normal by conventional microscopic histopathology.

Spectroscopy of elastic scattering is commonly used to probe tissue morphology [1]. However, the sensitivity of light scattering signal to refractive index fluctuations is significantly reduced when the size of the scattering structures falls below the wavelength (~500 nm). Recently, there has been significant interest in understanding biological systems at the nanoscale, which requires measurement of sub-wavelength refractive index fluctuations. According to mesoscopic light transport theory [2-4], for an object that is weakly disordered and weakly scattering, it is indeed possible to probe refractive index fluctuations of any length scale including those well below the wavelength [3, 4] if one analyzes a signal generated by the multiple interference of 1D-propagating waves reflected from the refractive index fluctuations within the object. The enhanced sensitivity of 1D-propagating waves to sub-wavelength correlation lengths of refractive index fluctuations l_c (i.e., l_c < wavelength λ) can be understood from the following consideration: while in 3D the scattering coefficient ~(l_c / λ)³ , and, thus, contribution from small length scales is weighted down as $l_c^2$, for 1D waves the scattering coefficient is ~ (l_c / λ) [5]. The 1D-propagating waves are one of many subset of waves (herein called 1D-partial waves) propagating within a scattering particle. Recently, we reported an optical system [6] capable of isolating 1D-partial waves from different parts of a homogeneous scattering particle. Here we show that the backscattering signal formed by these 1D-partial waves can be detected for heterogeneous objects, such as biological cells, and be used to probe the sub-wavelength refractive index fluctuations.

A detailed description of the PWS instrument is given elsewhere [6]. In brief, a broadband light with spatial coherence length <1 μm is focused onto the sample by a low-numerical aperture (NA) objective (Edmund Optics, NA of objective = 0.4, NA of illumination = 0.2, NA of collection = 0.4). The illumination beam diameter (~120 μm) is much larger than biological cells (~8 μm) and is well collimated within a cell located in the waist of the beam. The resulting backscattered image is projected with a 60x magnification onto the slit of an imaging spectrograph (10 μm slit width) coupled with a CCD camera (Coolsnap HQ, Roperscientific, 1392 × 1040 6.2 μm pixels) and mounted on a motorized linear scanning stage (Zaber Technologies). The backscattering image is acquired by linearly scanning the slit of the spectrograph with a 10 μm step. The size of a pixel in the image plane (image pixel) is 6.2 μm × 10 μm while the size of pixel in the object plane (cell pixel) is 100 nm × 165 nm. At each scanning step x, the CCD camera records a matrix with one axis corresponding to λ and the other to the spatial position of the image y resulting in a data cube (x,y, λ). The system contains a flipper mirror that directs the image into a digital camera for quick visualization. The backscattering spectrum I(λ; x, y) (λ=390-750nm, spectral resolution ~3nm, spectral sampling ~ 0.25nm; only signal from λ₁ = 500 nm to λ₂ = 670 nm is analyzed, due to the low illumination and transmission efficacy of the instrument) is recorded for each cell pixel (x,y). All spectra obtained from each cell pixel are normalized by the spectra of the incident light using mirror reflection. For each (x,y), I(λ) ( ≡ I(λ; x, y) ) is further processed to remove the high frequency spectral noise using a 6th order low-pass Butterworth filter with a normalized cut off frequency of 0.08 and the variations in the lamp spectrum using a low order polynomial I_p (λ) fit to I(λ). The normalized cut off frequency (cut off frequency/ sampling frequency) was chosen such that it removes all oscillations below the spectral resolution of the spectrometer. The resulting spectrum R(λ) = I(λ) - I_p (λ) is referred to as the fluctuating part of the reflection coefficient. It is important to realize that unlike traditional light scattering experiments where a scattering signal is formed by all waves propagating within a scattering particle and interfering in the far-field, the backscattering spectrum analyzed in PWS is formed by the subset of waves, in particular 1D partial waves. The properties of both the object and the instrument facilitate the detection of 1D waves. While the low NA of the objective restricts the illumination and collection of light to a narrow cone, the weak refractive index fluctuations and a small radius of curvature of a cell spread on a glass slide reduces the probability of the interference among adjacent 1D channel, which is further prevented by the low-coherence illumination. Thus, light interaction with a complex weakly disordered medium can be approximated as a combination of several independent parallel 1D channels with R(λ) generated by the multiple interference of photons propagating in these 1D channels.

Typical I(λ) and I_p (λ) obtained from a particular cell pixel (in this case, a cell isolated from human pancreatic epithelium) spread on a glass slide is shown in Fig. 1a. Fig. 1b shows the corresponding R(λ) . In order to show the noise level, the spectrum is compared with the one obtained from a glass slide. As seen, the intensity fluctuations seen in the spectrum from the cell are above the noise floor. Absorption does not play a significant role in these spectral fluctuations as the absorption coefficient μ_a ~ 1.5 cm^-1 [7] and the thickness of cell is ~ 4 μm. Similarly, the glass slide behind the cell does not contribute to the observed spectral fluctuations as the spectrum of the reflection from the slide is expected to be flat. This brings us to the question of how R(λ) is related to the properties of the object: thickness (L), average refractive index (n₀), the variance and the correlation length of refractive index fluctuations ( < Δn² > and l_c). In the regime where the approximation of 1D independent channels is valid, R(k) (where k = 2π/λ is the wave number) can be characterized using 1D mesoscopic light transport theory [2-4]. Accordingly, the root mean square average of R(k) can be written as: < R > ≡Lξ^-1 , where ξ^-1 is the scattering coefficient of a 1D channel. Although a complicated function of < Δn² > and l_c, ξ^-1 can be simplified for $k{l}_c<1:{\xi }^{-1}\infty 2k^2{L}_d∕n_0^2$ with L_d =< Δn² > l_c. Following terminology used in condensed matter physics, L_d is referred to as the disorder strength. In the following discussion we consider the case of kl_c<1 without the loss of generality [8]. If L and n₀ are known, L_d can be determined from $<R>\approx 2k^2{L}_{d}L∕n_0^2$ for each cell pixel. In turn, L can be estimated from the autocorrelation function C(Δk) = < R(k)R(k + Δk) >/< R(k)R(k) > [3, 4]: ln(C(Δk) = -(Δk)² f (L_d)AL^α , where A=const (in units of length) [4]. Function f and parameter α are numerically derived using FDTD simulations. In a weakly disordered medium and in the absence of strong localization, f is a slowly varying function of L_d (r² = 0.04) and is approximated as a constant (i.e., f ~ 1). α arises due to the finite spectral bandwidth (λ₂ - λ₁) of the spectrum that is being used to calculate C(Δk) (in the limit of a very large bandwidth, L(λ₂ - λ)/λ² 1 << 1 , α = 2; for the bandwidth in our system α ~1). C(Δk) is calculated for the entire spectrum with a center wavelength λ_mean = 585 nm for each cell pixel. Therefore, knowing the experimentally obtained quantities < R > and C(Δk) for a given cell pixel (x,y) and n₀ (assumed to be ~1.38), we can calculate L_d :

$$L_d=B\frac{n_0^2}{2k^2}\frac{<R>{\left(\Delta k\right)}^2}{-\ln \left(C\left(\Delta k\right)\right)},$$ (1)

where B is the calibration constant and ln(C(Δk)) (Δk)² is obtained by fitting a linear slope to - ln(C(Δk)) vs (Δk)².

Figure 1.

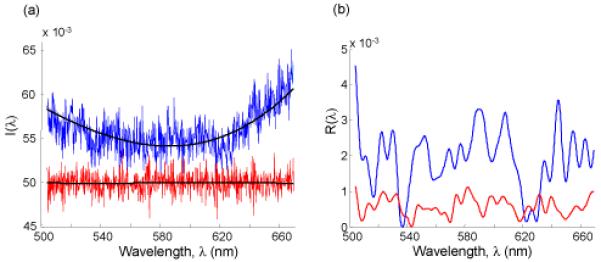
(a) The normalized backscattering spectrum I(λ) from a single pixel of a biological cell (blue) and a pure glass slide (red) with the Ip (λ) (black). (b) The corresponding spectrum R(λ) obtained from a biological cell (blue) and from a pure glass slide (red).

To confirm that L_d calculated using Eq. (1) is indeed sensitive to nanoscale refractive index fluctuations we performed rigorous numerical experiments using FDTD simulations [9]. We constructed a dielectric slab with n₀ = 1.38 as a model of a scattering object. We varied < Δn > between 0.02 and 0.05, l_c between 5 and 35 nm, and L between 0.5 and 4 μm. For each combination of < Δn > , l_c and L, FDTD was used to determine the backscattering spectrum and Eq. (1) was used to calculate L_d based on this spectrum. The results shown in Figs. 2(a,b) indicate that L_d is proportional to both l (r² = 0.94) and < Δn² > (r² = 0.98) thereby confirming the agreement with the mesoscopic theory.

Figure 2.

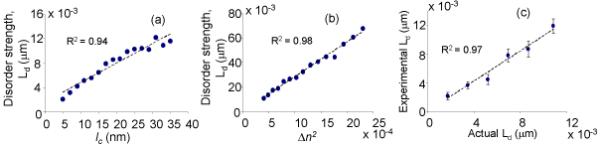
Validation of the nanoscale sensitivity of L_d using FDTD simulations (a,b) and experimental nanostructured model media (c).

To confirm the hypothesis that the PWS scheme enables collecting 1D propagating waves and Eq. (1) is valid, we performed experiments on a series of nanostructured model media comprised of aggregated polystyrene nanospheres. The fabrication protocol is described in detail in [10]. In brief, the aqueous suspension of monodispersed polystyrene nanospheres (Duke Scientific, Inc.) of volume ~ 50 μl was uniformly smeared on a glass slide. The self-assembled lattice formed after 15 minutes of evaporation. We used models with L varying from 0.3 to 13 μm and nanosphere sizes 20, 40, 60, 80, 100 and 125 nm (standard deviations of sizes ~10%). PWS measurements were obtained from 30 different combinations of L and nanosphere sizes. Since both l_c and Δn are known a priori in this model, i.e., l_c ~ the size of a nanosphere and Δn ~ the refractive index of a polystyrene, we were able to compare the actual L_d of the model with the L_d found from the experimental PWS data (Eq. (1)). As shown in Fig. 2c, there was a good agreement (r² = 0.97) between the experimentally observed and actual values of L_d . These experiments were also used to determine constant B in Eq. (1). Finally, this experiment demonstrated that the minimal length scale of refractive index fluctuations to which PWS is sensitive to is below 20 nm.

The nanoscale sensitivity of PWS could be critical to cell microscopy where cells are regularly imaged to understand disease processes. Conventional cytology is not sensitive to changes in cell nanoarchitecture (e.g. ribosomes, membranes, nucleosomes, just to name a few cell structures with subdiffractional dimensions). At the same time, these are some of the most fundamental building blocks of the cell. We hypothesized that PWS can detect nanoarchitectural alterations in cells that are undetectable by cytology. We considered pancreatic cancer as a case in point. Pancreatic cancer is the 4^th leading cause of cancer deaths in the US with an overall 5-year survival rate of <5%. For diagnosis, pancreatic cells are extracted using fine needle aspirations and subjected to a cytopathological analysis. However, the sensitivity of cytology is low for mass lesions in symptomatic patients (~70%) and much lower for early lesions due in part to the relative rarity of frankly malignant-appearing cells that can be identified by cytology. We performed a pilot study on archival pancreatic cells (fixed with alcohol) obtained from 16 patients (7 normal and 9 malignant). 6 cases from these 9 adenocarcinomas were cytologically diagnosed as cytologically normal. (We note that although fixation modifies the internal refractive index distribution compared to that of live cells, the intracellular morphology is expected to be maintained.) PWS measurements were obtained from three different cohorts of cells: cytologically normal cells from normal patients (N), cytologically malignant cells from cancer patients (C) and cytologically normal cells from cancer patients (CN). For each patient, ~ 40 cells were chosen at random. Typical bright field and PWS images (i.e. L_d (x, y) ) obtained for these three cell types are shown in Figs. 3(a,b). As seen, the L_d-image shows a clear difference between N and C cells. More importantly, L_d-images are different between N and CN cells too. Further statistical analysis was performed using the two parameters that are obtained from the L_d maps: the mean and the standard deviation the intracellular disorder strength $\left(L_d^{\left(c\right)}\text{and}{\sigma }^{\left(c\right)}\right)$. As shown in Figs. 3(c,d) both the $\langle L_d^{\left(c\right)}\rangle$ and 〈 σ^(c)〉 (〈〉 indicates the average taken over all the cells within a patient cohort) are highly significantly elevated in cancer patients compared to the control group (P < 0.001). A prediction rule developed using a linear regression model yielded 100% sensitivity and 100% specificity for cytologically normal patients vs cancer patients. Interestingly, the cytologically normal cells from cancer patients also had significantly elevated $\langle L_d^{\left(c\right)}\rangle$ P < 0.001) with 83% sensitivity and 100% specificity. We note that both $\langle L_d^{\left(c\right)}\rangle$ vary within a patient cohort as indicated by the error bars in Fig. 4a. However this variation (~ 50% in normal population) is much smaller than the difference between the patient cohorts (which is > 100%). A higher L_d in cancer patients may be due to the increase in < Δn² > and/or l_c. Higher < Δn² > can be associated with the increased density of intracellular macromolecular complexes [11] while the change in l_c may be due to the macromolecular aggregation.

Figure 3.

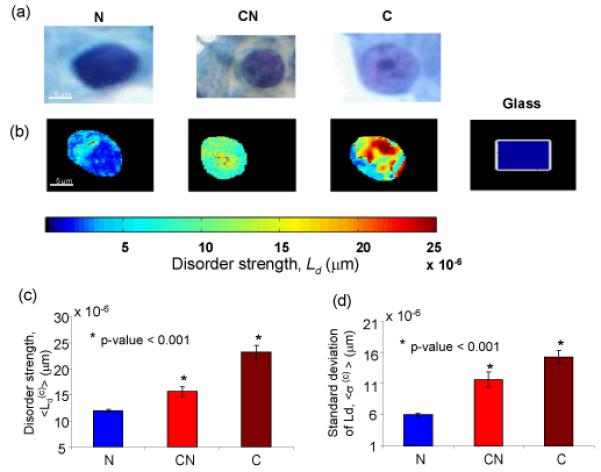
A representative bright field image (a) and the corresponding pseudo-color L_d map (b) recorded from three different cell types: N, C and CN. (c) and (d): $\langle L_d^{\left(c\right)}\rangle$ 〈 σ^(c)〉 for different cell types. Error bars are the standard errors of the mean.

In summary, the backscattering spectrum from a weakly disordered medium contains spectral fluctuations that can be used to measure the disorder strength of the refractive index fluctuations within the scattering object. The disorder strength is sensitive to sub-wavelength, nanoscale refractive index fluctuations. As an illustration of the potential capabilities of PWS, we showed that this technique may identify cancer cells by sensing microscopically undetectable alterations in cell architecture.