Abstract
Functional magnetic resonance imaging (fMRI) is a fairly new technique that has the potential to characterize and classify brain disorders such as schizophrenia. It has the possibility of playing a crucial role in designing objective prognostic/diagnostic tools, but also presents numerous challenges to analysis and interpretation. Classification provides results for individual subjects, rather than results related to group differences. This is a more complicated endeavor that must be approached more carefully and efficient methods should be developed to draw generalized and valid conclusions out of high dimensional data with a limited number of subjects, especially for heterogeneous disorders whose pathophysiology is unknown. Numerous research efforts have been reported in the field using fMRI activation of schizophrenia patients and healthy controls. However, the results are usually not generalizable to larger data sets and require careful definition of the techniques used both in designing algorithms and reporting prediction accuracies. In this review paper, we survey a number of previous reports and also identify possible biases (cross-validation, class size, e.g.) in class comparison/prediction problems. Some suggestions to improve the effectiveness of the presentation of the prediction accuracy results are provided. We also present our own results using a projection pursuit algorithm followed by an application of independent component analysis proposed in an earlier study. We classify schizophrenia versus healthy controls using fMRI data of 155 subjects from two sites obtained during three different tasks. The results are compared in order to investigate the effectiveness of each task and differences between patients with schizophrenia and healthy controls were investigated.
Keywords: Classification, Bias, Detection, Generalization, Schizophrenia, fMRI, Functional MRI
Introduction
Functional magnetic resonance imaging (fMRI) is a fairly new and unique tool that enables widespread, noninvasive investigation of brain functions (Kwong et al. 1992). The difference in magnetic susceptibility of oxygenated (diamagnetic) and deoxygenated (para-magnetic) blood is the basis for recording temporal and spatial alterations in the blood oxygen level dependant (BOLD) fMRI signal (Ogawa et al. 1990). There is much hope that fMRI data can be used to characterize and/or classify brain disorders such as Alzheimer's disease, schizophrenia, mild traumatic brain injury, addiction or bipolar disorder using the biologically measured quantity. For this purpose, responses to various types of stimuli in both healthy controls and patients with brain disorders have been measured, compared and analyzed.
Analyzing fMRI data for the ultimate goal of diagnosing schizophrenia is crucial in the sense that there are complications in diagnosis and there is no gold standard. The disorder is complex and different combinations of symptoms may be seen in some patients versus others or even in the same patient at different points in time. For example, a patient may meet the diagnosis via psychotic and disorganized symptoms while another patient may have predominantly negative symptoms. The interview and history are the main factors that determine the diagnosis and even the best expert might diagnose schizophrenia when it does not exist.
The nature of fMRI data presents numerous challenges for analysis and interpretation. FMRI may produce spatially overlapping functional networks activated during application of different tasks. During the same task, patients with schizophrenia might activate different brain regions that are part of the same network, or different networks, more than controls.
Moreover, the data are four dimensional, including 3 spatial dimensions changing over time, and includes tens of thousands of voxels that can be represented with vectors of time points. Each subject can be characterized by the voxel values varying in time and solution requires a very high dimensional analysis space (number of voxels × number of time points) where the number of subjects tested is many orders of magnitude smaller than dimensionality of the space. The data occupies only a small volume in the space because hypervolumes grow exponentially with increasing dimensionality. This is called “the curse of dimensionality” (Bellman 1961). The problem is difficult to solve because high dimensional space is mostly empty and discriminative information is usually in a lower dimensional subspace (Jimenez and Landgrebe 1998, 1999).
Efficient methods and tools are needed in order to draw generalizable and valid conclusions out of high-resolution measurements that usually include noise and redundancy due to correlations within the data set. When dealing with such high dimensional data, it is important to reduce the dimensionality of the data effectively, possibly with projections from high to low dimensional space, while preserving the class separability between healthy controls and patients. Then, the investigation of the differences between the classes can be carried out more effectively in a lower dimensional space and stable tools can be developed. The dimensionality reduction (e.g. elimination of voxels) should hence be specific enough to remove the redundancy but broad enough to keep the discriminative features of the subsets.
Most fMRI research studies that are not focused on diagnostic classification, use simple group averaging to differentiate between subject classes. In this case, the group averages do not necessarily explain the fMRI activation behavior across all subjects within the same class. These findings might provide a general representation of the investigated classes but classification problems require more difficult conditions to be satisfied since the findings should hold for each individual subject in the classes for good prediction accuracies. In addition, the results might not be generalizable to larger data sets and usually more advanced techniques are required for better and valid comparisons.
We believe that there are important issues to consider in analyzing fMRI data for the purposes of diagnostic classification / prediction and in the presentation of classification performances. Possible biases affect the prediction accuracies previously reported in the field and there is still much to be done, beginning with defining standards both in designing algorithms and in reporting the prediction accuracies in the classification problems.
There have been numerous efforts using fMRI, sometimes in conjunction with other imaging data, with a variety of methods to differentiate patients with brain disorders from healthy control subjects. Promising prediction performances have recently been reported in the literature with the claim that complex diseases can be diagnosed efficiently. We believe that some of those results, though promising, may be biased to the specific data set used and that generalization to other data will be difficult. In this paper we have attempted to emphasize some commonly occurring biases and suggest some possible solutions.
We would like to note that the selection of features used in the classification is crucial. Using selected voxels rather than brain regions might result in overfitting and the resulting findings might be specific to the data set employed. This is so because reproducibility of fMRI activations at a regional level tends to be more robust across test sites, techniques and subjects than is single voxel selection (Casey et al. 1998; Tegeler et al. 1999).
A key issue in the class comparison / prediction problems is less the choice of methods themselves than their correct application following appropriate cross validation rules. The use of cross-validation is very important. The examples we list in “Bias in classification” indicated that cross-validation methods should be applied correctly to obtain more accurate and generalizable conclusions. Cross validation should be properly applied in every stage of the analysis rather than only during the performance evaluation. Prediction accuracies with cross-validation should accompany the results for better validation of the distinguishing features. When the classification results are properly validated using approaches such as cross-validation, then results will be more likely to reproduce.
We also believe that the data sets that are utilized in such research studies are at least as important as the techniques employed. How subject selection is made and what criteria the subjects are required to meet should be detailed in the studies. This will not only prevent selection bias but help us interpret the results for improvements in diagnosis. The techniques should be applied to larger data sets, which should help generalization of the results. Multiple sites should be included in the analysis of the methods to help validation. The Function Biomedical Informatics Research Network (Friedman et al. 2006) and MIND Clinical Imaging Consortium (Demirci et al. 2008) studies are two such representatives of the combined efforts attempting to do this for fMRI data.
In this paper, in “Bias in classification,” we survey previously published work with a focus on identifying possible biases in class comparison / prediction problems and we make suggestions which we hope will be useful for future studies. In addition to our review on previous classification research, we also present a projection pursuit (PP) algorithm that we apply on fMRI data of 155 subjects obtained during three different tasks at two different sites in “A PP analysis model and classification performance comparison on tasks.” “Tasks and data” provides brief information about the tasks we employed and the data we used, and “Analysis methodology” explains the PP algorithm we introduced in our earlier work (Demirci et al. 2008). In “Results and discussion,” we discuss the results we obtained using data of three different tasks and compare them. “Extension to data from multiple sites” presents an extension with addition of data from another site, and investigates the change in the prediction accuracy with multiple sites and different subgroups. Finally, closing remarks are provided in “Conclusion.”
Bias in classification
Issues regarding interpretation and bias in reporting prediction accuracy during classification using gene expression data have been investigated earlier and are relevant to studies utilizing fMRI data. Wood et al. (2007) argue that some genetics research is not reliable although their presented results suggest that most complex diseases can be accurately diagnosed with an effective selection of genetic data such as gene expression measures. Problems are often due to a lack of reporting certain important details (number of subjects in each class, specificity, sensitivity, etc.) related to the analysis performed. We discuss issues related to the presentation of prediction results in recent fMRI studies and present suggestions for improvement.
We divide the possible causes for bias into two main parts, described separately here. In “Class size biases and examples from schizophrenia fMRI literature,” we concentrate on the bias related to data sets employed in the analyses and in “Biases in cross-validation and examples,” we emphasize the bias that can originate due to misapplication of cross validation.
Class size biases and examples from schizophrenia fMRI literature
Classifiers typically use the observations obtained from a training data set and develop the most effective predictive function selecting the most suitable features to assign class memberships to a test (validation) data set. The prediction accuracy is then based on the performance of the classifier in the assignment of the members in the test set. When the results from such an analysis are reported, it is important to present the classification performance for each individual class. Wood et al. (2007) indicates the need to present prediction accuracy separately for each class (e.g., sensitivity and specificity) especially when the classes contain unequal numbers of samples. An overall estimated prediction accuracy does not give information on the performance for each class. In two-class problems this corresponds to presenting both specificity and sensitivity so that the performance of the classifier on both subsets can be interpreted. An overall estimated error rate can still be reported using the proportions of each class in the whole data set.
Another important point in the design of classifiers is the number of subjects used in the training set. The conclusions based on classifiers estimated using a small sample size will likely not represent all the characteristics of the whole population. These classifiers may highlight the distinguishing characteristics of the smaller set but miss the more important properties of the whole population. This is especially so in a disorder such as schizophrenia which is defined using clinical symptom reports.
We now present several examples of studies that offer valuable approaches for using fMRI to diagnose brain disorders, though they also suffer to varying degrees from the biases just described.
Often, detection performances on classes are not reported separately. Ford et al. (2002) combined structural and functional magnetic resonance imaging (MRI) data for classification purposes. They extracted hippocampal formation by applying a mask and then extracted the functional and structural data within the mask. The high dimensional data were then projected onto a lower dimensional space and Fisher's linear discriminant (FLD) analysis was used to maximize the ratio of between-class and within-class variability considering the training set. The prediction accuracy of the classifier was tested using a total of 23 subjects (15 schizophrenia patients and 8 healthy controls) with a leave-one-out method. One of the subjects were removed from the whole set for validation purposes (K=1, 1-fold cross-validation) and the rest of the subjects were used as training data. A maximum classification accuracy of 83-87% was presented, which is reasonable. However, it would also be informative to know prediction performances on both classes separately, especially in this case where the number of subjects in the two groups differ. For example, for this particular set, 85% overall prediction performance could possibly be obtained with 100% detection performance on schizophrenia patients and only a 57% detection performance on healthy controls (43% false alarm), which would indicate a poor performance on healthy controls.
In a similar study, Ford et al. also proposed to use principal component analysis (PCA) to represent subjects in a lower dimensional space with maximal variance and uncorrelated samples, based on the idea that fMRI activation patterns show differentiations among healthy controls, patients with schizophrenia, Alzheimer's disease and mild traumatic brain injury. The FLD classifier was applied to fMRI brain activation maps in this lower dimensional space to differentiate patients from healthy controls (Ford et al. 2003). The prediction accuracy of the schizophrenia patients varied between 60% and 80% for different numbers of principal components on a set of 25 subjects (10 healthy controls and 15 patients with schizophrenia). Specificity and sensitivity performances were not reported separately. The authors appropriately pointed out that their results should be interpreted cautiously because of the small data set.
Detailed subject selection criteria are also important to include in research studies. Job et al. (2006) investigated whether structural changes in the brain over time provide a better indication of disease than behavioral measures for the prediction of schizophrenia and asserted that reduction in gray matter, especially in the temporal lobe, helps predict schizophrenia. It is mentioned that the Edinburgh High Risk study prospectively examined 150 young people with a high risk of developing schizophrenia based on familial history over a 10 year period. Twenty-one of these subjects developed schizophrenia and 60 had transient, partial or isolated psychotic symptoms on at least one occasion. In their research study, they selected 65 high-risk subjects from this set, 8 of whom developed schizophrenia an average of 2.3 years after their first scan. They concluded that they had only a limited number of subjects and the findings required an independent replication for validation. We believe a more detailed explanation on how the selection was made would be beneficial and further strengthen the validation of the results.
Shinkareva et al. (2006) identified the groups of voxels showing temporal dissimilarity using an RV-coefficient (Robert and Escoufier 1976) (a measure of temporal dissimilarity) and worked directly with fMRI time series data from brain regions of interest. They presented a prediction accuracy of 85.71% using a leave-one-out cross-validation on 14 subjects (7 schizophrenia patients and 7 healthy controls) using functional activity in brain frontal areas during a Stroop task, which involved presentation of task relevant (color) and task irrelevant (emotional meaning) attributes of different words. The results seemed promising. This set of 14 subjects was selected among a group of 32 available subjects (16 schizophrenia patients and 16 healthy controls). Providing more information on the selection procedure and why only 7 participants, but not more, from each subclass were used would be useful in interpreting the results. We were motivated by the effectiveness of the temporal data used and the method employed. When we carried out a similar analysis on a set of more than 100 subjects, we were not as successful.
Calhoun et al. (2008) combined temporal lobe and default mode components after an application of independent component analysis (ICA) on the fMRI data obtained during an auditory oddball task to discriminate subjects with bipolar disorder, chronic schizophrenia and healthy controls. 21 chronic schizophrenia patients, 14 bipolar Type I outpatients and 26 healthy controls were used in this analysis. The two spatially independent brain modes (temporal lobe and default mode) were concatenated into a single image. An adaptive step was employed to reduce the number of voxels used and subjects were represented in a reduced dimensional space. Each individual was assigned one of three class memberships with a leave-one-out approach based on the Euclidian distance between the individual and group means. Randomly selected subjects from each group were excluded from the whole data set, the classifier was designed using the remaining participants and tested on the three subjects. An average sensitivity and specificity of 90% and 95% were reported, respectively.
Separately, we applied a PP technique to decrease the dimensionality of fMRI data obtained during an auditory oddball task on 70 subjects (34 schizophrenia patients, 36 healthy controls) from New Mexico site of the MIND Research Network (Demirci et al. 2008). The technique included various data reduction stages including an application of an ICA and selection of different brain activation networks. Promising overall prediction accuracies varying between 80%-90% were obtained. We propose that including data from different sites would help validation of these results because each site brings variabilities like operators, scanning equipment and parameters, and population distribution.
Good examples of classification of 3D medical images were presented and corresponding performances were compared by Pokrajac et al. (2005). They used activation contrast maps of 18 subjects (9 Alzheimer's disease patients and 9 healthy controls) and highly activated regions were extracted utilizing an activation cut-off threshold. Statistical distance based techniques (Mahalanobis distance and KL divergence) and maximum likelihood methods were used for classification. The prediction accuracies obtained with a leave-one-out cross-validation varied between 68% and 80%. Best performance was achieved with k-means (k = 3) maximum likelihood approach with a 80% detection accuracy.
Other promising results were reported in Kontos et al. (2004). They applied Hilbert space filling curves on 3D fMRI activation contrast maps to transform them into a linear domain preserving the locality of the voxels during transformation. Nine healthy controls and 9 patients with Alzheimer's disease were analyzed. Neural networks were employed as a classification tool and almost 100% classification accuracy was achieved using a leave-one-out cross-validation. Wang et al. (2004) applied similar techniques on the time series domain to determine the discriminative spatial patterns in the fMRI data. They found accuracies above 90%.
Causes of bias in prediction problems are not limited to the data set employed, but could be due to the misapplication of the verification methods. In “Biases in cross-validation and examples,” we describe further possible causes and provide examples of this type from recent literature.
Biases in cross-validation and examples
Prediction performance of classifiers is usually measured using cross-validation but are likely to be biased when cross-validation is used in a way that provides a measure of generalizability error (Wood et al. 2007). K-fold cross-validation evaluates the prediction accuracy by splitting the data into K folds, separating one of these to be used as test fold, and utilizing the rest of the folds as training folds. In this case, the estimated parameters, and model should be computed using only the training folds and the prediction performance of the designed system be evaluated on the test fold. The operation can then be repeated K times where each of the folds is used as a test fold, and the average performance is then the unbiased estimate of the classifier. Using the full set of data during the design of the model and not building it from scratch for each different test group biases the results (Simon 2004; Wood et al. 2007). A two-level cross-validation method is proposed where the data set is divided into portions in two consecutive steps where the second division ensures that the model parameters for the classifier are unbiased (Wood et al. 2007).
Simon pointed out the difficulty of designing an effective classifier using gene expression data, due to the fact that candidate predictors have a dimensionality that is orders of magnitude greater than the number of subjects available (Simon 2004; Simon et al. 2003). This problem presents unique challenges as the solution requires analysis of tens of thousands of noisy data points in a very high dimensional space, and turning them into dependable and understandable conclusions. He also raises the issue that research done in this field is usually based in only one institution and microarray assay's conducted in one laboratory. In spite of these restrictions, he also agrees that prediction accuracy of the classifiers should be presented along with certain criteria. He supports using k-fold cross validation methods and agrees that this is more efficient than split-sample validation. The validity of the classifier should be measured with cross-validation to provide precise estimates of specificity and sensitivity. It is very important to select subjects from a prospective multicenter clinical network so that the results can be generalized to multiple locations.
Supervised classifiers usually assume that certain data points among the whole data set are associated with class distinction (Simon et al. 2003). These points should be selected as a first step of designing an effective classifier. The appropriate subsets can either be assigned weights depending on their distinctive strengths or a PCA can be applied as a dimensionality reduction technique. The general problem of designing an effective classifier is overfitting to the training data set. This is a very general problem in cases where the number of training samples are small compared to the number of data points to represent them. The presented prediction accuracies are usually misleading as the classifier over-fits to the original data set (especially the unimportant random variations) and can result in highly variable results when applied to new data. This requires an effective presentation of prediction performance for the designed classifiers. Simon et al. (2003) indicates that it is crucial to apply cross-validation when selecting discriminative data, decreasing dimensionality and designing the predictor. Failing to cross validate in any of these steps produces biased results.
K-fold cross-validation techniques should be applied in all steps of designing a classifier including feature selection. For example, Job et al. (2006) extracted three brain areas in a comparison between 8 schizophrenia subjects and 57 control subjects. The same subjects used in the region selection were also used in the classification. Such an approach tends to bias the results as the information on the classes has been used to select the brain areas. Areas showing possible differentiations between schizophrenia and control subjects can be selected with minimal to no bias by determining the regions without using the test subject in each iteration and then performing classification of the left out subject only.
Georgopoulos et al. (2007) presented a classification method using magnetoencephalography (MEG) and assigned group memberships to subjects with various illnesses (Alzheimer's disease, schizophrenia, multiple sclerosis, Sjogren's syndrome, chronic alcoholism, facial pain). They used 248 axial gradiometers on 142 human subjects and obtained 30628 partial zero-lag cross-correlations between sensors for all sensor pairs and used them as the predictor set. They looked for subsets of this predictor set and investigated if any such predictor subsets correctly classified subjects into their respective groups. This was a dimensionality reduction problem. They indicated that a subset of 12 predictors (correlations) gave a prediction accuracy of 86.6% and assigned 86.6% of the subjects to their respective groups correctly. They used this same set of 12 predictors and presented `cross-validation' results around 77-79% with two different jackknifed methods, k-fold and leave-one-out, respectively. Though these results are encouraging, especially given the specificity of the approach to multiple different groups, they appear to be biased to the data at hand because the same set of 12 predictors were used for each different training set, and a different set of predictors were not obtained for each training set separately.
Application of k-fold cross-validation at each step is crucial. Failing to do so on only one such step will bias the results. Pardo et al. (2006) used linear discriminant analysis (LDA) to differentiate patients with schizophrenia and bipolar disorder. They used 22 neuropsychological test scores and 23 quantitative structural brain measurements obtained with cerebral structural MRI to classify 28 subjects into three groups (8 healthy controls, 10 schizophrenia and 10 bipolar disorder patients). Multiple regression analyses were used before LDA to adjust the data for demographic and medication influences. A subset from the whole 45 variables was chosen each time and these subsets included varying number of variables (2 to 12). The prediction performance of each subset was tested using a leave-one-out method on the 28 subjects, resulting in the average of 28 different cases. 9 subsets with 12 variables provided a classification rate of 96.4%, misclassifying only one of the subjects out of the entire 28. Pardo et al. assert that the results are robust because a leave-one-out method was employed in the analysis. However, the fact that these subsets (12 variables) were determined using all 28 subjects is ignored. A more robust result would be obtained by using only the 27 subjects to reduce the number of features and testing the performance of this subset on the left-out subject.
Fan et al. (2007) applied a multivariate classification approach combining data from both a functional feature map (cerebral blood flow) and structural MRI data to detect brain abnormality associated with prenatal cocaine exposure in adolescents. Regions with voxels of similar correlation to the disease were obtained using a Pearson correlation coefficient for three different feature maps separately. A leave-one-out method was employed and an effective cross-validation strategy was followed to measure the overall correlation of a feature to class label. Then, statistical regional features (histograms) and a PCA were used to represent each region with a feature vector. Subjects were represented with the vectors from three different feature maps. Promising results were obtained on 49 subjects (25 prenatal cocaine-exposed subjects and 24 normal controls). Fan et al. (2007) mention the possibility that obtained classification accuracy might be an indication of over-fitting based on the random permutation tests they performed.
Nakamura et al. (2004) used structural brain images of 104 subjects (57 patients with schizophrenia and 47 healthy controls) to investigate the differences between the healthy controls and schizophrenia patients. 81% overall detection accuracy was obtained using a discriminant function analysis.
Previous research topics mentioned in this paper are summarized in Table 1. It is important to note here that there are numerous other classification studies based on structural data (Golland et al. 2000; Gerig et al. 2001; Shen et al. 2004) in the brain imaging field but we are mostly concentrating on studies using fMRI data in this paper.
Table 1.
List of previous research with the data and the methods used, and the performances obtained
| # subjects | Best Performance | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Author | Title | Data | Method | (c+d) | (a+b) | (a+c)/(a+b+c+d) | a/(a+b) | c/(c+d) | a/(a+d) | c/(b+c) | a | b | c | d |
| Healthy Control | Patient (SZ, AD, CA, ..) | Prediction Accuracy (%) (overall) | Sensitivity, (PD,%) (%) | Specificity, (1-PFA,%) | PPV (+ predictive value | NPV (- predictive value | TP (true +) | FP (false +) | TN (true -) | FN (false -) | ||||
| Ford et al. (2002) | A combined structural-functional classification of schizophrenia using hippocampal volume plus fMRI activation. | fMRI-sMRI | Fisher's linear discriminate (FLD) analysis | 8 | 15 | 83-87 | ? | ? | ? | ? | ? | ? | ? | ? |
| Ford et al. (2003) | Patient Classification of fMRI Activation Maps. | fMRI | Fisher's linear discriminate (FLD) analysis | 10 | 15 | 60-80 | ? | ? | ? | ? | ? | ? | ? | ? |
| Job et al. (2006) | Grey matter changes can improve the prediction of schizophrenia in subjects at high risk. | vMRI | Measure of change in grey matter with masks and thresholding in ROIs. | 57 | 8 | 89 | 38 | 96 | 60 | 92 | 3 | 5 | 55 | 2 |
| Shinkareva et al. (2006) | Classification of functional brain images with a spatio-temporal dissimilarity map. | fMRI | Temporal dissimilarity using an RV-coefficient | 7 | 7 | 86 | 86 | 86 | 86 | 86 | 6 | 1 | 6 | 1 |
| Calhoun et al. (2007) | Temporal lobe and default hemodynannic brain modes discriminate between schizophrenia and bipolar disorder. | fMRI | ICA, Euclidian distance | 26 | SZ 21 BP 14 |
91 | 90 | 95 | ? | ? | ? | ? | ? | ? |
| Demirci et al. (2007) | A Projection Pursuit Algorithm to Classify Individuals Using fMRI Data: Application to Schizophrenia. | fMRI | ICA and Projection Pursuit | 36 | 34 | 80-90 | 91-97 | 89 | 89 | 91 | 31 | 3 | 32 | 4 |
| Pokrajac etal. (2005) | Applying spatial distribution analysis techniques to classification of 3D medical images. | fMRI | Mahalanobis distance, Kullback-Leibler (KL) divergence and maximum likelihood | 9 | 9 | 68-80 | 77-79 | 57-83 | 70 | 75 | 7 | 2 | 6 | 3 |
| Kortos et al. (2004) | Detecting discriminative functional MRI activation patterns using space filling curves. | fMRI | Hilbert space filling curves, neural networks | 9 | 9 | 82-100 | 79-100 | 74-100 | 100 | 100 | 9 | 0 | 9 | 0 |
| Wang et al. (2004) | Application of time series techniques to data mining and analysis of spatial patterns in 3D images. | fMRI | Time series domain techniques (Euclidian distance, Singular Value Decomposition) | 9 | 9 | 80-100 | ? | ? | ? | ? | ? | ? | ? | ? |
| Georgopoulos et al. (2007) | Synchronous neural interactions assessed by magnetoencephalography: a functional biomarker for brain disorders. | MEG | Autoregressive integrative moving average (ARIMA) model | 89 | SZ 19 AD 9 CA 3 SS 1D MS 12 |
77 | ? | ? | ? | ? | ? | ? | ? | ? |
| Pardo etal. (2006) | Classification of adolescent psychotic disorders using linear discriminant analysis. | sMRI | Linear Discriminant Analysis (LDA) | 8 | SZ 10 BP 10 |
96.4 | ? | ? | ? | ? | ? | ? | ? | ? |
| Fan et al. (2007) | Multivariate examination of brain abnormality using both structural and functional MRI. | fMRI-sMRI | Pearson correlation coefficient, statistical regiona features {histograms) and PCA | 24 | 25 | 88-92 | ? | ? | ? | ? | ? | ? | ? | ? |
The missing data in some cells are approximated using the data in others when possible.
fMRI: functional MRI, sMRI: structural MRI, vMRI: volumetric MRI, MEG: Magnetoencephalography
Finally, we would like to summarize possible different reasons for bias in the prediction problems using fMRI data. Table 2 lists different types of bias, reasons, possible solutions and examples in each group. “Selection Bias” and “Parameter Selection Bias” may seem very similar to each other. “Selection Bias” involves the use of all subjects that we try to classify in any stage of the classification algorithm and may result in overfitting. This is a misapplication of cross-validation. “Parameter Selection Bias” involves the change of the parameters in the classification algorithm and application of the specific set of parameters giving the best result in the final design. This could result from deciding what part of the data to use, and what parameter values to prefer (optimum set) based on the multiple runs of the test.
Table 2.
Different causes of bias in prediction problems
| Type of Bias | Reason | Solution | Example |
|---|---|---|---|
| Limited number of available subjects | The results are obtained based on a small data set (whole group or one of the classes) and are not always generalizeable to larger data sets. A small set does not necessarily represent all characteristics of populations of interest. | Collecting data for more subjects (either locally or via multi-site studies) | 9 patients and 9 healthy controls or 5 patients and 27 healthy controls. |
| Presenting only the overall prediction accuracy (all classes together) | The classes in a data set might not have equal number of subjects. A lower prediction performance on the subclass with smaller number of subjects will have less weight and overall performance will look high due to the higher performance of the sublass with larger number of subjects. Poor performance on the class with smaller number of subjects will be concealed. | Including a separate prediction accuracy for each subclass, and an overall prediction accuracy. | Reporting 90% overall prediction accuracy on 5 patients and 35 controls could be either, 1) 90% on patients, 90% on controls 2) 41% on patients, 97% on controls |
| Selection Bias (ovefitting) | Cross validation is often used incorrectly. Design of a classifier is composed of the stages: 1- selecting a subset of discriminative subjects, 2- applying PCA / assigning weights to voxels based on their discriminative strengths, 3-defining prediction rules. Using full set of available subjects in any of these steps causes bias. |
External cross-validation at each step of the classifier design. Classifier should be built from scratch (from step 1 to step 3) for each training set. | Using all subjects available (including the class information) to reduce the number of voxels from 50000 to 50 and then running an analysis with external cross-validation. |
| Parameter Selection (Optimization) Bias | Selecting a set of parameters based on the prediction accuracy obtained and using the set of parameters with the best performance in the final classifier, (e.g. even if cross-validation is applied, running the experiment multiple times with the same data ) | 2-level cross-validation: A portion of the data (1/P1) is left out to assess the prediction performance. P2-fold external cross-validation is applied on the remaining portion of the data. | Running the same analysis multiple times considering varying number of principal components, and using the most optimum number of PCs in the further steps. |
Although it is not always possible to extend the data set, especially for patients, the number of healthy controls used in the analysis can be increased to obtain more generalizable results especially when there are only a very limited number of patients. As long as the specifics of the subgroups remain the same and prediction accuracies for the subclasses are reported, the number of subjects in the subgroups do not necessarily need to be equal. Using multi-site data from different studies will also increase the effectiveness of the results.
In our own experience, including the test subjects in the feature elimination steps increased the performance considerably (10%-15%). Our experience verified the necessity of the correct application of k-fold cross-validation. Thus, classifiers should be designed from scratch for each different training set, and test subjects only used for validation purposes.
A PP analysis model and classification performance comparison on tasks
Tasks and data
The fMRI data used in this research discussed below were obtained via the MIND Research Network, a consortium founded to help diagnosis of mental illnesses and other brain disorders, including understanding the course and neural mechanisms of schizophrenia. The data presented here were obtained from four different sites (New Mexico, Harvard, Iowa and Minnesota). The aim was to collect as many data as possible with a cooperative team approach and to incorporate the differences in the multi-site design. Representatives from investigative teams from each of the sites worked together for calibration and standardization of imaging designs and techniques so that more reliable measurements of brain structure and functions across sites could be obtained.
We used functional data sets obtained when subjects were scanned during performance of three different tasks. These tasks are auditory oddball (AOD), Sternberg item recognition paradigm (SIRP) and Sensorimotor (SM) tasks. Sections “Auditory oddball discrimination (AOD) task”, “Sternberg item recognition paradigm (SIRP) task” and “Sensorimotor (SM) task” describe the tasks briefly followed by a description of the method we followed and results we obtained.
Auditory oddball discrimination (AOD) task
It is hypothesized that an important deficit in schizophrenia involves information processing (Braff 1993). Patients with schizophrenia complain that they are subject to more stimuli than they can interpret (McGhie and Chapman 1961). They misperceive, confuse internal with external stimuli (hallucinations), or do not respond at all to external stimuli. Patients sometimes cannot allocate attentional resources relevant to tasks (resource allocation). Alternatively, patients may be unable to suppress irrelevant stimuli (inhibit) in order to focus on more significant ones (Watersa et al. 2003). This is why the auditory oddball task is widely used to assess sensory processing ability (McCarley et al. 1993; Shankardass et al. 2001; Tecchio et al. 2003; Symond et al. 2005).
During auditory oddball tasks, our participants wore sound-insulated earphones (Avotec, Stuart, FL. Avotec Inc.. 603 N. W. Buck Hendry Way) that present the auditory stimuli while shielding from noise due to vibration of the gradient coil. Subjects are asked to respond by pressing a button with their right index finger every time they hear a target stimulus and not to respond to other standard tones or novel computer generated sounds. The same auditory stimuli have been found to be effective in differentiating healthy controls from schizophrenia subjects in previous fMRI studies (Kiehl and Liddle 2001; Kiehl et al. 2005). Standard stimuli occur with a probability of p = 0.82 and are represented with 1 kHz tones. Target and novel stimuli are infrequent and each occurred with a probability of p = 0.09 (Fig. 1). Target stimuli are represented with 1.2 kHz tones and novel stimuli are computer generated, complex sounds. Each stimulus is presented with a pseudorandom order and last for 200 ms. The inter-stimulus interval changes randomly in the interval 550-2050 ms with a mean of 1200 ms. A total of four runs were acquired per session and each run comprised 90 stimuli. The sequences for target and novel stimuli were exchanged between runs to balance their presentation and to ensure that the activity evoked by the stimuli were not because of the type of the stimulus used.
Fig. 1.

Auditory oddball experiment. Three different stimuli are represented with different colors and unevenly spaced to indicate the pseudorandom generation (Demirci et al. 2008)
Sternberg item recognition paradigm (SIRP) task
A working memory (WM) deficit is consistent with some of the symptoms of schizophrenia, since performing cognitive operations using WM permits individuals to respond in a flexible manner, to formulate and modify plans, and to base behavior on internally-held ideas and thoughts rather than being driven by external stimuli (Baddeley 1992). The SIRP task was utilized as it is a choice reaction time task that requires working memory. Participants in the SIRP task are asked to memorize targets (digits) during the “encode” epoch and then are asked to respond by indicating whether the probe is a target (a member of the memorized set) or a foil (not a member of the memorized set). Figure 2 shows one of those blocks during an experiment.
Fig. 2.
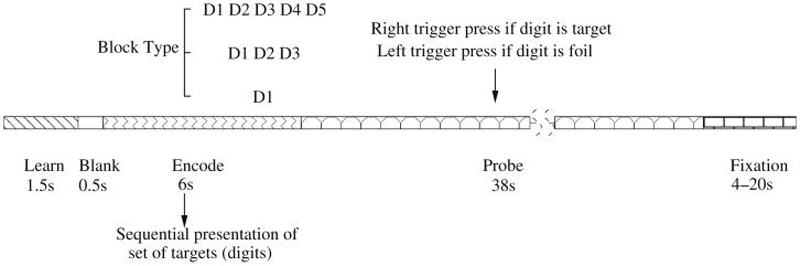
Representation of a block in SIRP (Sternberg Item Recognition Paradigm). Two blocks of each of the three conditions with {1, 3, 5} digits (in a pseudorandom order) constitute a run
Each block is composed of three epochs. During the encode epoch, one of the three possible WM blocks are pseudorandomly selected and the targets (digits) presented sequentially. Subjects are asked to respond to the probes (single digits) presented during the “probe” epoch and asked to respond with a right trigger press if the digit is a target (a member of the memorized set) or a left trigger press if the digit is a foil (not a member of the memorized set). In each of the probe epochs half the probes are targets and half are foils. A “fixation” epoch follows where a point is shown on the screen and subject is asked to relax and get ready for the next trial. The duration of the fixation epochs within a run is random, changing between 4 and 20 seconds. Six blocks (two blocks of each of the 3 conditions in a pseudorandom order) constitute a run and each run lasts approximately 6 minutes requiring the sum of fixation epochs to be 78 seconds.
Sensorimotor (SM) task
The sensorimotor task was designed for calibration purposes. The task includes 8 different tones with different pitches which are presented with 0.2s duration and 0.5s stimulus onset asynchrony (SOA) in a pattern such that pitches of the tones increases and decreases stepwise (see Fig. 3). The pattern of ascending and descending pitch scales continues till the end of a block with “on” cycle. Subjects are asked to push a button of an input device with their right thumb after each tone. No tone is presented during the blocks with “off” cycles. The total task duration is 240s (120 TRs, TR = 2s).
Fig. 3.

Representation of a block in Sensorimotor (SM) task
fMRI data
For this study, we analyzed data from two sites as an initial effort in a larger multi-site analysis. Incorporating data from other sites is planned in our next research study. The first data set included 70 subjects from the New Mexico site of the MIND research network; 34 patients with schizophrenia and 36 healthy controls. Patients with schizophrenia were receiving stable treatment with atypical antipsychotic medications (aripiprazole(7), olanzapine(2), risperidone(1), ziprasidone(1), clozapine(1)). Twenty eight subjects in each class were males. There were no significant between-group differences in age. The healthy controls ranged in age from 18 to 54 years (mean=28.9, SD=12.3). The patients ranged in age from 18 to 60 years (mean=31.4, SD=11.6).
A larger data set was generated with the addition of subjects from the Iowa site to the previously described New Mexico data and included a total of 138 subjects; 57 schizophrenia patients and 91 healthy controls. Patients with schizophrenia were receiving stable treatment with atypical antipsychotic medications (aripiprazole(13), olanzapine(7), risperidone(12), ziprasidone(4), clozapine(1), quetiapine(5)). 60 of the healthy controls (61%) and 38 of the patients (83%) were males. Healthy participants ranged in age from 18 to 57 years (mean=30.2, SD=10.6). Patients ranged in age from 18 to 60 years (mean=32.4, SD=12.3). In the second data set, there was no significant difference in the average ages of the two groups.
Schizophrenia patients in the data set were limited to those with a DSM-IV diagnosis of schizophrenia on the basis of a structured clinical interview and review of the case file (First et al. 1995). The healthy volunteer subjects were recruited from communities through newspaper advertising and carefully screened using a structured interview to rule out medical, neurological, and psychiatric illnesses, including substance abuse. Subjects with history of neurologic or psychiatric disease other than schizophrenia, head injury resulting in prolonged loss of consciousness and/or neurological sequelae, skull fracture, epilepsy, except for childhood febrile seizures, prior neurosurgical procedure, and IQ less than or equal to 70, based on a standard IQ test or the ANART were excluded from the study. All subjects were fluent in English, provided written, informed, IRB approved consent at the scanning locations in New Mexico and Iowa, and were paid for their participation.
All scans were acquired at the MIND Research network sites in New Mexico and Iowa on Siemens Sonata 1.5T and Siemens 3T Trio dedicated head scanners equipped with 40mT/m gradients and standard quadrature head coils, respectively. The functional scans were acquired using gradient-echo echoplanar-imaging with the parameters: repeat time (TR)= 2 s, echo time (TE)= 40 ms ((TE)= 30ms for Iowa), field of view= 22 cm, acquisition matrix= 64 × 64, flip angle= 90°, voxel size= 3.44 × 3.44 × 4 mm3, gap= 1 mm, 27 slices, interleaved acquisition.
FMRI data were preprocessed using the software package SPM5 (SPM5 2008). Images were realigned using INRIalign a motion correction algorithm unbiased by local signal changes (Freire et al. 2002). Data were spatially normalized into the standard Montreal Neurological Institute space (Friston et al. 1995), spatially smoothed with a 9 × 9 × 9 mm3 full width at half-maximum Gaussian kernel. The data (originally acquired at 3.44 × 3.44 × 4 mm3) were slightly sub-sampled to 3 × 3 × 3 mm3, resulting in 53 × 63 × 46 voxels.
Behavioral data
The demographics of the data set used in this study was explained in detail in “fMRI data.” Tables 3 and 4 present behavioral data for AOD and SIRP tests, respectively. The presented hit percentages consider all subjects from the two sites, but the reaction times were evaluated using only the subjects from the New Mexico site due to a hardware measurement error at the Iowa site.
Table 3.
Comparison of schizophrenia patients and healthy controls in AOD test using the hit percentages in targets and average reaction times. Both mean and standard deviations are listed
| Hits in targets % |
Avg. reaction time (s) |
|||
|---|---|---|---|---|
| Patients | Controls | Patients | Controls | |
| Mean | 82.36 | 81.47 | 484.36 | 451.66 |
| Std | 18.38 | 20.67 | 131.65 | 79.37 |
Table 4.
Comparison of schizophrenia patients and healthy controls in SIRP test using the hit percentages in targets and average reaction times. Both mean and standard deviations are listed
| All correct % |
Target RT all (s) |
Load 1 target RT (s) |
Load 3 target RT (s) |
Load 5 target RT (s) |
||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Patients | Controls | Patients | Controls | Patients | Controls | Patients | Controls | Patients | Controls | |
| Mean | 94.59 | 98.57 | 665.97 | 583.62 | 556.59 | 497.89 | 685.55 | 607.10 | 775.76 | 645.87 |
| Std | 5.61 | 0.91 | 92.50 | 62.82 | 65.86 | 60.75 | 89.71 | 61.86 | 135.51 | 77.51 |
Table 3 lists the hit accuracies of the targets and average reaction times of both patients and controls based on four different runs included in an AOD experiment. The results indicate that patients have longer average reactions times and standard deviations compared to controls, although the accuracies are similar to each other.
Table 4 lists average hit accuracies and average response times of both patients and controls based on runs where three different block types were presented. These behavioral results also show that patients have longer average reaction times and standard deviations compared to controls, and hit accuracies are essentially the same, similar to those obtained in AOD experiment.
Analysis methodology
Background and related work
ICA is a technique that is used on multivariate data to define a generative model as linear or nonlinear mixtures of some unknown sources with an unknown mixing system. ICA decomposes the data into mutually independent, nongaussian sources, which are called sources or independent components. Various algorithms such as maximization of nongaussianity, minimization of mutual information, maximization of maximum likelihood estimation can be employed (Hyvarinen et al. 2001). It has been a fruitful tool in the fMRI field by helping delineate the spatiotemporal structure of fMRI data. Using ICA, the change in the fMRI signal is factored into a set of time courses and corresponding spatial patterns where either the spatial patterns or the time courses are a priori independent. Spatial ICA extracts the non-overlapping, temporally coherent brain activation networks without constraining the temporal domain (McKeown et al. 1998; Calhoun et al. 2001c).
ICA has been used on fMRI data mostly to identify networks associated with schizophrenia. Calhoun et al. (2004) used ICA on fMRI data to identify aberrant localization of hemodynamic coherence in schizophrenia and suggested that abnormal patterns of coherence in temporal lobe cortical regions characterize schizophrenia. Garrity et al. (2007) also employed ICA of fMRI data to identify the default mode component, which is thought to reflect the resting state of the brain, and examined the differences in temporal and spatial aspects of the default mode. Significant spatial and temporal differences were observed between healthy controls and patients with schizophrenia in the default mode component.
We also employed ICA to separate the data into maximally independent groups and identify the networks most related to schizophrenia as one of the steps of our PP algorithm (Demirci and Calhoun 2007; Demirci et al. 2007, 2008). Time progress of voxels during the auditory oddball task were factored into 20 independent spatial components and a set of time courses through ICA. After the application of ICA on the data obtained during various tasks, independent spatial components (the default mode network, temporal lobe network, visual mode, frontal temporal, frontal parietal, lateral frontal parietal, etc.) were selected for each task. For this paper, we chose to focus only on the main task-related components, but much more is possible. Although default mode is the baseline condition when the brain is idling, each task can yield a default mode component that can be chosen from among the other networks. The independent components were used to represent N subjects in a high dimensional space (number of voxels in the whole brain, m, ≈ 150000 voxels) separately. An m × N dimensional mean removed data matrix (m ⪢ N), X, whose columns included all voxels in the network was formed and PCA was applied to the covariance matrix, CXX = (1/N - 1)XXT, as an effort to transform the data into a lower dimensional space with maximal variability. PCA decomposes the data into uncorrelated components. An alternative eigen-analysis method was preferred due to the extensive size of CXX and PCA was applied on instead. The two covariance matrices, CXX and shared the same N nonzero eigenvalues with the assumption that there were only N independent observations. Eigenvectors, vi, of the covariance matrix CXX were obtained applying a transformation on the eigenvectors, , of ,
| (1) |
The classification performance obtained on the subjects using all brain data with a leave-one-out cross validation method was poor (results not shown). This indicated the necessity of reduction of the voxels (m ⇒ m′), and considering only those features that discriminated the healthy controls and patients with schizophrenia. A mask was proposed to eliminate voxels that demonstrated indifferent activation patterns between classes. Remaining voxels (features) were used to represent the subjects in a lower dimensional space. Classification results were promising and PP algorithm was shown to be effective (Demirci and Calhoun 2007). The performance of the classifier was compared using different activation networks and the temporal lobe network provided better and more stable performance among the others (Demirci et al. 2008).
Methods
During our research study, we applied three group ICA operations (Calhoun et al. 2001a, b; GIFT 2008) on the data from three different tasks and obtained 20 independent spatial components and a set of time courses for each task. In light of the previous findings, two different criteria have been used to select the activation networks (independent components) to be used in further analysis in two different methods. In the first of such method, we inspected the independent components visually and labeled them as a temporal lobe network, default mode network, etc based on the activation. We would like to clarify that labeling operation causes no bias and each of the independent components looks similar to one of the brain activation patterns. The selection is not based on visual appearance quality. In the second method, the independent components were ordered based on the fit to the regressors used in the task. In this paper we performed these two analyses, first using only the temporal lobe network and the second using the component with the best fit to the regressors for each of the tasks.
The selected independent components were used in the developed PP algorithm separately (Demirci et al. 2008). The number of all brain voxels from each individual independent component were reduced to around 6000 using a mask to eliminate the voxels that demonstrated little difference between the two classes. Employing a stepwise algorithm, 10 patients with schizophrenia and 10 healthy controls were picked randomly from their training groups at each step. Differences between the averages of the two subsets each with 10 subjects were examined to retain the voxels showing higher activation for either schizophrenia patients or healthy controls. Voxels that were retained in the set consistently were kept until the number of voxels was less than 6000. These voxels were used to represent the training subjects and the covariance matrix was computed in the PCA to find the spatial patterns (eigenvectors) that maximized variability. The first M eigenvectors representing the largest variance were kept and each of the subjects was projected onto these eigenvectors to determine the principal components (PCs) in the M dimensional space. An optimization algorithm was employed to find the direction, , that maximized the separation of the healthy controls and patients with schizophrenia based on the PP index defined (Demirci et al. 2008). Another PP stage followed to decrease the number of features to be considered. Components of the unit length vector were used and M/2 eigenvectors giving more separation between the classes were kept. A similar optimization stage was employed to find another direction, , that maximized the separation of classes in the M/2 dimensional space. All training subjects were represented with scalars after projecting their coordinates onto in the M/2 dimensional space. A test subject was also projected onto and represented with another scalar. A decision was given objectively based on the projection of the test subject on the unit length vector compared with the distribution of the training set.
In this study, we extend our research efforts to find performance differences among the data obtained during three different tasks, AOD, SIRP and SM, to examine their usefulness in discriminating healthy controls from patients with schizophrenia. Detailed descriptions of the tasks were provided in Sections “Auditory oddball discrimination (AOD) task”, “Sternberg item recognition paradigm (SIRP) task” and “Sensorimotor (SM) task.”
A leave-one-out approach was performed on 70 subjects (36 healthy controls and 34 patients with schizophrenia) from New Mexico site of the MIND research network. The same test was repeated for different values of M to investigate the effect of number of PCs considered on the performance accuracy.
In “Results and discussion,” we present results obtained using the fMRI data and applying a previously published PP technique (Demirci et al. 2008).
Results and discussion
Probability of detection (PD), probability of false alarm (PFA) and overall detection accuracy (PAll) are tabulated in Table 5 for various activation networks of three different tasks. The results are presented for various predicted false alarm rates (10%, 20%, 30%, 40%) obtained using the Gaussian approximation to the histograms on the direction. For the AOD and SM tasks, the components with temporal lobe activation and the component with best fit to regressors were the same, 12th and 17th components, respectively. In SIRP task, component with temporal lobe activation was the 16th one and best fit to regressors method gave two highly likely components, 11th and 3rd.
Table 5.
Prediction performances obtained with various number of components, (M/2, M), and activation networks from three differnet tasks: A PCA step is used to find the first M PCs of the training set, for M = 4, 6, 10, 14, 20, 30, 40, 50
| Temporal |
Temporal |
Best Fit to Regress. |
Best Fit to Regress. |
Temporal |
||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Odd comp12 |
Sirp comp16 |
Sirp comp11 |
Sirp comp03 |
Sm comp17 |
||||||||||||||||||
| 10% | 20% | 30% | 40% | 10% | 20% | 30% | 40% | 10% | 20% | 30% | 40% | 10% | 20% | 30% | 40% | 10% | 20% | 30% | 40% | |||
| Number of Components Used | (25,50) | PD | 0.97 | 0.97 | 1.00 | 1.00 | 0.94 | 0.97 | 0.97 | 0.97 | 0.97 | 0.97 | 1.00 | 1.00 | 0.94 | 0.97 | 0.97 | 0.97 | 1.00 | 1.00 | 1.00 | 1.00 |
| PFA | 0.53 | 0.61 | 0.69 | 0.75 | 0.56 | 0.68 | 0.76 | 0.76 | 0.53 | 0.59 | 0.62 | 0.76 | 0.53 | 0.68 | 0.74 | 0.76 | 0.46 | 0.54 | 0.63 | 0.69 | ||
| Pall | 0.71 | 0.67 | 0.64 | 0.61 | 0.68 | 0.64 | 0.59 | 0.59 | 0.71 | 0.68 | 0.68 | 0.61 | 0.70 | 0.64 | 0.61 | 0.59 | 0.78 | 0.74 | 0.69 | 0.67 | ||
| (20,40) | PD | 0.94 | 0.94 | 1.00 | 1.00 | 0.88 | 0.97 | 0.97 | 0.97 | 0.84 | 0.91 | 0.94 | 0.97 | 0.91 | 0.94 | 0.97 | 0.97 | 0.97 | 1.00 | 1.00 | 1.00 | |
| PFA | 0.33 | 0.56 | 0.67 | 0.78 | 0.32 | 0.59 | 0.71 | 0.71 | 0.47 | 0.59 | 0.62 | 0.65 | 0.47 | 0.65 | 0.71 | 0.79 | 0.40 | 0.46 | 0.60 | 0.63 | ||
| Pall | 0.80 | 0.69 | 0.66 | 0.60 | 0.77 | 0.68 | 0.62 | 0.62 | 0.68 | 0.65 | 0.65 | 0.65 | 0.71 | 0.64 | 0.62 | 0.58 | 0.79 | 0.78 | 0.71 | 0.69 | ||
| (15,30) | PD | 0.80 | 0.94 | 0.94 | 0.94 | 0.75 | 0.88 | 0.94 | 0.97 | 0.84 | 0.84 | 0.88 | 0.97 | 0.88 | 0.91 | 0.97 | 1.00 | 0.97 | 1.00 | 1.00 | 1.00 | |
| PFA | 0.28 | 0.36 | 0.58 | 0.75 | 0.26 | 0.44 | 0.62 | 0.65 | 0.29 | 0.41 | 0.53 | 0.56 | 0.38 | 0.53 | 0.68 | 0.68 | 0.37 | 0.46 | 0.51 | 0.63 | ||
| Pall | 0.80 | 0.79 | 0.67 | 0.59 | 0.74 | 0.71 | 0.65 | 0.65 | 0.77 | 0.71 | 0.67 | 0.70 | 0.74 | 0.68 | 0.64 | 0.65 | 0.81 | 0.78 | 0.75 | 0.69 | ||
| (10,20) | PD | 0.79 | 0.91 | 0.94 | 0.97 | 0.66 | 0.88 | 0.91 | 0.97 | 0.81 | 0.88 | 0.88 | 1.00 | 0.75 | 0.88 | 0.94 | 0.97 | 0.89 | 1.00 | 1.00 | 1.00 | |
| PFA | 0.17 | 0.31 | 0.50 | 0.67 | 0.18 | 0.29 | 0.62 | 0.71 | 0.26 | 0.35 | 0.44 | 0.59 | 0.26 | 0.47 | 0.50 | 0.65 | 0.20 | 0.46 | 0.57 | 0.63 | ||
| Pall | 0.81 | 0.80 | 0.71 | 0.64 | 0.74 | 0.79 | 0.64 | 0.62 | 0.77 | 0.76 | 0.71 | 0.70 | 0.74 | 0.70 | 0.71 | 0.65 | 0.85 | 0.78 | 0.72 | 0.69 | ||
| (7,14) | PD | 0.65 | 0.82 | 0.91 | 0.97 | 0.50 | 0.69 | 0.81 | 0.84 | 0.81 | 0.91 | 0.91 | 1.00 | 0.81 | 0.84 | 0.91 | 0.94 | 0.92 | 0.97 | 1.00 | 1.00 | |
| PFA | 0.19 | 0.22 | 0.42 | 0.61 | 0.12 | 0.29 | 0.47 | 0.68 | 0.21 | 0.32 | 0.50 | 0.56 | 0.21 | 0.38 | 0.41 | 0.53 | 0.20 | 0.43 | 0.54 | 0.63 | ||
| Pall | 0.73 | 0.80 | 0.74 | 0.67 | 0.70 | 0.70 | 0.67 | 0.58 | 0.80 | 0.79 | 0.70 | 0.71 | 0.80 | 0.73 | 0.74 | 0.70 | 0.86 | 0.78 | 0.74 | 0.69 | ||
| (5,10) | PD | 0.50 | 0.74 | 0.76 | 0.88 | 0.53 | 0.72 | 0.78 | 0.91 | 0.75 | 0.91 | 0.91 | 0.94 | 0.81 | 0.88 | 0.91 | 0.91 | 0.95 | 0.95 | 1.00 | 1.00 | |
| PFA | 0.17 | 0.22 | 0.33 | 0.44 | 0.09 | 0.24 | 0.32 | 0.50 | 0.18 | 0.24 | 0.38 | 0.50 | 0.18 | 0.32 | 0.50 | 0.56 | 0.20 | 0.43 | 0.51 | 0.60 | ||
| Pall | 0.67 | 0.76 | 0.71 | 0.71 | 0.73 | 0.74 | 0.73 | 0.70 | 0.79 | 0.83 | 0.76 | 0.71 | 0.82 | 0.77 | 0.70 | 0.67 | 0.88 | 0.76 | 0.75 | 0.71 | ||
| (3,6) | PD | 0.44 | 0.65 | 0.76 | 0.85 | 0.53 | 0.66 | 0.75 | 0.84 | 0.84 | 0.94 | 0.94 | 0.97 | 0.59 | 0.72 | 0.81 | 0.88 | 0.78 | 0.95 | 0.95 | 1.00 | |
| PFA | 0.11 | 0.22 | 0.28 | 0.44 | 0.12 | 0.18 | 0.32 | 0.47 | 0.12 | 0.21 | 0.32 | 0.50 | 0.15 | 0.24 | 0.33 | 0.47 | 0.17 | 0.34 | 0.46 | 0.51 | ||
| Pall | 0.67 | 0.71 | 0.74 | 0.70 | 0.71 | 0.74 | 0.71 | 0.68 | 0.86 | 0.86 | 0.80 | 0.73 | 0.73 | 0.74 | 0.71 | 0.70 | 0.81 | 0.81 | 0.75 | 0.75 | ||
| (2,4) | PD | 0.35 | 0.53 | 0.68 | 0.85 | 0.44 | 0.59 | 0.69 | 0.81 | 0.78 | 0.88 | 0.94 | 0.94 | 0.56 | 0.69 | 0.81 | 0.88 | 0.65 | 0.78 | 0.92 | 0.95 | |
| PFA | 0.11 | 0.17 | 0.39 | 0.47 | 0.12 | 0.24 | 0.32 | 0.47 | 0.03 | 0.18 | 0.26 | 0.53 | 0.12 | 0.21 | 0.29 | 0.47 | 0.11 | 0.29 | 0.37 | 0.46 | ||
| Pall | 0.63 | 0.69 | 0.64 | 0.69 | 0.67 | 0.68 | 0.68 | 0.67 | 0.88 | 0.85 | 0.83 | 0.70 | 0.73 | 0.74 | 0.76 | 0.70 | 0.76 | 0.75 | 0.78 | 0.75 | ||
Following this, PP was used to reduce the number of dimensions to M/2. Probability of detection (PD = TP/(TP+FN) = sensitivity), probability of false alarm (PFA = FP/(FP+TN) = false discovery rate), overall detection performance (PAll = (TP+TN)/(TP+FP+TN+FN)) were reported for different predicted false alarm rate thresholds (10%, 20%, 30%, 40%). A total of 70 subjects (36 healthy controls and 34 patients with schizophrenia) from the New Mexico site of the MIND network were used. Performances for components with temporal lobe activation (AOD 12th, SIRP 16th and SM 17th) and components with best fit to regressors (AOD 12th, SIRP 11th and SM 17th or AOD 12th, SIRP 3rd and SM 17th) can be compared. After elimination 6000 voxels were obtained and then noise in the masks was removed with a filter
Three different comparisons can be made using the three possible independent component choices from the SIRP task and keeping the independent components from AOD and SM tasks the same. One of the comparisons with the choice of components with temporal lobe activations from all three tasks are presented in Fig. 4 for a 10% predicted false alarm rate threshold choice.
Fig. 4.
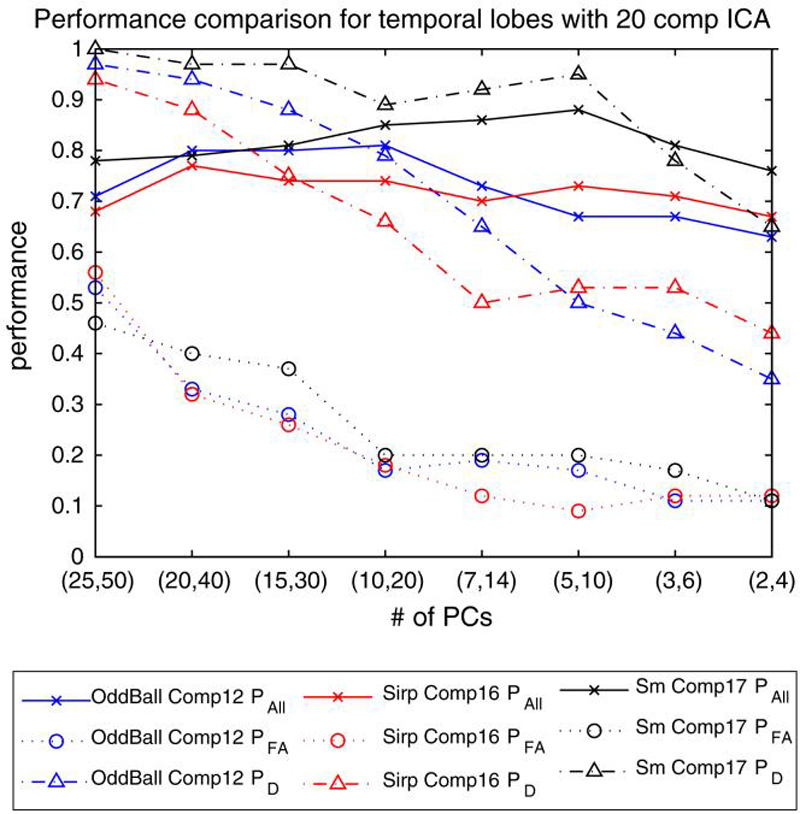
Performance comparison of 3 different tasks (AOD, SIRP and SM) with temporal lobe activation networks for varying (M/2,M). PAll, PFA and PD are reported for predicted PFA = 10% threshold. A t-test was employed to eliminate the number of voxels to consider on a group of 70 subjects from NM site
The results indicate that PFA rates are high for all three tasks especially for higher M values. The PFA rates fall as lower M values are used and stay almost constant for M lower than 20. PD values show a similar trend for all three comparisons and detection performance falls down as M values lower than 20 are considered. The decrease in the values for PFA and PD compensate each other and Pall does not show a large change as the number of PCs considered varies. Nevertheless, it can be seen that optimal number of M is either 14 or 10 for this data giving the best possible overall performance accuracy. When we compare the performances of the three tasks, it can be seen that SM task does better than AOD and SIRP tasks for almost all choices of M. This is an interesting result as SM task was designed as a calibration paradigm but in fact helps us obtain better performances compared to the other two tasks. The AOD task seem to be performing better for choices of M > 14, and SIRP task performs better for M ≤ 14. Low performance of SIRP task for other M values could be because working memory deficits can appear better in other scenarios.
Extension to data from multiple sites
In “Bias in classification,” we mentioned the difficulty of generalizations for small subject numbers and indicated the need to extend the sets, possibly by using subjects from different sites. Previous comparison results presented in “A PP analysis model and classification performance comparison on tasks” were based on 70 subjects only from the NM site of the MIND Research Network. We wanted to extend our data set using additional subject data possibly from other sites to investigate the stability of these results and to further validate them. These variations can originate from, but not limited to, operator variability, scanning equipment and parameters, population distribution, etc. In this section, we first give brief information on the data set used and present three sets of results to investigate the effect of a larger data set, differences between chronic and standard patients and brain activation pattern explaining the difference between patients and controls, respectively.
Tasks and data
In our next analysis, we extended our data set in “Results and discussion” and included the data from the Iowa site. The data and task descriptions given in “A PP analysis model and classification performance comparison on tasks” are still valid. A total of 138 (57 patients with schizophrenia and 81 healthy controls) subjects were employed. The number of subjects included in the new data set was almost twice as large as the number of subjects in the initial set, and included possible variations due to possible measurement differences in the two sites. The schizophrenia patients constituted less than half of the whole data set; hence the two classes included an unequal number of subjects.
Results and discussion
Variability in the prediction accuracies with data from two sites combined
The same masking technique in “Analysis methodology” has been applied on the temporal lobe activation networks from three different tasks and number of voxels considered was decreased to 6000 with the application of designed masks. The remaining voxels were used in the PP algorithm. Pall, PD and PFA values for a predicted false alarm rate of 10% are depicted in Fig. 5. Obtained PFA rates are smaller for M > 14, compared to the results with only 70 subjects. This is in fact in accordance with the number of subjects used as a bigger set included more variability in it and required a larger set of PCs to be represented. Similarly, PD performances decreased more rapidly as smaller M values were used compared to the results found for only 70 subjects. Pall performances are almost the same as previously, and around 80% overall prediction accuracies are obtained. Similar to the analysis in “A PP analysis model and classification performance comparison on tasks,” the overall prediction performances obtained using the SM task are higher than those obtained using the AOD and SIRP tasks.
Fig. 5.
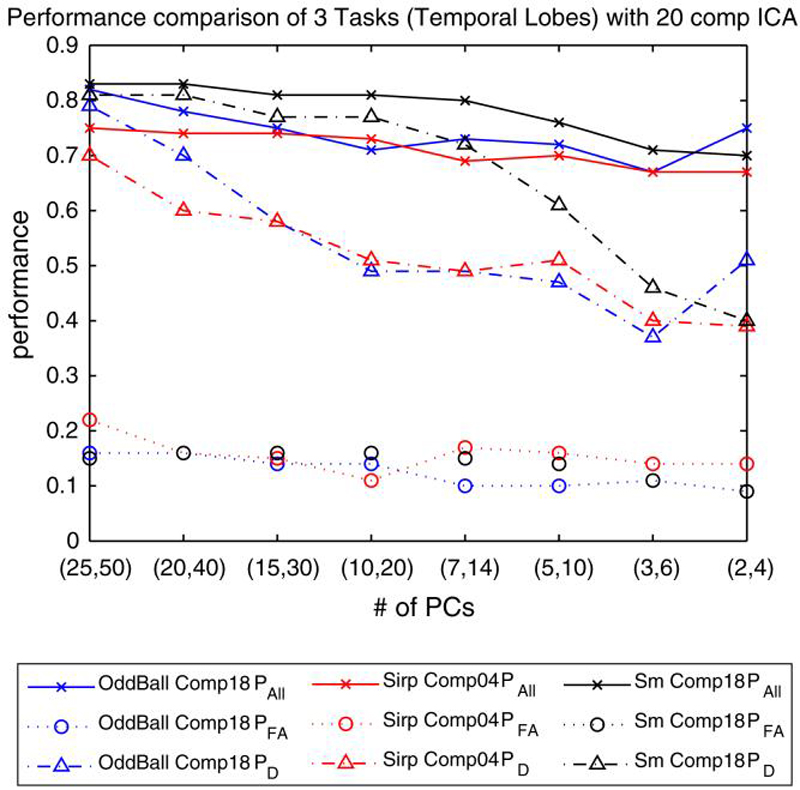
Performance comparison of 3 different tasks (AOD, SIRP and SM) with temporal lobe activation networks. PAll, PFA and PD are reported for predicted PFA = 10% threshold. A t-test was employed to eliminate the number of voxels to consider on a group of 138 subjects from NM and Iowa sites. 6000 voxels were used after elimination
The increased number of subjects used in the analysis motivated us to include a larger set of voxels than 6000. We modified the experiment slightly and applied a masking to represent each of the subjects by 8000 voxels. The remaining steps in the PP algorithm were unchanged. Pall, PD and PFA values for a predicted false alarm rate of 10% are depicted in Fig. 6. The results obtained using 8000 voxels were almost the same as before where only 6000 voxels were used to represent each of the subjects. Overall prediction accuracy of the SM task was still higher than the accuracies obtained using the AOD and SIRP tasks for almost all values of M.
Fig. 6.
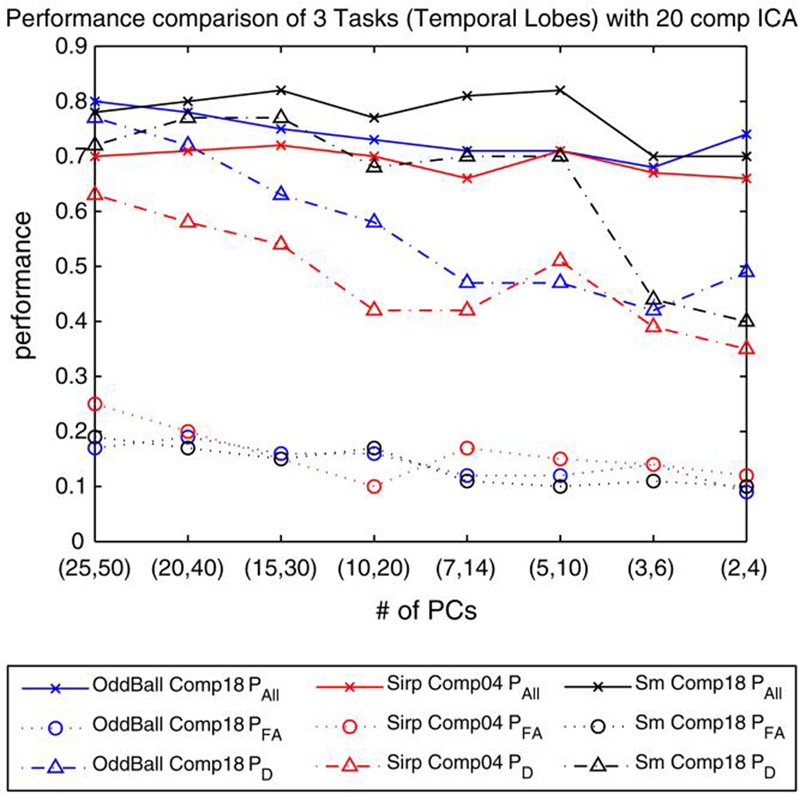
Performance comparison of 3 different tasks (AOD, SIRP and SM) with temporal lobe activation networks. PAll, PFA and PD are reported for predicted PFA = 10% threshold. A t-test was employed to eliminate the number of voxels to consider on a group of 138 subjects from NM and Iowa sites. 8000 voxels were used after elimination
Variability in the prediction accuracies with different subgroups
The results presented in “Results and discussion” and “Variability in the prediction accuracies with data from two sites combined” include the prediction performances of the PP algorithm and explain how well the two classes, schizophrenia patients and healthy controls, can be separated from each other. The class of patients with schizophrenia included both chronic and first episode cases. We designed another experiment to investigate whether the chronic patients could better be separated from the healthy controls and whether the group of selected healthy controls made any difference in the performance of the classifier.
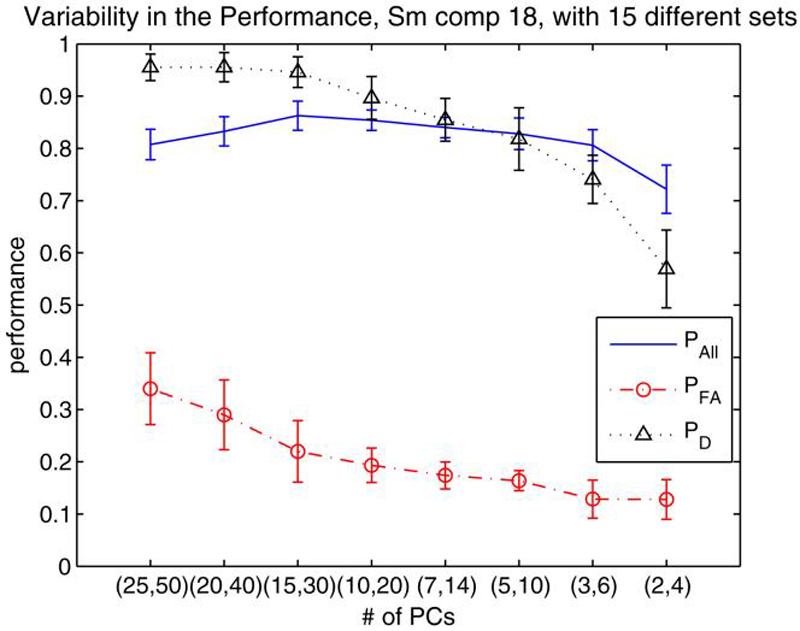
In this experiment, we used a total of 42 chronic schizophrenia patients and used them with 42 healthy controls selected randomly from a set of 56. The experiment was repeated a total of 15 times. In each of these experiments, the same set of 42 chronic schizophrenia patients were kept and were matched with a different set of 42 healthy controls among the 56 possible healthy subjects. The temporal lobe network for the SM task was used in the analysis. The average performance of PAll, PFA and PD are depicted in Fig. 7 for varying number of M's. The error bars indicate the standard deviation of the performances from the average performance in the 15 different trials.
Fig. 7.
Variability in the Performance of SM 18th component with 84 subjects (42 chronic patients, 42 healthy controls). The chronic patient set was kept the same but 15 different healthy control sets were determined (each with different 42 controls) using a total of 56 healthy controls. Variability in PAll, PFA and PD are reported for predicted PFA = 10% threshold. A t-test was employed to eliminate the number of voxels
The results show that overall average prediction accuracies (PAll) are slightly higher (just above 80%) than those obtained using all patients with schizophrenia, both chronic and first episode. PFA values are high for larger number of Ms and decrease as we use smaller values. The variability that we see in the performance indicate the differences among the healthy control subjects in their own group and point out the need for more efficient ways of feature selection. The variability in almost all PAll, PFA and PD is high for large and small values of M, and smallest for either M=14 or M=10. These values of M are indeed the values we achieve the best overall prediction accuracies and optimum for these experiments.
Spatial representation of the maximum separation direction,
We discussed the necessity of reducing the data dimensionality. It is crucial to decrease the number of features efficiently and keep only those that best discriminate classes for reliable classification. We applied a mask on the whole brain image and kept the voxels that showed consistently higher/lower activation for the two classes. The disadvantage of this approach was the fact that some regions in the brain did not contribute to the analysis at all, and were eliminated in the masking of the whole brain data. We also designed a different masking technique and divided the brain into 116 regions based on a Talairach map. The average of all subjects' brain data was divided into 116 regions. In each region, the top 10% of the most activated voxels were kept and others were eliminated to generate the mask. The obtained mask was used on each of the subjects and the remaining voxels were used in the PP analysis similarly (Demirci et al. 2008).
In the PP algorithm, the subjects are represented in a reduced dimensional space using the uncorrelated PCs and the direction maximizing the separation of patients with schizophrenia and healthy control distributions is found in two separate steps via unit length vectors involved in the optimization of a cost function. The detection performance of the PP algorithm is based on the objective classification of the test subjects according to where they fall on the maximum separation direction in a reduced (M/2)-dimensional space (Demirci et al. 2008). Although the decision is made in the reduced dimensional space, the technique actually compares each of the test subjects with the spatial pattern represented by the maximum separation direction, which maximizes the separation of patients with schizophrenia and healthy control cases using only the training set.
In the analysis, the two opposite ends of the maximum separation direction correspond to the patients with schizophrenia and healthy controls in the reduced dimensional space and we can term the spatial patterns as end point images of the maximum separation direction. It is noteworthy to investigate the spatial patterns that the maximum separation directions represent in the analyses. The spatial pattern represented the most important features in terms of separation and it is appropriate to investigate the spatial representation to make an easier visual comparison. This spatial pattern that the maximum separation direction represents might be more important than the prediction performances that we obtain and provides stronger validity for the designed PP algorithm.
The spatial pattern in the reduced dimensional space can be generated using the components of the maximum separation direction vector, , and the corresponding eigenvectors the reduced (M/2)-dimensional space. The common linear model that was subtracted before PCA represents the origin in the space and was added to these patterns and included in the comparison for a more credible discussion.
Figure 8 shows the spatial representation of the end points of the maximum separation direction in the (M/2)-dimensional space (M=6) at slices 19, 20, 29 and 36 (right to left) for a particular training set. Different sets of training subjects gave similar spatial masks since only one subject was removed from the whole group. We are presenting only one of those here. Comparison of activation in the temporal lobe for patient with schizophrenia, average and healthy control (from top to bottom) indicate that patients with schizophrenia have decreased activation in the temporal lobe activation component.
Fig. 8.
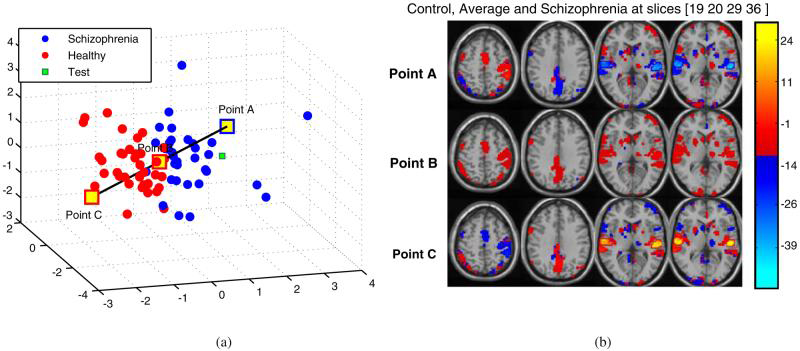
Spatial representation of the maximum separation direction,ŭ, in the reduced dimensional space. Points A-C are used to illustrate difference(s) in the activation of patient with schizophrenia, average and healthy control (from top to bottom) with 3/6 principal components at slices 19, 20, 29 and 36 (right to left) among the 46. Point A represents schizophrenia, Point B represents average, and Point C represents Healthy Control. a 3D distribution. b Regenerated slices
Similar analyses were repeated for other values of M. Although, different number of PCs were considered and gave us different classification accuracies, the maximum direction image found represented very similar appearing patterns (Figures not shown due to similarity).
In the future, we are planning to identify the impact of additional variables (scanning parameters, similar but not identical tasks) to investigate the variability of the methods. It would also be interesting to combine fMRI data with clinical variables like medication record, age, behavioral results. Unfortunately, we currently do not have the data for human-diagnosed cases available to compare the algorithmic sensitivity/specificity with the human diagnosed accuracies. Using only the chronic patients with a matching set of healthy controls increased the prediction accuracies slightly suggesting it may be possible to use classification approaches to identify subtypes of schizophrenia. Finally, application of various methods to fMRI data together with the results presented indicates that the optimal classification of subjects into distinct groups of patients and healthy controls is yet an unsolved problem. Considerable effort is still required for better and more generalizable results.
Conclusion
fMRI is a promising tool that could possibly be used for diagnostic / prognostic purposes. Various studies have been published in the fMRI field and patients with schizophrenia were successfully discriminated from healthy controls. We believe that there are important issues to consider both in analyzing fMRI data for classification and in presentation of the results. We have surveyed previous classification research and identified some issues to consider and present possible solutions.
We also presented a classification study based on a PP algorithm applied to an ICA analysis. FMRI data of 155 subjects from two different sites obtained during three different tasks were used in the algorithm in order to discriminate patients with schizophrenia from healthy controls. The SM task provided better results compared to AOD and SIRP tasks. Extension of the data to two sites provided similar results and proved to be generalizable. The spatial representation of the patients and controls in the reduced dimensional space suggested that schizophrenia patients had decreased activation in the temporal lobe component. In summary, with the use of proper validation techniques we believe that fMRI has great potential for use in clinical decision making, but there is still much work to be done.
Acknowledgements
The data collection was funded by the Department of Energy, grant DE-FG02-99ER62764. The authors would like to thank the MIND Research Network staff for their efforts during the data collection processes. This work was funded by the National Institutes of Health, under grants 1 R01 EB 000840 and 1 R01 EB 005846.
A Appendix
An observation matrix, X, including n subjects each represented with m voxels,
| (2) |
Two different covariance matrices can be defined, and two different eigendecompositions are possible,
| (3) |
| (4) |
where
| (5) |
and
| (6) |
Nonzero eigenvalues of covariance matrices X XT, {λ1,…λn}, and XT X, {l1,… ln}, are the same and eigenvectors corresponding to the higher dimensional covariance matrix, {q1,… qn}, can be derived from the eigenvectors of the smaller one, {p1,… pn}. This useful information number of can be used in cases where the data points is a lot higher than the number of observations. Here we present a proof of this fact.
Using Eq. 4 as a beginning point,
| (7) |
| (8) |
| (9) |
| (10) |
| (11) |
can be obtained. Equation 11 can be further used,
| (12) |
| (13) |
| (14) |
| (15) |
| (16) |
| (17) |
| (18) |
and a relationship between P and Q can be reached. Using Eq. 4 again,
| (19) |
| (20) |
| (21) |
| (22) |
| (23) |
| (24) |
| (25) |
| (26) |
| (27) |
can be obtained. The same equation is valid for every column separately and can be expressed as,
| (28) |
References
- Baddeley A. Working memory. Science. 1992;255(5044):556–559. doi: 10.1126/science.1736359. [DOI] [PubMed] [Google Scholar]
- Bellman R. Adaptive control processes - A guided tour. Princeton University Press; Princeton: 1961. p. 255. [Google Scholar]
- Braff DL. Information processing and attention dysfunctions in schizophrenia. Schizophrenia Bulletin. 1993;19:233–259. doi: 10.1093/schbul/19.2.233. [DOI] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar J. ICA2001. San Diego, CA: 2001a. Group ica of functional MRI data: Separability, stationarity, and inference. [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ. A method for making group inferences from functional mri data using independent component analysis. Human Brain Mapping. 2001b;14:140–151. doi: 10.1002/hbm.1048. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Adali T, Pearlson GD, Pekar JJ. Spatial and temporal independent component analysis of functional MRI data containing a pair of task-related waveforms. Human Brain Mapping. 2001c;13:43–53. doi: 10.1002/hbm.1024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Kiehl KA, Liddle PF, Pearlson GD. Aberrant localization of synchronous hemodynamic activity in auditory cortex reliably characterizes schizophrenia. Biological Psychiatry. 2004;55:842–849. doi: 10.1016/j.biopsych.2004.01.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Calhoun VD, Maciejewski PK, Pearlson GD, Pearlson GD, Kiehl KA. Temporal lobe and default hemodynamic brain modes discriminate between schizophrenia and bipolar disorder. Human Brain Mapping. 2008 doi: 10.1002/hbm.20463. in press. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casey B, Cohen J, O'Craven K. Reproducability of fMRI results across four institutions using a spatial working memory task. NeuroImage. 1998;8(3):249–261. doi: 10.1006/nimg.1998.0360. [DOI] [PubMed] [Google Scholar]
- Demirci O, Calhoun VD. IEEE international workshop on machine learning for signal processing. Thessaloniki; Greece: 2007. Detection of schizophrenia using fMRI data via projection pursuit. [Google Scholar]
- Demirci O, Clark V, Calhoun VD. A projection pursuit algorithm to classify individuals using fMRI data: Application to schizophrenia. NeuroImage. 2008;39:1774–1782. doi: 10.1016/j.neuroimage.2007.10.012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Demirci O, Tyo JS, Ritchie EA. Spatial and spatiotemporal projection pursuit techniques to predict the extratropical transition of tropical cyclones. IEEE Transactions on Geoscience and Remote Sensing. 2007;45:418–425. [Google Scholar]
- Fan Y, Rao H, Hurt H, Gianetta J, Korczykowski M, Shera D, et al. Multivariate examination of brain abnormality using both structural and functional MRI. NeuroImage. 2007;36:1189–1199. doi: 10.1016/j.neuroimage.2007.04.009. [DOI] [PubMed] [Google Scholar]
- First MB, Spitzer RL, Gibbon M, Williams JBW. Biometrics Research Department, New York State Psychiatric Institute; New York: 1995. Structured clinical interview for Dsm-Iv axis I disorders—patient edition (Scid-I/P, Version 2.0) [Google Scholar]
- Ford J, Farid H, Makedon F, Flashman L, McAllister T, Megalooikonomou V, et al. Patient classification of fMRI activation maps. Proc. of the 6th annual international conference on medical image computing and computer assisted intervention (MICCAI'03).2003. [Google Scholar]
- Ford J, Shen L, Makedon F, Flashman LA, Saykin AJ. A combined structural-functional classification of schizophrenia using hippocampal volume plus fMRI activation. Second joint EMBS/BMES conference; Houston, TX. 2002. [Google Scholar]
- Freire L, Roche A, Mangin JF. What is the best similarity measure for motion correction in fMRI time series? IEEE Transactions on Medical Imaging. 2002;21:470–484. doi: 10.1109/TMI.2002.1009383. [DOI] [PubMed] [Google Scholar]
- Friedman L, Glover GH, FBIRN Reducing interscanner variability of activation in a multicenter fMRI study: Controlling for signal-to-fluctuation-noise-ratio (sfnr) differences. NeuroImage. 2006;33:471–481. doi: 10.1016/j.neuroimage.2006.07.012. [DOI] [PubMed] [Google Scholar]
- Friston K, Ashburner J, Frith CD, Poline JP, Heather JD, Frackowiak RS. Spatial registration and normalization of images. Human Brain Mapping. 1995;2:165–189. [Google Scholar]
- Garrity AG, Pearlson GD, McKiernan K, Lloyd D, Kiehl KA, Calhoun VD. Aberrant “default mode” functional connectivity in schizophrenia. American Journal of Psychiatry. 2007;164(3):450–457. doi: 10.1176/ajp.2007.164.3.450. [DOI] [PubMed] [Google Scholar]
- Georgopoulos AP, Karageorgiou E, Leuthold A, Lewis SM, Lynch J, Alonso AA, et al. Synchronous neural interactions assessed by magnetoencephalography: A functional biomarker for brain disorders. Journal of Neural Engineering. 2007;4:349–355. doi: 10.1088/1741-2560/4/4/001. [DOI] [PubMed] [Google Scholar]
- Gerig G, Styner M, Shenton ME, Lieberman JA. Shape versus size: Improved understanding of the morphology of brain structures. Proc. MICCAI 2001. Lecture Notes in Computer Science 2208.2001. pp. 24–32. [Google Scholar]
- GIFT Group ICA of fMRI Toolbox (GIFT) 2008 http://icatb.sourceforge.net/
- Golland P, Grimson WEL, Shenton ME, Kikinis R. Small sample size learning for shape analysis of anatomical structures. Proceedings of MICCAI. Third international conference on medical robotics, imaging and computer assisted intervention, LNCS.2000. pp. 72–82. [Google Scholar]
- Hyvarinen A, Karhunen Y, Oja E. Independent component analysis. Wiley-Interscience; New York: May 18, 2001. [Google Scholar]
- Jimenez LO, Landgrebe DA. Supervised classification in high-dimensional space: Geometrical, statistical, and asymptotical properties of multivariate data. IEEE Transactions on Systems, Man, and Cybernetics-Part C. 1998;28:39–54. [Google Scholar]
- Jimenez LO, Landgrebe DA. Hyperspectral data analysis and supervised feature reduction via projection pursuit. IEEE Transactions on Geoscience and Remote Sensing. 1999;37:2653–2667. [Google Scholar]
- Job DE, Whalley HC, McIntosh AM, Owens DG, Johnstone EC, Lawrie SM. Grey matter changes can improve the prediction of schizophrenia in subjects at high risk. BioMed Central. 2006;4:29. doi: 10.1186/1741-7015-4-29. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kiehl KA, Liddle PF. An event-related functional magnetic resonance imaging study of an auditory oddball task in schizophrenia. Schizophrenia Research. 2001;48:159–171. doi: 10.1016/s0920-9964(00)00117-1. [DOI] [PubMed] [Google Scholar]
- Kiehl KA, Stevens MC, Celone K, Kurtz M, Krystal JH. Abnormal hemodynamics in schizophrenia during an auditory oddball task. Biological Psychiatry. 2005;57:1029–1040. doi: 10.1016/j.biopsych.2005.01.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kontos D, Megalooikonomou V, Ghubade N, Faloutsos C. Detecting discriminative functional MRI activation patterns using space filling curves. Proc. of the 25th annual international conference of the IEEE engineering in medicine and bilogy society (EMBC); Cancun, Mexico. 2004. [Google Scholar]
- Kwong KK, Belliveau JW, Chesler DA, Goldberg IE, Weisskoff RM, Poncelet BP, et al. Dynamic magnetic resonance imaging of human brain activity during primary sensory stimulation. Proceedings of the National Academy of Sciences. 1992;89:5675–5679. doi: 10.1073/pnas.89.12.5675. [DOI] [PMC free article] [PubMed] [Google Scholar]
- McCarley RW, Shenton ME, O'Donnell BF, Faux SF, Kikinis R, Nestor PG, et al. Auditory p300 abnormalities and left posterior superior temporal gyrus volume reduction in schizophrenia. Archives of General Psychiatry. 1993;50:190–197. doi: 10.1001/archpsyc.1993.01820150036003. [DOI] [PubMed] [Google Scholar]
- McGhie A, Chapman J. Disorders of attention and perception in early schizophrenia. British Journal of Medical Psychology. 1961;34:103–116. doi: 10.1111/j.2044-8341.1961.tb00936.x. [DOI] [PubMed] [Google Scholar]
- McKeown MJ, Makeig S, Brown GG, Jung TP, Kindermann SS, Bell AJ, et al. Analysis of fmri data by blind separation into independent spatial components. Human Brain Mapping. 1998;6:160–188. doi: 10.1002/(SICI)1097-0193(1998)6:3<160::AID-HBM5>3.0.CO;2-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nakamura K, Kawasaki Y, Suzuki M, Hagino H, Kurokawa K, Takahashi T, et al. Multiple structural brain measures obtained by three-dimensional magnetic resonance imaging to distinguish between schizophrenia patients and normal subjects. American Journal of Psychiatry. 2004;158:1809–1817. doi: 10.1093/oxfordjournals.schbul.a007087. [DOI] [PubMed] [Google Scholar]
- Ogawa S, Lee TM, Kay AR, Tank DW. Brain magnetic resonance imaging with contrast dependent on blood oxygenation. Proceedings of the National Academy of Sciences. 1990;87:9868–9872. doi: 10.1073/pnas.87.24.9868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pardo PJ, Georgopoulos AP, Kenny JT, Stuve TA, Findling RL, Schulz SC. Classification of adolescent psychotic disorders using linear discriminant analysis. Schizophrenia Research. 2006;87:297–306. doi: 10.1016/j.schres.2006.05.007. [DOI] [PubMed] [Google Scholar]
- Pokrajac D, Megalooikonomou V, Lazarevic A, Kontos D, Obradovic Z. Applying spatial distribution analysis techniques to classification of 3D medical images. Artificial Intelligence in Medicine. 2005;33:261–280. doi: 10.1016/j.artmed.2004.07.001. [DOI] [PubMed] [Google Scholar]
- Robert P, Escoufier Y. A unifying tool for linear multivariate statistical methods: The RV-coefficient. Applied Statistics. 1976;25:257–265. [Google Scholar]
- Shankardass A, Nicolson R, Fawcett A. A combined structural-functional classification of schizophrenia using hippocampal volume plus fMRI activation. 5th BDA international conference; University of York, UK. 2001. [Google Scholar]
- Shen L, Ford J, Makedon F, Saykin A. A surface-based approach for classification of 3d neuroanatomic structures. Intelligent Data Analysis, An International Journal. 2004;8(6):519–542. [Google Scholar]
- Shinkareva SV, Ombao HC, Sutton BP, Mohanty A, Miller GA. Classification of functional brain images with a spatio-temporal dissimilarity map. NeuroImage. 2006;33:63–71. doi: 10.1016/j.neuroimage.2006.06.032. [DOI] [PubMed] [Google Scholar]
- Simon R. When is a genomic classifier ready for prime time? Nature Clinical Practice. 2004;1:4–5. doi: 10.1038/ncponc0006. [DOI] [PubMed] [Google Scholar]
- Simon R, Radmacher MD, Dobbin K, McShane LM. Pitfalls in the use of DNA Microarray Data for Diagnostic and Prognostic Classification. Journal of the National Cancer Institute. 2003;95(1):14–18. doi: 10.1093/jnci/95.1.14. [DOI] [PubMed] [Google Scholar]
- SPM5 Statistical parametric mapping (SPM) 2008 http://www.fil.ion.ucl.ac.uk/spm/
- Symond MB, Harris AWF, Gordon E, M. W. L. Gamma synchrony in first-episode schizophrenia: A disorder of temporal connectivity? American Journal of Psychiatry. 2005;162:459–465. doi: 10.1176/appi.ajp.162.3.459. [DOI] [PubMed] [Google Scholar]
- Tecchio F, Benassic F, Zappasodia F, Gialloretid LE, Palermoe M, Serif S, et al. Auditory sensory processing in autism: A magnetoencephalographic study. Biological Psychiatry. 2003;54:647–654. doi: 10.1016/s0006-3223(03)00295-6. [DOI] [PubMed] [Google Scholar]
- Tegeler C, Strother S, Anderson J, Kim S. Reproducability of BOLD-based functional MRI obtained at 4T. Human Brain Mapping. 1999;7(4):267–283. doi: 10.1002/(SICI)1097-0193(1999)7:4<267::AID-HBM5>3.0.CO;2-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang Q, Kontos D, Li G, Megalooikonomou V. Application of time series techniques to data mining and analysis of spatial patterns in 3D images. Proc. of the 2004 IEEE international conference on acoustics, speech, and signal processing (ICASSP 2004).2004. [Google Scholar]
- Watersa FAV, Badcockb JC, Mayberya MT, Michiea PT. Inhibition in schizophrenia: Association with auditory hallucinations. Schizophrenia Research. 2003;62:275–280. doi: 10.1016/s0920-9964(02)00358-4. [DOI] [PubMed] [Google Scholar]
- Wood I, Visscher P, Mengersen K. Classification based upon gene expression data: Bias and precision of error rates. Bioinformatics. 2007;23:1363–1370. doi: 10.1093/bioinformatics/btm117. [DOI] [PubMed] [Google Scholar]