The adaptive accuracy of flowers: measurement and microevolutionary patterns

Abstract

Background and Aims

From Darwin's time onward, biologists have thought about adaptation as evolution toward optimal trait values, but they have not usually assessed the relative importance of the distinct causes of deviations from optima. This problem is investigated here by measuring adaptive inaccuracy (phenotypic deviation from the optimum), using flower pollination as an adaptive system.

Methods

Adaptive accuracy is shown to have at least three distinct components, two of which are optimality (deviation of the mean from the optimum) and precision (trait variance). We then describe adaptive accuracy of both individuals and populations. Individual inaccuracy comprises the deviation of the genotypic target (the mean phenotype of a genotype grown in a range of environments) from the optimum and the phenotypic variation around that genotypic target (phenotypic imprecision). Population inaccuracy has three basic components: deviation of the population mean from the optimum, variance in the genotypic targets and phenotypic imprecision. In addition, a fourth component is proposed, namely within-population variation in the optimum. These components are directly estimable, have additive relationships, and allow exploration of the causes of adaptive inaccuracy of both individuals and populations. Adaptive accuracy of a sample of flowers is estimated, relating floral phenotypes controlling pollen deposition on pollinators to adaptive optima defined as the site most likely to get pollen onto stigmas (male inaccuracy). Female inaccuracy is defined as the deviation of the position of stigma contact from the expected location of pollen on pollinators.

Key Results

A surprising amount of variation in estimated accuracy within and among similar species is found. Some of this variation is generated by developmental changes in positions of stigmas or anthers during anthesis (the floral receptive period), which can cause dramatic change in accuracy estimates. There seem to be trends for higher precision and accuracy in flowers with higher levels of integration and dichogamy (temporal separation of sexual functions), and in those that have pollinators that are immobile (or immobilized) during pollen transfer. Large deviations from putative adaptive optima were observed, and these may be related to the effects of conflicting selective pressures on flowers, such as selection against self-pollination promoting herkogamy (spatial separation of pollen and stigmas).

Conclusions

Adaptive accuracy is a useful concept for understanding the adaptive significance of phenotypic means and variances of floral morphology within and among populations and species. Estimating and comparing the various components of adaptive accuracy can be particularly helpful for identifying the causes of inaccuracy, such as conflicting selective pressures, low environmental canalization and developmental instability.

INTRODUCTION

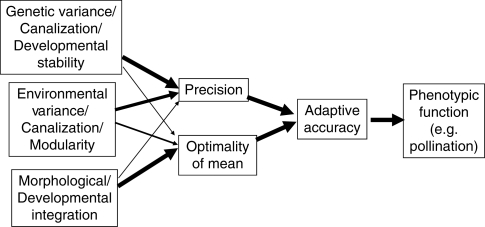
Adaptive accuracy is an evolutionary concept that attempts to increase the testability of optimality models by allowing the explicit assessment of the degree to which populations and individuals in a population phenotypically match their adaptive optima (Orzack and Sober, 1994a; Armbruster et al., 2004; Hansen et al., 2006; Pélabon and Hansen, 2008). It ties together diverse concepts from evolutionary development, functional morphology, quantitative genetics and ecology in the context of natural selection (Fig. 1). One major advantage of the adaptive accuracy concept, both conceptually and empirically, is that it allows partitioning of inaccuracy into its sources, including the effects of developmental noise and lack of genetic and environmental canalization (imprecision) vs. the effects of constraints and conflicting selective pressures that cause population mean departure from the optimum (Fig. 1).

Fig. 1.

Flow diagram indicating the relationship between adaptive accuracy and various evolutionary developmental concepts. Natural selection acts on the phenotype as measured by adaptive accuracy, but response to selection occurs through changes in precision and optimality, as effected by changes in genetic and developmental functions, including developmental stability and genetic and environmental canalization.

The concept of adaptive accuracy is particularly useful for analysing the adaptive significance of flower morphology and pollination function. A notable advantage of flowers is that their adaptive optima can often be estimated, at least under some simplifying assumptions. This represents a starting point for more detailed analyses. For example, the optimal length of a floral tube might be directly related to the proboscis length of the main pollinators, which can be measured in the field. Geographical variation in this environmental parameter leads to explicit predictions of variation in floral optima and hence geographical differentiation (e.g. Johnson and Steiner, 1997; Anderson and Johnson, 2008). Similarly, the optimal location of pollen placement on a pollinator should be related to the expected location of pollinator contact with stigmas of other conspecific flowers (Armbruster et al., 2004).

The study of adaptive accuracy in flowers begins at least as early as Sprengel (1793), although he thought of accuracy as a design issue rather than an evolutionary phenomenon. The concept received attention from Darwin (1862) in connection with the adaptive fit of flowers to their pollinators, and reward-seeking insects in relation to their flowers. Studies of adaptation routinely test the adaptive value of a trait by (1) comparing phenotypic means to putative fitness optima (optimality studies), (2) associating changes in fitness with changes in individual phenotypic values (phenotypic selection studies) or (3) analysing the differences in phenotypic means among populations or species with assumed differences in fitness optima (comparative studies). However, these approaches leave us with very few empirical assessments of deviation from fitness optima (maladaptation) in natural populations (Orzack and Sober, 1994a, b). Furthermore, the deviation of a population from its adaptive optimum has several components (e.g. ontogenetic, environmental and genetic variances), but almost no one has tried to assess their contributions to maladaptation (Armbruster et al., 2004; Hansen et al., 2006; Pélabon and Hansen, 2008). Flower–pollinator fit is a system well suited for studying maladaptation because it is possible reliably to identify fitness optima a priori, namely the match of pollinator and flower morphologies and the correspondence of male and female floral parts (Armbruster et al., 2004).

At least three distinct aspects of adaptive accuracy in pollination can be considered: (1) the adaptive fit of pollinator-reward structures to the morphology and behaviour of the pollinator, (2) the adaptive fit of tongues or legs of pollinators to the reward-bearing structures of the flower (e.g. nectar spur or floral tube and stamens in pollen-reward flowers), (3) the adaptive fit of pollen-dispensing and pollen-receiving structures to the pollinator, in relation to where pollen is picked up from, or deposited on it, respectively. Because of the relative ease of measurement and analysis, in this treatment we focus only on the third aspect, the adaptive fit of stigmas to the expected site of pollen deposition on pollinators, and the adaptive fit of stamens to the expected site of stigma contact with pollinators. The optimality function of this relationship is both intuitively and empirically straightforward in most, but not all, flowers. For pollen to get to an appropriate stigma, it must be placed on the pollinator in a location that will later be touched by stigmas of conspecific flowers. If the pollinator moves rather little in the pollination process, this may be a restricted area on its body. If it does move, this might be a broad area, selecting for higher rather than lower variance in stigma and/or anther positions (see Campbell et al., 1994, 1998; Wolf et al., 2001; and discussion below). In turn, for a stigma to pick up pollen, it must usually contact the pollinator in the location that conspecific pollen has been deposited. If this is a small area, a narrow, mathematically concave fitness function will be established. If the pollinator moves a lot during the pollination process and pollen is distributed over a wide area, a broad, flattened fitness function may be established.

In this context, Armbruster et al. (2004) proposed that adaptive accuracy could be decomposed into precision and mean optimality in a manner that resembles the decomposition of statistical inaccuracy into imprecision (trait variance, σ²) and bias (deviation of the trait mean, μ, from the optimum θ):

i.e.

Armbruster et al. (2004) then made some qualitative comparisons of pollination accuracy and its components across flowers from plant groups with different degrees of morphological integration, although they did not measure the proposed components in a way that permitted additivity.

Precision and deviation from the optimum are affected differentially by various ‘control’ processes considered by evolutionary-developmental biology, such as genetic and environmental canalization, developmental stability and environmental variance (Fig. 1). Hansen et al. (2006) developed this idea further by distinguishing the accuracy of a population (population variation around an optimum) from the accuracy of an individual (departure of an individual from an optimum). The total inaccuracy of a population can thus be decomposed into the departure from the optimum caused by variation among genotypic ‘targets’ (the ideal or mean phenotype expressed by a genotype; see Table 1 for definitions), and variation in genotypic expression caused by developmental instability and environmental variance (Hansen et al., 2006).

Table 1.

Key terms and components relating to adaptive accuracy of individuals and populations

Term	Definition	Derivation/symbol
Adaptive optimum	Predefined or estimated point in phenotypic space yielding maximum fitness	θ, E[θ]
Variance in adaptive optimum	Population variance in value of optimum	Var[θ]
Individual: adaptive inaccuracy	A genotype's average squared phenotypic distance from optimum	s(zT – E[θ])2 + sVar[θ] + sVd
Population: maladaptation (population inaccuracy or load)	A population's average squared phenotypic distance from optimum	s(E[z]–Eθ[θ])2 + sVT + sVar[θ] + sE[Vd]
Genotypic target	Expected phenotype produced by a genotype, i.e. mean phenotype across a range of environments	zT
Mean genotypic deviation from optimum	The difference between the population mean and the optimum	zT – E[θ]
Phenotypic imprecision	Phenotypic variance around the genotypic target, caused by developmental noise, environmental variance, etc.	Vd
Population mean deviance (from optimum)	The difference between the population mean and the optimum	E[z] – Eθ[θ]
Population imprecision	Phenotypic variance in population caused by genetic variation (genotypic target variance), environmental variance, and developmental noise (phenotypic imprecision)	VT + E[Vd]

The goal of the present paper is to (1) expand further the theory of adaptive accuracy to include variance in the adaptive optimum, (2) suggest ways to measure and scale the components of adaptive accuracy, and (3) measure components of floral accuracy in a sample of plant species with varying degrees of floral integration, using as a model the positional correspondence of pollen deposition on, and pick-up from, the pollinator. Using this sample of species, we then address questions about how accuracy is affected by the dynamic relationship with pollinators and by floral integration, i.e. the extent to which different parts of the flower co-vary, which may increase accuracy and pollination efficiency (Armbruster et al., 2004). We also consider how sources of within-population variance, such as ontogenetic and environmental variation, affect measurements of inaccuracy.

Prior studies of floral accuracy and precision

The adaptive fit of floral tubes (or spurs) to pollinators, and pollinators to floral tubes, has been discussed in considerable detail in the context of the pollination and coevolution of orchids and other specialized flowers and their pollinating insects (usually moths). Evidence has largely been derived from the correspondence of population means of plant and pollinator structures (e.g. Steiner and Whitehead, 1990, 1991; Johnson and Steiner 1997), although there are also a few studies of relative fitness and phenotypic selection within populations (Nilsson, 1988; Maad and Alexandersson, 2004). Very few studies have actually attempted to measure floral precision or accuracy, however.

Armbruster et al. (2002) considered floral precision numerically, focusing on the variation in position of dehisced anthers in species of Collinsia and Tonella (Plantaginaceae). These authors hypothesized that the tendency of stamens to converge on a similar length just prior to dehiscence was an adaptive response to selection for precision in pollen placement on bees. When the range in dehisced anther position was scaled to the range of undehisced anther positions, outcrossing species tended to be more precise than their respective self-pollinating sister species (Armbruster et al., 2002). These authors did not, however, analyse other components of floral accuracy.

A numerical approach to floral accuracy has been developed for heterostylous flowers. This is a special case, where flowers occur in two morphs, and the optimal placement of the pollen of one morph on the pollinator is that location that contacts the stigmas of the other morph. Similarly, because of intra-morph incompatibility, the optimal position of the stigmas is one that causes them to contact the pollinator where the pollen of the opposite morph is deposited. This relationship is captured by measuring ‘reciprocity’, for which several quantitative metrics have been proposed, the most useful of which are those of Richards and Koptur (1993) and Eckert and Barrett (1994). Reciprocity in this sense is identical to the correspondence of the locations of pollen deposition on, and pollen pick-up from, pollinators (optimality) in homostylous (normal) flowers, as described below, except that the target values of reciprocity are derived from the target structure on the alternative morph. Eckert and Barrett (1994) and Sánchez et al. (2008) also considered the precision (variance) of reciprocity. Sánchez et al. (2008) proposed a number of significant refinements to the Richards and Koptur (1993) metric, and these even more closely approach adaptive accuracy as we describe it here. Although the reciprocity measure they propose captures critical characteristics of both optimality and precision of heterostylous flowers, it does not have the additive properties of the adaptive accuracy metric we describe, nor the generality of application to other kinds of organisms. A few studies on homostylous flowers have tried to analyse the degree to which the locations of pollen deposition on, and stigma contact with, pollinators correspond (Armbruster, 1988; Campbell et al., 1994, 1998; Ladd, 1994; Wolf et al., 2001; Castro et al., 2008).

The evolution of floral precision and accuracy has also been discussed in the context of the evolution of adaptations that permit species coexistence and loss of gametes to other species (Armbruster et al., 1994; Muchhala and Potts, 2007; Muchhala, 2008; Armbruster and Muchhala, 2009). High precision and accuracy of pollen placement and pick-up is associated with divergence in location of pollen placement among related sympatric species. This association may reflect the ability of precise flowers to respond to selection for reduced loss of pollen to foreign stigmas by specializing on where pollen is placed on pollinators, the evolution of floral precision in response to this selective pressure, or the effects of both evolutionary processes.

Dynamic geometry and ecology of flower–pollinator fit

As noted above, most assessments of the fit of flowers to their pollinators have concerned the match of floral tubes or spurs with the length of the pollinator's appendages or vice versa. Other aspects of flower–pollinator fit have received much less attention and deserve further scrutiny, especially in the context of accuracy. Indeed, the diversity of interactive dynamics of flower–pollinator fit and its effect on the accuracy of pollen deposition and pick-up remains largely unexamined. Although much uncertainty is introduced by behaviour and movement of pollinators on flowers, we can attempt to simplify these dynamics and hope that patterns emerge. Below we attempt to do this.

There are at least seven different ways in which flowers and pollinators physically interact during the pollination process. This variation relates to how pollinators and flowers move relative to each other during pollination. This movement affects pollen placement and pick-up and, hence, floral accuracy. We describe briefly these seven dynamic interaction ‘classes’ based on the shape and movement of the flower and on the movement of the pollinator relative to the flower (see Table 2 for summary). These categories are not fixed, however, and many plant species show intermediate characteristics or mixtures of the traits.

Table 2.

A classification of flower–pollinator dynamics based on the interaction of pollinator and flower-part movements, determining over how broad an area pollen is deposited and the expected precision of pollen deposition and stigma contact

Floral class	Floral characteristics	Pollinator movement during pollination	Area of pollen deposition	Expected precision (consistency of pollen placement, stigma contact)	Example(s)
1	Open, fixed platform	Crawls across flower	Broad area	Low	Passiflora spp.
2	Fixed position, broadly tubular or gullet	Crawls down tube	Broad area	Low	Penstemon, Mimulus, Linum, Rubiaceae
3	Fixed platform or narrow tube	Hovers, landing into fixed position without subsequent movement (‘helicoptering’)	Small area	High	Dalechampia
4	Motile flower parts	Nearly immobile at time of contact with sexual parts	Small area	High	Salvia, Collinsia, papilionoid legumes
5	‘Explosively’ motile flower parts	Completely immobile at time of contact with sexual parts	Small area	Very high	Hyptis, Stylidium, Catasetum
6	Secondary pollen presentation, immobile flower parts	Mobile or immobile	Often small area?	Often medium to high?	Polygala, Asteraceae, Campanulaceae
7	Secondary pollen presentation, motile flower parts, often ‘explosive’	Nearly or completely immobile at time of contact with sexual parts	Small area	Very high	Calathea

(1) Fixed platform, moving pollinator. Some plants have open flowers over which pollinators move when accessing rewards. In the process, the pollinators slide across the sexual parts, with pollen being deposited in a broad area on the body, e.g. the entire dorsal side of an insect thorax. For example, in Passiflora, bees land on the platform formed by petals and crawl across the platform to access nectar in a central trough. If the bees are the right size they slide under the anthers and/or stigmas, contacting them with the entire dorsal surface of their thorax (W. S. Armbruster, unpubl. res.). Both actinomorphic (radially symmetrical) flowers and open zygomorphic (bilaterally symmetrical) flowers may be involved.

(2) Pollinator slides down a tube. A similar relationship to 1 above involves either zygomorphic or actinomorphic gullet flowers, where the pollinator slides past the sexual parts as it crawls, or inserts part of its body, down a gullet. Pollen is deposited on and removed from a large area of the pollinator's dorsal surface. For example, in the distylous Linum suffruticosum, pollinating bombyliid flies get thrum (long stamens, short style) pollen deposited on a broad area of the thorax and abdomen, from where it is harvested by pin (long style, short stamens) stigmas as the flies slide past them on entering a pin flower for nectar. Correspondingly, pin pollen is deposited over a broad area of the ventral surface of the flies, from where it is harvested by thrum stigmas as the flies enter thrum flowers (Armbruster et al., 2006).

(3) Immobile flower parts, ‘helicoptering’ pollinator. Some flowers (or blossoms) are zygomorphic with open platforms, but have relatively fixed points of contact with pollinators as they ‘helicopter’ down onto the flower and then remain largely immobile while collecting the reward. This interaction results in moderately consistent contact of anthers/stigmas with a more precise location on the pollinator than in the two previous classes. An example is seen in species of Dalechampia pollinated by resin-collecting euglossine bees (Armbruster and Herzig, 1984; Armbruster, 1988; Armbruster et al., 2004; see below). This form of interaction intergrades with classes 1 and 2, depending on the degree of movement of the pollinator after it comes into contact with the flower's sexual parts.

(4) Motile flower parts (powered by pollinator), relatively immobile pollinator. This class is a variant of 3, wherein flowers have consistent orientation relative to a largely immobile pollinator (at the time of pollination), but the contact with sexual parts involves some type of floral movement. A good example is Salvia (Lamiaceae); here the pollinator moves initially into the floral tube, but is then contacted by motile anthers or stigmas only after it has largely ceased movement and has engaged a lever mechanism. This results in consistent placement of pollen in a precise location and contact by the stigma in approximately the same place (Classen-Bockhoff et al., 2004; Walker and Sytsma, 2007). In the case of Collinsia (Plantaginaceae) and many papilionoid legumes, the insect pollinator ‘helicopters’ onto the flower, orientating itself consistently so that it can reach the nectar. As it does so, the pollinator's weight causes a portion of the flower to move, exposing or shifting the sexual parts so that pollen is deposited or picked up in a relatively consistent place (Armbruster et al., 2002). This class intergrades into the next.

(5) ‘Explosive’ pollination (powered by the flower), relatively immobile pollinator. This involves actinomorphic, or more often zygomorphic, flowers that have immobile pollinators at the time of stigma/anther contact. This is achieved by a combination of little pollinator movement (e.g. the pollinator ‘helicoptering’ in and staying put), a precise location of a ‘trigger’ point, and/or rapid movement of the structure depositing, and sometimes picking up, pollen. This system has the potential to result in extremely precise pollen placement and extremely high male (and often female) floral accuracy. Examples include most flowers with autonomously powered, moving parts (but see class 7), including Hyptis (Lamiaceae; male accuracy; Brantjes and Devos, 1981; Keller and Armbruster, 1989), Catasetum and some other orchids (male accuracy), and Stylidium (Stylidiaceae; male and female accuracy; Armbruster et al., 1994). The remarkable floral accuracy of Stylidium in both male and female function is analysed below.

(6) Immobile flower, secondary pollen presentation. This class includes plants, like most Asteraceae, Campanulaceae and Polygala (Polygalaceae), that have flowers with little or no floral movement and with secondary pollen presentation, where pollen is placed by the anthers onto another floral structure, which then in turn places the pollen on the pollinator (for a review, see Ladd, 1994). It is generally argued that secondary pollen presentation has evolved to improve floral precision and/or decrease the likelihood of self-pollination. These effects have almost never been measured, however (but see Castro et al., 2008).

(7) ‘Explosive’ secondary pollen presentation. The final class also includes flowers with secondary pollen presentation, but the flowers have some kind of self-powered floral movement. An example is Calathea spp. (Marantaceae), wherein the style is spring loaded and places pollen on the pollinator with great speed and apparent precision (Kennedy, 1978, 1983; Ladd, 1994; Armbruster et al., 2002; Classen-Bockhoff and Heller, 2008).

An understanding of these flower–pollinator dynamics is a first step towards understanding floral accuracy, and especially floral precision. If pollinators move across the flower as they pollinate (classes 1 and 2), pollen is smeared over a relatively large area. Plants with such flowers could be expected to experience weaker selection for, or even selection against, uniform positioning of anthers or stigmas (precision).

THEORY

Accuracy and precision

We first summarize the model developed in Hansen et al. (2006). This model assumes the existence of a fixed optimum for a given phenotypic trait, and considers the accuracy and precision with which a given genotype can produce a phenotypic state corresponding to this optimum. Following Nijhout and Davidowitz (2003), we first define the phenotypic target value as the average phenotype reached by this genotype in a particular distribution of environments. Target optimality is then a function of the distance of the phenotypic target to the adaptive optimum and the reliability with which the genotype is able to attain its target. Consider a quadratic fitness function W(z) = W_max – s(z – θ)², where z is the trait value, θ is the optimum and s is the strength of stabilizing selection around the optimum. The phenotypic expression of the trait can then be broken down to a genotypically set target value, z_T, and a developmental error, z_d, as z = z_T + z_d, where z_d is a random variable with mean zero and variance V_d. The expected fitness of this genotype is then

where E_d[ ] denotes expectation over developmental realizations of this genotype. Hence, there are two components of individual maladaptation, one that is proportional to the deviance of the target from the optimum, (z_T−θ)², and one that is proportional to the imprecision, V_d. These combine into the adaptive inaccuracy as

or

The inaccuracy is measured in units of fitness (the units of s are the inverse of the units of the trait squared). The population maladaptation, or load (i.e. population-level inaccuracy), also depends on variation among genotypes in their target phenotypes and in their reliability. If E[z] is the population mean and V_T is the population variance in the target phenotype, then population maladaptation can be decomposed as follows:

or

where E[ ] without subscript denotes population expectation. Pélabon et al. (2004) show how individual variation in reliability affects imprecision, but we ignore this here.

Note that these decompositions are based on a quadratic fitness function. This is done for illustration, and we may think of the quadratic term as the first part of a Taylor expansion around the optimum. If the fitness function is asymmetric or has other more complex non-linearities, the equations for maladaptation will have to be modified with additional terms depending on skew and higher moments of the trait realization and population variation. The existence of an optimum and mathematical concavity of the fitness function around this optimum is, however, crucial. If the fitness function is mathematically convex, trait variation will be favoured.

Accuracy with variation in the optimum

To refine our model to describe adaptations for deposition and pick-up of pollen from pollinators, we need to treat the optimum as a random variable (i.e. one with random variation). This is because the optimal position of anthers for placing pollen on a pollinator will depend on the position of the stigma in the flowers that the pollinator visits next, and these vary within and across plants. Similarly, the optimal position for the stigma will vary due to variation in where pollen is deposited on the pollinator and in the behaviour of the pollinator.

Let θ be a random variable. If we take anther position as our focal trait, then θ represents the position of the stigma to which the pollen is to be transferred, and if we take stigma position as the focal trait, then θ represents anther position. In either case, both anther and stigma position should be measured in relation to the landmark that controls pollinator position, and if there are systematic pollinator movements relative to structures depositing pollen on the pollinator (as discussed above), then the value of the optimum must be adjusted for them. The inaccuracy of an individual flower with target value z_T and imprecision V_d is then

This shows that we simply need to add the variance in the fitness optimum as a third component of the inaccuracy. Random pollinator movements relative to structures depositing pollen may also add to the variation of the optimum. On the population level we get the following equation for maladaptation:

Thus, we have four components of maladaptation (population inaccuracy) to consider: (1) the deviance of the mean target phenotype from the mean optimum, (2) the population variation in the target phenotype, (3) the variation in the optimum and (4) the expected variance in realizing the phenotypic target.

We note again that this model considers maladaptive variation in relation to a mathematically concave fitness function. There can be many situations in pollination where variation in the positions for placement and pick-up of pollen may be advantageous, for example as a bet-hedging strategy. It may also be advantageous to spread the pollen widely on the pollinator to increase the chance of transfer.

MATERIALS AND METHODS

We focus on floral accuracy related to the locations of pollen deposition on, and pick-up from, pollinators. For this analysis, we assume that the male fitness optimum is the mean stigma position in the population and the female fitness optimum is the mean anther position in the population, as measured from a consistent landmark (see Figs 2 and 3). In all study systems but one, the landmark used was the part of the flower or blossom where the pollinator places its head when collecting the reward. In the case of Linum, a sliding system, the landmark was the petal surface, across which the pollinator crawls. Individual and population inaccuracy were calculated as deviation from these optima.

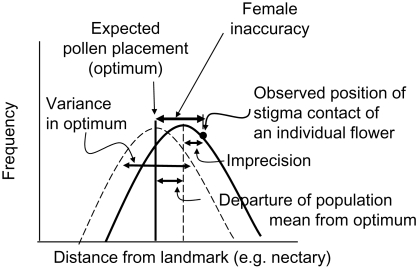
Fig. 2.

A graphical model illustrating female floral accuracy and its components. In this depiction, the optimum (expected location of pollen on the pollinator) also has a variance. Female floral inaccuracy has three components here: (1) the departure of the mean stigma position from the expected location of pollen on the pollinator (as estimated by the mean distance of the anthers from the landmark), (2) variance in the stigma position and (3) variance in the optimum (= variance in the position of the anthers). Very roughly normal distributions were drawn because most morphometric traits tend to have normal distributions.

Fig. 3.

Graphical depiction of how floral optimality and precision are manifested on the pollinator. The distribution of pollen on the bee is determined by the population variance in gland–anther distance (GAD) and the distribution of stigma contacts is determined by the population variance in gland–stigma distance (GSD). The departure from optimum (the difference between the means of the two distributions) reflects, in turn, the difference between population mean GAD and population mean GSD. The bee is a male Euglossa viridissima, pollinator of Dalechampia spathulata, the females of which pollinate D. scandens.

Although maladaptation and inaccuracy are logically measured on individuals, they are also properties of populations, and it is the latter application we use here. In field studies, and to simplify greenhouse studies, we pooled the population variation in the target phenotype with the expected variance in realizing the phenotypic target; we measured them jointly as the within-population phenotypic variance of the trait. We therefore calculated maladaptation (or population inaccuracy or load) as:

Because the variance of morphological measurements usually scales with trait values, we need to scale inaccuracy calculations in order to make comparisons between study systems with flowers of different sizes. We scaled inaccuracy by the square of the trait mean (see Sokal and Rohlf, 1981; Hansen et al., 2003a). We also calculated the CV of each trait as the standard deviation divided by the mean to promote comparison with other studies. In order to compare precision among our study systems we also partition inaccuracy into it components, presented as per cents. The 95 % confidence intervals for accuracy estimates were computed by bootstrapping, where the data were resampled 1000 times.

Floral integration

We were interested in ascertaining if there is an evolutionary relationship between floral integration and floral accuracy. Integration of flower parts that function together is one way that higher optimality can be achieved (e.g. Conner and Via, 1993; Armbruster et al., 2004). We therefore needed an estimate of the integration of the flowers in each study system. We used two different indices of integration and compared the results. The first one is based on the variance of the eigenvalues λ of the correlation matrix (Wagner, 1984; Cheverud et al., 1989). Because each eigenvalue represents the amount of variance distributed along its corresponding eigenvector, morphological integration, i.e. in this case correlation among traits, will provoke a concentration of the variation among few eigenvectors and therefore increase the variance among eigenvalues (for a review see Pavlicev et al., 2009). This integration index can be expressed as a fraction of its maximal value, M − 1, for a given number of traits M. It is often also adjusted for sampling bias by subtraction of its expected value of the eigenvalue variance under the null-hypothesis of no correlation. However, because this is not a correct adjustment for bias under other hypotheses, we did not use it. For example, although sampling error may introduce integration when none is present, it may also reduce integration where it is very strong.

The second measure of integration was recently developed by Hansen and Houle (2008) and builds on comparing the conditional evolvability (Hansen et al., 2003b) to the unconditional evolvability of a trait. The conditional evolvability is a measure of the evolvability of a focal trait when a set of other correlated traits are under stabilizing selection. The degree of integration of the focal trait, y, with other constraining traits, x, can then be defined as the fraction by which the evolvability of y is reduced by x. If e(y) is evolvability of y, and c(y|x) is the conditional evolvability of y relative to x, then the integration of y relative to x is defined as i(y|x) = (e(y) – c(y|x))/e(y). Although developed as a description of genetic integration, this measure can also be computed based on phenotypic variation by using the variance of the trait as evolvability, and the conditional variance as conditional evolvability. Then i(y|x) simply measures how much of the variance in y is tied up with x. Note that this index computes the integration of a specific trait with the rest. To get a general measure of integration we use the average integration of the traits. Hansen and Houle (2008) discussed two ways of doing this. One was to take the average across all possible directions in morphospace (by taking y to be a random vector), and the other was to take the average across a specific set of traits. Here we take the second approach and calculate integration of traits with different, well-defined functions. Our aim was, then, to study the integration among those functions.

Specifically, to compute the average integration, ī, from a variance matrix, V, we note that the conditional variance of a trait with respect to all the others is the inverse of the corresponding diagonal element of the inverse of V (Hansen and Houle 2008). Hence, we get

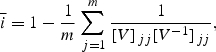1

where m is the number of traits, V_jj is the variance of the jth trait, and V⁻¹_jj is the jth diagonal element of the inverse of V. This index varies between 0 for a set of uncorrelated traits and approaches 1 in the limit when no traits can vary independently of the others. If only two traits are involved, it reduces to the square of the correlation between those traits. Note that this differs from the Wagner integration also by being based on the variance matrix and not the correlation matrix.

We analysed separately patterns of phenotypic integration among (1) traits that interact directly in pollen placement and pick-up and show homology or functional analogy across systems (‘male–female integration’; e.g. stamen and style lengths), and (2) floral parts that do not interact but do show some homology or functional analogy across study systems (e.g. perianth and pistil traits). Characters in the latter set included: a pistil trait [style length in Collinsia, gland–stigma distance (GSD) in Dalechampia and column length in Stylidium], a trait related to the reward function (nectar-tube length in Collinsia, resin-gland area in Dalechampia and nectar-tube length in Stylidium), and one trait related to the size of the petals or petaloid bracts (keel length in Collinsia, lower bract length in Dalechampia and lower-petal length in Stylidium).

Study systems

We employed eight species from four genera, belonging to four of the above pollination-movement classes: classes 2–5. We made new measurements in the field and laboratory and also used unpublished field-collected raw data for which summary statistics have been previously reported (see below). These data are drawn from (1) three populations of Linum suffruticosum (Linaceae; class 2; Fig. 4; summary statistics for two populations presented in Armbruster et al., 2006; new data for one population), (2) four populations of Dalechampia scandens and one of D. schottii (Euphorbiaceae; class 3; Fig. 5A; new data), (3) one population each of Collinsia sparsiflora and C. concolor (Plantaginaceae; class 4; Fig. 5B; new data) and (4) one population each of Stylidium brunonianum, S. hirsutum and S. bicolor (Stylidiaceae; class 5; Fig. 5C–E; summary statistics in Armbruster et al., 1994). Greenhouse-grown material was used only in the test of environmental effects on accuracy in D. scandens. Measured flowers were nearly always from different plants except for measurements of D. scandens at La Mancha and Puerto Morelos, where approx. 120 flowers were measured on 25 and 23 plants, respectively. The traits measured and the respective landmarks in each study system are presented in Table 3. Landmarks were selected based on observations of pollinator behaviour: the landmark was usually where the pollinator placed its head when pollination occurred. In the case of Linum, however, the landmark was the petal surface across which the pollinator crawled during pollination. With Dalechampia, all analyses were based on measurements made at floral stage 1 (beginning of bisexual phase, one staminate flower open), except for those made for the ontogenetic analysis and the data set from Tulum, Mexico (stages 0–3 used).

Fig. 4.

Flowers of Linum suffruticosum. (A) Pin morph, with pollinating Usia sp. (Bombyliidae), which slides past the stigmas and stamens as it enters the floral chamber to obtain nectar. (B) Thrum morph.

Fig. 5.

Flowers of three additional study systems. (A) Dalechampia scandens with the first staminate flower open and three receptive styles visible. The whitish structure is the resin gland. (B) Collinsia concolor, a whorl of six flowers. Note stamens and styles, as well as nectar, are hidden from view and inaccessible to insects other than medium-sized to large bees. (C) Stylidium schoenoides in cocked and discharged positions. (D) Stylidium bicolor in staminate phase, with column in cocked position. (E) Stylidium bicolor in female phase (column cocked).

Table 3.

Measurements and landmarks used to calculate male and female inaccuracies and their components in the four study systems

Study system	Landmark	Male accuracy trait	Male fitness optimum	Female accuracy trait	Female fitness optimum	Calculation of mean-scaled accuracy index
Linum suffruticosum (class 2)	Inner face of petal	Petal–anther gap (thrum)	Petal–stigma gap (pin)	Petal-stigma gap (pin)	Petal–anther gap (thrum)	[(mean gappin – mean gapthrum)2 + VARgap-pin + VARgap-thrum]/(trait mean)2
Dalechampia spp. (class 3)	Resin gland	Gland–anther distance (GAD)	Population mean gland–stigma distance (GSD)	GSD	Population mean GAD	[(mean GSD –mean GAD)2 +VARGSD + VARGAD]/(trait mean)2
Collinsia spp. (class 4)	Throat of floral tube	Throat–anther distance (TAD)	Population mean throat–stigma distance (TSD)	TSD	Population mean TAD	[(mean TSD – mean TAD)2 + VARTSD +VARTAD]/(trait mean)2
Stylidium spp. (class 5): column length	Sensitive trigger point on column	Trigger–anther distance with column sprung (‘length’)	Population mean trigger–stigma distance (column sprung)	Trigger–stigma distance (column sprung)	Population mean trigger–anther distance (column sprung)	[(mean lengthmale – mean lengthfemale)2 + VARlength-male + VARlength-female)]/(trait mean)2
Stylidium spp. (class 5): column reach	Sensitive trigger point on column	Location of pollen on artificial pollinator (‘reach’)	Population mean column reach	Column reach	Population mean location of pollen on pollinator	[(mean reachmale – mean reachfemale)2 + VARreach-male + VARreach-female]/(trait mean)2

Measurements were made on fresh flowers of Linum, Dalechampia and Stylidium with dial or digital callipers precise to 0·01 mm, and on FAA-fixed (formaldehyde, glacial acetic acid, 99 % ethyl alcohol; 1 : 1 : 18) flowers of Collinsia (preserved in 70 % ethyl alcohol after approx. 1 week of fixation) with an ocular micrometer on a dissecting microscope. Stylidium column reach was measured as follows. The column was triggered with a fine-paintbrush handle onto which a grid had been etched (the ‘artificial pollinator’). The handle was orientated consistently, parallel to the axis of the landing platform, in the same fashion as the real pollinators. Reach was measured with callipers as the distance from the handle tip (which touched the trigger point) to the centre of the spot of pollen on the handle grid. See Armbruster et al. (1994, 2002, 2004, 2006) and Hansen et al. (2003a) for additional information on measurements and population locations.

RESULTS

Are some flowers more accurate than others?

Linum suffruticosum has actinomorphic flowers with unfused parts (except for the pistil, which is syncarpous). The pollination dynamics are class 2. Due to this lack of fusion, flowers have low structural integration, although we lack a statistical estimate of this due to the nature of the measurements taken. Imprecision, as calculated from the trait variance, was relatively high (CV = 12–25 %) and mean-scaled inaccuracy measurements (4–11 %) were in the middle of the range seen across other species (Table 4).

Table 4.

Inaccuracy statistics for Linum suffruticosum, Dalechampia spp., Collinsia spp. and Stylidium spp.

Species (location; no. of flowers measured)	Sexual function	Overall floral integration: relativized standardized Wagner–Cheverud Integration Index (%)	Overall floral integration: Hansen–Houle Integration Index (%)	Male–female integration: Hansen–Houle Integration Index (%)/(95 % CI)	Departure from optimum (mm)/% total inaccuracy	Imprecision: trait variance/(CV)/% total inaccuracy	Variance in optimum/(CV)/% total inaccuracy	Raw inaccuracy	Mean2-scaled inaccuracy (95 % CI)
Linum suffruticosum (Ronda, Spain; n = 24)	Thrum	–		–	0·14/7·76 %	0·096/(20·1 %)/38·0 %	0·137/(22·0 %)/54·2 %	0·253	10·65 % (–)
(n = 31)	Pin				0·14/7·76 %	0·137/(22·0 %)/54·2 %	0·096/(20·1 %)/38·0 %	0·253	8·95 (–)
Linum suffruticosum (Grazalema, Spain; n = 14)	Thrum	–		–	0·16/8·06 %	0·176/(25·1 %)/55·5 %	0·116/(18·6 %)/36·4 %	0·318	11·39 (–)
(n = 14)	Pin				0·16/8·06 %	0·116/(18·6 %)/36·4 %	0·176/(25·1 %)/55·5 %	0·318	9·48 (–)
Linum suffruticosum (Malaga, Spain; n = 24)	Thrum	–		–	0·147/15·7 %	0·069/(15·8 %)/49·9 %	0·137/(12·1 %)/34·4 %	0·137	5·03 (2·83–8·03)
(n = 21)	Pin				0·147/15·7 %	0·137/(12·1 %)/34·4 %	0·069/(15·8 %)/49·9 %	0·137	4·18 (2·58–6·01)
Dalechampia scandens (Tulum, Mexico; n = 13)	Male	19·1	21·7	47·0 (2·0–93·0)	0·48/13·0 %	0·715/(23·0 %)/40·4 %	0·824/(21·8)/46·6 %	1·77	13·07 (6·23–20·5)
(n = 19)	Female				0·48/13·0 %	0·824/(21 %)/46·6 %	0·715/(23·0 %)/40·4 %	1·56	9·85 (5·63–13·71)
Dalechampia scandens (Pto Morelos, Mexico; n = 115)	Male	28·1	27·0	12·2 (2·0–25·0)	0·39/9·56 %	0·798/(19·7 %)/50·19 %	0·640/(17·3 %)/40·25 %	1·59	7·72 (6·04–9·46)
(n = 120)	Female				0·39/9·56 %	0·640/(17·3 %)/40·25 %	0·798/(19·7 %)/50·19 %	1·59	6·54 (5·37–7·82)
Dalechampia scandens (La Mancha, Mexico; n = 127)	Male	14·7	22·0	28·0 (8·0–49·0)	1·32/52·52 %	0·589/(22·9 %)/17·76 %	0·99/(21·3 %)/29·72 %	3·32	29·56 (24·0–36·3)
(n = 131)	Female				1·32/52·52 %	0·99/(21·3 %)/29·72 %	0·589/(22·9 %)/17·76 %	3·32	15·21 (13·2–17·6)
Dalechampia schottii (Puerto Morelos, Mexico; n = 43)	Male	6·42	8·11	21·0 (4·0–42·0)	3·547/79·80 %	0·563/(28·0 %)/3·57 %	2·622/(26·0 %)/16·63 %	15·77	219·5 (166·7–287·7)
(n = 51)	Female				3·547/79·80 %	2·622/(26·0 %)/16·63 %	0·563/(28·0 %)/3·57 %	15·77	40·66 (36·3–44·8)
Collinsia sparsiflora (Pop. 5, Lower Lake, CA, USA, n = 111)	Male	13·5	22·3	62·1 (–)	0·57/7·58 %	0·34/(13·8 %)/33·1 %	0·61/(16·3 %)/58·3 %	1·28	6·38 (3·75–9·18)
(n = 21)	Female				0·57	0·61/(16·3 %)	0·34/(13·8 %)	1·28	4·68 (2·93–6·43)
Collinsia concolor (San Jacinto Mtns, CA, USA, n = 96)	Male	16·9	26·4	14·0 (0·0–0·41)	1·59/44·44 %	0·376/(11·2 %)/6·61 %	2·78/(43·1 %)/48·95 %	5·69	19·08 (13·6–24·8)
(n = 19)	Female				1·59/44·44 %	2·78/(43·1 %)/48·95 %	0·376/(11·2 %)/6·61 %	5·69	37·99 (22·2–64·5)
Stylidium brunonianum (South Boundary, Stirling Range, WA, Australia, n = 6)	Column length (male & female)	29·1	42·1	100·0 (–)	0/0 %	0·154/(6·15 %)/50 %	0·154/(6·14 %)/50 %	0·308	0·757 (0·01–1·08)
(n = 16)	Column reach (male)				0/0 %	0·118/(10·82 %)/50 %	0·118/(10·82 %)/50 %	0·236	2·33 (0·17–5·28)
Stylidium bicolor (Yanchep, WA, Australia, n = 10)	Column length (male& female)	8·1	10·8	100·0 (–)	0/0 %	0·543/(5·60 %)/50 %	0·543/(5·60 %)/50 %	1·09	0·628 (0·15–0·91)
(n = 9)	Column reach (male)				0/0 %	1·16/(16·5 %)/50 %	1·16/(16·5 %)/50 %	2·31	5·46 (0–10·46)
Stylidium hirsutum (South Boundary, Stirling Range, WA, Australia, n = 8)	Column length (male & female)	17·3	29·1	100·0 (–)	0/0 %	0·426/(10·1 %)/50 %	0·426/(10·1 %)/50 %	0·852	2·02 (0·90–3·24)
(n = 11)	Column reach (male)				0/0 %	0·077/(5·8 %)/50 %	0·077/(5·8 %)/50 %	0·154	0·668 (0·10–0·98)

The standardized integration index is calculated as the percentage maximal integration, corrected for the number of traits (see Methods). Abbreviations: CV = coefficient of variance, CV² = mean-squared scaled variance, additive to the percentage departure from the optimum to obtain the mean-squared-scaled inaccuracy; CI = confidence interval.

Dalechampia spp. have unisexual flowers united into blossom inflorescences (pseudanthia). These pollination units are loosely organized in comparison with flowers, but they are probably more integrated than other types of inflorescences. The pollination dynamics are class 3. The species surveyed here have relatively low integration indices [relative Wagner–Cheverud (W-C) I = 6–27 %; Hansen-Houle (H-H) i = 8–27 %; male–female HH i = 12–47 %], low precision (CV = 17–28 %) and often large inaccuracies (7–220 %; Table 4), as might be expected from blossom inflorescences compared with flowers.

Collinsia spp. have flowers as pollination units, and these flowers have considerable fusion of perianth parts: connation (fusion within a whorl: synsepaly and sympetaly) and adnation (fusion of different whorls: epipetaly, filaments fused to corolla). There is no connation of staminate and pistillate tissues, however. Thus, the level of structural integration is much greater than in Dalechampia, although this is not particularly evident from the integration statistics (relative W-C I = 13–17 %, H-H i = 22–26 %, male–female HH i = 14–62 %). The pollination dynamics are class 4. Precision (CV = 14–43 %) and inaccuracy indices (5–38 %) are highly variable (see below, Table 4), but are generally a little smaller than in Dalechampia.

Stylidium has single flowers as pollination units, with extensive fusion of parts, through both connation and adnation. Although the statistical integration of perianth parts and pistil is not particularly high (relative W-C I = 8–29 %, H-H i = 10–42 %), the integration of the stamens and style, which are fused into the motile column, is extremely high (male-female HH i ≈ 100 %). The pollination dynamics are class 5. This group shows virtually no deviation from the optimum (anthers and stigmas are in the same location, but separated in time; Fig. 5C–E), relatively high precision (CV = 6–10 %) and very small floral inaccuracies (0·8–2·0 %; column measurements; Table 4).

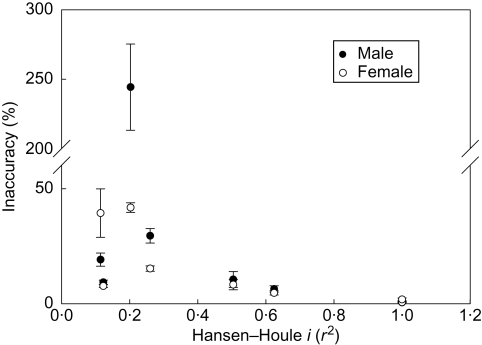
If these four genera are representative of their pollinator-movement classes, they suggest a weak trend for classes with completely immobile pollinators (at time of pollination: classes 4 and 5) to have evolved higher floral precision than classes with weakly immobile (class 3) and mobile pollinators (class 2), although accuracy does not particularly follow this pattern (Table 5). Although the sample is inadequate, pseudanthial blossoms appear to be less precise than flowers, even after correcting for size (Table 5). Comparison of genera also shows an apparent trend of decreasing inaccuracy with increasing integration of the stamens and pistils, as measured by the male–female integration index, H-H i, (Fig. 6).

Table 5.

Mean accuracy components across the four genera representing four pollinator-interaction classes. Note, numbers in rows 1–3 sum to the numbers in line 4

Metric	Linum suffruticosum (Class 2 flower)	Dalechampia spp. (Class 3 pseudanthium)	Collinsia spp (Class 4 flower)	Stylidium spp. (Class 5 flower)*
Mean mean2-scaled deviation from optimum (%)	0·870	16·58	4·34	0·0
Mean mean2-scaled imprecision (=CV2) (%)	3·96	11·98	3·31	0·43
Mean mean2-scaled variance in optimum (%)	3·46	14·25	9·04	0·43
Mean mean2-scaled inaccuracy (%)	8·29	42·81	16·69	0·85

* Based on column length, not column reach.

Fig. 6.

Relationship between calculated floral inaccuracy and integration of male and female structures as measured by their correlation (r²).

Why does accuracy vary so much within species?

Effect of ontogenetic variation on accuracy metrics

Because the length of floral parts often changes during late (post-anthesis) floral development, the accuracy of flowers may be sensitive to when measurements are made. The best measurement will capture overall means and variances in the population of receptive flowers, and this is what we have tried to indicate in Table 4. However, population means may obscure important patterns. This may be especially important when there are complex temporal dynamics in herkogamy (spatial separation of sexes,) or in sexual expression (dichogamy), both of which limit self pollination. These patterns were explored by looking at the effect of developmental stage on floral accuracy in one species of Dalechampia and two species of Collinsia.

Nearly all species of Dalechampia have partial dichogamy, each blossom spending the first 2–3 d of the receptive period in the female conditions (stigmas receptive, but no staminate flowers open), followed by about 1 week in the bisexual condition (stigmas receptive and one to several staminate flowers open). We wondered if floral changes during this period of development affected accuracy in any systematic way.

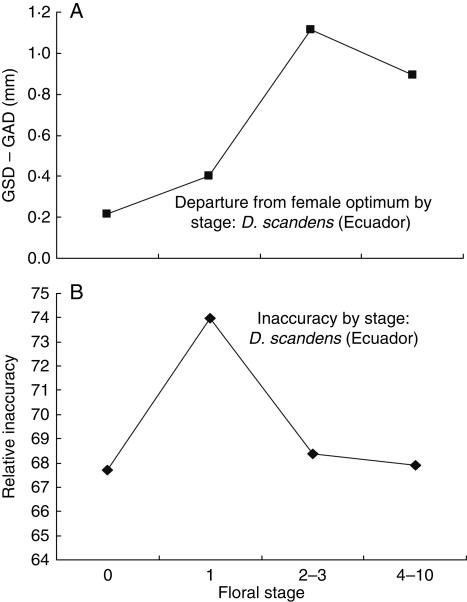
We suspected that in many species of Dalechampia, deviation from optimal might increase with blossom age. This is based on the fact that in some species stigma contact with bees mostly occurs in the female stage, and when this is the case, selection would act on GSD only at this stage. Subsequent growth of the styles, say associated with fruit development, would not be selected against. Thus, departure of stigma position from the optimal with increasing blossom age should be detected, although it would actually be adaptively irrelevant. (For this reason analyses reported in Table 4 were based mostly on style length from floral stage 1, which closely reflects the geometry in the female stage.) The expected decrease in optimality is exhibited by data collected from Dalechampia scandens var. hibiscoides in Ecuador (Fig. 7A). This decrease lowers floral accuracy, but the relationship is complicated by apparent developmental changes in precision, such that inaccuracy rises and then falls again (Fig. 7B).

Fig. 7.

Effect of blossom age in Dalechampia scandens var. hibiscoides (Ecuador) on: (A) departure from the optimum, and (B) inaccuracy. ‘Floral stage’ indicates the number of male flowers open, where 0 is the female stage, and 1 is the first day after the female stage. Stage 2–3 is generally 2 d after the female stage, and stage 4–10 is generally 3–7 d after the female stage.

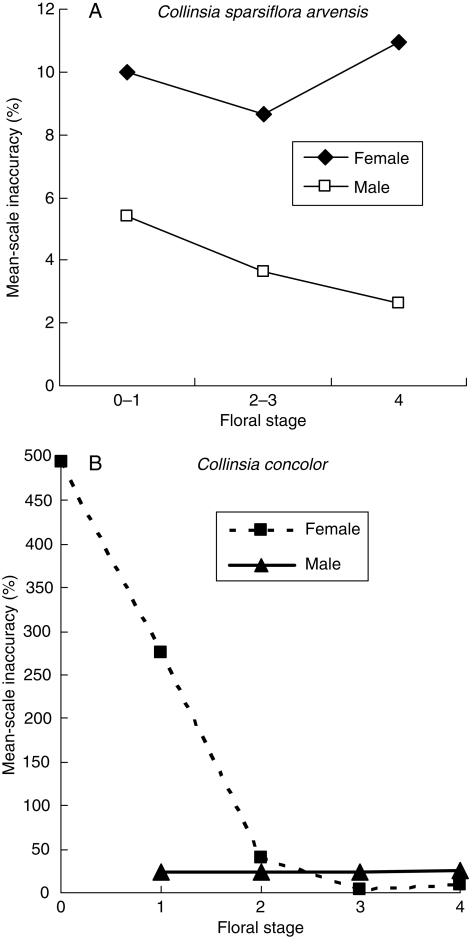
Some Collinsia species undergo changes in herkogamy during floral development, whereas others do not. In those species that do change, self-pollination is unlikely during the first few days a flower is open but becomes increasingly likely in the last day or two (Armbruster et al., 2002). Collinsia sparsiflora var. arvensis is a facultative selfer, with only slight herkogamy and little change in style length with flower age. As expected, C. sparsiflora shows consistent and moderately high accuracy throughout floral development (Fig. 8A). In contrast, C. concolor appears to promote outcrossing for the first 2–3 d of flower development by having short styles and marked separation between the stigma and dehiscing anthers (early herkogamy). The flowers undergo selfing in the final 1–2 d of receptivity (delayed selfing). Not surprisingly, C. concolor flowers show dramatic changes in inaccuracy value with development, from a remarkable 490 % on the first day of anthesis to less than 10 % on the final days of anthesis (Fig. 8B).

Fig. 8.

Changes in male and female relative (mean-scaled) inaccuracy occurring with late floral development in: (A) Collinsia sparsiflora var. arvensis and (B) Collinsia concolor. Floral stage indicates the number of dehisced anthers in the measured receptive flowers. Each stage lasts approx. 0·5–1·0 d.

Effect of environment on accuracy metrics

We predicted that reducing the environmental variance experienced by plants would increase floral precision and hence accuracy. Thus, plants grown in a uniform greenhouse should have more precise flowers than representatives of the same population growing in the field, as the former experience a more uniform environment.

We compared floral precision from greenhouse and field samples from five populations of Dalechampia scandens. We did not detect any consistent differences in GSD precision between greenhouse and field environments (F_1,9 = 0·027, P = 0·877), although there was a weak possible trend for the gland–anther distance (GAD) of flowers in greenhouse environments (mean CV = 17·2 %) to be more precise than flowers in the field (mean CV = 21·3 %; F_1,9 = 2·81, P = 0·169; Table 6, Appendix). It is possible, however, that lower trait variances from greenhouse measurements are the result of greenhouse measurements being made with greater precision than field measurements.

Table 6.

Analysis of variance of population and environment effects on precision (coefficients of variation) of gland–stigma distance (GSD) and gland–anther distance (GAD) for five populations of Dalechampia scandens, as measured on plants in the field vs. the greenhouse (GH)

Source of variation	SS	d.f.	MS	F	P-value
(a) Precision of GSD
Population	0·013789	4	0·003447	0·912626	0·534238
Field vs. GH	0·000103	1	0·000103	0·027232	0·876932
Error	0·015109	4	0·003777
Total	0·029001	9
(b) Precision of GAD
Population	0·020052	4	0·005013	3·310499	0·136489
Field vs. GH	0·004259	1	0·004259	2·81261	0·168832
Error	0·006057	4	0·001514
Total	0·030368	9

Accuracy of floral morphology vs. accuracy of pollen placement on pollinators

In our analyses of floral accuracy, we have made the assumption that the distances between the anthers and stigmas and the floral landmark that orientates the pollinator are indicative of the position on the pollinator where pollen is deposited and picked up, respectively (Figs 2 and 3). In turn, patterns of optimality, precision and accuracy derived from these measurements are assumed to be representative of those that directly relate to pollination. Although these assumptions seem reasonable, Stylidium flowers provide an opportunity to test their validity. We made field measurements of both the length of the column (the tip of which bears initially a pair of anthers and subsequently a stigma) and the position of pollen placement on an artificial pollinator. Thus, we are able to compare precision and accuracy indices based on floral measurements directly with those based on measurements of pollen position on pollinators, assuming that the artificial pollinator ‘behaves’ like a real one. This assumption seems reasonable in this case because we were careful to orientate the artificial pollinator in the same position as the real ones. In both cases, the column releases only when the pollinator is in the right position and touches the sensitive trigger point with enough pressure. Because the pollen is placed on the back, side or ventral surface of the pollinator within 15–30 ms of it touching the trigger, the pollinator does not have time to move out of the ‘correct’ position (Findlay, 1978, 1982; Armbruster et al., 1994).

In general, floral precision and accuracies measured in the two ways were reasonably close, at least as compared with the differences among species and study systems. The estimates of precision (variance) were especially close in Stylidium brunonianum (column length vs. reach: 0·154 vs. 0·118), although a little less so for S. bicolor (0·543 vs. 1·16) and S. hirsutum (0·426 vs. 0·077; Table 4). In two of the three cases the pollen placement was more precise than predicted from floral measurements. Because population-mean departure from the optimal was estimated as 0, the raw floral inaccuracy measurements followed exactly the same pattern. (Mean-squared standardized values showed a different pattern simply because differences in column length and reach led to scaling by different means.)

DISCUSSION

Adaptive accuracy makes both theoretical and intuitive sense. It measures the departure of individuals and populations from hypothesized optima, and allows partitioning of this departure into components generated by developmental and environmental noise (imprecision), genetic variation in the population, variance inherent in the adaptive target, and the optimality of the population mean. This approach is particularly useful for understanding the evolution of flowers in terms of measuring adaptation and relating floral morphology to pollination performance. The present survey reveals these strengths, but also some limitations, especially as related to the importance of measuring the most appropriate traits at the right time in floral development.

It is a little hard to interpret variation between study systems and pollinator-interaction classes because there is large variation within both. Despite these limitations, we will attempt to make some interpretations, although these are only preliminary and must be interpreted with caution. Comparable data from many more plants are needed before any firm conclusion can be drawn. We first discuss possible sources of within-species and within-class variation.

Effects of ontogenetic and environmental variation on accuracy metrics

In Dalechampia scandens and Collinsia concolor, the ontogenetic state of the measured flowers had a huge effect on accuracy measurements. These acted on accuracy primarily through effects on departure from the optimum. This variation makes it difficult to characterize and compare species and study systems, but it seems to be a real characteristic of these systems. Some of the variation appears to be related to features that prevent or promote self-pollination (through partial dichogamy or staged herkogamy). For example, D. scandens var. hibiscoides showed a five- to six-fold increase in departure from the optimal style length with increasing blossom age (Fig. 7). C. concolor, a species with early-stage herkogamy, showed a decrease of female inaccuracy with flower age, from about 500 % to less than 5 %, while male inaccuracy stayed fairly constant (Fig. 8B). In contrast, both male and female inaccuracies in C. sparsiflora, a related species lacking pronounced herkogamy, were fairly low and constant (Fig. 8A).

We expected significantly higher precision in greenhouse-grown than field-grown plants because the environmental variance of each trait should be lower in the semi-uniform environment of the greenhouse. Although there was a weak trend in this direction in one trait, it was far from significant. This may be because of small sample sizes of the comparison and/or unmeasured genotype-by-environment or population-by-environment interactions. Alternatively, the strong environmental canalization generally observed in floral traits compared with vegetative traits (Hansen et al., 2007) may decrease the potential effect of environmental variation on inaccuracy, and its detectability would be especially low because of the large effects of ontogenetic variation.

Effect of pollinator-interaction class on precision and accuracy

Although study system (genus) and pollinator-interaction class are confounded, only the latter has an ordinal trend (from loose interactions to tighter). It may thus be possible to make some inference about the relationship between interaction class and accuracy and its components. Floral imprecision (as measured by the variance in points of stamen and stigma contact with pollinators) appears to be lower in pollination classes that have completely immobile pollinators (classes 4 and 5; Table 5). This does not reflect a circular relationship, as it at first seems, because imprecision was measured on the flower traits themselves (except for column reach which was measured on an artificial pollinator, which was not included in the means in Table 5). This trend is instead expected because selection for precision should be stronger when pollinators themselves interact more consistently. There is no clear ordinal trend, however, between mean-scaled inaccuracy and the pollination class. This is probably because other factors that characterize the study systems, such as breeding system, dichogamy and herkogamy, have important effects on inaccuracy via the departures from optima (see below).

Why does floral accuracy vary so much among species within pollination classes?

The adaptive accuracy of the flowers surveyed here varied from quite high to surprisingly low. At least two possible reasons for low accuracy of flowers come to mind. One is that there are limits on precision because of genetic variation or environmental or developmental noise (i.e. poor canalization; see Hansen et al., 2007). A second possible reason is that conflicting selective pressures prevent populations from attaining adaptive optima for pollination transfer, which, in turn, lowers accuracy. Accuracy may be further eroded if the phenotype departs so much from the adaptive optimum that there is selection against precision (Armbruster et al., 2004; Hansen et al., 2006; Armbruster and Muchhala, 2009).

The data set presented here provides some clues about the possible roles of conflicting selective pressures. Species that are largely outcrossing, but are self-compatible and do not have sexual functions separated in time (not dichogamous), seem to have relatively low optimality and accuracy (e.g. D. scandens, C. concolor). This appears to be the result of selection for herkogamy (spatial separation of the sexes) as a way of reducing self-pollination. Largely selfing species, such as C. sparsiflora, are able to achieve higher optimality and accuracy. Even higher accuracy is possible for species with complete dichogamy, e.g. Stylidium spp.

Another way in which herkogamy and outcrossing can be promoted without extreme departure from the adaptive optimum is for anthers and styles to depart at different angles from the landmark, i.e. diverge in other dimensions. For example, consider Dalechampia: the hypothesized adaptive optimum is where GAD and GSD are equal. If the anthers and stigmas extend away from the adaptive optimum in a linear dimension, then herkogamy (anther–stigma distance or ‘ASD’) = GSD – GAD. Thus, selection for herkogamy will drive phenotype away from the optimum and thus lower floral accuracy. This relationship largely holds for D. schottii and the La Mancha population of D. scandens, which have relative inaccuracies of 41–219 and 15–30 %, respectively (Table 4). Other populations of D. scandens (e.g. Tulum and Puerto Morelos), in contrast, utilize an additional dimension, with the styles extending at a different angle than the staminate flowers. Thus, ASD ≠ GSD – GAD, and, as expected, these two populations have much lower relative inaccuracies (7–13 %; Table 4).

One way that plants appear to generate floral precision and sometimes optimality is by fusion of floral parts (structural integration). Indeed, in this small survey the more integrated flowers (i.e. with more fusion of parts and more correlated variation of structures) generally show higher floral accuracy. Stylidium has single flowers as pollination units with extensive fusion of parts (general floral H-H i = 11–42 %), especially the stamens and style, which form the motile column (male–female H-H i ≈ 100 %). This group has floral inaccuracies of only 0·6–2·0 % (Table 4). In contrast, Dalechampia has blossom inflorescences (clusters of unisexual flowers) as pollination units, hence largely lacking floral fusion (general floral H-H i = 8–27 %, male–female H-H i = 12–47 %). This group has floral inaccuracies of 7–220 %. Collinsia spp. have intermediate integration [flower as pollination unit, fusion of perianth, epipetaly (filaments fused to corolla), but no fusion of staminate and pistillate tissues; general floral H-H i = 22–26 %, male–female H-H i = 14–62 %] and highly variable (see below), but largely intermediate, inaccuracies (5–38 %; Table 2).

Accuracy of floral morphology vs. accuracy of pollen placement on pollinators

The Stylidium system allowed us to examine the relationship between adaptive accuracy based on measurements of floral morphology (column length) vs. those derived from measurements of pollen placement on (artificial) pollinators (column ‘reach’). In two of the three populations examined, the pollen placement on the artificial pollinator was more accurate than was estimated from floral measurements. If this indicates a trend, it might reflect the action of unmeasured compensatory traits that help to ‘correct’ for variation in column length.

In contrast, however, S. bicolor showed greater imprecision and inaccuracy for column reach than length, and did so quite dramatically (1·16 vs. 0·54 for imprecision, 2·31 vs. 1·08 for raw inaccuracy and 5·47 % vs. 0·63 % for mean-standardized inaccuracy). We suspect this reflects the large difference between the column reach and length, with reach being only 49·4 % of length, in contrast to most species (where the ratio is in the range 60–95 %). Thus, for reasons not entirely clear, the S. bicolor column is in a more arched position when it strikes the insect to deposit or pick-up pollen. There may therefore be considerable extra variation (imprecision) introduced by variation in the degree of column arching.

General remarks and conclusions

Adaptive accuracy and its components of optimality and precision appear, on theoretical grounds, to be a useful way to assess individual and population adaptedness. Challenges arise when trying to operationalize and measure components of accuracy. Two of the biggest challenges are deciding when in floral development to measure structures and how to measure and assess conflicting selective pressures (e.g. for outcrossing). In some cases, the approach described here seems to work quite well, but in others it is probably overly simplistic. Even in the latter situation, however, quantification of accuracy and its components provides a starting point for further detailed study. Measurements of accuracy can be improved by careful consideration of the detailed mechanics and dynamics of flower–pollinator interactions, especially in the context of the movement of pollinators and floral parts during pollination and floral development during the period the flower is receptive. Interestingly, one insight that comes out of the present survey is that one of the best ways to reduce the imprecision caused by pollinator movement may be to place and pick-up pollen very quickly. Thus, flowers in effect immobilize pollinators through explosive pollination, and thus explosive pollination may be an adaptation to increase precision and accuracy.

When there are constraints or conflicting selective pressures on floral accuracy, decomposition of accuracy into its components can help us identify and distinguish between possible causes. For example, conflicting selective pressure, such as selection against self-pollination, is likely to affect optimality, at least initially, whereas constraints generated by low floral integration or poor canalization are likely to affect precision. In some cases, integration may also promote optimality, as is the case for Stylidium, but this is easily recognized by careful analysis of floral function and pollinator movement (or lack thereof). In the sample of species examined here, there may be a trend towards higher accuracy in flowers that are more integrated. However, this relationship will be more appropriately tested in future surveys that are able to control other variables such as pollinator-movement dynamics, plant breeding and mating systems, and plant phylogeny.

Further work is also needed as to how to quantify the effect of variation in pollinator movement and entry into flowers on pollen placement, position of stigma contact, and ultimately male and female accuracies. Clearly, movement and instability add to positional variance and increases in the size of the pollen ‘spot’ on the pollinator. At present, however, our metrics do not take this into account. Thus, we may be overestimating precision in flowers like Linum and other members of pollination classes (1 and 2) with pollination by pollinators that slide past fertile parts, while at the same time underestimating the dramatic improvements in accuracy seen in flowers like Stylidium and other members of the specialized pollination classes (5 and 7) with trigger systems and ‘explosive’ pollen placement.

In summary, the adaptive accuracy approach to studying the evolution of flower morphology and function has strengths and weaknesses. The weaknesses highlight areas where we need much more detailed information on the mechanics of pollination. The variety of interaction mechanics between flowers and pollinators makes it hard to generalize, especially in light of the limited data available thus far. Future generalization will depend on broader surveys, perhaps through meta-analysis of published studies, although these are presently problematic because original data are so rarely published. In this connection, we urge scientific publishers to make raw data available more generally (e.g. as electronic appendices), so that detailed accuracy analyses such as these can be performed on existing data sets. Other advancements will accrue from refining theory so that it can accommodate more complex selective scenarios, such as conflicting selection, frequency-dependent selection and complex fitness surfaces, in which cases selection for increased variance may impede evolution towards higher accuracy.

APPENDIX

Components of inaccuracy in five populations of Dalechampia scandens in the field vs. a semi-uniform greenhouse environment for gland–stigma distance (GSD = female) and gland–anther distance (GAD = male) for five populations

	Field							Greenhouse
Population	n (m/f)	Deviation from optimum	GSD CV	Inaccuracy	Female relative inaccuracy	GAD CV	Male relative inaccuracy	Deviation from optimum	GSD CV	Inaccuracy	Female relative inaccuracy	GAD CV	Male relative inaccuracy
Tulum	19/13	0·575	0·211	1·850	10·223	0·230	13·668	−0·085	0·205	1·514	7·821	0·193	8·133
Caracas	27/20	0·490	0·161	0·854	8·986	0·234	12·705	1·066	0·244	2·768	13·690	0·191	23·513
Maracay (all blossoms used)		0·511	0·181	0·798	8·894	0·199	12·926	1·083	0·036	1·323	12·076	0·166	26·665
Puerto Ayacucho		0·875	0·162	1·361	7·363	0·096	11·606	0·760	0·149	1·128	6·768	0·127	10·218
Chetumal		0·592	0·166	1·126	12·725	0·306	19·841	0·312	0·214	1·890	7·894	0·182	9·006
Mean		0·6086	0·1762	1·1978	9·6382	0·213	14·1492	0·6272	0·1696	1·7246	9·6498	0·1718	15·507