Trapline foraging by pollinators: its ontogeny, economics and possible consequences for plants

Abstract

Background

Trapline foraging (repeated sequential visits to a series of feeding locations) has been often observed in pollinators collecting nectar or pollen from flowers. Although field studies on bumble-bees and hummingbirds have clarified fundamental aspects of this behaviour, trapline foraging still poses several difficult questions from the perspectives of both animals and plants. These questions include whether and how traplining improves foraging performance, how animals develop traplines with accumulating foraging experience, and how traplining affects pollen flow or plant reproduction.

Scope

First, we review our previous work performed by using computer simulations and indoor flight-cage experiments with bumble-bees foraging from arrays of automated feeders. Our findings include the following: (1) traplining benefits foragers that are competing for resources that replenish in a decelerating way, (2) traplining is a learned behaviour that develops over a period of hours and (3) the establishment of traplines could be hampered by spatial configuration of plants such as zigzags. Second, using a simulation model linking pollinator movement and pollen transfer, we consider how service by pollinators with different foraging patterns (searchers or trapliners) would affect pollen flow. Traplining increases mating distance and mate diversity, and reduces ‘iterogamy’ (self-pollination caused by return visits) at the population level. Furthermore, increased visitation rates can have opposite effects on the reproductive success of a plant, depending on whether the visitors are traplining or searching. Finally, we discuss possible consequences of traplining for plants in the light of new experimental work and modelling.

Conclusions

We suggest that trapline foraging by pollinators increases variation among plant populations in genetic diversity, inbreeding depression and contributions of floral traits to plant fitness, which should in turn affect the rates and directions of floral evolution. More theoretical and empirical studies are needed to clarify possible outcomes of such a neglected side of pollination.

INTRODUCTION

Many aspects of plant mating systems have been studied inferentially by interpreting patterns of genetic markers, but there is also a more ecological tradition of directly observing the pollination process. Specifically, evolutionary biologists have long studied pollinator movements to draw inferences about gene flow or reproductive success within plant populations (Levin and Kerster, 1968). At the most basic level, observed distributions of flight distances were assumed to be linked as random walks without pollen carryover; successive refinements included simple assumptions about carryover (Kerster and Levin, 1968), direct observations of carryover (Thomson and Thomson, 1989), models of correlated random walks (Kareiva and Shigesada, 1983) and considerations of geitonogamous self-pollination, whether within multi-flowered inflorescences (reviewed by de Jong et al., 1993) or clonal patches (Geber, 1985). Here, we propose further refinements to take into account the observation that some pollinators return repeatedly to small foraging areas (Ribbands, 1949; Manning, 1956; Gill and Wolf, 1977). Within those areas, some pollinators tend to visit particular plants in repeatable sequences or traplines. Both of these aspects, i.e. localized foraging and traplining, produce movement patterns with larger-scale properties that cannot be accurately represented by random-walk assumptions combined with distributions of flight distances. We have recently completed a series of experiments on how bumble-bees use space and develop traplines, and built simulation models to examine the consequences of different spatial-use tactics for the efficiency of foraging by the bees. With some additional programming, these models can be redirected to address the consequences of different spatial-use tactics of pollinators for the mating system of the plants.

The first section of this paper reviews our recent work on the development of traplines and their significance to pollinators. The second section extends the foraging model to address how spatial use of pollinators would translate into plant mating. We are particularly interested in typical situations where a pollinator begins its foraging life in searching mode and gradually develops a fixed trapline within a small area. The model shows how gene-flow distance and numbers of mates are indeed affected by whether pollinators adopt searching or traplining tactics. Furthermore, we explore how spatial use of pollinators would affect ‘iterogamy’, a previously undescribed manifestation of geitonogamy: self-pollination caused by revisitation with an extensive pollen carryover. In the light of these updates, the third section discusses the significance of traplining for plants. In this paper, we have focused on bumble-bees because no other pollinator has more information available on both pollen carryover and traplining, but the general concepts should be applicable to a wider range of pollinators as we learn more about their behavioural ecology.

PREVIOUS WORK: HOW AND WHY DO POLLINATORS TRAPLINE?

Functional significance of trapline foraging: theoretical evaluations

Trapline foraging has been reported for various animals collecting foods from renewable resource patches, such as bumble-bees (Manning, 1956; Heinrich, 1976; Thomson et al., 1982, 1987; Thomson, 1996; Comba, 1999), euglossine bees (Janzen, 1971; Ackerman et al., 1982; Dressler, 1982), butterflies (Gilbert, 1980), hummingbirds (Gill, 1988; Tiebout, 1991; Garrison and Gass, 1999), wagtails (Davies and Houston, 1981), bats (Lemke, 1984; Racey and Swift, 1985) and primates (Janson et al., 1981; Garber, 1988; Janson, 1998; Watts, 1998). Such prevalence suggests that traplining is an efficient harvesting tactic, but it is not obvious why.

To consider the value of traplining, we developed a simulation model of foragers with different patterns of spatial use (Ohashi and Thomson, 2005). In our model, one or more foragers harvest food from isolated patches that are randomly scattered in a two-dimensional space. The distance between patches is measured as a unit, t. A habitat contains 30 patches within a square, 1500t on a side. We also modelled the effects of decreasing forager density using a larger square (3000 × 3000t²) containing 120 patches. Foragers are assumed to move between these patches, following one of four spatial-use patterns: (1) moving stochastically without using any information from past experiences (random searching, RS); (2) moving stochastically, but going longer distances after encountering lower reward (area-restricted searching, ARS); (3) repeatedly moving along a fixed route (complete traplining, CT); and (4) traplining, but sampling novel patches and shifting to neighbouring rewarding patches after encountering low reward (sample-and-shift traplining, SST). In the following summary, we call a forager adopting RS or ARS a ‘searcher’, and a forager adopting CT or SST a ‘trapliner’. The movement distance is measured as the amount of space traversed between sequential patches, not the overall displacement from the original location which would be shorter when foragers turn. Because foragers move one unit of distance per unit of time, time and distance are measured with a single unit, t. During one foraging trip, each forager starts from any one of the patches in the habitat, and continues to travel until its cumulative travel time or distance reaches a fixed value, 30 000t.

Resource renews within each patch according to either of two renewal schedules: an infinite linear increase (‘linear renewal’) or a linear increase toward a fixed maximum (‘non-linear renewal’). These options were made to reflect the actual data that renewal schedules of resources within flowers often differ greatly among plant species (Castellanos et al., 2002, 2006). An arriving forager instantly depletes all the accumulated resource at a patch and leaves immediately. Thus, the standing crop of resource in a patch is determined by the resource renewal schedule (linear or non-linear) and the elapsed time since the last visit. We tracked both the resources actually harvested by a focal forager (i.e. rewards) and the standing crops of resources that accumulated at patches.

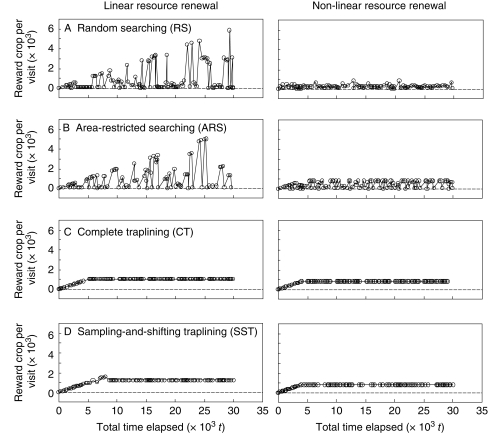
An important result for solo foraging concerns elapsed time between visits to a patch. A trapliner returns to each patch at regular intervals, but a searcher frequently makes short-interval revisitations to the same patches, while occasionally encountering patches that have not been visited for a long time. Consequently, a trapliner obtains the same reward from every patch (Fig. 1). In contrast, a searcher encounters a mixture of many near-empties, and a few rare ‘jackpots’ (Fig. 1). Both tactics perform equally well when resource renewal is linear. When resource renewal is non-linear, however, a searcher suffers because ‘jackpots’ are capped. A trapliner does better because it does not depend on ‘jackpot’ patches. This advantage is identical to that of ‘systematic foraging’ or periodic returns to a patch proposed by Possingham (1989), and confirms his suggestion that traplining is one possible mechanism of producing such a systematic pattern.

Fig. 1.

Rewards obtained at each visit by simulated foragers in solo foraging situations. Each line plot shows a representative example of one foraging trip for the tactic. Linear and non-linear resource renewals are considered (Ohashi and Thomson, 2005). Note that the jackpots are encountered by RS and ARS foragers (searchers) but not by CT or SST (trapliners). Redrawn, with permission, from Ohashi and Thomson (2005).

We found that this characteristic of solo traplining has another advantage in competitive situations (Ohashi and Thomson, 2005). When trapliners and searchers compete, trapliners always outperform searchers. Foraging performance of searchers greatly decreases with the intensity of competition, because the existence of competitors reduces the number of ‘jackpot’ patches. As in the solo case, however, trapliners suffer less in competition because they do not depend on ‘jackpot’ patches. In other words, trapliners gain superiority in competitive situations by harvesting resource in patches before the arrival of other foragers.

Our model also illustrates the costs and benefits of information use: sample-and-shift trapliners use previous reward experiences as information, and respond to them in a ‘win-stay, lose-shift’ manner. This allows animals to shift their traplines to less-crowded patches within a habitat, relieving competition from other foragers. When the habitat is packed with many foragers and there is no competitor-free space, however, the exploratory component of sample-and-shift traplining makes it more costly than complete traplining; sampling and shifting will inevitably increase the average movement distance and the variation in elapsed time between visits.

Trapline foraging by bumble-bees: laboratory experiments

Ohashi and Thomson's (2005) model indicates that spatial use of pollinators would converge into traplining or quasi-traplining except in special circumstances, e.g. unless rewards renew without limit and pollinators do not compete. Under field conditions, however, patterns of spatial use often differ greatly among individual pollinators. For example, some bumble-bee workers establish highly repeatable traplines, while others – even conspecifics or nest mates – may not (Thomson et al., 1982, 1997; Makino et al., 2007). The causes and consequences of such variability are of great interest from the perspectives of both animals and plants.

The most likely reason for this variation is that trapline foraging is not caused solely by innate rules for choosing the distances and turning angles of successive flights (Pyke, 1978; Waddington, 1980) but also by spatial learning, and that it develops with individual experiences (Manning, 1956; Heinrich, 1976; Thomson, 1996). In this case, the difference in the amount of experience would cause behavioural variation among individuals. If spatial memory is involved, moreover, the establishment and persistence of traplines may be constrained by various factors other than experience, magnifying the variation among individuals. Possible influences include plant population size, growing density, spatial distribution, floral display size, resource renewal schedule, competition among pollinators and cognitive ability of pollinators (Manning, 1956; Heinrich, 1976; Thomson et al., 1987; Thomson, 1988; Comba, 1999; Makino and Sakai, 2005; Burns and Thomson, 2006; Temeles et al., 2006; Kapustjanskij et al., 2007).

We tested these ideas experimentally using a large flight cage, captive bumble-bee colonies (Bombus impatiens), and motor-powered artificial ‘flowers’ whose nectar secretion rates are known and controllable (Ohashi et al., 2007, 2008). Just as in Ohashi and Thomson's (2005) model, each flower serves as an isolated resource point or patch that gradually accumulates 30 % sucrose solution (‘nectar’), so that a bee has to make multiple visits to each flower to fill up its honeycrop and return to the hive. The flowers secrete nectar at a uniform rate, but we switch them off while bees are not active. Due to this intervention to prevent nectar overflow, the rate of nectar accumulation gradually decreases as the elapsed time since the last visit increases at a flower (Ohashi et al., 2008). This replenishment schedule would affect foraging performance of bees in an equivalent way to the ‘non-linear renewal’ (linear renewal with the maximum) in Ohashi and Thomson's (2005) model.

Ontogeny and geometry of traplines in the absence of competition

We first examined whether and how naive bumble-bees establish their own traplines as they accumulate foraging experience (Ohashi et al., 2007). We set out arrays of ten artificial flowers that secreted nectar at a uniform rate (2·2 µL min⁻¹ per flower) while the motors were turned on. In each trial, we let one naive bee forage in the cage and recorded the sequence of visits to flowers at which it probed for nectar. The bee normally made 10–30 flower visits to flowers, returned to the hive briefly to deposit her nectar load, and then came out again to repeat the process. Each bee was allowed to make 60–71 such foraging trips.

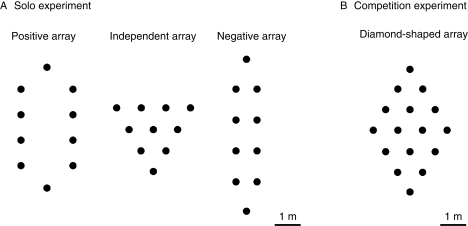
We tested three array geometries that varied with respect to two general preferences of bees: the preference to make short flights and the preference to continue moving in one direction (Fig. 2A). In the ‘independent’ array, flowers always had 2–6 equidistant nearest neighbours in different directions, and bees could choose movement distance and turning angle independently. In the ‘positive’ array, proximity and directionality were positively linked, i.e. the nearest neighbour (except the flower visited just before the current flower) could be reached by straight-ahead movements. In the ‘negative’ array, by contrast, proximity and directionality were negatively linked, i.e. a bee had to turn to choose the nearest neighbour.

Fig. 2.

The spatial arrangements of artificial flowers used in our laboratory experiments with bumble-bees. (A) The three types of arrays for the solo foraging experiment (Ohashi et al., 2007), and (B) the diamond-shaped array for the competition experiment (Ohashi et al., 2008). Closed circles indicate flowers. We also set out several landmarks beside and within each array to enhance spatial learning of bumble-bees, although not drawn in these schematic views.

Figure 3 shows examples of how often and in which direction the experienced bees moved between flowers in these arrays. Black arrows indicate significantly biased transitions, and white arrows indicate frequent, but non-biased transitions. In the positive and independent arrays, bees showed traplining tendencies, frequently retracing certain pathways and cycling back to the same flowers at long intervals. In the negative array, by contrast, bees tended to follow less repeatable, zigzag pathways with frequent revisitations at short intervals.

Fig. 3.

Examples of foraging paths frequented by individual bumble-bees in the solo foraging experiment (data from Ohashi et al., 2007). Arrows indicate how often and to which direction each bee moved between two flowers. Black arrows indicate significantly asymmetrical transitions (P < 0·05). Thick and thin arrows indicate frequent (>5 % of total) and infrequent (≤5 % of total) transitions, respectively. White double-headed arrows indicate frequent transitions without significant asymmetry.

We tested these visual impressions using several indices that were originally proposed by Thomson et al. (1997). As the practical measure of repeatable foraging routes, we calculated the coefficient of variation (CV) of ‘return cycle’ (= number of flower visits a bee made before returning to any particular flower) for each trip. If a bee repeated a fixed circuit, variation among return cycles would be small. As an alternative measure of repeatability, we also calculated a similarity index for flower-visit sequences derived from a global alignment method developed for DNA sequences (Waterman, 1989). Next, we calculated the average return cycle for each trip to assess the geometric efficiency of foraging routes. Because there were ten flowers, the optimal return cycle was nine. We then performed sampled randomization tests (Sokal and Rohlf, 1995) to see whether these indices significantly differed from those for null visit sequences produced by searching behaviour without knowledge of the locations of flowers, i.e. by simple rules for movement between successive flowers. For more details on the data analyses, see Thomson et al. (1997) and Ohashi et al. (2007).

These tests revealed two important aspects of foraging routes in bumble-bees. First, foraging routes of bees became more repeatable and geometrically efficient than expected from a combination of simple movement rules between successive flowers. It usually required 2–3 h for a bee to establish a significantly repeatable and efficient trapline, indicating that traplining is based on spatial memory of patches or sequences. Therefore, differences in foraging experience among individual pollinators may partly explain the observed variation in their spatial use under field conditions. Second, bees' innate preference to fly short distances outweighed their preference for straight moves, and there was little plasticity in this regard. In the negative array, where choosing nearest neighbours was inconsistent with choosing straightest movements, the repeatability and geometric efficiency of routes stayed low even after bees gained experience. These results suggest that a bee's ability to optimize its foraging route in nature may depend largely on how it selects a set of plants or patches in a large habitat. If there are sufficient options, therefore, a bee might select a configuration similar to our positive array: a circular or oval arrangement of plants in which choices of nearest neighbours are consistent with choices of directional movements. It would be interesting to test whether the established traplines of bumble-bees in the field meet these conditions.

Effects of experience and priority on trapline foraging in the presence of competition

Next, we examined how experience and priority of animals at a particular food site could affect their movement paths and resultant foraging performance in competitive situations (Ohashi et al., 2008). We set out 16 artificial flowers in a diamond-shaped array at intervals of 0·95 m (Fig. 2B). For automatic tracking and identification of individual bumble-bees, each flower was equipped with an infrared light-emitting diode and a phototransistor at its entrance, and also a radio-frequency-identification reader that read passive 2·5-mm square chips glued onto the bees' thoraces (the Coil-on-Chip RFID system^®, Hitachi Maxell, Ltd, Tokyo, Japan). Thus, our system recorded flower identity, bee identity, and arrival and departure times for each visit made by the bees throughout the experiment (K. Ohashi et al., in prep.). Flowers secreted nectar at a uniform rate (1·8 µL min⁻¹ per flower) while the motors were turned on, so we could estimate the amount of nectar obtained by the bees at each visit.

In the main experiment, we simulated a situation in which two bees entered a habitat at different times and competed for nectar. We first allowed one naive bee (early arrival) to forage alone until it made 30 foraging trips (‘solo phase’). We then let another naive bee (late arrival) compete with the early arrival (‘competition phase’). This phase was continued until the late arrival made 30 trips. We carried out such daily trials for eight pairs of bees, each of which took 6–8 h. As the collective terms, we refer to the early arrivals and the late arrivals as B1 and B2, respectively.

Competitive performance of paired bees depended on their arrival sequence in the cage. During the competition phase, the early arrivals (B1) with prior access to flowers consistently collected significantly more nectar per unit of time than the late arrivals (B2). B1 obtained 4–6 µL of extra nectar in any one minute compared with B2, which roughly corresponds to 7–10 % of the full capacity of a bee's honeycrop. The difference in performance between paired bees was significantly smaller (1–3 µL of difference per minute) during trips 31–60 in a control experiment where the two bees started foraging simultaneously.

In pairwise competition, early arrivals gained the upper hand in two ways. First, the greater experience of B1 conferred a double advantage: more repeatable foraging routes and faster travel speeds between flowers. As shown in Fig. 4, an increased repeatability of B1's foraging route (= CV of return cycle multiplied by −1) significantly reduced the variance of its return intervals to the same flower within trips. Such periodic returns directly increased B1's rate of nectar intake per trip by producing returns to flowers before the refilling rate diminished too much, as well as by increasing the chances of taking accumulated nectar in flowers before B2's arrival, as predicted by Ohashi and Thomson (2005). Fast travel also improved B1's performance, although it was not incorporated into Ohashi and Thomson's (2005) model. The effects of fast returns were very similar to those of periodic returns, i.e. they increased the chances of harvesting nectar in flowers before the refilling rate diminished too much, as well as the chances of taking accumulated nectar in flowers before B2's arrival (Fig. 4).

Fig. 4.

Path diagram for determinants of foraging performance of experienced bumble-bees (B1's gross rate of nectar intake) during the competition phase in Ohashi et al.'s (2008) experiment (n = 296 trips). Single-headed arrows represent the hypothesized effects of one variable on another; double-headed arrows represent unanalysed correlations between two variables, i.e. shared variation that is not explained within the model. Continuous lines indicate positive effects and dashed lines negative effects, with the magnitude of the coefficient determining their width. Numbers near the paths indicate standardized path coefficients. Asterisks (*P < 0·05, **P 0·01, ***P < 0·0001) denote standardized path coefficients that are significantly different from 0, as assessed by multivariate Wald tests. Residual variances of endogenous variables (those being affected by other variables) are also indicated by open arrows. χ² = 394·6, d.f. = 116, P < 0·00001; root-mean-square error of approximation, RMSEA = 0·061. Redrawn, with permission, from Ohashi et al. (2008).

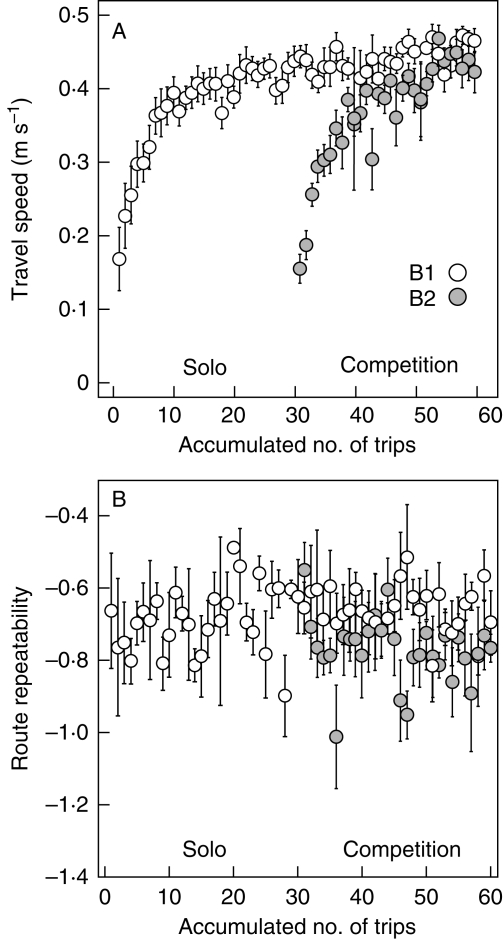
Second, the prior residence of B1 prevented B2 from establishing repeatable traplines. Although B1 significantly increased the route repeatability as they accumulated experience during the solo phase, B2 achieved hardly any increase during competition (Fig. 5). B1's route repeatability also decreased when B2 were added, but only slightly. Perhaps B2 were distracted from learning particular paths because the competitor prevented continuous reinforcement. Alternatively, B2 might be responding to their past reward experience in a ‘win-stay, lose-shift’ manner (Thomson, 1988), which would tend to increase their time spent in sampling and their variation in return intervals (Ohashi and Thomson, 2005). Whatever the mechanism, spatial overlap between the paired bees, measured by Pianka's (1973) symmetrical index of niche overlap, significantly decreased as the competition progressed (Ohashi et al., 2008). This spatial partitioning of flowers arose primarily from adjustments by the late arrivals, but those adjustments could not confer improved route repeatability for B2 because our small arrays did not offer sufficient scope. Thus, the advantages of early arrivals came not just from their experiences that enhanced traplining and fast travelling, but also from the prior residence in the habitat itself that effectively prevented the late arrivals from establishing their own traplines.

Fig. 5.

Changes in bee behaviour with accumulated foraging experience within trials. (A) Travel speed between flowers and (B) route repeatability (−CV of number of flower visits made before returns). Mean ± s.e. were calculated for each trip using data on multiple bees. Open circles represent B1 (early arrivals) and filled circles represent B2 (late arrivals). Data from Ohashi et al. (2008).

Although B1 increased both route repeatability and travel speed between flowers during the solo phase, these gains are not necessarily attributable to traplining. In fact, B2 also increased travel speed between flowers as it gained experience without increasing its route repeatability (Fig. 5). Furthermore, travel speed between flowers tended to be lower in trips where the bees followed more repeatable routes (Fig. 4). Such a ‘trade-off’ between speed and accuracy in traplining appears to contradict the fact that both fast movements and traplining rely on long-term spatial memory (Saleh and Chittka, 2007). One probable reason for this discrepancy is that traplining requires some additional information, such as the memory of sequential order of flowers along a route (Chameron et al., 1998), while fast movement only requires the memory of flower locations or spatial layout. If this were the case, the time cost needed for memory retrieval would have increased as bees retraced routes more precisely. In our situation, B1 followed accurate traplines because the advantages of traplining outweighed the costs. However, when circumstances make traplining cognitively difficult, as is probably the case when plants grow in dense homogeneous stands, when landmarks are absent, or when plants are arranged in confusing patterns such as zigzags (Ohashi et al., 2007), the best strategy may be for a bee to increase its travel speed without following an accurate trapline. Such factors may further increase variation in spatial use among individual pollinators and across different habitats. Burns (2005) discussed similar situations caused by speed–accuracy trade-offs in bumble-bee foraging, where the benefits of higher speed outweighed the costs of more accurate discrimination between flowers with different values.

It is also noteworthy that the bees adjusted their average return cycles in response to the presence or absence of competition, and to the rate of nectar renewal (Ohashi et al., 2008). Bees made longer cycles when a competitor was added, and shorter ones when nectar secretion rate increased from 1·8 to 2·3 µL min⁻¹ per flower. Making longer cycles, however, did not actually help bees in competition. Although longer cycles let bees encounter more reward when they arrived at flowers ahead of their competitor, they also increased the probability that the competitor would get there first (Fig. 4). Because these effects cancel out, longer cycles barely affect performance in competition, despite their obvious advantage in solo foraging. On the other hand, such cycle changes under competition could certainly affect patterns of pollen flow among plants.

NEW WORK: HOW DOES TRAPLINE FORAGING AFFECT PLANT MATING?

Traplining is evidently a learned behaviour that is influenced by time and experience (Ohashi et al., 2007). Therefore, the pollinators visiting a plant population at any one time should display behavioural variations according to their arrival sequence, and their movement patterns should change over time. These characteristics may produce predictable patterns in pollen flow within a plant population.

Furthermore, the costs of learning may vary among individuals according to their arrival sequences. For example, the availability of favourable spatial configurations of plants in a population may be lower for later arrivals (Ohashi et al., 2007). Plants surrounded by visual landmarks may also be less accessible for later arrivals because earlier arrivals have pre-empted them. Considering the speed–accuracy trade-off in traplining (Fig. 4), therefore, the late arrivals may choose to travel rapidly between flowers without establishing traplines (Ohashi et al., 2008). Such differences in cognitive difficulty may further increase variation in pollinator movements and, in turn, pollen flow.

Methods

The model

To examine how such variation in pollinator movements could affect pollen flow, we extended Ohashi and Thomson's (2005) simulation model by adding a new module for pollen transport. In this model, we considered pollinators collecting nectar from isolated plants that are randomly scattered in a two-dimensional space, just as the ‘patches’ modelled by Ohashi and Thomson (2005). The distance between plants is measured as a unit, t. Each plant is assumed to bear a single flower, setting one fruit containing many seeds. This simplification allowed us to focus on pollen flow among plants, aside from the other complicated problems associated with multiple flowers on individual plants (de Jong et al., 1993; Iwasa et al., 1995; Ohashi and Yahara, 2001; Harder et al., 2004). Each plant or flower secretes nectar linearly toward a fixed maximum (‘non-linear renewal’).

Each pollinator was assigned to perform either ARS (area-restricted searching) or SST (sample-and-shift traplining). Both types of pollinators use previous reward experiences as information, and respond to them in a ‘win-stay, lose-shift’ manner (Ohashi and Thomson, 2005). We adopted the same threshold value to classify ‘win’ and ‘lose’ visits for both types of foragers, so that the average movement distance between successive visits was similar in solo situations. We also adjusted the return interval time of traplines so that a trapliner gains as much as a searcher does per unit of time.

To simulate pollen flow, we adopted the ‘exponential decay’ model proposed by Rademaker et al. (1997), where pollen deposition, losses and removal are represented by four fixed parameters. Specifically, k₁ denotes the fraction of pollen on the bee's body deposited on the stigma per flower visit, k₂ the fraction of pollen removed from the anthers per flower visit, k₃ the fraction of pollen removed from the anthers that adheres to the pollinator and k₄ the fraction of pollen on the bee that is lost in the flight between two flowers. The fraction k₄ includes passive loss, grooming and the fraction of pollen lost on flower parts other than the stigma. As the baseline parameter values, we used estimates by Rademaker et al. (1997) for the Echium–Bombus system, where the ‘pollen carryover fraction’ (1 − k₁) (1 − k₄) was 94 %. We also modelled the effects of reducing this ratio to 80 %. For simplicity, we assumed that the flowers completely avoid autogamy and pollinator-facilitated intrafloral selfing, which corresponds to very effective ‘approach herkogamy’. We could also incorporate a constant amount of pollen grains transferred directly from anthers to the stigma within a flower at each visit, but it would not change our results at least in a qualitative term. We also assumed that the number of pollen grains, ovule number and stigma surface area are effectively large, so that all pollinator visits to plants would lead to pollen removal and deposition. In other words, patterns of pollen flow would directly translate into mating patterns. No pollen grains deposited on stigmas would be removed again by pollinators.

With the model described above, we simulated situations where either one or five pollinators with different spatial-use tactics foraged on plants. To determine how pollen flow changed as pollinators developed traplines, we simulated situations with varying fraction of trapliners within the five pollinators: 5ARS, 4ARS/SST, 3ARS/2SST, 2ARS/3SST, ARS/4SST and 5SST. We also modelled the effects of variation in pollinator density using a small population with 30 plants (1500 × 1500 t²) and a large population with 120 plants (3000 × 3000 t²). As in Ohashi and Thomson (2005), one foraging trip continued until a fixed amount of time (30 000t) elapsed. For each situation, we repeated such foraging trips 100 times. Simulated movement paths of each pollinator and the resultant pollen movements were all recorded for later analyses.

Quantification of pollen flow

We considered how the fraction of trapliners affected three aspects of pollen flow among plants: (1) mating distance, (2) mate diversity and (3) self-pollination rate. As an index of mating distance, we calculated the distance of pollen flow, i.e. Euclidean distance between mother (recipient) and father (donor) plants for each pollen grain delivered. This index measures the overall displacement of a pollen grain from the location of the donor plant, which would reflect both the movement paths of pollinators and pollen carryover. For the population-level analysis, we calculated a median value using data for all the pollen grains delivered to stigmas. For the plant-level analysis, we calculated a median value for pollen grains delivered from the focal plant to stigmas.

Next, as an index of mate diversity, we calculated the effective number of fathers for the ith plant (N_epi) . Because each plant received a finite number of pollen grains, we adopted the unbiased estimator of the mathematical definition of ‘effective paternity number’ (Starr, 1984):

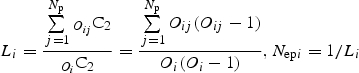where N_p is the total number of plants, O_i is the total number of pollen grains received by the ith plant from all plants, O_ij is the number of pollen grains received by the ith plant from the jth plant (including i = j) and _OC₂ is the choose function of O and 2 (also known as the combination or binomial coefficient:

i.e. the number of ways that two pollen grains can be chosen from a set of O pollen grains). L_i represents the probability that two pollen grains randomly and independently drawn from the ith plant's stigma are from the same father if we have N_epi ‘ideal fathers’, all contributing with the same probability. Real fathers are neither ideal nor do they contribute with equal probability, so N_epi computed from the above equation gives the ‘effective number’ of fathers, which means the number of idealized fathers that would give the same probability, L_i. N_epi ranges from zero to N_p, with greater values indicating higher levels of mate diversity. Because N_epi is mathematically equivalent to Simpson's index of diversity (Simpson, 1949), it is hardly affected by sample size (O_i) to the extent that O_i is larger than 100 as in our case (for the estimator of N_epi with smaller values of O_i, see Nielsen et al., 2003; García et al., 2005). We did not calculate the effective number of mothers (N_emi), because N_epi and N_emi would be symmetrical unless the number of pollen grains, ovule number or stigma surface area is limited.

Finally, self-pollination can occur in our model when a pollinator returns to a plant still carrying grains that it picked up at that same plant on a previous cycle. Although this type of self-pollination has received little prior attention, it may become important when pollinators frequently return to the same plants after short excursions. We therefore coined the new term ‘iterogamy’, and calculated the proportion of iterogamy for the ith plant (R_i) as follows:

R_i ranges from 0 to 1, with greater values indicating higher levels of self-pollination. We used the symbol R (‘returns’) for iterogamy because using I introduces a possible confusion with the i's used for indices.

For the population-level analysis, we calculated the mean and standard deviation (s.d.) of each index using 100 median values obtained from individual foraging trips. We then examined how these indices changed with varying pollinator abundance, spatial-use tactics and population size. For the plant-level analysis, we calculated each index for individual plants and performed a simple correlation analysis between the index and the pollinator visitation rate per plant in each foraging trip. Using the mean and s.d. of 100 values of Pearson's coefficient of correlation (r), we carried out one-sample t-tests for the mean (H₀: r = 0). We compared the results between searcher-dominant and trapliner-dominant populations to see how spatial-use tactics of pollinators could affect the significance of ‘pollinator attraction’ to plants.

Results and discussion

Population-level effects

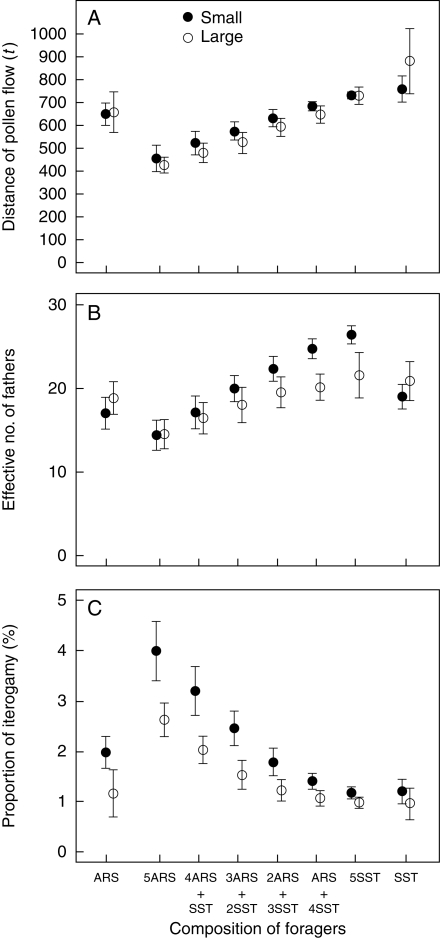
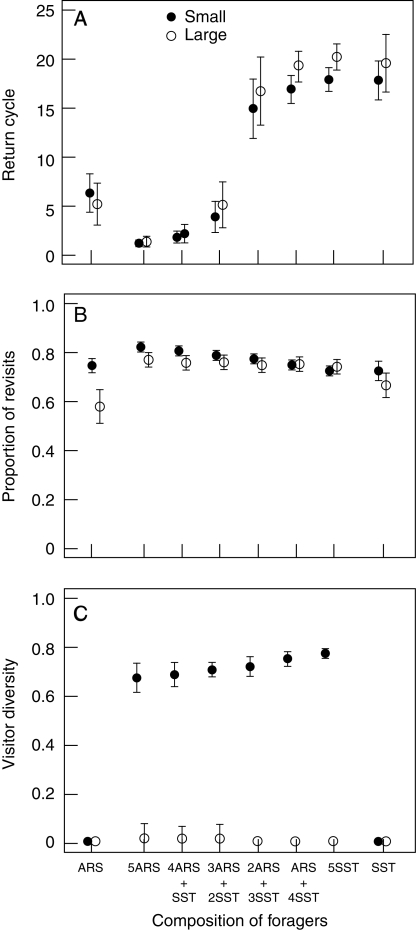
Our model revealed consistent effects of the fraction of trapliners. In both small and large plant populations, the average distance of pollen flow and the effective number of fathers increased as the pollinator assemblage changed from searcher-dominant to trapliner-dominant (Fig. 6). The increases in mean values were up to 71 % in pollen-flow distance and up to 83 % in effective number of fathers. These results oppose some intuitive predictions, such as those by Thomson et al. (1982), that traplining would tend to localize gene flow. It should be noted that those expectations envisaged a comparison of locally restricted trapliners to possible long-distance vagabonds that lacked ties to localized foraging areas. In the model presented here, both trapliners and searchers are restricted to local operations.

Fig. 6.

Expected relationships between composition of trapliners (SST) and searchers (ARS) and (A) distance of pollen flow, (B) effective number of fathers and (C) proportion of iterogamy (= self-pollination caused by return visits) at the population level. Filled circles indicate averages of median values for 100 foraging trips in a small population (30 plants) and open circles indicate those in a large population (120 plants). Error bars indicate s.d.

Moreover, the proportion of iterogamous self-pollination exponentially decreased as trapliners became more dominant (Fig. 6). Iterogamy was minor (6 % or less), but even this amount could lead to substantial losses of opportunities for superior mating when pollen grains, ovules or stigma surface areas are limited, and when selfed progeny suffer strong inbreeding depression. Note that the total number of zygotes (= number of pollen grains sired and received) did not change with the fraction of trapliners, because the difference in spatial use had no significant effect on the total number of visits made during a trip (results not shown). Therefore, establishment of traplines by pollinators tends to promote gene flow among plants, thereby increasing effective population sizes and reducing both uniparental and biparental inbreeding. That difference persisted even when we increased the threshold value to classify ‘win’ and ‘lose’ visits for searchers, so that they would frequently travel between distant plants.

These differences in the effects on plant mating between trapliners and searchers arise because the average return cycle per trip (= number of plant visits made before returning to any particular plant) was nearly three times longer in trapliners than in searchers (Fig. 7A). When searchers compete with one another, the exploitative component of their behaviour produced more short returns. With a certain level of pollen carryover, both mate diversity and mating distance (overall displacement of a pollen grain from its origin) would increase with an extended return cycle even though movement distance (the amount of space traversed by pollinators) between successive visits does not change. Moreover, this fundamental difference led to changes in the other two aspects of visitation patterns. First, the proportion of revisits out of all the visits made during a trip declined with the fraction of trapliners, although the difference was at most 10 % (Fig. 7B). Second, the number of pollinators sharing a plant, and the evenness of their visit frequencies, increased with the fraction of trapliners, because traplines developed to include plants spread widely in space. We calculated the simplest measure of such ‘visitor diversity’ per plant (V_D), using Lande's (1996) modified version of Simpson's index of diversity:

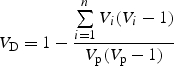where n is the number of pollinators, V_p is the total number of visits to the focal plant, and V_i is the number of visits made by the ith pollinator. V_D ranges between 0 and 1, with greater values indicating greater diversity of visitors. As shown in Fig. 7C, the average V_D increased linearly with the fraction of trapliners in the small plant population (the mean values increased up to 15 %), while it remained near zero in a large plant population where most plants were unvisited. Thus, the increased visitor diversity also contributed to the high mate diversity in the small plant population predominated by trapliners.

Fig. 7.

Expected relationships between composition of trapliners (SST) and searchers (ARS) and (A) return cycle (= number of plant visits made before returning to any particular plant), (B) proportion of revisits (= total number of revisitations divided by total number of plant visits) and (C) visitor diversity (V_D). Filled circles indicate averages of proportion of revisits or averages of median values of return cycle and visitor diversity for 100 foraging trips in a small population (30 plants) and open circles indicate those in a large population (120 plants). Error bars indicate s.d.

Comparing single ARS runs to 5ARS runs shows possible negative consequences of attracting too many searching pollinators. Although the increased visitation promoted zygote (seed) production, it entailed a cost in the quality of pollen flow: mating distance and mate diversity decreased (the reduction in mean values were up to 35 and 23 %, respectively), and iterogamous self-pollination increased up to 1·3-fold (Fig. 6). In contrast, increasing the number of trapliners increased mate diversity (up to 1·4-fold), while hardly affecting mating distance and iterogamous self-pollination (SST vs. 5SST in Fig. 6).

Searching versus traplining also alters the total effect of pollen carryover on plant fitness when iterogamy is considered (Fig. 8). It has been frequently suggested that more extensive pollen carryover would increase mating distance and mate diversity, and reduce geitonogamous self-pollination (Waser and Price, 1984; Galen and Rotenberry, 1988; Robertson, 1992). These predictions on mating distance and mate diversity were supported in our model, irrespective of the spatial-use tactics of pollinators (Fig. 8A, B). However, extensive pollen carryover will also increase iterogamy. With a high fraction of trapliners, the proportion of iterogamy did increase with the pollen carryover fraction (Fig. 8C). When searchers (or pollinators with short return cycles) were dominant, by contrast, the proportion of iterogamy decreased as plants had higher fractions of pollen carryover (Fig. 8C). When pollinators trapline, therefore, the increased iterogamy may counteract the positive effects of pollen carryover and decrease the optimal fraction of pollen carryover for plants. The optimal fraction of pollen carryover might also differ between male and female perspectives in real systems where pollen and ovule fates are asymmetric (Harder and Routley, 2006).

Fig. 8.

Expected effects of changes in pollen carryover on (A) distance of pollen flow, (B) effective number of fathers and (C) proportion of iterogamy in searcher-dominated (5ARS) and trapliner-dominated (5SST) populations. High and low pollen carryover represents the fraction 94 % and 80 %, respectively. Filled circles indicate averages of median values for 100 foraging trips in a small population (30 plants) and open circles indicate those in a large population (120 plants). Error bars indicate s.d.

Plant-level effects

Although plants that receive more visits should exchange more pollen with others, increased visitation need not confer higher reproductive success. High visitation rates can be achieved by frequent returns made by one or a few individuals, or by occasional visits by many different individuals (Williams and Thomson, 1998; Makino et al., 2007). These two components of pollinator visitation may have different consequences.

Even though all the plants in our model were assumed to have a uniform rate of nectar secretion, plants in more crowded areas tended to receive more visits because pollinators preferred to move short distances. This trend did not vary with the fraction of trapliners, but the relative contributions of return visits by individual pollinators and the number of visitors differed between the searcher-dominant (5ARS) and the trapliner-dominant (5SST) simulations. When searchers dominated, a plant's visitation rate was uncorrelated with its visitor diversity (V_D; Table 1). This indicates that an increase in relative visitation in the searcher-dominant population was caused mainly by frequent returns by the same individuals. With a high fraction of trapliners, by contrast, each trapliner chose plants spread widely in space to increase its return cycles, so that the visitation rate was correlated with V_D (Table 1). Consequently, the effects of high visitation rate on a plant's mate diversity greatly differed between the searcher-dominant and the trapliner-dominant populations. When searchers predominated, plants that received more visits attained lower mate diversity (Table 1). When trapliners predominated, by contrast, plants that received more visits enjoyed higher mate diversity (Table 1).

Table 1.

Expected relationships between pollinator visitation rate to a plant and the plant's reproductive components

	5ARS			5SST
Index	r	t	P	r	t	P
Visitor diversity	−0·023 ± 0·28	−0·82	>0·05	0·81 ± 0·063	128·57	<0·0001
Distance of pollen delivery	−0·46 ± 0·17	−27·06	<0·0001	−0·29 ± 0·25	−11·60	<0·0001
Effective no. of fathers	−0·12 ± 0·23	−5·22	<0·0001	0·81 ± 0·063	128·57	<0·0001
Proportion of iterogamy	0·69 ± 0·17	40·59	<0·0001	−0·19 ± 0·32	−5·94	<0·0001

Pearson's coefficient of correlation (r, mean ± s.d.) of each index with visitation rate per plant is calculated in each trip, and r-values are averaged for 100 foraging trips in searcher-dominated (5ARS) and trapliner-dominated (SST) populations, respectively. The significance of r was tested with a one-sample t-test for the mean (H₀; r = 0).

On the other hand, plants that received more visits tended to have shorter mating distances, irrespective of the fraction of trapliners (Table 1). In addition, an increase in plant visits reduced iterogamy when trapliners were dominant, while it had an opposite effect when searchers were dominant (Table 1). These counterintuitive results may be explained by the algorithm we used to simulate trapline development: a trapliner chooses a set of plants by moving between close plants that it has never visited before, and by returning to the starting plant after a certain amount of time has elapsed and nectar has been replenished to a sufficient level (Ohashi and Thomson, 2005). The resultant traplines therefore had a negative relationship between the average distance between plants and the number of plant visits made before returns (return cycle). In other words, a trapliner that chose closely located and popular plants tended to visit more plants before returning; conversely, a trapliner visited fewer plants when it occasionally chose more distant and less crowded plants in the population. Thus, the increased visitation by trapliners resulted in shorter mating distances and less iterogamy at the plant level.

In our model, therefore, the development of traplines enhances outcrossing and potential mate diversity. Although a trapliner repeatedly visits a restricted set of plants, it would limit the level of iterogamous self-pollination by invariably visiting many plants before returning. When circumstances lead trapliners to add plants to their circuits, the new plants are spread widely in space, which further boosts mating distance and mate diversity. Under competition, shared plants at which two or more traplines overlap would enjoy even greater potential mate diversity. Note that our simulations might have overlooked a possible disadvantage of trapline foraging for plants with two or more flowers. Williams and Thomson (1998) showed that regular visitors (trapliners) of bumble-bees on a Penstemon plant tended to probe more flowers during plant visits than occasional visitors did. Similarly, more frequent visitors of Bombus diversus probed significantly more flowering heads per plant visit on six Cirsium purpuratum (T. T. Makino, University of Tsukuba, Japan, pers. comm.). If a trapliner probes more flowers on a plant, relatively less pollen may leave the plant per visit, due to geitonogamous self-pollination and grooming losses (Thomson, 1986; Harder and Barrett, 1995; Karron et al., 2004).

IMPLICATIONS: WHEN DOES TRAPLINE FORAGING MATTER?

Our early papers on Aralia hispida speculated on possible consequences of traplining for plants (Thomson et al., 1982; Thomson, 1988). Here we will reconsider this issue in the light of much new experimental work and modelling.

Gene flow within and among plant populations

Pollinators visiting a plant population may differ greatly in their spatial use depending on various factors associated with their learning processes. When plants attract cognitively sophisticated pollinators, replenish their floral rewards, grow in populations with rich visual landmarks and are distributed in ways that aid spatial learning of pollinators (Ohashi et al., 2007), for example, visitors would quickly learn to follow traplines with long return cycles. A moderate level of ‘traplining’ (or frequenting foraging circuits with long return cycles) could be reached without spatial memory by following simple movement rules for choosing the distances and turning angles of successive flights. If pollinators can learn the locations and sequences of patches more easily, however, even longer and more stable return cycles may be achieved (Ohashi et al., 2007). As our simulations have suggested, plants blooming under such conditions would experience increased mating distance, mate diversity and outcrossing rate due to the increased fraction of trapliners.

Because animals often have difficulty in learning multiple locations in close proximity (Burns and Thomson, 2006), larger distances between neighbouring plants may also encourage pollinators to trapline, thereby promoting pollen flow among plants at the population level. When plants are considerably isolated, however, some other forces are likely to be simultaneously hampering pollen flow, which could complicate the eventual outcome for mating patterns. First, if plants have inconspicuous flowers, developing traplines on scattered plants may entail heavy time and energy costs of learning exact plant locations (Manning, 1956). Such increased costs could reduce the fraction of trapliners. Second, numerous studies have shown that pollinators probe more flowers on larger floral displays (reviewed by Goulson, 2000; Ohashi and Yahara, 2001), which would increase the wastage of pollen that could otherwise be used for outcrossing (Thomson, 1986; Harder and Barrett, 1995; Karron et al., 2004). Third, our simulations suggest that a trapliner may increase iterogamous self-pollination by visiting fewer plants before returning when its foraging route includes one or more isolated plants (Table 1). Such a reduction of return cycle could benefit animals when resource renewal is non-linear or when there are competitors, by producing returns to plants before the refilling rate tapers off and before other foragers take the accumulated resources (Ohashi and Thomson, 2005; Ohashi et al., 2008). Although we need to test it empirically, it is thus possible that trapliners exacerbate iterogamy in low-density plant populations by visiting fewer plants before returning. The increase in iterogamy would be greater in some animals that cause higher levels of pollen carryover than the apid bees for which our model's parameters were estimated; hummingbirds might be an example (Castellanos et al., 2003).

At larger scales, another indirect effect of traplining may arise when pollinators respond to competition. Bees that establish traplines earlier retain their foraging areas tenaciously (Ohashi et al., 2008). When a plant population is not packed with pollinators, therefore, late arrivals can fit in uncrowded areas and establish their own traplines. If the population is packed, however, late arrivals will have to forage inefficiently unless they find underused plants or increase their travel speeds enough to compensate for their lack of traplines. If they cannot achieve an acceptable level of intake, they may decide to leave the current population to find another, or they might work two different localities alternately (see Thomson and Chittka, 2001, p. 193). This could contribute to gene flow between plant populations. Pollen-mediated gene flow between populations may increase the effective size of populations and reduce the threat of genetic drift-based hazards such as the depletion of genetic variation and inbreeding depression, but may also limit local adaptation (Ellstrand, 1992; Lenormand, 2002). In this way, we suggest that various biotic and abiotic factors related to trapline foraging may contribute to genetic diversity and inbreeding depression in plant populations, which should in turn affect the rates and directions of floral evolution. The importance of these factors in gene flow is rather hypothetical at this time, and awaits further theoretical and empirical exploration.

Counterintuitive interactions between pollinator attraction and plant fitness

The foraging tactics adopted by pollinators may interact with visitation rates in unexpected ways. As we have seen, increased visitation by trapliners and searchers may have opposite effects on pollen flow from plants (Table 1). Attracting more searchers reduces mate diversity and outcrossing rates, while attracting more trapliners increases both of those aspects of mating. Because trapliners and searchers are indistinguishable by casual observation, such differences have received virtually no attention. One needs to break ‘visitation’ down into its components – the number of individuals sharing the plant and the number of return visits by each individual – as has been attempted in very few studies (Williams and Thomson, 1998; Makino et al., 2007). This finding reinforces our conviction that pollination biologists would benefit from treating pollinators as individuals (Thomson and Chittka, 2001).

The complicated relationship between pollinator visitation and pollen flow forces us to reconsider the significance of pollinator attraction for animal-pollinated plants. Researchers have implicitly assumed that floral traits that increase collective pollinator visits to a plant would equivalently contribute to plant fitness. This notion may not hold true if these traits vary in attraction toward pollinators with different patterns of spatial use, i.e. trapliners and searchers. Indeed, bumble-bees change their preference for plants with accumulating foraging experience at a food site; Makino and Sakai (2007) showed that inexperienced foragers initially prefer artificial inflorescences with more conspicuous displays, but later learn to override that early preference with a learned preference for more rewarding inflorescences. Therefore, floral traits that increase pollinator visits may vary in their contributions to plant fitness: conspicuous cues will recruit inexperienced foragers that are searching, and substantive rewards will retain experienced foragers that are developing traplines. For example, Aralia inflorescences with many small umbels received more bumble-bee visits than did inflorescences with the same number of flowers deployed across fewer, larger umbels (Thomson, 1988). Assuming that the flowers were equally rewarding, this preference reflects a difference in conspicuousness. Similarly, production of sterile flowers or large petals would increase conspicuousness (Bell, 1985; Ishii and Harder, 2006). Production of nectarless flowers should also increase conspicuousness and attract inexperienced foragers, whereas it would repel experienced foragers by decreasing substantive reward value (Bell, 1986; Gilbert et al., 1991). On the other hand, increased nectar flow would contribute to substantive reward value, but not to conspicuousness (Thomson, 1988; Makino and Sakai, 2007). Floral display size (number of open flowers per plant or inflorescence) would apparently contribute to superficial attractiveness (Makino and Sakai, 2007), but it would also increase substantive reward value. Not only are there more flowers available, but because the proportion of flowers probed by a pollinator declines with display size, flowers on large displays offer more accumulated reward on average than those on small displays (Ohashi and Yahara, 2002).

When a plant population is commonly visited by a mixture of pollinators with different preferences and spatial-use patterns, then, what kind of advertisement strategy is optimal for plants to maximize their fitness? The formal answer to this question could be very complex, because the success of any particular phenotype could be affected by the phenotypes of other plants in the vicinity. Without considering such local frequency dependence, our simulations suggest that plants could produce more offspring simply by increasing substantive rewards, i.e. catering to trapliners by offering higher rewards. Local populations of insect pollinators, however, may undergo substantial turnover as individuals die and are replaced by new recruits (Rodd et al., 1980; Thomson et al., 1987). Therefore, plants may also benefit from some level of conspicuousness to economically gain the recognition of newcomers. Even experienced bumble-bees tend to choose plants with large displays or plants growing in dense stands when they sample outside their own traplines (Thomson et al., 1982; Makino et al., 2007). In low-density populations, moreover, pollinators may prefer to visit conspicuous plants, because they can travel between distant plants without remembering the exact locations (Manning, 1956). Given these perspectives, plants would generally benefit from having both types of floral traits. By contrast, when there are so many pollinators that plants would not suffer from reduced return visits, when circumstances make traplining cognitively difficult, when pollinators have poor cognitive abilities or when pollinators are not site-faithful and travel across landscapes, it would become advantageous for plants to allocate more energy to floral traits that increase only conspicuousness to searchers (see also discussion in Makino and Sakai, 2007). Thus, plants may have evolved different combinations of floral traits to maximize the efficiency of pollen flow, by ‘choosing’ among behaviourally variable pollinators under given circumstances. This situation may have some resemblance to diffuse coevolution between plants and multiple pollinator taxa (e.g. Aigner, 2001), but it is more complicated in that the same pollinators would change their behaviour with time and experience. Furthermore, different levels of selection are likely to be operating: by producing more reward, an individual plant may attract more visitations not only to itself but also to its neighbours. Clearly, more theoretical and empirical studies are needed to clarify possible outcomes of such dynamic evolution in angiosperms.