Skip to main content
PMC home page
Annals of Botany logoLink to Annals of Botany
. 2009 Feb 18;103(9):1459–1469. doi: 10.1093/aob/mcp027

Size-specific interaction patterns and size matching in a plant–pollinator interaction web

Martina Stang 1,*, Peter G L Klinkhamer 1, Nickolas M Waser 2, Ingo Stang 1, Eddy van der Meijden 1
PMCID: PMC2701768  PMID: 19228701

Abstract

Background and Aims

Many recent studies show that plant–pollinator interaction webs exhibit consistent structural features such as long-tailed distributions of the degree of generalization, nestedness of interactions and asymmetric interaction dependencies. Recognition of these shared features has led to a variety of mechanistic attempts at explanation. Here it is hypothesized that beside size thresholds and species abundances, the frequency distribution of sizes (nectar depths and proboscis lengths) will play a key role in determining observed interaction patterns.

Methods

To test the influence of size distributions, a new network parameter is introduced: the degree of size matching between nectar depth and proboscis length. The observed degree of size matching in a Spanish plant–pollinator web was compared with the expected degree based on joint probability distributions, integrating size thresholds and abundance, and taking the sampling method into account.

Key Results

Nectar depths and proboscis lengths both exhibited right-skewed frequency distributions across species and individuals. Species-based size matching was equally close for plants, independent of nectar depth, but differed significantly for pollinators of dissimilar proboscis length. The observed patterns were predicted well by a model considering size distributions across species. Observed size matching was closer when relative abundances of species were included, especially for flowers with openly accessible nectar and pollinators with long proboscises, but was predicted somewhat less successfully by the model that included abundances.

Conclusions

The results suggest that in addition to size thresholds and species abundances, size distributions are important for understanding interaction patterns in plant–pollinator webs. It is likely that the understanding will be improved further by characterizing for entire communities how nectar production of flowers and energetic requirements of pollinators covary with size, and how sampling methods influence the observed interaction patterns.

Key words: Plant–pollinator community, flower morphology, generalization, nectar, pollination network, body size, size matching, specialization

INTRODUCTION

Most angiosperm species attract animals to pollinate their flowers (e.g. Renner, 1988; Nabhan and Buchmann, 1997). Attraction is usually achieved by providing rewards of nectar, pollen or other substances. In some flowers, these rewards are easily accessible, but in others they are obtained only by animals with particular behaviours or morphologies. Perhaps the clearest example is the concealment of nectar within deep tubes or other floral structures. Leaving aside those animals that ‘rob’ the nectar (Irwin et al., 2001), it is expected that concealed nectar will be accessible only to animals with mouthparts as long as or longer than the depth of the structure that holds the nectar (hereafter termed the ‘nectar depth’).

In previous studies of a Spanish community of nectar-producing plant species and nectar-searching animal species (Stang et al., 2006, 2007), we were able to predict several topological properties of the actual web of interactions by assuming the existence of a threshold proboscis length for each plant species. Specifically we could predict the observed distribution of the degree of generalization of plants and pollinators, the nestedness of interactions between plants and pollinators (the degree to which more specialized species interact with a sub-set of the partners of more generalized species) and the degree of interaction asymmetry, i.e. whether specialists interact with generalists (asymmetry) or with other specialists (symmetry). Here we explore the success of size thresholds in combination with size distributions in explaining an additional topological property, namely the patterns of interaction as a function of size. These patterns can be expressed as a bivariate frequency distribution of interactions across size classes of proboscis lengths and nectar depths, along with the average degree of size matching between depths and lengths for each species separately.

In our earlier studies, it was found that the proboscis lengths of flower visitors to a given plant species were indistinguishable from a random selection from all the potential visitors in the local species pool, i.e. those insects that conformed to the nectar depth of the plant species (Stang et al., 2006). In such a case, observed size matching should be influenced not only by the size threshold ‘rule’, but also by the frequency distributions of nectar depths and proboscis lengths in the community (compare Cohen et al., 1993). For example, if flower visitors with short proboscises are more abundant than those with long proboscises, visits to flowers with openly accessible nectar might be dominated by the former. This could lead to high degrees of size matching for such plants, even in the absence of innate preferences of pollinators or of preferences resulting from interpecific competition for nectar (e.g. Ranta and Lundberg, 1980; Harder, 1985; Rodríguez-Gironés and Santamaría, 2005, 2006).

The few published studies of size-specific interaction patterns and size matching in communities of plants and pollinators have restricted their focus to groups of closely related animal species such as hoverflies (Gilbert, 1981), long-proboscid flies (Goldblatt and Manning, 2000), euglossine bees (Borrell, 2005), solitary bees (Armbruster and Guinn, 1989), bumble-bees (Brian, 1957; Ranta and Lundberg, 1980; Harder, 1985), butterflies (Corbet, 2000) and hawkmoths (Haber and Frankie, 1989). Overall, these studies revealed that animal species with long proboscises visit on average a wider range of flowers than species with short proboscises, as one would expect based solely on size thresholds. All studies also reported a positive relationship between proboscis lengths of animals and average nectar depths of plants visited, indicating size matching. However, none of these studies tested whether the observed size-specific interaction patterns and average size matching could result from the actual frequency distributions of proboscis lengths or nectar depths in the local community. Furthermore, these animal-centred studies do not allow an extrapolation to how well plant species match the morphology of their visitors (the plants' rather than the animals' perspective), because most plants were probably visited by more than the animal taxa under investigation (Herrera, 1996; Waser et al., 1996; Olesen, 2000).

Here the Spanish web was used to explore factors that contribute to observed size-specific interaction patterns and size matching. After characterizing the actual size distributions of proboscis lengths and nectar depths, the frequency distribution of observed interactions across size classes of plants and animals is described and the average degree of size matching for each plant and animal species is calculated separately. The observed patterns are then compared with theoretical expectations based on joint probability distributions. In this modelling approach, which differs from those used in previous such studies, it is assumed that the probability of observing any interaction is inversely proportional to the number of potential interaction partners of both the plant and animal species involved, given that the threshold rule is met. The goals are 3-fold: (1) to explore how well the simple considerations of size thresholds and size distributions can reproduce size-specific interaction patterns at the community level and size matching at the level of species; (2) to determine whether the inclusion of the relative abundances of species changes the observed patterns and its predictability; and (3) to see whether the degree of size matching differs between morphologically generalized and specialized species, as could be expected when trait distributions are uniform and interactions are proportional to abundance.

MATERIALS AND METHODS

Study system and sampling methods

The study community in the southeast of Spain comprised 25 nectar-producing plant species from 11 plant families, and 111 nectar-collecting pollinator species from five insect orders (Stang et al., 2006). The number of pollinator species and individuals at flowers was determined during 6 weeks in March and April 2003 by using a modified transect walk. Ten sampling plots of 200 m2 (most of them 4 × 50 m) were established and we walked through them at a slow pace. As soon as an insect was observed visiting a plant species that was in good flower, we determined if the insect was searching for nectar and/or pollen and touching the flower's reproductive organs. After catching that insect, we continued observing this plant species for the next 2–7 min, depending on visitation activity and the number of flowering plant individuals in that plot. During this interval, each additional insect individual visiting that plant species was recorded. All observed insects contacted stigmas and anthers during their visits, so they were all counted as pollinators. After each observation interval, we switched to another plant species that was in good flower. Each plant species was observed for 60 min, spreading the observation intervals per species equally over four 2 h periods between 1000 h and 1800 h (i.e. 15 min per 2 h period). We distributed observation intervals randomly over different plots [3·6 ± 1·6 plots per species (mean ± s.d.)] and sampling days (within a period of 15 d per plant species) so that each plant species was sampled only once per plot and per 2 h period within 1 d.

During the peak of each plant species' flowering season, the number of flowering individuals was counted. It was assumed that the sample of individual plants observed to interact with pollinators was representative of the overall plant community during the observation period. This approach simplifies the comparison with previously published quantitative studies, almost all of which are based on the observed number of interacting individuals. Similarly, it was assumed that our sample of 887 individual nectar-searching pollinators comprising 111 different species could be taken as representative of the overall pollinator community during the study period. Most individual pollinators that were observed were caught for identification, but only one specimen from each animal species per plant species and sampling interval was retained for size measurement (in total 278 individuals), to minimize the impact on pollinator populations. The honeybee Apis mellifera was the most abundant species, comprising one-third of observed individuals. For this species, we caught only a tiny fraction of observed individuals, making our estimate of the number of individual honey bees less reliable than that of the other pollinator species.

A pollinator species was observed on average 8·0 ± 28·5 times (or 5·4 ± 7·5 excluding honey bees). A total of 34 % of the pollinator species were represented by only a single individual during the entire study period. Per plant species, on average 36 ± 25 pollinator individuals (or 24 ± 18 excluding honeybees) were observed.

Species traits and trait distributions

Nectar depth was measured for 5–10 flowers of each plant species as the distance from the position in the flower that a pollinator's head could reach to the base of the flower part containing the nectar (Stang et al., 2006). Nectar standing crops were generally small, so these measurements will be close to actual nectar accessibility. In all analyses, the minimum nectar depth value measured for each plant species was used, to allow the most liberal interpretation of the threshold that would exclude potential pollinators (Stang et al., 2006). Proboscis length and body length of all pollinators captured at flowers were also measured. Body mass of pollinators was estimated as M = 0·0305L2·62, with M = dry mass in mg and L = body length in mm (Rogers et al., 1976).

The width of the floral structure containing the nectar and the proboscis diameter of pollinators were also measured, as these might impose an additional size constraint on interactions (Stang et al., 2006). However, these morphological traits are not discussed further, since they did not enter as a major factor in the analyses presented below (Stang, 2007).

Observed and expected frequency distributions of interactions

The observed frequency distributions of numbers of interactions as functions of size were determined by dividing the ranges of proboscis lengths and nectar depths into size classes of 2 mm and counting the observed numbers of interacting species or individuals as each analysis required (see below). The expected frequency distributions of interactions were derived using two algorithms derived from our sampling regime in the field. The first ‘species-based’ algorithm assumes that all species are equally abundant and that the probability of observing an interaction between any given species pair depends solely on the number of other species that may potentially interact with each member of the pair. That is, we assume that species with many potential interaction partners will be observed infrequently with any one of these partner species, and vice versa for species with few potential partners (see also the Appendix). The second ‘abundance-based’ algorithm adds in the observed number of interacting individuals per species, so that abundant species have a higher chance of interacting than do rare species.

For the first, species-based approach, the joint probability pij that pollinator species i is visiting a plant species j is calculated as:

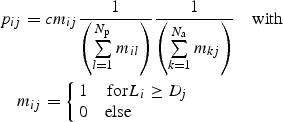graphic file with name mcp02705.jpg 1

where c is a normalization factor, mij is the threshold operator that indicates whether the interaction is possible, Li is the proboscis length of pollinator species i, and Dj is the nectar depth of plant species j. The first quotient in the equation is the probability that the pollinator species of interest visits the plant species of interest, among all Np plant species that this pollinator can visit. Given that pollinator i can indeed visit plant j, this quotient is one divided by a sum taken across all Np plant species in the community, in which only those with mij = 1 are counted. The second, parallel term is the probability that the pollinator to the plant species of interest is the pollinator species of interest, among all the Na pollinator species that can visit this plant species, with a form analogous to that of the first quotient. Consider an example: a pollinator species i with a proboscis of 3 mm can exploit all plant species j with nectar depth ≤3 mm; if five plant species meet this criterion, the probability of observing this pollinator on any given one of these five plant species is (1/5) = 0·2. Conversely, a nectar depth of 3 mm is accessible to pollinators i with a proboscis ≥3 mm; if 20 pollinator species meet this criterion, the probability of observing any particular pollinator species is (1/20) = 0·05. These probabilities are multiplied to find the joint probability (0·01) of observing exactly that plant species visited by that pollinator species.

For the second, abundance-based approach, we include the relative abundances of species, thus assuming that the joint probability pij is proportional to the number of observed interacting individuals instead of species, so that:

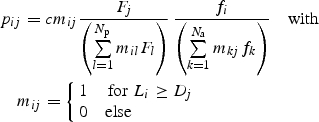graphic file with name mcp02706.jpg 2

where Fj is the number of observed interacting individuals of plant species j, and fi is the number of observed interacting individuals of pollinator species i.

Multiplication of the probabilities pij by the observed number of species–species or individual–individual interactions (231 and 887, respectively) yields the expected frequencies of interactions across species and individuals. It is straightforward to transform these expected frequency distributions into the expected numbers of species or individuals per size class, by adding all frequencies across the species pairs of one bivariate size class (e.g. nectar depths of 2–4 mm combined with proboscis lengths of 6–8 mm).

Observed and expected degrees of size matching

The observed degree of size matching was calculated for each species separately, based on the mean and standard deviation of trait values for its mutualistic partners. From the plants' perspective, this means the average proboscis lengths of visitors to their flowers, whereas from the pollinators' perspective it means the average nectar depths of flowers they visited. To calculate expected nectar depths and proboscis lengths, we used either species- or abundance-based matrices of probabilities pij of interaction between pollinator species i and plant species j. Hence the expected mean proboscis length 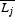Inline graphic of pollinators from the perspective of plant species j is calculated as:

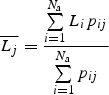graphic file with name mcp02707.jpg 3

In the same way the mean nectar depth 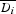Inline graphic from the perspective of pollinator species i is calculated as:

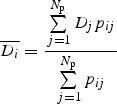graphic file with name mcp02708.jpg 4

Least-squares linear regression was used to assess the degree of size matching across species. Size thresholds by themselves may be expected to produce a decreasing variance of observed or expected data points with increasing nectar depth or decreasing proboscis length, since greater nectar depths allow access by a smaller range of proboscis lengths, and shorter proboscises allow access to a smaller range of nectar depths. Thus, we expect triangular distributions of depth on length or of length on depth (Stang et al., 2007; compare Cohen et al., 1993). This heterogeneity of variance does not in fact occur when using means of proboscis lengths and nectar depths, so that such data met the statistical criteria for regression analysis. Model I least-squares linear regression was used because it was assumed that mean proboscis lengths or nectar depths of single species (x-variates) were measured with less error than the means of trait values of the multiple interaction partners for each such species (y-variates).

To test whether size thresholds and observed frequency distributions of size (nectar depth and proboscis length) could jointly explain the observed degree of matching, we compared the observed slope of the regressions just described with the expected slopes based on the two algorithms (species-based and abundance-based). To compare the degree of matching of generalized species with that of specialized species, and to compare observed and expected slopes, partial F-tests following Potthoff (1966) were used. Statistical analyses were performed in SPSS 12·0 (SPSS Inc., Chicago, IL, USA).

RESULTS

Observed trait distributions and covariation among species traits

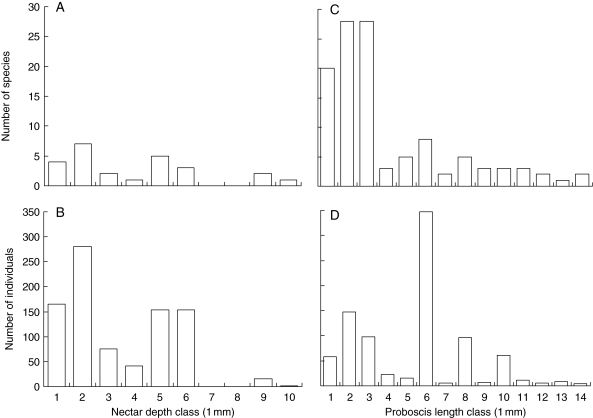
Nectar depths ranged from 0 to 9·5 mm, with a mean of 3·5 mm and a median of 2·7 mm (Fig. 1A). The frequency distribution of depths was slightly right-skewed (kurtosis = –0·25, skewness = 0·73) but could not be distinguished statistically from a normal distribution (Kolmogorov–Smirnov z = 0·84, P = 0·49, n = 25). The distribution of the number of interacting individuals across plant species (Fig. 1B) was also slightly right-skewed (kurtosis = –0·44, skewness = 0·51); a log transformation did not normalize it (z = 9·39, P < 0·001, n = 887). The number of interacting plant individuals (which equals the number of individual pollinators observed on a plant species) and the total number of open flowers were positively correlated (rs = 0·58, P = 0·002, n = 25).

Fig. 1.

Fig. 1.

Open in a new tab

Observed distributions of nectar depths and proboscis lengths. Shown are the numbers of interacting species (A, C) and individuals (B, D) per size class interval of 1 mm. Honey bees (Apis mellifera, mean proboscis length = 5·95 mm) contribute 295 individuals to proboscis length class 6 in (D).

Observed proboscis lengths of the 111 pollinator species ranged from 0·1 to 14·0 mm, with a mean of 3·5 mm and a median of 2·3 mm. Mean and median values were similar to those of nectar depths, but the maximum proboscis length was 4·5 mm greater than the maximum nectar depth (Fig. 1C). The distribution was unimodal and right-skewed (kurtosis = 1·36, skewness = 1·43). After log transformation, the proboscis lengths were normally distributed (z = 1·01, P = 0·26, n = 111). The frequency distribution based on the number of individuals resembles the distribution based on the number of species, but only when A. mellifera is excluded. The distribution with Apis was slightly right-skewed (kurtosis = –0·19, skewness = 0·23, Fig. 1D); a log transformation did not normalize it (z = 9·4, P < 0·001, n = 887). Without Apis the distribution was slightly more right-skewed (kurtosis = –0·61, skewness = 0·65); again a log transformation did not normalize it (z = 3·16, P < 0·001, n = 592).

Estimated dry body mass of the pollinator species ranged from 0·1 to 67·4 mg, with a mean of 12·7 mg and a median of 7·8 mg. The distribution was right-skewed and was normalized by log transformation (z = 0·90, P = 0·39, n = 111). Log proboscis length and log body mass were significantly positively correlated across pollinator species; hence the former size trait exhibits positive allometric scaling with the latter (length = 0·72 mass0·61, r2 = 0·67, P < 0·001, n = 111).

Observed and expected frequency distributions of interactions

Observed and expected frequency distributions of plant–pollinator interactions across 2 mm size classes are given in Table 1. Matrices in the top section (a, c) represent observed frequency distributions across size classes and show that most interactions were observed in the upper left triangle of the matrix. The leading diagonal from the lower left corner to the top right corner represents size classes for which nectar depth and proboscis length match. Matrices in the bottom section (b, d) represent expected frequency distributions of interactions. In both sections, the left-hand matrix (a, b) represents the species-based perspective and the right-hand matrix (c, d) represents the abundance-based perspective. For the species-based analysis there were no significant differences between observed and expected values in non-zero cells of these matrices (χ2 = 10·62, d.f. = 12, P = 0·56), i.e. for interactions that were both possible given the threshold rule and actually represented in the Spanish community. For the abundance-based analysis, the differences were significant (χ2 = 105·34, d.f. = 12, P < 0·001). The largest contribution to these differences came from cells in the left upper corner of the matrices: interactions between plants with openly accessible nectar and pollinators with long proboscises were observed far less frequently than expected.

Table 1.

Observed and expected frequency distributions of plant–pollinator interactions across size classes of 2 mm, with pollinators in rows and plants in columns

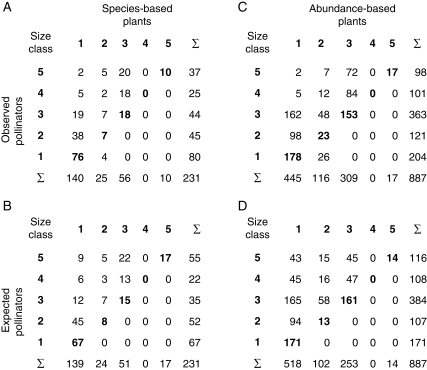graphic file with name mcp02704.jpg
Open in a new tab

Size increases from bottom to top (pollinators) and left to right (plants).

Size class 5 for pollinators combines all proboscis lengths between 8 and 14 mm in order to obtain frequencies large enough to meet assumptions of χ2 tests.

Observed and expected degrees of size matching

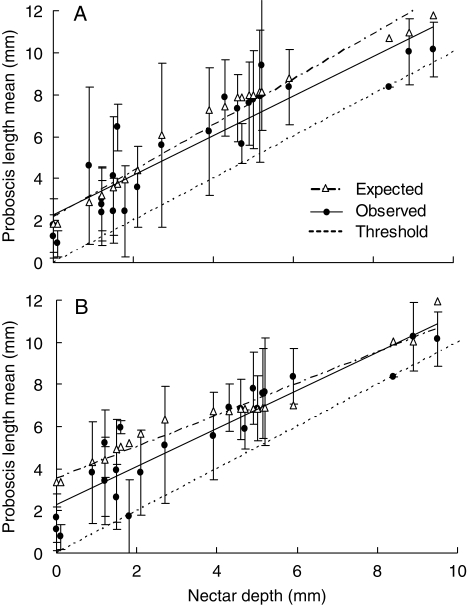
Regressing observed mean proboscis length on nectar depth (the plants' perspective) yields a significant positive slope for both species-based (= 0·95) and abundance-based (= 0·90) means, with an intercept in both cases of about 2·2 mm (Fig. 2 and Table 2, plants). Neither slope differed significantly from unity, but the intercepts in both cases differed significantly from zero. This means that proboscis length did not perfectly match nectar depth on average, but the difference was quite small, and the degree of matching was independent of nectar depth (i.e. the degree of matching was similar across the range of depths). The observed slopes also did not differ significantly from the expectations of the species-based (slope = 1·09) or abundance-based (slope = 0·75) algorithms, even though the latter slope differed by 0·15 from the observed slopee and the intercept was about 1 mm larger. Overall, the combination of size thresholds and observed frequency distributions of proboscis length closely reproduced the observed degree of size matching.

Fig. 2.

Fig. 2.

Open in a new tab

Observed and expected proboscis lengths in relation to nectar depths of flowers based on species (A) or individuals (B). Each data point corresponds to a single plant species (n = 25) and is shown as the mean proboscis length of pollinators observed at that plant (filled circles) ±1 s.d. (vertical lines), along with the mean length predicted by the appropriate (species-based or abundance-based) model (open triangles). The threshold line is the line at which proboscis length equals nectar depth.

Table 2.

Degree of observed and expected morphological matching based on the mean trait values of the interaction partners, according to the species-based and abundance-based algorithms

Model Slope Intercept r2 Δ t P
Plants' perspective
 Species-based
  Observed 0·95 +2·26 0·82 – – –
  Expected 1·09 +2·18 0·97 –0·14 –1·422 0·162
  Threshold line 1·00 0·00 1·00 –0·05 –0·949 0·348
 Abundance-based
  Observed 0·90 +2·27 0·85 – – –
  Expected 0·75 +3·54 0·95 +0·15 +1·770 0·083
  Threshold line 1·00 0·00 1·00 −0·10 −1·638 0·108
Pollinators' perspective
 Species-based
  Observed 0·53 +0·14 0·70 – – –
  Expected 0·52 –0·01 0·96 +0·01 +1·910 0·849
  Threshold line 1·00 0·00 1·00 –0·47 –14·170 <0·001
 Abundance-based
  Observed 0·54 +0·11 0·72 – – –
  Expected 0·36 –0·18 0·95 +0·18 +5·300 <0·001
  Threshold line 1·00 0·00 1·00 –0·46 –14·570 <0·001
Open in a new tab

The table gives the slope, intercept and r2 of the best linear fits to the observed data and to model predictions, corresponding to the fits shown in Figs 2 and 3. Δ indicates the difference in slope between these regression lines, and between the observed regression and a slope of unity expected under perfect size matching; t gives the t value and P the significance of these differences.

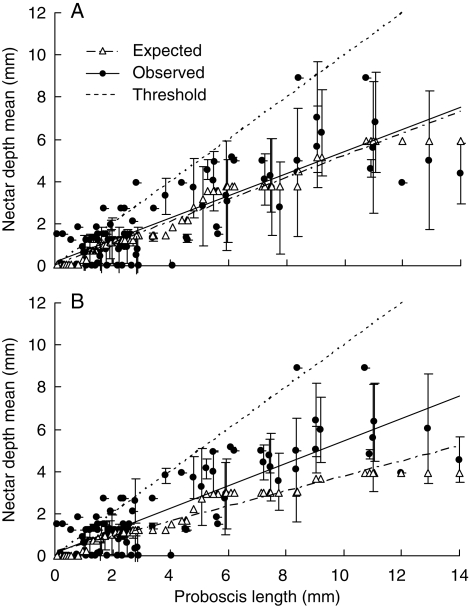
Fig. 3.

Fig. 3.

Open in a new tab

Observed and expected nectar depths in relation to proboscis lengths of pollinators based on species (A) or individuals (B). Each data point corresponds to a single pollinator species (n = 111) and is shown as the mean nectar depth of flowers visited by that pollinator (filled circles) ±1 s.d. (vertical lines), along with the mean depth predicted by the appropriate (species-based or abundance-based) model (open triangles). The threshold line is the line at which nectar depth equals proboscis length.

Regressing observed mean nectar depths on proboscis lengths (the pollinators' perspective) again yields a significant positive slope for both species-based and abundance-based means (Fig. 3 and Table 2, pollinators). Both slopes were significantly less than unity, i.e. pollinators with short proboscises matched the flowers they visited more closely than did pollinators with long proboscises. The observed slope based on species means (= 0·53) was not significantly different from the expected slope (= 0·52), whereas the slope based on abundance (= 0·54) was significantly steeper than expected (= 0·36). The latter result indicates that with increasing proboscis length pollinators matched the flowers they visited slightly but significantly more closely than expected. Nevertheless, the difference between observed and expected was small compared with the difference with a slope of unity.

DISCUSSION

Mutualistic ecological webs studied to date, including pollination webs, exhibit some remarkably consistent features: an excess of relative specialists compared with extreme generalists (i.e. scale-free or truncated scale-free degree distributions; e.g. Jordano et al., 2003; Vázquez and Aizen, 2003), asymmetry in the interactions of specialists and generalists (i.e. most specialists interacting with generalists rather than other specialists; e.g. Vázquez and Aizen, 2004) and nestedness (i.e. more specialized species tending to interact with sub-sets of the partners of their more generalized counterparts; e.g. Bascompte et al., 2003), with little evidence for highly exclusive compartments (e.g. Dicks et al., 2002; Lewinsohn et al., 2006). Recognition of these shared features has led to a variety of mechanistic attempts at explanation. To date, the causal assumptions have been (a) that interactions occur at random, and reflect primarily the (log-normal) abundance distribution of plant and animal species (Vázquez and Aizen, 2004; Vázquez et al., 2007; Krishna et al., 2008); (b) that trait complementarity (such as phenological matching) and/or exploitation barriers (such as a nectar depth threshold) determine network topology (Jordano et al., 2006; Rezende et al., 2007; Santamaría and Rodríguez-Gironés, 2007); or (c) that a combination of exploitation barriers (nectar depth threshold) and random interactions proportional to the observed abundance of species is important (Stang et al., 2007).

Here an additional feature of pollination webs was considered, i.e. size-related distribution patterns, that could help to discriminate between the different causal assumptions. We explored how well the frequency distributions of interactions across size classes, and the average degree of size matching for individual species in an actual pollination web, can be explained by two simple rules: (1) nectar searching pollinators will only visit flowers when their mouthparts suffice to reach the nectar (the size threshold rule); and (2) the probability of an interaction depends on the relative abundances of plants and pollinators of the size classes in question (the rule that the actual frequency distributions of flower and pollinator sizes of the species pool in the local community determine the frequencies of interactions). These two rules did quite well in predicting the observed size-specific interaction patterns from the perspective of both plants and pollinators. This result suggests that, along with the size threshold and interaction proportional to species abundance [the two rules that can explain the degree of generalization, nestedness and interaction asymmetry (Stang et al., 2007)], size distributions play an important and hitherto unrecognized role in structuring pollination webs.

Trait distributions and morphological matching

A right-skewed distribution, lognormal and unimodal, is the prevailing distribution for body mass across animal species (e.g. Hutchinson and Macarthur, 1959; Brown, 1995, and references therein; Kozlowski and Gawelczyk, 2002; Allen et al., 2006; Ulrich, 2006). A right-skewed distribution of proboscis lengths also should prevail in pollination webs, insofar as length correlates across species with body mass. Such a positive correlation has been reported for solitary bees, bumble-bees, butterflies and sphingid moths (Harder, 1985; Haber and Frankie, 1989; Shmida and Dukas, 1990; Corbet, 2000; Agosta and Janzen, 2005; see also Inouye and Pyke, 1988). It was also found in the Spanish community, and, indeed, proboscis lengths in this community were distributed lognormally across species, with most species having a short proboscis. As a result, the majority of pollinators of morphologically generalized plants (those with relatively accessible nectar) matched the nectar depth of flowers very closely. Visual inspection suggests that nectar depths in our community also were right-skewed. A right-skewed distribution was reported in alpine communities in North America, Austria and Australia (Inouye and Pyke, 1988), and for flowers visited by Costa Rican dry forest moths (Agosta and Janzen, 2005).

These features of size distributions appear to explain the observed patterns of size matching from the perspective of both plants and pollinators. Because pollinators with short proboscises were common, the average degree of size matching was relatively high for generalized plants. However, the longest proboscises were longer than the deepest flowers by >4 mm. As a result, relatively specialized flowers (those with concealed nectar) also received visits representing a range of proboscis lengths, especially at the species level. Thus the linear regressions of proboscis length on nectar depth have slopes near unity, but both the predicted and observed slopes, while paralleling the threshold line, lie about 2 mm above it. Turning to the regressions of nectar depth on proboscis length, the presence of pollinators with extra-long proboscises necessarily will depress the slope of a straight line fit, which is consistent with our finding of slopes less than unity.

Deviations between expected and observed matching

Despite the good agreement between observed and predicted relationships, there was some variation in how closely the mean of single species agreed with theoretical expectation based on our simple rules. Some of the deviation of observed means from predicted values might be an artefact that would have disappeared with more extensive sampling of the community. However, in the regression of nectar depth on proboscis length, using the abundance-based algorithm, there also appears to be a systematic deviation in the direction that longer tongued pollinators fell increasingly above the predicted line. Such a deviation suggests that our approach has limitations, a likely one being that it fails to capture all the elements that determine the value or utility of different flowers from the pollinators' perspective. Selection of flowers by pollinators is likely to be based on more than just accessibility of nectar, since pollinators appear in general to be sensitive to finer details of floral reward such as caloric value and ease of extraction (e.g. Pyke, 1984; see also Stephens and Krebs, 1986).

Complicating the picture are the potential intercorrelations of size with components of resource quality and energy requirements. For example, plant species with accessible nectar probably produce less nectar on average than those with deep tubes or spurs. Conversely, pollinators with long proboscises tend to have larger body mass (in general, and as we have shown, in the Spanish community), which confers larger energy requirements (Heinrich and Raven, 1972; Corbet, 2006). The combination of these factors could impose an additional energetic threshold on pollinators, restricting species with long proboscises to flowers with nectar depths exceeding a certain value, since these would also contain caloric rewards above a certain value (see Corbet et al., 1995). An energetic threshold of this kind would be consistent with the under-representation of long-tongued pollinators at open flowers and the systematic deviation of such pollinators in the regression of nectar depth on proboscis length, relative to expectation from the abundance-based model.

Finally, we recognize that pollinators often search flowers not only for nectar but also for pollen. The importance of pollen as a reward differs greatly across pollinator taxa (e.g. butterflies vs. bees), as do the accessibility and amounts of pollen across plant species. Both aspects might influence flower selection by pollinators that are probing a flower for nectar, and this might contribute to the observed deviation from expectations. Future studies should estimate the impact of pollen vs. nectar visits on network structure, and should more explicitly distinguish insects that are seeking nectar alone, pollen alone or some combination.

Model assumptions

Our central assumption that pollinators follow a size threshold in visits to flowers requires that they quickly learn which flowers have accessible nectar, so that the probability of observing them on inappropriate flowers is low. Learning of this kind has been studied more extensively in some pollinator taxa than in others, but appears to be rapid in most cases (e.g. Chittka and Thomson, 2001). We also assumed that pollinators choose randomly from among the appropriate plants. This assumption is in good accord with actual observations from the Spanish web (Stang et al., 2006, 2007) and more generally it corresponds to the behaviour expected of optimal foragers that are relatively unconstrained in floral choice, as appears to be a good first approximation for many pollinators (e.g. Pyke, 1984; Waser et al., 1996). We further assumed that the chance of observing a given plant species is independent of the chance of observing a given pollinator species, once the size threshold rule is met, and that an observer cannot see an interaction when it is with a plant that is not chosen by the observer (see Appendix).

Implications for ecological generalization, floral evolution and conservation

We have shown that a size threshold is not at odds with a relatively high degree of morphological matching for plants with open flowers. In principle, the rewards of such flowers are accessible to a wide range of proboscis lengths, but pollinators with short proboscises outnumber those with longer proboscises and thus predominate as pollinators. Thus the potential for ecological generalization, which characterizes open flowers, is not at odds with an empirical observation of strong size matching. Because many small pollinators (especially flies, beetles and wasps) are not as efficient as larger pollinators (especially bees) in transferring pollen during each visit to a flower (e.g. Herrera, 1987, 1989), generalization on a diversity of pollinators might be important for the pollination of open flowers. Turning to the pollinators' perspective, a longer proboscis confers the potential for greater generalization, which may be important for supporting a higher metabolic cost, even if most visits are to deep flowers.

If a size threshold and a seemingly ubiquitous right-skewed frequency distribution of proboscis lengths ensure substantial size matching between flowers and pollinators, this may lead to further evolutionary change. Even if a relatively tight match might not originally be essential for successful pollination, the high number of species and individuals with a predictable morphology might increase the probability that plant species will adapt to the most common morphological type of pollinator (which might comprise numerous insect species), insofar as this increases per-visit pollination efficiency. For example, upright, shallow flowers might adapt the distance between the opening to their nectar chamber and their exposed anthers to match the average distance by which pollinator mouthparts exceed nectar depth, because pollen might attach better to hairy body parts than to a smooth proboscis. This could tighten the match of flowers to pollinators, especially if floral evolution is coupled with an increase in preference of pollinators for flowers that have nectar depths that match their mouthparts or are only slightly shorter.

Indeed, a relatively close morphological ‘fit’ between flower depth and length of mouthparts often appears to correlate with high rates of visitation to flowers (Inouye, 1980; Ranta and Lundberg, 1980; Peat et al., 2005), and also with high rates of pollen transfer during each visit (Nilsson, 1988; Campbell et al., 1996; Johnson and Steiner, 1997; but see Wilson, 1995). Assuming that morphological fit usually does benefit plant reproduction, these results, and the results of our study, imply that a right-skewed distribution of proboscis lengths may be important for the maintenance of intact plant communities. Loss of short-tongued pollinator species, or reduction in their abundances, should reduce the degree of size matching, and might thereby reduce pollination success of shallow flowers. Trait distributions that provide an optimal morphological matching for all plant species could serve as a testable reference point to estimate the potential health of a plant–pollinator web in terms of resilience to species loss.

Caveats and future directions

We have argued here, and in previous papers (Stang et al., 2006, 2007), that size thresholds and size distributions together do well in explaining topological features of the Spanish pollination web. However, this is far from the final word, in several regards. First, it seems imperative to apply this same approach to other interaction webs in distinct types of habitats. We are in the process of doing so ourselves, and we also urge other workers to measure trait distributions across species and individuals, and to include such information in attempts to explain observed interactions. Secondly, there is little known about the impact of sampling methods on observed interaction patterns. For example, how does sampling proportional to plant abundance (transect walks, e.g. Memmott, 1999), sampling until saturation points of finding new pollinator species are reached (adaptive sampling, e.g. Ollerton and Cranmer, 2002) or equal sampling effort per plant species (focal species approach, e.g. this study) affect estimates of generalization, interaction asymmetry and size matching? These questions need further investigation, especially if one wants to quantify links and compare the results of different studies (manuscript in preparation). Thirdly, and more generally, there is a logical pitfall in assuming that a given causal model is correct because it does a good job in predicting what one observes. There is no accepted criterion as to how good the prediction must be in order that one gains confidence in given causal factors. Furthermore, it is logically fallacious to conclude that because A predicts B, B implies A. In other words, although size thresholds and size distributions appear plausible as causal components of actual visitation patterns, and although our confidence increases along with the number of features we can explain in actual webs, ultimately we cannot exclude other causal factors as important, without further work.

Among the causal factors that might be important are several that have been hinted at above: the energetic value of individual flowers, the number and clustering of flowers on plants (which influences energetic cost of travel among them), energetic requirements of pollinators and costs of resource extraction as a function of the match or mismatch between flower and pollinator size (e.g. Inouye, 1980; Smith et al., 1996), as well as interspecific resource competition among pollinators and consequent shifts in resource use (e.g. Rodríguez-Gironés and Santamaría, 2006). It also would be worth studying how floral advertisement such as colour and odour influence flower choice and thus interaction patterns within a network (Raguso, 2008; Riffell et al., 2008). Extending observational studies such as ours to new communities is one step toward exploring the roles of all such factors, but we would argue, in conclusion, that experimental manipulation (of plant and pollinator size distributions, nectar rewards, and so on) is also feasible, and ultimately necessary, for further progress in determining which mechanistic factors give rise to the patterns we see in pollination webs.

ACKNOWLEDGEMENTS

Many thanks to Tom de Jong, Mary Price, Axel Rossberg, Miguel Rodrígues-Gironés, Laura Burkle and Ruben Alarcón for discussion and for comments on the manuscript, and to Annals of Botany and the Ecological Society of America for financial support to M.S. to attend the Symposium on which this Special Issue is based.

APPENDIX

Our modelling approach (the formulae described in the text) corresponds to the following scenario: (a) a plant is selected [with equal probability for all plant species (species-based approach) or individuals (abundance-based approach)]; (b) a pollinator is selected out of the pollinators that meet the threshold criterion for that plant [each particular pollinator species (or individual) has an equal probability of being selected]; (c) the selected pollinator randomly chooses one of the plants for which it has access to nectar; (d) whether the plant chosen by the observer and the plant chosen by the pollinator are the same is checked; (e) if they are the same, this interaction is counted as 1, if not this interaction is discarded and counted as zero; (f) the procedure is repeated until each plant species (or individual) is sampled the same number of times.

This approach assumes (a) that all plant and pollinator species overlap in time and space and can potentially interact (see Stang et al., 2006); (b) that each plant species (or individual) is observed for the same amount of time and that each pollinator species (or individual) has the same amount of time available for visitation; (c) that the pollinators arrive sequentially (so that only one pollinator individual is in the area per time interval); (d) that a pollinator chooses only a plant to which it has access to nectar (i.e. a pollinator wastes no time visiting flowers with inaccessible nectar); (e) that the pollinator chooses randomly among plants that meet the threshold criterion (i.e. pollinators show no preferences, as if, for example, plants do not differ in effective reward offered); (f) that the pollinator chooses a plant independently from the observer; and (g) that an interaction cannot be seen by an observer when the pollinator chooses a plant different from that chosen by the observer (because the observation is spatially restricted; the observer cannot see everything at once).

LITERATURE CITED

  1. Agosta SJ, Janzen DH. Body size distributions of large Costa Rican dry forest moths and the underlying relationship between plant and pollinator morphology. Oikos. 2005;108:183–193. [Google Scholar]
  2. Allen CR, Garmestani AS, Havlicek TD, et al. Patterns in body mass distributions: sifting among alternative hypotheses. Ecology Letters. 2006;9:630–643. doi: 10.1111/j.1461-0248.2006.00902.x. [DOI] [PubMed] [Google Scholar]
  3. Armbruster WS, Guinn DA. The solitary bee fauna (Hymenoptera, Apoidea) of interior and arctic Alaska – flower associations, habitat use, and phenology. Journal of the Kansas Entomological Society. 1989;62:468–483. [Google Scholar]
  4. Bascompte J, Jordano P, Melian CJ, Olesen JM. The nested assembly of plant–animal mutualistic networks. Proceedings of the National Academy of Sciences, USA. 2003;100:9383–9387. doi: 10.1073/pnas.1633576100. [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Borrell BJ. Long tongues and loose niches: evolution of euglossine bees and their nectar flowers. Biotropica. 2005;37:664–669. [Google Scholar]
  6. Brian AD. Differences in the flowers visited by four species of bumble-bees and their causes. Journal of Animal Ecology. 1957;26:71–98. [Google Scholar]
  7. Brown JH. Macroecology. Chicago: The University of Chicago Press; 1995. [Google Scholar]
  8. Campbell DR, Waser NM, Price MV. Mechanisms of hummingbird-mediated selection for flower width in Ipomopsis aggregata. Ecology. 1996;77:1463–1472. [Google Scholar]
  9. Chittka L, Thomson JD. Cognitive ecology of pollination: animal behaviour and floral evolution. Cambridge: Cambridge University Press; 2001. [Google Scholar]
  10. Cohen JE, Pimm SL, Yodzis P, Saldana J. Body size of animal predators and animal prey in food webs. Journal of Animal Ecology. 1993;62:67–78. [Google Scholar]
  11. Corbet SA. Butterfly nectaring flowers: butterfly morphology and flower form. Entomologia Experimentalis et Applicata. 2000;96:289–298. [Google Scholar]
  12. Corbet SA. A typology of pollinations systems: implications for crop management and the conservation of wild plants. In: Waser N, Ollerton J, editors. Plant–pollinator interactions: from specialization to generalization. Chicago: The University of Chicago Press; 2006. pp. 315–340. [Google Scholar]
  13. Corbet SA, Saville NM, Fussell M, PrysJones OE, Unwin DM. The competition box: a graphical aid to forecasting pollinator performance. Journal of Applied Ecology. 1995;32:707–719. [Google Scholar]
  14. Dicks LV, Corbet SA, Pywell RF. Compartmentalization in plant–insect flower visitor webs. Journal of Animal Ecology. 2002;71:32–43. [Google Scholar]
  15. Gilbert FS. Foraging ecology of hover-flies – morphology of the mouthparts in relation to feeding on nectar and pollen in some common urban species. Ecological Entomology. 1981;6:245–262. [Google Scholar]
  16. Goldblatt P, Manning JC. The long-proboscid fly pollination system in southern Africa. Annals of the Missouri Botanical Garden. 2000;87:146–170. [Google Scholar]
  17. Haber WA, Frankie GW. A tropical hawkmoth community: Costa Rican dry forest Sphingidae. Biotropica. 1989;21:155–172. [Google Scholar]
  18. Harder LD. Morphology as a predictor of flower choice by bumblebees. Ecology. 1985;66:198–210. [Google Scholar]
  19. Heinrich B, Raven PH. Energetics and pollination ecology. Science. 1972;176:597–602. doi: 10.1126/science.176.4035.597. [DOI] [PubMed] [Google Scholar]
  20. Herrera CM. Components of pollinator quality – comparative analysis of a diverse insect assemblage. Oikos. 1987;50:79–90. [Google Scholar]
  21. Herrera CM. Pollinator abundance, morphology, and flower visitation rate – analysis of the quantity component in a plant–pollinator system. Oecologia. 1989;80:241–248. doi: 10.1007/BF00380158. [DOI] [PubMed] [Google Scholar]
  22. Herrera CM. Floral traits and plant adaptation to insect pollinators: a devil's advocate approach. In: Lloyd DG, Barrett SCH, editors. Floral biology. Studies on floral evolution in animal-pollinated plants. New York: Chapman and Hall; 1996. pp. 65–87. [Google Scholar]
  23. Hutchinson GE, Macarthur RH. A theoretical ecological model of size distributions among species of animals. American Naturalist. 1959;93:117–125. [Google Scholar]
  24. Inouye DW. The effect of proboscis and corolla tube lengths on patterns and rates of flower visitation by bumblebees. Oecologia. 1980;45:197–201. doi: 10.1007/BF00346460. [DOI] [PubMed] [Google Scholar]
  25. Inouye DW, Pyke GH. Pollination biology in the Snowy Mountains of Australia – comparisons with montane Colorado, USA. Australian Journal of Ecology. 1988;13:191–210. [Google Scholar]
  26. Irwin RE, Brody AK, Waser NM. The impact of floral larceny on individuals, populations, and communities. Oecologia. 2001;129:161–168. doi: 10.1007/s004420100739. [DOI] [PubMed] [Google Scholar]
  27. Johnson SD, Steiner KE. Long-tongued fly pollination and evolution of floral spur length in the Disa draconis complex (Orchidaceae) Evolution. 1997;51:45–53. doi: 10.1111/j.1558-5646.1997.tb02387.x. [DOI] [PubMed] [Google Scholar]
  28. Jordano P, Bascompte J, Olesen JM. Invariant properties in coevolutionary networks of plant–animal interactions. Ecology Letters. 2003;6:69–81. [Google Scholar]
  29. Jordano P, Bascompte J, Olesen JM. The ecological consequences of complex topology and nested structure in pollination webs. In: Waser N, Ollerton J, editors. Plant–pollinator interactions: from specialization to generalization. Chicago: The University of Chicago Press; 2006. pp. 173–199. [Google Scholar]
  30. Kozlowski J, Gawelczyk AT. Why are species' body size distributions usually skewed to the right? Functional Ecology. 2002;16:419–432. [Google Scholar]
  31. Krishna A, Guimarães PR, Jr, Jordano P, Bascompte J. A neutral-niche theory of nestedness in mutualistic networks. Oikos. 2008;117:1609–1618. [Google Scholar]
  32. Lewinsohn TM, Prado PI, Jordano P, Bascompte J, Olesen JM. Structure in plant–animal interaction assemblages. Oikos. 2006;113:174–184. [Google Scholar]
  33. Memmott J. The structure of a plant–pollinator food web. Ecology Letters. 1999;2:276–280. doi: 10.1046/j.1461-0248.1999.00087.x. [DOI] [PubMed] [Google Scholar]
  34. Nabhan GP, Buchmann SL. Pollination services: biodiversity's direct link to world food stability. In: Daily GC, editor. Nature's services: societal dependence on natural ecosystems. Washington, DC: Island Press; 1997. pp. 133–150. [Google Scholar]
  35. Nilsson LA. The evolution of flowers with deep corolla tubes. Nature. 1988;334:147–149. [Google Scholar]
  36. Olesen JM. Exactly how generalized are pollination interactions? De Norske Videnskaps–Akademi. I. Matematisk Naturvidenskapelige Klasse, Skrifter, Ny Serie. 2000;39:161–178. [Google Scholar]
  37. Ollerton J, Cranmer L. Latitudinal trends in plant–pollinator interactions: are tropical plants more specialised? Oikos. 2002;98:340–350. [Google Scholar]
  38. Peat J, Tucker J, Goulson D. Does intraspecific size variation in bumblebees allow colonies to efficiently exploit different flowers? Ecological Entomology. 2005;30:176–181. [Google Scholar]
  39. Potthoff RF. Statistical aspects of the problem of biases in psychological tests. Chapel Hill, NC: University of North Carolina, Department of Statistics; 1966. [Google Scholar]
  40. Pyke GH. Optimal foraging theory – a critical review. Annual Review of Ecology and Systematics. 1984;15:523–575. [Google Scholar]
  41. Raguso RA. Start making scents: the challenge of integrating chemistry into pollination ecology. Entomologia Experimentalis et Applicata. 2008;128:196–207. [Google Scholar]
  42. Ranta E, Lundberg H. Resource partitioning in bumblebees – the significance of differences in proboscis length. Oikos. 1980;35:298–302. [Google Scholar]
  43. Renner SS. Effects of habitat fragmentation on plant–pollinator interactions in the tropics. In: Newbery DM, Prins HHT, Brown ND, editors. Dynamics of tropical communities. Oxford: Blackwell Science; 1988. pp. 339–360. [Google Scholar]
  44. Rezende EL, Jordano P, Bascompte J. Effects of phenotypic complementarity and phylogeny on the nested structure of mutualistic networks. Oikos. 2007;116:1919–1929. [Google Scholar]
  45. Riffell JA, Alarcón R, Abrell L, Davidowitz G, Bronstein JL, Hildebrand JG. Behavioral consequences of innate preferences and olfactory learning in hawkmoth–flower interactions. Proceedings of the National Academy of Sciences, USA. 2008;105:3404–3409. doi: 10.1073/pnas.0709811105. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Rodríguez-Gironés MA, Santamaría L. Resource partitioning among flower visitors and evolution of nectar concealment in multi-species communities. Proceedings of the Royal Society B: Biological Sciences. 2005;272:187–192. doi: 10.1098/rspb.2005.2936. [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Rodríguez-Gironés MA, Santamaría L. Models of optimal foraging and resource partitioning: deep corollas for long tongues. Behavioral Ecology. 2006;17:905–910. [Google Scholar]
  48. Rogers LE, Hinds WT, Buschbom RL. General weight vs length relationship for insects. Annals of the Entomological Society of America. 1976;69:387–389. [Google Scholar]
  49. Santamaría L, Rodríguez-Gironés MA. Linkage rules for plant–pollinator networks: Trait complementarity or exploitation barriers? PloS Biology. 2007;5:354–362. doi: 10.1371/journal.pbio.0050031. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Shmida A, Dukas R. Progressive reduction in the mean body sizes of solitary bees active during the flowering season and its correlation with the sizes of bee flowers of the mint family (Lamiaceae) Israel Journal of Botany. 1990;39:133–141. [Google Scholar]
  51. Smith CE, Stevens JT, Temeles EJ, Ewald PW, Hebert RJ, Bonkovsky RL. Effect of floral orifice width and shape on hummingbird–flower interactions. Oecologia. 1996;106:482–492. doi: 10.1007/BF00329706. [DOI] [PubMed] [Google Scholar]
  52. Stang M. The structure of flower visitation webs: how morphology and abundance affect interaction patterns between flowers and flower visitors. The Netherlands: Leiden University; 2007. PhD Thesis. [Google Scholar]
  53. Stang M, Klinkhamer PGL, van der Meijden E. Size constraints and flower abundance determine the number of interactions in a plant–flower visitor web. Oikos. 2006;112:111–121. [Google Scholar]
  54. Stang M, Klinkhamer PGL, van der Meijden E. Asymmetric specialization and extinction risk in plant–flower visitor webs: a matter of morphology or abundance? Oecologia. 2007;151:442–453. doi: 10.1007/s00442-006-0585-y. [DOI] [PubMed] [Google Scholar]
  55. Stephens DW, Krebs JR. Foraging theory. Princeton, NJ: Princeton University Press; 1986. [Google Scholar]
  56. Ulrich W. Body weight distributions of European Hymenoptera. Oikos. 2006;114:518–528. [Google Scholar]
  57. Vázquez DP, Aizen MA. Null model analyses of specialization in plant–pollinator interactions. Ecology. 2003;84:2493–2501. [Google Scholar]
  58. Vázquez DP, Aizen MA. Asymmetric specialization: a pervasive feature of plant–pollinator interactions. Ecology. 2004;85:1251–1257. [Google Scholar]
  59. Vázquez DP, Melian CJ, Williams NM, Blüthgen N, Krasnov BR, Poulin R. Species abundance and asymmetric interaction strength in ecological networks. Oikos. 2007;116:1120–1127. [Google Scholar]
  60. Waser NM, Chittka L, Price MV, Williams NM, Ollerton J. Generalization in pollination systems, and why it matters. Ecology. 1996;77:1043–1060. [Google Scholar]
  61. Wilson P. Selection for pollination success and the mechanical fit of Impatiens flowers around bumblebee bodies. Biological Journal of the Linnean Society. 1995;55:355–383. [Google Scholar]

Articles from Annals of Botany are provided here courtesy of Oxford University Press

RESOURCES