Plant Light Interception Can Be Explained via Computed Tomography Scanning: Demonstration with Pyramidal Cedar (Thuja occidentalis, Fastigiata)

Abstract

Background and Aims

Light interception by the leaf canopy is a key aspect of plant photosynthesis, which helps mitigate the greenhouse effect via atmospheric CO₂ recycling. The relationship between plant light interception and leaf area was traditionally modelled with the Beer–Lambert law, until the spatial distribution of leaves was incorporated through the fractal dimension of leafless plant structure photographed from the side allowing maximum appearance of branches and petioles. However, photographs of leafless plants are two-dimensional projections of three-dimensional structures, and sampled plants were cut at the stem base before leaf blades were detached manually, so canopy development could not be followed for individual plants. Therefore, a new measurement and modelling approach were developed to explain plant light interception more completely and precisely, based on appropriate processing of computed tomography (CT) scanning data collected for developing canopies.

Methods

Three-dimensional images of canopies were constructed from CT scanning data. Leaf volumes (LV) were evaluated from complete canopy images, and fractal dimensions (FD) were estimated from skeletonized leafless images. The experimental plant species is pyramidal cedar (Thuja occidentalis, Fastigiata).

Key Results

The three-dimensional version of the Beer–Lambert law based on FD alone provided a much better explanation of plant light interception (R² = 0·858) than those using the product LV*FD (0·589) or LV alone (0·548). While values of all three regressors were found to increase over time, FD in the Beer–Lambert law followed the increase in light interception the most closely. The delayed increase of LV reflected the appearance of new leaves only after branches had lengthened and ramified.

Conclusions

The very strong correlation obtained with FD demonstrates that CT scanning data contain fundamental information about the canopy architecture geometry. The model can be used to identify crops and plantation trees with improved light interception and productivity.

INTRODUCTION

Light interception by the leaf canopy is at the core of photosynthesis in higher plants (Thornley, 2002). In particular, this process is vital for our environment because it contributes to recycling of atmospheric CO₂ (Sage and Coleman, 2001). Using the digital data and graphics of Keeling and Whorf (2005), the increase rate of atmospheric CO₂ concentration in the last decade can be estimated to be approx. 1·8 ppm per year. From within-year fluctuations, plants, via photosynthesis, appear to contribute to reducing atmospheric CO₂ concentration, between a peak and a trough, by approx.14 ppm every year. A 35 % increase of plant biomass, with 10 % of this sequestered into the soil C pool after plant senescence, would result in a decrease in atmospheric CO₂ concentration by 3·5 % or approx. 0·5 ppm, which represents >25 % of the current yearly increase rate of atmospheric CO₂. Thus, while plants perform many extremely important functions, such as providing energy to the biosphere, a very timely example of global function is net removal of the greenhouse gas CO₂ from the atmosphere, via photosynthesis. Light and CO₂ being the major inputs of this process, it follows that improving plant light interception is the key to optimization, and a better modelling of plant light interception, a prerequisite. The reported study addresses this question.

Within the constraints of their environment, plants array their foliage in space to optimize light interception and gas exchange. Different approaches have been proposed to study canopy development, empirically (Foroutan-pour et al., 1999a, 2001; Purcell, 2000) and by computer simulation (Perttunen et al., 2001; Kikuzawa et al., 2004; Niklas, 2004). The new approach proposed here is model-based and spatio-temporal, and makes use of real data collected by a technology that is novel to plant science.

The relationship between light interception and leaf area was traditionally modelled with the Beer–Lambert law, borrowed from physics (Monsi and Saeki, 1953), until the spatial distribution of leaves was incorporated through the fractal dimension of leafless plant structure photographed from the side that allowed the maximum appearance of branches and petioles (Foroutan-pour et al., 2001). Despite good results, there are a number of problems with this approach: photographs of leafless plants are two-dimensional projections of three-dimensional structures; sampled plants are cut at the stem base before leaf blades are detached manually, so canopy development cannot be followed for individual plants.

Therefore, the new approach and modelling, which were developed to explain plant light interception more completely and precisely, are based on the appropriate processing of computed tomography (CT) scanning data collected for developing canopies. X-ray CT scanning technology was recently shown to have potential for developmental studies in plant science if the CT scanner used is of the medical type (Dutilleul et al., 2005). In fact, medical CT scanners capture changes in material density of relatively light and large objects, such as plant canopies, better than industrial CT scanners can do. Because leaves and branches possess different densities, branches can be isolated on the computer after leaves have been removed digitally, and the plant is allowed to grow between CT scanning sessions. In the following sections, the successive steps in the collection and processing of CT scanning data for developing canopies of pyramidal cedars, including the construction of three-dimensional images and the statistical analyses involved in the application of three-dimensional versions of the Beer–Lambert law, are explained. Finally, the efficacy of the new approach in modelling the ability of plant canopies to intercept light is discussed, and perspectives for future studies are elaborated.

MATERIALS AND METHODS

Plant material

The experimental plants were four approx. 5-year-old pyramidal cedars (Thuja occidentalis, Fastigiata) or an equivalent expression. This plant species was chosen because its branching pattern clearly meets the fractal assumption, i.e. branches subdivide into sub-branches, sub-branches into sub-sub-branches, etc. in a regular dichotomous manner (Fig. 1); it follows that the same structure is reproduced over a range of scales. The cedars were already potted when purchased (Pépinière Saltarelli Enr., Vaudreuil-Dorion, Québec, Canada) on 16 May 2005. After purchase, they were kept in a greenhouse environment, except on the days their canopies were submitted to CT scanning. Fertilizer (30–10–10) had been applied at the tree nursery and no other fertilizer was applied thereafter. The potted cedars were watered on a weekly basis. During the course of their growth, the cedars showed no signs of nutrient deficiency, disease pressure or insect damage.

Fig. 1.

Branch sample of a cedar (Thuja occidentalis). The length of the scale (bottom right) corresponds to 5 cm.

Collection and processing of CT scanning data

The complete canopy (i.e. branching pattern and foliage) of each of the four experimental cedars was scanned three times at the CT Scanning Laboratory for agricultural and environmental research of McGill University. The dates of CT scanning were 14 and 15 June 2005 (time 1), 27 and 28 July 2005 (time 2) and 6 and 7 September 2005 (time 3). Two cedars were CT scanned per day, following the same order throughout the experiment.

CT scanning configuration parameters were: scan time, 4 s; tube current, 50 mA; tube voltage, 120 kV (Dutilleul et al., 2005). Because of the growth of cedars from time 1 to time 3, the field of view (i.e. diameter of the cylindrical volume to be CT scanned) was increased from 24 cm (time 1) to 32 cm (time 2) and 40 cm (time 3). Slice thickness was 1 mm at time 1. To optimize resolution at the following times, the couch, on which a cedar was placed, moved by 1 mm after each X-ray exposure at time 2 and by 1·5 mm at time 3. The intervals of CT numbers (i.e. indirect measures of density) used for the identification of leaf and branch voxels were adjusted accordingly; a voxel is the volumetric extension of a pixel.

Raw three-dimensional images of the complete canopies were constructed from CT scanning data, using the MATLAB software (The MathWorks Inc., Natick, MA, USA). Leaf volume (LV) was evaluated from this type of image, by multiplying the number of leaf voxels counted in an image by the corresponding volume of one voxel. For fractal dimension estimation, three-dimensional images of the sole branching patterns were skeletonized, i.e. each branch in those images was reduced to one-voxel thickness, because there would be biasing thickness effects otherwise (Foroutan-pour et al., 1999b).

Light energy measurements and data processing

Following each CT scanning session, light energy (μmol s⁻¹ m⁻²) was recorded with a Line Quantum Sensor (LI-COR Inc., Lincoln, NE, USA) in the measurement room, at four given positions forming a square in the horizontal plane above and below the cedar canopy. Light interception (%) of a cedar canopy at a given position was calculated as (1 – I/I₀) × 100, where I₀ is the irradiance above canopy and I is the irradiance under the same canopy (Purcell, 2000). For use in a three-dimensional variant of the Beer–Lambert law, where light interception is transformed by using the natural logarithm (referred to as logarithm and denoted log hereafter), the variable to explain (LI) was evaluated as log[(1−Ī/Ī₀)×100], with Ī and Ī₀, the mean values of I and I₀ over the four positions.

Statistical analyses

Fractal dimension (FD) was estimated on skeletonized three-dimensional images of branching patterns, with the cube-counting procedure available in the CATSIVA software; this software has been used for root systems in recent studies (Lontoc-Roy et al., 2005, 2006), but was designed for quantitative analysis of plant CT scan data in general. The logarithm of the numbers of cubes of decreasing size that intersected the image was plotted against the logarithm of the inverse of the corresponding cube side lengths, and an FD estimate was provided by the slope of the straight line fitted to the data points in this log–log plot. Differences between means at different times were assessed by repeated measures ANOVA (Crowder and Hand, 1990), using GLM procedure (REPEATED option) of the SAS package (SAS Institute Inc., Cary, NC, USA). The regression models of LI on each of the three candidate explanatory variables (i.e. LV, FD, LV*FD) were without intercept. The significance of correlations was assessed with a modified t-test (Dutilleul, 1993), because the data (i.e. temporal repeated measures) did not satisfy the assumptions of independence and homogeneity of the variance of the classical test.

RESULTS

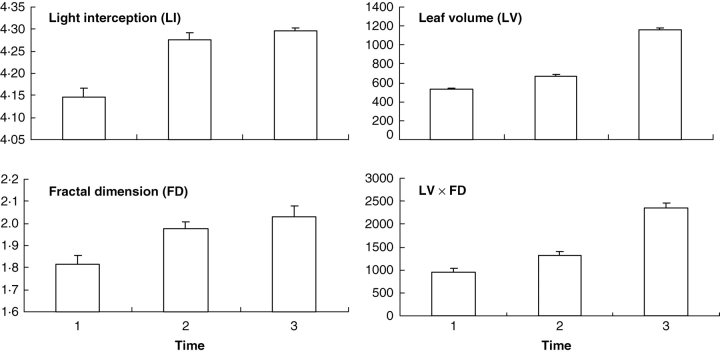
For each of the experimental cedars, three raw and three skeletonized three-dimensional images were constructed (Fig. 2). The use of three-dimensional images for fractal analysis produced FD estimates greater than 2·0 at time 3, and to a lesser extent at time 2 (Fig. 3). Variations of LI and FD over time look smaller than those of LV (Fig. 3), but the former two variables are expressed in a logarithmic scale; the percentage of intercepted light (i.e. before log-transformation) was already greater than 60 % at time 1, and FD values in the three-dimensional space cannot be greater than 3·0. For all variables, however, time main effects were declared highly significant (P < 0·005) by the repeated measures ANOVA. Pairwise comparisons of means detected significant differences at the same level, with the exceptions of times 1 and 2 (P < 0·01) and times 2 and 3 (P < 0·10) for LI and of times 2 and 3 for FD (P < 0·10).

Fig. 2.

False-coloured three-dimensional renderings of the complete canopies (top) and the sole branching patterns skeletonized (i.e. branches are reduced to one-voxel thickness) (bottom) of the same four pyramidal cedars (Thuja occidentalis, Fastigiata) at 6-week intervals (A–D). Height (cm) mean values (± s.e.) for complete canopies are 45·8 (±0·5), 50·7 (±0·4) and 55·5 (±1·2) at the three consecutive times. Complete canopy images were constructed from CT scanning data and show canopy development over time. Skeletonized leafless images were used for fractal dimension estimation and show the increasing complexity of branching patterns over time.

Fig. 3.

Mean values (with standard error bars) at the three times of CT scanning for the variable to explain (LI, or logarithm of the proportion of intercepted light expressed as a percentage; Purcell, 2000) and the three candidate explanatory variables used separately in variants of the three-dimensional version of the Beer–Lambert law. Variables LI and FD are unit-less, while LV and LV*FD are in cubic millimetres.

Concerning the joint fluctuations of variables in time (Fig. 3), the increase in LI was important between times 1 and 2, and corresponded to an increase of similar importance in the complexity of branching patterns, as shown by the FD estimates. Thereafter, LI and FD increased more slowly. Accordingly, the correlation between LI and FD was declared highly significant (P < 0·005) by the modified t-test, and the model based solely on the fractal geometric component provided the best goodness-of-fit (R² = 0·858). By comparison, the increase in LV was more important between times 2 and 3, so the correlation between LI and LV was non-significant (P > 0·10) and the goodness-of-fit was moderate (R² = 0·548). The product LV*FD provided an intermediate goodness-of-fit (R² = 0·589) and its correlation with LI was declared significant (P < 0·05) by the modified t-test.

DISCUSSION

The new approach presented here is spatio-temporal because the development of a given plant canopy is followed in space and time (Fig. 2), and the spatial variables LI, LV and FD are analysed in time (Fig. 3). Light interception was directly measured in the reported study, which distinguishes it from computer simulation studies (Kikuzawa et al., 2004; Niklas, 2004). The information necessary to analyse the foliage volume (LV) and canopy architecture complexity (FD) was contained in the three-dimensional images constructed from CT scan data. It could be, but does not have to be, decomposed and expressed in terms of position, shape and angle of each leaf and branch as in three-dimensional digitizing procedures (Sinoquet et al., 1998). Unlike photographs, the three-dimensional images of plant canopies constructed from CT scanning data do not suffer from the distortion that occurs in two-dimensional projections, and depict the actual spatial distribution of leaves and the branching pattern through which they are arrayed.

The observed delay in the increase of LV relative to FD reflects the appearance of new leaves only after branches have lengthened and ramified. The presence of sun and shade leaves in the canopy (Thornley, 2002) may also explain the weaker correlation between LI and LV, which represents the total leaf volume. The very strong correlation obtained with FD demonstrates that CT scanning data contain fundamental information about the canopy architecture geometry.

The reported canopy experiment is the first of its kind (i.e. plant CT scan) to be completed over a growing season. The results presented here can be used to undertake future plant CT scan studies of canopies for a variety of plant species, using similar procedures in the same approach. Cedar was chosen because its branching pattern meets the fractal assumption. Other natural candidates include soybean, a field crop plant (Foroutan-pour et al., 1999b, 2001), and some bonsai trees, with possible extension of results to other tree species using simulation models such as LIGNUM (Perttunen et al., 2001). The present study demonstrated that a geometric model, based on the physical Beer–Lambert law and the fractal dimension estimated on three-dimensional images constructed from CT scanning data, explains plant light interception during canopy development. With due attention to interaction and competition effects between individuals and intrinsic differences in photosynthesis between species (Ehleringer and Pearcy, 1983; Furbank and Taylor, 1995), such a model could be used to identify crops and young plantation trees with improved light interception and productivity.