Random Effects Models in a Meta-Analysis of the Accuracy of Two Diagnostic Tests Without a Gold Standard

Abstract

In studies of the accuracy of diagnostic tests, it is common that both the diagnostic test itself and the reference test are imperfect. This is the case for the microsatellite instability test, which is routinely used as a prescreening procedure to identify individuals with Lynch syndrome, the most common hereditary colorectal cancer syndrome. The microsatellite instability test is known to have imperfect sensitivity and specificity. Meanwhile, the reference test, mutation analysis, is also imperfect. We evaluate this test via a random effects meta-analysis of 17 studies. Study-specific random effects account for between-study heterogeneity in mutation prevalence, test sensitivities and specificities under a nonlinear mixed effects model and a Bayesian hierarchical model. Using model selection techniques, we explore a range of random effects models to identify a best-fitting model. We also evaluate sensitivity to the conditional independence assumption between the microsatellite instability test and the mutation analysis by allowing for correlation between them. Finally, we use simulations to illustrate the importance of including appropriate random effects and the impact of overfitting, underfitting, and misfitting on model performance. Our approach can be used to estimate the accuracy of two imperfect diagnostic tests from a meta-analysis of multiple studies or a multicenter study when the prevalence of disease, test sensitivities and/or specificities may be heterogeneous among studies or centers.

1. INTRODUCTION

The performance of a binary diagnostic test is usually represented by sensitivity (Se) and specificity (Sp). Sensitivity is also referred to as the true positive fraction, defined as the probability of testing positive given the person is diseased. Specificity is also known as the true negative fraction, defined as the probability of testing negative given the person is not diseased (Zhou, Obuchowski, and McClish 2002; Pepe 2003). Disease status is usually measured by a reference test, which may also be prone to measurement error. In this case, a “gold standard” is not available. There is a considerable literature discussing the challenges and approaches to assess the performance of diagnostic tests from a single population in the absence of a “gold standard” (Gart and Buck 1966; Joseph, Gyorkos, and Coupal 1995; Andersen 1997; Johnson, Gastwirth, and Pearson 2001). Even under the assumption that two tests are conditionally independent given disease status, estimating five parameters (i.e., prevalence, two sensitivities, and two specificities) from three unconstrained cells in a two by two table induces nonidentifiability. In this context, even Bayesian approaches, which can incorporate prior knowledge on model parameters, do not generally converge to the true values as sample size increases (Johnson, Gastwirth, and Pearson 2001). To overcome the identifiability problem, sampling from a second population with a different prevalence was suggested (Hui and Walter 1980). Assuming that the tests have the same accuracy in both populations, there are six unconstrained cells, and sufficient degrees of freedom to estimate the six parameters (two prevalences, two sensitivities, and two specificities).

The growth of evidence-based medicine has led to an increase in attention to meta-analytic studies of diagnostic test accuracy (Egger, Smith, and Altman 2001). When a “gold standard” is available, random effects models including the hierarchical summary receiver operating characteristic model (Rutter and Gatsonis 2001) and the bivariate random effects meta-analysis on sensitivities and specificities (van Houwelingen, Arends, and Stijnen 2002;Reitsma et al. 2005; Chu and Cole 2006), which are very closely related and sometimes identical (Harbord, Deeks, Egger, Whiting, and Sterne 2007), have been recommended to take into account the potential heterogeneity between studies (Zwinderman and Bossuyt 2008).

The literature on meta-analytic studies of diagnostic test accuracy when a gold standard is not available is very sparse. In a recent meta-analysis of 17 studies to evaluate the accuracy of microsatellite instability testing (MSI) in predicting Lynch syndrome, the most common familial colorectal cancer syndrome, a Bayesian approach was proposed to handle missing data resulting from partial testing (Chen, Watson, and Parmigiani 2005). However, the meta-analysis assumed that the sensitivity and specificity of both tests do not differ from study to study. Furthermore, after categorizing the studies into a registry-based recruitment group and a family-based recruitment group (based on whether subjects were recruited from population-based colorectal cancer registries or from individuals with a family or personal history of colon, rectum, or endometrial cancers) the prevalence is assumed homogeneous within each group. However, because of differences in study design, study population, and laboratory techniques, between-study heterogeneity is intrinsic in many meta-analyses (Egger et al. 2001).

To our knowledge, when a gold standard is not available, meta-analysis using random effects models has not been previously described in the literature. In this article, we investigate such models in the presence of between-study heterogeneity in test sensitivities, specificities and/or the prevalence of disease by reanalyzing existing meta-data on the diagnosis of Lynch syndrome and through simulations. This article is organized as follows. In Section 2, we introduce the study background and review the meta-data. In Section 3, we present our modeling approach and explain the assumptions and choices that were made. In Section 4, we report the results of the case study, including three sensitivity analyses: (1) on the choice of prior distributions; (2) on the handling of a suspected outlier, and (3) on the conditional independence assumption. Section 5 includes a comprehensive simulation study to illustrate the performance of our approach under a variety of conditions. Finally, we discuss our findings and implications for future analyses in Section 6.

2. STUDY BACKGROUND

2.1 Lynch Syndrome

The DNA mismatch repair (MMR) system consists of a group of genes that are in charge of repairing the mismatches in the genome that occur during cell duplication. When a person inherits a pathogenic (i.e., disease-causing) mutation in one of these genes, the impaired mismatch repair mechanism gives rise to Lynch syndrome. Lynch syndrome, also known as Hereditary Nonpolyposis Colorectal Cancer, is the most common familial colorectal cancer syndrome. Lynch syndrome individuals have an up to 80% lifetime risk of cancer of the colon or rectum, as well as an elevated risk of cancer at the stomach, small bowel, endometrium, and a number of other sites compared to the general population. It is estimated that 600,000 individuals in the United States have Lynch syndrome but may not know it. It is of great public health importance to accurately diagnose Lynch syndrome for cancer prevention and early detection (Chen et al. 2006).

Diagnosing Lynch syndrome is equivalent to mutation finding in the MMR genes. Therefore, mutation analysis of the MMR genes is considered the reference test for Lynch syndrome. Finding mutations involves obtaining blood samples and performing laboratory tests on blood DNA. Available commercial mutation analysis currently costs a hefty $2,000-$3,000 per individual, which precludes it use in widespread screening. To increase cost effectiveness, a relatively inexpensive test ($200-$300 per individual) was proposed as a prescreening test (Thibodeau, Bren, and Schaid 1993). This test aims at detecting a tumor phenotype, called “microsatellite instability” (MSI), which exists in most tumors that arise from inherited MMR mutations. MSI testing is performed on DNA extracted from tumor tissues. The MSI test is now routinely used as a part of international Lynch syndrome diagnostic guidelines (Umar et al. 2004); it is therefore important to accurately evaluate its sensitivity and specificity to support informed clinical diagnosis.

2.2 Overview of the Meta-Studies

A number of research groups have attempted to evaluate accuracy of the MSI test by comparing it to the mutation analysis results in subjects with tumors. In the meta-analysis by Chen et al. (2005), 17 studies were identified from a systematic review of literature on the evaluation of the accuracy of the MSI test in diagnosing Lynch syndrome. Studies either recruited subjects from population-based colorectal cancer registries or selected individuals with a family or personal history of colon, rectum, or endometrial cancers. The former tend to have a lower chance of having Lynch syndrome, because they are often the only case of colorectal cancer in the family. Tumor tissue was collected for MSI testing, and blood samples were obtained for mutation analysis. Most studies tested subjects for MSI and conducted subsequent mutation analysis on all or a subset of subjects. More details regarding the studies can be found in Chen et al. (2005). See Table 1 for the list of studies.

Table 1.

A list of the studies included in the meta-analysis

Study ID	Family Recruitment*	Complete data				Missing data
		ni11	ni10	ni01	ni00	ni1m	ni0m	nim1	nim0
1	Y	16	1	2	20	0	0	0	0
2	Y	8	8	0	9	0	0	0	0
3	Y	8	15	0	0	12	43	0	0
4	Y	5	4	1	15	0	0	0	0
4	N	0	5	0	38	0	0	0	0
5	N	0	0	0	0	18	130	0	0
6	Y	7	7	0	2	0	0	0	0
6	N	0	0	0	7	0	0	0	0
7	Y	13	22	2	10	0	0	0	0
8	Y	16	6	1	36	0	0	0	0
9	N	10	53	0	0	0	446	0	0
10	N	0	0	0	0	28	308	0	0
11	Y	0	0	0	0	0	0	89	75
12	N	0	0	0	0	22	159	0	0
13	Y	0	1	4	22	0	0	0	0
14	N	18	48	0	0	0	469	0	0
15	Y	21	11	0	0	0	63	0	0
16	Y	14	14	0	20	0	0	0	0
17	Y	92	88	0	0	0	188	0	0

NOTE: MSI = microsatellite instability testing, MUT = mutation analysis testing. The (n_i11, n_i10, n_i01, n_i00, n_i1m, n_i0m, n_im0) correspond to the number of subjects with MSI = 1 and MUT = 1, MSI = 1 and MUT = 0, MSI = 0 and MUT = 1, MSI = 0 and MUT = 0, MSI = 1 and MUT = missing, MSI = 0 and MUT = missing, MSI = missing and MUT = 1, and MSI = missing and MUT = 0, respectively.

^*Recruitment can be family-based (high risk) or registry-based (low risk).

After examining the studies in detail, several challenges emerge. (1) The absence of a gold standard: the reference test, mutation analysis, is not perfect. The main reason is that most mutation analysis techniques fail to detect large genomic deletions and rearrangements, which constitute a significant fraction of all MMR mutations (Yan et al. 2000). (2) Potential heterogeneity: studies differ in their subject recruitment methods and in the laboratory techniques or quality. Such between-study heterogeneity is likely to affect parameter estimates. Not accounting for it may result in bias in relevant point estimates or underestimation of uncertainty or both. (3) Missing data: because of the perceived high negative predictive value of MSI testing, many studies did not perform subsequent mutation analysis once the subjects were tested MSI negative. Other patterns of missing data also exist (see Section 3.1). In this article, we introduce an approach to address these challenges that commonly arise in meta-analyses of diagnostic tests that lack a gold standard.

3. STATISTICAL METHODS

We present an analytic approach to estimating the accuracy of MSI testing and mutation analysis in a meta-analytic setting. Here we measure the accuracy of a test by two quantities: sensitivity, denoted as Se = Pr (test positive | true mutation), and specificity, denoted as Sp = Pr (test negative | no mutation). According to convention, we focus on dichotomized test results as the outcome of interest, as follows. For the MSI test, MSI = 1 denotes a positive result (i.e., a high level of microsatellite instability), and MSI = 0 for a negative result (i.e., low instability or stable) (Boland et al. 1998). For mutation analysis, MUT = 1 denotes finding a pathogenic mutation, and MUT = 0 for failure to find any.

For study i (i = 1, 2, ..., I), let P_ijk = Pr (MSI = j, MUT = k) be the joint probability of test results and n_ijk be the corresponding observed count, j, k = 0, 1. Let π_i be the study-specific disease prevalence, and let (Se_iA, Se_iB, Sp_iA, Sp_iB) be the corresponding sensitivities and specificities for MSI and MUT. Under the assumption that the two tests are independent conditional on the true disease status, study-specific prevalences, sensitivities, and specificities, we have the following relationship:

$$\begin{array}{c}\hfill P_{i11}={\pi }_{i}S{e}_{iA}S{e}_{iB}+(1-{\pi }_i)(1-S{p}_{iA})(1-S{p}_{iB}),\hfill \\ \hfill P_{i10}={\pi }_{i}S{e}_{iA}(1-S{e}_{iB})+(1-{\pi }_i)(1-S{p}_{iA})S{p}_{iB},\hfill \\ \hfill P_{i01}={\pi }_i(1-S{e}_{iA})S{e}_{iB}+(1-{\pi }_i)S{p}_{iA}(1-S{p}_{iB}),\hfill \\ \hfill P_{i00}={\pi }_i(1-S{e}_{iA})(1-S{e}_{iB})+(1-{\pi }_i)S{p}_{iA}S{p}_{iB}.\hfill \end{array}$$ (1)

In this context, the conditional independence assumption is arguably likely to be valid. Because all pathogenic mutations disrupt the MMR mechanism that leads to MSI tumors, those that are likely to be missed by MUT (i.e., large genomic deletions and rearrangements) do not differ from others in their ability to generate MSI tumors. In other words, biologically there do not seem to be subjects who are more likely to be missed (or picked up) by both tests (Rodriguez-Bigas et al. 1997). However, we shall relax this assumption and discuss a method to allow conditional dependence in Section 3.4.

3.1 Missing Data and the Likelihood

Several studies had missing data as a result of partial testing. The most common scenario is that because of the perceived high negative predictive value of MSI testing, studies did not perform mutation analysis once the subjects were tested MSI negative. Partial testing can be grouped into the following patterns: (A) MSI measured, MUT missing; (B) MSI missing, MUT measured. We denote the probabilities of study i to fall in categories A and B by ω_iA and ω_iB. Table 2 presents a typical data structure and notation for a study with partial testing.

Table 2.

Typical data displays for study i (i = 1, ..., I) with missing data

MSI	MUT
	Positive (+)	Negative (-)	Missing
Positive (+)	ni11(1-ωiA-ωiB)Pi11	ni10(1-ωiA-ωiB)Pi10	ni1mωiA(Pi11+Pi10)
Negative (-)	ni01(1-ωiA-ωiB)Pi01	ni00(1-ωiA-ωiB)Pi00	ni0mωiA(Pi01+Pi00)
Missing	nim1ωiB(Pi11+Pi01)	nim0ωiB(Pi10+Pi00)	—

NOTE: In each cell, the first line shows the observed count, the second line the corresponding probability. MSI = microsatellite instability testing, MUT = mutation analysis testing.

Of the 17 studies with a total of 2,750 subjects, 9 studies with a total of 2,050 subjects have missing data on either MUT or MSI tests. Among them, three studies had MUT completely missing and one study had MSI completely missing (a total of 829 subjects). They can be considered missing completely at random (MCAR). Five studies had missing MUT on all subjects with MSI = 0 for a total of 1,209 subjects, and can be considered missing at random (MAR). Only one study (i.e., Study 3) had MUT missing on 12 of 35 subjects with MSI = 1 due to unavailability of blood samples. Assuming that blood sample availability is independent of mutation analysis result conditioning on MSI result, then the missing mechanism for those 12 subjects can also be regarded as MAR. Therefore, we focus on methods under the MAR assumption for the selection process (Rubin 1976; Little and Rubin 2002).

Under the MAR assumption, the likelihood function can be factored into L(θ_i, ϑ_i | data) = L (θ_i | data) × L (ϑ_i | data) where θ_i, = (π_i, Se_iA, Se_iB, Sp_iA, Sp_iB) and ϑ_i = (ω_iA ω_iB). Assuming independence among subjects conditional on θ_i, the log-likelihood for θ = (θ₁, θ₂, ... , θ₁) is the summation of the contribution from each study, that is

$$\begin{array}{cc}\hfill \mathrm{Log}L(\theta \mid \text{data})=& \sum _i\{n_{i11}\log \left(P_{i11}\right)+n_{i10}\log \left(P_{i10}\right)\hfill \\ \hfill & +n_{i01}\log \left(P_{i01}\right)+n_{i00}\log \left(P_{i00}\right)\hfill \\ \hfill & +n_{i1m}\log (P_{i11}+P_{i10})+n_{i0m}\log (P_{i01}+P_{i00})\hfill \\ \hfill & +n_{im1}\log (P_{i11}+P_{i01})+n_{im0}\log (P_{i10}+P_{i00})\},\hfill \end{array}$$ (2)

where the relations among the components of θ_i and P_ijk are summarized in (1).

3.2 Accounting for Heterogeneity Through Random Effects Models

Between-study heterogeneity commonly exists in a meta-analysis because studies usually differ in their subject recruitment methods and laboratory techniques as well as arguably in overall study quality, as reflected in the study protocol and adherence to the protocol. Thus, measurements within a study tend to be correlated beyond what would be anticipated for measurements between studies. Not adequately accounting for this heterogeneity when it is present may result in biased estimation or underestimation or both of uncertainty (Egger et al. 2001; Molenberghs and Verbeke 2005). To take into account the potential between-study heterogeneity of the prevalence, sensitivity and specificity, we consider a random effects model. In line with Section 2, we introduce a covariate X_ij = 1 if recruitment is family-based and X_ij = 0 if recruitment is registry-based. The model can then be specified as follows:

$$\begin{array}{cc}\hfill \mathrm{logit}({\pi }_i\mid {\epsilon }_i)=& {\eta }_0+{\eta }_1{X}_{ij}+{\epsilon }_i,\hfill \\ \hfill \mathrm{logit}(S{e}_{iA}\mid {\mu }_{iA})=& {\alpha }_A+{\mu }_{iA},\hfill \\ \hfill \mathrm{logit}(S{e}_{iB}\mid {\mu }_{iB})=& {\alpha }_B+{\mu }_{iB},\hfill \\ \hfill \mathrm{logit}(S{p}_{iA}\mid {\nu }_{iA})=& {\beta }_A+{\nu }_{iA},\hfill \\ \hfill \mathrm{logit}(S{p}_{iB}\mid {\nu }_{iB})=& {\beta }_B+{\nu }_{iB},\hfill \\ \hfill {({\epsilon }_i,{\mu }_{iA},{\mu }_{iB},{\nu }_{iA},{\nu }_{iB})}^{\prime }\sim & N(0,\Sigma ),\hfill \end{array}$$ (3)

where logit(p) = log(p) - log(1 - p). In epidemiological studies, the prevalence of disease is usually assumed to be independent of sensitivity and specificity of a diagnostic test, in other words, a study with higher prevalence does not imply higher (or lower) accuracy in testing (Szklo and Nieto 2004). Under the assumption that the prevalence of Lynch syndrome is independent of the test accuracy of MUT and MSI, the variance-covariance matrix Σ in Equation (3) can be specified as

$$\Sigma =\left(\begin{array}{ccccc}\hfill {\sigma }_{\epsilon }^2\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ \hfill \hfill & \hfill {\sigma }_{{\mu }_A}^2\hfill & \hfill {\rho }_{{\mu }_A{\nu }_A}{\sigma }_{{\mu }_A}{\sigma }_{{\nu }_A}\hfill & \hfill {\rho }_{{\mu }_A{\mu }_B}{\sigma }_{{\mu }_A}{\sigma }_{{\mu }_B}\hfill & \hfill {\rho }_{{\mu }_A{\nu }_B}{\sigma }_{{\mu }_A}{\sigma }_{{\nu }_B}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\sigma }_{{\nu }_A}^2\hfill & \hfill {\rho }_{{\nu }_A{\mu }_B}{\sigma }_{{\nu }_A}{\sigma }_{{\mu }_B}\hfill & \hfill {\rho }_{{\nu }_A{\nu }_B}{\sigma }_{{\nu }_A}{\sigma }_{{\nu }_B}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill {\sigma }_{{\mu }_B}^2\hfill & \hfill {\rho }_{{\mu }_B{\nu }_B}{\sigma }_{{\mu }_B}{\sigma }_{{\nu }_B}\hfill \\ \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill \hfill & \hfill {\sigma }_{{\nu }_B}^2\hfill \end{array}\right).$$ (4)

The parameters (ρ_μAνA, ρ_μAμB, ρ_μAνB, ρ_νAμB, ρ_νAνB, ρ_μBνB) capture the pairwise correlation among random effects. If prevalence is suspected to be associated with test accuracy in a specific meta-analysis, the corresponding correlations can be specified above instead of the zero entries. However, unless there are many studies of reasonable size with considerable variation, there is typically little information on the correlation parameters even in the presence of a gold standard (Harbord et al. 2007). Therefore, their estimation may be troublesome and a simple Σ is preferred. The diagonal elements of the matrix $({\sigma }_{{\mu }_A}^2,{\sigma }_{{\mu }_B}^2,{\sigma }_{{\nu }_A}^2,{\sigma }_{{\nu }_B}^2,{\sigma }_{\epsilon }^2)$ capture the extent of heterogeneity of the parameters of interest across studies. If there is statistical or scientific evidence of homogeneity, that is, $({\sigma }_{{\mu }_A}^2,{\sigma }_{{\mu }_B}^2,{\sigma }_{{\nu }_A}^2,{\sigma }_{{\nu }_B}^2,{\sigma }_{\epsilon }^2\approx 0)$, the corresponding study-specific random effect(s) can be dropped from the model.

3.3 Model Implementation

We adopted two approaches to make inference from the previous random effects model. The first is a nonlinear mixed effects model (NLMM) (Davidian and Giltinan 1995; Vonesh and Chinchilli 1997; Molenberghs and Verbeke 2005) fitted using SAS PROC NLMIXED; the second is a Bayesian hierarchical model (Carlin and Louis 2000; Gelman, Carlin, Stern, and Rubin 1995) fitted using WinBUGs (Spiegelhalter, Thomas, and Best 2002). Because these two approaches use different frameworks and different software, they can be considered complementary. In most instances, inferences obtained by Bayesian and frequentist methods agree when weak prior distributions are specified. However, the Bayesian framework is particularly attractive when suitable proper prior distributions can be constructed to incorporate known constraints and subject-matter knowledge on model parameters (Davidian and Giltinan 2003). Furthermore, the Bayesian framework provides for direct construction of 100(1 - α)% equal tail and highest probability density (HPD) credible intervals of general functions of the estimated parameters without having to rely on asymptotic approximations.

To avoid over-fitting the data with an excess of random effects, we used a forward selection procedure based on information criteria. Specifically, Akaike’s information criterion (AIC) and the Bayesian information criterion (BIC) were used as the guideline (Burnham and Anderson 1998) for NLMM, and the deviance information criterion (DIC) was used for the Bayesian hierarchical model (Spiegelhalter, Thomas, Carlin, and van der Linde 2002). At each forward step, we added a random-effect component that provided the largest improvement based on the previous model selection criteria.

3.3.1 Nonlinear Mixed Effects Model (NLMM)

The nonlinear mixed effects model was fitted using PROC NLMIXED in SAS version 9.1 (SAS Institute Inc., Cary, NC). PROC NLMIXED maximizes an adaptive Gaussian quadrature approximation to the likelihood integrated over the random effects (Pinheiro and Bates 1995) using dual quasi-Newton algorithm optimization techniques, and then computes empirical Bayes estimates of the random effects. We used the PROC NLMIXED built-in delta method to compute the population estimates of the back-transformed parameters of interest and their confidence intervals (CIs) based on a normal approximation. In the presence of random effects, the back-transformed estimates represent the population median estimates. To obtain the population means, numerical integration over the estimated distributions of random effects can be performed (Halloran, Preziosi, and Chu 2003). Furthermore, the NLMM implemented in SAS PROC NLMIXED enables us to use the estimated model for constructing predictions of arbitrary functions using empirical Bayes estimates of the random effects. This often produces more concentrated predictions than a fully Bayesian procedure because NLMM does not fully take into account the uncertainty associated with the estimation, especially for the random effects. In this situation, the full Bayesian approach is expected to provide more appropriate assessment of uncertainty.

3.3.2 Bayesian Hierarchical Model (BHM) and the Choice of Priors

In the Bayesian hierarchical model, computation was done using Markov chain Monte Carlo (MCMC) (Gelfand and Smith 1990) in WinBUGS (Spiegelhalter, Thomas, and Best 2002). Burn-in consisted of 100,000 iterations; 400,000 subsequent iterations were used for posterior summaries. Convergence of Markov chains was assessed using the Gelman and Rubin convergence statistic (Gelman and Rubin 1992; Brooks and Gelman 1998). We selected proper but diffuse prior distributions for the hyper-parameters, because noninformative prior distributions can lead to inaccurate posterior estimates (Natarajan and McCulloch 1998). The hyper-priors for the precision parameters were assumed to be as follows: (1) ${\sigma }_{\epsilon }^{-2}\text{Gamma}(1,1)$, which corresponds to a 95% interval of (0.27, 39.50) for the variance parameter ${\sigma }_{\epsilon }^2$ allowing large heterogeneity for the prevalence; (2) $({\sigma }_{{\mu }_A}^{-2},{\sigma }_{{\mu }_B}^{-2},{\sigma }_{{\nu }_A}^{-2},{\sigma }_{{\nu }_B}^{-2})\sim \text{Gamma}(2,2)$, which corresponds to a 95% interval of (0.36, 8.26) for the variance parameters, $({\sigma }_{{\mu }_A}^2,{\sigma }_{{\mu }_B}^2,{\sigma }_{{\nu }_A}^2,{\sigma }_{{\nu }_B}^2)$, providing moderate heterogeneity for the latent sensitivities and specificities. Vague priors of N(0, 2²) were assumed for the fixed effects (η₀, α_A, α_B, β_A, β_B), which correspond to a 95% interval for the log-odds ranging from 0.02 to 50 (Chu, Wang, Cole, and Greenland 2006). A vague prior of N(0, 2²) was used for η₁ on the log scale to ensure the constraint that the prevalence of the family-history recruitment group is greater than that in the registry-based recruitment group for any study i.

3.4 The Conditional Independence Assumption

It is well known that if the conditional independence assumption is falsely assumed, parameter estimates can be biased (Vacek 1985; Torrance-Rynard and Walter 1997; Dendukuri and Joseph 2001). When the possibility of conditional dependence cannot be completely ruled out, as a sensitivity analysis to the conditional independence assumption, we extended the model in Equation (1) to allow dependence. Specifically, we incorporated the residual dependence of the two tests given the latent disease status and study-specific random effects by assuming homogenous residual dependence across all studies. Let ρ₁ and ρ₀ denote the correlation of the two tests when the true disease status is positive and negative, respectively, Equation (1) becomes (Vacek 1985; Shen, Wu, and Zelen 2001; Dendukuri and Joseph 2001),

$$\begin{array}{c}\hfill P_{i11}={\pi }_i(S{e}_{iA}S{e}_{iB}+{\delta }_{1i})+(1-{\pi }_i)\left[(1-S{p}_{iA})(1-S{p}_{iB})+{\delta }_{0i}\right],\hfill \\ \hfill P_{i10}={\pi }_i\left[S{e}_{iA}(1-S{e}_{iB})-{\delta }_{1i}\right]+(1-{\pi }_i)\left[(1-S{p}_{iA})S{p}_{iB}-{\delta }_{0i}\right],\hfill \\ \hfill P_{i01}={\pi }_i\left[(1-S{e}_{iA})S{e}_{iB}-{\delta }_{1i}\right]+(1-{\pi }_i)\left[S{p}_{iA}(1-S{p}_{iB})-{\delta }_{0i}\right],\hfill \\ \hfill P_{i00}={\pi }_i\left[(1-S{e}_{iA})(1-S{e}_{iB})+{\delta }_{1i}\right]+(1-{\pi }_i)[S{p}_{iA}S{p}_{iB}+{\delta }_{0i}],\hfill \end{array}$$ (5)

where ${\delta }_{1i}={\rho }_1\sqrt{S{e}_{iA}S{e}_{iB}(1-S{e}_{iA})(1-S{e}_{iB})}$ and ${\delta }_{0i}={\rho }_0\sqrt{S{p}_{iA}S{p}_{iB}(1-S{p}_{iA})(1-S{p}_{iB})}$ are the covariances between two tests among the diseased and nondiseased subjects in study i, respectively. The feasible range of correlations is determined by the sensitivities among diseased subjects and specificities among nondiseased subjects in each study. Specifically, the correlation coefficients ρ₁ and ρ₀ satisfy

$$\begin{array}{c}\hfill \underset{i}{\max }\left\{-\sqrt{\frac{S{e}_{iA}S{e}_{iB}}{(1-S{e}_{iA})(1-S{e}_{iB})}},-\sqrt{\frac{(1-S{e}_{iA})(1-S{e}^{iB})}{S{e}_{iA}S{e}_{iB}}}\right\}\le {\rho }_1\hfill \\ \hfill \le \underset{i}{\min }\left\{\sqrt{\frac{S{e}_{iA}(1-S{e}_{iB})}{(1-S{e}_{iA})S{e}_{iB}}},\sqrt{\frac{(1-S{e}_{iA})S{e}_{iB}}{S{e}_{iA}(1-S{e}_{iB})}}\right\},\text{and}\hfill \\ \hfill \underset{i}{\max }\left\{-\sqrt{\frac{S{p}_{iA}S{p}_{iB}}{(1-S{p}_{iA})(1-S{p}_{iB})}},-\sqrt{\frac{(1-S{p}_{iA})(1-S{p}_{iB})}{S{p}_{iA}S{p}_{iB}}}\right\}\le {\rho }_0\hfill \\ \hfill \le \underset{i}{\min }\left\{\sqrt{\frac{S{p}_{iA}(1-S{p}_{iB})}{(1-S{p}_{iA})S{p}_{iB}}},\sqrt{\frac{(1-S{p}_{iA})S{p}_{iB}}{S{p}_{iA}(1-S{p}_{iB})}}\right\}.\hfill \end{array}$$

Although negative associations are possible, it seems more plausible that ρ_i ≥ 0 (i = 0, 1), which corresponds to positive dependence conditional on the latent disease status and study-specific random effects. If homogenous conditional dependence between studies looks suspicious, methods allowing more complex dependent errors need to be considered, for example, by considering study-specific correlation coefficients ρ_1i and ρ_0i in Equation (5).

Furthermore, we propose a simple graphical method, the Kappa agreement plot, to quantitatively validate the conditional dependence assumption for each study based on the final model. This plot is obtained by plotting the model-based marginal agreement between the two tests for study i measured by the Kappa statistics (κ_i) with 95% confidence (or credible) intervals, which corrects the agreement that may occur by chance alone, against the observed marginal agreement between the two tests for study i. The model-based Kappa statistics for study i can be computed by

$${\kappa }_i=\frac{P_{i11}+P_{i00}-(P_{i11}+P_{i10})(P_{i11}+P_{i01})-(P_{i00}+P_{i10})(P_{i00}+P_{i01})}{1-(P_{i11}+P_{i10})(P_{i11}+P_{i01})-(P_{i00}+P_{i10})(P_{i00}+P_{i01})}.$$

If the model based 95% confidence (or credible) intervals include the observed Kappa statistics at close to the nominal rate, then there is not enough evidence to reject the conditional independence assumption.

4. CASE STUDY

We searched for the best fitting model, starting with the model that assumes no random effects (referred to as Model I), which was presented in Chen et al. (2005). Based on the forward-selection procedure in Section 3.3, Table 3 presents the goodness of fit statistics including the -2 log (likelihood) statistic AIC, and BIC for the nonlinear random effects model, and DIC for the Bayesian hierarchical model.

Table 3.

Selection of random effects using a forward selection procedure

Random effects models	NLMM using NLMIXED			BHM using WinBUGS
	-2logL*	AIC*	BIC*	DIC*	pD
I	91.3	103.3	108.3	104.2	5.6
IIa (εi)	44.5	58.5	64.4	34.8	17.7
IIb (μiA)	67.9	81.9	87.7	67.0	14.5
IIc (νiA)	81.7	95.7	101.5	119.9	10.8
IId (μiB)	64.0	78.0	83.8	65.0	14.6
IIe (νiB)	66.0	80.0	85.8	68.4	8.5
IIIa (εi, μiA)	39.8	55.8	62.4	23.1	15.9
IIIb (εi, νiA)	44.2	60.2	66.9	24.3	17.3
IIIc (εi, μiB)	36.8	52.8	59.4	19.5	24.8
IIId (εi, νiB)	42.6	58.6	65.3	27.3	17.8
IVa (εi, μiB, μiA)	30.6	48.6	56.1	9.9	24.0
IVb (εi, μiB, νiB)	34.9	52.9	60.4	16.1	21.2
IVc (εi, μiB, νiA)	36.5	54.5	62.0	14.8	26.2
IVd (εi, μiB, μiA, ρμBνB)	30.9	50.9	59.2	14.2	24.2
IVe (εi, μiB, νiB, ρμBνB)	34.6	54.6	63.0	22.7	25.9
IVf (εi, μiB, νiA, ρμBνA)	36.7	56.7	65.0	43.9	27.8
Va (εi, μiB, μiA, νiA)	31.0	51.0	59.3	12.1	24.9
Vb (εi, μiB, μiA, νiB)	30.9	50.9	59.2	8.5	23.0

NOTE: A and B correspond to the microsatel-lite instability (MSI) and mutation analysis (MUT) testing, respectively. NLMM = nonlinear mixed effects model; BHM = Bayesian hierarchical model; AIC = Akaike’s information criterion; BIC = Bayesian information criterion; DIC = deviance information criterion; and ρ_D = the effective number of parameters. For the Bayesian analysis, priors for precision parameters of random effects are specified as ${\sigma }_{\epsilon }^{-2}\sim \text{Gamma}(1,1)$ and $({\sigma }_{{\mu }_A}^{-2},{\sigma }_{{\mu }_B}^{-2},{\sigma }_{{\nu }_A}^{-2},{\sigma }_{{\nu }_B}^{-2})\sim \text{Gamma}(2,2)$ · The random effects (ε_i, μ_iA, ν_iA, μ_iB, ν_iB) correspond to study-specific prevalence, MSI sensitivity, MSI specificity, MUT sensitivity, and MUT specificity, respectively.

^*Thirty-three hundred points have been subtracted from -2logL, AIC, BIC, and DIC for presentation. For example, the actual AIC for model I is 3300 + 103.3 = 3,403.3. The bolded cells represent the selected models based on the forward selection procedure.

In the first step, adding any random-effect improved the goodness of fit under all criteria, with the exception of Model IIc using DIC. The largest improvement was achieved by allowing for study-specific prevalence ε_i, referred to as Model IIa. For example, the DIC decreased by 69.4 points compared with Model I. This revealed an important characteristic of this meta-analysis, that is, the studies varied considerably in their recruitment criteria, resulting in different mutation prevalences across studies. Based on the Bayesian hierarchical Model IIa, the posterior mean prevalence ranged from 0.125 to 0.860 for the twelve studies in the family-recruitment group, and from 0.016 to 0.098 for the seven studies in the registry-recruitment group.

In the second step, the largest improvement was seen by adding a random-effect for the mutation analysis sensitivity μ_iB (Model IIIc). The improvement was modest compared with adding the initial random-effect, but still notable (e.g., the DIC decreased by 15.3 points compared with Model IIa). This is plausible because studies were conducted in different laboratories using a variety of mutation analysis techniques. As a result, the mutation analysis sensitivities ranged from 0.424 to 0.871 for the 17 studies based on the Bayesian hierarchical Model IIIc.

The last forward step that produced meaningful improvement included random effects for microsatellite instability testing sensitivity μ_iA (Model IVa). The DIC decreased by 9.6 points compared with Model IIIc. The final model included the random-effects on (1) prevalence ε_i; (2) mutation analysis sensitivity μ_iB; and (3) microsatellite instability testing sensitivity μ_iA. In this case study, model selection proceeded identically under the nonlinear mixed effects model and the Bayesian hierarchical model. Table 3 shows that no improvements were obtained by including additional random effects.

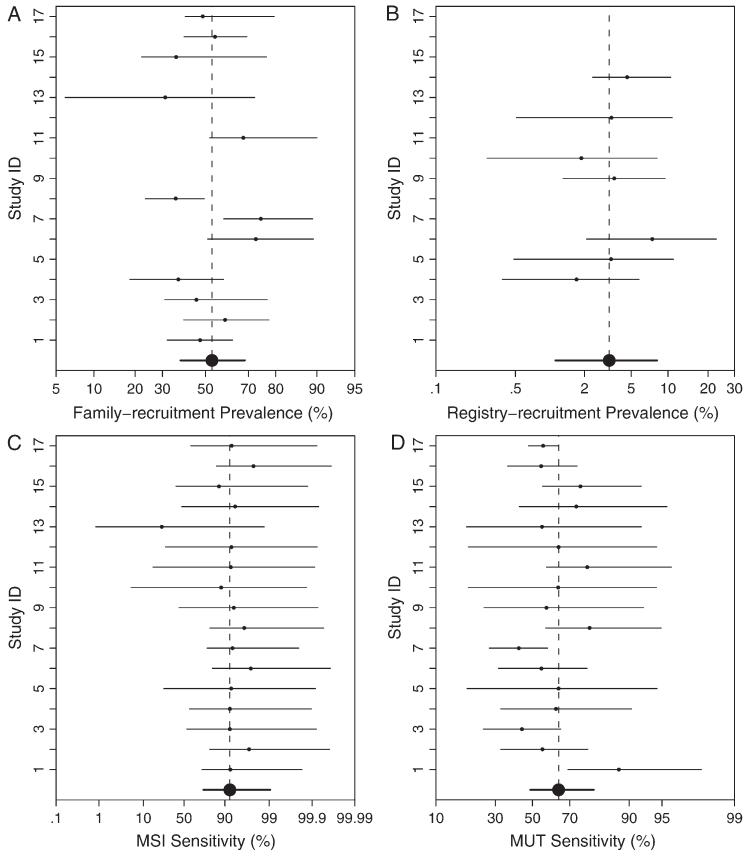
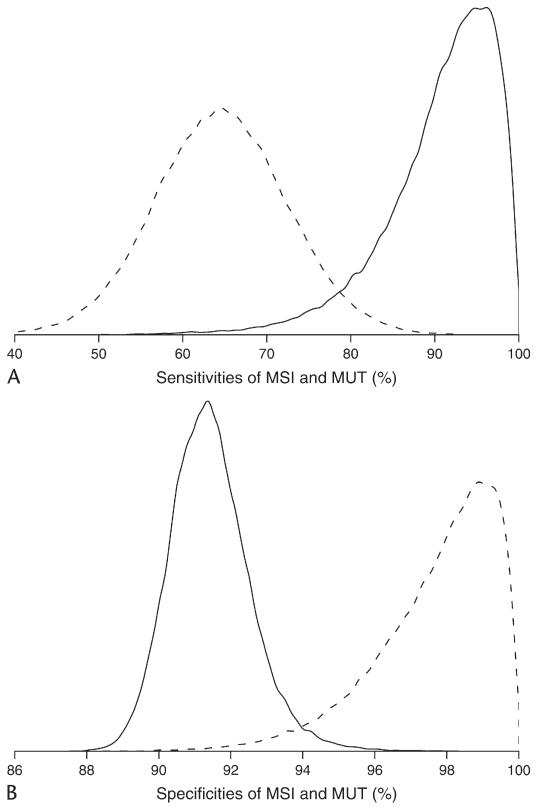
Estimated fixed effects (MSI sensitivity, MSI specificity, MUT sensitivity, MUT specificity, prevalence in the family-recruitment group, and prevalence in the registry-recruitment group) from Model I, Model IIa, Model IIIc, and Model IVa are presented in Table 4. Estimates were highly concordant between the two approaches, except for some difference in the estimates of MSI sensitivity. We used the triple of percentiles, _2.550_97.5, as an effective way to display a parameter estimate (or posterior median) with its 95% confidence (or equal tail credible) interval, as suggested by Louis and Zeger (2008). Based on the final model IVa, the posterior estimate of MSI sensitivity from BHM was _0.740.92_0.99, whereas the estimate from NLMM was _0.920.97_1.00. The random effect of MSI sensitivity has a standard deviation of 2.53 by NLMM or 1.65 by BHM on the logit scale. The standard deviation is relatively large is because most study-specific sensitivity estimates were close to 0.9, whereas one study (i.e., study 13) had a much lower estimate of _0.010.23_0.99 (see Figure 2C). When study 13 is removed from the analysis (see Section 4.2), there is no longer enough evidence to support heterogeneous MSI sensitivity. Figure 1 presents the posterior kernel smoothed density of MSI sensitivity, MSI specificity, MUT sensitivity, and MUT specificity based on the final Bayesian hierarchical Model IVa, suggesting a skewed posterior density of MSI sensitivity, which helps explain the difference in MSI sensitivity estimates between the nonlinear mixed effect model and the Bayesian hierarchical model.

Table 4.

Summary of parameter estimates using the nonlinear random effects models and the Bayesian hierarchical models

Random effects models	Non-linear Random Effects Models* Using NLMIXED				Bayesian hierarchical models using WinBUGS
	I None	IIa εi	IIIc εi, μiB	IVa εi, μiB, μiA	I None	IIa εi	IIIc εi, μiB	IVa εi, μiB, μiA
MSI specificity	902920937	893912932	889909929	894914934	898917936	898916934	893912938	895914939
MSI sensitivity	735819904	8929781000	8809821000	9229681000	745842951	843934985	872957996	740922990
MUT specificity	100010001000	906953999	8989521000	9479861000	917980998	926968996	916958990	935981998
MUT sensitivity	564622679	536594653	508656805	495641786	565621678	537590645	531630726	488645801
Family-recruitment prevalence	491555618	318495673	302465629	442532622	460536610	354520694	328476641	380532685
Registry-recruitment prevalence	284765	01843	01739	82847	244266	92975	92772	113382
σε (prevalence)	—	44510341624	3549041454	311601890	—	67210601790	6059591626	4977981384
σμA (MSI sensitivity)	—	—	—	88025294177	—	—	—	73716493766
σνA (MSI specificity)	—	—	—	—	—	—	—	—
σμB (MUT sensitivity)	—	—	1117421375	1377561375	—	—	6019441650	5979321610
σνB (MUT specificity)	—	—	—	—	—	—	—	—

NOTE: The triple notation of _LP_U denotes the point estimate P with 95% confidence limits (L, U) for the nonlinear random effects models, or the posterior median P with 95% equal tailed credible limits (L, U) using Bayesian hierarchical models. The numbers have been multiplied by 1,000 for presentation.

^*95% confidence intervals based on normal approximation.

Figure 2.

Study-specific posterior means with 95% equal tail credible sets of the prevalence of family (A), and registry (B), recruitment groups, MSI (C), and MUT (D) sensitivities based on the Bayesian hierarchical model IVa. Large dots and bold lines are population averaged posterior estimates with their corresponding 95% credible intervals.

Figure 1.

Posterior distributions of MSI and MUT sensitivities (A), MSI and MUT specificities (B). It is based on the kernel smoothed density estimation of 400,000 Monte Carlo samples. Solid lines are for MSI, dashed lines are for MUT.

Although mutation analysis has been regarded as the reference test, with a median sensitivity of 64%, it does not offer the level of accuracy as a gold standard should. In fact, these tests missed one-third of all MMR mutations, a value that is consistent with the proportion of large genomic mutations that cannot be detected by conventional mutation analysis techniques.

4.1 Sensitivity Analysis to Prior Distributions for BHM

As a sensitivity analysis to the specification of prior distributions, we repeated our analyses using two additional sets of priors for the variance parameters of random effects that are more diffuse than the ones presented earlier. Although estimation of other parameters remains of interest, because of space limitations we focus here on MSI sensitivity and specificity estimates, because they are of primary scientific interest. Specifically, we have chosen Gamma(1, 1) and Gamma(0.5, 0.5) as the priors for the precision parameters $({\sigma }_{\epsilon }^{-2},{\sigma }_{{\mu }_A}^{-2},{\sigma }_{{\mu }_B}^{-2})$. When $({\sigma }_{\epsilon }^{-2},{\sigma }_{{\mu }_A}^{-2},{\sigma }_{{\mu }_B}^{-2})\sim \text{Gamma}(1,1)$, which corresponds to a 95% interval of (0.27, 39.50) for the variance parameters, the posterior estimate of MSI sensitivity was _0.710.93_0.99. When $({\sigma }_{\epsilon }^{-2},{\sigma }_{{\mu }_A}^{-2},{\sigma }_{{\mu }_B}^{-2})\sim \text{Gamma}(0.5,0.5)$, which corresponds to a 95% interval of (0.2, 1,018.3) for the variance parameters, the posterior estimate of MSI sensitivity was _0.680.93_0.99. Under both priors, the posterior estimate of MSI specificity was _0.890.91_0.94. In summary, for the priors considered, results are consistent.

4.2 Sensitivity Analysis to an “Outlier” Study

Bayesian posterior means with 95% equal tail credible sets of the study-specific effects from the final model are shown in Figure 2. The study-specific MSI sensitivity estimates were quite homogeneous, with study 13 being the only exception (see Figure 2C), which is consistent with the expert belief that MSI is a relatively standard and simple test and that measurement variability associated with it is low. On the other hand, the study-specific estimates of mutation prevalence are quite heterogeneous, highlighting differences in the study populations. The wide range of MUT sensitivity estimates suggests differences in the nature and quality of the laboratory work for mutation analysis. Closer examination of study 13 reveals that it is a study of missense mutations. A missense mutation only results in a single amino acid substitution, which may or may not be pathogenic. Such mutations are currently all treated as MUT = 1, whereas functionally some of them should be classified as MUT = 0. This led to a smaller than expected number of MSI = 1 subjects in study 13 and was reflected in the low study-specific MSI sensitivity.

To investigate sensitivity to a potential outlier, we excluded study 13 and reran our forward random-effects selection procedures. The algorithm identified Model IIa in the first step and IIIc in the second step using both NLMM and BHM. Under all model selection criteria, the forward selection algorithm did not proceed to select an additional random-effect on MSI sensitivity, as there was no longer enough evidence supporting such heterogeneity once study 13 is removed.

From the final Model IIIc using the NLMM, MSI sensitivity and specificity were estimated to be _0.870.93_0.99 and _0.890.91_0.93, respectively. The MUT sensitivity and specificity were respectively estimated to be _0.510.66_0.81 and _1.001.00_1.00. The standard deviations of random effects for prevalence σ_ε and MUT sensitivity σ_μB were estimated to be _0.220.60_0.98 and _0.130.74_1.35. When using the Bayesian hierarchical model, posterior estimates of MSI sensitivity and specificity were _0.870.94_0.99 and _0.890.91_0.94, respectively. The posterior estimates of MUT sensitivity and specificity were _0.500.65_0.81 and _0.940.98_1.00. The posterior estimates of the standard deviations of random effects for prevalence σ_ε and MUT sensitivity σ_μB are estimated to be _0.490.75_1.25 and _0.600.94_1.65, respectively.

In summary, the two approaches yielded similar estimates of model parameters. Moreover, none of the estimates changed notably from the original estimates when the “outlier” (i.e., study 13) was included in the analysis, especially when using BHM.

4.3 Sensitivity Analysis to the Conditional Independence Assumption

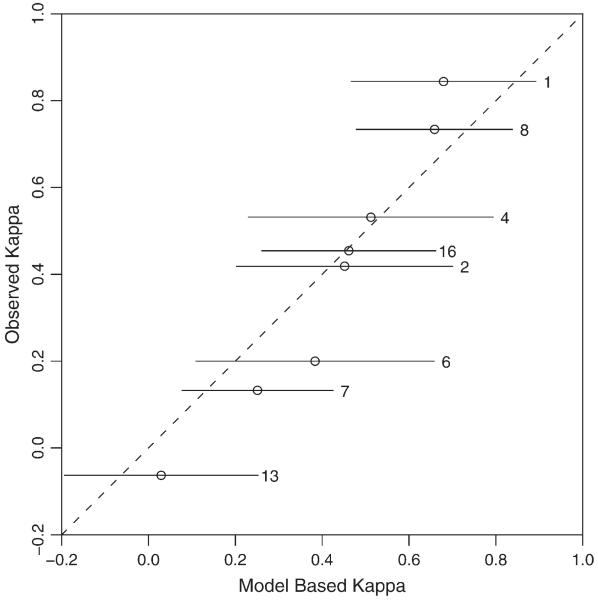
As a graphical check, Figure 3 presents the model-based versus observed Kappa statistics for those studies with complete data using NLMM. It suggests that the conditional independence assumption is likely to be valid here because all of the 95% CIs of model-based Kappa statistics contain the observed Kappa statistics. As expected, the model-based estimates are shrunk toward the mean.

Figure 3.

Model-based Kappa versus observed Kappa statistics for assessing the conditional dependence assumption.

In Section 3.4, we restricted the final model (IVa using NLMM) to homogeneous conditional dependence across studies as specified in Equation (5). Specifically, under ρ₁ = ρ₀ = ρ, which corresponds to equal conditional dependence for true positives and true negatives, the negative twice log-likelihood (-21ogL) was 3,330.0. It did not improve the goodness of fit over model IVa in Table 3 (i.e., -21ogL = 3,330.6) significantly (p-value = 0.44 based on likelihood ratio test). The estimated correlation coefficient ρˆ = _-0.340.012_0.37. When ρ₁ ≠ρ₀, -2logL is estimated to be 3,329.3 (p-value = 0.52), which did not improve the goodness of fit either. The estimated correlation coefficient ρˆ₁ for true positives was _-0.500.002_0.50, and the ρˆ₀ for true negatives was _-0.180.26_0.71. No further sensitivity analyses of more complex conditional dependence structures were pursued.

5. SIMULATION STUDIES

To evaluate the performance of our modeling approach and to study the impact of misspecification of random effects, we performed four sets of simulations. For ease of presentation and interpretation, we generated data with random effects only on disease prevalence or test sensitivities (ε_i, μ_iA, μ_iB) and fitted models with up to two random effects. Specifically, data were generated from the following four models: (1) no random effects; (2) random effect on prevalence (ε_i); (3) random effect on MSI sensitivity (μ_iA); and (4) random effects on prevalence and MSI sensitivity (ε_i, μ_iA). Simulations represent realistic scenarios that researchers are likely to encounter, such as those in the case study.

For each simulation, 20 meta-studies were generated, each with 7 studies having only a family-recruitment group, 7 studies having only a registry-recruitment group, and 6 studies having both a family-recruitment group and a registry-recruitment group. For each study, there were 80 observations in the family-recruitment group and 250 observations for each study in the registry-recruitment group, roughly matching the sample sizes in our case study. Each study in the registry-recruitment group was assigned a probability of 0.40 of missing MUT test results for those with MSI = 0, which corresponds to a common scenario in diagnostic testing when the reference test is expensive or invasive. In the absence of random effects, the prevalences of true mutation were set to be 50% for the family-recruitment group and 10% for the registry-recruitment group. The sensitivity and specificity were taken to be 70% and 98% for MUT, respectively, and were both taken to be 90% for MSI testing. In the presence of random effects, the variances of (ε_i, μ_iA) were set to be 0.5², which gives the prevalence a 95% interval of 27%-73% for the family-recruitment group and 4%-23% for the registry-recruitment group and the MSI sensitivity a 95% interval of 77%-96%.

For each generated dataset, we fitted seven models using both NLMIXED and BHM: (1) no random effect; (2) one random effect (on ε_i, μ_iA, or μ_iB); and (3) two random effects (on [ε_i, μ_iA], [ε_i, μ_iB], or [μ_iA, μ_iB]). Model selection was based on AIC and BIC for the nonlinear random effects model using SAS PROC NLMIXED and DIC for the Bayesian hierarchical model using WinBUGs.

Table 5 summarizes the Monte Carlo frequency of selecting each candidate model as the “best” model in each set of simulations. In summary, DIC has a probability of 0.55-0.70 to identify the true random effects model, whereas the performance of AIC and BIC is highly variable with a probability of 0.25-0.95. Closer examination of the results reveals that the Bayesian approach with DIC has a stronger tendency to select additional random effect(s) not included in the true model than does the nonlinear random effects approach (overall probability of 0.17 for DIC, 0.06 for AIC, and 0.03 for BIC, averaging over all four scenarios). Meanwhile, the average probability that the Bayesian approach misses a true random effect (0.17) was lower than that of the nonlinear random effects approach (0.30 based on AIC and 0.36 based on BIC). A possible explanation for this is that BHM fully accounts for the uncertainty in estimation and thus produces a more appropriate selection of random effects.

Table 5.

The empirical probability of selecting a candidate model as the final model using AIC, BIC, or DIC^* based on simulation studies with 2,000 replicates

True random effects model		Selected random effects model
		None	εi	μiA	μiB	εi, μiA	εi, μiB	μiA, μiB
None	AIC	885	30	41	42	1	1	1
	BIC	940	16	21	24	0	0	0
	DIC	707	21	188	58	7	3	18
εi	AIC	1	914	0	1	34	50	1
	BIC	2	961	0	1	16	21	0
	DIC	0	701	1	1	200	97	1
μiA	AIC	602	24	321	31	9	1	12
	BIC	711	14	247	19	4	0	5
	DIC	335	13	554	29	20	2	49
εi, μiA	AIC	0	632	0	0	324	44	1
	BIC	1	731	1	1	248	20	0
	DIC	0	330	1	0	605	64	1

NOTE: The bolded cells represent the probability of identifying the correct model. The numbers have been multiplied by 1,000 for presentation.

^*AIC = Akaike’s informationcriterion; BIC = Bayesian information criterion; DIC = deviance iinformation criterion.

The prevalence random effect (ε_i) was almost always identified, if present. Under-fitting was mainly a result of the failure to include the random effect in MSI sensitivity (μ_iA) (i.e., 95% interval = 77%-96%), which had a narrower range than that of the prevalence ε_i (i.e., 95% interval = 27%-73% for the family-recruitment group and 4%-23% for the registry-recruitment group) by simulation design due to the logit transformation. Overall, the probability of selecting completely incorrect random effects (i.e., including invalid random effects while failing to include true random effects) was very low under all criteria (0.03 for DIC, 0.03 for AIC, 0.01 for BIC, respectively).

Table 6 records the means, standard errors, 95% interval lengths, and coverage probabilities for the MSI sensitivity under each model. Although estimation of other parameters is also of interest, because of space limitations we present only MSI sensitivity. In general, the standard errors are larger when including more random effects. Over-fitting (including a random effect when there is none) or under-fitting (not including the random effect when it is present) can generate biased point estimates of MSI sensitivity. Moreover, over-fitting tends to produce larger standard errors, whereas under-fitting can provide biased standard error estimates in both directions. Specifically, if the true model contains no random effects, the 95% CI length can be 25% wider in the BHM or 14% wider in the NLMM when random effects are included. On the other hand, when the true model contains random effects on both prevalence (ε_i) and MSI sensitivity (μ_iA), the 95% CI length is 20% narrower by NLMM or 25% narrower by BHM when no random effects are included, and 25% wider by NLMM or 25% wider by BHM when we only include random effects for MSI sensitivity (μ_iA).

Table 6.

The estimation and coverage performance of each model on MSI sensitivity (true value = 0.90) based on simulation studies with 2,000 replicates

True models		Random effects models using NLMIXED							Bayesian hierarchical models using WinBUGS
		None	εi	μiA	μiB	εi, μiA	εi, μiB	μiA, μiB	None	εi	μiA	μiB	εi, μiA	εi, μiB	μiA, μiB
None	Mean	902	900	903	900	901	900	902	897	900	919	902	918	902	922
	95% CI length*	83	89	98	89	96	89	97	79	84	105	83	101	81	101
	95% CICP*	961	968	975	964	977	969	976	938	949	944	951	942	946	920
εi	Mean	902	900	897	896	902	900	890	897	900	902	897	916	902	896
	95% CI length*	85	86	123	92	96	87	129	80	81	126	86	103	79	130
	95% CICP*	961	966	972	956	977	968	956	941	958	981	946	950	945	977
μiA	Mean	893	891	900	891	898	891	899	888	892	911	894	911	895	915
	95% CI length*	85	91	111	91	111	91	111	81	86	112	85	108	83	108
	95% CICP*	864	879	949	873	942	876	950	829	879	959	890	951	875	948
εi, μiA	Mean	893	892	890	887	899	892	882	889	893	894	888	909	895	887
	95% CI length*	85	86	132	92	106	87	139	82	84	134	88	110	81	138
	95% CICP*	860	885	944	852	952	886	898	831	873	977	855	957	866	963

NOTE: The numbers have been multiplied by 1,000 for presentation. The bolded cells represent the correctly chosen model.

^*95% CICp = 95% confience interval coverage probability 95% CICP, and 95% CI length are based on logit-normal assumption for the random effects models using NLMIXED and equal tail credible intervals for the Bayesian hierarchical models using WinBUGS.

We note the following for the coverage probabilities: (1) under the correct model, or when over-fitting occurs, the coverage probabilities are all close to the nominal value of 0.95; (2) when under-fitting occurs, failure to include random effects in prevalence (ε_i) does not substantially affect the coverage probabilities for MSI sensitivity; but failure to include random effects on MSI sensitivity itself reduces coverage notably. In summary, there is a need to select appropriate random effects carefully to account for potential cross-study heterogeneity on the estimation of diagnostic accuracy measurements from a meta-analysis without a gold standard.

6 DISCUSSION

In this application of random effects models for meta-analysis of the accuracy of two diagnostic tests without a gold standard, we focused on methods that assume conditional independence between two tests given the true mutation status and the study-specific random effects. In the case study, this assumption is biologically plausible, because large genomic deletions and rearrangements do not differ from other mutations in their ability to generate tumors with microsatellite instability. Furthermore, the assumption seems reasonable based on the Kappa agreement plot and the homogenous conditional dependence models that we have considered in Section 3.4. However, if the homogenous conditional dependence looks suspicious, methods incorporating heterogeneous dependent errors across studies need to be considered, for example, by considering study-specific correlation coefficients ρ_1i and ρ_0i in Equation (5).

We demonstrate improved estimation of the sensitivity and specificity by taking into account heterogeneity across studies through study-specific random effects. All model selection criteria consistently indicated that allowing for appropriate random effects improves goodness of fit, and their inclusion did affect estimates of the sensitivity and specificity of MSI and MUT. In particular, estimated MSI sensitivity increased noticeably from the model without random effects. The medical literature suggests that all tumors except a small fraction from Lynch syndrome individuals exhibit positive MSI phenotype (see Vasen and Boland 2005). Therefore, a MSI sensitivity estimate of 0.93 based on NLMM or 0.94 based on BHM from the final model after deleting the “outlier” study might be more biologically plausible than the lower estimate (0.82 based on NLMM or 0.84 based on BHM) obtained from the model without random effects. Random effects models can be effective in identifying outlier studies, for example study 13.

Simulations show that our approach has a good chance of identifying the correct model, with the DIC being more likely to favor expanded models relative to AIC and BIC, which tend to penalize random effects. Our simulations identify a noticeable variance inflation from over-fitting and meaningful decrements in coverage when between-study heterogeneity is present but not included in a model. Therefore, when there is uncertainty about whether to include a random effect or when different statistical criteria give different recommendations, we recommend including the random effect to reduce the chance of omitting an important source of variability. However, variance inflation cautions against generically including all five random effects. From the design perspective, one potential way to improve the selection of competing models with multiple tests in a meta-analysis is to extend the methods recently proposed by Albert and Dodd (2008) for the meta-analysis setting when some study participants are verified by a gold standard.

The nonlinear random effects model as implemented by SAS PROC NLMIXED involves maximizing an approximation to the likelihood integrated over the multidimensional random effects. Particularly in the presence of missing data, convergence may be an issue. For example, about 0.1-0.5% simulations did not converge. Moreover, we were not able to fit all five random effects using PROC NLMIXED.

Finally, when dealing with multiple tests from a single population, several alternative models have been proposed to incorporate conditional dependence induced by characteristics other than latent disease status. The basic idea is to include a subject-specific random effect, with test results independent conditional on both this random effect and latent disease status. Examples include a Gaussian random effects model (Qu, Tan, and Kutner 1996; Qu and Hadgu 1998), and the extended finite mixture model (Albert, McShane, and Shih 2001). In a meta-analysis involving multiple tests, one may consider adding additional random effects at the subject level and nesting such an effect within the study level to account for the potential residual dependence after conditioning on the latent disease status and study-specific random effects.

We did not study this extension because it is known that when conditional dependence between imperfect measurements is misspecified in a single study, estimated sensitivity, specificity, and prevalence can be biased, and a large number of imperfect measurements are needed to distinguish among different models (Albert and Dodd 2004). Furthermore, it is computationally complex to include subject-specific random effects nested within study-specific random effects. SAS NLMIXED SAS version 9.1 cannot handle nested random effects and the MCMC setting may have convergence problems. Further research and development is needed to incorporate these effects.