Noninvasive Three-dimensional Cardiac Activation Imaging from Body Surface Potential Maps: A Computational and Experimental Study on a Rabbit Model

Abstract

Three-dimensional (3-D) cardiac activation imaging (3-DCAI) is a recently developed technique that aims at imaging the activation sequence throughout the 3-D volume of myocardium. 3-DCAI entails the modeling and estimation of the cardiac equivalent current density (ECD) distribution from which the local activation time within myocardium is determined as the time point with the peak amplitude of local ECD estimates. In this paper, we report, for the first time, an experimental study of the performance and applicability of 3-DCAI as judged by measured 3-D cardiac activation sequence using 3-D intra-cardiac mapping, in a group of 4 healthy rabbits during ventricular pacing. During the experiments, the body surface potentials and the intramural bipolar electrical recordings were simultaneously measured in a closed-chest condition to allow for a rigorous evaluation of the noninvasive 3-DCAI algorithm using the intra-cardiac mapping. The ventricular activation sequence non-invasively imaged from the body surface measurements by using 3-DCAI was generally in agreement with that obtained from the invasive intra-cardiac recordings. The overall difference between them, quantified as the root mean square (RMS) error, was 7.42±0.61 ms, and the normalized difference, quantified as the relative error (RE), was 0.24±0.03. The distance from the reconstructed site of initial activation to the actual pacing site, defined as the localization error (LE), was 5.47±1.57 mm. In addition, computer simulations were conducted to provide additional assessment of the performance of the 3-DCAI algorithm using a realistic-geometry rabbit heart-torso model. Averaged over 9 pacing sites, the RE and LE were 0.20±0.07 and 4.56±1.12 mm, respectively, for single-pacing, when 20 μV Gaussian white noise was added to the body surface potentials at 53 body surface locations. Averaged over 8 pairs of dual pacing, the RE was 0.25±0.06 for 20 μV additive noise. The present results obtained through both in vivo experimentation and computer simulation suggest that 3-DCAI can non-invasively capture important features of ventricular excitation (e.g. the activation origin and the activation sequence), and has the potential of becoming a useful imaging tool aiding cardiovascular research and clinical diagnosis and management of cardiac diseases.

1. Introduction

Noninvasive imaging of cardiac electrical activity is of importance and significance for better understanding the mechanisms of cardiac physiology and pathophysiology, and for guiding therapeutic treatments of cardiac disorders in clinical medicine. A number of efforts have been made to solve the inverse problem of electrocardiography (ECG) in order to estimate the equivalent cardiac sources from body surface potential maps (BSPMs). Such inverse approaches include moving dipole fitting [1], [2], epicardial potential imaging [3]-[5], and heart surface activation imaging [6]-[9].

Recently the ECG inverse problem has been extended to imaging the three-dimensional (3-D) cardiac electrical activity, including both computational studies [10]-[15], [17] and experimental studies [16]. In these studies, 3-D cardiac electrical activity is estimated with the aid of either a heart cellular automaton model [11]-[13], [16] or an imaging algorithm inverting an imaging equation [10], [14], [15], [17]. While the distributed current density source model was used to estimate 3-D cardiac electrical activity [10], the direct reconstruction of the 3-D current density distribution has been challenging. A cellular automaton heart model based inverse imaging approach has been used to localize the site of origin of activation [11], estimate the activation sequence [12], [16] and estimate the distribution of trans-membrane potentials (TMPs) [13].

Among the existing 3-D cardiac electrical imaging algorithms, Liu et al [17] recently reported a biophysical model based 3-DCAI algorithm in which the 3-D distributed equivalent current density (ECD) is first estimated and then the cardiac activation time is derived from the time course of current density estimate at each imaging location within the myocardium. While the computer simulation results are promising in a human heart-torso model [17], the performance of this algorithm in an experimental setting remains unclear.

The purpose of the present study was to rigorously and quantitatively evaluate the imaging performance of the biophysical model based 3-DCAI algorithm [17] using a 3-D intra-cardiac mapping procedure [16], [18], [19] in a rabbit model. Four healthy New Zealand white rabbits were studied during left ventricular (LV) and right ventricular (RV) pacing. Plunge-needle electrodes were placed in the ventricles, and the body surface potentials and intra-cardiac bipolar recordings were measured simultaneously in a closed-chest condition. The 3-DCAI imaging results were quantitatively compared with intra-cardiac mapping results and imaging performance was assessed.

2. Methods

A. Spatial Gradient of Trans-membrane Potential

The activation time of a myocardial cell is the time point at which the TMP rises almost instantaneously from the resting potential of −90 mV to a plateau potential typically around 0 mV for a normal or an abnormal cell. Regardless of the regional difference of the action potential amplitude, the activation time is classically characterized by the maximum temporal derivative of the TMP waveform. Although this temporal feature allows deriving the heart surface activation sequence from the non-invasively estimated heart surface TMP [8] or epicardial potentials [4], its applicability to the 3-D activation imaging has not been suggested or maybe not feasible due to some intrinsic technical challenges.

Other than the maximum temporal derivative of the TMP, the TMP spatial gradient provides an alternative and equally effective feature for deriving the activation time. Cardiac excitation propagates as a moving wavefront separating the depolarized and non-depolarized myocardium. For a given myocardial cell, the activation time can be thought of as the time point at which the excitation wavefront passes through the cell. Since a considerable difference of the TMP amplitude only exists across the excitation wavefront, a cell at its activation time is also characterized by the maximum TMP spatial gradient. This concept is mathematically expressed as Eq. (1).

$$\tau \left(\mathbf{r}\right)=\underset{t}{\text{arg max}}\mid \nabla {\varphi }_m(\mathbf{r},t)\mid$$ (1)

where ϕ_m (r,t) is the TMP at location r and time t.

Note that Eq. (1) also points to the biophysical principle of a well established intra-cardiac mapping technique based on intramural bipolar recordings. The electrical potential difference between two closely spaced electrodes (i.e. the bipolar potential) is approximately a directional component (along the intramural needle) of the TMP spatial gradient. Therefore, the time instant with the peak value of the absolute bipolar potential precisely corresponds to the activation time with the maximum TMP spatial gradient, as defined in Eq. (1).

B. Equivalent Current Density

For any myocardial location r and any time t, we define the equivalent current density ${\overrightarrow{\mathbf{j}}}_{eq}(\mathbf{r},t)$ to be proportional to the local TMP spatial gradient, as expressed by Eq. (2)

$${\overrightarrow{\mathbf{j}}}_{eq}(\mathbf{r},t)=-{\mathbf{G}}_i\left(\mathbf{r}\right)\nabla {\varphi }_m(\mathbf{r},t)$$ (2)

where G_i (r) is the intracellular effective conductivity tensor.

By definition, we have Eq. (3) as a consequence of Eq. (1) and Eq. (2).

$$\tau \left(\mathbf{r}\right)=\underset{t}{\text{arg max}}\mid {\overrightarrow{\mathbf{j}}}_{eq}(\mathbf{r},t)\mid$$ (3)

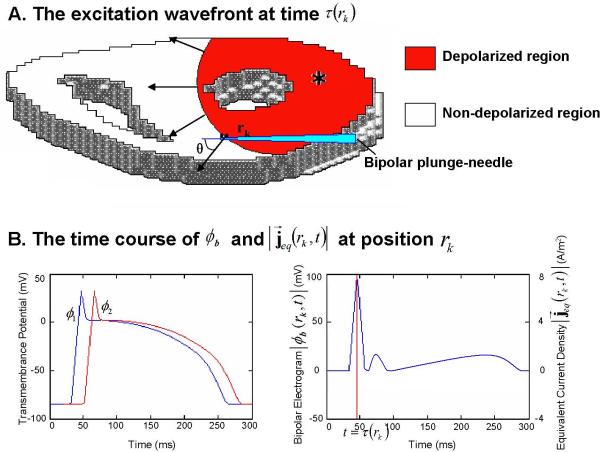
Therefore, the activation time is also characterized by the maximum magnitude of the ECD [17]. The relationship among the activation time, the TMP and its spatial gradient, the ECD and the intramural bipolar potential is illustrated in Fig. 1. The electrode 1 and electrode 2 record the potentials ϕ₁ and ϕ₂, and the recorded time course bipolar electrogram at point r_k is given as |ϕ_b (r_k, t)| = |ϕ₁ – ϕ₂|. At the instant t = τ (r_k), the cardiac cell at point r_k is undergoing depolarization, which is represented by equivalent current density ${\overrightarrow{\mathbf{j}}}_{eq}(r_k,t)$. The angle between the direction of the transmural needle and the direction of equivalent current density ${\overrightarrow{\mathbf{j}}}_{eq}(r_k,t)$ is θ. The relationship between the magnitude of local equivalent current density and recorded bipolar electrogram can be mathematically described as

$$\mid {\overrightarrow{\mathbf{j}}}_{eq}(r_k,t)\mid =\frac{g\left(r_k\right)\mid {\varphi }_b(r_k,t)\mid }{d\text{cos}\theta }$$ (4)

where d is the distance between electrode 1 and electrode 2, and g(r_k) is the conductivity at position r_k.

Fig. 1.

(A) An axial slice of the ventricles, in which the cardiac cells are undergoing depolarization. The red region behind the excitation wavefront represents the depolarized muscle cells, while the local equivalent current density field over each point along this wavefront, indicated by black arrow, represents propagation direction of the wavefront at these points. A transmural needle is inserted in the ventricular myocardium. (B) Left panel shows the time course of the TMPs ϕ₁ and ϕ₂ at electrode 1 and electrode 2. Right panel shows the time course to recorded bipolar electrogram |ϕ_b(r_k,t)| through electrode 1 and electrode 2 and the magnitude of local equivalent current density $\mid {\overrightarrow{\mathbf{j}}}_{eq}(r_k,t)\mid$. The activation time τ(r_k) at position r_k is indicated by red line at right panel.

C. Forward Problem

Based on the bidomain theory [20], [21], the 3-D distributed ECD can be regarded as the electrical “source” model accounting for the extracellular potential “field”, as shown in the following governing equation.

$$\nabla \cdot [({\mathbf{G}}_i\left(\mathbf{r}\right)+{\mathbf{G}}_e\left(\mathbf{r}\right))\nabla {\varphi }_e(\mathbf{r},t)]=\nabla \cdot {\overrightarrow{\mathbf{j}}}_{eq}(\mathbf{r},t)$$ (5)

where G_i(r) and G_e(r) are the intracellular and extracellular effective conductivity tensors respectively, and ϕ_e(r,t) is the extracellular potential.

Given a tessellated geometrical heart-torso model and the prior knowledge of the electrical conductivity of relevant tissues and organs, the extracellular potentials measurable over the body surface is linearly related to the 3-D ECD distribution. Eq. (6) expresses this linear relationship using a matrix-vector notation.

$$\Phi \left(t\right)=\mathbf{LJ}\left(t\right)$$ (6)

where Φ(t) and J(t) are the vectors of body surface potential distribution and 3-D ECD distribution respectively, and L is the source-to-sensor transfer matrix.

D. Inverse Problem

The concept of the ECD as well as its “source” interpretation according to the bidomain theory allows us to relate the imaging contrast (i.e. activation time) to the measurement (i.e. body surface potentials) through well defined equations from Eqs. (3) through (6). In the present study, we solved the linear inverse problem of Eq. (6) to estimate the spatiotemporal ECD distribution from the body surface potentials and then derived the activation time from the estimated ECD time course for each individual myocardial location.

Our previous computer simulations [17] have suggested that the activation time at each myocardial location is well aligned with the maximum local ECD estimate resulting from the lead-field normalized weighted minimum norm (LFN-WMN) estimation [22], [23] in combination with a spatiotemporal regularization [5]. In the present study, we solved the inverse problem of Eq. (6) by using the same algorithm as detailed in [17]. Briefly, the singular value decomposition (SVD) is employed to decompose the spatiotemporal ECG data matrix into orthogonal spatial and temporal components. The spatial components that do not satisfy the discrete Picard condition [24] are assumed to be dominated by noise perturbation, and thereby are truncated. The LFN-WMN estimation is applied to each remaining spatial component. The LFN-WMN solutions multiplied with the corresponding singular values and temporal components are summed to obtain the spatiotemporal ECD estimates. The activation time at each myocardial site is then determined from the time course of the estimated local ECD, by finding the maximum ECD estimate according to Eq. (3).

E. Rabbit Model and In Vivo Mapping

Four healthy New Zealand rabbits were studied using a protocol approved by the Institutional Animal Care and Use Committees of the University of Minnesota and the University of Illinois at Chicago. The experimental protocol was detailed in [16]. In brief, for each rabbit, two sets of Ultra Fast Computer Tomography (UFCT) images were obtained before the in vivo mapping. One without intravenous (IV) contrast was used to construct the rabbit torso model, and another one with IV contrast was obtained for construction of a detailed ventricle model. Later, 40−60 breathable BSPM electrodes were uniformly placed to cover the anterior-lateral rabbit chest up to the mid-axillary line. The heart was exposed via median sternotomy, and 20−25 transmural needle electrodes were inserted in the left and right ventricles of the rabbit. Each needle electrode contains 8 bipolar electrode-pairs with an inter-electrode distance of 500 μm [18], [19]. The difference in the sampling density of the needles was taken into account [16]. Around the pacing locations, the intramural bipolar electrodes were more densely positioned. The chest and skin were closed, and rapid ventricular pacing was then performed via bipolar electrode pairs on selected plunge needle electrodes, and the bipolar electrograms were continuously recorded from all plunge electrode pairs together with body surface potentials from surface electrodes. At the completion of mapping, the plunge needle electrodes were carefully localized as described in [16] by replacing each with a labeled pin. The heart was then excised, fixed in formalin, and underwent a post-operative UFCT scan to obtain precise 3-D localization of the transmural electrodes.

F. In Vivo Data Analysis

Fig. 2 schematically depicts the experimental protocol and the flow of data analysis. The realistic geometry rabbit heart-torso model was built in each animal from two sets of CT images obtained before in vivo mapping. The rabbit ventricles were tessellated into 12376±5374 evenly spaced grid points. The spatial resolution of the ventricle models was 1 mm (rabbit 1, 2, 3) or 0.75 mm (rabbit 4). There were 178±29 bipolar electrodes during 3-D intra-cardiac mapping and 53±6 surface electrodes on the rabbit body surface.

Fig. 2.

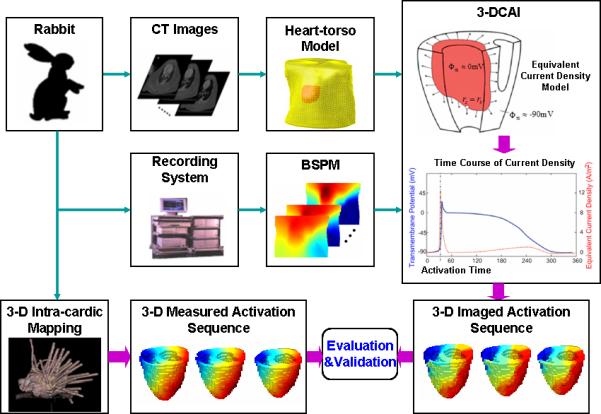
Schematic diagram of the experimental protocol. Simultaneous 3-dimentional (3-D) intra-cardiac mapping and body surface potential mapping were conducted and the measured activation sequence from 3-D intra-cardiac mapping is compared with the imaged activation sequence obtained by the 3-D cardiac activation imaging technique.

Single-beat BSPM signals were extracted from the pacing onset (identified by a pacing artifact observable on the ECG recordings) to the end of the QRS interval. Fig. 3.A. shows an example of multi-channel BSPM signals with a red box highlighting an extracted single-beat data. 3-DCAI was applied to each of the extracted single-beat data, resulting in the underlying activation sequence within the ventricular myocardium. From the simultaneously recorded intra-cardiac data, the activation times at discrete recording sites were measured by using a peak criterion [18], [19]. The activation time was then interpolated onto all non-recording sites by using the method described in [16].

Fig. 3.

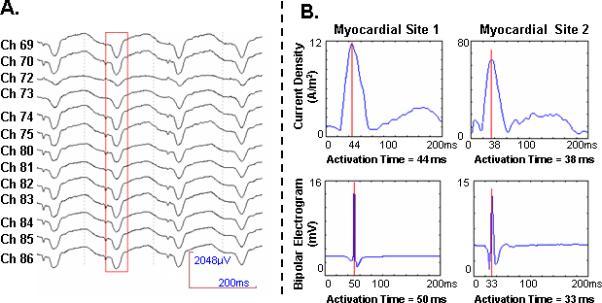
(A) An example of electrocardiograms (ECGs) recorded from the anterior chest during ventricular pacing at left lateral wall of rabbit 4. The red block starting from the pacing stimuli represents a single beat that was applied in 3-DCAI. (B) Comparison between the time course of the estimated current density (top row) and the recorded bipolar electrograms in 3-D intra-cardiac mapping (bottom row) at two myocardial sites in ventricles of rabbit 2. Site 1 is located at left lateral wall. Site 2 is located at posterior wall. Red line marks the estimated activation time.

The activation sequence measured from the intra-cardiac data was taken as the golden standard to evaluate the performance of 3-DCAI. The root mean square (RMS) error was computed to quantify the difference between the invasively measured activation sequence and the non-invasively imaged activation sequence. The RMS is defined as

$$RMS=\sqrt{\frac{\sum _{i=1}^n{(A{T}_i^E-A{T}_i^M)}^2}{n}}$$ (7)

where n is the number of grid points of the heart model, and $A{T}_i^E$ and $A{T}_i^M$ are the estimated activation time and measurement constructed activation time at the i-th myocardial grid point, respectively. The relative error (RE) was computed to provide the normalized difference between the invasively measured activation sequence and the non-invasively imaged activation sequence. RE is defined as

$$RE=\sqrt{\frac{\sum _{i=1}^n{(A{T}_i^E-A{T}_i^M)}^2}{\sum _{i=1}^n{\left(A{T}_i^M\right)}^2}}.$$ (8)

The localization error (LE), which is defined as the distance from the pacing site to the center of mass of the myocardial region with the earliest imaged activation time, was computed to evaluate the performance of 3-DCAI in localizing the site of origin of activation.

G. Computer Simulation

In order to comprehensively evaluate the performance of 3-DCAI and help interpret the data from the in vivo experiments, computer simulations were conducted on a realistic rabbit geometry and piece-wise homogeneous heart-torso model. There were 7,625 grid points evenly spaced by 1 mm throughout the whole 3-D ventricular myocardial volume. To simulate the body surface electrode setup in the in vivo experiment, 53 body surface electrode locations were selected to uniformly cover the anterior-lateral chest of the rabbit body surface.

A cellular automaton heart model [11]-[13] was employed to simulate the ventricular electrical activity using both single-site and dual-site pacing protocols. In the single-site pacing, 9 representative pacing sites were selected throughout the 3-D myocardium of ventricles, which included basal left wall (BLW), basal right wall (BRW), basal anterior (BA), basal posterior (BP), middle left wall (MLW), middle right wall (MRW), middle anterior (MA), middle posterior (MP), and apex. A dual-site pacing protocol was used to simulate more complex excitation than that of the single-site pacing. 8 pairs of pacing sites were selected throughout the 3-D myocardium of ventricles. With the setting that maximum peak-peak value was 3 mV determined from actual ECG data, Gaussian white noise (GWN) of 20 μV was added to the BSPMs generated by the boundary element method (BEM) based forward computation. Considering the maximum noise level of instrumentation is 10 μV, this represents a conservative estimate of experimental noise. RE was calculated to evaluate the dissimilarity between the imaged activation sequence and simulated “true” activation sequence. LE was calculated to measure the capability of localizing the origin of excitation during single-site pacing.

3. Results

In the Methods section, we reveal the physical correlation between the ECD and the intramural bipolar potential. This correlation suggests that the ECD estimates should ideally be proportional to the recorded intramural bipolar potentials. Therefore, we compared the time course of the ECD estimates at a given myocardial site with the intramural bipolar electrogram recorded at the same site. In Fig. 3.B, both the intramural electrograms and the local ECD estimates at two representative locations are displayed as functions of time. Note that both time courses were normalized before comparison since the activation time was magnitude-independent. It was found that the bipolar electrogram always appeared as a delta function, which indicated a transient TMP spatial gradient as a consequence of the steep upstroke of the TMP undergoing depolarization. Although it was anticipated that the real ECD waveform should be similar to the intramural electrogram, the estimated ECD by solving the linear inverse problem evolved much slower than the intramural bipolar potential. This is in line with our findings obtained in previous computer simulation studies in a human heart-torso model [17]. Nevertheless, the activation times, determined as the instant with peak amplitude in the intra-cardiac bipolar electrogram [18], [19], [25] and as the instant with maximum ECD estimate [17] respectively, aligned well around the same time point for both examples shown here.

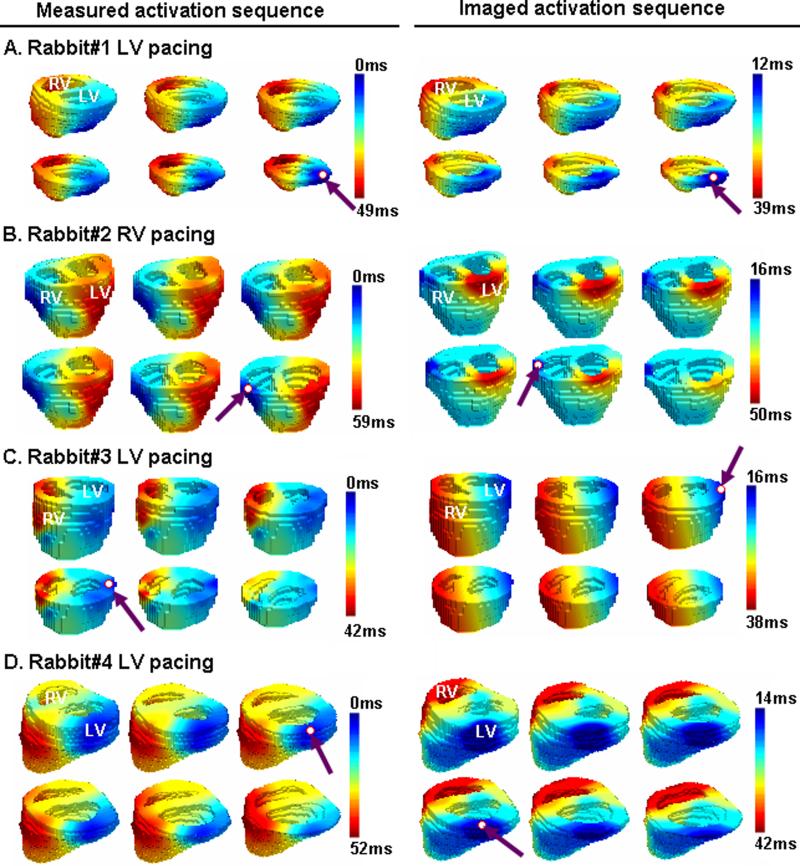
Fig. 4 shows examples of comparison between the measured and imaged activation sequences for 4 paced beats recorded from all 4 rabbits (one pacing beat per rabbit). For each beat, the activation time distributions on six representative axial slices were displayed along with the 3-D realistic heart geometry. We found that the imaged activation sequences (left column) were qualitatively consistent with the measured ones (right column). The origin of activation was localized to be around the true pacing site, whereas the imaged activation origin tended to be slightly closer to the epicardium or the base. This tendency probably represents a localization bias of the current 3-DCAI algorithm. In the imaged activation sequences, the regions in the middle activation (shown in light blue and yellow) are also found to be larger than in the measured activation map, particularly for Fig. 4.B. The imaged excitation process appeared to be more discrete instead of being continuous and smooth as observed in the intra-cardiac measurements, suggesting the limited spatial resolution of the current 3-DCAI algorithm. The quantitative comparison returned a RMS of 6.78 ms, a RE of 0.21, and a LE of 3.67 mm for rabbit 1, a RMS of 7.02 ms, a RE of 0.26, and a LE of 7.48 mm for rabbit 2, a RMS of 7.97 ms, a RE of 0.21 and a LE of 5.20 mm for rabbit 3, and a RMS of 7.90 ms, a RE of 0.27 and a LE of 5.51 mm for rabbit 4, respectively. On average, RMS, RE, and LE were 7.42±0.61 ms, 0.24±0.03, and 5.47±1.57 mm, respectively, for this pilot study.

Fig. 4.

Comparison between the 3-D activation sequence measured via 3-D intra-cardiac mapping (left column) and the 3-D activation sequence imaged by using 3-DCAI (right column). The activation sequence is color coded from blue to red, corresponding to earliest and latest activation. The pacing site and the estimated initial site of activation are marked by a red circle and a purple arrow. (A) Activation was paced at left posterior wall of ventricle in rabbit 1. A realistic geometry of ventricle for rabbit 1 is displayed (top left view). (B) Activation was induced by pacing at right lateral wall of ventricle in rabbit 2 (top anterior view). (C) Activation was induced by pacing at left lateral wall of ventricle in rabbit 3 (top anterior view). (D) Activation was induced by pacing at left lateral wall of ventricle in rabbit 4 (top left view).

Fig. 5 shows examples of comparison between the imaged activation sequence and simulated “true” activation sequence during computer simulation. As shown in Fig. 5.A, the imaged pattern coincided well with the simulated activation sequence, with RE = 0.16. The LV pacing site was localized with a 3.86mm LE. Similar imaging performance was observed when the activation was induced by pacing at the middle lateral wall of the right ventricle, as shown in Fig. 5.B, with RE = 0.19 and LE = 4.69mm. Fig. 5.C shows an example of simultaneous dual-site pacing. The imaged activation sequence is consistent with the simulated activation sequence, with RE = 0.17 which shows that 3-DCAI can reconstruct the activation sequence throughout the ventricles for dual-site pacing at two separate locations. Quantitative comparison between imaged activation sequence and simulated “true” activation sequence under both single-site pacing and dual-site pacing with respect to the different location of the origin of the ventricular excitation are summarized in Table I and Table II. On average, RE was 0.20±0.07 and LE was 4.56±1.12 mm for single-site pacing. For dual-site pacing, averaged RE was 0.25±0.06.

Fig. 5.

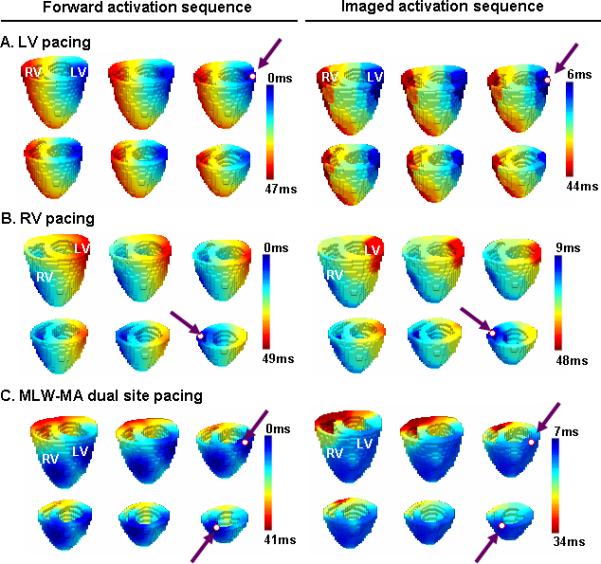
Comparison between the forward simulation activation sequence and imaged activation sequence (right column) during the computer simulation. A realistic geometry of ventricles is displayed, from a top anterior view. (A) Activation was paced at basal lateral wall of the LV. (B) Activation was paced at middle lateral wall of RV. (C) Activation was simultaneously paced at middle left wall (MLW) and middle anterior (MA) of ventricles.

TABLE I.

Simulation Results of Imaging the 3-D Ventricular Activation Sequence Induced by Single-site Pacing

Pacing Site	RE	LE (mm)
BLW	0.16	3.86
BRW	0.20	4.32
BA	0.19	3.61
BP	0.32	6.40
MLW	0.18	3.61
MRW	0.19	4.69
MA	0.14	3.61
MP	0.31	6.40
Apex	0.15	4.58
Mean	0.20	4.56
STD	0.07	1.12

TABLE II.

Simulation Results of Imaging the 3-D Ventricular Activation Sequence Induced by Dual-site Pacing

Pacing Site 1	Pacing Site 2	RE
BP	BLW	0.38
MRW	MLW	0.26
BP	MLW	0.28
BRW	MA	0.21
BR	MLW	0.24
MLW	MLW	0.23
MLW	MA	0.17
MP	MLW	0.25
Mean		0.25
STD		0.06

4. Discussion

The present study is aimed at rigorously and quantitatively evaluating the biophysical model based 3-D cardiac activation imaging (3-DCAI) algorithm, detailed in [17], through both in vivo animal experiments and computer simulation studies. The present study represents the first experimental study assessing the performance of the 3-DCAI algorithm by comparing with simultaneously recorded intra-cardiac data, although the in vivo rabbit data were obtained in the experiment presented in [16]. The comparison between the non-invasively imaged activation sequence based on 3-DCAI and the measured activation sequence based on the intra-cardiac mapping suggests that: 1) 3-DCAI is capable of reconstructing the overall pattern of the 3-D ventricular excitation profile induced from a single pacing site, 2) the localization error of 3-DCAI for localizing the origin of ventricular activation was 5.47±1.57 mm, and 3) 3-DCAI has relatively lower spatial resolution than the intra-cardiac mapping.

The fact that both the intramural bipolar recording and the equivalent current density are proportional to the spatial gradient of the TMP points to the common physical principle shared by 3-DCAI [17] and the intra-cardiac mapping [18], [19] in terms of estimation and visualization of the activation sequence throughout the entire myocardium. This commonality also justifies the use of the 3-D intra-cardiac mapping as an ideal way to evaluate the activation sequences imaged by using 3-DCAI.

The intra-cardiac mapping technique based upon intramural bipolar recording has been employed to investigate ventricular tachycardia (VT) [18], [19]. These successful applications have confirmed the efficacy of using the TMP spatial gradient to detect the activation time for both normal and abnormal myocardial cells. Note that the TMP spatial gradient is essentially proportional to the imaging contrast (i.e. the equivalent current density) of the present 3-DCAI algorithm. Therefore, 3-DCAI can be thought of as a noninvasive alternative technique for the intra-cardiac mapping. More importantly, it also suggests that 3-DCAI is in principle applicable to image the intrinsic cardiac activation under pathological conditions when the intra-cardiac mapping is applicable.

However, the need to solve a highly ill-posed linear inverse problem in order to estimate the ECD from body surface measurements poses a great challenge to 3-DCAI. Solving such an inverse problem is essentially a task of seeking a spatial filter (or inverse operator) that projects the recorded data in the sensor space to the solution in the source space. It is often experienced in the ECG (as well as EEG/MEG) inverse problem that applying such a spatial filter cannot lead to a source reconstruction in perfect agreement with the true source distribution [26]. Instead, the source estimates may appear as a spatially blurred image, from which one may still resolve the true sources if they are distributed in a discrete or focal manner [10]. But when the current sources are continuously distributed over a wavefront during the paced ventricular activation, the imaged ECD distribution at any specific time point is highly distinct from being a transmural surface as one may expect for the instantaneous excitation wavefront, and it is difficult to accurately reconstruct the instantaneous ECD distribution.

In 3-DCAI the activation time is determined exclusively from the time course of local ECD estimates. Surprisingly, we found that the ill-posed nature caused much less distortion to the normalized temporal waveform of ECD estimates than it does to the instantaneous ECD spatial distribution. At a noisy condition, the ECD spatial distribution was found to be hardly interpretable, whereas the estimated ECD waveform at each individual myocardial site still demonstrated a clear peak instant that was determined as the activation time. Regarding this finding, our speculated explanation is two fold. First, the activation time is a magnitude-independent temporal feature of local ECD estimates; therefore it is less sensitive to the spatial distortion of the inverse solution. It is true that the torso volume conductor behaves as a spatial filter and the estimation of the equivalent current density is essentially the de-convolution of this spatial filter. However, even though both forward and inverse procedures operate upon the spatial domain, the bias and blurring of the inverse solution in space also necessarily affects the time course of the source estimate. This effect may be well accounted for by a low-pass filter. Importantly, this effect does not significantly bias the peak instant which marks the activation time, since the “peak instant” of the source time course is a “low-frequency” feature. But this effect may cause the ambiguity and potential bias of other competitive methods based on determining the activation time from the maximum positive or minimum negative derivative, which is a “high-frequency” feature, of the estimated TMPs, or the estimated epicardial or endocardial potentials. In this sense, it represents another technical merit and robustness of 3-DCAI. Second, the cardiac excitation process is typically continuous and smooth in nature and so is the point spread (or cross-talk) function of the 3-D ECG inverse solution. In other words, the source estimates at any specific location are primarily affected by the source activities at neighboring sites with similar activation times. In future studies, we will attempt to provide more rigorous theoretical insights with regards to these interpretations.

The ill-posed problem of the ECD estimation is still the primary source of the activation imaging bias of 3-DCAI [17]. Because of the spatial blurring and bias of the inverse solution, the estimated ECD time course was also smooth over time, whereas a delta function was observed in the intramural bipolar recording at the same site. This distinction accounted for the reduced specificity of activation time estimation. As a consequence, different myocardial locations within an extended region, particularly those that are activated around the middle of the QRS interval, often had the identical activation time, although they were actually activated progressively. In addition, it also caused the total activation time (TAT) obtained from the imaged activation sequence to be shorter than the TAT determined from the intra-cardiac data.

In the present study, we have only demonstrated experimentally the feasibility of 3-DCAI in imaging ventricular activation induced by single-site pacing. Such single-site pacing provides a well-controlled experimental setting for evaluating the performance of 3-DCAI in imaging ventricular activity with focal activation, such as ectopic beats or automatic VT. The present results suggest the potential use of 3-DCAI in guiding interventional procedures (e.g. catheter ablation) in treatment of automatic VT of focal nature [19]. As we described in the Methods section, the imaging principles of 3-DCAI is not limited to single-site pacing induced activities. 3-DCAI is in principle applicable to imaging complex cardiac activation. Further in vivo experimentation will need to be conducted to image more complex cardiac activation such as reentry VT or other arrhythmias.

In the present study, computer simulation study was also conducted to provide additional assessment to the performance of the 3-DCAI algorithm and help in data interpretation of our experimental results. We have obtained an averaged LE of 4.56 mm in singe-site pacing during computer simulation, which is smaller than the averaged LE of 5.49 mm on a human model [17]. However, the LE does not linearly scale to the geometry size of heart-torso model. The primary source for these errors is caused by the intrinsic ill-posedness of the inverse problem. For example, the imaged area of early activation is a region rather than a single point. The shape of the time course of the estimated ECD is much smoother than the shape of “delta function” that simulates the “true” time course of ECD. Also, in our present computer simulation, we used 53 body surface electrodes to simulate the real in vivo experimental setup, while in the previous simulation study on a human model [17], there were 200 body surface electrodes. Such imaging parameters may influence our imaging results.

The averaged LE of 5.47 mm in the in vivo experiments is larger than our computer simulation results of 4.56 mm. Various reasons related to the in vivo experimental procedures may account for the slightly larger error, including the localization errors of body-surface electrodes, the localization errors of plunge-needle electrodes, and the volume conductor modeling errors [16], [27]. These inherited experimental errors are mainly determined by experimental procedures, and do not necessarily scale to the geometry size of the subject in a linear manner. Considering the area of catheter ablation typically ranges from 5 to 8 mm [28], the present results represent reasonable accuracy in assessing the imaging ability of the 3-DCAI technique using in vivo models.

Compared with our previous in vivo study of a cellular automaton heart model based approach [16], the 3-DCAI approach has obtained similar results in terms of LE and RE, but lower resolution, considering that TAT obtained from imaged activation sequence is shorter than the TAT obtained from measured activation sequence. The cellular automaton heart model based approach utilizes the a priori electrophysiological knowledge as a constraint and thus is capable of producing higher resolution imaging results. In comparison, 3-DCAI does not need to build a sophisticated heart model. It only uses the general biophysical relationships governing the cardiac electrical activity, and has a notable feature of minimal dependence on the physiological knowledge of cardiac electrical properties. Therefore, 3-DCAI is potentially applicable to imaging various cardiac activity including sinus rhythm and arrhythmias.

In the present study, we have used a well established 3-D intra-cardiac mapping procedure to test the feasibility of the 3-DCAI algorithm in imaging activation sequence under an in vivo situation. Compared with other previous experimental studies reported in literature [4], [8], [29], [30] for heart surface imaging approaches, the 3-D intra-cardiac mapping represents a desirable validation protocol as the 3-DCAI results are distributed within the 3-D myocardium. A limitation of this approach is its complexity of the procedures and validation experimentation.

Last but not least, 3-DCAI provides the functional data throughout the entire myocardium instead of only over the epicardium and/or endocardium, which is distinct from existing heart surface activation imaging techniques [4], [7], [8]. The intramural cardiac function is of great interest when the excitation profile propagates transmurally from the endocardium to the epicardium. To account for a more accurate volume conductor modeling, it may be preferable to use the finite element method (FEM) rather than the BEM [31], given the recent development of diffusion tensor imaging (DTI) which holds a potential to obtain the information of anisotropic conductivity [32].

In summary, the present study suggests the feasibility and applicability of the biophysical source model based 3-DCAI in imaging the 3-D ventricular activation sequence, as assessed by the invasive 3-D intra-cardiac mapping. The present results obtained from both computer simulations and in vivo experimental studies indicate a reasonable performance of the 3-DCAI algorithm in reconstructing the overall activation sequence and localizing the site of origin of activation. The computer simulation results in a rabbit model confirm the experimental findings. The present experimental finding is encouraging and suggests that the biophysical model based 3-DCAI technique merits further investigation and may have potential to become a useful noninvasive imaging means for mapping cardiac electrical activity non-invasively throughout the 3-D myocardium.