Nanoscale imaging of chemical interactions: Fluorine on graphite

Abstract

Using C₆₀-functionalized scanning tunneling microscope tips, we have investigated the adsorption of fluorine on graphite. Based on characteristics of the accompanying electron standing waves, we are able to distinguish the fluorine adatoms that have bonded ionically to the graphite surface from those that have formed covalent bonds with the surface. This result permits determination of the ratio of ionic to covalent C–F bonds on graphite obtained by gas phase fluorination, which seems to be temperatureindependent between 200 and 300°C under the reaction conditions used.

Fluorinated carbon materials are an area of intense research because of their important practical applications as lubricants, water repellants, and battery cathodes. The chemical composition of fluorinated carbons depends on both the structure of the starting material and the fluorination conditions (1, 2). One of the most intriguing aspects of fluorinated graphite is the variability of its electrical conductivity. This variability is due to the ability of the fluorine atoms to form both ionic and covalent bonds with the carbon atoms (3, 4). Electrical conduction in fluorinated graphite can be enhanced by the ionic bond between the fluorine and carbon atoms because of an increase in hole carriers, whereas covalent bonding produces a decrease in the overall carrier concentration (4). In this report, we use scanning tunneling microscopy (STM) to identify the ionic and covalent C–F bonds on graphite by the differences induced by each bonding configuration in the surrounding local density of states of the graphite substrate.

STM has become an invaluable technique for probing the electronic properties of materials on the nanometer scale. Of particular interest is its ability to observe the standing electron wave patterns (Friedel oscillations) generated by scattering from defects and steps on certain surfaces (5–7). The observation of these scattered electron states has proved beneficial in exploring adsorption on surfaces (8), the depth of impurities in solids (9–11), and the mixing of surface and bulk electron states (12). Previously, it has been shown that it is necessary to narrow the STM tip local density of states to image electron standing waves on graphite (13). This narrowing can be done either by cooling to cryogenic temperatures (14) or by the adsorption of a C₆₀ molecule onto the tip apex (15). As in the case of electron scattering on noble metal surfaces, which can be observed in the (dI/dV)/(I/V) (where I is the tunneling current and V is the tip sample voltage difference) measurements made with a metal STM tip (16, 17), it should also be possible to observe the 3-fold scattering on graphite by imaging the differential conductivity with a metal tip at room temperature. Fourier space lattice-superlattice filtering of these 3-fold electron-scattering images enables the exact determination of the defect position relative to the underlying graphite lattice (18). In this report, we demonstrate the ability to identify two different bonding configurations of fluorine atoms adsorbed onto graphite via the easily distinguishable differences in their surrounding electron-scattering patterns.

Experimental Procedures

The fluorinated graphite samples were prepared by placing freshly cleaved highly oriented pyrolytic graphite (ZYA grade) in a Monel flow reactor and exposing it to fluorine gas diluted with helium at elevated temperatures. The HF impurity of the fluorine gas was removed by passing it through an HF trap containing sodium fluoride pellets. The F₂ and He flow rates for these reactions were 1 and 100 standard cm³/min (sccm), respectively. The reaction time in each case was 2 min unless otherwise noted. The fluorination reactions were carried out at 200, 250, and 300°C. The surfaces were then imaged under ambient conditions with a home-built STM controlled by RHK Technology (Troy, MI) electronics and software. Scanning was performed with both bare, mechanically cut Pt/Rh (87/13) tips and the same tips functionalized with C₆₀ molecules as described (19). All graphite samples were scanned before the fluorination procedure to compare the density and structure of naturally occurring defects with those generated from the formation of C–F bonds.

Results and Discussion

Imaging the fluorinated graphite surfaces with a C₆₀-functionalized STM tip yields highly reproducible images of the local fluorination sites and allows for clear distinction between the two types of bonding. Fig. 1 is an STM image of a graphite sample fluorinated at 300°C with an STM tip that has been functionalized by the adsorption of a C₆₀ molecule at its apex. This procedure facilitates the imaging of the predicted 3-fold electron scattering around graphite defects at room temperature.

Figure 1.

An image of graphite fluorinated at 300°C obtained with a C₆₀-functionalized STM tip. The prominent 3-fold defect in the lower right is attributed to a covalent C–F bond, whereas the other defects represent fluorine atoms adsorbed with an ionic bond. The spacing between the atomic sites in the unperturbed areas of the image is 2.46 Å. (Inset) Fourier transform of the topographic image. The six outer peaks are caused by the graphite lattice, whereas the six inner peaks correspond to the electronic superlattice. The tunneling parameters were 1-nA and +100-mV sample bias voltage.

Fig. 1 Inset is the center of its Fourier transform. Besides the six outer peaks caused by the graphite lattice, there are a set of six very strong inner peaks corresponding to a 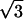× 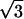R30° superlattice (where a = 2.46 Å). This superlattice represents a perturbation to the graphite electronic structure caused by the presence of the fluorine adsorbate. The feature in the lower right corner of the topographic image shows a strong 3-fold electron-scattering pattern, whereas the other features in this image are surrounded by much weaker electronic perturbations. Shown in Fig. 2 is an STM image of graphite fluorinated at 250°C obtained with a bare metal STM tip. In this case, a fairly blunt STM tip is scanned over the adsorbates yielding images of the STM tip at each bonding site. The appearance of the superlattice in the topographic images is highly dependent on the metal tip structure and is typically much weaker than the superlattice detected with a C₆₀ tip. In Fig. 2, virtually no superlattice modulation is detected in the topographic image, although weak superlattice points are visible in the Fourier transform of this image (Fig. 2 Inset). Observation of the superlattice by metal tips has also been reported in the vicinity of adsorbed metal clusters (20) and defects induced by ion damage (21). In correlating the number of features in each image observed with C₆₀-functionalized STM tips to the number of features imaged by bare metal tips, we discover that the strong 3-fold scattering features shown in Fig. 1 correspond to the larger sized features imaged in Fig. 2. This result is in agreement with previous experiments that ascribed the large size of graphite defects in STM images to electronic, not topographic, effects (22). For either metal or C₆₀ STM tips, two distinct types of features were imaged on the fluorinated surfaces. Only the overall density, not the relative proportion, of these features varied with increasing fluorination temperature. In addition, a control sample exposed to F₂ at room temperature for 10 min showed no change in the defect coverage or type when compared with the freshly cleaved graphite surfaces.

Figure 2.

A constant current topographic image of graphite fluorinated at 250°C imaged with a bare metal STM tip. The differences in defect size correspond to differences in the C–F bonds. (Inset) This image is the corresponding Fourier transform. Although much weaker than in Fig. 1, the six superlattice peaks are still present. The tunneling parameters were 1-nA tunneling current and +100-mV sample bias voltage.

Comparing the C₆₀-tip-obtained experimental images to theory allows the identification of the C–F bonding configuration. The theoretical images in Fig. 3 A and B representing the local density of states of graphite near the Fermi energy illustrate the variations in the electron scattering caused by differences in the adsorbate bond strength. These images were generated with a tight-binding calculation of a 2,917-atom bilayer cluster with periodic boundary conditions with one π-electron per atom. The on-site energies of all atoms were set equal to zero. The hopping parameter, V_ppπ, was set equal to −3 eV between in-plane neighbors and −0.3 eV between interplane neighbors. These values have been shown to provide a good fit to the graphite π-bands (23). Following the theoretical approximations made by Tersoff and Hamann (24, 25) regarding the electronic structure of the STM tip, the STM image therefore reflects the local density of states of the surface. Fig. 3A was calculated by assuming strong bonding of the adsorbate to a single carbon by setting its coupling strength equal to that of the in-plane neighbors. For Fig. 3B, V_ppπ was reduced by a factor of three to reflect a decrease in the adsorbate bond strength. These images are in very good agreement with the experimental results displayed in Fig. 1. Based on this agreement, we assign the defects demonstrating long-range electron scattering to fluorine atoms having covalent bonds to the graphite surface. For weakly coupled adsorbates, which we attribute to ionic bonding, the intensity of the scattered wave is reduced relative to the background lattice. As a result, the electronic perturbation surrounding the fluorine appears more isotropic. However, the structure of the scattered wave is strongly correlated with the Fermi surface of graphite and remains trigonally symmetric. An analogous situation is seen for the scattered electron waves on the (111) surface of noble metals (12) and the (101̄0) surface of beryllium (26), which remain spherically and elliptically symmetric, respectively. Although these images qualitatively reflect the experimental results, a more thorough calculation is necessary for a quantitative determination of the electronic structure and relative bonding energies.

Figure 3.

Theoretical images reflecting changes in the adsorbate interaction with the graphite surface. (A) The interaction of the adsorbate with the surface is set equal to that of the neighboring atoms. (B) The strength of that interaction is decreased by a factor of three.

We also investigated the HF-catalyzed fluorination of a graphite surface at room temperature. In this case, the fluorine would be expected to bond to the graphite surface in a predominantly ionic fashion. This sample was exposed for 10 min to an atmosphere consisting of 100 He sccm, 1 HF sccm, and 1 F₂ sccm at room temperature. The HF catalyzes the fluorination process by forming HF₂⁻ species in the presence of molecular fluorine, which subsequently reacts with the graphite (27). On this sample, we observed a decrease in the strongly 3-fold scattering defects and an increase in the weakly scattering defects. This observation is consistent with previous results that indicate that fluorination in the presence of HF yields primarily ionic C–F bonds (27). Additionally, a control sample of graphite was fluorinated with 1 sccm F₂ and 100 sccm He at room temperature and showed neither type of defect to be present on the graphite surface. This result confirms that uncatalyzed fluorination of graphite does not occur under these conditions. We attribute neither of the defects to molecular fluorine, because it is generally assumed that fluorine adsorbs only to the graphite surface in an atomic state (28). These results seem to confirm our assignment of the scattered states to the different bonding configurations.

Table 1 summarizes the defect density and the ratios of covalently bonded to ionically bonded fluorine for the different fluorination conditions as determined from the STM images. These results can be compared with previous investigations that probed the nature of the C–F bond through nonlocal techniques such as x-ray photoelectron spectroscopy (29) and nuclear magnetic resonance spectroscopy (30). The defect density demonstrates that the amount of fluorine reacted with the graphite is highly temperature-dependent, which is in good agreement with previous studies. However, a striking feature for the noncatalyzed fluorination is the fairly constant ratios of ionic versus covalent bonding over the temperature range studied. This result is very unexpected, considering previous studies on fluorinated graphite. Although this represents a very dilute coverage of fluorine on the graphite, it has been suggested previously that the transformation to a covalent solid does depend on the presence of large amounts of fluorine (28).

Table 1.

Summary of fluorination results

Ratios of reaction gases, sccm	Sample temperature, °C	Defect density, per Å2	Percentage of F atoms with covalent bonds
99 He:1 F2	200	9.4  × 10−7	18.7  ± 1
99 He:1 F2	250	5.0  × 10−5	19.2  ± 1
99 He:1 F2	300	1.4  × 10−4	17.3  ± 1
98 He:1 HF:1 F2	23	4.2  × 10−5	11.5  ± 1

A summary of the results for the different fluorination conditions. The reaction times were 2 min for the uncatalyzed fluorination and 10 min for the sample treated with HF. Although there is a noticeable increase in fluorine adatoms with temperature for the uncatalyzed samples, the ratio of ionic to covalent C–F bonds remains relatively constant. However, fluorination with HF shows a reduced percentage of covalent bonds. For comparison, the density of naturally occurring defects observable by the STM on freshly cleaved graphite was always less than 5⁻⁸ per Ų. 

Conclusion

In summary, the fluorination of graphite has been investigated with bare metal and C₆₀-adsorbed STM tips. We have found that, with C₆₀ molecularly functionalized tips, the chemical nature of the bonding sites can be clearly and consistently distinguished at room temperature. In addition, we have found that the percentage of covalent C–F bonds is independent of the fluorination temperature up to 300°C, in contrast with results obtained with HF-catalyzed fluorination. This finding, combined with the ability to determine the exact adsorbate binding site on the substrate lattice, should prove a highly detailed technique for imaging other adsorbates and for studying other important chemical interactions on graphite surfaces, such as oxidation (31). It may also prove useful in analyzing other fluorinated graphene structures such as single-walled nanotubes (32, 33).

Abbreviations

STM

scanning tunneling microscopy

sccm

standard cubic centimeters per minute