Origin of the Activity Drop with the E50D Variant of Catalytic Antibody 34E4 for Kemp Elimination

Abstract

In enzymes, multiple structural effects cooperatively lead to the high catalytic activity, while individually these effects can be small. The design of artificial enzymes requires the understanding and ability to manipulate such subtle effects. The 34E4 catalytic antibody, catalyzing Kemp elimination of 5-nitrobenzisoxazole, and its Glu50Asp (E50D) variant are the subject of the present investigation. This removal of only a methylene group yields an approximately 30-fold reduction in the rate for the catalyzed Kemp elimination. Here, the aim is to understand this difference in the catalytic performance. The mechanism of Kemp elimination catalyzed by 34E4 and the E50D mutant is elucidated using QM/MM Monte Carlo simulations and free energy perturbation theory. In both proteins, the reaction is shown to follow a single-step, concerted mechanism. In the mutant, the activation barrier rises by 2.4 kcal/mol, which corresponds to a 62-fold rate deceleration, in good agreement with the experimental data. The positions and functionality of the residues in the active site are monitored throughout the reaction. It is concluded that the looser contact with the base, shorter base-Asn58 contact, less favorable π-stacking with Trp91 in the transition state of the reaction, and different solvation pattern all contribute to the reduction of the reaction rate in the E50D variant of 34E4.

Introduction

Substantial efforts are being directed toward the design of artificial enzymes.^1-12 Biological catalysts are remarkable in their specificity and high activity under mild conditions.¹³ Hence, enzyme design presents a great challenge. It is a multivariable task, because a large number of degrees of freedom are involved, and because many parts of the protein may function synergistically, while their individual contributions to the catalysis may be small. In order to be able to properly choose and manipulate the structure of artificial enzymes, it is important to understand in detail the microenvironment phenomena at the active site and their cooperative effect on the catalytic performance.

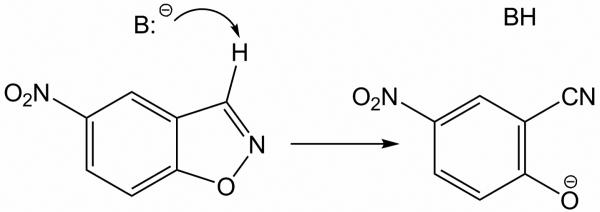
Recently, a series of active artificial enzymes^1,12 and catalytic antibodies^16-19 for the Kemp elimination of 5-nitrobenzisoxazole (Scheme 1)^14,15 has been reported. In these protein catalysts, Asp, Glu, or His play the role of the catalytic base (B); in some cases an acidic residue or residues are introduced near the N-O bond of the substrate, and the remaining residues of the binding site play structural roles.^1,12,16-19 However, despite this success, more detailed understanding of why some of these catalysts are more active than others is desirable. Here, two catalytic antibodies for Kemp elimination, 34E4^16-19 (PDB-code 1Y0L, 2.50 Å resolution), and its Glu^H50Asp variant (PDB-code 1Y18, 2.80 Å resolution) are studied. The 34E4 antibody was raised against a benzimidazolium hapten.¹⁶ Glu50 is the key residue in 34E4, which plays the role of the base abstracting the C3 proton. 34E4 and its E50D variant make an interesting case for the present investigation, because the single Glu to Asp substitution leads to a 30-fold reduction in catalytic activity.¹⁷ Both proteins are active catalysts with 34E4 providing a striking rate acceleration of greater than 10⁶-fold over background.¹⁸

Scheme 1.

Kemp elimination in 5-nitrobenzisoxazole.

On the basis of the crystal structure with the bound hapten, qualitatively, the difference in activity in these antibodies was attributed to less optimal positioning of the base and less favorable π-stacking interaction between the substrate and Trp91 in the binding site of the mutant.¹⁷ However, upon mutation, the entire binding pocket is likely to undergo a structural rearrangement, and the differences in the positions of all residues in the binding site should contribute to the difference in activity. Furthermore, the crystal structures only provide direct information on the binding of the hapten, while the present computations can address all points along the reaction path. Examination of how the structures of the entire active sites of 34E4 and its E50D variant change in progressing from the reactants to transition states and products is desirable to fully understand the variation in the reaction rate.

In order to elucidate further the mechanism of the reaction catalyzed by 34E4 and its E50D variant, the catalyzed Kemp eliminations of 5-nitrobenzisoxazole are investigated here using QM/MM Monte Carlo simulations and free energy perturbation theory. Observations from such detailed investigations are necessary to strengthen the basis for further rational design of artificial enzymes.

Methods

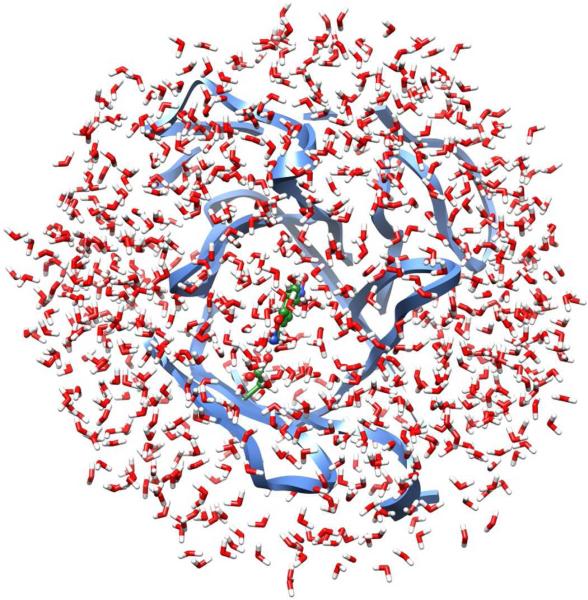
The initial structures of the two antibodies with the bound hapten were taken from the 1Y0L and 1Y18 entries, which were deposited in the Protein Data Bank in 2005.¹⁷ Each crystal structure contains a tetramer, and a monomer was used in the MC simulations. In preparation for the simulations, the hapten in the binding site was replaced with 5-nitrobenzisoxazole, and the complex of the catalytic antibody under consideration was truncated such that only protein residues with any atom within ca. 15 Å of the substrate were retained. This left 126 residues out of the 447 in the monomer. The overall charge was set to zero via neutralization of residues remote from the active site. The substrate was initially positioned with the hydrogen on C3 oriented towards the putative base. Both systems were relaxed using 50-step conjugate gradient minimizations. Subsequently, a 20-Å cap containing TIP4P water molecules²⁰ was centered on the substrate, and ca. 800 water molecules remained after removal of ones with their oxygen atom within 2.5 Å of any non-hydrogen atom of the complex. Figure 1 illustrates a system prepared in this way.

Figure 1.

A truncated protein-substrate complex with ca. 800 TIP4P water molecules; the QM region (green) consists of the side chain of the catalytic base and the substrate. The nearest 126 residues of the protein and the solvent form the MM region.

Initial simulations for the systems were carried out using QM/MM/MC statistical mechanics calculations, as implemented in the MCPRO program.²¹ Each simulation consisted of 5 × 10⁶ configurations of solvent equilibration, 10 × 10⁶ configurations of full equilibration, and 35 × 10⁶ configurations of averaging at 25 °C. All degrees of freedom for the substrate and the side chain of the catalytic base were variable, bond angles and dihedral angles were sampled for the side chains of all other residues, and the TIP4P water molecules could translate and rotate. The protein backbone was held fixed after the initial conjugate-gradient relaxation. Fixing the backbone during the MC simulations is an approximation, the validity of which was justified in earlier work on similar systems, artificial enzymes for Kemp elimination.¹² It had been shown that, when the backbone is extensively sampled (50 × 10⁶ configurations of MC) with a concerted rotation algorithm, the deviations of the backbone position in the resulting structures are minor. This holds in both the comparison of the reactant to the transition state configurations, and of either to the available crystal structures without the substrate. The overall backbone RMSD was below 0.16 Å.¹² The final configurations from these initial QM/MM/MC calculations were then used as starting points for the mechanistic investigations.

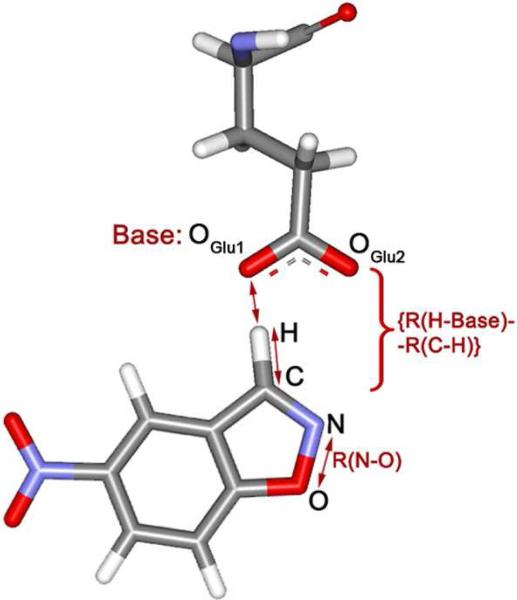
Potential of mean force (PMF) calculations were carried out for the Kemp eliminations by perturbing along reaction coordinates using MC/FEP calculations. Two distances were chosen as reaction coordinates, and two-dimensional free-energy maps were created. The increment between simulations was 0.04 Å for preliminary scanning, and 0.02 Å for refinement near stationary points. Double-wide sampling was used so two free-energy changes were obtained for each window by incrementing in both the forward and reverse directions. One reaction coordinate was the length of the breaking C-N bond. The reaction coordinate for the hydrogen transfer was chosen as the difference between the lengths of the forming and breaking bonds to the hydrogen, {R(H-Base) - R(C-H)}, where the sum, {R(H-Base) + R(C-H)}, was fixed at the value obtained in the initial QM/MM MC simulation (Figure 2). The combined reaction coordinate for hydrogen transfer reduces the dimensionality for creation of the free-energy surfaces from three to two. The approach has been previously validated; it was shown that the error for the barrier to hydrogen transfer thus obtained is insignificant for a wide variety of proton donor-acceptor combinations.²² In addition, for the hydrogen transfers, the quadrature method of Tubert-Brohman et al.^22a was also followed whereby the free energy changes are fit by cubic polynomials using free-energy derivatives obtained from only five windows of double-wide sampling (i.e., ten free energy changes in all). Analytical integration then yields the free energy profile. This approach was shown to introduce errors in the activation barrier of no greater than 0.5 kcal/mol versus conventional results using 25−30 windows.^22a In the present case, this treatment for hydrogen transfers reduced the computational effort from roughly 36,000 to 7,200 hours for construction of each two-dimensional free energy surface on 3-GHz Pentium processors.

Figure 2.

Choices for the reaction coordinates: R(N-O) and {R(H-Base) - R(C-H)}. An oxygen atom of the ionized Glu plays the role of the base in this case.

In the QM/MM implementation, the energy of the QM region was computed using the PDDG/PM3 semiempirical molecular orbital method.²³ PDDG/PM3 has been extensively tested for gas-phase structures and energetics,²³ and it has performed well in QM/MM/MC studies for numerous pericyclic,²⁴ substitution,²⁵ and elimination reactions in solution.^22b,26,27 Notably, the previous study of Kemp eliminations of benzisoxazole-3-carboxylates yielded free energies of activation within 2−3 kcal/mol of experimental data in water and methanol, and revealed the importance of ion-pairing in aprotic media.²⁷ In the present study, the QM-region consisted of the substrate, 5-nitrobenzisoxazole, and the side chain of the putative base, Glu or Asp (Figure 1). The linking hydrogen atom for the side chain was made coincident with C_α of the basic residue. The energy of the QM region was computed for every attempted move of the solute, i.e., every 10 configurations. The rest of the system was treated using the OPLS-AA force field.²⁸ To compute the electrostatic part of the interaction energy between the QM and MM regions, CM3P atomic charges were used for the QM atoms and the MM charges for the MM atoms.²⁹ The CM3P charges were unscaled as the QM region had a net charge of −1 for the cases examined here.³⁰ Interactions were truncated using a 10-Å residue-based cutoff based on distances between non-hydrogen atoms. Each FEP window entailed 5 × 10⁶ configurations of solvent equilibration, 10 × 10⁶ configurations of full equilibration, and 25 × 10⁶ configurations of averaging. At each point on the free energy surface, configurations from the Monte Carlo runs were saved. They are used to analyze and illustrate the structural variations along the reaction paths.

Results and Discussion

1. 34E4 catalytic antibody

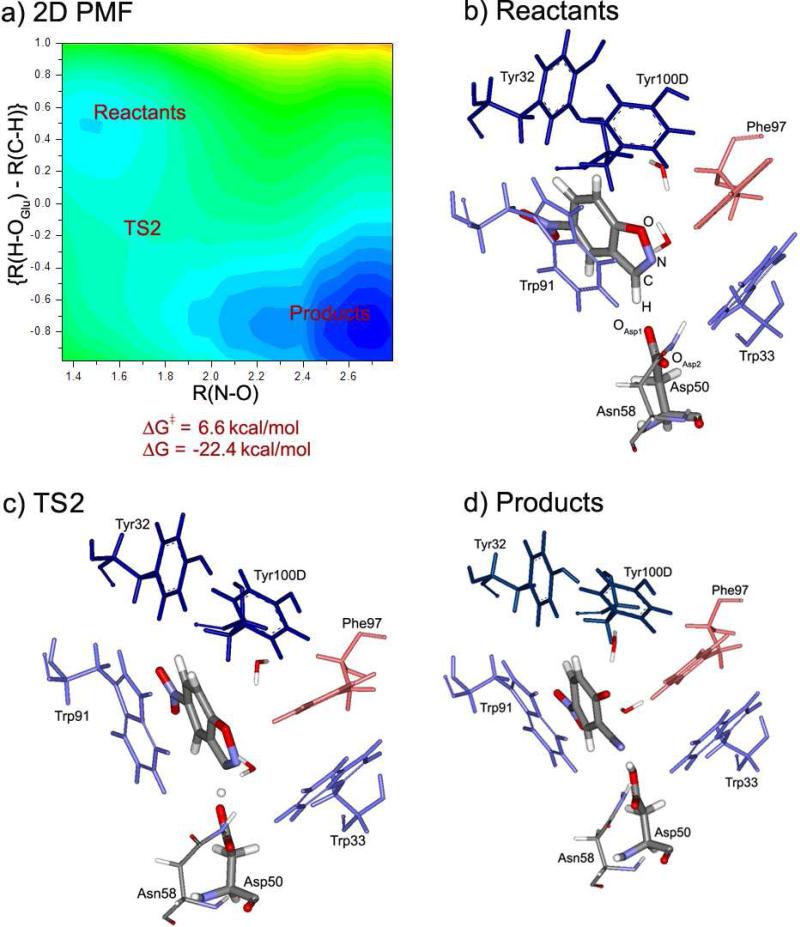
Figure 3 summarizes the QM/MM/FEP results for the original 34E4 catalytic antibody. The 2D PMF for the catalyzed reaction is shown in Figure 3a, and Figure 3b shows the structure of the initial complex with 5-nitrobenzisoxazole, as obtained from the QM/MM Monte Carlo relaxation. Typical structures of the transition state and the final product are illustrated in Figures 3c and 3d.

Figure 3.

Kemp elimination of 5-nitrobenzisoxazole catalyzed by the 34E4 antibody: (a) 2D PMF, showing the location of the reactants, transition state (TS1) and products; (b) QM/MM/MC relaxed structure of the initial complex; (c) TS1, and (d) the product complex from the QM/MM/MC/FEP simulations.

As can be seen from Figure 3b, 5-nitrobenzisoxazole is well-positioned in the binding site. It forms a short hydrogen bond to the base, Glu50 ({R(H-O_Glu1) + R(C-H)} is 2.68 Å), and a tight π-stacking contact with Trp91. There is an additional extended π-stacking network, Tyr32 – Tyr100D – Phe97 – Trp33, where Tyr100D interacts with Tyr32 and Phe97 in a T-fashion, while Trp33 and Phe97 form a shifted π-complex. These bulky aromatic residues perform the function of steering the substrate toward the base. In addition, there is a hydrogen bond between Asn58 and O_Glu2 (R(H-O_Glu2) = 2.16 Å). Several solvent water molecules are present in the binding site. Two of them are shown in Figure 3b. One is forming a hydrogen bond to the isoxazolyl oxygen of the substrate, and the other is simultaneously coordinated to O_Glu2 and the isoxazolyl nitrogen atom.

Starting from this complex the Kemp elimination was driven along the two reaction coordinates as described above. In the constructed free energy map in Figure 3a, the N-O bond opens to the right, and hydrogen transfers downward. The upper left corner of the map corresponds to the well of the reactants, and bottom right corner corresponds to the products. The reaction follows a single-step, concerted mechanism. In transition state TS1, the transferring hydrogen is half way between the donor C and the acceptor O atoms, and the O-N distance is 1.67 Å in TS1, while it is 1.43 Å in the reactants and 2.75 Å in the products. Therefore, the hydrogen transfer is more advanced in the transition state than the N-O bond breaking. The activation barrier for the reaction is 4.2 kcal/mol, and ΔG is −10.5 kcal/mol. The estimated uncertainty in these figures is ±0.5 kcal/mol. This error is known to be introduced by the polynomial approximation for computing free energies for hydrogen transfer processes.^22a The actual standard deviations from the fluctuations in the free-energy averages from the FEP simulations were approximately an order of magnitude smaller.

From the structure of the reactants, TS1, and products, it can be seen how the important contacts between the substrate and the residues of the active site evolve during the reaction. Mostly, all interactions are preserved. π-stacking between the substrate and Trp91 is well maintained, as is the Tyr-Tyr-Phe-Trp cluster. One of the solvent water molecules follows the oxygen atom of the substrate, which becomes formally negatively charged in the product. The other water molecule loses its coordination to N and retains a hydrogen bond to the O_Glu2 atom of the carboxyl group. It may be noted that the nitro group of the substrate rotated to be perpendicular to the phenyl ring early in the MC simulations and it retained this orientation through the course of the reaction. With PDDG/PM3, the planar form of nitrobenzene is lower in energy than the perpendicular rotamer by 2.25 kcal/mol, so the observed effect reflects a response to the environment.

2. E50D mutant

Figure 4 depicts results for the Kemp elimination catalyzed by the mutant protein. In Figure 4b, the equilibrated structure of the initial complex is shown. The orientation of 5-nitrobenzisoxazole in the binding pocket is very similar to that in 34E4. It forms the hydrogen bond to Asp50 ({R(H-O_Asp1) + R(C-H)} is 2.74 Å). A π-stacking interaction is also present between Trp91 and the substrate. The extended chain of residues, interacting with their π-systems, Tyr32 – Tyr100D – Phe97 – Trp33, is also retained. O_Asp2 forms a shorter hydrogen bond to Asn58 than in 34E4. The solvation pattern is somewhat different in the mutant than in 34E4; now two water molecules are coordinated to the isoxazolyl oxygen atom of the substrate, and no water molecule is hydrogen bonded to Asp50.

Figure 4.

Kemp elimination of 5-nitrobenzisoxazole catalyzed by the E50D mutant of the 34E4 antibody: (a) 2D PMF, showing the locations of the reactants, transition state (TS2) and products; (b) QM/MM/MC relaxed structure of the initial complex; (c) TS2, and (d) the product complex from the QM/MM/MC/FEP simulations.

The 2D PMF (Figure 4a) is similar to the one for 34E4. The transition state, TS2, is observed at R(N-O) = 1.63 Å, and the transferring hydrogen is again roughly midway between the donor C and the acceptor O_Asp1 atoms. The computed ΔG^‡ of the reaction is 6.6 kcal/mol, and ΔG is −22.4 kcal/mol. The predicted increase of the activation barrier corresponds to a 62-fold reduction in the reaction rate at 25 °C as compared to the original 34E4 antibody. This is in the overall good agreement with the experimental finding of a 30-fold reduction in k_cat at 20 °C.¹⁸ The overall ΔG for the reaction is notably 11.9 kcal/mol more exergonic. Although providing additional thermodynamic driving force for the reaction, this effect might lead to more pronounced product inhibition.

The structure of the binding site does not undergo dramatic rearrangement during the reaction. All contacts observed in the reactants are still present in TS2 and the product. Neither do any striking differences emerge immediately between the structures of the transition states TS1 and TS2, and the products of reaction for 34E4 and its E50D modification. Nevertheless, upon the E50D mutation, the energetics of the reaction undergo significant alteration. Therefore, the structural reasons for this effect need further exploration.

However, before pursuing this, it is noted that both calculated absolute free energies are 10−15 kcal/mol lower than from the experimental report.¹⁸ Such discrepancies can arise from many sources including inaccuracies in the QM method, though PDDG/PM3 has done well previously for several elimination reactions,^22b,26,27 treatment of the electrostatics in the simulations including choices of ionization states for all residues and the lack of explicit polarization in the MM region, and inconsistencies between the experimental and modeled conditions including use of buffers and added salts. Importantly, the difference in the barrier heights is well reproduced by the FEP results. The origin of this difference is the focus here and it is anticipated that the factors contributing to the discrepancies with the absolute free energies of activation are similar for 34E4 and its E50D variant.

3. Structural Analysis

The structural results and energetics reported in this section were produced by averaging over configurations saved at regular intervals during the averaging phase of QM/MM/MC simulations. Once stationary points were identified on the free energy surfaces, additional sampling was performed for these structures. The present analyses were carried out by averaging the results over 500 saved configurations.

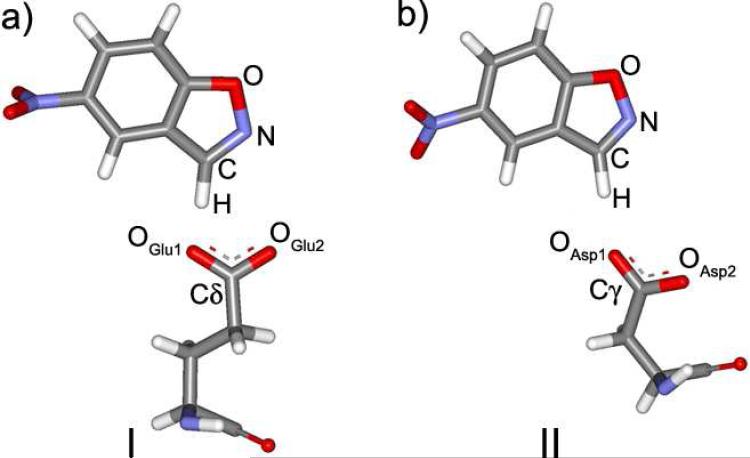
The contacts between the substrate and the catalytic base residues in the two proteins are first to be investigated. The discussion is illustrated by Figure 5, showing the structures of these contacts, and Table 1. A few differences between structures I and II (Figure 5) can be pointed out. First of all, the distance between Glu50 and the acidic hydrogen of 5-nitrobenzisoxazole is 0.06 Å shorter in the original antibody than in theAsp50 mutant. This is particularly interesting since a much greater discrepancy, ca. 0.3 Å, was found in the crystal structures for the hapten complexes.¹⁷ Thus, the protein and substrate adjust in response to removal of the methylene group to maintain catalytic activity at a higher level than might be expected. In any event, the elongation of the contact is still consistent with an increase in the activation barrier for hydrogen transfer in the mutant as compared to 34E4.

Figure 5.

The contact of 5-nitrobenzisoxazole with the base in (a) 34E4, and (b) the E50D mutant.

TABLE 1.

Average geometries of the contacts between 5-nitrobenzisoxazole and Glu/Asp in the reactant complexes from QM/MM/MC simulations.

34E4		E50D mutant
Parameter	Value	Parameter	Value
R(C-H), Å	1.19 ± 0.00	R(C-H), Å	1.17 ± 0.00
R(OGlu1-H), Å	1.49 ± 0.00	R(OAsp1-H), Å	1.57 ± 0.00
{R(C-H)+R(H-OGlu1)}, Å	2.68 ± 0.00	{R(C-H)+R(H-OAsp1)}, Å	2.74 ± 0.00
∠(H-OGlu1-Cδ), °	110.91 ± 0.06	∠(H-OAsp1-Cγ), °	154.75 ± 10.28
Dih(H-OGlu1-Cδ-OGlu2), °	12.65 ± 0.04	Dih(H-OAsp1-Cγ-OAsp2), °	28.91 ± 14.18

Furthermore, the orientation of the substrate for the hydrogen transfer can be analyzed as defined by the position of the hydrogen relative to the lone-pair on the O_Glu1 atom, i.e., the hydrogen acceptor. The angle H-O_base-C should be close to 120°, and the substrate and carboxylate group of the base should be in one plane. In the original antibody, the angle H-O_Glu1-Cδ is 110.9°, which is 9.1° away from the presumably optimal value. In the mutant, however ∠(H-O_Asp1-Cγ) is 154.8°, which is 34.8° greater than optimal. The dihedral angle determining the mutual orientation of the carboxylate group and 5-nitrobenzisoxazole should be close to 0 °. In 34E4 it is 12.7°. In the mutant it is 28.9°, which again is a larger deviation. The standard deviations for both the angle and the dihedral in the mutant are much larger, which suggests a less well-defined, floppier contact between the substrate and the base. Hence, overall, in 34E4, the contact is more favorable.

Another prominent contact in the binding pocket is between the substrate and the indole fragment of Trp91. Through electrostatic effects including polarization and charge-transfer, Trp91 is expected to stabilize the negative charge developing on the substrate during the reaction. The contact with Trp91 should stabilize the transition state, and thus contribute to the catalytic effect. It is important to bear in mind that Trp91 belongs to the MM-region of the system, and thus its electronic density cannot be polarized in response to the changes in the electronic structure of the substrate. Therefore, the observations here are made on the basis of the static atomic charges for Trp91.

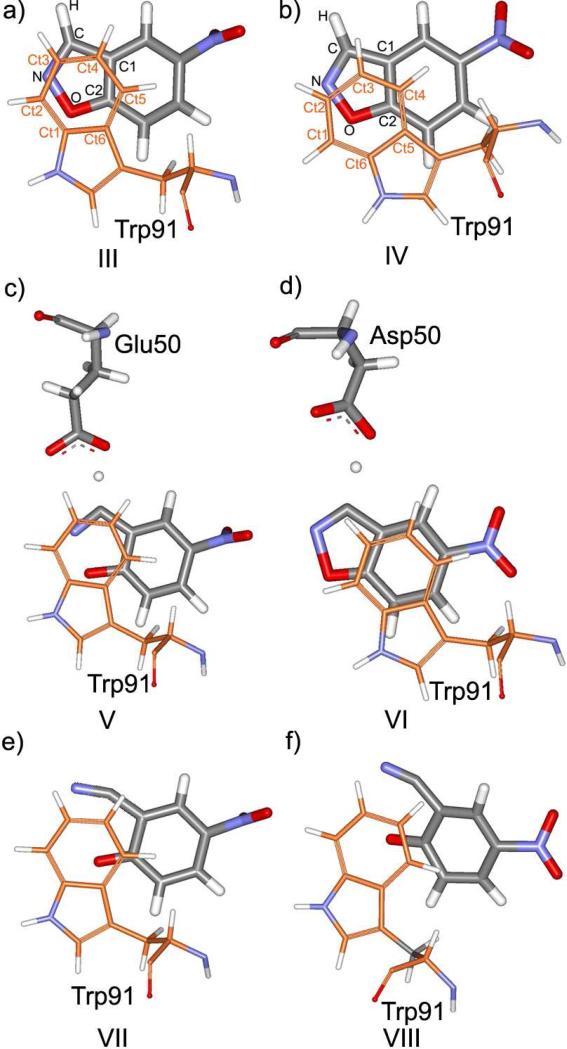
Figure 6 shows the mutual orientation of 5-nitrobenzisoxazole and the side chain of Trp91 in the reactants, transition states, TS1 and TS2, and the products. Table 2 contains corresponding contact distances for the reactants and transition states, and also the MM interaction energies between the substrate and Trp91. The latter were calculated using the QM charges on the substrate, as obtained from QM/MM/MC, and the OPLS-AA parameters for all atoms.

Figure 6.

The contact between 5-nitrobenzisoxazole and Trp91 in the reactant states of (a) 34E4, and (b) E50D mutant; (c) TS1, and (d) TS2; and in the products (e) for 34E4, and (f) for E50D.

TABLE 2.

Average characteristics of the contact displacements between 5-nitrobenzisoxazole and Trp91 from QM/MM/MC simulations.

Parameter	Value in 34E4 (reactants)	Value in E50D (reactants)	Value in 34E4 (TS1)	Value in E50D (TS2)
ΔE, kcal/mol[a]	−3.62 ± 0.69	−2.55 ± 0.56	−3.93 ± 0.60	−2.03 ± 0.53
R(Ct1-O), Å	3.52 ± 0.10	3.64 ± 0.18	3.52 ± 0.09	3.78 ± 0.21
R(Ct2-O), Å	3.76 ± 0.10	3.44 ± 0.16	3.77 ± 0.10	3.43 ± 0.17
R(Ct6-O), Å	3.39 ± 0.06	3.99 ± 0.23	3.39 ± 0.06	4.32 ± 0.28
R(Ct2-N), Å	3.70 ± 0.13	3.78 ± 0.18	3.70 ± 0.12	3.76 ± 0.16
R(Ct3-N), Å	3.41 ± 0.11	3.47 ± 0.16	3.41 ± 0.10	3.52 ± 0.16
R(Ct3-C), Å	3.77 ± 0.02	3.69 ± 0.13	3.76 ± 0.14	3.51 ± 0.15
R(Ct4-C), Å	3.45 ± 0.12	3.61 ± 0.16	3.44 ± 0.12	3.66 ± 0.15
R(Ct4-C1), Å	3.61 ± 0.13	3.80 ± 0.14	3.61 ± 0.13	3.86 ± 0.17
R(Ct5-C1), Å	3.59 ± 0.10		3.57 ± 0.10
R(Ct5-C2), Å	3.32 ± 0.01	3.69 ± 0.14	3.32 ± 0.09	3.74 ± 0.12
R(Ct6-C2), Å	3.57 ± 0.06	4.20 ± 0.11	3.57 ± 0.09	4.16 ± 0.10
R(Ctr1-Ctr2), Å[b]	3.52 ± 0.09	3.58 ± 0.12	3.51 ± 0.09	3.61 ± 0.13

^[a]The average MM energy of interaction between the substrate and Trp91.

^[b]The average distances between the geometrical centers of the 5-membered ring of the substrate and the 6-membered ring of Trp91.

In 34E4, Trp91 forms a parallel, not-shifted π-stacking interaction with the isoxazole ring of the substrate (Figure 6a). In the mutant, however, the phenyl ring of Trp91 is noticeably shifted from the orientation observed in the original antibody (structure IV, Figure 6b). There is an overall greater separation between the phenyl ring of Trp91 and the isoxazole ring of the substrate in the mutant as compared to 34E4 (interatomic distances are compared in Table 2). This effect was also seen in the crystal structure.¹⁷ The interaction energy between Trp91 and the substrate is more favorable in the original antibody (Table 2).

The π-stacking interaction with Trp91 should be especially important in the transition state and the product, when the five-membered ring of the substrate acquires much of the negative charge. In the transition state, a more dramatic effect can be observed (Figure 6c and 6d, Table 2). In TS1 of 34E4, Trp91 maintains the contact with the isoxazole ring of the substrate. In contrast, in TS2 of E50D, the phenyl ring of Trp91 and the isoxazole ring of the substrate are displaced. Trp91 now overlaps more with the phenyl ring of the substrate and now seems less well positioned to stabilize the region of increasing negative charge. The substrate-Trp separation is smaller, and the interaction energy is more favorable in the original antibody, as presented in Table 2.

Figures 6e and 6f show the Trp91-product contacts. In both cases, the center of the phenyl ring of Trp91 lies directly above the formally negatively charged oxygen, although in the case of the mutant, Trp91 and the oxygen are slightly further separated.

The mutual orientations of Trp91 and the substrate, especially in structures V-VIII in Figure 6, influence the magnitude of the activation barrier and catalytic performance of the antibodies. Importantly, it would not be possible to detect the noted differences in the analysis of crystal structures of only complexes of the proteins and haptens or even substrates.

The interaction of the carboxylate group of the base residue (Glu50/Asp50) with the NH₂-group of Asn58 is also expected to be significant.¹⁷ Structurally, the side chain of Asn58 assists in proper positioning of the base in the binding site. On the other hand, this hydrogen bond should stabilize the base, thus reducing its ability to efficiently abstract the proton from the substrate. In 34E4, the Glu50-Asn58 hydrogen bond is quite long (R(H_NH2-O_Glu2) = 2.29 ± 0.23 Å). The shorter side chain of Asp50 in the mutant, however, promotes a closer contact with Asn58, and the H_NH2-O_Asp2 distance is significantly reduced to 1.94 ± 0.16 Å. Therefore, the ionized Asp50 should be a weaker base and the barrier to hydrogen transfer should increase, all else being equal. This is another potential contributor to the poorer catalytic performance of E50D.

Furthermore, Asn58 is more exposed to the binding pocket in E50D than in the original 34E4, where it is enclosed by the longer side chain of Glu50. In fact, in the product of the mutant, after the opening of the N-O bond, the N-atom of the cyano group forms a hydrogen bond to the NH₂-group of Asn58. This contributes to the more negative ΔG of the reaction.

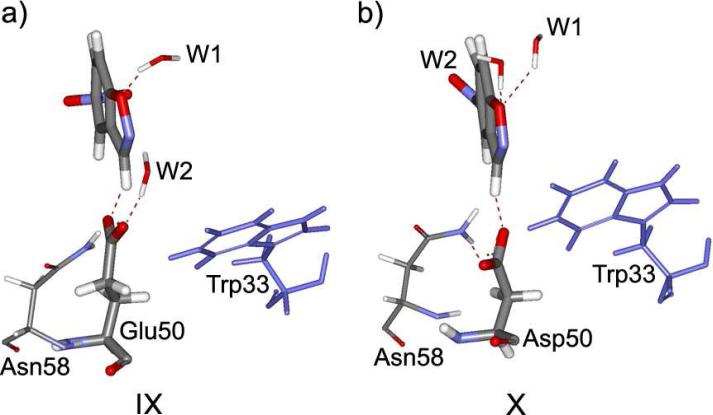
An additional difference between 34E4 and its E50D modification can be found in the water placement in the active sites. In both proteins, two solvent water molecules are coordinated to the substrate. Figure 7 illustrates their positioning. In the original antibody, one water molecule, W1, forms a hydrogen bond to the isoxazolyl oxygen atom of the substrate (structure IX, Figure 7). However, in the E50D variant, both W1 and W2 are coordinated to this oxygen atom (X, Figure 7). The contact between the oxygen and the water molecules becomes tighter as the oxygen acquires more negative charge. Since the N-O bond cleaves relatively late in the reaction, the energy of the transition state should be primarily defined by the hydrogen transfer. Therefore, hydration of isoxazolyl oxygen leads to stabilization of the product to a greater extent than of the transition state. Hence, a more negative ΔG should result from the better hydration of the oxygen, while ΔG^‡ should be less sensitive to it. This is consistent with what is computed for the E50D mutant, whose ΔG is more negative than that of 34E4.

Figure 7.

Hydrogen bonding to solvent water in the reactant states of the complex of 5-nitrobenzisoxazole and (a) 34E4, and (b) its E50D mutant.

The other water molecule in 34E4, W2, forms a hydrogen bond to the carboxylate group of Glu50. W2, in combination with Asn58, participates in the positioning of Glu50 to perform its catalytic function. In the mutant, the Asp50 residue, having a shorter side chain, is buried deeper in the binding site, and shielded by the bulky side chains of Trp33 and Asn58. No solvent water can get in contact with it. Asp50 is, however, tightly coordinated to Asn58 through a short hydrogen bond. This tight contact, not compensated by the interaction with a structural solvent water, results in the position of Asp50 being less favorable for the reaction, as was already suggested (see Figure 5 and Table 1). On the other hand, the interaction of W2 with the carboxylate group of Glu50 should reduce its basicity and offset the poorer interaction with Asn58. Indeed, the pK_a values for Glu50 and Asp50 in the two antibodies are both high, but similar at 6.4 and 6.6.¹⁸ Hence, the better performance of the original 34E4 is not based so much on the actual basicity of the catalytic base, which does not differ greatly from that in the mutant, but rather on the structural factors in the active site that tighten the base-substrate contact.

Conclusions

The mechanism of Kemp elimination of 5-nitrobenzisoxazole catalyzed by the catalytic antibody 34E4 and its E50D variant has been studied using free-energy perturbation calculations in conjunction with QM/MM/MC simulations. The computed activation barrier for the mutant was found to be 2.4 kcal/mol higher than for the original antibody. This corresponds to a 62-fold rate deceleration for the mutant, which is similar to the experimental factor of 30. In both cases the computations find that the reactions follow a concerted path, where the hydrogen transfer from 5-nitrobenzisoxazole to the base (Glu50/Asp50) is more advanced at the transition state than the N-O bond opening. Structural analysis of the complex of the substrate with both proteins was performed. In addition to the catalytic base, residues Trp91 and Asn58, the π-quartet of Tyr32, Tyr100D, Phe97, and Trp33, and two solvent water molecules form the specific microenvironment of the binding sites.

Further, the structural origin of the reduced catalytic activity for the mutant was analyzed. A combination of structural effects in the reactants, transition states, and products appears to be responsible for the rate deceleration in the mutant. The relative positions of the substrate and the base, including the length and orientation of the hydrogen bond, were shown to be less optimal in the mutant than in 34E4. Trp91, although performing similar π-stacking interactions with the reactant in both proteins, shifts in the transition state TS2 for the mutant protein (Figure 6, structure VI). In TS2, it appears to be less well positioned to stabilize the developing negative charge on the substrate. Furthermore, solvent water and the Asn58 residue play roles by forming hydrogen bond contacts to the substrate and the carboxylate group of the base. In 34E4, one water molecule and a weakly coordinated Asn58 position Glu50 for the efficient proton abstraction. However, in the E50D variant, Asp50 is deeply buried in the pocket, and shielded from the solvent by the side chains of Trp33 and Asn58. This yields a less favorable position of the base, including the longer separation between the H-donor and H-acceptor and the less optimal angular orientation. The carboxylate group of Asp50 also forms a short hydrogen bond to the NH₂-group of Asn58, though this effect on the basicity of the carboxylate is likely offset by the hydrogen bond between the water molecule and Glu50 in 34E4. As a result, the experimental pK_a values of Glu50 and Asp50 in the two proteins are close. Therefore, the actual strength of the catalytic base does not play as much of a role in rate deceleration in the mutant as the structural effects leading to the looser contact between the base and the substrate. In addition, in the mutant, the NH₂-group of Asn58 is more exposed to the binding pocket and interacts with the nitrogen atom of the forming cyano group. This contributes to greater product stabilization and more negative ΔG for the E50D variant. Better solvation of the phenolate oxygen in the product with the mutant is identified as another factor leading to product stabilization.

Overall, the identified structural effects along the reaction paths in the binding sites of the two antibodies consistently explain the observed rate deceleration upon the modest mutation of Glu50 to Asp. Such insights significantly expand the information available from the crystal structures for hapten complexes. Additionally, the present study points to several structural factors of relevance for further design of efficient protein catalysts for Kemp elimination.