Assessment of Programs for Ligand Binding Affinity Prediction

Abstract

The prediction of the binding free energy between a ligand and a protein is an important component in the virtual screening and lead optimization of ligands for drug discovery. To determine the quality of current binding free energy estimation programs, we examined FlexX, X-Score, AutoDock and BLEEP for their performance in binding free energy prediction in various situations including co-crystallized complex structures, cross docking of ligands to their non-co-crystallized receptors, docking of thermally unfolded receptor decoys to their ligands and complex structures with “randomized” ligand decoys. In no case was there a satisfactory correlation between the experimental and estimated binding free energies over all the datasets tested. Meanwhile, a strong correlation between ligand molecular weight-binding affinity correlation and experimental-predicted binding affinity correlation was found. Sometimes the programs also correctly ranked ligands’ binding affinities even though native interactions between the ligands and their receptors were essentially lost due to receptor deformation or ligand randomization, and the programs could not decisively discriminate randomized ligand decoys from their native ligands; this suggested that the tested programs miss important components for the accurate capture of specific ligand binding interactions.

Introduction

The prediction of the binding free energy between a ligand and its protein target is an important component in the virtual screening/lead optimization of ligands for drug discovery. Many scoring functions for binding free energy estimation have been developed. These can be grouped into three categories: force field methods^1,2, empirical scoring functions^3-6 and knowledge-based potentials^7,8. Usually, the quality of binding free energy prediction has been assessed by Pearson's correlation coefficient⁹, CC, defined as the covariance between the calculated and observed binding energies for ligand-receptor complexes divided by the product of their respective standard deviations. Several studies on the performance of current binding energy scoring functions have been reported^10-12, which indicated that the CC at the state-of-the-art is around 0.5¹¹ and is at best 0.7^10,12 when the binding energies of native (co-crystallized) complex structures were estimated. Since native complex structures should be the easiest cases for binding energy prediction, the current prediction limit of binding energy scoring functions with a CC of 0.5−0.7 for native complex structures suggests that additional improvements might be required for them to be used in the approaches where the comparison of binding energies are important.

One of the known problems occurring in rigid receptor docking is called the “cross docking” problem^10,13,14. Cross docking refers to the docking of a ligand to a receptor whose structure has not been determined by co-crystallization with that ligand. The structure of the binding pocket of the receptor is usually slightly different when it is co-crystallized with the ligand than when it is not. This slight change in receptor structure can sometimes cause a dramatic change in the top-scoring ligand conformation compared to when the co-crystallized receptor structure is used^10,15. A possible cause of the failure of a rigid receptor approach in cross docking might be the scoring functions’ sensitivity to steric repulsions¹¹, which produces a large repulsive energy if ligand atoms slightly intrude into the receptor's side chain positions. However, slight modifications of the locations of the clashing atoms of ligands and proteins to avoid steric repulsion are apparently not performed in rigid receptor docking¹⁰. In this regard, flexible receptor docking has been suggested as a means for the more accurate assessment of binding free energy^16-21.

The problem with flexible receptor docking is that it is computationally expensive. For example, in a rotamer-based approach to flexible receptor docking which is considered to be one of the fastest methods, 96 alternative receptor structures were used to account for the side chain flexibility of three residues in the protein tyrosine phosphatase 1B binding pocket¹⁶. In an ingenious approach, the receptor structure was divided into immobile and mobile parts, the ligand was docked to each part, and the binding energy was calculated by combining the partial docking scores²². However, when we do not know the location of the binding pocket in a given protein and accordingly do not know which residues should be treated as rigid or mobile, the number of alternative receptor structures could easily become very large, tremendously increasing the computational cost. Thus, before discarding rigid docking as a means of estimating binding energy, it must be certain that there is no way to improve upon it, since the sequencing of the human as well as other genomes^23-28 has necessitated the formulation of faster and better approaches to drug development via virtual screening and lead optimization.

Regarding virtual screening and lead optimization on a proteomic scale, the practicality of achieving this goal has been hindered by the fact that there is no general method that can produce very accurate protein structures without a known structure of high homology²⁹. In practice, many proteins will have predicted structures whose Cα root-mean-square-deviation (RMSD) from native is in the 3−6 Å range³⁰, even when the proteins have homologs of known structure. Thus, for many proteins, virtual screening and lead optimization must be performed with inaccurately predicted structures. The question is: “How close is close enough for relatively accurate binding affinity prediction”? As far as we know, this question has not yet been addressed; the prediction of binding free energy is different from and requires more elaborate functions than those for binding pose prediction. Although many studies on the performance of docking/scoring schemes have been published^{10,11,14,31-33}, virtually none examined binding energy prediction performance in cross docking or predicted receptor structure-based docking. Thus, to address this issue, we examined several docking/binding affinity scoring programs. Also, we performed a benchmark on the binding affinity prediction programs with ligand decoys whose atoms were shuffled while maintaining their chemical composition and heavy atom covalent bond geometry. To our knowledge, there has been no study of this kind.

The performance of any algorithm may be assessed in a variety of ways. Here, we address the following questions: how good are current docking/scoring algorithms in predicting the binding affinity for (1) co-crystallized complex structures, (2) cross docking datasets, (3) datasets comprised of ligands and the deformed decoys of their receptors and (4) datasets comprised of “randomized” ligand decoys. To answer these questions, we examined four programs on twelve datasets compiled from two databases.

Material and Methods

Overview

A summary of the datasets, docking and ranking programs used in this study is shown in Table 1. Each of the datasets had the complex structures of the same receptor and a set of its ligands (CDS sets: CDS1 to CDS12). Four programs were used in this study. They employed physics-based (AutoDock 3.0.5³⁴), knowledge-based (BLEEP³⁵) and empirical (FlexX 2.0.2⁸, X-Score 1.2.1⁶) scoring functions. FlexX and AutoDock were used in docking simulations and for ranking ligand conformations according to their binding scores. X-Score could only rank ligand conformations. The performance of BLEEP was assessed with the data obtained by the authors of BLEEP, extracted from the Protein Ligand Database v1.3³⁶. We considered binding energy predictions in four contexts: 1) native complex structures, 2) cross docking, 3) deformed receptor structures and 4) randomized ligand decoys.

Table 1.

Summary of evaluated datasets and docking and ranking programs

Type of study	Dataset	Docking program	Ranking program
Native complex structures	CDS1 to CDS7	None	AutoDock
			FlexX
			X-Score
	CDS8 to 12	None	BLEEP
Cross docking	CDS6 CDS7	AutoDock	AutoDock
		FlexX	FlexX
			X-Score
Deformed receptor structures	CDS6 CDS7	AutoDock	AutoDock
		FlexX	FlexX
			X-Score
Randomized decoys	CDS1 to CDS7	None	AutoDock
			FlexX
			X-Score

Dataset compilation

Seven datasets of the one receptor-many ligands type (the CDSk, k=1,7 sets), each containing the structures of the complexes of the same receptor and a set of its ligands, were prepared from PDBbind database v2005³⁷ according to the following steps: (1) The complex structures in the database were grouped into datasets according to the amino acid sequences of their receptors so that the receptor structures in each dataset had the exactly same amino acid sequences. (2) In some datasets, some complex structures had experimentally determined pKi values and others pKd. Although pKi and pKd values are often used interchangeably, to ensure as much consistency of binding affinity data as possible in each dataset, we selected the complex structures so that all the complex structures in a dataset had pKi values or all of them had pKd values. Thus, we determined which between pKi and pKd was the majority in each dataset and removed the complex structures with the minority binding constant type. (3) The datasets whose number of complex structures was less than 10 were removed. (4) The datasets whose range of experimentally determined pKd or pKi was less than 3.0 were removed. (5) Only one entry of the duplicated entries with the same receptor and the same ligand was left.

After applying the above criteria, 7 datasets, CDS1 to CDS7, remained. For CDS6, two subsets, CDS6a and CDS6b, were made by preserving the Zn atom in the active site (CDS6a) or removing it (CDS6b). CDS1 to CDS7 are shown in Table 2. The range of the experimentally determined pKd or pKi values in each dataset was equal or more than 3.48. When the receptor structures in each dataset were aligned using the structural alignment program TM-align³⁸, the average Cα root-mean-square-deviation, RMSD, between any two receptor structures in a dataset was 0.30 Å. Also, the entries in CDS1 to CDS7, except CDS6b, were combined to make a larger dataset, CDSa. CDSa's ranges of molecular weight and pKd (pKi) were 831 Da and 9.17, respectively. Water was removed from all the receptor structures. The ligands had MMFF94 charges³⁹ and these MMFF94 charges were used throughout this study except in the section of binding affinity estimation with randomized decoys, where Gasteiger-Marsili charges were assigned to the native ligands and their decoys.

Table 2.

Datasets used in this study

Dataset	Receptor	PDB ID's	NL1	RMW2	HET3	NC4	REE5
CDS1	Carbonic anhydrase II	1bcd, 1g1d, 1g52, 1g53, 1g54, 1ttm, 1xpz, 1xq0, 1if7, 1if8	10	300	Zn	1	4.18
CDS2	Endothiapepsin	1eed, 1epo, 1epp, 1epq, 2er6, 2er9, 3er3, 4er1, 4er2, 5er2, 5er1	11	423	None	1	4.51
CDS3	HIV-1 protease	1g2k, 1g35, 1gno, 1hbv, 1hos, 1hps, 1hpv, 1hpx, 1hsg, 1hvi, 1hvj, 1hvk, 1hvl, 1ohr, 1w5v, 2bpv, 2bpy, 2bqv, 7upj, 1ajv, 1ajx, 1c70, 1hih, 1dif, 1w5w, 1w5y, 1iiq, 1nh0	28	351	None	2	4.29
CDS4	Oligo-peptide binding protein	1b05, 1b0h, 1b1h, 1b2h, 1b32, 1b3f, 1b3g, 1b3h, 1b3l, 1b40, 1b46, 1b4h, 1b4z, 1b51, 1b58, 1b5h, 1b5i, 1b5j, 1b6h, 1b7h, 1b9j, 1jet, 1jeu, 1jev, 1qka, 1qkb, 2olb	27	140	None	1	3.48
CDS5	Ribonuclease a	1jn4, 1o0f, 1o0h, 1o0m, 1o0n, 1w4o, 1w4p, 1w4q, 1z6s, 1afk, 1afl, 1o0o, 1qhc	13	485	None	1	3.48
CDS6a,b6	Thermolysin	1qf0, 1qf1, 1qf2, 1tlp, 1tmn, 1z9g, 1zdp, 4tln, 5tln, 1os0	10	394	Zn	1	3.83
CDS7	Beta trypsin	1c5t, 1g36, 1ghz, 1lqe, 1oyq, 1ppc, 1pph, 1tng, 1tnh, 1tni, 1tnj, 1tnk, 1tnl, 1gi1, 1gi4, 1gi6, 1gj6, 1o2j, 1o2n, 1o2o, 1o2p, 1o2q, 1o2r, 1o2s, 1o2t, 1o2u, 1o2v, 1o2w, 1o2x, 1o2z, 1o30, 1o32, 1o35, 1o36, 1o37, 1o39, 1o3b, 1o3d, 1o3e, 1o3h, 1o3i, 1o3j, 1o3l, 1qb1, 1qbn, 1qbo, 1tx7	47	450	None	1	6.47
CDS8	Beta trypsin	1tpp, 1tni, 1tnj, 1tnk, 1tnl, 1yyy, 1zzz	7	350	None	1	5.39
CDS9	Carbonic anhydrase II	1am6, 1bcd, 1bn1, 1bn3, 1bn4, 1bnm, 1bnn, 1bnq, 1bnt, 1bnu, 1bnv, 1cil, 1cim, 1cin, 1bnw	15	328	Zn	1	6.10
CDS10	Endothiapepsin	2er6, 2er7, 2er9, 3er3, 4er4, 5er2, 1epo, 2er0	8	414	None	1	2.62
CDS11	HIV-1 protease	1hpv, 1htf, 1hvi, 1hvj, 1hvk, 1hvl	6	289	None	2	2.36
CDS12	Thrombolysin	1thl, 1tlp, 1tmn, 2tmn, 4tln, 4tmn, 5tln, 5tmn, 6tmn	9	410	Zn	1	6.47

¹Number of ligands

²The difference between the maximum and minimum ligand molecular weight

³Hetero atoms in the binding pockets

⁴Number of chains in the receptors

⁵The difference between the maximum and minimum pKd or pKi

⁶CDS6a maintained the Zn atom in the active sites while CDS6b was prepared by removing the Zn atom from the active sites.

Another group of datasets (CDS8 to 12) was constructed from the Protein Ligand Database v1.3³⁶, applying the same criteria as for CDS1 to 7, except that the minimum number of complex structures and the minimum pKd or pKi difference for a dataset was lowered to 7 and 2.3, respectively, so that 5 datasets result. These datasets are also shown in Table 2.

Docking and ranking programs

FlexX 2.0.2⁸ and AutoDock 3.0.5³⁴ were used to generate the docked conformation of ligands and to rank the conformations according to their binding scores. X-Score 1.2.1⁶ has ranking functionality but not docking capability. Thus, in cross docking and decoy docking studies, the docked conformations from FlexX were used as an input to X-Score to obtain X-Score estimations of binding affinity. Since we obtained binding scores by BLEEP from the Protein Ligand Database v1.3, we did not perform actual scoring with BLEEP.

Binding affinity estimation with native X-ray complex structures

The binding energies of the X-ray complex structures were estimated by FlexX, X-Score and AutoDock. Each complex structure of the datasets had two files, one receptor structure file in pdb format and one ligand structure file in mol2 format. For the binding energy estimation with X-Score, the files were processed as follows. The mol2 format files of the ligand structures were processed with fixmol2 option of X-Score to correct any atom or bond typing error and the resulting files were used as the input files for X-Score. The pdb files of the receptor structures were processed with fixpdb option of X-Score and used as the input files for X-Score. All default parameters of X-Score were used, and the binding energies were calculated with the score command of X-Score. Among X-Score's three scoring functions, HMScore showed the best CC over our datasets (data not shown). However, since the average of the values by X-Score's three scoring functions showed similar prediction performance and lower variance over our datasets (data not shown), we used this average as the predicted binding score throughout this study.

Binding energy estimation for the X-ray complex structures with FlexX was performed as follows: Since applying FlexX's transformation rule on ligands gave better binding affinity prediction than when it was not applied (data not shown), this transformation option was applied in every FlexX calculation. All histidines in the receptors were treated as the neutral his type. All arginines and lysines were treated as having a +1 charge and all aspartates and glutamates were treated as having a −1 charge. Only metal ions inside the binding pockets were included in the binding energy calculation. Cysteines not in disulfide bonds were separately treated as the cysh type. The center of mass of the ligand was used as the probe location for each complex. All residues of a receptor were considered in the binding score calculation. The binding energy was estimated with the score fix command.

Binding energy estimation of the X-ray complex structures with AutoDock was performed as follows. The receptor structure files were converted to pdbqs format with pmol2q⁴⁰ and used as the input files. The ligand structure files were processed with AutoDockTools⁴¹ to produce pdbq format input files. Grids of length 30.0 Å were placed around the center of ligands with a spacing of 0.375 Å. The gpf and dpf parameter files were generated with gpf3gen and dpf3gen provided in the AutoDock package, respectively. The binding energy evaluation was performed with epdb command on the native receptor and ligand structures. Even though we used high resolution X-ray complex structures, AutoDock produced positive non-bonded energy for close contacts between ligand and receptor atoms. We examined non-bonded energy of each ligand atom, and ignored it if it was positive. However, in cross docking and decoy docking studies described below, this step was not performed, since AutoDock moved ligands to resolve close contacts during docking simulation. Binding energy estimation for X-ray complex structures with BLEEP was obtained from the Protein Ligand Database v1.3³⁶.

The programs’ performance in binding affinity prediction for a dataset was assessed by calculating CC, the Pearson's correlation coefficient⁴² between the experimental binding affinity and estimated binding score. For CDS1 to 7, PDBbind v2005 provided pKd or pKi for each complex structure. Since X-Score gave estimated pKd, its output was directly used to calculate the CC. Since FlexX and AutoDock provide the estimated binding free energy in kJ/mol and kcal/mol, respectively, the experimental pKd or pKi was converted to the experimental binding free energy with the following formula: experimental binding free energy = RT log_e (10^{−pKd or pKi}) where RT = 0.59 kcal/mol. For CDS8 to 12, since Protein Ligand Database v1.3 provided both experimental and estimated binding energies in kJ/mol, these values were compared directly. We also measured the correlation coefficient between the logarithm of ligand molecular weight and experimental binding affinity.

Cross docking dataset/evaluation approach

Dataset

Over the long term, we would like to be able to predict binding affinity using inaccurate protein models that are generated by protein structure prediction algorithms such as TASSER⁴³. Logically, a binding energy prediction program should be first capable of predicting binding energy with co-crystallized X-ray complex structures and the X-ray structures of receptors and their ligands which were not co-crystallized with them; if not, then predictions on inaccurate models would be expected to be very unreliable. As explained in Results and Discussion, only CDS6a,b and CDS7 showed a satisfactory CC for X-ray complex structures with all of FlexX, X-Score and AutoDock (Table 3). However, since CDS6a contained zinc in the binding pockets of the receptor structures and thus could not be used as it was for cross docking study, we used its Zn-free version, CDS6b, for the cross docking study. CDS6b behaved similarly to CDS6a in binding affinity estimation with X-ray complex structures (Table 3). For ease of docking simulation and analysis, we translated and rotated the receptor structures in CDS6b and CDS7 so that they all could be superimposed on the receptor structure of the complex structures 1tlp and 1oyq, respectively. 1tlp and 1oyq were the complex structures with the largest ligands in the respective datasets. The receptor structures’ mean Cα RMSD from the receptor structures of 1tlp and 1oyq was 0.16 and 0.24 Å for CDS6b and CDS7, respectively. The ligands of CDS6b and 7 were also translated and rotated according to their native receptor structures so that their relative position to their native receptor structures did not change.

Table 3.

Correlation between experimental and predicted binding affinities for the X-ray complex structures in CDS1 to 7

Dataset	CC1						CCMW2
	FlexX6		X-Score		AutoDock
	NL5	OL5	NL5	OL5	NL5	OL5
CDS1	0.80	0.77	−0.04	−0.05	0.33	−0.42	−0.16
CDS2	0.06	−0.10	−0.08	−0.13	−0.28	0.15	0.04
CDS3	0.36	0.25	0.42	0.41	0.43	0.44	0.49
CDS4	−0.17	0.14	0.15	0.17	−0.04	0.06	0.07
CDS5	0.43	0.54	0.48	0.38	0.71	0.50	0.73
CDS6a	0.76	0.79	0.79	0.78	0.85	0.80	0.87
CDS6b	0.79	ND4	0.79	ND4	0.87	ND4	0.87
CDS7	0.74	0.75	0.79	0.77	0.70	0.74	0.71
Avg3	0.43	0.45	0.36	0.33	0.39	0.32	0.39
CDSa	0.10	0.14	0.61	0.61	0.40	0.60	0.62
	BLEEP
CDS8	0.95						0.77
CDS9	0.89						0.94
CDS10	0.08						0.05
CDS11	0.64						0.63
CDS12	0.76						0.70

¹Correlation coefficient between experimental pKd or pKi and predicted binding score

²Correlation coefficient between the logarithm of ligand molecular weight and experimental pKd or pKi

³Average of the seven CC's above, excluding CDS6b

⁴Not determined

⁵NL: native ligands, OL: Open Babel native-like ligands

⁶The full and "clashless" scores were used for the native and Open Babel native-like ligands, respectively.

Docking simulation and Ranking

Docking simulation and ranking with FlexX were performed as follows: For each receptor structure in CDS7 and CDS6b, all of its residues were considered in docking simulation and binding score calculation. The probe location of a receptor structure was defined as the center of mass of its native ligand. Amino acid typing was the same as in the binding score calculation with the native X-ray complex structures. Base fragments of a ligand were selected with selbas a command, placed with placebas 3 command and grown with complex all command. Default values were used for all the other parameters. Among the generated ligand conformations, the top scoring conformation was selected as the “best scoring” conformation of the ligand for the receptor structure it was docked to. One hundred top scoring ligand conformations were also saved for the ranking analysis with X-Score. Re-scoring and ranking of the ligand conformations with X-Score was performed with the docked ligand conformations obtained with FlexX and their receptor structure as was done for the native complexes. The top scoring conformation was selected as the “best scoring” conformation of the ligand for the receptor. Since we did an “all ligands to all receptor structures” type of cross docking, we obtained as many best-scoring complex structures for a ligand as the number of the receptor structures in its dataset. We chose the complex with the best score among them and named it the “best-of-best scoring” complex for the ligand and also called the ligand conformation in this complex the “best-of-best scoring” conformation of the ligand.

Docking simulation and ranking with AutoDock were performed as follows: The superimposed receptor and ligand structure files used for FlexX were converted to pdbqs (with pmol2q) and pdbq (with AutoDockTools) files, respectively, as described in the section of binding affinity estimation with native X-ray complex structures. Grids of length 30.0 Å were placed around the center of ligands with a spacing of 0.375 Å. The gpf and dpf parameter files were generated with gpf3gen and dpf3gen provided in the AutoDock package, respectively. A Lamarckian genetic algorithm search was performed to find the best scoring conformation with the following parameters: ga_pop_size 50, ga_num_evals 250000, ga_num_generations 27000, ga_elitism 1, ga_mutation_rate 0.02, ga_crossover_rate 0.80, ga_window_size 10, set_ga, la_search_freq 0.06, set_psw1 and ga_run 10. Default values were used for all the other parameters. “Best scoring” ligand conformations and “best-of-best scoring” complex structures and ligand conformations were obtained in the same way as with docking and ranking with FlexX.

RMSD from native of the cross-docked ligands. Since the receptor structures in CDS6b and CDS7 were superimposable without big deviation, the cross-docked conformation and the native one of a ligand could be compared straightforwardly with the root-mean-square distance between the equivalent atom pairs in the two conformations (RMSD from native).

Contact map

We made a two-dimensional matrix for each ligand-receptor complex. The columns and rows corresponded to the ligand atoms and the receptor amino acids, respectively. We considered that there was a contact between a ligand atom and a receptor residue if the distance between the ligand atom and any of the atoms of the receptor residue was less than 6 Å. We chose the rather generous 6 Å as the contact distance cutoff to allow ligands some freedom to move inside the binding pockets. We set each element of the matrix (each corresponding to ligand atom-receptor residue pair) to 1 if there was a contact or 0 if not, to obtain the contact map for the ligand and the receptor structure. The change in ligand-receptor contact in two contact maps was calculated as the percentage of the number of the elements which were 1 in both contact maps over the number of the elements which were 1 in the reference contact map. For the estimation of the change in ligand conformation due to cross docking, the contact maps from the docked complexes were compared to those from the native X-ray complex structures, which were used as the reference contact maps.

Decoy docking dataset/evaluation approach

Dataset

For the same reason as that for the cross docking, CDS6b and CDS7 were chosen as the datasets for the decoy docking study. Again the receptor structures of 1tlp and 1oyq were chosen as the reference receptor structures. One hundred decoys were generated from each of the reference receptor structures for each 1, 2 and 3 ± 0.5 Å Cα RMSD from native (decoy RMSD) bin with our in-house program which employed Monte Carlo sampling applied to an all atom protein model⁴⁴. The receptor residues were randomly moved and new conformations were accepted or discarded using the Cα RMSD from native of the ligand-contacting residues (determined as the residues which had atoms within 5.0 Å from the ligand atoms in 1tlp or 1oyq complex structure) of the new structures as the “energy” and a kT value of 0.1. The unfolding simulation continued until the atoms of the ligand-contacting residues had been moved on average by 1, 2 or 3 ± 0.5 Å from their original locations. The decoys were briefly energy-minimized with the program MINIMIZE in TINKER⁴⁵ until their Cα RMSD gradient from native reached 1.0 kcal/mole/Å. This minimization changed the Cα RMSD from native of the decoys and thus the minimized decoys were grouped again into 1, 2 and 3 ± 0.5 Å Cα RMSD bins. There were 93, 101 and 97 decoys and 100, 99 and 95 decoys in 1, 2 and 3 ± 0.5 Å Cα RMSD bins for CDS6b and CDS7, respectively.

Docking simulation and ranking

Docking simulation with FlexX was performed as follows: All the residues of the receptor structures of 1tlp and 1oyq were used in docking simulation. The probe locations for the receptor structures of 1tlp or 1oyq, defined in cross docking study, often could not be used in decoy docking study, since the locations often overlapped with those of decoy receptor atoms. In these cases, the probe location was randomly translated by the step size of 0.3 Å until it reached a location where the minimum distance between the probe and the receptor atoms was between 3.5 and 4.5 Å. Docking simulation and ranking of the conformation of the docked ligands with FlexX were performed as in the cross docking study. X-Score ranking of the ligand conformations generated with FlexX was also done as in cross docking. The docking simulation and ranking with AutoDock was performed as in cross docking study except that decoys were used instead of the cross docking receptor structures. The “best scoring” conformation of a ligand for a decoy was the conformation of the ligand that produced the best score with the decoy. The “best-of-best scoring” complex structure for a ligand in a decoy Cα RMSD from native bin was the complex structure of the ligand and a decoy in the given bin that had the best binding score among the complex structures which had the ligand and the decoys in the bin. The ligand conformation in this complex structure was termed as the “best-of-best scoring” conformation of the ligand in the bin.

Contact map

The contact map was obtained with the “best-of-best scoring” complex for each ligand and decoy Cα RMSD bin, as in cross docking.

Binding affinity estimation with randomized ligand decoys

Each ligand in CDS1 to CDS7 was “randomized” by “swapping” the chemical entities of the ligand atoms according to the following rules: 1) halogens could be swapped only with hydrogens, 2) an oxygen in a carboxyl group could be swapped with a hydrogen, 3) heavy atoms could be swapped with heavy atoms only when the connectivity among heavy atoms could be maintained by, if needed, adding and/or deleting hydrogens after the swap. Due to swapping of heavy atoms, the atomic charges of decoy atoms needed to be recalculated. We used the Open Babel⁴⁶ package for the recalculation of atomic charges, by first deprotonating the decoys and protonating them with the Gasteiger-Marsili charge assignment⁴⁷. In this procedure, we found that Open Babel occasionally changed the atom types of heavy atoms during the protonation; for example, when the two carbons in CH₃-CH₂- were deprotonated and protonated, Open Babel sometimes changed their atom types from two sp3 carbons to two sp2 carbons, resulting in CH₂=CH-. In addition, the native ligands, which we used and were collected from the PDBbind database, had MMFF94 charges instead of Gasteiger-Marsili charges. Thus, for fair comparison, we also deprotonated the native ligands from the PDBbind database with Open Babel and protonated them with Gasteiger-Marsili charge assignment. We termed the resulting molecules “Open Babel native-like ligands.” On average, the Open Babel native-like ligands had one less hydrogen than the native ligands. The Open Babel native-like ligands produced correlation coefficients between experimental binding affinity and predicted binding score that were very similar to those obtained with the native ligands from the PDBbind database in CDS1 to CDS7 (see Table 3). Thus, in the study with randomized decoys, we used these Open Babel native-like ligands as the “native ligands,” and derived the randomized decoys from these Open Babel native-like ligands.

The similarity of a decoy to its native ligand was evaluated by its Tanimoto index⁴⁸ to the native ligand. The term “Tanimoto index of a decoy” means the “Tanimoto index of a decoy with respect to its native ligand as a reference.” Since the Tanimoto index ranges from 0 to 1, we made 10 bins with an interval of 0.1, and up to 100 ligand decoys with different Tanimoto indexes were prepared in each Tanimoto index bin for each ligand. Some ligands could have less than 100 decoys in certain Tanimoto index bins, due to their chemical composition and covalent bond geometry. In this case, we obtained as many decoys as possible by extensive decoy generation with the number of swaps ranging from 1 to 200. More than 200 swaps did not produce any new decoy with any native ligand.

Calculation of binding score of a decoy-receptor complex was performed in the same way as that for the calculation of binding affinity of a native ligand-receptor complex with the following difference: Due to heavy atoms swapped with hydrogens and the hydrogens added by Open Babel, the clashes between a receptor atom and a decoy atom could happen. However, we did not modify the location of the decoys to avoid the clashes, since 1) moving the decoys to avoid the clashes could generate additional breaks in native ligand-receptor contacts and 2) if the programs could capture specific ligand-receptor interactions, it should still give these decoy-receptor complexes worse scores than those for native ligand-receptor complexes. Thus, we ignored a positive van der Waals energy contribution from these clashes as follows: FlexX had a separate score term for these clashes, and thus we ignored this clash score (dG_clash) and summed the other score terms to obtain a binding score for a decoy-receptor complex. We termed this score, which ignored the clashes, the “clashless” FlexX score. In fact, the clashless score-Open Babel native-like ligand pairs performed as well as the full score-PDBbind native ligand pairs (Tables 3). Thus, this clashless score was used for both ligand decoys and native ligands in this study with randomized decoys. X-Score was not sensitive to this clash, and thus we used X-Score scores without modification. Ignoring the clashes detected by AutoDock was performed as with X-ray complex structures.

Evaluation of the CC with decoy-receptor complexes was performed as follows. In each dataset/ligand/Tanimoto index bin, we randomly picked a decoy among all the decoys in the bin (when there was no decoy in the bin, we left the bin empty), and calculated the CC for each dataset/Tanimoto index bin with the binding scores of selected decoy-receptor complexes. If less than 90% of the ligands in a dataset had decoys in a Tanimoto index bin, we did not calculate the CC for the dataset/Tanimoto index bin. We repeated this process 10,000 times to obtain the distribution of CC's in each dataset/Tanimoto index bin, and compared this distribution with the CC obtained with the Open Babel native-like ligands that had at least one decoy in the dataset/Tanimoto index bin.

Results and Discussion

Binding energy prediction from the native complex structures of CDS datasets

First, we examined the correlation between the experimental and predicted binding affinities of the X-ray complex structures in CDS1 to 7 for FlexX, X-Score and AutoDock and in CDS8 to 12 for BLEEP (Table 3). The CC varied greatly among the datasets and only CDS6a,b and CDS7 showed high CC's in all of the three programs. Although BLEEP performed well in four out of the five datasets, we could not conclude that BLEEP was better than the other programs, as we explain below. For the time being, we will confine our discussion to FlexX, X-Score and AutoDock.

The variation in the accuracy of binding affinity prediction in different datasets was also demonstrated by Ferrara et al.¹⁰ and Warren et al.⁴⁹. Although average of the datasets’ CC's was similar in all the programs, when the complex structures in CDS1 to 7 were pooled into a bigger dataset (CDSa), only X-Score showed moderately good binding affinity prediction ability. X-Score's better overall performance was expected, since it had been specifically trained to predict binding affinities. X-Score's CC for CDSa was comparable to those reported by Wang et al. (0.66 to 0.77)^6,12. However, even X-Score failed to accurately rank binding affinities in datasets other than CDS6a,b and CDS7. Interestingly, FlexX performed exceptionally well with CDS1 compared to the other programs, while it was almost as good as random prediction with CDSa.

Regarding the variation of CC in CDS1 to CDS7, a similar variation of the CC according to receptor family was reported by Ferrara et al.¹⁰. The receptors of CDS6 (thermolysin) and CDS7 (beta trypsin) are members of metalloprotease and serine protease families, respectively, and Ferrara et al. obtained average CC's of 0.68 and 0.69 for these families with 9 binding energy prediction programs. Here, the averages of the CC's obtained by the three programs were 0.80 and 0.74 for CDS6a and CDS7, respectively. The other CDS's belonged to Ferrara et al.'s low CC categories and did not produce high CC's in our study, either.

We are interested in elucidating why the programs could rank binding affinities well in some datasets and not others. Regarding this, the correlation between the logarithm of ligand molecular weight and experimental binding energy reported by Velec et al.⁵⁰ and Ferrara et al.¹⁰ caught our attention. We examined this correlation, viz. the correlation coefficient with logarithm of ligand molecular weight, CCMW, in each dataset (Table 3). While CCMW also varied across the datasets, surprisingly, the value of CCMW was as high as the CC's obtained with the programs; the mere logarithm of ligand molecular weight was as good a predictor of ligand binding affinity as the scoring functions employed by the programs; Related to this, it is notable that Ishchenko and Shakhnovich found a strong correlation of a non-specific potential and experimental binding affinity in metalloproteases, serine proteases and carbonic anhydrase II, to which our CDS6, CDS7 and CDS1 belong, respectively⁵¹. In our study, the CC and CCMW were high in CDS6 and CDS7 and low in CDS1, with the exception of a high CC of CDS1 by FlexX. Thus, the data from the two groups agreed in the cases of metalloprotease and serine protease but differed in carbonic anhydrase II. Examining the origin of the difference between the two sets of results, when we calculated the CCMW of the dataset for carbonic anhydrase II in the study of Ishchenko and Shakhnovich, its CCMW was very high (0.95), while the CCMW of our CDS1 is very low (−0.16). Thus, it appears that the study by Ishchenko and Shakhnovich on the correlation between non-specific potential and experimental binding affinity agree with our notion of the relationship between CCMW and CC. Also, it was noticed that all the four datasets where BLEEP performed well also had high CCMW's. Thus, we could not exclude the possibility that BLEEP also captured mainly non-specific interactions, which could be inferred from high CCMW's.

Since CCMW would have become much lower if the ligands which could not fit into the binding pockets had been included in the datasets and also since the molecular weight of a ligand alone without its geometric information would not be sufficient to determine whether the ligand will fit into a binding pocket or not, molecular weight of a ligand alone could not be used as a predictor of binding affinity. However, this observation suggests that non-specific interactions might play a big role in determining the performance of all the programs examined.

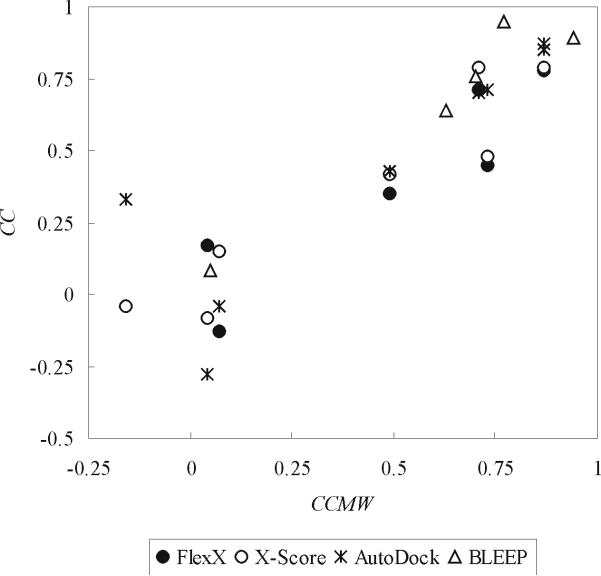
Although the relationship between CCMW and CC had been implied^10,50, we were interested in examining their strong correlation. When we examined this correlation, it was found that CCMW's indeed were well correlated with the CC's obtained with all the four programs (Figure 1). BLEEP's CCMW-CC correlation data obtained with different datasets nicely fit with those from the other three programs. The correlation coefficient between CCMW's and CC's was 0.91 when one outlier (FlexX's CC for CDS1) was excluded, again suggesting the major role of non-specific interactions in determining the performance of the programs’ scoring functions.

Figure 1.

Correlation between CC (correlation coefficient between experimental pKd or pKi and predicted binding score) and CCMW (correlation coefficient between the logarithm of ligand molecular weight and experimental pKd or pKi). The binding scores of the native X-ray complex structures in CDS datasets were calculated with FlexX, X-Score and AutoDock. Binding scores by BLLEP and corresponding experimental pKd's or pKi's were obtained from the Protein Ligand Database. CDS1 was omitted from FlexX results since it was a significant outlier. The correlation coefficient between CC and CCMW was 0.93, 0.95, 0.85 and 0.97 for FlexX, X-Score, AutoDock and BLEEP, respectively.

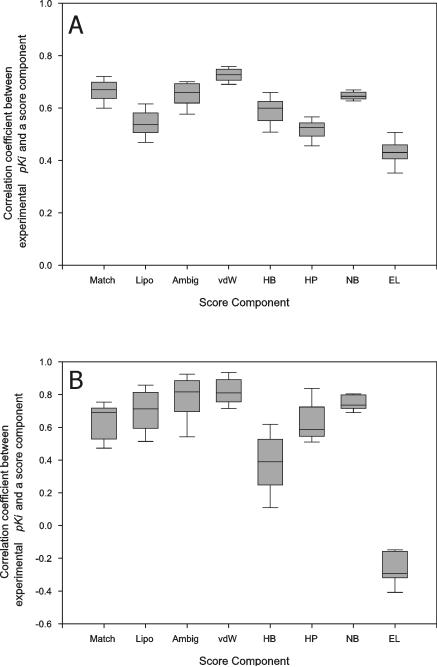
To further examine the role of non-specific interactions, we analyzed the correlation between experimental binding affinity and the programs’ individual score components (Table 4). The correlation between the experimental binding affinity and most of the various score components varied greatly across CDS1 to CDS7; moreover there was no individual score component which had a consistently high or consistently low correlation with experimental binding affinity in all of our datasets. Also, it was evident that van der Waals interaction alone was not sufficient for correct scoring in Table 4, where X-Score's van der Waals score and AutoDock's non-bonded score did not correlate well with experimental binding affinity, contrary to the suggestion by the study of Fahmy and Wagner⁵². In CDSa, the lipophilic score in FlexX, the van der Waals and hydrophobic scores in X-Score and the van der Waals and hydrogen bond score in AutoDock were correlated with the experimental binding affinity better than the other score components in the respective programs. These score components were mostly related to non-specific interactions such as van der Waals and hydrophobic interaction.

Table 4.

Correlation coefficients between experimental pKd or pKi and binding score components

	FlexX			X-Score			AutoDock
	Match1	Lipo1	Ambig1	vdW1	HB1	HP1	NB1	EL1
CDS1	0.81	0.22	0.04	−0.26	0.78	0.19	0.19	0.49
CDS2	0.11	0.00	0.23	−0.04	0.22	−0.17	−0.27	−0.06
CDS3	0.24	0.56	0.55	0.44	0.17	0.41	0.45	0.12
CDS4	−0.21	0.16	0.14	0.06	−0.18	0.28	0.08	−0.43
CDS5	0.61	0.51	0.63	0.56	0.68	−0.21	0.53	0.71
CDS6a	0.79	0.70	0.84	0.84	0.66	0.69	0.84	0.56
CDS6b	0.85	0.70	0.85	0.84	0.67	0.63	0.86	0.35
CDS7	0.54	0.70	0.78	0.72	0.73	0.48	0.71	0.40
CDSa	0.12	0.57	0.36	0.54	0.01	0.62	0.51	0.19

¹The binding score components meant the following according to the developers⁶,⁸,³⁴; Match: ionic, hydrogen bond and aromatic interaction score, Lipo: lipophilic contact score, Ambig: hydrophilic-lipophilic contact score, vdW: van der Waals interaction score, HB: hydrogen bond score, HP: hydrophobic interaction score, NB: van der Waals interaction and hydrogen bond score, EL: electrostatic interaction score.

Based on these results, the binding affinity prediction performance of FlexX, X-Score and AutoDock was largely dependent on how well experimental binding affinities were correlated with non-specific van der Waals and hydrophobic interaction scores between ligands and receptors. Considering the agreement between the CCMW-CC correlation by BLEEP and that by the other three programs (Figure 1), we could not exclude the possibility that BLEEP also had the same limitation. Thus, the programs might have been missing other important aspects of ligand-receptor interactions, whose absence leads to the inconsistency in the binding affinity prediction performance of the programs observed with our datasets.

Binding energy prediction with cross docking CDS6b and CDS7

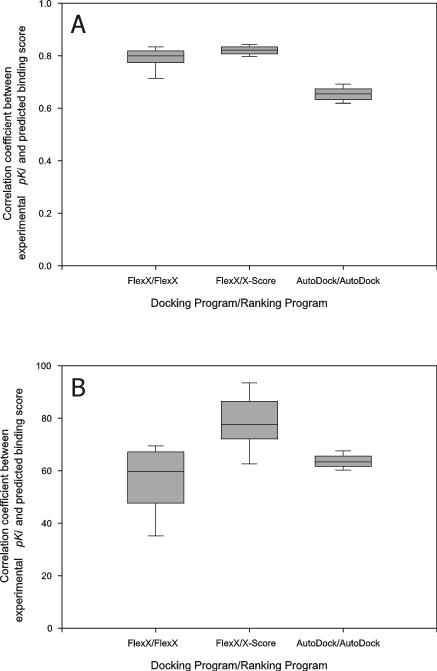
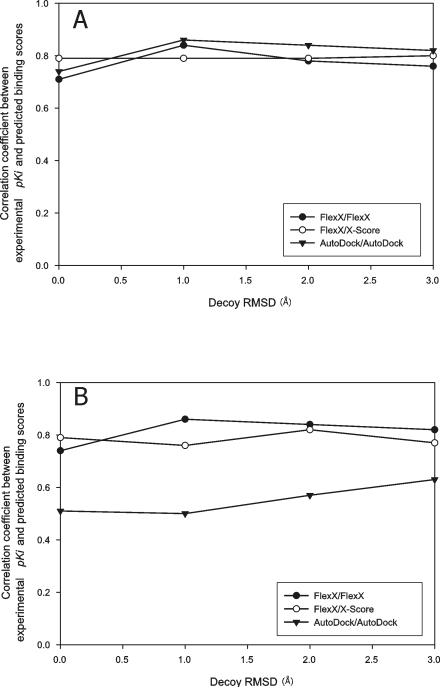
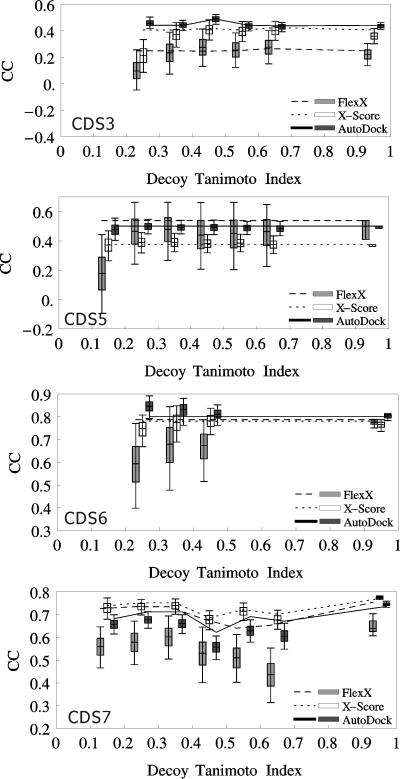
All of the receptor structures of CDS6b (CDS7) were docked to all of the ligands of CDS6b (CDS7) using the rigid receptor-flexible ligand docking capabilities of FlexX and AutoDock, and the resulting docked conformations of the ligands were ranked with FlexX, AutoDock and X-Score as described in Material and Methods. The CC between the binding scores of the “best-of-best scoring” ligands and their experimental binding affinities was high: 0.62, 0.83 and 0.63 for (docking program/ranking program) FlexX/FlexX, FlexX/X-Score and AutoDock/AutoDock, respectively, in CDS6b and 0.83, 0.81 and 0.67 for FlexX/FlexX, FlexX/X-Score and AutoDock/AutoDock, respectively, in CDS7. Moreover, the CC between the binding scores of the “best scoring” ligands docked to each receptor and the experimental binding affinities of the native conformations of the ligands complexed with their native receptor structures was also high (Figure 2); the average CC over the receptor structures was 0.57, 0.79 and 0.62 for FlexX/FlexX, FlexX/X-Score and AutoDock/AutoDock, respectively, for CDS6b and 0.82, 0.83 and 0.66 for FlexX/FlexX, FlexX/X-Score and AutoDock/AutoDock, respectively, for CDS7. Thus, except CDS6b with FlexX, slight changes in receptor structure did not seem to have disturbed the CC of CDS6b and CDS7 significantly. Rather, CC increased with cross docking/ranking with FlexX/X-Score in CDS6b and FlexX/FlexX and FlexX/X-Score in CDS7, relative to those from X-ray complex structures.

Figure 2.

Distribution of the correlation coefficient between experimental pKi and predicted binding score from cross docking. The ligands of CDS7 (A) and CDS6b (B) were docked to the receptor structures in CDS7 and CDS6b, respectively, then the “best scoring” conformations of the ligands for each receptor structure were pooled and the CC was calculated with these best scores and the experimental pKi's. This calculation of CC was repeated for each receptor, the CC's were pooled and their distribution was plotted. Box boundaries represent the 25^th and 75^th percentiles, and whiskers the 10^th and 90^th percentiles. Bars in the boxes represent median values.

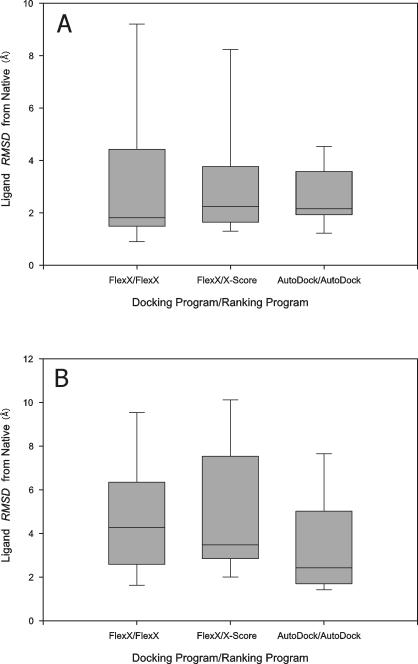
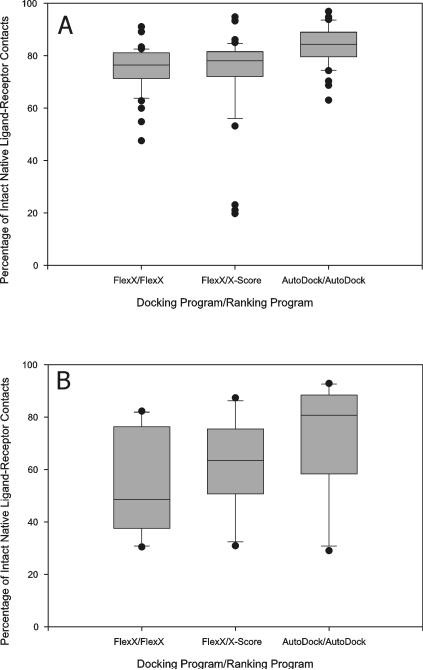
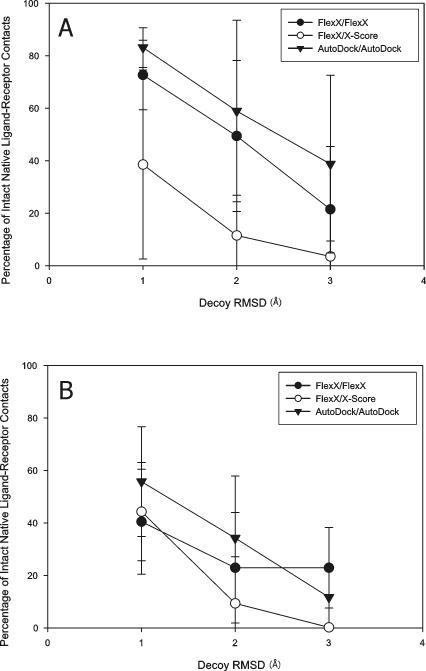
Meanwhile, the best-of-best scoring conformation of a ligand (the top scoring ligand conformation among the ligand conformations docked to all the receptor structures) was significantly different from its native conformation in the X-ray complex structure (Figure 3) and the native contacts between the ligands and the receptor structures were found to have been lost for many ligands due to cross docking (Figure 4). Thus, even though the cross-docked structures lost significant parts of the native contacts between the ligands and the receptor structures, the correlation coefficient between experimental binding affinity and predicted binding score was not abolished and rather slightly increased with certain programs. Thus, although as reported by others^10,15 cross docking often produced significant changes in ligand conformations and ligand-receptor binding interactions, CDS6b and CDS7 with their high native CC's could endure that distortion and still produced fairly high CC's.

Figure 3.

The distribution of RMSD from native (ligand conformations in the X-ray complex structures) of the “best-of-best scoring” conformations of the ligands of CDS7 (A) and CDS6b (B), cross-docked to the receptor structures of CDS7 and CDS6b, respectively. Box boundaries represent the 25^th and 75^th percentiles, and whiskers the 10^th and 90^th percentiles. Bars in the boxes represent median values.

Figure 4.

Percentage of intact native ligand-receptor contacts in “best-of-best scoring” cross docking complexes. The ligands of CDS7 (A) and CDS6b (B) were docked to the receptor structures in CDS7 and CDS6b, respectively. The “best-of-best scoring” complex was obtained for each ligand, and the contact maps of the best-of-best scoring complexes were obtained and compared to the contact maps from the native X-ray complex structures containing the same ligands, to obtain the percentages of intact native ligand-receptor contacts. Box boundaries represent the 25^th and 75^th percentiles, and whiskers the 10^th and 90^th percentiles. Dots represent outliers outside of the 5^th and 95^th percentiles.

We analyzed the correlation between individual score components and experimental binding affinity (Figure 5). The most noticeable feature was that non-specific interaction terms, such as van der Waals interaction term in X-Score and non-bonded term in AutoDock, correlated with experimental binding affinity better than the other score components in the programs, while all of FlexX's score components similarly correlated with experimental binding affinity. This indicated that non-specific interaction played a more important role in binding affinity prediction of X-Score and AutoDock than other score components.

Figure 5.

The distribution of the correlation coefficients between score components and experimental pKi's. The ligands of CDS7 (A) and CDS6b (B) were cross-docked to the receptor structures of CDS7 and CDS6b, respectively, with FlexX (for Match, Lipo, Ambig, vdW, HB and HP columns) or AutoDock (for NB and EL columns) and their docked conformations ranked with FlexX (for Match, Lipo and Ambig columns), X-Score (for vdW, HB and HP columns) or AutoDock (for NB and EL columns) as described in Material and Methods. The best scoring conformations of the ligands for each receptor structure were collected and the correlation coefficient between score components and experimental pKi was calculated for each receptor and its best-scoring ligand conformations. The correlation coefficients from all the receptor structures were pooled to obtain the shown distribution. The binding score components meant the following according to the developers⁶,⁸,³⁴; Match: ionic, hydrogen bond and aromatic interaction score of FlexX, Lipo: lipophilic contact score of FlexX, Ambig: hydrophilic-lipophilic contact score of FlexX, vdW: van der Waals interaction score of X-Score, HB: hydrogen bond score of X-Score, HP: hydrophobic interaction score of X-Score, NB: van der Waals interaction and hydrogen bond score of AutoDock and EL: electrostatic interaction score of AutoDock.

Binding energy prediction from docking deformed receptor structures from CDS6b and CDS7 to their ligands

Originally, we were interested in the estimation of the binding affinities of ligands for predicted receptor structures. However, since the tested programs did not perform well even with X-ray complex structures it was apparent that we could not study this. Thus, we instead further examined whether the high CC's observed with CDS6b and CDS7 were caused mainly by the capture of non-specific interactions. As described in Material and Methods, we deformed the receptor structures of the complex structures 1tlp and 1oyq of CDS6b and CDS7, respectively, to generate deformed decoys with the binding site residues’ Cα RMSD from native of 1, 2 and 3 ± 0.5Å and docked the ligands of the respective datasets to the deformed decoys. Our purpose was to break native ligand-receptor contacts and to examine if the high CC's of CDS6b and CDS7 could still be maintained.

As shown in Figure 6, all the programs could rank binding affinities with deformed decoys as correctly as with native receptor structures, even when the decoys had the Cα RMSD from native of 3 ± 0.5 Å. However, as shown in Figure 7, the native contacts between the ligands and their native receptor structures were rapidly lost with the deformation of the receptor structures; the ligands that were docked to the areas completely out of their original binding pockets were also observed. These results indicated that the good binding affinity ranking performance of the programs with the decoy structures was not based on their accurate retrieval of the native interactions present in the native X-ray complex structures, but probably resulted from mainly non-specific interactions.

Figure 6.

Correlation between experimental pKi and predicted binding score from decoy receptor structure docking. The ligands of CDS7 (A) and CDS6b (B) were docked to the deformed decoys of the receptor structures of the complex structures 1oyq of CDS7 and 1tlp of CDS6b, respectively. For each ligand, the “best-of-best scoring” complex was chosen in each decoy Cα RMSD from native bin and the binding affinity estimate from this complex was used to calculate CC. The legend indicates docking/ranking programs used. Decoy RMSD of 0 Å means native receptor structures.

Figure 7.

Percentage of intact native ligand-receptor contacts in the “best-of-best scoring” complex structures. The ligands of CDS7 (A) and CDS6b (B) were docked to the decoy receptor structures. The best-of-best scoring complex structure was obtained for each ligand in each decoy Cα RMSD from native bin. The contact map for the best-of-best scoring complex structure was compared to that of its native X-ray counterpart to obtain the percentage of intact native ligand-receptor contacts, as described in Material and Methods. The percentages were collected for each decoy Cα RMSD from native bin and plotted. The symbols and bars represent the mean values and standard deviations, respectively.

Binding affinity estimation with randomized ligand decoys

We further investigate the idea that non-specific interactions govern the binding affinity prediction performance of the tested programs by examining these programs’ performance with the “randomized” decoys that were prepared as described in Material and Methods.

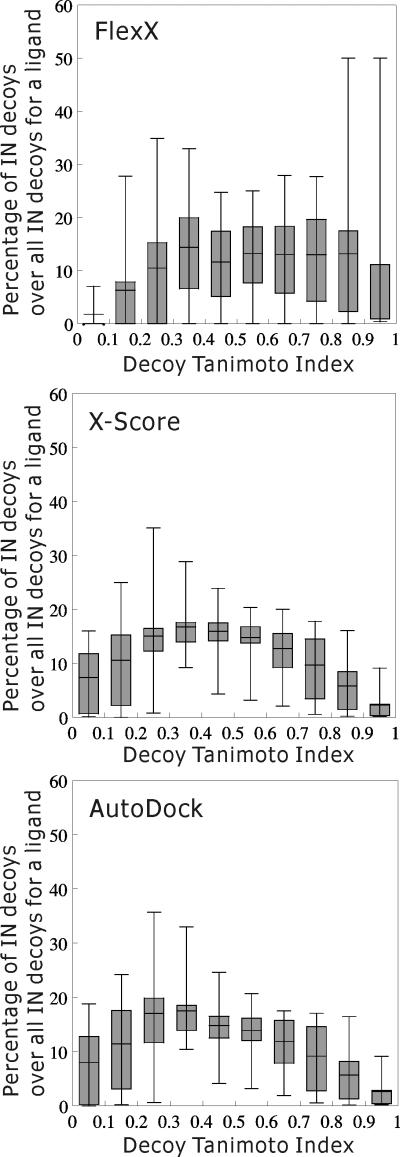
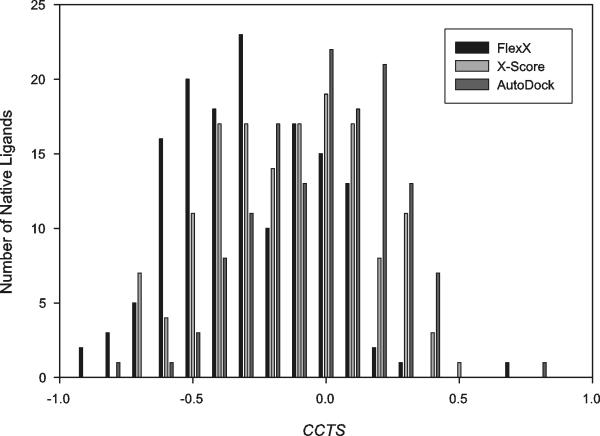
First, we examined if the programs could discriminate the randomized decoys from their native ligands as follows: For each native ligand, we collected its decoys whose predicted binding affinities were below that of the native ligand plus one kT (2.5 kJ/mol). We termed these decoys “IN” decoys. Then, the percentage of the IN decoys for a native ligand in each decoy Tanimoto index bin over all the IN decoys for the native ligand was calculated. The distribution of these percentages across the whole native ligands is plotted for each decoy Tanimoto index bin in Figure 8. For an ideal binding affinity prediction program, the percentage of IN decoys should be the highest in the highest decoy Tanimoto index bin and decrease as the decoy Tanimoto index is reduced. However, with all the three programs, the percentage of IN decoys peaked in the decoy Tanimoto index bin of 0.3∼0.4, and its distribution was far from that of an ideal binding affinity scoring function; with the decoy Tanimoto index of 0.6 as the criterion of a decoy's being native-like, there were more “non-native-like” IN decoys than “native-like” IN decoys.

Figure 8.

Percentage of IN decoys. Randomized decoys were prepared and their binding affinities were calculated as described in Material and Methods. For each native ligand, decoys whose predicted binding affinities were below that of the native ligand plus one kT (2.5 kJ/mol) were collected (“IN” decoys). The percentage of the IN decoys for a native ligand in a decoy Tanimoto index bin over all the IN decoys for the native ligand was calculated. The distribution of these percentages across the whole native ligands is plotted for each decoy Tanimoto index bin. Box boundaries represent the 25^th and 75^th percentiles, and whiskers the 5^th and 95^th percentiles. The bar in a box represents the average of the percentages in each decoy Tanimoto index bin.

Secondly, if a program could capture specific interaction between ligand and receptor atoms, it would give worse scores to decoys which are more dissimilar to their native ligand. Thus, we examined the correlation coefficient, CCTS, between the Tanimoto indexes of the decoys of a native ligand and their binding scores (Figure 9). A perfect CCTS would be −1, and with a CCTS of −0.6 as the criterion for good correlation, all the three programs produced CCTS worse than −0.6 with the majority of the native ligands; the percentage of the native ligands having the CCTS of less than −0.6 was 17.8, 7.5 and 1.5% by FlexX, X-Score and AutoDock, respectively.

Figure 9.

Histogram of CCTS, the correlation coefficient between the Tanimoto indexes of the randomized decoys of a native ligand and their binding scores. Generation of the randomized decoys and evaluation of the binding scores of the decoy-receptor complexes were performed as described in Material and Methods. For each native ligand, all the Tanimoto index-binding score pairs were collected from its decoy-receptor complexes and CCTS was calculated with these pairs. A histogram was plotted with the CCTS's of all the native ligands.

Lastly, we examined if the CC changed by using decoy-receptor complexes instead of native ligand-receptor ones. Figure 10 shows the distribution of CC over 10,000 test datasets composed of randomized decoy-receptor complexes in each dataset/Tanimoto index bin. We examined CDS3, CDS5, CDS6a and CDS7 for which most programs produced CC's of more than 0.4. With the criterion of 0.1 for the difference between the CC from native ligand-receptor complexes and the top 25^th percentile of the CC's from decoy-receptor complexes, only FlexX for CDS7 could discriminate decoy-receptor complexes from native ligand-receptor ones. All the other program/dataset combinations could not discriminate native complexes from decoy-receptor ones.

Figure 10.

Distribution of CC over 10,000 test datasets composed of randomized ligand decoy-receptor complexes in each decoy Tanimoto index bin. Generation of the randomized ligand decoys, estimation of the binding affinities of the decoy-receptor complexes and calculation of the CC in each decoy Tanimoto index bin were performed as described in Material and Methods. Box boundaries represent the 25^th and 75^th percentiles, and whiskers the 5^th and 95^th percentiles. The bar in a box represents the average of the CC's in each Tanimoto index bin. A box between decoy Tanimoto index 0.1 and 0.2 represents the distribution of CC's obtained in the Tanimoto index bin 0.1∼0.2, and so on. Lines represent the CC's obtained with the Open Babel native-like ligands that had at least one decoy in the decoy Tanimoto index bin. Gray, White and Black boxes represent the CC's obtained with FlexX, X-Score and AutoDock, respectively. Dashed, dotted and solid lines represent the CC's obtained with FlexX, X-Score and AutoDock, respectively.

Conclusion

We examined four programs, FlexX, X-Score, AutoDock, and BLEEP, for their ability to accurately predict ligand-receptor binding affinity for 12 datasets and found that none of the programs performed well in predicting binding affinities for all of the datasets.

One interesting observation is that CC, the binding affinity prediction performance of the programs, is very highly correlated with CCMW, the correlation between the logarithm of ligand molecular weight and experimental binding affinity (Figure 1). This result suggests that the programs might not be correctly capturing specific interactions in ligand binding, as exemplified by the finding that even though native contacts were greatly lost in decoy-ligand docking, CC was still maintained at high levels for CDS6b and CDS7 datasets (Figures 6 and 7). Also, in general, FlexX, X-Score and AutoDock could not decisively discriminate native ligands from their “randomized” ligand decoys, which were generated by “shuffling” the locations of the atoms of each of the native ligands while maintaining its chemical composition and heavy atom covalent bond geometry (see Figures 8, 9 and 10). Thus, the tested programs do not capture the specific interactions between ligand and receptor atoms.

Since FlexX performed the best with randomized ligand decoys, X-Score with X-ray complex structures and AutoDock with preserving native ligand conformation and native ligand-receptor contacts in cross docking, we could not conclude which program was the best one.

Considering the “high CCMW to high CC” correlation and our results with deformed receptor decoys and randomized ligand decoys, we surmise that these programs will perform well in binding energy prediction on the datasets which have high correlation between the molecular weights of binding ligands and their experimental binding affinities, due to higher contribution of non-specific interaction to binding affinity, and vice versa.

There are many success stories and good benchmarks about docking and ranking programs in virtual screening and the prediction of the binding conformations of ligands^12,22,49,53. However, the prediction of the binding affinities of ligand-receptor complex structures appears to be a more difficult task than the prediction of the binding conformations of ligands^10,49. The reports of the lack of correlation between experimental and predicted binding energies for many ligand-receptor complex structures and prediction programs^10,49, the similar result by us (Table 3) and our finding of the role of non-specific interactions in the binding affinity prediction performance of the examined programs (see Figures 1, 6, 7, 8 and 10) clearly suggest that improvement of the ranking/scoring functions for ligand binding affinity prediction may come from a more complete and accurate capture of specific interactions in ligand binding.

Also, since the programs examined in this study could not consistently predict ligand binding affinities even with X-ray complex structures, the question of whether rigid-receptor docking is suitable for ligand binding affinity prediction or not could not be answered in this study and is still an open question. The question of “how close to native structures is close enough for predicted protein structures for relatively accurate binding affinity prediction” also could not be answered in this study, since the binding scores (by the tested programs) of the ligands in CDS6a,b and CDS7 appeared to be governed by non-specific interaction terms and thus neither changing receptor structures nor “randomizing” ligands could significantly affect the binding affinity ranking of the ligands. To answer this question, we need the dataset that has a low CCMW and high CC's by binding affinity prediction programs.

In summary, we found that 1) there is a strong correlation between CCMW (ligand molecular weight-binding affinity correlation of a dataset) and CC (predicted and experimental binding affinities correlation of the dataset) and thus binding affinity prediction programs performed well only with the datasets having high CCMW's, 2) for the datasets having high CCMW's, loss of native ligand-receptor contacts did not significantly perturb correct ranking of ligands according to their binding affinities and 3) in general, the tested programs could not decisively distinguish native ligands from their randomized decoys.