Abstract
The transient potassium A-current is present in most neurons and plays an important role in determining the timing of action potentials. We examine the role of the A-current on the activity phase of a follower neuron in a rhythmic feed-forward inhibitory network with a reduced three-variable model and conduct experiments to verify the usefulness of our model. Using geometric analysis of dynamical systems, we explore the factors that determine the onset of activity in a follower neuron following release from inhibition. We first analyze the behavior of the follower neuron in a single cycle and find that the phase plane structure of the model can be used to predict the potential behaviors of the follower neuron following release from inhibition. We show that, depending on the relative scales of the inactivation time constant of the A-current and the time constant of the recovery variable, the follower neuron may or may not reach its active state following inhibition. Our simple model is used to derive a recursive set of equations to predict the contribution of the A-current parameters in determining the activity phase of a follower neuron as a function of the duration and frequency of the inhibitory input it receives. These equations can be used to demonstrate the dependence of activity phase on the period and duty cycle of the periodic inhibition, as seen by comparing the predictions of the model with the activity of the pyloric constrictor PY neurons in the crustacean pyloric network.
Keywords: Oscillation, central pattern generator, phase plane, stomatogastric, phase
1. Introduction
Bursting oscillations occur in many neurons and other cell types and underlie rhythmic activity in many networks of the central nervous system. In the mammalian thalamocortical system, for example, bursting occurs in the thalamocortical neurons during EEG-synchronized sleep (McCormick and Bal, 1997). Other examples include the circadian rhythmicity which results from the interaction of the circadian pacemaker, comprising of the neurons of the suprachiasmatic nucleus and other neurons such as the photoreceptors (Moore, 1999). Bursting oscillations are particularly prevalent in neurons of central pattern generators (CPGs) that produce rhythmic motor activity. These types of neurons include, for instance, the respiratory neurons in the pre-Botzinger complex of the brain stem that exhibit pacemaker bursting activity (Johnson et al., 1994).
The activity of oscillatory networks of neurons is determined by the oscillation frequency as well as the activity phase of the component neurons within each cycle. In many oscillatory networks, the relative bursting phase among neurons plays an important in determining the normal or dysfunctional output of the network. In CPGs, for instance, the relative phase of neurons or groups of neurons determines the order of muscle contractions and therefore the motor behavior (Marder and Bucher, 2007). It has also been shown that the motor system dysfunction associated with Parkinson’s disease, is critically dependent on how the phase relationships between basal ganglia nuclei are affected by the loss of dopamine (Walters et al., 2007). The phase difference between neurons is often maintained over a wide range of frequencies (Marder and Calabrese, 1996; Marder et al., 2005).
The A-current is a transient outward potassium current that is present in most neuronal types and contributes to spike timing. The A-current is an essential factor in determining the frequency-current response of neurons, as was first shown in the seminal paper of Connor and Stevens (Connor and Stevens, 1971). In the CA3 pyramidal cells in the hippocampus, the activation of the A-current underlies the propagation failure of action potentials in axons (Debanne et al., 1997). The A-current has been shown to be important in determining the post-inhibitory rebound bursting phase of neurons and its effect on determining this phase is subject to the neuromodulation of the current by dopamine (Harris-Warrick et al., 1995).
In order to investigate how the A-current interacts with other intrinsic and synaptic factors to affect the activity phase of a follower neuron, we focused on a simple inhibitory network consisting of a pacemaker neuron and a follower neuron. The prototype of our model includes two neurons, the pyloric dilator (PD) and the pyloric constrictor (PY), of the pyloric CPG in the stomatogastric nervous system of the crab Cancer borealis. The PD neurons are members of the pyloric pacemaker ensemble and produce very regular bursting activity with a period of around 1 sec. The follower PY neurons are also members of the pyloric system which oscillate due to the synaptic inhibition they receive from the pacemaker neurons.
The activity phase of pyloric follower neurons such as PY has been partially attributed to the presence and extent of the A-currents in these neurons (Harris-Warrick et al., 1995; MacLean et al., 2005). In the current study, we use the dynamic clamp technique to verify the role of the A-current in setting the activity phase of follower PY neurons. Based on these results, we construct a 3-variable model to analyze how the interaction between the A-current and other intrinsic properties of the follower neuron determine the post-inhibition activity phase of this neuron. Our model, which is based on the model of Bose et al (Bose et al., 2004), focuses on the bursting envelope of the follower neuron and the spiking properties are ignored.
We use phase space analysis and separation of time scales to determine the factors that determine the fate of the follower neuron trajectory following inhibition in a single cycle of oscillation. We then use these results to derive a set of equations that describe the steady-state phase of the follower neuron in response to a repetitive periodic input. These equations depend on a set of model parameters, including the active and inactive durations of the pacemaker neurons. Finally, we compare the phase of the follower neuron as predicted by these equations with the phase of the biological PY neurons when the network cycle period is varied using different protocols.
2. Post-inhibition phase of an oscillatory neuron and the role of the A-current
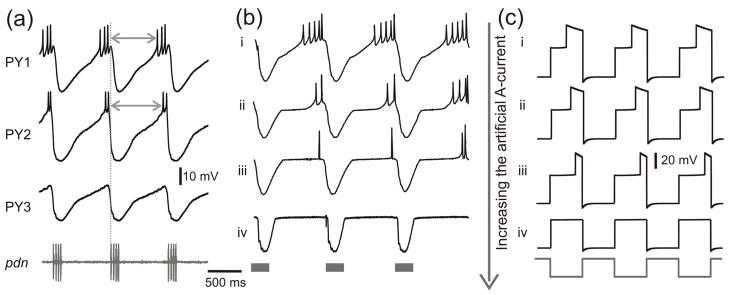
This study is motivated by the observation that different neurons in a CPG network are active at different phases of each cycle of oscillations. These distinct phases often command the contraction phases of distinct muscles which, in a coordinated fashion, produce meaningful movements. CPG network neurons are typically subject to inhibitory inputs and produce activity upon rebound from this inhibition. An example of this type of activity is shown for the PY neurons in Figure 1a. There are three to five PY neurons in the pyloric CPG and these neurons can have fairly distinct activity phases. As seen in Figure 1a, PY1 has a more advanced phase than PY2, while PY3 does not spike at all. It has been shown that the activity phase of the PY neuron is affected by the strength of the A-current (Harris-Warrick et al., 1995). Our study is based on the hypothesis that the strength and kinetics of the A-current in individual PY neurons can determine their distinct activity phases.
Figure 1.
The effect of the A-current on the activity phase of biological and model PY neurons. (a) Simultaneous recording of three biological PY neurons in the crab STG. All PY neurons receive periodic inhibitory synaptic input from the pyloric pacemaker neurons. The activity of the pacemaker neurons can be seen in the extracellular nerve recording (pdn, bottom trace). Note that the PY neurons burst with different time delays (arrows) with respect to onset of the pacemaker input (vertical dotted line). PY2 has a more delayed phase than PY1, while PY3 does not spike at all. (b) An artificial A-current was injected into a PY neuron, using the dynamic clamp technique, and its strength (gA, the maximum conductance) was increased from top to bottom (in nS: i: 0, ii: 50, iii: 100, iv: 200), resulting in an increase in the delay to the active state. When the maximum conductance was too large (iv), the PY neuron was not able to reach the active state and there were no action potentials. Note that even without the dynamic clamp A-current, there was a delay to the active state of the PY neuron presumably due to its intrinsic biological A-current. (c) The effect of the A-current shown in panel b can be mimicked by simulating the three-variable model with different values of gA. Note that this model represents only the envelope of slow oscillations and the spikes seen in the biological neuron are smoothed over. Model parameters: (in ms) Tin = Tact = 500, τhl = 495, τhm = 810, τhh = 1000, τwl = 40, τwm = 100, τwh = 800; (in mV) EL = −60, ECa = 120, vm = −1.2, km = −18, EK = −84, vw = 15, kw = −5, vn = −6, kn = −0.5, vh = −10, kh = 0.1, Einh= −80; (in nS) gL = 2, gCa = 4, gK = 8, gA = 3.5(i), 3.7(ii), 4(iii), 5(iv), ginh = 2; (in pA) Iext = 75.
In order to quantitatively demonstrate how the A-current affects the activity phase, we injected an artificial A-current into a single PY neuron using the dynamic clamp technique (see Experimental Methods) and measured the shift in the PY neuron activity phase while varying the maximum conductance (gA) of the A-current. Figure 1b shows the experimental results. In Case i, gA is equal to zero and therefore the trace shows the membrane potential of the PY neuron without any additional input. In Cases ii–iv we increased gA gradually, and the activity of the PY neuron is shifted to a later phase. When the maximum conductance was too large (Case iv), there were no action potentials and the active phase of the PY neuron was effectively suppressed. This case was similar to the ongoing activity of the PY3 neuron in Figure 1a.
In the following sections, we will use a simplified neuronal model to analytically explore the role of the A-current in determining the activity phase of CPG neurons such as the PY neuron. We will then use these analytical results to predict this phase for the biological neuron as a function of the frequency and duty cycle of the oscillatory inhibition it receives.
3. Model
3.1 General equations
Our model is based on the model of Bose et al (2004) which includes three variables to determine the bursting envelope: two variables (v and w) are from the Morris-Lecar (ML) model representing the membrane potential of the follower neuron and the activation variable of the potassium current, and one variable h describing the A-current inactivation. This model represents only the envelope of the oscillatory activity in the PY neurons; the spikes shown in Figs. 1a and 1b are smoothed over as they do not play an important role in determining the effect of the A-current. The equations for the model are given as
| (1) |
where
| (2) |
represents the ML terms, and w∞(v), n∞(v) and h∞(v) are sigmoidal functions respectively representing the steady state values of the activation variable for the potassium current, the activation and inactivation variables for the A-current. Each sigmoidal function has the form:
| (3) |
Here kx is negative for activation variables and positive for deactivation variables. We say the sigmoid is steep when the parameter kx ~ O(ε1) where 0 < ε1 ≪ 1. In our model kn and kh are set to be small (~ O(ε1)), but kw, which determines the shape of the w-nullcline, can be small or large. The time constants τw(v) and τh(v) determine the speed with which the variables w and h change in different voltage regions.
The synaptic current has the following expression:
| (4) |
We set s∞(v0) as a steep sigmoid in order to simplify the synaptic mechanics.
Figure 1c shows the voltage traces simulated by the model for different values of gA. As in the model of Bose et al, we simplified the activity of the pacemaker neuron by defining the membrane potential v0 of the PD neuron as a square wave oscillating periodically between −50 mV and 0 mV with active duration Tact and inactive duration Tin (Fig. 1c, bottom trace). As seen in Figure 1c, the model neuron membrane potential oscillations consist of three voltage ranges (low, medium and high) and transitions between these three states. The low voltage state corresponds to the inhibition from the pacemaker; the high voltage state represents the spiking or active state and the medium voltage state represents the post-inhibition state before spiking occurs. As with the biological neuron (Fig. 1b), when the value of gA is increased from top to bottom, the duration spent in the high voltage state decreases (Fig. 1c, Cases i–iii) and thus the active phase is more and more delayed. For large enough gA the active phase is suppressed (Case iv).
3.2 The role of the A-current and the inhibition in the v-w and w-h phase planes
We can analyze the trajectory of the follower neuron in its three-variable phase space by considering the dynamics of the trajectory on two distinct 2-dimensional manifolds: the v-w plane and the w-h plane (described further below). The dynamics of the trajectory in the v-w plane are described using a family of “phase planes” parameterized by the slow variable h which represents the inactivation of the A-current.
Without the A-current term, the ML model is described by a cubic v-nullcline and a sigmoidal w-nullcline in the v-w phase plane (Rinzel and Ermentrout, 1998). When a trajectory lies near the left branch the neuron is said to be silent; when it is near the right branch the neuron is called active. The left and right branches of the v-nullcline correspond, respectively, to the low- and high-voltage states as described in Figure 1c. In the ML model, if a fixed point lies on the sections of the v-nullcline that have negative slope (i.e. the left or right branch) it is stable and if it is in the section with the positive slope (between the minimum and maximum) it is unstable (Rinzel and Ermentrout, 1998).
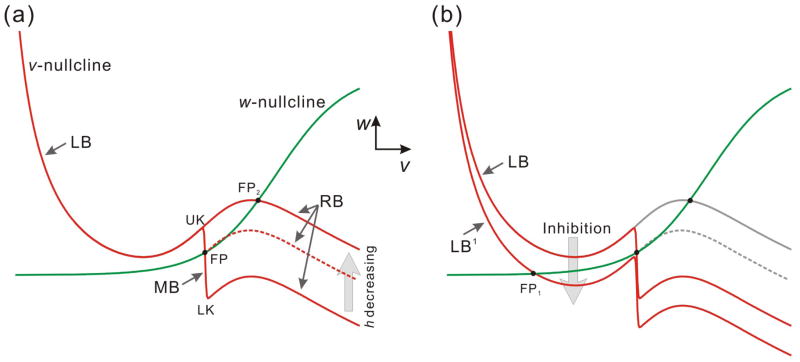
With the parameters used in Figure 1c, in the absence of an A-current, the v- and w-nullclines intersect on the right branch at a stable fixed point (FP2 in Fig. 2a), which implies that without inhibition, the model neuron is always active. This corresponds to the fact that the PY neurons are active (spike tonically) when they do not receive inhibition from the pacemaker (Rabbah and Nadim, 2005).
Figure 2.
The changes of the nullclines caused by the A-current and the inhibition in the v-w phase plane. (a) The presence of the A-current term causes an additional middle branch on the v-nullcline that has negative slope and therefore the nullcline shape is quintic. LB, MB and RB represent the left, middle and right branches of the v-nullcline respectively. UK and LK denote the upper and lower knee of MB. As the inactivation fraction h decreases, MB shrinks from LK. The dashed nullcline represents an intermediate value of h. (b) The inhibition from the pacemaker neuron causes the v-nullcline to move down vertically for a distance depending on the strength of the inhibitory synapse. FP, FP1 and FP2 represent fixed points in the v-w phase plane.
In the presence of the A-current term, however, there is an additional “middle branch” on the v-nullcline that has negative slope and therefore the nullcline shape is quintic (Fig. 2a). Due to the negative slope of this branch, any fixed point that lies on it would also be stable. We will use the notations LB, MB and RB respectively to denote the left branch, middle branch and right branch (Fig. 2a). Our assumption that the steady-state inactivation curve of the A-current is steep (kn is small) implies that MB is almost vertical. In fact, for the remainder of this manuscript we assume that MB is vertical (ε1 = 0). We have examined the consequences of relaxing this assumption in a separate study (Zhang et al., 2008). We refer to the lower knee, the upper knee and the fixed point (when present; FP in Fig. 2a) on MB as LK, UK and FP. When h decreases (i.e. the A-current inactivates), LB is unchanged, but MB shrinks (LK moves up), and RB moves up as well (Fig. 2a).
The inhibition from the pacemaker neuron causes the v-nullcline to move down vertically for a distance depending on the strength of the inhibitory synapse (Fig. 2b), as seen by the influence of the negative term Iinh in Equation (1). For large enough inhibition, this shift always results in a stable fixed point (FP1) on the left branch (called LB1 for the inhibited nullcline; Fig. 2b). In this study, we assume that the onset and decay of inhibition is fast and therefore the inhibition is only important during the active state (Tact) of the pacemaker.
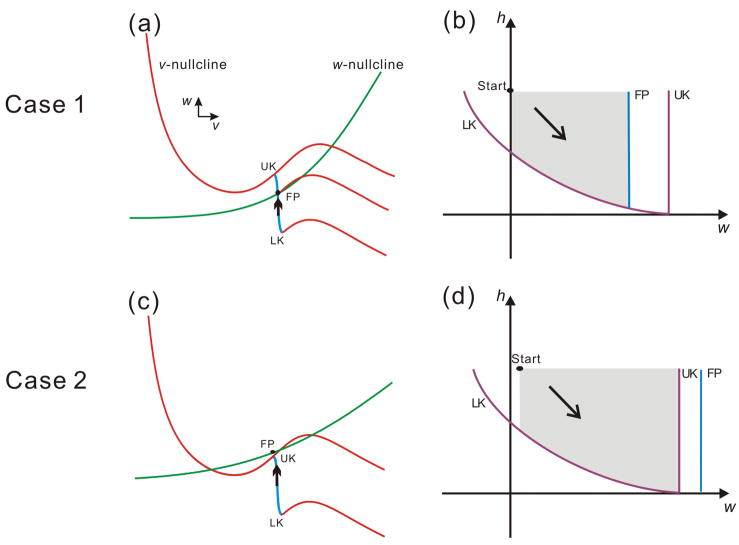
In the v-w phase plane, the steepness and midpoint of the w-nullcline determine the existence of a stable fixed point on MB. If there is an intersection on MB (Fig. 3a), then the fixed point exists and is locally stable. If the w-nullcline sits above MB, there will be no fixed point on MB. However, in this case the flow on MB is still attracted by the w-nullcline and, although there is no fixed point on MB, for each point on MB there is a “pseudo-fixed point” on the w-nullcline above MB (Fig. 3c). The pseudo-fixed point can be formally defined for any point (v, w) located on the middle branch as the point (v, w′) with the same v-coordinate on the w-nullcline. We label any fixed point or pseudo fixed point by FP.
Figure 3.
The parameters of the A-current, in conjunction with other intrinsic model parameters, can determine the fate of the follower neuron trajectory. Two qualitatively distinct cases are shown in the phase space based on the shape and relative position of the nullclines which are in turn determined by the relative positions of w∞(v) and MB (blue segment of the v-nullcline). Panels a and c show these two cases in the v-w phase plane; panels b and d show the same cases in the w-h phase plane respectively. In the w-h phase plane (b and d), the curves LK, FP and UK correspond to the lower knee LK, the upper knee UK and the fixed point FP in the v-w phase plane. The point “Start” denotes the entrance of the trajectory into the w-h phase plane and the grey area represents the potential paths of the trajectory. Case 1 (a & b; fixed point on MB): (a) In the v-w phase plane, the two nullclines intersect at FP on the middle branch (MB). (b) In the w-h phase plane, the trajectory is blocked by FP and can never reach UK. Case 2 (c & d; no fixed point on MB): (c) In the v-w phase plane, there is no intersection on the middle branch of the v-nullcline. (d) In the w-h phase plane, FP is to the right of UK and therefore the trajectory may reach UK.
The w-h phase plane is used to analyze the dynamics of the trajectory following the release from inhibition, when the A-current is large enough to prevent an immediate jump to the active state. In this case, the trajectory lands on MB (corresponding to the middle-voltage state in Fig. 1c). MB is a one-dimensional curve in the v-w phase plane and, in this plane, MB shrinks when h decays. However, the dynamics of the trajectory on MB are in fact determined primarily by the two slow variables, h and w. Thus, it is simpler to analyze the fate of the trajectory on MB by examining its evolution in the w-h phase plane where the curves of LKs, UKs and FPs can be properly visualized (Fig. 3b and 3d).
Figures 3b and 3d show the curves representing LK UK and FP in the w-h phase plane, corresponding, respectively, to the two cases shown in Figures 3a and 3c. The curves LK, UK and FP represent the lower and upper knees of MB and the fixed point as seen in the v-w phase plane. The shadowed areas represent the possible ranges of the trajectories. UK and FP are vertical lines as their positions in the w-direction are not changed. LK is a curve with negative slopes since the h value deceases as the w value is increasing when the trajectory is moving on MB. Consistent with the locations of FP and UK shown in the v-w phase plane (Figs. 3a and 3c), in Figure 3b, FP is on the left of UK while, in Figure 3d, FP is on the right of UK. The black arrow in each of these two figures shows the flow direction in the w-h phase plane.
3.3 The singular perturbation assumption and the reduced equations
The membrane potential of the follower neuron can be mapped to a trajectory on the v-w phase plane. For ε small enough (see Eq. (1)), the system is singularly perturbed (Mishchenko and Rosov, 1980). As a consequence, in some regions of phase space, v changes very quickly while w and h remain nearly constant. In other regions, the behavior of v can be slaved to that of w and h. Equations to describe either can be obtained by setting ε = 0 in Equation (1) or a time-rescaled version of Equation (1). These two sets of equations are respectively referred to as the slow and the fast equations and can be obtained as follows.
The slow equations are found by setting ε = 0 in Equation (1):
| (5) |
Note that the first equation in (5) describes the v-nullcline, thus indicating that the slow equations describe the dynamics of the trajectory on this nullcline.
The fast equations are obtained by rescaling t = εξ in Equation (1) and then setting ε = 0:
| (6) |
These equations control the trajectory during the jumps between the branches of the v-nullcline. Note that the last two equations in (6) imply that the values of w and h do not vary during these jumps.
Each cycle of the trajectory is pieced together using solutions of Equation (5) to determine the movement on the branches of the v-nullcline and of Equation (6) to determine the jumps between these branches. For instance, during the inhibition by the pacemaker, the trajectory moves toward FP1 on LB1 during Tact, and it stays near FP1 due to its stability (Fig. 4a). When the inhibition ends, the v-nullcline is raised (as described in Fig. 2b). FP1 no longer exists therefore the trajectory can jump to MB. In fact the trajectory is able to jump when it reaches the knee on any branch. For example, when the trajectory encounters the lower knee of MB, it jumps to RB. These jumps correspond to saddle-node bifurcation in the fast equations (Eq. (6)) (Rinzel and Ermentrout, 1998). The existence of a trajectory to the full system (Eq. (1)) that is close to the “pieced-together” trajectory obeying the lower-dimensional slow and fast Equations (5) and (6) follows from the results of geometric singular perturbation theory as described by Mishchenko and Rosov (1980).
Figure 4.
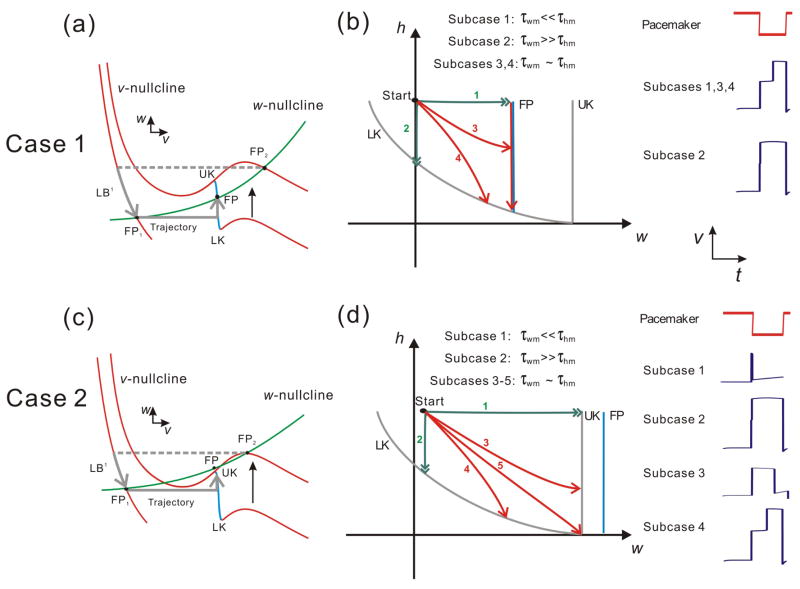
The dynamics of Cases 1 (a & b) and 2 (c & d) in the v-w and w-h phase planes. (a) In Case 1, the trajectory jumps to the left branch (LB1) from FP2 at the onset of inhibition and then moves along LB1 to FP1 during Tin. When the inhibition ends, the trajectory jumps to the middle branch MB and moves toward FP. At the same time, MB shrinks from LK due to the decay of h. (b) In the w-h phase plane, four subcases are possible based on the relative size of the two time constants τwm and τhm. Note, however, that the only way the trajectory can leave this phase plane is by reaching LK. (c) In Case 2 the shape of the w-nullcline causes wFP > wUK on MB. After landing on MB, the trajectory moves toward FP, and LK rises simultaneously as the MB shrinks. (d) Five subcases can be achieved in the w-h phase plane based on the relative size of τwm and τhm. In this case, trajectories 1 and 3 leave the phase plane by reaching UK whereas trajectories 2 and 4 leave from LK. The fate of trajectory 5 is unclear since it reaches the intersection of LK and UK. Insets on the right of panels b and d show the time traces of the pacemaker and the follower neuron in each subcase.
The trajectories of interest are restricted to three branches of the v-nullcline: the left branch LB1 in the presence of inhibition and the middle and right branches (MB and RB) in its absence, and the jumps between these branches. The slow equations for the trajectory moving on LB1, MB and RB are given as:
On LB1:
| (7) |
On MB:
| (8) |
On RB:
| (9) |
Our simplifying assumption that h∞(v) is steep (kh is small) implies that h∞(v) = 1 on LB1 and h∞(v) = 0 on MB and RB. The time constants for w and h on the left branches (LB and LB1), the middle branch (MB) and the right branch (RB) are set as τwl and τhl, τwm and τhm, and τwh and τhh respectively. All time constants are assumed to be of the same order of magnitude as Tact (O(Tact)) unless otherwise specified in the Results. In cases where two time constants are assumed to be of different orders of magnitude (i.e. τ1 ≪ τ2), the larger one (τ2 in this case) is assumed to be O(Tact).
4. Results
As described above, a numerical simulation of our model (Eq. (1)) with different parameter sets can reproduce the variety of phase delays observed in the biological PY neurons. Our goal in this study is to determine which parameters result in the distinct values of activity phase delay in the model neuron following inhibition, and to derive the relationships among parameters that would allow us to predict this activity phase as a function of the activity of the pacemaker neuron. We begin by describing the behavior of the trajectory in a single cycle and then use this information to derive the activity phase in response to a periodic input. Because the activity phase of the neuron following inhibition is determined by the time it spends on the middle branch MB, we will first focus on how the trajectory lands on MB, the factors that determine its fate on MB and where it goes after leaving MB.
4.1 The fate of the trajectory on MB
We begin with the trajectory at FP2 (Fig. 4a). Assume at t = 0 the follower neuron is inhibited and the trajectory lands on LB1. For the duration of inhibition (Tact), the trajectory moves downwards along LB1 towards the stable fixed point FP1 (Fig. 4a). We assume that τwl is small enough on LB1 such that, during the inhibited state, the trajectory reaches a small neighborhood of FP1. At the same time, the inactivation variable h of the A-current increases with time constant τhl. The growth of h does not affect the shape of LB1, but does result in a larger MB1. In fact, the size of MB1 is related to how long the follower neuron stays in the inactive state. At the end of the inhibition, the trajectory in the v-w plane is released from a neighborhood the fixed point FP1 and jumps horizontally to MB. Once the trajectory lands on MB, h begins to decay with the time constant τhm which causes MB to shrink from the lower knee LK. At the same time, the trajectory moves at the rate τwm towards the fixed point FP.
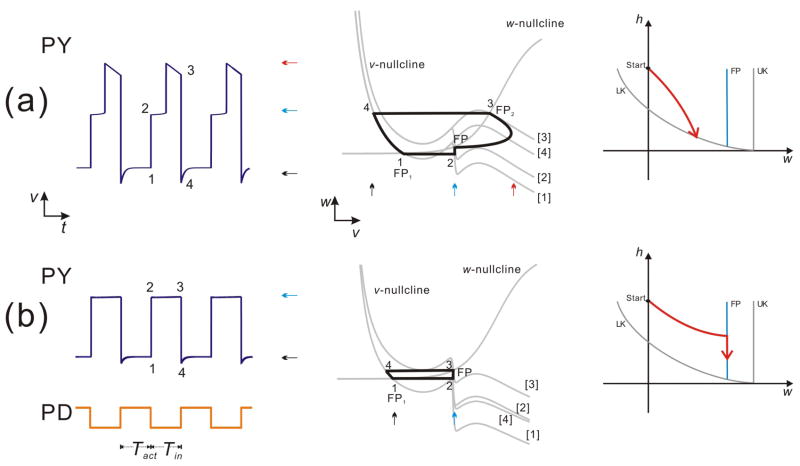
Figures 4a and 4c show two possible cases – Case 1 and Case 2 – depending on the shape and relative position of the v and w nullclines in the v-w phase plane. In Case 1 the w-nullcline crosses the v-nullcline on the middle branch and UK is always higher than FP in the w direction, while in Case 2 UK is lower than FP as the w-nullcline is above the middle branch of the v-nullcline. The trajectory cannot reach UK in Case 1 therefore it can only jump to the right if LK moves fast enough during Tin. In Case 2, however, FP is above the middle branch, which allows the trajectory to jump left if it moves fast enough to reach UK during Tin. Although these two possibilities are not exhaustive, they indicate how the structure of the nullclines can determine the fate of the trajectory on MB.
Figures 4b and 4d show the possible trajectories of Case 1 and Case 2, respectively, in the w-h phase plane. The curves LK, UK and FP are as defined in Figure 3. The difference between Cases 1 and 2 is that, in the w-h phase plane, the FP curve lies to the left of the UK curve in the former case but to its right in the latter (Figs. 4b and 4d). Thus, from the relative positions of the LK, UK and FP curves, it immediately follows that, in Case 1, the trajectory can only leave MB by jumping from LK to RB (because FP blocks the access to UK), whereas in Case 2, a trajectory could leave MB either by reaching LK and jumping to RB or by reaching UK and jumping to LB.
3.1.1 Case 1
The trajectory arrives on MB through a horizontal jump (in the v-w plane) and therefore the initial w value on MB is the same as the last value on LB1. The movement of the trajectory in the w-h phase plane is determined by the time constants τwm and τhm. According to these time constants, several subcases can be defined that represent all possible trajectories on MB. Each subcase is shown as an arrowed curve on the w-h manifold (Fig. 4b). In Case 1, for instance, there are four subcases: Subcase 1 satisfies the condition τwm ≪ τhm which causes a fast motion in the w direction, therefore the trajectory rapidly moves to FP immediately after landing on MB, and it follows the FP curve vertically down until it reaches the LK curve. Subcase 2 satisfies the condition τwm ≫ τhm, which makes the trajectory move rapidly in the h direction until it reaches the LK curve. In Subcase 3 and 4, τwm and τhm are of the same order and therefore there is no rapid movement in either the w or the h direction. The trajectory either reaches FP first and then moves vertically down to LK (Subcase 3) or moves directly to LK without encountering FP (Subcase 4). Note that in all four subcases, the trajectory eventually reaches LK and jumps to RB. Subcases 1 and 3 are distinguished from 2 and 4 by the fact that the fixed point is playing a role in determining the movement of the trajectory. Bose et al (Bose et al., 2004) examined only Subcase 1 as defined here.) Note also that Subcases 1, 3 and 4, but not 2, result in a measurable delay to activity of the follower neuron (insets in Fig. 4b).
3.1.2 Case 2
We use a similar method to analyze Case 2. In this case, because the w-nullcline is relatively shallow, it does not intersect MB in the v-w plane. In Subcase 1 the trajectory moves quickly in the w-direction and reaches UK almost immediately after landing on MB, which leads to a left jump back to LB. Subcase 2 is the same as that in Case 1, in which the trajectory reaches LK fast and then jumps to RB. Subcase 3 and 4 show the cases when τwm and τhm are of the same order. The trajectory reaches UK and jumps left in the former and it reaches LK and jumps right in the latter. Subcase 5 shows a rare possibility that the trajectory reaches UK and LK at the same time when MB shrinks to a point or when h = 0. In this case the fate of the trajectory remains ambiguous.
Note that in Case 1, although the delay to activity in Subcases 1, 3 and 4 can be quite similar, Subcase 1 is inherently distinct from the other two. In this subcase, the delay to the active phase is caused only by the presence of the fixed point FP and the delay caused by the time spent in MB would completely disappear if the FP disappeared (e.g. if gCa is increased in Eq. (1)), in which case the behavior of the follower neuron would be identical to that of Subcase 1 of Case 2 (Fig. 4d).
3.1.3 Simulation of the biological neurons
We now use the geometric setup described in Figure 4 to demonstrate the distinct behaviors of the biological PY neurons. In order to simulate the biological PY neurons, we only need to consider the subcases in Case 1, since the membrane potential of PY never moves to the inactive state without receiving inhibition. Therefore in the v-w phase plane, the trajectory can only jump to the right or stay on MB (till the next cycle of inhibition) after landing on it. Figures 5a and 5b show these two possibilities. In Figure 5a, the left panel shows the model solution which represents the activity of PY1 in Figure 1a and Case i in Figure 1b; the middle panel shows the trajectory of the solution in the v-w phase plane; and the right panel shows the trajectory in the w-h phase plane describing the activity on MB. In this case the trajectory moves faster in the h direction than in the w direction (as in Subcase 4 of Fig. 4b) and therefore it reaches LK directly and then jumps to the right.
Figure 5.
The periodic solutions in Case 1 when the A-current is moderate (a) or strong (b). (a) Left panel: a modest A-current causes a phase delay to the active state. Middle panel: the periodic solutions in the v-w phase plane. Right panel: The trajectory in the w-h phase plane, which shows the dynamics on the middle branch. The trajectory reaches the curve of the lower knee (LK) during Tin, therefore the membrane potential reaches the active state after a phase delay. (b) Left panel: the follower neuron cannot reach the active state when the A-current is strong. Middle panel: the periodic solutions in the v-w phase plane. The trajectory jumps back to the left branch when the inhibition starts. Right panel: The trajectory reaches the curve of the fixed point (FP), and then it moves downward along FP. It does not reach LK during Tin, therefore the membrane potential does not reach the active state. The arrows in the left and middle panels denote the inactive (black), active (red) and intermediate (blue) states. The labels [1–4] in the middle panels denote the v-nullcline corresponding to the times denoted by the same label in the left panel.
Figure 5b shows a simulation with a stronger A-current corresponding to PY3 in Figure 1a and Case iv in Figure 1b. The three panels show the same information as in Figure 5a. It is clear (especially in the right panel) that in this case, the trajectory does not move fast in the h direction: it reaches FP first and then moves along it. It fails to reach LK during Tin, thus it cannot jump to the right. The trajectory remains near FP on MB until the next cycle of inhibition arrives (see PY trace in Fig. 5b). The inhibition moves the v-nullcline down and the trajectory jumps to the left.
3.2 Periodic solutions
The analysis on the w-h manifold gives us a clear view of the possible fates of the trajectory on the middle branch in a single cycle. However, the determination of this fate does not guarantee knowledge of the long-term behavior of the follower neuron. This is because the values of w or h may vary from cycle to cycle and may also depend on the history of these variables in previous cycles. It is possible that these variables converge to a stationary value (dynamic equilibrium) after a number of cycles. In order to determine the long-term behavior of the follower neuron, it is necessary to track the values of w and h over multiple cycles. In the following sections we derive analytic expressions for each variable as a function of the pacemaker and other network parameters. We will derive these expressions for a representative case discussed above.
We first examine the accumulation of the inactivation variable h in Case 1, which provides a vertical MB and a stable fixed point FP on it (Figs. 3a and 4a). For simplicity, we assume the movement in the w direction on MB is fast compared to the movement in the h direction (Subcase 1 or 3 in Fig. 4b) and that τwl, τwh and τhh are set properly to guarantee the trajectory lands on MB only from LB1 in every cycle. Under these two conditions we do not need to consider the variability of the w value in each cycle. Suppose at t = 0 the pacemaker becomes active, and therefore the follower neuron moves to its inactive state due to inhibition. We suppose the trajectory starts in the v-w plane on the left branch with h(0) = 0. During 0 < t < Tact, the trajectory moves downwards and obeys Equation (7); therefore at t = Tact:
| (10) |
Following t = Tact, the follower neuron is released from inhibition, which is reflected in the v-w phase plane as a jump from LB1 to MB. When the trajectory lands on the middle branch, it moves to FP and the lower knee LK begins to rise with time constant τhm. (Our assumptions above require that the trajectory does not reach LK before it reaches FP.) The time tm spent on the middle branch is determined by the equation
| (11) |
Here vθ is the v value of the middle branch and tm represents the time the trajectory spends on the middle branch, which can be calculated explicitly (see also (Bose et al., 2004)) as
| (12) |
If the trajectory is able to jump to the right branch during (Tact, P−εα) where P ≡ Tact+Tin, then at t = P
| (13) |
Here εα represents the time the trajectory takes to exceed the w value of the upper knee of MB1, wUK1, in the w direction while it is moving along RB. εα equals to zero if wFP ≥ wUK1; when wFP < wUK1, if the trajectory jumps from MB to RB at a moment in (P−εα, P), then when the inhibition starts at t = P, the trajectory will return to MB1 instead of LB1. εα can be calculated by the following equation:
| (14) |
In order to avoid the trajectory landing on MB1, we set τwh and τhh to be small thereby forcing εα to also be small. Under this condition the interval (P−εα, P) can be ignored for simplicity.
If the trajectory is unable to jump to the right branch during (Tact, P−εα), then at t = P
| (15) |
Based on the above steps we conclude the following recursive equations describing the values of h in cycle n (hn) at the moments that the inhibition from the pacemaker is removed at t = (n−1)P + Tact:
| (16a) |
| (16b) |
where tmn denotes the time spent on the middle branch in the nth cycle. Note that if the time spent on the left branch is too short, h would not become large enough (MB does not grow enough) in that cycle and the log term in Equation (16b) can be negative. In this case, the trajectory would not land on the middle branch and tmn is defined to be 0. The activity phase ϕ in each cycle can be calculated by
| (17) |
This iteration scheme converges to the steady state values h* and tm* which satisfy
| (18a) |
| (18b) |
In these equations, h* denotes the steady state value of h (inactivation of the A-current) at the end of the inhibition from the pacemaker in each cycle and tm* is the steady state value of the time spent on the middle branch. Therefore the steady state activity phase is
| (19) |
Equations (16)–(19) show that h, tm and ϕ can be represented as functions of Tin and Tact, and therefore the cycle period (P) and the duty cycle (Tact/P) of the pacemaker neurons play an important role in determining the activity phase of the follower neuron.
A natural question that arises from these calculations is whether we can use these simplified Equations (16)–(19) to predict the activity phase of the biological PY neurons. We addressed this question by using an experimental protocol to measure the activity phase of the biological PY neurons as a function of the cycle period of the pacemaker neurons. We performed this experiment using two PY neurons. In order to control the cycle period, we blocked the biological synapses from the pacemaker neurons to the PY neurons (Rabbah and Nadim, 2005) and used the dynamic clamp technique to produce an artificial synaptic input (from a model pacemaker neuron) to the PY neurons. This allowed us to change the values of Tin and Tact (and therefore the cycle period) in a controlled manner. We used three different protocols for changing the cycle period.
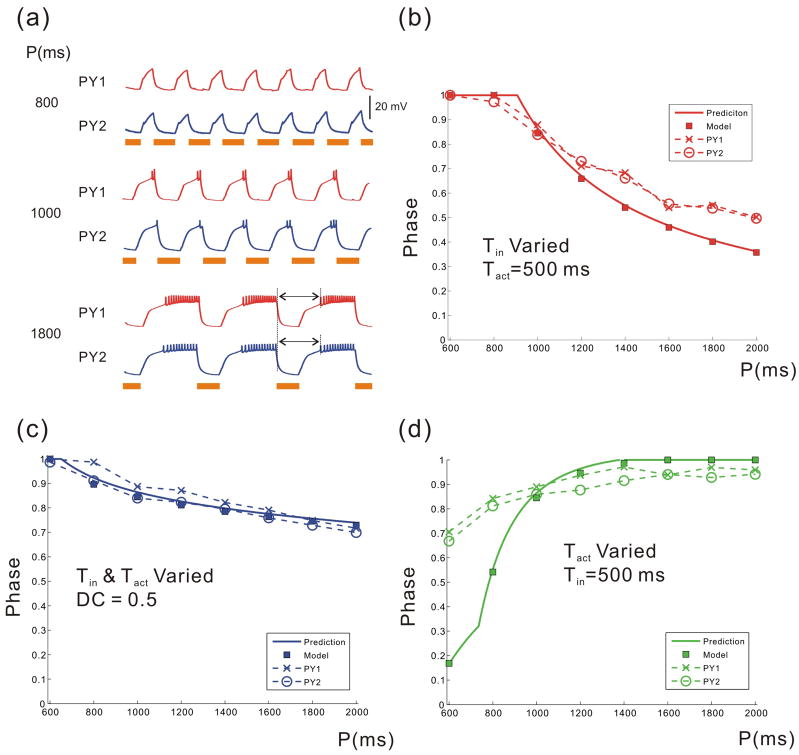
In the first protocol, we changed cycle period by varying Tin but keeping Tact fixed. Figure 6a shows the membrane potentials of the two PY neurons when Tact = 500 ms and Tin = 300, 500, 1300 ms. Figure 6b shows the comparison of steady state phases as predicted by Equations (16)–(19) and the activity phase of the biological PY neurons. It is clear that the activity phase decreases with Tin. In the second protocol, we changed the cycle period by changing both Tin and Tact while keeping the duty cycle constant. In the third protocol, we changed the cycle period by keeping Tin fixed and varying Tact. The results of the model and experiments for these two protocols are shown, respectively, in Figures 6c and 6d. As seen in Figures 6b–d, our model provides a good qualitative prediction of the activity phase of the PY neurons for all three protocols. For the first two protocols and a large range of periods in the third protocol, there is also very good quantitative agreement between the model and the experiments. Note that in many central pattern generators, including the pyloric network, variations of cycle period are similar to the protocol shown in Figure 6c, where the duty-cycle of the pacemaker neurons remains constant (Abbott et al., 1991; Bucher et al., 2005). Despite the fact that our equations were derived using several simplifying assumptions Figure 6 indicates that they can faithfully predict the activity phase of the biological neurons. Note, however, that the model does not quantitatively match the biological phase in Figure 6d for the smallest values of Tact. At these small values the A-current does not de-inactivate sufficiently and the middle branch is very short. As a result, the trajectory either does not land on the middle branch at all or barely spends time on that branch. This inability of the model to predict the phase for may be due to the fact that our model only includes a single inactivation variable for the potassium A-current whereas this current in the biological PY neurons may involve multiple inactivation variables with distinct kinetics, as suggested by Harris-Warrick et al (1995).
Figure 6.
The recursive equations predict the activity phase of the model neuron and the biological PY neurons in a reasonable accuracy: (a) The time traces of two biological PY neurons when P is varied by varying Tin (Tact is fixed). The solid bars denote the active duration of the pacemaker input. The phase-period plot when P is varied by varying Tin and keeping Tact fixed (b); by varying Tin and Tact but keeping the duty cycle fixed (c); by varying Tact and keeping Tin fixed (d). In (b–d), the solid curve shows the phase calculated from Equations (16–19); the filled squares show the phase of the 3-variable model; the two dashed curves show the burst phase of the biological PY neurons. Give parameters for the simulation.
4. Discussion
The transient potassium current or A-current has been shown to exist in various types of neurons (Huguenard et al., 1991; Herrington and Lingle, 1994; Wustenberg et al., 2004) and is known to be important in setting the timing of action potentials (Gerber and Jakobsson, 1993), especially following inhibitory input (Harris-Warrick et al., 1995). The A-current is known to contribute to the generation of a coordinated motor pattern (Hess and El Manira, 2001) and acts as a bursting trigger in the absence of a slow variable (Tabak et al., 2007; Toporikova et al., 2007). In a network of bursting neurons, the A-current often acts to delay the onset of the burst, thus setting the activity phase of different neurons within the network (Harris-Warrick et al., 1995).
In a previous modeling study, we examined how the A-current can interact with short-term synaptic depression to promote phase maintenance in a follower neuron when the frequency of the periodic input is varied (Bose et al., 2004). Because the focus of the study of Bose et al was on synaptic depression, only a single set of parameters associated with the A-current were considered. In the current study, our focus is to understand how the various parameters associated with the A-current lead to different activity phases of a follower neuron. Our study is done in two stages. First, we use dynamical systems analysis to determine the fate of the trajectory of the follower neuron following inhibition in a single cycle. We then use this information to derive a set of equations that describe the steady-state activity phase of this neuron in response to a periodic input. The activity phase predicted by these equations matched the activity phase of follower PY neurons in the crab pyloric network when cycle period was varied through different experimental protocols.
How does the A-current affect the behavior of the neuron following inhibition?
A typical response of a follower neuron in an inhibitory network is to rebound to an active state following the inhibition, but the transition to the active state may be delayed by the amount and kinetics of the A-current. For example, in the crustacean pyloric network, the follower LP and PY neurons show different burst phases, which is partially determined by the different amount and specific properties of the A-current (Tierney and Harris-Warrick, 1992). It has been suggested that the variation in the phase of different PY neurons can be due to the different levels of A-current expressed in these neurons (Hooper, 1998). In fact, our experiments show that different PY neurons in the same preparation burst in different phases. Furthermore, their burst phases can be modulated by injecting an artificial A-current (Fig. 1, 2).
Our study focuses on two important questions regarding the phase of the follower neurons. First, following inhibition, how do the parameters of the A-current interact with other intrinsic properties to determine the time delay before the burst (active state)? Second, during rhythmic activity, how do different network parameters, including the cycle period, duration of inhibition and the strength and kinetics of the A-current interact to determine the activity phase of the follower neuron?
When we examined the factors that determine the delay before the burst, we found that, although the dominant factors in determining the delay are the maximal conductance and inactivation time constant of the A-current, the time constant governing the intrinsic properties of the neuron (w: the activation of the K current in the Morris-Lecar model) also contributes to this delay. Thus, the voltage-gated currents other than the A-current that are active in the time interval following the inhibition can prolong or shorten this delay. For example, when the time constant (τwm) of the recovery variable w is of the same order of magnitude of the inactivation time constant of the A-current, increasing (decreasing) τwm will lead to an increase (decrease) of the time delay to the active state.
More importantly, these other intrinsic currents can be a determining factor in whether a burst even occurs. As seen in our analysis of Figure 4d, if the intrinsic recovery variable w activates too fast, the neuron can return to its inactive phase even before the arrival of the next cycle of inhibition. Interestingly, such a possibility may be relatively easy to check in a biological neuron by inspecting whether the follower neuron can ever return to an inactive state without receiving inhibition, for example by blocking synaptic inputs or using a dynamic clamp synapse.
Our analysis of the A-current in this study is based on the simplifying assumption that the activation and inactivation steady-state curves are steep. Although a more gradual activation of the A-current is not considered here, a shallow activation curve could result in qualitative changes of the phase plane (e.g. the vertical curves in Figure 4) that may result in additional potential fates of the trajectory following inhibition. One example is that the follower neuron may produce non-periodic or even chaotic behaviors in which it only bursts in some cycles but not others, a behavior that is not possible in the current simplified model. A more detailed analysis requires examining all possible phase-plane structures that could arise due to the various model parameters (Zhang et al., 2008) and is beyond the scope of this study. However, it is useful to note that the simple phase-plane analysis techniques such as the one shown in Figure 4 can be used to explore such potential outcomes.
Our results on the steady-state activity phase of this neuron in response to a periodic input indicate that the phase of the follower neuron is not only a function of the period (P) of the input it receives but also a function of how P is changed. For example, if P is doubled, the phase of the follower neuron can become larger or smaller, depending on whether the duration of the synaptic input is increased or not. This is because the extent to which the A-current recovers from inactivation depends both on P (= Tact + Tin) and on the duration for which the neuron remains inhibited (Tact). Although there are many possible methods for changing P, we focus on three protocols. We show that if P is changed but Tact or the duty cycle (Tact/P) is fixed, the phase of the follower neuron decreases as P increases. Both these mechanisms of changing period occur in CPG networks, for example in the swing phase of locomotion which remains constant (constant Tact) despite a ten-fold variation in the cycle frequency (Grillner, 2006) or the lobster pyloric pacemaker ensemble (constant duty cycle) (Abbott et al., 1991). However, if P is changed by keeping Tin fixed, the phase of the follower neuron would increase as P is increased. Our theoretical predictions were then verified through a set of experiments conducted in follower PY neurons showing a close match between experiment and theory. Thus, our analysis provides a basic explanation for how the changes in phase depend not only on P but on how P is changed.
What do our results imply for the biological system?
The activity phases of CPG neurons are often determined by the frequency of network oscillations. In some cases, such as fish swimming, strict phase maintenance is required to produce a meaningful motor output (Grillner, 2006). In other cases, the activity phase of different neurons, and therefore the muscles that they control, increases or decreases as a function of network frequency (Hooper, 1997). Because there is a dominance of inhibitory connections in CPG networks (Friesen, 1994; Marder and Bucher, 2001; Marder et al., 2005) and the potassium A-current is a common current present in most neurons, our analysis can be applied in a variety of CPG and other oscillatory networks. In fact, our model can be used to determine (at least approximately) the phase of any follower neuron (with A-current) receiving rhythmic inhibition. To do so, the main factors that should be determined are the time constant of A-current inactivation which can be readily determined in voltage-clamp measurements, the timing of synaptic inhibition (Tact and Tin) and whether the neuron is active or silent in the absence of inhibition.
Conclusions
Rhythmic biological networks in general and the crustacean pyloric network in particular may have many follower neurons that both receive periodic driving input and interact with one another. Moreover, the presence of neuromodulators results in intrinsic or synaptic modifications and therefore changes the activity phase of the follower neurons. For example, dopamine can reduce the strength of the A-current therefore prolonging the duration of bursting (Harris-Warrick et al., 1995). Our results show that the factors that determine the post-inhibitory delay to bursting may include other voltage-gated currents that interact with the A-current. Additionally, during rhythmic activity, the timing of the inhibition is crucial in determining the steady-state activity phase of the follower neuron. Our modeling work provides a mathematical framework for understanding the activity of the individual follower neurons. Similar techniques can be used to account for inputs from other network neurons in order to determine the activity phase of these neurons and the long-term fate of their trajectories. As the number of neurons involved and thus the complexity of the network is increased, the simplifying techniques utilized in this study may be of critical importance for understanding the underlying dynamics.
Acknowledgments
This work is supported by the National Science Foundation Grant 0615168 (AB) and the National Institutes of Health Grant MH-60605 (FN).
5. Appendix: Experimental Methods
5.1 Dynamic clamp
The dynamic clamp experiments such as the one shown in Figure 1 were performed in the Nadim lab (unpublished data) on C. borealis PY neurons in two-electrode current clamp mode as described in (Rabbah et al., 2005). An artificial A-current was implemented in dynamic clamp (Manor and Nadim, 2001; Rabbah et al., 2005) and injected in the PY neurons with a sampling rate of 4 kHz. The equations describing the artificial clamp A-current are given by
The dynamic clamp software used here has been developed in the Nadim laboratory and is available for free download at (http://stg.rutgers.edu/software/index.htm).
Contributor Information
Yu Zhang, Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102.
Amitabha Bose, Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102.
Farzan Nadim, Department of Mathematical Sciences, New Jersey Institute of Technology, Department of Biological Sciences, Rutgers University, Newark, NJ 07102.
References
- Abbott LF, Marder E, Hooper SL. Oscillating Networks: Control of burst duration by electrically coupled neurons. Neural Comput. 1991;3:487–497. doi: 10.1162/neco.1991.3.4.487. [DOI] [PubMed] [Google Scholar]
- Bose A, Manor Y, Nadim F. The activity phase of postsynaptic neurons in a simplified rhythmic network. J Comput Neurosci. 2004;17:245–261. doi: 10.1023/B:JCNS.0000037685.71759.1a. [DOI] [PubMed] [Google Scholar]
- Bucher D, Prinz AA, Marder E. Animal-to-animal variability in motor pattern production in adults and during growth. J Neurosci. 2005;25:1611–1619. doi: 10.1523/JNEUROSCI.3679-04.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connor JA, Stevens CF. Prediction of repetitive firing behaviour from voltage clamp data on an isolated neurone soma. J Physiol. 1971;213:31–53. doi: 10.1113/jphysiol.1971.sp009366. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Debanne D, Guerineau NC, Gahwiler BH, Thompson SM. Action-potential propagation gated by an axonal I(A)-like K+ conductance in hippocampus. Nature. 1997;389:286–289. doi: 10.1038/38502. [DOI] [PubMed] [Google Scholar]
- Friesen WO. Reciprocal inhibition: a mechanism underlying oscillatory animal movements. Neurosci Biobehav Rev. 1994;18:547–553. doi: 10.1016/0149-7634(94)90010-8. [DOI] [PubMed] [Google Scholar]
- Gerber B, Jakobsson E. Functional significance of the A-current. Biol Cybern. 1993;70:109–114. doi: 10.1007/BF00200824. [DOI] [PubMed] [Google Scholar]
- Grillner S. Biological pattern generation: the cellular and computational logic of networks in motion. Neuron. 2006;52:751–766. doi: 10.1016/j.neuron.2006.11.008. [DOI] [PubMed] [Google Scholar]
- Harris-Warrick RM, Coniglio LM, Barazangi N, Guckenheimer J, Gueron S. Dopamine modulation of transient potassium current evokes phase shifts in a central pattern generator network. J Neurosci. 1995;15:342–358. doi: 10.1523/JNEUROSCI.15-01-00342.1995. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herrington J, Lingle CJ. Multiple components of voltage-dependent potassium current in normal rat anterior pituitary cells. J Neurophysiol. 1994;72:719–729. doi: 10.1152/jn.1994.72.2.719. [DOI] [PubMed] [Google Scholar]
- Hess D, El Manira A. Characterization of a high-voltage-activated IA current with a role in spike timing and locomotor pattern generation. Proc Natl Acad Sci U S A. 2001;98:5276–5281. doi: 10.1073/pnas.091096198. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hooper SL. The pyloric pattern of the lobster (Panulirus interruptus) stomatogastric ganglion comprises two phase-maintaining subsets. J Comput Neurosci. 1997;4:207–219. doi: 10.1023/a:1008867702131. [DOI] [PubMed] [Google Scholar]
- Hooper SL. Transduction of temporal patterns by single neurons. Nat Neurosci. 1998;1:720–726. doi: 10.1038/3721. [DOI] [PubMed] [Google Scholar]
- Huguenard JR, Coulter DA, Prince DA. A fast transient potassium current in thalamic relay neurons: kinetics of activation and inactivation. J Neurophysiol. 1991;66:1304–1315. doi: 10.1152/jn.1991.66.4.1304. [DOI] [PubMed] [Google Scholar]
- Johnson SM, Smith JC, Funk GD, Feldman JL. Pacemaker behavior of respiratory neurons in medullary slices from neonatal rat. J Neurophysiol. 1994;72:2598–2608. doi: 10.1152/jn.1994.72.6.2598. [DOI] [PubMed] [Google Scholar]
- MacLean JN, Zhang Y, Goeritz ML, Casey R, Oliva R, Guckenheimer J, Harris-Warrick RM. Activity-independent coregulation of IA and Ih in rhythmically active neurons. J Neurophysiol. 2005;94:3601–3617. doi: 10.1152/jn.00281.2005. [DOI] [PubMed] [Google Scholar]
- Manor Y, Nadim F. Synaptic depression mediates bistability in neuronal networks with recurrent inhibitory connectivity. J Neurosci. 2001;21:9460–9470. doi: 10.1523/JNEUROSCI.21-23-09460.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marder E, Calabrese RL. Principles of rhythmic motor pattern generation. Physiol Rev. 1996;76:687–717. doi: 10.1152/physrev.1996.76.3.687. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D. Central pattern generators and the control of rhythmic movements. Curr Biol. 2001;11:R986–996. doi: 10.1016/s0960-9822(01)00581-4. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D. Understanding circuit dynamics using the stomatogastric nervous system of lobsters and crabs. Annu Rev Physiol. 2007;69:291–316. doi: 10.1146/annurev.physiol.69.031905.161516. [DOI] [PubMed] [Google Scholar]
- Marder E, Bucher D, Schulz DJ, Taylor AL. Invertebrate central pattern generation moves along. Curr Biol. 2005;15:R685–699. doi: 10.1016/j.cub.2005.08.022. [DOI] [PubMed] [Google Scholar]
- McCormick DA, Bal T. Sleep and arousal: thalamocortical mechanisms. Annu Rev Neurosci. 1997;20:185–215. doi: 10.1146/annurev.neuro.20.1.185. [DOI] [PubMed] [Google Scholar]
- Mishchenko EF, Rosov NK. Differential equations with a small parameter and relaxation oscillations. New York: Plenum Press; 1980. [Google Scholar]
- Moore RY. A clock for the ages. Science. 1999;284:2102–2103. doi: 10.1126/science.284.5423.2102. [DOI] [PubMed] [Google Scholar]
- Rabbah P, Nadim F. Synaptic dynamics do not determine proper phase of activity in a central pattern generator. J Neurosci. 2005;25:11269–11278. doi: 10.1523/JNEUROSCI.3284-05.2005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rabbah P, Golowasch J, Nadim F. Effect of electrical coupling on ionic current and synaptic potential measurements. J Neurophysiol. 2005;94:519–530. doi: 10.1152/jn.00043.2005. [DOI] [PubMed] [Google Scholar]
- Rinzel J, Ermentrout GB. Analysis of neural excitability and oscillations. In: Koch C, Segev I, editors. Methods in Neuronal Modeling: From Ions to Networks. Cambridge, MA: MIT Press; 1998. pp. 251–291. [Google Scholar]
- Tabak J, Toporikova N, Freeman ME, Bertram R. Low dose of dopamine may stimulate prolactin secretion by increasing fast potassium currents. J Comput Neurosci. 2007;22:211–222. doi: 10.1007/s10827-006-0008-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tierney AJ, Harris-Warrick RM. Physiological role of the transient potassium current in the pyloric circuit of the lobster stomatogastric ganglion. J Neurophysiol. 1992;67:599–609. doi: 10.1152/jn.1992.67.3.599. [DOI] [PubMed] [Google Scholar]
- Toporikova N, Tabak J, Freeman ME, Bertram R. A-Type K(+) Current Can Act as a Trigger for Bursting in the Absence of a Slow Variable. Neural Comput. 2007 doi: 10.1162/neco.2007.08-06-310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Walters JR, Hu D, Itoga CA, Parr-Brownlie LC, Bergstrom DA. Phase relationships support a role for coordinated activity in the indirect pathway in organizing slow oscillations in basal ganglia output after loss of dopamine. Neuroscience. 2007;144:762–776. doi: 10.1016/j.neuroscience.2006.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wustenberg DG, Boytcheva M, Grunewald B, Byrne JH, Menzel R, Baxter DA. Current- and voltage-clamp recordings and computer simulations of Kenyon cells in the honeybee. J Neurophysiol. 2004;92:2589–2603. doi: 10.1152/jn.01259.2003. [DOI] [PubMed] [Google Scholar]
- Zhang Y, Bose A, Nadim F. A detailed mathematical analysis of the interaction between the A-current and other intrinsic properties in setting the phase of a follower neuron in an inhibitory network. 2008 In preparation. [Google Scholar]