Abstract
Registration based mapping of geometric differences in MRI anatomy allows the detection of subtle and complex changes in brain anatomy over time that provides an important quantitative window on the process of both brain development and degeneration. However, methods developed for this have so far been aimed at using conventional structural MRI data (T1W imaging) and the resulting maps are limited in their ability to localize patterns of change within sub-regions of uniform tissue. Alternative MRI contrast mechanisms, in particular Diffusion Tensor Imaging (DTI) data are now more commonly being used in serial studies and provide valuable complementary microstructural information within white matter. This paper describes a new approach which incorporates information from DTI data into deformation tensor morphometry of conventional MRI. The key problem of using the additional information provided by DTI data is addressed by proposing a novel mutual information (MI) derived criterion termed diffusion paired MI. This combines conventional and diffusion data in a single registration measure. We compare different formulations of this measure when used in a diffeomorphic fluid registration scheme to map local volume changes. Results on synthetic data and example images from clinical studies of neurodegenerative conditions illustrate the improved localization of tissue volume changes provided by the incorporation of DTI data into the morphometric registration.
Keywords: Diffeomorphic fluid registration, Deformation morphometry, Mutual information, Multi channel mutual information, Diffusion tensor imaging, Dense feature morphometry
1. Introduction
The spatial and temporal patterns of tissue volume loss and integrity change occurring in neurodegenerative conditions are not only of scientific interest aimed at understanding neurodegenerative processes, but are also of key clinical interest for disease diagnosis and treatment monitoring. By relating brain anatomy to cognitive performance, such findings contribute on a more fundamental level to a better understanding of brain function and dys-function. Tracking of change in brain anatomy over time from MRI has emerged as a powerful tool in detecting and studying changes relating to disease diagnosis and progression in neurodegeneration and development. In particular, non-rigid registration based methods have been developed to map subtle geometric changes in brain anatomy and separate true volume changes from tissue displacements (Freeborough and Fox, 1998; Studholme et al., 2006; Cardenas et al., 2007). Such methods have been almost entirely focused toward the analysis of conventional T1 weighted (T1W), T2 weighted (T2W) or proton density weighted (PDW) structural MRI data. These images provide basic contrast between gray matter, white matter and cerebrospinal fluid, but are limited in their ability to spatially localize geometric change within regions of uniform tissue. In particular, current serial morphometry of MRI cannot probe within the bulk of white matter that holds the underlying connections between functional brain regions. White matter is known to be lost during normal aging (Jernigan et al., 2001) and many forms of dementia, and its volume can change in substance abuse and recovery. White matter tracts are critically important in relating structural changes occurring over time in different anatomical regions, in a range of neurodegenerative conditions including Alzheimer's, Semantic (Studholme et al., 2004) and Frontotemporal Dementia (Cardenas et al., 2007), alcohol abuse and HIV.
DTI data (Basser et al., 1994) provides significant microstructural information about tissues in the brain, which significantly compliments that provided by high resolution T1W imaging. There has been significant recent work on the alignment of diffusion tensor imaging to diffusion tensor imaging, both within and between subjects. The alignment problem of DTI is more complex than the alignment of conventional scalar MRI values because the inherent local geometry of the diffusion measurements is modified by spatial transformation of images. DTI data itself, unlike T1W imaging, provides relatively calibrated measurements which are consistent between studies and this motivates the direct application of tensor metrics to evaluate their alignment. Recent work has seen the incorporation of these ideas into deformable DTI registration algorithms such as the elegant work of Cao et al. (2005). The work of Zhang et al. (2000) derives a novel method of incorporating the diffusion rotational information into an elastic registration scheme to align tensor orientations and locations simultaneously. These methods importantly are aimed at using not just scalar measures of diffusion, but the directional diffusion information within the registration process. This allows the registration and any resulting morphometric analysis to localize changes to regions that may have the same scalar diffusion properties as their neighbours, and simply differ from surrounding tissues in their diffusion orientation. In particular, the recent work of Zhang et al. (2007) shows the importance of using directional diffusion information in the registration, as opposed to simple scalar metrics (such as fractional anisotropy) of diffusion properties derived from diffusion measurements. This motivates our interest in making use of the full diffusion tensor information in the registration.
This paper examines a related but different problem: one of incorporating DTI alignment information within high resolution deformation morphometry of conventional T1W MRI data, in order to provide additional spatial constraints in deformation morphometry. A key challenge here is that T1W data is not directly compatible with the geometrically derived local diffusion measurements, but provides much greater spatial resolution in many areas of the brain (basic tissue boundaries and grey matter structure). The initial ideas for this work were originally presented at the Information Processing in Medical Imaging conference in 2007 (Studholme et al., 2007), and are expanded and applied here to both synthetic and clinical imaging data.
2. Method
2.1. Measures of registration of MRI and DTI
Entropy based methods, such as those using mutual information, have been used to form a robust measure of image similarity between T1W images for accurate deformation morphometry, where, unlike the DTI tensor components, the intensity and contrast is essentially un-calibrated and can vary between imaging studies. Given a pair of conventional T1 weighted images, with intensities m1(x) and m2(x) (superscripts denoting time point) in the same common space x ∈ X, we can derive a measure of the mutual information between the sets of intensities M1 and M2 occurring together in the two images:
| (1) |
where H(M) = ∑m∈M – p(m) log(p(m)) is the marginal entropy and H(M1, M2) = ∑m1∈M1 ∑m2∈M2 – p(m1, m2) log(p(m1, m2)) is the joint entropy of intensities m1 and m2 occurring together. The local gradient of this criterion (Hermosillo et al., 2002) can be used to drive a fluid registration allowing non-rigid diffeomorphic alignment of images as in (D'Agostino et al., 2003). In this work, we want to build on this by introducing information from DTI data.
If we assume that we additionally have sets of reconstructed diffusion tensor values D1 and D2 over the same field of view of the T1 weighted MRI data at each time point, then we want to evaluate both MRI and DTI similarity simultaneously. In practice, here we will assume that the tensor contains six individual diffusion measures D = {Dxx, Dyy, Dxy, Dxz, Dyz, Dzz}, but the methods can be extended to larger numbers of directions. For DTI data these calibrated tensor components can be related geometrically using a range of different approaches (Zhang et al., 2000; Cao et al., 2005), to derive a measure of similarity for DTI alignment. However, these measurements cannot be directly related to conventional scalar image data. Ideally, a combined similarity measure is needed, which takes into account the changing relationship between the local orientation of the DTI data and the conventional structural data, as well as between the DTI information. A direct approach would be to evaluate the mutual information between all seven image pairs (T1W intensity and the six diffusion tensor components) acquired for two imaging studies. This would make use of multi-channel mutual information methods previously proposed (Studholme et al., 1996; Studholme et al., 1996; Pluim et al., 2003) to evaluate the collective mutual information between studies. For conventional matching where there is some shared information between image types, as illustrated in the upper part of Fig. 1, we can consider the shared information due to a combination of all the images. Given that the spatial relationships within studies is fixed (Studholme et al., 1996), the registration similarity between studies can be evaluated from the mutual information between the two studies collectively,
| (2) |
where H(M1, D1) is the collective information provided by the first study, H(M2, D2) is the collective information provided by the second study, and H(M1, D1, M2, D2) is the joint information of the combined studies. However, this criterion requires, for six DTI directions, the estimation of the (6 + 1) × 2 = 14 dimensional joint probability distribution for the joint entropy H(M1, D1, M2, D2), i.e. we need to estimate the probability of co-occurrence of all possible combinations of 14 different values . Any estimate of this distribution would be sparsely populated and require expensive computational methods to store and evaluate. One alternative approach is to simply ignore changes in shared information between different types of images and form a measure from a simple summation of MI between image pairs, each derived from the matching of one image type in one study to the same image type in the second study,
| (3) |
This simplification however clearly ignores any influence that one image type may have in explaining the structure in the other image types. An alternative formulation explored here is to use a simplification of the general case of Eq. (2). This simplification is based on the fact that the information provided by the different diffusion directions within a study is relatively un-correlated. For example, in conventional multi-channel MI based image registration, meaningful shared information between channels occurs when regions of a given intensity in one modality co-occur with intensities in a second modality (e.g. grey matter intensities in MRI co-occur with some fraction of a ‘soft tissue’ intensity range within CT). In DTI data complex, curved tracts are exhibited as different combinations of diffusion strengths in each axis along its length. Thus, within a single DTI study, high values of diffusion components in the X axis Dxx would not be expected to co-occur more frequently with a particular diffusion strength in the Y-axis Dyy (i.e. given a diffusion strength in direction X, we cannot guess what the diffusion strength in direction Y is going to be). However, considering the pairing of conventional MRI with diffusion measurements: within regions of white matter as seen in T1W MRI, there will be a certain fraction of voxels exhibiting a specific level of X-axis diffusion Dxx, and a certain fraction exhibiting Y-axis diffusion Dyy, reflecting, for example anterior–posterior or inferior–superior connections within white matter. In addition, low MRI T1W intensities delineate regions of unreliable diffusion measurements in CSF and bone. Thus, the statistical co-occurrence of DTI diffusion components and conventional structural MRI intensity can provide a meaningful partitioning of diffusion information to clarify the alignment measure.
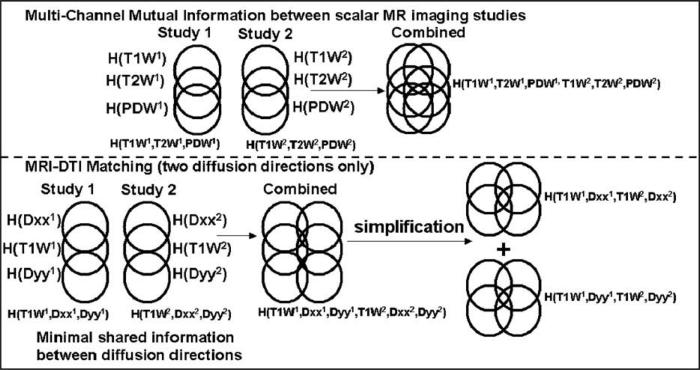
Fig. 1.
An illustration of the derivation of different MI measures of similarity between multiple sets of images for conventional scalar images (top) and combined scalar and DTI data types (bottom). In conventional MRI data sets (T1W, PDW, T2W) there is appreciable shared information. For DTI data, there is little shared information between individual diffusion direction maps. We can therefore consider the simplified relationship between DTI directional measurements separately paired with conventional MRI.
In order to account for shared structure between MRI and DTI at both time points, a measure formed by combining mutual information measures evaluated between T1/Diffusion image pairs, say (M1, ), at each time point can be considered. For each diffusion image, its match to the same diffusion direction at the later time point can be evaluated, together with the match of the high resolution T1W image intensities at each time point such that a single measure is formed by summing mutual informations over paired directions,
| (4) |
where ϕ ∈ {xx, xy, yy, xz, yz, zz} are the set of tensor components considered. There are different approaches to formulating the paired measure I(M1, , M2, ) of shared information between image pairs at each time point. Two direct approaches we consider here are illustrated in Fig. 2.
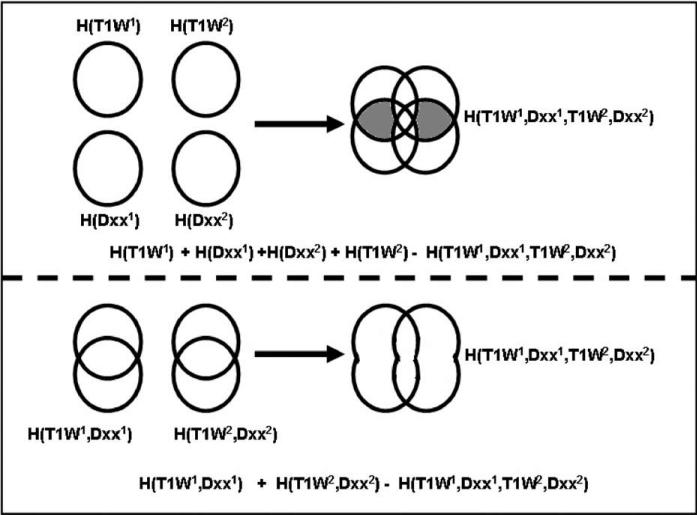
Fig. 2.
An illustration of different multi-channel formulations for measures relating the change in information in pairs of images. We can either consider the change in information between each of the images considered independently and when combined (top), or consider the change in information content between separately paired images and pairs combined (bottom). We name these diffusion paired mutual information (DPMI) and diffusion paired joint mutual information (DPJMI) respectively. The key difference is the constant factor indicated in grey for the DPMI measure, which is not a function of the mapping between studies.
The first approach (upper row in Fig. 1) is to use the difference in uncertainty between all four images (MRI and a DTI tensor component at each time point) when considered separately and then considered collectively, such that
| (5) |
We can term this as Diffusion Paired Mutual Information (DPMI). Because the first two terms are in the fixed coordinate system of the first time point and we assume the overlap does not change during the local deformable registration, this can be simplified by considering only changes in the second time point scans such that
| (6) |
An alternative is to use the differences in uncertainty when considering T1W-diffusion images paired at the first and second time points and then collectively over both time points such that,
| (7) |
We can term this as Diffusion Paired Joint Mutual Information, as we are considering joint densities only in this case. As above, for the purposes of serial registration, we can assume the first term remains constant during alignment so that the measure,
| (8) |
is maximised during registration.
Importantly, both of these formulations (8 and 6) require only four-dimensional joint intensity distributions to be estimated, but take into account the co-occurrence of structural and diffusion measures as image alignment is evaluated. Considering the effect of the spatial transformation on these two formulations, from Fig. 2, we can see that the only difference in their value should be from the shared information between the DTI-MRI data values within a given study (highlighted in grey). These factors should be independent of the spatial transformation between the studies, if there is no change in overlap between the images (which would change the marginal entropies). This is reasonable to assume for the local non-rigid registration step, which is bounded to the region of brain within the common overlap of all the image acquisitions.
2.2. Derivation of image registration forces
For these experiments in deformation based morphometry, a dense field diffeomorphic image registration scheme is used, where the local voxel mapping from one image to the other is described by the concatenation of a sequence ι = 1,...,S of diffeomorphic displacement fields xι+1 = xι + uι(xι) which are steps along a fluid flow. To estimate this sequence of displacement fields, the local gradient of a registration measure, , with respect to the current local displacement parameters u is evaluated to drive the images into alignment. These forces can be derived from the sum of the gradients of each of the paired MI terms . These, in turn, can be derived using the approach of Hermosillo et al. (2002), to create a single force field driving the image sets into alignment.
Diffusion paired MI (Eq. 6) can be expressed as an integration over the space of image values co-occurring in the four images such that
| (9) |
This can be differentiated with respect to u to form a force on a given point x1 of
| (10) |
Here, the first set of terms, which are a function of the 4D joint probability of intensity pairs, cluster intensity values in 4D by seeking deformations which move points to locations that form more probable DTI-MRI intensity combinations. This tends to reduce uncertainty and therefore joint information content in the collective image. The later terms containing marginal probabilities penalize for deformations which decrease uncertainty in the individual images, maximising information in the deforming images. Substituting this into Eq. 4 gives, for each point, a summation over the gradients in each diffusion direction pairing:
| (11) |
Diffusion paired Joint MI (Eq. 8) can be similarly expressed as an integration over intensities:
| (12) |
Differentiation with respect to the deformation field u then provides a registration force field of the form,
| (13) |
As with DPMI, the first set of terms cluster intensity values in 4D, by seeking deformations which move points to locations that form more probable DTI-MRI intensity combinations. The later terms containing 2D joint probabilities penalize for deformations which decrease uncertainty in paired images at each time point. Substituting this into Eq. (4) gives, for each point a summation over the gradients in each diffusion direction pairing,
| (14) |
2.3. Fluid registration methodology
The initial deformation between imaging studies is set to a zero displacement field, which is composed with a rigid transformation between the T1W images. Each iteration step can be broken down into separate parts: Firstly, the set of six 4D joint probability distributions between the structural T1W MRI data paired with each of the diffusion measurements at each time point is estimated for the current deformation estimate, using cubic intensity interpolation. A discrete binned estimate, using 64 bins in each intensity range, is then formed by passing through the 3D volume and interpolating values of the second time point into the coordinate system of the first time point. From this probability distribution, a force field is estimated from the observed intensities and intensity gradients of the T1W and diffusion images, forming a vector field at each voxel in the coordinate system and sampling of first time point T1W image. To provide a continuous model of the probability distribution for a given set of MRI and DTI intensities, the histogram is first smoothed. This 4D joint probability distribution p(i1, i2, i3, i4) is then used to form discrete 2D and 1D marginal probability distributions p(i3, i4), p(i3) and p(i4) by summing counts across the appropriate dimensions of the 4D distribution. For a given set of intensities at each voxel, the joint and marginal probabilities and their gradients with respect to intensity are estimated. To ensure continuity of the gradients, a probability approximation scheme is used. In this case we have used 4D, 2D and 1D Cubic B-Spline approximations (Wahba, 1990) for the corresponding 4D, 2D joint, and 1D marginal probabilities, respectively. As described by Thevenaz and Unser (2000), the B-spline provides a positive function of data values essential for a continuous approximation model of probability values.
A registration force field is then derived from the local gradient of the similarity measure with respect to the local displacement estimate, making use of the spatial derivatives of intensity values estimated by finite differences across the image space, and intensity derivatives of the joint and marginal probability values estimated using differentiated B-Spline kernels. This map of registration force vectors is then used to drive a velocity based, viscous fluid deformation model to ensure topology preservation. The solution to the registration is formed by integrating steps along an instantaneous velocity field which is itself derived from a balance between the registration force field F(x) and the energy of a flowing viscous fluid. The instantaneous velocity vector v(x) of a point in the image is estimated such that
| (15) |
where μ and λ are constants determining the relationships between stresses in the flow field. This is solved numerically in a similar way to Christensen et al. (1996) and Freeborough and Fox (1998), using Successive Over Relaxation (Press et al., 1992). From this velocity field estimate, a gradient ascent approach is used to refine the displacement estimate at each iteration. We include an updating of the local diffusion directions using the method of preserving the principal directions of diffusion (Alexander et al., 1999), during the iterative registration.
2.4. Data pre-processing for human image data
The DTI data of each human study was reconstructed into a rank 2 tensor and the b = 0 image was rigidly and then non-rigidly aligned to the T1 MPRAGE data using a method derived from Studholme et al. (2000). The non-rigid deformation estimate of the data was then applied to bring the diffusion tensors into the coordinate system and sampling resolution of the MPRAGE data (using cubic interpolation), taking into account the local change in geometry using the method of preservation of principal directions (Alexander et al., 1999). The initial rigid transformation mapping between the two MPRAGE images of the two studies was then estimated by maximization of normalized mutual information between scans (Studholme et al., 1999).
3. Experimental setup
3.1. Synthetic image data
In order to explore the basic behavior of the registration process and resulting morphometric maps created, we constructed a set of synthetic 3D T1W and DTI image pairs of simple geometric scenes with 1mm cubic voxel size. These images were smoothed to simulate a realistic resolution for image data. The scenes contained contrasting structure in the conventional T1W and DTI components in the form of spheres of tissue with sizes modified between the two studies. These data are illustrated by the images in Fig. 3.
Fig. 3.
Digital phantom data for evaluation: Top two rows show orthogonal slices through synthetic image volumes created to simulate loss of tissue in T1W MRI data. Lower two rows show additional synthetic diffusion data in the form of an overlay of principal diffusion directions, illustrating the different diffusion properties in the left and right halves of the partially contracting sphere. These two diffusion regions have the same fractional anisotropy, but differ simply in their orientation. This simulates neighbouring tracts with different directions, but with the same strength of connectivity.
3.2. Human image data
For these experiments longitudinal imaging data was used that was acquired by investigators Dr. M. Weiner and Dr. D. Meyerhoff in their imaging studies of neurodegenerative disease and substance abuse at the center for imaging of neurodegenerative disease at the VA hospital in San Francisco. Each imaging study included 3D T1 weighted MPRAGE acquisition with a resolution of 1 × 1 × 1 mm (256 × 256 FOV with 256 × 256 matrix, 176 slices) acquired with a sagittal orientation with RF spoiling. The scan time is 5 min 30 s. The phase encoding direction is anterior to posterior. The TR/TE/TI/flip angle = 2300 ms/3.37 ms/950 ms/7°. The acquisition was carried out using an 8 channel coil, using Grappa encoding and an acceleration factor of 2, with 50 reference lines of phase encoding. A diffusion tensor imaging protocol was then acquired consisting of a 2D double refocused spin echo EPI sequence with a spatial resolution of 2 × 2 × 3 mm with 4 averages. The overall scan time was 3 min with an axial acquisition of 40 slices without a gap between slices. The field of view 256 × 224 mm and the slice thickness is 3 mm. The acquisition uses an interleaved scan with TR/TE = 6 s/77 ms and a Matrix size of 128 × 128. An 8 channel coil is used with Grappa reconstruction using 2 acceleration factors and 35 reference lines. For directional encoding of diffusion, two b-values (0 and 800 s/cm2) and six diffusion directions were used.
4. Results
4.1. Results on synthetic data: comparison of MI, DPMI and DPJMI
The fluid registration procedure was applied using different registration measures to the synthetic image data using the T1W data only and incorporating diffusion information. The Jacobian of the resulting sequence of transformations was calculated and its determinant mapped over the image space to indicate the pattern of volume increases and decreases required to adapt the first time point image to match the second. Dark regions here indicate contraction, white regions indicate expansions and grey indicate no volume change. For the purposes of registration, the evaluation of the deformation field was limited to a spherical region 10 voxels outside the sphere itself. The results, shown in Fig. 4, clearly show the contribution of the additional diffusion information in the morphometric maps when using DPMI and DPJMI compared to MI of T1W images alone. The division of the internal space of the sphere into different diffusion directions provides a strong boundary creating a clear contrast in the pattern of contractions occurring within the uniform sphere. This illustrates how these measures can be used to localize volume changes in the brain. In addition we found, as would be expected from their derivation, that experimentally the two formulations for the diffusion paired measures (DPMI and DPJMI) behaved in a very similar way, with differences varying only at a level of numerical rounding errors. For the results of our later experiments, maps are presented using DPMI only, since equivalent results were found using both formulations.
Fig. 4.
Resulting maps of volume changes estimated when driving the fluid registration using conventional Mutual information (top) based on the T1W images only and using Diffusion Paired Mutual Information (DPMI) middle and Diffusion Paired Joint MI (DPJMI) bottom. Volume changes are shown as a simple grey scale with dark indicating contraction of the first time point to match the second, mid grey no change and white indicating expansion. Without the diffusion data there is no image structure to constrain the deformations within the bulk of tissue making up the sphere, resulting in a smooth gradient of contractions across the sphere. With DTI data, the orientation information provided by the diffusion tensors strongly partitions the pattern of contractions within the sphere so there is no inferred contractions in the opposite half of the sphere. The maps provided by DPMI and DPJMI (bottom two columns) are, within numerical rounding, the same, which confirms our observations in the derivation of the two measures.
4.2. Mapping brain volume increases: recovery from alcohol abuse
In previous work (Cardenas et al., 2007), T1W based morphometry has been used to study patterns of volume change over the brain in recovery from alcohol abuse using repeated T1W 1.5 T imaging. In more recent work combined DTI and MRI imaging has begun to be used at 4 T to study the same changes. In this paper, data were used from a cigarette smoking alcohol dependent volunteer enrolled in a program of treatment for alcohol dependence, who was imaged 6 days after his last alcoholic drink and then again after 39 days. We applied conventional T1W MRI morphometry and DTI-MRI morphometry using DPMI. Fig. 5 illustrates the data and changes observed. Firstly, the left two columns show the structural changes in terms of a simple subtraction of rigidly aligned T1W MRI data after accurate registration. This indicates ventricular CSF volume decreases from the shift in CSF-white matter boundaries. Slices through the 3D DTI and morphometric estimates are then shown on the right two columns. Conventional deformation based morphometry (bottom right column) indicates large scale volume changes distributed over white matter, with no ability to localize the volume change pattern. DPMI driven morphometry (top right column) highlights focal changes. A display of the corresponding DTI data in terms of the principal direction of diffusion is included to show the additional structure in the same region of tissue. A second example slice from these studies is shown in Fig. 6, again illustrating the significant localization of volume changes by the tissue diffusion structure. Both of these DPMI derived maps show focal increases in white matter volume that correspond to regions that have previously been shown in cross-sectional studies of alcohol dependent individuals to have lower fractional Anisotropy that light drinking controls (Yeh et al., 2007).
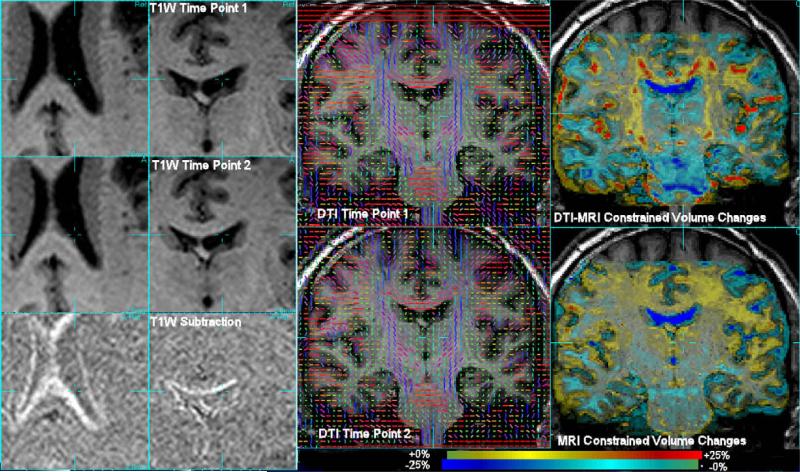
Fig. 5.
Data and results of applying deformation tensor morphometry to studies acquired on a subject before and after a period of abstinence from heavy drinking. Left two columns show enlarged view of the subtraction of rigidly aligned T1W MRI data. Right column shows estimated volume changes as a colour overlay on the first time point MRI of the determinant of the jacobian of the deformation sequence. Gross increases of tissue volume over bulk white matter are observed from T1W imaging alone. DTI-MRI morphometry created by maximising DPMI (top right) provides significant localisation of tissue volume changes, localizing changes in patterns around the ventricles and following the white matter tract structure seen in the DTI data.
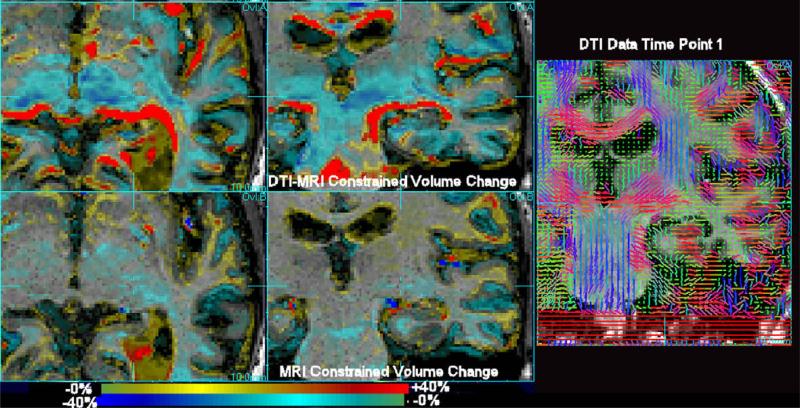
Fig. 6.
Axial slices through DTI (shown as principal diffusion direction) and MRI (left) at the two time points before and after abstinence from heavy drinking. Right: corresponding slices though volume change maps derived from MRI and MRI-DTI combined (using DPMI) displayed as a colour scale of percentage change overlaid onto the first time point MRI. Volume changes constrained by MRI data alone show diffuse increases in white matter volume after abstinence from heavy drinking. DTI-MRI constrained results show significantly localized volume increase patterns constrained to regions of tracts. Localization of greater changes are particularly visible in the corpus callosum (seen in mainly in red on the diffusion tensor maps).
4.3. Mapping brain volume decreases: Alzheimer's disease
A subject with an initial clinical diagnosis of Alzheimer dementia was imaged on a 4T Siemens imaging system twice over a period of 9 months. MI and DPMI driven fluid registration was applied to the data and the determinant of Jacobian matrix of the estimated deformation field was evaluated at each point in the first time point image and used to create a map of relative expansions and contractions required to force the anatomy at the first study to match the anatomy of the second. Results comparing the use of the proposed approach with conventional T1W deformation morphometry are shown in Fig. 7, for a subject diagnosed with Alzheimer's disease. This figure shows an improved localization of tissue contractions around the medial temporal lobe, when incorporating a measure of DTI alignment into the mapping process. Without DTI information, contractions of white matter around the expanding ventricle are significantly less constrained by the T1W imaging alone. We include a slice of the DTI data in the same region of the brain to illustrate the directional structure available in this region.
Fig. 7.
A subject diagnosed with Alzheimer's dementia scanned twice with an interval of 9 months (MMSE 25, age 61.7), exhibiting tissue loss and ventricular expansion. The scan pairs were fluidly aligned using MI (bottom row) and DPMI (top row). Sagittal and axial slices are shown along with a corresponding coronal slice through the DTI data at the same location. Here, in contrast to the alcohol recovery study, mainly tissue contractions are observed (blue). The incorporation of the additional structural information in white matter provided by DTI assists in constraining the local volume changes mapped by the fluid registration within a more focal region. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)
5. Discussion
A new general approach to the problem of localizing tissue volume changes in morphometric studies was proposed. This work is motivated by the need to localize patterns of tissue volume change within bulk regions of tissue visible in conventional MRI data. Such types of morphometric analyses are becoming increasingly important as DTI data is more routinely being acquired in imaging studies of anatomy and its change over time. We can classify such approaches, that make use of multiple contrast mechanisms such as DTI and MRI, as dense feature morphometry. They in effect attempt to make use of features at almost every voxel in the brain to localize tissue volume changes, as opposed to those methods driven only by the location of basic tissue boundaries. Developing and refining such approaches will allow us to probe for focal losses within the bulk of white matter holding connections between functional brain regions, and may provide an important new understanding of structural and functional changes occurring over time in neurodegenerative conditions and during their treatment.
This paper describes the first approach to making combined use of both DTI and MRI in deformation based morphometry. The approach is based on multi-channel mutual information and uses the complimentary information provided by the different modalities. It contrasts to DTI only registration methods in that it must deal with balancing conventional MRI alignment with DTI alignment. The new approach makes use of the relative independence of DTI components to derive a registration measure based on four-dimensional joint intensity probability estimates, making its implementation computationally more tractable. Two closely related criteria are formulated: diffusion paired mutual information (DPMI) and diffusion paired joint mutual information (DPJMI), and expressions are derived for their derivative with respect to the local deformation field. These derivatives are then used as force fields to drive a diffeomorphic registration between imaging studies.
A mutual information based approach to deriving measures was used because of the known issue of changing tissue contrast in many neurodegenerative conditions. Evolving tissue properties can influence both conventional T1W contrast between different tissue types, as well as relative diffusion strength within tissues measured in DT imaging. As a result, repeated imaging of brain anatomy may differ both in shape and contrast as a degenerative or developmental process proceeds. As discussed and illustrated in Studholme et al. (2006), it is important for a morphometric registration to separate changes in tissue contrast from true geometric changes in order to provide physically meaningful quantitative shape measurements. Information theory based approaches provide robustness to global changes in relative contrast, which simpler measures such as intensity correlation (Freeborough and Fox, 1998), that assume a linear relationship between intensities, cannot provide.
The process of pairing DTI with MRI directly improves the evaluation of DTI alignment: Many regions in brain diffusion images contain low or zero signal, particularly within fluid spaces, where they provide unreliable directional information. However, regions of low or high diffusion signal correspond to different intensities within the structural MRI data (dark CSF and bright tissue). At its simplest level, the use of the paired MI of values between structural and diffusion images can be seen as partitioning the DTI data into more and less useful regions of directional information. The conventional structural MRI data provides the majority of shared content between the two studies, since it has highest resolution and contrast to noise. However, in regions of uniform white matter, the gradient of the similarity measure will contain stronger contributions from the DTI data.
The methodology was applied to synthetic image data to evaluate the basic approach and to compare the behavior of the alternative formulations of DPMI and DPJMI. The methods were then applied to clinically typical imaging data acquired in cases of both tissue volume increase and volume loss. These two cases clearly show the promise of the technique with the possibility of new findings in the pattern of tissue volume change that may contribute to an improved understanding of neurodegenerative and neurodevelopmental processes. The improvement in the localization of volume changes is particularly important in relating any anatomical changes to specific functional measures, and understanding, for example how different subjects respond differently in the recovery from alcohol dependence.
An alternative approach to the registration problem would have been to derive scalar, orientation independent measures of image values from the DTI data, and combine these with conventional image data. However, sub-structures in white matter are characterized by both rotationally invariant microstructural tissue integrity (FA, diffusivity) and the microstructural orientation. Neighboring regions of white matter may have identical integrity but differing orientation of tracts. This information is provided by the orientation components of the diffusion tensor, not FA or diffusivity. By using the diffusion values directly, but including their re-orientation during the warping process, we can use their relationship between studies to more fully constrain the deformation solution within white matter.
One key issue in any quantitative morphometric analysis making use of DTI data, especially when acquired at higher fields, is the presence of geometric distortion, particularly those distortions arising from susceptibility effects in Echo Planar imaging. In this paper we have used imaging protocols currently used at the VAMC in San Francisco which do not incorporate additional acquisition techniques such as reverse gradient or field mapping to allow direct correction of DT imaging. As a result, we have used retrospective correction of the DTI data to structural MRI derived from earlier work on spin echo EPI imaging (Studholme et al., 2000; Studholme et al., 1999), which incorporates a physical model of the distortion process occurring in spin echo EPI to constrain the geometric mapping to a T1W image. Further work is underway to explore how distortions and their correction can influence the measurements of anatomical changes seen in clinical imaging studies.
From the initial work here, the general approach taken appears to provide promising results and motivates work on a new area of morphometric analysis. Such approaches promise to provide significantly refined maps of brain shape changes and improve our understanding of anatomy and brain function in different clinical conditions. Further work is underway to extend this methodology to improve the registration, allow improved spatial normalisation for group comparisons, deal with geometric and intensity distortions and evaluate the quantitative accuracy of the approach on a larger range of clinical data.
Acknowledgements
This methods development work was primarily funded by Grant NIH R01 NS 055064. The author would like to Thank Dr. Dieter J. Meyerhoff and Dr. Michael W. Weiner for making data available from their 4T imaging studies at the center for imaging of neurodegenerative disease at the VA hospital in San Francisco. This work would not have been possible without image data acquired as part of the NIH funded Grants AA10788, AG10897, P01 AG12435, P01 AG19724, PO1 AA11493, additional imaging acquired by Dr. Lara Stables, and help from the faculty and staff of the center for imaging of neurodegenerative disease at the VA in San Francisco. The author would also like to thank Dr. Corina Drapaca for discussions on the presentation of the mathematical derivations, the anonymous reviewers of the paper and for attendees of the IPMI conference for valuable comments and suggestions.
References
- Alexander DC, Gee JC, Bajcsy RK. Strategies for data reorientation during nonrigid warps of diffusion tensor images. Proceedings of MICCAI. 1999;99:463–472. [Google Scholar]
- Basser P, Mattiello J, le Bihan D. Estimation of the effective self-diffusion tensor from the NMR spin echo. Journal of Magnetic Resonance. 1994;103:247–254. doi: 10.1006/jmrb.1994.1037. [DOI] [PubMed] [Google Scholar]
- Cao Y, Miller M, Winslow R, Younes L. Large deformation diffeomorphic metric mapping of vector fields. IEEE Transactions on Medical Imaging. 2005;24(9):1216–1230. doi: 10.1109/tmi.2005.853923. [DOI] [PubMed] [Google Scholar]
- Cardenas VA, Studholme C, Gazdzinski S, Durazzo TC, Meyerhoff DJ. Deformation based morphometry of brain changes in alcohol dependence and abstinence. Neuroimage. 2007;34:879–887. doi: 10.1016/j.neuroimage.2006.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardenas V, Studholme C, Gazdzinski S, Meyerhoff TDD. Deformation based morphometry of brain volume changes during recovery from alcohol dependence. Neuroimage. 2007;34:879–887. doi: 10.1016/j.neuroimage.2006.10.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cardenas V, Boxer A, Chao LL, Gorono-Tempini M, Miller B, Weiner MW, Studholme C. Deformation morphometry reveals brain atrophy in frontotemporal dementia. Archives of Neurology. 2007;64(6):873–877. doi: 10.1001/archneur.64.6.873. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Christensen G, Miller M, Vannier M. Individualizing neuroanatomical atlases using a massively parallel computer. Computer. 1996:32–38. [Google Scholar]
- D'Agostino E, Maes F, Vandermeulen D, Suetens P. A viscous fluid model for multimodal non-rigid image registration using mutual information. Medical Image Analysis. 2003;7:565–575. doi: 10.1016/s1361-8415(03)00039-2. [DOI] [PubMed] [Google Scholar]
- Freeborough P, Fox N. Modeling brain deformations in Alzheimer's disease by fluid registration of serial 3D MR images. Journal of Computer Assisted Tomography. 1998;22(5):838–843. doi: 10.1097/00004728-199809000-00031. [DOI] [PubMed] [Google Scholar]
- Hermosillo G, Chefd'hotel C, Faugeras O. Variational methods for multimodal image matching. International Journal of Computer Vision. 2002;50(3):329–343. [Google Scholar]
- Jernigan T, Archibald S, Fennema-Notestine C, Gamst A, Stout J, Bonner J, Hesselink J. Effects of age on tissues and regions of the cerebrum and cerebellum. Neurobiology of Aging. 2001;22(4):581–591. doi: 10.1016/s0197-4580(01)00217-2. [DOI] [PubMed] [Google Scholar]
- Pluim J, Maintz J, Viegever M. Mutual-information-based registration of medical images: a survey. IEEE Transactions on Medical Imaging. 2003;22(8):986–1004. doi: 10.1109/TMI.2003.815867. [DOI] [PubMed] [Google Scholar]
- Press W, Flannery B, Teukolsky S, Vetterling W. Numerical Recipes in C. Cambridge University Press; Cambridge, England: 1992. [Google Scholar]
- Studholme C. Proceedings of Information Processing in Medical Imaging. Vol. 4584. Springer Verlag; Kerkrade, The Netherlands: 2007. Incorporating DTI data as a constraint in deformation tensor morphometry between T1 MR images. pp. 223–232. LNCS. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Studholme C, Hill D, Hawkes D. Proceedings of the IEEE Workshop on Mathematical Methods in Biomedical Image Analysis. IEEE Computer Society Press; 1996. Incorporating connected region labelling into automated image registration using mutual information. pp. 23–31. [Google Scholar]
- Studholme C, Hill D, Maisey MN, Hawkes D. Proceedings in Image Fusion and Shape Variability Techniques. Leeds University Press; 1996. Registration measures for automated 3D alignment of PET and intensity distorted MR images. pp. 186–193. [Google Scholar]
- Studholme C, Hill D, Hawkes D. An overlap invariant entropy measure of 3D medical image alignment. Pattern Recognition. 1999;32(1):71–86. [Google Scholar]
- Studholme C, Constable RT, Duncan J. Incorporating an image distortion model in non-rigid alignment of EPI with conventional MRI. In: Kuba A, Samal M, Todd-Pokropek A, editors. Proceedings of Information Processing in Medical Imaging. Springer-Verlag; 1999. pp. 454–459. visegrad Hungary. [Google Scholar]
- Studholme C, Constable RT, Duncan JS. Accurate alignment of functional EPI data to anatomical MRI using a physics based distortion model. IEEE Transactions on Medical Imaging. 2000;19(11):1115–1127. doi: 10.1109/42.896788. [DOI] [PubMed] [Google Scholar]
- Studholme C, Cardenas V, Blumenfeld R, Schuff N, Rosen H, Miller B, Weiner M. Deformation tensor morphometry of semantic dementia with quantitative validation. Neuroimage. 2004;21:1387–1398. doi: 10.1016/j.neuroimage.2003.12.009. [DOI] [PubMed] [Google Scholar]
- Studholme C, Drapaca C, Iordanova B, Cardenas V. Deformation based mapping of volume change from serial brain MRI in the presence of local tissue contrast change. IEEE Transactions on Medical Imaging. 2006;25(5):626–639. doi: 10.1109/TMI.2006.872745. [DOI] [PubMed] [Google Scholar]
- Thevenaz P, Unser M. Optimization of mutual information for multiresolution image registration. IEEE Transactions on Image Processing. 2000;9(12):2083–2099. doi: 10.1109/83.887976. [DOI] [PubMed] [Google Scholar]
- Wahba G. Spline Models for Observational Data. Society for Industrial and Applied Mathematics. Philadelphia: 1990. [Google Scholar]
- Yeh H, Simpson K, Gazdzinski S, Durazzo T, Meyerhoff D. Proceedings of ISMRM. Berlin, Germany: 2007. 2007. Voxelwise analysis of mr diffusion data from recovering alcoholics using tract-based spatial statistics. p. 3737. 2007. [Google Scholar]
- Zhang H, Yushkevich P, Alexander D, Gee J. Deformable registration of diffusion tensor MR images with explicit orientation optimization. Medical Image Analysis. 2000;10(5):764–785. doi: 10.1016/j.media.2006.06.004. [DOI] [PubMed] [Google Scholar]
- Zhang H, Avants B, Yushkevich P, Woo J, Wang S, McCluskey L, Elman L, Melhem E, Gee J. High-dimensional spatial normalization of diffusion tensor images improves the detection of white matter differences: an example study using amyotrophic lateral sclerosis. IEEE Transactions on Medical Imaging. 2007;26(11):1585–1597. doi: 10.1109/TMI.2007.906784. [DOI] [PubMed] [Google Scholar]