Abstract
Accurate prediction of survival rates of cancer patients is often key to stratify patients for prognosis and treatment. Survival prediction is often accomplished by the TNM system that involves only three factors: tumor extent, lymph node involvement, and metastasis. This prediction from the TNM has been limited, because other potential prognostic factors are not used in the system. Based on availability of large cancer datasets, it is possible to establish powerful prediction systems by using machine learning procedures and statistical methods. In this paper, we present an ensemble clustering-based approach to develop prognostic systems of cancer patients. Our method starts with grouping combinations that are formed using levels of factors recorded in the data. The dissimilarity measure between combinations is obtained through a sequence of data partitions produced by multiple use of PAM algorithm. This dissimilarity measure is then used with a hierarchical clustering method in order to find clusters of combinations. Prediction of survival is made simply by using the survival function derived from each cluster. Our approach admits multiple factors and provides a practical and useful tool in outcome prediction of cancer patients. A demonstration of use of the proposed method is given for lung cancer patients.
1. Introduction
Accurate prediction of outcomes or survival rates of cancer patients is often key to stratify patients for prognosis and treatment. Outcomes of patients are usually generated using standard survival functions and various factors recorded in the database (such as SEER [1] or NCDB [2]) that have prognostic potential. All prognostic factors become integrated through determination of the outcome according to the survival rate. This integration leads to a prognostic system that can be used to predict outcomes of any new patients. Clearly, a crucial question is how can one form a powerful prognostic system for cancer patients? The traditional answer to this question is to use the TNM system [3] that involves only three factors: tumor extent, lymph node involvement, and metastasis. However, the outcome prediction from the TNM has been limited, mainly because any other potential prognostic factors are not used in the system.
In this paper, we propose a computer-based prognostic system for cancer patients that admit multiple prognostic factors. Here is idea of our approach: (i) we partition patients from a cancer dataset into “natural” groups such that patients in the same group are more similar in survival than patients from different groups; (ii) once “natural” groups are obtained, a survival function for each group can be estimated by a standard method. Our prognostic system then consists of groups of patients and survival functions associated with the groups.
The first step (i) is the key to the entire process. Mathematically, this step is equivalent to performing a cluster analysis on a cancer dataset. However, this type of cluster analysis is different from traditional clustering approaches, which may be elaborated below. Suppose, after some simple management, a typical record for a patient contained in a cancer dataset is of the form: X, X1,…, Xm, where X is the recorded patient's survival time, which can be a censored time, and X1,…, Xm are measurements made on m risk factors or variables such as tumor size, gender, and age. Cluster analysis rising in (i) means that clusters of patients are sought such that patients in the same cluster are more similar in their lifetime T than patients from different groups. Here the connection between T and the observed time X is described as follows: T = X if X is an actual time to death due to the cancer under study; T > X otherwise (in this case X is a censored time). Therefore, cluster analysis from (i) is not equivalent to partitioning the set of vectors {(X, X1,…, Xk)} or the set {(X1,…, Xk)} which could be suggested by traditional clustering methods.
The above discussed difference between the cluster analysis in (i) and the traditional clustering indicates that clustering required in (i) may not be a trivial task. Other potential challenges in accomplishing (i) include presence of a high percentage of censored observations, different types of risk factors or variables, and a large dataset size [4–6]. For example, an SEER dataset of lung cancer patients diagnosed from 1973 through 2002 has more than 500 000 patients, comprises more than 30% records with censored survival times, and involves more than 80 variables that are either on the continuous, or ordinal, or nominal scale.
To overcome the above mentioned possible difficulties, we consider subsets of a cancer data, based on combinations of levels of some known key factors. This reduces the complexity in establishing prognostic systems. We then group these subsets by a hierarchical clustering algorithm, where the distance measure between two subsets is learnt through multiple clustering based on Partitioning Around Medoids (PAM) of Kaufman and Rousseeuw [7].
The rest of the paper is organized as follows. In Section 2, we briefly review some necessary elements of clustering and survival analysis. In Section 3, we present our algorithm of clustering of cancer data. An application of our algorithm to establishing a prognostic system for lung cancer patients is provided in Section 4. And finally our conclusion is given in Section 5.
2. Some Elements of Clustering and Survival Analysis
Clustering may be viewed as a process of finding natural groupings of objects. Commonly used clustering procedures fall into two categories: partitioning approaches and hierarchical approaches. A partitioning approach assigns objects into a group or cluster through optimizing some criterion. A hierarchical approach produces a hierarchy of groups or clusters. In this paper, we will use the PAM algorithm (a partitioning algorithm) and linkage methods (special cases of Hierarchical clustering techniques). They will be briefly reviewed in this section. Also reviewed in this section are some notations of censoring and survival functions. Censored survival times often occur in a cancer dataset and represent on type of incomplete data. A survival function provides a probability of survival to certain times for a cancer patient.
2.1. PAM
Partitioning is one of the major clustering approaches. PAM is a partitioning method operating on a dissimilarity matrix, a matrix of pairwise dissimilarities or distances between objects. It starts from selecting initial K (a predetermined number) representative objects, or medoids, assigning each data object to the nearest medoid, and then iteratively replaces one of the medoids by one of the nonmedoids which leads to a reduction in the sum of the distances of the objects to their closest medoids. The similarity measure here includes, as a special case, the Euclidean distance, which is used with the K-means algorithm. PAM is more robust than the K-means approach, because it employs as cluster centers the medoids not the means, and minimizes a sum of dissimilarities instead of a sum of squared Euclidean distances.
2.2. Linkage Methods
Hierarchical clustering procedures are the most commonly used clustering methods in practice. Commonly used linkage methods include single linkage (SL), complete linkage (CL), and average linkage (AL). They are special cases of agglomerative clustering techniques, operate on a given dissimilarity matrix, and follow the same procedure beginning with the individual objects, at each intermediate step two least dissimilar clusters are merged into a single cluster, producing one less cluster at the next higher level [8]. The difference among the linkage methods lies in the dissimilarity measures between two clusters, which are used to merge clusters. SL, CL, and AL define, respectively, the dissimilarity between two clusters to be the minimum distance between objects from these two clusters, the maximum distance between objects from these two clusters, and the average distance between objects in the two clusters. The output of a linkage method is often summarized into a plot where the nested clusters are graphically represented as a tree, called a dendrogram. The branches in the tree represent clusters. Two clusters merge at a height along a dissimilarity axis that is equal to the dissimilarity between the two clusters.
2.3. Censoring
Cancer data are often time-to-event data that present themselves in different ways, imposing great challenges in analysis. One special feature of a large cancer data set is censoring [9]. Censored observations come from the mechanism of monitoring the progress of patients from some point in time, such as the time a surgical procedure is performed or a treatment regimen is initiated, until the occurrence of some predefined event such as death. Censoring comes in many different forms and right censoring is widely used in clinical studies. Right censoring is used to record the amount of time elapsing between the point at which the patient entered the study and the point at which he or she experienced one of the following three events: the event of interest (e.g., death for most of the cancer studies); loss to follow-up for some reason such as death caused by a health problem other than the one being considered or having moved to another locality; alive at the time the study is terminated. The time elapsing between enrollment in the study and experiencing one of these three events is called the patient's survival time. A survival time is censored if it is not the actual time between enrollment and experiencing the event of interest. Given a censored survival time for a patient, all we know about the lifetime of the patient is that it is greater than some value. Censored survival times provide only a portion of information on the actual lifetimes.
2.4. Survival Function
A patient's lifetime T is a random variable having a probability distribution. In addition to the commonly used probability density function, the distribution of T can also be characterized by the survival function, defined to be S(t) = P(T > t). The function S(t) provides the probability of surviving beyond t. The survival function is usually estimated by a nonparametric method referred to as the Kaplan-Meier estimator [10]. An estimated survival function may be portrayed visually in a survival curve graph. A direct comparison of several survival curves can be conducted by examining the curves appearing in a single graph. A theoretical comparison of several survival functions can be made by conducting a commonly used test such as the log-rank test, Gehan's test [11], Breslow's test [12], and test of Tarone and Ware [13].
3. Algorithm of Clustering of Cancer Data
A key issue related to clustering is how one measures the dissimilarity between objects. Most clustering algorithms presume a measure of dissimilarity. For example, the K-means clustering uses Euclidean distance as a dissimilarity measure. Since cancer data involve censored survival times, a direct use of existing clustering algorithms is not applicable. With cancer data, it is important to find a way to define objects and dissimilarity between objects prior to execution of any clustering algorithm.
Suppose, for a cancer data set, a certain number of factors have been selected for consideration. Various combinations can then be formed by using levels of factors. Specifically, a combination is a subset of the data that correspond to one level of each factor. Suppose there are available a total of N combinations x1, x2,…, xn. A combination plays a role of an object in the cluster analysis. When developing a prognostic system, we need to find groups of patients such that patients within each group are more similar in survival than patients from different groups. Assuming that all patients coming from the same combination have a similar survival rate, then this is equivalent to finding natural groups of combinations.
After objects become available, we can start to define a dissimilarity measure between objects. A dissimilarity measure dis(xi, xj) is a nonnegative function that is symmetric with respect to xi and xj. For cancer data, a direct method is to define the dissimilarity between two combinations in light of the difference between the two corresponding survival functions, and the details follow below. Given two combinations xi and xj, testing if there is a difference between the corresponding two survival functions can be done by conducting a commonly used test such as the log-rank test. It is known that a smaller value of a test statistic shows a stronger evidence of no difference. Thus we can define dissimilarity or “distance” between xi and xj to be
| (1) |
Clearly, dis0(xi, xj) > 0. This dissimilarity measure in (1) is not the one we actually use when developing cancer predictive systems. In fact, we will use the dissimilarity (1) for the PAM algorithm only and generate a learnt dissimilarity measure for the cancer data through combining assignments from multiple clusterings based on the PAM algorithm. A learnt measure should be more realistic than that in (1). This learnt dissimilarity will then be used with a hierarchical clustering algorithm to produce prognostic systems.
Below we first discuss learning dissimilarity from the use of PAM. And then we present an ensemble clustering algorithm using the learnt dissimilarity and linkage methods to develop prognostic systems for cancer patients.
3.1. Learning Dissimilarity from Data
Different choices of dissimilarity functions can lead to quite different clustering results. Prior knowledge is often helpful in selecting an appropriate dissimilarity measure for a given problem. However, it is possible to learn a dissimilarity function from the data. We describe such a procedure as follows.
Partitioning methods are usually not stable in the sense that the final results often depend on initial assignments. However, if two objects are assigned to the same cluster by a high percentage of the times of use of the same partitioning method, it is then very likely that these two objects come from a common “hidden” group. This heuristic implies that the “actual” dissimilarity between two objects may be derived by combining the various clustering results from repeated use of the same partitioning technique. Here we formalize this combining process using the PAM partitioning method.
For the data {x1, x2,…, xn}, we can select K initial medoids and then run PAM with the dissimilarity measure (1) to partition the data into K clusters. It is known that the final assignment usually depends on the initial reallocation. Now we run PAM N times. Each time a number K is randomly picked from a given interval [K1, K2]. By doing this, we may end up with N possibly different final assignments. Given two objects xi and xj, let pij denote the probability that they are not placed into the same cluster by the final assignment of a run of PAM. This probability pij can be estimated by using the results of repeated PAM clustering. Define δl(i, j) = 1 if the lth use of the PAM algorithm does not assign xi and xj into the same cluster; and δl(i, j) = 0 otherwise. Then δ1(i, j), δ2(i, j),…, δN(i, j) are i.i.d Bernoulli (pij). It is well known that the best unbiased estimator of pij is ∑l = 1Nδl(i, j)/N. This estimate will be used as the dissimilarity measure between xi and xj, that is,
| (2) |
A smaller value of dis(xi, xj) is expected to imply a bigger chance that xi and xj come from the same “hidden” group.
3.2. Clustering of Cancer Data
With the learnt dissimilarity (2) between the combinations, we can choose a clustering method to form “natural” groups of the combinations. For flexibility and easy interpretation in practice, we choose a hierarchical clustering approach. The final ensemble algorithm of clustering of cancer data (EACCD) is shown in Algorithm 1. Here the word ensemble refers to the sequence of the PAM procedures involved in the method.
Algorithm 1.
Ensemble algorithm of clustering of cancer data.
Early issues on ensemble clustering were discussed in [14] from the perspective of evidence accumulation. The work in [15] combined the K-means algorithm and linkage methods to form an ensemble method of discovering sample classes using gene expression profiles.
4. Results on Lung Cancer
4.1. Dataset
In this study, we used the SEER data [1] containing records of lung cancer patients diagnosed from the year 1988 through 1998 and examined the following factors: AJCC stage, grade, histological type, and gender. We considered four factors, X1, X2, X3, and X4 that were set to be stage, grade, histological type, and gender, respectively. For simplicity, we only investigated the following four important levels of X3: adenocarcinoma, squamous cell carcinoma, large cell carcinoma, and small cell carcinoma. The levels of other three variables were those commonly used in the lung cancer study. Factor X1 had four levels: I, II, III, and IV; factor X2 had four levels: 1, 2, 3, and 4; and factor X4 had two levels: 1 (male) and 2 (female). The final data we actually used involve 90,214 patients. A portion of the data, in terms of X(survival time), X1, X2, X3, and X4, is provided in Table 1.
Table 1.
Lung cancer data of 90,214 patients. Survival time is measured in months. Here, adeno, squamous, large, and small represent adenocarcinoma, squamous cell carcinoma, large cell carcinoma, and small cell carcinoma, respectively.
| Patient | Survival time (X) | Stage (X1) | Grade (X2) | Histology (X3) | Gender (X4) |
|---|---|---|---|---|---|
| 1 | 64 | 1 | 2 | squamous | 1 |
| 2 | 24 | 1 | 3 | large | 1 |
| 3 | 24 | 2 | 3 | squamous | 1 |
| 4 | 8 | 1 | 2 | squamous | 1 |
| 5 | 16 | 3 | 3 | squamous | 2 |
| 6 | 143 | 3 | 2 | adeno | 2 |
| 7 | 6 | 3 | 3 | small | 2 |
| 8 | 1 | 4 | 4 | small | 1 |
| 9 | 9 | 1 | 3 | adeno | 2 |
| — | — | — | — | — | — |
| — | — | — | — | — | — |
| 90211 | 1 | 1 | 3 | squamous | 1 |
| 90212 | 2 | 1 | 2 | adeno | 1 |
| 90213 | 62 | 2 | 3 | adeno | 1 |
| 90214 | 4 | 4 | 4 | squamous | 2 |
Before running our algorithm EACCD, we used the levels of four factors X1, X2, X3, and X4 to partition the dataset into 128(= 4 × 4 × 4 × 2) combinations, shown in Table 2. Due to the approximation of the chi-square distribution to the log-rank test statistic, a combination containing less than 100 patients was dropped from our study. In this case, no further analysis was done for these combinations, and our attention was paid to all the other combinations that have a size equal to or larger than 100. For example, Comb 5, Comb 6, Comb 7, Comb 8, Comb 124, as shown in Table 2, were dropped from our study. Under this restriction we only kept 80 combinations, leaving out a total of 1,264 patients.
Table 2.
A list of 128 combinations based on factor levels. Here, adeno, squamous, large, and small represent adenocarcinoma, squamous cell carcinoma, large cell carcinoma, and small cell carcinoma, respectively.
| Group name | Stage (X1) | Grade (X2) | Histology (X3) | Gender (X4) | Sample size |
|---|---|---|---|---|---|
| Comb 1 | I | 1 | adeno | 1 | 1008 |
| Comb 2 | I | 1 | adeno | 2 | 1426 |
| Comb 3 | I | 1 | squamous | 1 | 430 |
| Comb 4 | I | 1 | squamous | 2 | 187 |
| Comb 5 | I | 1 | large | 1 | 8 |
| Comb 6 | I | 1 | large | 2 | 4 |
| Comb 7 | I | 1 | small | 1 | 2 |
| Comb 8 | I | 1 | small | 2 | 2 |
| Comb 9 | I | 2 | adeno | 1 | 2389 |
| Comb 10 | I | 2 | adeno | 2 | 2662 |
| — | — | — | — | — | — |
| — | — | — | — | — | — |
| Comb 123 | IV | 4 | squamous | 1 | 163 |
| Comb 124 | IV | 4 | squamous | 2 | 70 |
| Comb 125 | IV | 4 | large | 1 | 1503 |
| Comb 126 | IV | 4 | large | 2 | 911 |
| Comb 127 | IV | 4 | small | 1 | 4246 |
| Comb 128 | IV | 4 | small | 2 | 3368 |
4.2. Setting of the Algorithm
To run our algorithm EACCD, we chose parameters as follows. The choice of N depends on the rate at which dis in (2) converges to pij. A large number should be chosen for N, and for this purpose we set N = 10000. Any theoretically possible choices of K was used in running PAM, and thus we set K1 = 2 and K2 = 79, due to availability of 80 objects. In addition, the log-rank test was used to obtain the measure (1) for the PAM algorithm. And the average linkage was employed as a hierarchical clustering method.
4.3. Results from Cluster Analysis
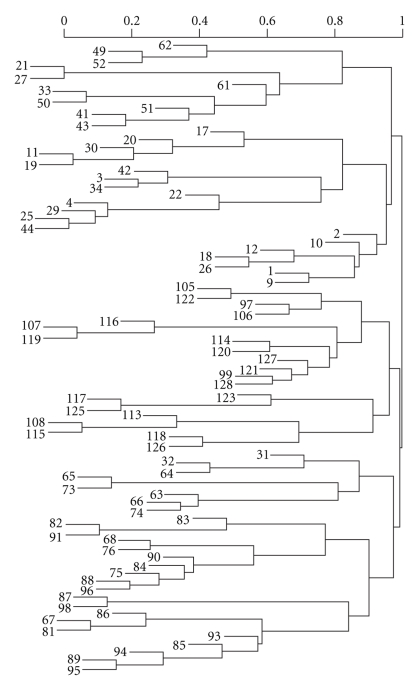
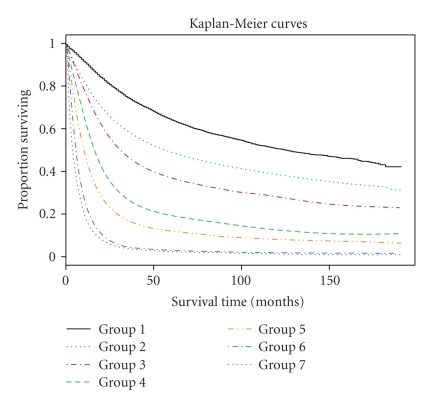
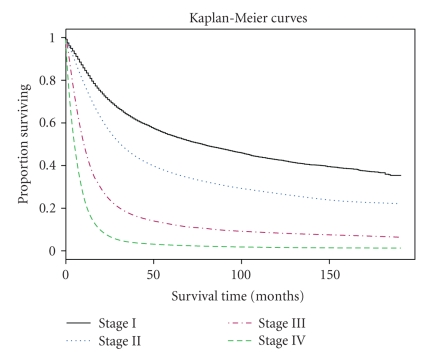
The output of cluster analysis for these 80 combinations is shown in Figure 1, where for simplicity Comb has been removed from each combination or label. It is straightforward to use the dendrogram shown in Figure 1. Cutting off the dendrogram at a specified height of the dissimilarity axis partitions data into disjoint clusters or groups. Cutting at different heights usually leads to different numbers of groups. As an example, if we cut the dendrogram in Figure 1 at a height slightly above 0.90, then we obtain 7 groups shown in Table 3. The log-rank test shows that any two groups differ significantly (using a significance level of 0.01) in their survival functions. Figure 2 shows the Kaplan-Meier estimates of the survival curves for the 7 groups. These 7 groups and their survival curves constitute a prognostic system for lung cancer patients, as discussed in step (ii) of the Section of Introduction. Prediction using this system is then carried out in the usual way. In comparison, those 4 survival curves from the TNM system, based on all the patients from the 80 combinations, are provided in Figure 3.
Figure 1.
Dendrogram from clustering of lung cancer data.
Table 3.
Seven groups produced by cutting the dendrogram in Figure 1 at the height 0.93.
| Group | Combinations | Sample size |
|---|---|---|
| Group 1 | Stage I, Grade 1, adeno | 11303 |
| Stage I, Grade 2, adeno | ||
| Stage I, Grade 2, squamous, female | ||
| Stage I, Grade 3, adeno, female | ||
| Stage I, Grade 4, adeno, female | ||
| Group 2 | Stage I, Grade 1, squamous | 13431 |
| Stage I, Grade 2, squamous, male | ||
| Stage I, Grade 3, adeno, male | ||
| Stage I, Grade 3, squamous | ||
| Stage I, Grade 3, large cells, female | ||
| Stage I, Grade 4, adeno, male | ||
| Stage I, Grade 4, large cells | ||
| Stage II, Grade 1, adeno, female | ||
| Stage II, Grade 2, adeno, female | ||
| Stage II, Grade 2, squamous, female | ||
| Group 3 | Stage I, Grade 1, squamous, male | 4522 |
| Stage I, Grade 3, large cells, male | ||
| Stage I, Grade 4, squamous, male | ||
| Stage II, Grade 1, adeno, male | ||
| Stage II, Grade 2, adeno, male | ||
| Stage II, Grade 2, squamous, male | ||
| Stage II, Grade 3, adeno | ||
| Stage II, Grade 3, squamous | ||
| Stage II, Grade 4, large cells | ||
| Group 4 | Stage I, Grade 4, small cells | 4291 |
| Stage II, Grade 4, small cells | ||
| Stage III, Grade 1, adeno | ||
| Stage III, Grade 2, adeno | ||
| Group 5 | Stage III, Grade 1, squamous | 24951 |
| Stage III, Grade 2, squamous | ||
| Stage III, Grade 3 | ||
| Stage III, Grade 4, adeno | ||
| Stage III, Grade 4, squamous, male | ||
| Stage III, Grade 4, large cells | ||
| Stage III, Grade 4, small cells | ||
| Group 6 | Stage IV, Grade 1, adeno, male | 18215 |
| Stage IV, Grade 1, squamous, male | ||
| Stage IV, Grade 2, adeno | ||
| Stage IV, Grade 2, squamous, male | ||
| Stage IV, Grade 3, adeno, female | ||
| Stage IV, Grade 3, squamous, female | ||
| Stage IV, Grade 3, small cells | ||
| Stage IV, Grade 4, adeno | ||
| Stage IV, Grade 4, small cells | ||
| Group 7 | Stage IV, Grade 2, squamous, female | 12237 |
| Stage IV, Grade 3, adeno, male | ||
| Stage IV, Grade 3, squamous, male | ||
| Stage IV, Grade 3, large cells | ||
| Stage IV, Grade 4, squamous, male | ||
| Stage IV, Grade 4, large cells | ||
Figure 2.
Survival curves of seven groups in Table 3.
Figure 3.
Survival curves of four TNM stages.
Some observations come immediately from Table 3. Group 1, 5, 6, and 7 only contain some cases from Stage I, III, IV, and IV, respectively. Both groups 2 and 3 contain Stage I cancer cases, indicating that additional relevant parameters are associated with increased relative biologic aggressive tumor behavior. Group 4 consists of some cases from Stage I, II, and III, suggesting that localized biologically aggressive cancers may have the same survival as more indolent advanced staged cancers.
5. Conclusion
In this paper we have introduced an ensemble clustering based approach to establish prognostic systems that can be used to predict an outcome or a survival rate of cancer patients. An application of the approach to lung cancer patients has been given.
Generalizing or refining the work presented in this paper can be done in many ways. Our algorithm EACCD actually is a two-step clustering method. In the first step, a dissimilarity measure is learnt by using PAM, and in the second step, the learnt dissimilarity is used with a hierarchical clustering algorithm to obtain clusters of patients. These clusters of patients form a basis of a prognostic system. Improvement of dissimilarity measures (1) and (2), as well as the effect of different algorithms used in each step will be investigated in our future work. Refined algorithms, based on EACCD, will be sought and resulting prognostic systems with clinical applications will be reported. This constitutes our main research work in the future.
Acknowledgment
This work was partially supported by the National Science Foundation Grant CCF-0729080.
References
- 1.SEER. http://seer.cancer.gov/.
- 2.NCDB. http://www.facs.org/cancer/ncdb/index.html.
- 3.Greene FL, Compton CC, Fritz AG, Shah JP, Winchester DP, editors. AJCC Cancer Staging Atlas. New York, NY, USA: Springer; 2006. [Google Scholar]
- 4.Chen D, Xing K, Henson D, Sheng L. Group testing in the development of an expanded cancer staging system. In: Proceedings of the 7th International Conference on Machine Learning and Applications (ICMLA '08); December 2008; San Diego, Calif, USA. pp. 589–594. [Google Scholar]
- 5.Chen D, Xing K, Henson D, Sheng L, Schwartz AM, Cheng X. A clustering-based approach to predict outcome in cancer patients. to appear in International Journal of Data Mining and Bioinformatics. [Google Scholar]
- 6.Xing K, Chen D, Henson D, Sheng L. A clustering-based approach to predict outcome in cancer patients. In: Proceedings of the 6th International Conference on Machine Learning and Applications (ICMLA '07); December 2007; Cincinnati, Ohio, USA. pp. 541–546. [Google Scholar]
- 7.Kaufman L, Rousseeuw P. Finding Groups in Data: An Introduction to Cluster Analysis. New York, NY, USA: John Wiley & Sons; 1990. [Google Scholar]
- 8.Hastie T, Tibshirani R, Friedman J. The Elements of Statistical Learning. New York, NY, USA: Springer; 2001. [Google Scholar]
- 9.Klein JP, Moeschberger ML. Survival Analysis: Techniques for Censored and Truncated Data. 2nd edition. New York, NY, USA: Springer; 2003. [Google Scholar]
- 10.Kaplan EL, Meier P. Nonparametric estimation from incomplete observations. Journal of the American Statistical Association. 1958;53(282):457–481. [Google Scholar]
- 11.Gehan EA. A generalized Wilcoxon test for comparing arbitrarily singly-censored samples. Biometrika. 1965;52:203–223. [PubMed] [Google Scholar]
- 12.Breslow N. A generalized Kruskal-Wallis test for comparing K samples subject to unequal patterns of censorship. Biometrika. 1970;57(3):579–594. [Google Scholar]
- 13.Tarone RE, Ware J. On distribution free tests for equality of survival distributions. Biometrika. 1977;64(1):156–160. [Google Scholar]
- 14.Fred ALN, Jain AK. Data clustering using evidence accumulation. In: Proceedings of the 16th International Conference on Pattern Recognition (ICPR '02), vol. 4; August 2002; Quebec, Canada. pp. 276–280. [Google Scholar]
- 15.Chen D, Zhang Z, Liu Z, Cheng X. An ensemble method of discovering sample classes using gene expression profiling. In: Pardalos PM, Boginski VL, Vazacopoulos A, editors. Data Mining in Biomedicine. Vol. 7. New York, NY, USA: Springer; 2007. pp. 39–46. (Springer Optimization and Its Applications). [Google Scholar]