Fieldmap-Free Retrospective Registration and Distortion Correction for EPI-based Functional Imaging

Abstract

We describe a method for correcting the distortions present in echo planar images (EPI) and registering the EPI to structural MRI. A field map is predicted from an air/tissue segmentation of the MRI using a perturbation method and subsequently used to unwarp the EPI data. Shim and other missing parameters are estimated by registration. We obtain results that are similar to those obtained using fieldmaps, however neither fieldmaps, nor knowledge of shim coefficients is required.

1 Introduction

Echo-planar imaging (EPI) is one of the most widely used pulse sequences in functional magnetic resonance imaging (fMRI) due to its high temporal resolution. The ability to acquire an entire volume within seconds makes it a valuable, non-invasive tool for probing dynamic physiological processes such as the blood-oxygenation-level-dependent (BOLD) response. As a result, EPI has become widely used in basic neuroscience studies as well as in clinical research in areas such as pre-surgical planning and MR-guided intervention.

A significant limitation of EPI is its sensitivity to magnetic field inhomogeneity. Perturbations in the field result in signal loss and geometric distortion in EPI data [1]. Previous studies have shown that correcting geometric distortion in functional images increases the accuracy of co-registration to structural MR [2, 3]. Precise anatomical localization of functional activation is especially important in single-subject studies (ie. pre-surgical evaluation) and in cases where the structural MR is used as a reference to sample the functional data (ie. cortical-surface-based analysis) [3]. Therefore, field inhomogeneity and distortion is a significant problem in fMRI.

Field inhomogeneity results in distortion because the MR image reconstruction assumes that the magnetic field within the scanner is a superposition of known linear gradient fields and a uniform B₀ field. In practice, gradient linearity is compromised to achieve high gradient strength and fast switching [4] and main field homogeneity is compromised due to constraints on the design and manufacture, resulting in B₀ field inhomogeneities as high as several hundred parts per million (ppm) [5]. Furthermore, materials placed in the magnet perturb the applied field depending on their intrinsic magnetic susceptibility.

To improve magnetic field homogeneity, MR systems use superconducting active shims, ferromagnetic passive shims, and room-temperature spherical harmonic shim coils. The superconducting active shims and ferromagnetic passive shims can reduce field inhomogenity to within a few ppm before subjects or samples are placed in the magnet [5]. The placement of a sample in the scanner results in perturbations of the field that are greatest near boundaries between materials with large susceptibility differences.

For biological samples, there is an important susceptibility difference between tissue and air. Soft tissue and bone have similiar susceptibilities of (χ_t ≈ −9.1×10⁻⁶) [6] and (χ_b ≈ −11.4 × 10⁻⁶) [7], which counteract the applied field, while air interacts only weakly with the field (χ_a ≈ 0.4×10⁻⁶) [6]. This is critical in human studies where air-tissue interfaces in the sphenoid and ethmoid sinuses and auditory canals produce large perturbations in the field in the frontal and temporal lobes of the brain. To compensate for this, MR systems typically have a set of room temperature shim coils consisting of the three linear gradients and five second order shims. These coils produce fields based on the spherical harmonic series to remove low order spatial perturbations of the field [5]. Imperfect shimming and higher order perturbations, however, result in residual subject-specific inhomogeneity and subsequent distortion of the acquired images.

These distortions are subject, pulse-sequence, and field strength dependent. The problem of signal loss in EPI has been addressed elsewhere [8] as well as the effects of B₀ inhomogenity on other functional imaging acquisitions such as spiral pulse sequences [4, 9] and will not be discussed here. For single-shot EPI acquisitions there are several existing techniques for correcting geometric distortion. The majority of these are fieldmap based methods [10, 1, 3]. A fieldmap provides a direct measure of the B₀ inhomogeneity at each point in the image and can be obtained from a variety of pulse sequences. Due to the low bandwidth of EPI in the phase encode direction, the geometric distortion is basically a voxel-wise translation restricted to the phase-encode direction, which can be computed directly from the fieldmap. Fieldmap techniques, however, have several limitations. First, they require additional scan time, which may be difficult to accomodate in certain clinical studies. Second, a single fieldmap may not be valid for unwarping each EPI volume if there are significant effects due to motion or respiration in the timeseries. Finally, fieldmaps are not available in many retrospective studies.

Other correction methods have been proposed including the acquisition of bipolar field gradient images [11], the use of a multi-reference scan for correction during reconstruction [12], and k-space energy spectrum analysis [13]. Correction techniques based on modified EPI acquisitions also increase scan time [11] while ones that require retention of the complex EPI data may not be practical [13].

More recently, magnetic field models have been developed to estimate the static field inhomogeneity from subject specific susceptibility models [6, 14]. Koch et al. has extended these models beyond estimating the field to applying them for distortion correction. Their method, however, relies on registering another subject’s CT data to the subject of interest in order to generate the air/tissue susceptibility model, and therefore may not account well for differences in individual anatomy. It also requires detailed knowledge of the shim system to implement the unwarping.

In this paper we describe a method to correct distortion without obtaining fieldmaps, modifying EPI acquisition parameters, requiring CT data for the subject of interest or having detailed knowledge of the shim system. Our approach consists of two parts. First, an MR classifier is used to segment structural MR into an air/tissue susceptibility model. This is used as input to a first order perturbation field model [6] to compute a subject-specific fieldmap. Second, a simultaneous shim estimation and registration algorithm is used to solve for the lower order field perturbations (shim parameters) needed to accurately unwarp and register the EPI data.

2 Methods

2.1 Fieldmap based unwarping

Structural MR, EPI and dual gradient echo fieldmaps were acquired for six subjects. Neurosurgery patients were selected so that CT data would be available for validation and training (section 2.2). Fieldmap-based unwarping techniques were used to provide a standard with which to compare our results. All NMR imaging was done in the Radiology department at Brigham and Women’s Hospital on a 3T GE magnet. The NMR acquisition protocol included (1) whole-brain axial 3D-SPGR, slice thickness=1mm, TE/TR=3/8msec, matrix=512×512, voxel size=0.5×0.5×1mm (2) single-shot EPI, slice thickness=4mm, TE/TR=40/2000 msec, matrix=128×128, voxel size=2×2×4mm (3) dual gradient echo fieldmap, slice thickness=4mm, TE1/TE2/TR=5/15/600msec, matrix=256×256, voxel size=1×1×4mm. Analysis was carried out using FEAT, part of FSL 3.3 (FM-RIB’s Software Library, www.fmrib.ox.ac.uk/fsl). The EPI was pre-processed: spatial smoothing using a Gaussian kernel of FWHM 5mm, mean-based intensity normalisation, and highpass temporal filtering was applied. Brain extraction of the structural MR was done using BET [15]. Fieldmap-based unwarping of the EPI was done using PRELUDE [16] to unwrap the phase and FUGUE [17] to compute the distortion by:

$$\mathrm{\Delta }y=\frac{\gamma \mathrm{\Delta }{B}_0(x,y,z)N_y{t}_{\mathit{dwell}}}{2\pi },$$ (1)

where ΔB₀(x, y, z) is the B₀ field inhomogeneity (which is proportional to the difference in phase and inversely proportional to the ΔT E of the gradient echo images), γ is the gyromagnetic ratio, Δy is the pixel shift in the phase encode direction, N_y is the number of voxels in the y direction, and t_dwell is the dwell time of the EPI sequence. Registration of the unwarped EPI to the high resolution structural MR was carried out using a seven DOF (rigid-body + scaling) transformation via the FLIRT registration algorithm using correlation ratio as the cost function [18, 19]. The signal loss was calculated and used for cost function weighting (to prevent FLIRT from trying to achieve agreement in regions of signal dropout) according to:

$$SL=\int \frac{\mathit{exp}(i\gamma \mathrm{\Delta }{B}_0(x,y,z)TE)}{L}dz,$$ (2)

where z is the through slice direction, L is the slice thickness, and T E is the echo time. Registration without unwarping was also carried out using FEAT and FLIRT. Both seven DOF rigid-body/scaling and twelve DOF affine transformations were applied.

2.2 MR derived Segmentation: Training via CT

CT data sets for subjects 1 and 2 were acquired with 0.46 × 0.46 × 4.8 mm voxels spanning 36 slices and 512×512 in-plane voxels. The CT data was registered to the fieldmap magnitude image for each subject using FLIRT so the estimated field maps would be in the same space as the acquired fieldmaps for validation. The CT data was also resampled to 1×1×1 mm voxels and ROIs surrounding the head were extracted to improve the speed of subsequent fieldmap estimation. The CT from both subjects was thresholded to obtain an accurate air/tissue segmentation of the entire FOV. The air/tissue labels and structural MR intensity values from subject 1 were used to train a classifier that calculates the probability of tissue given MR intensity according to:

$$P(T\mid I_i)=\frac{P(I_i\mid T)P(T)}{P(I_i\mid T)P(T)+P(I_i\mid T^c)P(T^c)}.$$ (3)

P (T) and P (T^c) are the prior probabilities of tissue and air, respectively. The conditional and prior probabilities were obtained from intensity histograms. The resulting segmenter was then applied to the structural MR of subjects 2–6. The CT from subject 2 was used for validation of subject 2’s segmented MR.

2.3 Fieldmap estimation and registration

The fieldmap estimation in this paper builds on the B₀ field model described in [6]. In this model, a first order perturbation solution of Maxwell’s equations is estimated from an air/tissue susceptibility model, where each voxel takes continuous values between 0 (air) and 1 (tissue). The field calculations are implemented as a simple linear convolution, which is fast and requires knowledge of only the voxel-based susceptibility model and MR field strength. The CT and MR derived segmentations for subject 2 were used as input to this model to compute corresponding ground truth and estimated fieldmaps.

Current field modeling techniques, including the one described in [6], do not account for the shim fields that reduce the B₀ inhomogeneity prior to fieldmap acquisition. Therefore, in order to compare an estimated fieldmap to an acquired one, the shim fields must be factored out of the acquired fieldmap. Each shim field consists of a baseline value plus subject specific offset, both of which, in principle, are known. The baseline value can be obtained by calibration with a phantom, the offset is recorded in the fieldmap dicom header. Factoring these known values out of the acquired fieldmap for validation purposes will still result in significant error between the estimated and acquired fieldmaps. This is because the estimated fieldmap does not include lower order spatial variations of the perturbation (or susceptibility induced) field that are caused by anatomy outside the FOV (ie. the segmentation does not include the neck and torso). However, these neglected susceptibility fields from the body can be modeled using the same lower order basis functions used to model the shims. Both can then be estimated and factored out by least squares fitting of the basis functions to the residual map (the difference between the estimated and acquired fieldmaps). This approach works well for validation purposes [6], but presents a problem when the goal is to use an estimated fieldmap in place of an acquired fieldmap for distortion correction. Then both the shims and neglected susceptibility fields are unknown and cannot be obtained from a simple fitting of the basis functions, since an acquired fieldmap is not available. To overcome this problem, we model the shims and lower order susceptibilty fields using the first and second order spherical harmonics and apply a simultaneous field estimation and registration algorithm to solve for the coefficients (shim parameters) which maximize the agreement between the EPI and structural MR.

All calculations were programmed and executed in Matlab 2007a on a PC workstation with four 3.2 GHz Intel Xeon processors and 3 GB of RAM running Debian Linux. An initial estimate of the shim parameters was obtained from the training data set of subject 1 using the least squares fitting method described previously. The initial estimate of the shim fields obtained from the training data was then added to the estimated fieldmap for subject 2. The fieldmap was masked to exclude non-brain voxels and a modified version of the Matlab fminsearch algorithm (unconstrained nonlinear Nelder-Mead direct search method) was used to solve for the shim parameters which optimized the agreement between the undistorted EPI and structural MR. All unwarping and registration was done using FUGUE and FLIRT as described previously in section 2.1. Agreement was quantified using correlation ratio as the cost function. This was repeated to compute final MR-derived fieldmaps for subjects 3–6.

3 Experimental Results

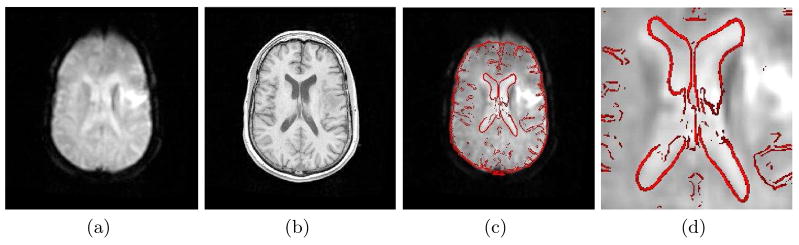
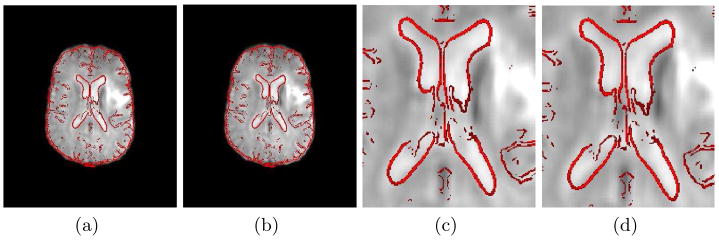
The importance of correcting distortion in EPI prior to registration is illustrated in Fig. 1. Distorted EPI from subject 2 is shown adjacent to the corresponding structural MR. Attempting to register the EPI directly to the structural MR using a 12 DOF affine transformation results in significant disagreement, which is most evident in the anterior region of the brain and the ventricles. In Fig. 3a and Fig. 3c the EPI is first unwarped using the fieldmap based method described in section 2.1. This significantly improves the agreement between the images, which is consistent with previously published work on this topic [2, 3]. The results of the MR classifier and fieldmap estimation algorithm for subject 2 are shown in Fig. 2. While the CT (Fig. 2a) can clearly distinguish between bone and air, regions of the skull and sinuses have similar intensities in the MR (Fig. 2c), making segmentation more difficult. Segmentation using the MR classifier (Fig. 2d), however, agrees reasonably well with the segmented CT (Fig. 2b).

Fig. 1.

Registration without unwarping. Registration of distorted EPI (a) to structural MR (b) using a 12 DOF affine transformation results in significant disagreement (c,d). An edge strength image of the structural MR (red) is overlaid on the registered EPI (c,d) for visualization.

Fig. 3.

Registration Results. An edge strength image of the structural MR is overlaid on the registered EPI (a–d). Unwarping and registration with the acquired fieldmap is shown in (a,c). Unwarping and registration using the MR-derived fieldmap (shim fields included) (b,d) results in excellent agreement between the EPI and structural MR.

Fig. 2.

Results of the Classifier and Fieldmap Estimation Algorithm. The CT (a) is thresholded to produce an air/tissue map (b) and the T1 (c) is segmented using the MR classifier (d). The CT-derived fieldmap (e, g-top) and MR-derived fieldmap (f, g-bottom) show excellent agreement. The absolute difference in the CT and MR derived fieldmaps is given in units of voxel shift in row 1 of the table and in Hz in row 2. P90 is the 90th percentile, etc. Results of Koch et al. [14] are given in Hz in row 3. The acquired fieldmap (h,j-top) and final MR-derived fieldmap (with shim)(i,j-bottom) show good overall agreement. The scale of the fieldmaps is ±200 Hz.

The CT and MR derived segmentations were used as input to the perturbation field model to produce a fieldmap from the CT and an estimated fieldmap from the MR. The fieldmap computed from the segmented CT is shown in Fig. 2e and the top of Fig. 2g, while the MR-derived fieldmap is shown in Fig. 2f and the bottom of Fig. 2g. The fieldmaps show excellent qualitative agreement. Quantitative analysis of the absolute error in the B₀ field between these images is given in the table in Fig. 2. Subvoxel error is achieved in 85% of voxels while the Mean and 90^th percentile values are significantly decreased relative to the error measurements reported by Koch et al [14].

The optimal shim fields were estimated using the simultaneous shim estimation and registration algorithm and added to the MR-derived fieldmap to produce the final fieldmap shown in Fig. 2i and the bottom of Fig. 2j. This result can now be compared to subject 2’s acquired fieldmap shown in Fig. 2h and the top of Fig. 2j. While some difference between the fieldmaps can be seen in the region closest to the air-filled sinuses, this does not result in a significant difference in the registration results. Visual inspection of the registration results (Fig. 3) shows equally good agreement between the EPI and T1 using either the MR-derived fieldmap (with shim) or acquired fieldmap. Quantititive comparison of the correlation ratio between the EPI and T1 also supports this conclusion. A value of 0.1516 was obtained when the acquired fieldmap was used for unwarping prior to registration versus a value of 0.1477 when the MR-derived fieldmap (with shim) was used. The discrepancy in the fieldmaps does not translate to the registration results because it occurs in areas in which there is severe signal loss in the EPI. In these areas there is little to no information to drive the estimation of more accurate shim parameters. Essentially, this region of the EPI is not sensitive to inaccuracies in the fieldmap because much of the signal intensity was lost during acquisition. Results similar to those shown in Fig. 2(c,d,h–j) and Fig. 3 were obtained for subjects 3–6.

4 Conclusions

We have demonstrated a novel EPI unwarping and registration algorithm. CT data was used to train an MR classifier and evaluate its performance on new data given only the relevant T1-weighted MR. A simultaneous shim estimation/registration algorithm was used to update the estimated fieldmap until optimal agreement between the EPI and structural MR was obtained. These registration results showed excellent agreement with standard fieldmap-based methods. This approach overcomes limitations of current unwarping strategies such as additional scan time, pulse-sequence modification, acquisition of CT data, or knowledge of shim parameters. Therefore, this provides a fieldmap-free, subject-specific EPI unwarping and registration technique particularly suitable for clinical applications and retrospective functional neuroimaging research.