Statistical Characterization of a 1D Random Potential Problem – with applications in score statistics of MS-based peptide sequencing

Abstract

We provide a complete thermodynamic solution of a 1D hopping model in the presence of a random potential by obtaining the density of states. Since the partition function is related to the density of states by a Laplace transform, the density of states determines completely the thermodynamic behavior of the system. We have also shown that the transfer matrix technique, or the so-called dynamic programming, used to obtain the density of states in the 1D hopping model may be generalized to tackle a long-standing problem in statistical significance assessment for one of the most important proteomic tasks – peptide sequencing using tandem mass spectrometry data.

1 Introduction

Important in both fundamental science and numerous applications, optimization problems of various degrees of complexity are challenging (see [1] for an excellent introduction). Optimization conditioned by constraints that may vary from event to event is of especial theoretical and practical importance. As a first example, when dealing with a system under a random potential, each realization of the random potential demands a separate optimization resulting in a different ground state. The thermodynamic behavior of such a system in a quenched random potential crucially depends on the random potential realized. A similar but practical problem may arise in routing passengers at various cities to reach their destinations. In the latter case, the optimal routing depends on the number of passengers at various locations, the costs from one location to the others, which likely to vary from time to time. This type of conditional optimization also occurs in modern proteomics problem, that is, in the mass spectrometry (MS) based peptide sequencing. In this case, each tandem MS (MS²) spectrum constitute a different condition for optimization which aims to find a database peptide or a de novo peptide to best explain the given MS² spectrum.

When the cost function of an optimization problem can be expressed as a sum of independent local contributions, the problem usually can be solved using the transfer matrix method that is commonly employed in statistical physics. A well-studied example of this sort in statistical physics is the directed polymer/path in a random medium (DPRM) [2,3,4]. Even when a small non-local energetics is involved, the transfer matrix approach still proves useful [5]. As an example, the close relationship between the DPRM problem and MS-based peptide sequencing, where a small nonlocal energetics is necessary to enhance the peptide identifications, was sketched in an earlier publication [5] and the cost value distribution from many possible solutions other than the optimal one is explored. Indeed, obtaining the cost value distribution from all possible solutions in many cases is harder than finding the optimal solution alone. In this paper, we will provide the solution to a generic problem that enables a full characterization of the peptide sequencing score statistics, instead of just the optimal peptide. The 1D problem considered is essentially a hopping model in the presence of a random potential. The solution to this problem may also be useful in other applications such as in routing of passengers and even internet traffic.

In what follows, we will first introduce the generic 1D hopping model in a random potential, followed by its transfer matrix (or dynamic programming) solution. We then discuss the utility of this solution in the context of MS-based peptide sequencing, and demonstrate with real example from mass spectrum in real MS-based proteomics experiments. In the discussion section, we will sketch the utility of the transfer matrix solution in other context and then conclude with a few relevant remarks.

2 1D hopping in random potential

Along the x-axis, let us consider a particle that can hop with a set of prescribed distances ${\left\{m_i\right\}}_{i=1}^K$ towards the positive x̂ direction. That is, if the particle is currently at location x₀, it can move to location x₀ + m₁, x₀ + m₂, … x₀ + m_K in the next time step. At each hopping step, the particle will accumulate an energy −s(x) from location x that it just visited. The score s(x) (negative of the on-site potential energy) is assumed positive and may only exist at a limited number of locations. For locations that s(x) do not exist, we simply set s(x) = 0 there. The energy of a path starting from the origin specified by the sequential hopping events p ≡ {m_h1 m_h2,…, m_hL} would have visited locations {x₁,x₂,…,x_L} with $x_i\equiv {\sum }_{j=1}^i{m}_{h_j}$ and has energy

$$E_p(x=x_L)\equiv -\sum _{i=1}^{L-1}s(x_i)\equiv -S_p(x).$$

In general, there can be more than one path terminated at the same point. Treating each path as a state with energy given by E_p, one ends up having the following recursion relation for the partition function Z(x) ≡ Σ_pe^−βE_p(x)

$$Z(x)=\sum _{i=1}^K{e}^{\beta s(x-m_i)}Z(x-m_i),$$ (1)

where β = 1/T plays the role of inverse temperature (with k_B = 1 chosen). If one were only interested in the best score terminated at point x, it will be given by the zero temperature limit β → ∞ and the recursion relation may be obtained by taking the logarithm on both sides of (1) and divided by β then taking β → ∞ limit to reach

$$S_{\text{best}}(x)=\underset{1\le i\le K}{max}\{s(x-m_i)+S_{\text{best}}(x-m_i)\},$$ (2)

where S_best(x) records the best path score among all paths reaching position x. This update method, also termed dynamic programming, records the lowest energy and lowest energy path reaching a given point x. The lowest energy among all possible at position x is simply −S_best(x) and the associated path can be obtained by tracing backwards the incoming steps. It is interesting to observe that one can also obtain the worst score at each position via dynamical programming

$$S_{\text{worst}}(x)=\underset{1\le i\le K}{min}\{s(x-m_i)+S_{\text{worst}}(x-m_i)\}.$$ (3)

The full thermodynamic characterization demands more information than the ground state energy. In principle, one may obtain the full partition function using eq. (1) evaluated at various temperatures. This procedure, however, hinders analytical property such as determination of the average energy

$$\langle E\rangle \equiv -\frac{\partial lnZ}{\partial \beta }.$$

A better starting point may be achieved if one can obtain the density of states D(E). In this case, we have

$$\begin{array}{l}Z\equiv \int dE{e}^{-\beta E}D(E)\\ \langle E\rangle =\frac{\int dE{e}^{-\beta E}ED(E)}{\int dE{e}^{-\beta E}D(E)}.\end{array}$$

Note that if the ground energy E_grd of the system is bounded from below, the partition function is simply a Laplace transform of a modified density of states given by

$$Z=e^{-\beta E_{\text{grd}}}\underset{0}{\overset{\infty }{\int }}dE{e}^{-\beta E}\stackrel{\sim }{D}(E)$$

where D̃ (E) ≡ D(E − E_grd) and

$$\langle E\rangle =E_{\text{grd}}+\frac{{\int }_0^{\infty }dE{e}^{-\beta E}E\stackrel{\sim }{D}(E)}{{\int }_0^{\infty }dE{e}^{-\beta E}\stackrel{\sim }{D}(E)}$$

This implies that the density of states D(E) together with the ground state energy E_grd determine all the thermodynamic behavior of the system. In the next section, we will explain how to obtain the density of states using the dynamical programming technique as well as how to extend this approach to more complicated situations that will be useful in characterizing the score statistics in MS-based peptide sequencing.

3 Obtaining the Density of States

The density of states is related to the energy histogram in a simple way. The number of states between energies E and E + η (with η ≪ 1) is given by D(E)η. If we happen to use η as the energy bin size for energy histogram, the count C(E) in the bin with energy E is simply D(E) η and the density of states D(E) = C(E)/η. For simplicity, we will assume that the all the on-site energies −s(x) are integral multiple of η. This implies that each path energy/score is also an integral multiple of η. In the following subsections, we will use score density of states instead of energy density of states.

3.1 The Simplest Case and its Application

We denote by C(x, N) the number of paths reaching position x with score Nη. With this notation, we can easily write down the recursion relation for C(x, N) as follows

$$C(x,N)=\sum _{i=1}^{K}C(x-m_i,N-\frac{s(x-m_i)}{\eta }).$$ (4)

This recursion relation allows us to compute the density of states in the same manner as computing the partition function (1) except that we need to have an additional dimension for score at each position x. As an even simpler application of this recursion relation, suppose that one is only interested in the number of paths reaching position x, one may sum over the energy part on both side of (4) and arrives at

$$C(x)=\sum _{i}C(x-m_i),$$ (5)

which enables a very speedy way to compute the total number of paths reaching position x. In the context of de novo peptide sequencing [6], this number corresponds to the total number of all possible de novo peptides within a given small mass range. Although simply obtained, this number may be useful for providing rough statistical assessment in de novo peptide sequencing.

3.2 The More Realistic Case

In general, one may wish to associate with each hop an energy h or one may wish to introduce some kind of score normalization based on the number of hopping steps. This is indeed the case when applying this framework to MS-based peptide sequencing where a peptide length factor adding or multiplying to the overall raw score is a common practice. In this case, it becomes important to keep track the number of hops made in each path. We may further categorize the counter C(x, N) into Σ_L C(x, N; L). That is, we may separate the paths with different number of steps from one another and arrive at a finer counter C(x, N, L) which records the number of paths reaching position x with score Nη and with L hopping steps.

It is rather easy to write down the recursion relation obeyed by this fine counter

$$C(x,N,L)=\sum _{i=1}^{K}C(x-m_i,N-\frac{s(x-m_i)}{\eta },L-1).$$ (6)

This recursion relation allows us to renormalize the raw score based on the number of steps taken. For example, for RAId_DbS [7], a database search method we developed, we divide the raw score obtained by 2(L − 1) for any peptide (path) of L amino acids (hopping steps) to get better sensitivity in peptide identification.

In principle, the recursion relations given by (4–6) are all one-dimensional updates. The only difference is the internal structure of counters at each position x. For (5), the counter is just an integer and has no further structure. For (4), the counter at each position has a 1D structure indexed by the score. For (6), the counter at each position x has a 2D structure indexed by both the score and the number of hopping steps. This means that in terms of solving the problem using dynamical programming, it is always a 1D dynamical programming with different degrees of internal structure that may lengthen the execution time when shifting from the simplest case (5) to the more complicated case (6). Obviously at each position x, there is an upper bound and a lower bound for score and also for the number of hopping steps accumulated. We shall call them S_best(x), S_worst(x), L_max(x) and L_min(x) respectively. The first two quantities may be obtained by eqs. (2) and (3) respectively. We provide the recursions for the two latter quantities below

$$L_{max}(x)=\underset{1\le i\le K}{max}\{L_{max}(x-m_i)\}+1,$$ (7)

$$L_{min}(x)=\underset{1\le i\le K}{min}\{L_{min}(x-m_i)\}+1.$$ (8)

Eqs. (2–3) and (7–8) provides the ranges for both the scores and the number of cumulative hopping steps at each position x via simple dynamic programming. As we will discuss later, this information enables a memory-efficient computations of score histograms.

4 Application in MS-based Peptide Sequencing

In this section, we focus on an important subject in modern biology – using MS data to identify the numerous peptides/proteins involved in any given biological process. Because of the peptide mass degeneracies and the limited measurement accuracy for the peptide mass-to-charge ratio, using MS² spectra is more effective in peptide identifications. In a MS² setup, a selected peptide with its mass identified by the first spectrometer is fragmented by noble gas, and the resulting fragments are analyzed by a second mass spectrometer. Although such MS²-based proteomics approaches promise high throughput analysis, the confidence level assignment for any peptide/protein identified is challenging.

The majority of peptide identification methods are so-called database search approaches. The main idea is to theoretically fragment each peptide in a database to obtain the corresponding theoretical spectra. One then decides the degree of similarity between each theoretical spectrum and the input query spectrum using a scoring function. The candidate peptides from the database are ranked/chosen according to their similarity scores to the query spectrum. Although one may assign relative confidence levels among the candidate peptides via various (empirical) means, an objective, standardized calibration exists only recently [8]. In our earlier publications [5,9], we proposed to tackle this difficulty by using a de novo sequencing method to provide an objective confidence measure that is both database-independent and takes into account spectrum-specific noise. In this paper, we will provide concrete algorithms for such purpose.

To begin, consider a spectrum σ with parent ion mass range [w − δ, w + δ], we denote by Π(w, δ) the set of all “possible” peptides with masses in this range. Given a peptide π from Π(w, δ), the associated quality score S(π, σ) is defined by a prescribed scoring system. The score distribution of S(π, σ) within Π(w, δ) provides naturally a likelihood measure for any given peptide π to the the correct one.

However, as described earlier [5], this seemingly straightforward idea faces two difficulties in terms of implementations. First, unlike the DPRM problem for which the function to be optimized is defined without ambiguity, the choice of the scoring function is somewhat empirical because the parameters used in the scoring must be trained using a training data set. Further, because of different instruments and experimental setups, it seems impossible to design a scoring system such that the correct peptide for each spectrum has the highest score among all possible peptides; the application of a given scoring function to general cases may require a leap of faith. Second, even after the scoring function is chosen, it is not known how to find the peptide π_o that maximizes S(π, σ) as well as the score distribution pdf(S) within Π(w, δ) other than by the generally impractical procedure of examining all members of Π(w, δ).

The first difficulty can be alleviated by validating high scoring de novo peptides via database searches [9] and is not the main focus of the current paper. Note that a partial solution to the second problem via iterative mapping when nonlocal score contributions exist is provided earlier [5]. Here we tackle the second problem head on when the scoring function used does not contain nonlocal contribution other than a final renormalization with respect to the peptide length. Our algorithms contains two parts: computer memory allocations and dynamical programming update. Prior to discussing these two parts, however, we first address the important issue of choosing a good mass unit.

4.1 Choosing a Good Mass Unit

The goal here is to choose a mass unit Δ and expresses the molecular mass of each amino acid as an integral multiple of this unit. For example, one may choose Δ to be 0.1 Dalton (Da), and round the molecular mass of each amino acid to be an integral multiple of 0.1 Da. Once a mass unit is chosen, all the masses under consideration are integral multiples of this unit. It turns out that different choices of the mass unit leads to different maximum cumulative mass error. As a specific example, consider using Δ = 0.1 Da as the mass unit. The mass of Alanine, with true mass 71.03711538 Da, is now represented as 710Δ. This molecular mass expression is 0.03711538 Da smaller than the true molecular mass of Alanine. When this happens, the integral mass representation has a mass smaller than the true mass, and we call such type of mass error a down-error. Now the amino acid Tryptophan with molecular mass 186.07931613 Da will be assigned an integral mass of 1861Δ, which has an extra of (0.1 – 0.07931613) Da compared to the true mass. We call this type of mass error the up-error.

The ratio of the mass error to the real molecular mass when multiplied by 3000 Da provides the cumulative maximum error that can be induced by a single amino acid at 3, 000 Da mass. For a fixed mass unit, we went over this mass error analysis for each of the twenty amino acids and documented the largest up-error and down-error. The larger one between the maximum up-error and the maximum down-error is called the max-error. To search for best mass units that minimize the max-error at 3,000 Da, we went over all possible mass unit ranging from 0.005 Da to 1.005 Da in step of 10⁻⁶ Da. Interestingly enough, we found a discrete list of mass units that have smaller max-error compared to their nearby mass units. These numerically found magic mass units are summarized in table 1.

Table 1.

A list of best mass units in Da. The abbreviation “m.u.e.” stands for “maximum up-error,” while “m.d.e.” stands for “maximum down-error.” The maximum up-error, maximum down-error, and max-error are evaluated in extrapolation to 3, 000 Da as described in the text. The abbreviation “a.a.w.m.u.” stands for “amino acid with maximum up-error,” while “a.a.w.m.d.” stands for “amino acid with maximum down-error.”

mass unit	m.u.e.	a.a.w.m.u.	m.d.e.	a.a.w.m.d.	max-error
0.006070	0.041980	Tryptophan	0.037455	Cysteine	0.041980
0.007300	0.041495	Methionine	0.061276	Asparagine	0.061276
0.017540	0.094183	Cysteine	0.121977	Proline	0.121977
0.021500	0.199585	Arginine	0.182283	Asparagine	0.199585
0.054470	0.453793	Asparagine	0.347792	Alanine	0.453793
0.065400	0.553492	Lysine	0.536989	Alanine	0.553492
0.109450	0.908287	Proline	0.900898	Lysine	0.908287
0.110300	0.962781	Histidine	0.858742	Lysine	0.962781
0.110320	0.960176	Aspartate	0.907801	Histidine	0.960176
0.500208	0.980357	Cysteine	0.983149	(Iso)Leucine	0.983149
1.000416	0.980357	Cysteine	0.983149	(Iso)Leucine	0.983149

Once a mass unit is chosen, all the amino acid masses are effectively integers. To obtain the score histogram of all de novo peptides when queried by a spectrum σ with parent molecular mass w (with N- and C- terminal groups of the peptide stripped away), we first construct a mass array where index k corresponds a molecular mass kΔ. To encode all possible peptides with molecular mass up to w, we need to have an array of size w/Δ+1. Apparently, when a larger mass unit is used, the size of the mass array is smaller and thus reduces computation time. However, as one may see from table 1, the larger mass unit is also accompanied by a larger max-error and might not be preferred when high mass accuracy is the first priority.

4.2 Efficient Memory Allocation

The basic idea of our algorithm is to encode all possible peptides in the mass array by linking pointers, analogous to the consecutive hopping steps in the 1D hopping model. For an amino acid a, let n(a) represents its corresponding integer mass in unit of Δ. For a peptide made of [a₁, a₂,…, a_M], it will have a hopping trajectory in the molecular array given by [0, x₁, x₂, …, x_M] with $x_{i\ge 1}\equiv {\sum }_{j=1}^{i}n(a_j)$. Let us also denote x_M by x_F to indicate that it is the terminating point of the path. Apparently, all possible peptides with molecular masses equal to x_F Δ will all have corresponding hopping paths starting at the origin and terminating at x_F. Through appropriate pointer linking, one may therefore encode all possible peptides with molecular mass x_F Δ in a one-dimensional mass array.

For a given spectrum σ, depending on the score function used, one may calculate local score contributions at each mass index. This step is done once only for the whole mass array, and need not be repeated for each candidate peptide. In a typical MS² experimental spectrum, there always exists some level of parent ion mass uncertainty. Once the size of the mass uncertainty is specified, we only need to examine de novo peptides whose corresponding hopping paths terminating at a few consecutive mass indices. This indicates that some of the mass indices of the aforementioned mass array may not even be used in this context. Below we describe how to efficiently obtain relevant mass indices and only allocate computer memories for those masses.

Assume that the possible terminating points are F₁,F₂,…,F_k with F_j+1 = F_j + 1. The update rules described in Eqs. (2–3), (5), and (7–8) will also be used at this stage. The following pseudocode describes our algorithm.

Initialize the mass_index = 0 entry

S_best = S_worst = L_max = L_min = 0; C=1;

REMARK: Max_aa is the maximum number of amino acids considered

for (aa_index = 0; aa_index < Max_aa; aa_index ++) {

label occupancy of n(aa_index);

at n(aa_index) attach a pointer back to 0;

update S_best, S_worst, L_max, L_min, C at n(aa_index);

}

for (mass_index = 1; mass_index <= F_k; mass_index ++) {

if (mass_index occupied ?) {

for (aa_index = 0; aa_index < Max_aa; aa_index ++) {

label occupancy of (mass_index + n(aa_index));

at mass_index+n(aa_index) attach a pointer to mass_index;

update S_best, S_worst, L_max, L_min, C at (mass_index + n(aa_index));

}

}

}

for (mass_index = F_k; mass_index >= F₁; mass_index −−) {

backtrack all possible paths → final occupied entries;

}

The last step in the algorithm above identifies relevant mass indices, mass indices that will be traversed by the hopping paths of all peptides with molecular masses in the range [F₁Δ, F_kΔ]. We only need to allocate computer memory associated with those sites. For each of these relevant sites, we also know the values of S_best, S_worst, L_max, L_min, and the total number of peptides reaching that site through the algorithm above. One may therefore allocate a 2D array of size (S_best(i)−S_worst(i))/η × (L_max(i) − L_min(i)) for each relevant mass_index i for later use.

4.3 Main Algorithm and some Results

Once memory allocation for relevant mass indices is done, we can efficiently go through those relevant sites to obtain the 2D score histogram that we mentioned. In the pseudocode below, update is performed using eq. (6). We now demonstrate the very simple main algorithm

Initialize all the fine counters C(x, N, L) = 0

except C(x = 0, N = 0, L = 0)=1;

for (aa_index = 0; aa_index < Max_aa; aa_index ++) {

update C(x, N, L) at x = n(aa_index);

}

for (mass_index in ascendingly ordered relevant mass indices) {

for (aa_index = 0; aa_index < Max_aa; aa_index ++) {

update C(x, N, L) at x =(mass_index + n(aa_index));

}

}

We now define the final 2D counter

$$Y(N,L)\equiv \sum _{i=1}^{k}C(F_i,N,L).$$ (9)

Apparently, in the 1D hopping model when allowing k consecutive terminating points, the resulting density of states D(E) can now be expressed as D(E = − Nη) = Σ_L Y (N, L)/η. If one were interested in normalizing the final score in a path-length dependent manner, one will has the following generic transformation

$$H(E)=\sum _L\int d{E}^{\prime }\frac{Y(E^{\prime }=-N\eta ,L)}{\eta }\delta (E-f(E^{\prime },L))$$ (10)

where f(E′, L) is a generic length-normalized energetic function that takes the raw energy E′ with L hopping steps and turn them into a new energy f(E′, L), and ∫dE′ → ηΣ_N is understood.

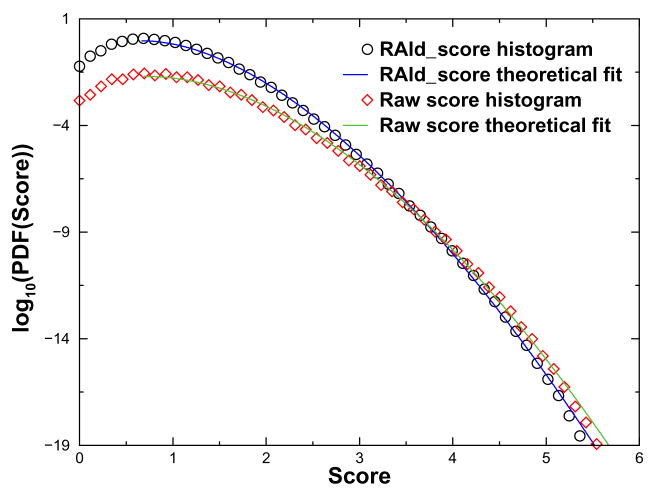
Using a real experimental MS² spectrum of parent ion mass 2254.7 ± 3.0 Da and a raw scoring function (RAId_DbS [7] raw score without divided by 2(L − 1) with L being the peptide length), we obtained a 2D score histogram. From this 2D score histogram, we can compute the average peptide length 〈L〉 as well. We then transform the 2D score histogram using two different f functions. In the first case, f(E′, L) = E′/2(〈L〉 − 1), meaning that one just divides the score by a constant given by 2(〈L〉 − 1). In the second case, we use the RAId_DbS scoring function where f(E′, L) = E′/2(L − 1). In Figure 1, we show the two resulting score histograms along with the fits to theoretical distribution function [7]. As one may see from the figure, both histograms are well fitted by the theoretical distribution function over at least 15 order of magnitudes. There is difference, however, in the histograms obtained. In the first case, where the score is merely divided by the average length, we have a wider score distribution than that of the second case. This implies that a high scoring hit out of the first type of scoring function will have a larger P-value than that of the second type. This is perfectly reasonable because when using the first type of raw scoring, very long peptides which by random chances are more likely to hit on fragment peaks in the mass spectrum are less penalized than the shorter peptides. As a consequence, one anticipates more false long peptides out of the first type of scoring method than that of the second scoring method. Therefore, one should assign a larger P-value to the former case and a smaller P-value to the latter case. It is apparently important to be able to obtain score histograms of the second scoring method. However, this can only be achieved if one keeps the length information in the dynamical programming update, see eq. (6).

Figure 1.

Score histograms for raw score and RAId_DbS score. Note that the two histogram cross each other at large score regime, indicating that the raw score function might not be as effective as the RAId_DbS score, see text for details.

5 Discussion, Summary, and Outlook

Our method may also be extended to other applications. In the case of passenger routings, the x-axis actually represents time. The local score may be viewed as the additional cost that may vary for different stops. Once the problem is laid out, the 2D histogram obtained from our solution indicates the number of equivalent routes in terms of additional costs and the total number of stops. This problem should be interesting in its own right.

In this paper, we developed a new approach to obtain the density of states of a 1D hopping problem in random potential. We have extended the simplest case scenario and have shown that we can apply this method to provide a complete score histogram for MS-based peptide sequencing problem. This important information may be used for a more objective statistical significance assignment in peptide identification. Our algorithm may also serve as a speedy de novo algorithm. If one is only interested in getting the best scoring peptide with length normalized score, one only needs to keep track of S_best(x, L). Furthermore, it is straightforward to include in our de novo algorithm post-translationally modified amino acids. The effect is simply an enlargement of the alphabet. That is, instead of having 20 amino acids, we will simply have more allowed masses but without needing to change any part of the algorithm.

In the near future, we would like to build a web application that allows the users to obtain information of interest. For example, a user might be interested in knowing: given a parent ion molecular mass and a mass error tolerance, how many de novo peptides can there be? Furthermore, we plan to provide users with the full score histogram when a query spectrum is provided and a scoring method is chosen. Our approach, founded on statistical physics, can easily address this type of questions to provide useful information for biological researches.