Modelling and spatial discrimination of small mammal assemblages: an example from western Sichuan (China)

Abstract

We investigate the relationship between landscape heterogeneity and the spatial distribution of small mammals in two areas of Western Sichuan, China. Given a large diversity of species trapped within a large number of habitats, we first classified small mammal assemblages and then modelled the habitat of each in the space of quantitative environmental descriptors. Our original two step “classify then model” procedure is appropriate for the frequently encountered study scenario: trapping data collected in remote areas with sampling guided by expert field knowledge.

In the classification step, we defined assemblages by grouping sites of similar species composition and relative densities using an expert-class-merging procedure which reduced redundancy in the habitat factor used within a multinomial logistic regression predicting species trapping probabilities. Assemblages were thus defined as mixtures of small mammal frequency distributions in discrete groups of sampled sites.

In the modelling step, assemblages’ habitats and environments of the two sampled areas were discriminated in the space of remotely sensed environmental descriptors. First, we compared the discrimination of assemblage/study areas by linear and non-linear forms of Discriminant Analysis (Linear Discriminant Analysis versus Mixture Discriminant Analysis) and of Multiple Regression (Generalized Linear Models versus Multiple Adaptive Regression Splines). The “best” predictive modelling technique was then used to quantify the contribution of each environmental variable in discriminations of assemblages and areas.

Mixtures of Gaussians provided a more efficient model of assemblage coverage in environmental space than a single Gaussian cluster model. However, non-linearity in assemblage response to environmental gradients was consistently predicted with lower deviance and misclassification error by Multiple Adaptive Regression Splines. The two study areas were mainly discriminated along vegetation indices. However, although the Normalized Difference Vegetation Index (NDVI) could discriminate forested from non-forested habitats, its power to discriminate assemblages in Maerkang, where a greater diversity of forest habitat was observed, was seen to be limited, and in this case NDVI was outperformed by the Enhanced Vegetation Index (EVI). Our analyses highlight previously unobserved differences between the environments and small mammal communities of two fringe areas of the Tibetan plateau and suggests that a biogeograph-ical approach is required to elucidate ecological processes in small mammal communities and to reduce extrapolation uncertainty in distribution mapping.

1 Introduction

1.1 Modelling distributions of assemblages

Modelling spatial distributions of species is a developed and promising research field which can both explain and predict the effects of environmental descriptors on species presence/absence in space. This relies on defining species’ habitats (Guisan and Zimmerman, 2000) following Hutchinson’s concept of ecological niche (1957). Recent reviews are found in Pulliam (2000) and Hirzel et al. (2002).

In situations where a large number of species co-occur in a large number of sampled sites, habitat definition for individual species can be complicated by species interactions. Defining habitat for rare or “shy” species can be impossible when presence is difficult to detect. By contrast, the full extent of habitats for dominant species can be elusive when the species is found in a large proportion of sampled sites. In these situations community level modelling constitutes a useful tool that provides a synthesis of such data sets by reducing their complexity to a much smaller set of higher-level entities. One such higher level entity can be that of an assemblage, i.e. a group of taxonomically related species which share the same habitat (Ferrier and Guisan, 2006). The habitat of an assemblage can therefore be defined in reference to a group of sites in which similar species composition and densities are observed.

Community-level spatial modelling involves three main steps (Ferrier and Guisan, 2006): i) classification of species and/or sites into groups, ii) statistical formulation to assess relationships between groups and environmental descriptors, and iii) predictive mapping of groups. Classification (i) is often realized through ordination methods without incorporating environmental information, e.g. the TWINSPAN algorithm (Hill, 1979; Legendre and Legendre, 1998). Grouping species into discrete assemblages involves making assumptions on species distributions (Olden, 2003): first, grouped species are treated in a similar way regarding their responses to environmental descriptors; then, species are assumed to belong to discrete mutually exclusive groups. In regards to Hutchinson’s concepts of ecological niche and associated species’ niche specificity and marginality, such assumptions seem at odds with species distributions in nature (Doledec et al., 2000; Hirzel et al., 2002). Moreover, clustering procedure can be biased by the subjective choice of similarity criterion and decision threshold (Anderson and Clements, 2000). In the modelling step (ii) groups are typically modelled against environmental variables, individually via GLM or GAM, or simultaneously using polychotomous regression or discriminant analysis (Lehmann et al., 2002; Gibson et al., 2004; Ferrier and Guisan, 2006). Modelling techniques have been deeply investigated in a “model then classify” approach by which species responses are grouped into assemblages after prediction of their occurrences (Lehmann et al., 2002; Gibson et al., 2004; Ferrier and Guisan, 2006). Joint modelling of multi-species responses has been recently developed to account for species interactions. This can help elucidate those variables that have strong effects on the whole community but might not be identified relevant in species level analyses (Leathwick et al., 2006). This has been successfully achieved through non-linear models such as Multiple Adaptive Regression Splines (MARS) (Friedman, 1991; Moisen and Frescino, 2002; Leathwick et al., 2006) and Artificial Neural Networks (Olden, 2003; Olden et al., 2006). However, these methods consider the model response to be presence of the individual species in each sampled site, defined using a threshold probability (usually 0.5) on observation frequencies, which can be viewed as a constraint for rarely observed species or sparse data sets.

1.2 Modelling landscape disturbance effects on small mammal distributions

Effects of landscape disturbances on small mammal communities have been investigated by defining assemblages using several classification methods on the basis of species trapping data. For example, Butet et al. (2006) used ordination methods and species/sites proximity in co-inertia axes while Giraudoux et al. (1998) defined assemblages by subjective criteria. Clustering algorithms have also been used to classify habitats into groups according to species composition dissimilarity (Krasnov et al., 1996).

On the basis of an a priori expert defined and qualitative habitat nomenclature, Raoul et al. (2008) produced an objective and reproducible classification of assemblages. The set of sampled habitat classes was reduced into a smaller set using information theory and assuming a multinomial model for the small mammal trapping data. Each a posteriori habitat class plus associated estimates of species trapping frequencies defined an assemblage. This approach presents several advantages over currently popular classification methods in the “Classify then model” approach: first, classification of assemblages was performed via a reclassification of sampled habitat classes a priori identified in the field and thus incorporates information gained from an expert oriented sampling strategy (Pearce et al., 2001); secondly, by considering each assemblage as a localised picture of species composition and relative densities, classification was performed at the habitat level instead of the species level, thus the crude assumptions of species responses mentioned above were avoided; finally, in the reclassification step, models were compared and selected using Akaike Information Criterion (AIC) which can be viewed as an objective method (Burnham and Anderson, 1998). However, this classification method limits the definition of assemblages’ habitats to qualitative and a priori habitat classes limited to the sampling design. Consequently it suffers from predictive power limitations, i.e. assemblage definitions cannot be spatially extrapolated beyond the sampled sites.

1.3 Context, hypothesis and objectives

In China, the spatial distribution of small mammal species has been shown to be modified by landscape disturbances such as overgrazing and fencing practices on the Tibetan plateau (Wang et al., 2004; Raoul et al., 2006), deforestation in Gansu (Giraudoux et al., 1998) and afforestation in Ningxia (Raoul et al., 2008). We aimed to investigate the relationship between landscape heterogeneity and the spatial distribution of small mammal assemblages in two forested areas located in the fringes of the Tibetan plateau (Sichuan, China). There, forest management leads to landscape heterogeneity and likely drives changes in the spatial distributions of small mammals.

Our main methodological challenge was to develop a predictive model for trapping data sets of diverse taxon, realized in remote areas and thus constrained by a limited sampling effort, a large number of rare species trapped with low frequency and an expert oriented sampling design. There is currently a need to adapt habitat modelling methodologies in order to fit and extract the maximum information possible from such data sets which is common in conservation studies. Here, we developed an original two step “Classify then model” procedure to address these issues.

In the classification step, we applied the Raoul et al. (2008) expert-class-merging procedure to summarise our trapping data by defining assemblages. Then, our major technical contribution was to incorporate such assemblage definitions into a predictive modelling framework. In the modelling step, the predictive limitations of the initial expert-class-merging assemblage definitions was overcame by extending the definition of the habitat associated with each assemblage using a set of quantitative variables extracted from remote sensors. By doing so, we addressed some currently debated methodological issues in the field of species distribution modelling. The modelling step aimed to answer two questions:

1. which modelling technique and associated response-factor relationships predict assemblage occurrence with lowest prediction error?

2. what are the contributions of each environmental variable in assemblage discrimination and prediction?

Among the theoretical hypothesis supporting current species modelling methodological frameworks, the shape of response curves has often been neglected and there is a need to consider it at the interface between statistical methods and ecological realism (Austin, 2002, 2007; Guisan et al., 2006). The richness of existing statistical models offers the opportunity to compare different ecological theories underlying observed patterns of species distribution in environmental space. While previous studies have shown non-linear models provide better fits and predictions of multiple species responses than linear models (Doledec et al., 2000; Olden, 2003; Leathwick et al., 2006), we tested if this observed pattern could hold when species responses are considered as a whole, i.e when assemblages and not species are used as the response variable. Several methods exist to discriminate known groups by continuous variables. We compared the discrimination ability of two widely used classifiers, multiple logistic regression and discriminant analysis, and tested several forms of assemblage response curves: linear versus non-linear and single Gaussian versus Gaussian mixture respectively.

The selection of a relevant set of predictors for building predictive models also remains an active current issue which is complicated by the nature of environmental predictors (direct/indirect) and their interactions (Austin, 2007). Here, instead of selecting a single “best” model, we investigated the overall contribution of each environmental variable within a set of models.

Because trapping data were collected in two distinct areas, the same questions were answered at the regional spatial extent to investigate discrimination of the two study areas in the environmental space.

2 Material and methods

2.1 Small mammal species data sets

2.1.1 Study areas

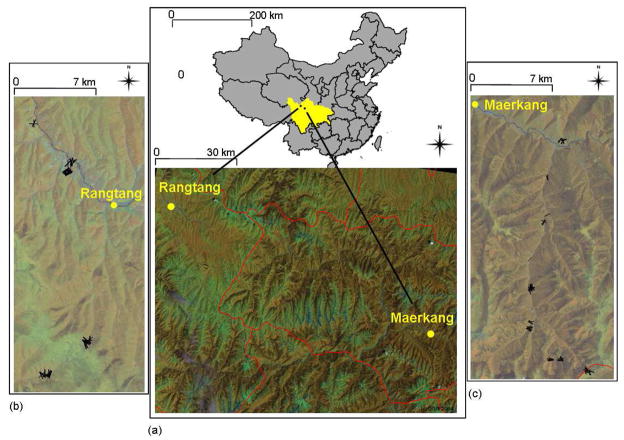
Two study sites were investigated in western Sichuan province (central China) in the vicinities of Rangtang and Maerkang cities, (approximatively 100 kilometres apart) (figure 1), in June 2004 and July/September 2005 respectively. The sampling area in Maerkang ranged from 2950 to 4100 meters altitude. The 2005 mean annual temperature and yearly average rainfall were 8.9 °C and 811.5 mm respectively (data source: Maerkang Center for Disease Control). Forested areas were either coniferous or birch and oak. Afforestation measures were in place and a large number of young plantation forests were found. Rhododendron forests and pastures were observed at higher elevations. Villages were often surrounded by ploughed fields and were situated close to rivers with abandoned terraced fields at higher elevation. In Rangtang, elevation of sampled area ranged from 3350 to 3900 meters and in 2005 yearly average temperature and yearly average rainfall were 5.4 °C and 854.3 mm respectively. Landscape was mainly composed of grassland and shrub. Forest was less abundant than in Maerkang and was more frequently coniferous than broad-leaf.

Figure 1.

a) Location of Maerkang and Rangtang study areas in Sichuan province, China. Lines delineate province and county boundaries. (b) and (c) represent locations of traplines (lines) around Rangtang and Maerkang cities respectively. Locations are plotted on a false colour composite satellite image in which red, green and blue correspond to Landsat ETM bands 4, 5 and 3.

2.1.2 Sampling protocol

Sampling was undertaken in a priori defined habitats identified in the field i.e. habitats classified on the basis of apparent dissimilarities in vegetation structure and dominant genus composition. In Maerkang and Rangtang, 18 and 12 habitats were sampled respectively (table 2). Four habitats were found to be similar in the two locations: “Forest Rhododendron/coniferous”, “Forest coniferous willow bushes understory”, “Stream bushes” and “Slope bushes” (table 2).

Table 2.

Maerkang (M1 to M4) and Rangtang (R1 to R4) assemblages obtained from expert-class-merging procedure. The number of traplines (Nb lines), habitat composition, number of trap-nights per sampled habitat (Nb trap-nights), species trapped (Dominant and Other) and Simpson diversity index are reported for each assemblage.

Assemblage	Nb lines	Habitat composition	Nb Trap-nights	Dominant species	Others species	Simpson diversity
M1	20	Bushes North Slope	75	Niviventer Confucianus	Chodsigoa hypsibia	2.60
		Bushes former Terrace	744		Apodemus latronum
		Bushes Birch Culture	300
		Grassland	447
		Forest Oak near Village	301
		Set a side Field	749
		Stream near Culture	300
M2	7	Culture	1050	Micromys minutus	Eozapus setchuanus	2.08
					Eo spalax fontanieri
					Apodemus latronum
M3	34	Forest Regeneration & Plantation	719	Qchotona cansus	Apodemus peninsulae	7.86
		Stream Bushes & Trees	325		Apodemus draco
		Forest Coniferous & Willow Bushes	600		Apodemus latronum
		Forest Oak	444		Chodsigoa hypsibia
		Stream Willow Bushes	294
		Stream Bushes	444		Sorex thibetantus
		Forest Rhododendron	746		Sorex cylindricauda
		Forest Rhododendron & Coniferous	747		Uropsilus soricipes
					Sicista concolor
					Microtus irene
M4	5	Forest white Birch wet	306	Apodemus draco	Apodemus latronum	1.97
		Forest red Birch Understorey	438		Niviventer confucianus
					Uropsilus soricipes
R1	23	Field bank	717	Apodemus peninsulae	Microtus limnophilus	1.07
		Slope grass & Sparse bushes	300		Eozapus setchuanus
		Field bank	369
		Culture border	671
R2	18	Bottom valley grassland & bushes	600	Apodemus peninsulae	Microtus limnophilus	1.25
		Bottom valley grassland & bushes (Namuda)	577
		Village garden	599
		Forest coniferous & willow bushes	898
R3	2	Fenced grassland	48	Microtus limnophilus	Apodemus peninsulae	1.25
R4	14	Forest rhododendron & coniferous	175	Qchotona cansus	Microtus irene	2.48
		Slope bushes	746		Apodemus peninsulae
		Stream bushes	1041		Microtus limnophilus

Extensive standard trapping (Giraudoux et al., 1998, Raoul et al, 2006) was undertaken in each habitat. Each standardized trapline consisted of 25 traps spaced three meters apart. Two types of traps were used: small break back traps (SBBT), for animals not heavier than 100g and big break back traps (BBBT) for larger individuals. Each trap was set for three nights (unless non-controlled factors dictated otherwise, e.g. trap theft), checked every morning and re-set/re-baited as necessary. We use the term trap-night to refer to a single trap set for one night. A total of 8095 trap-nights (4603 in Maerkang; 3492 in Rangtang) in 122 traplines (66 in Maerkang; 56 in Rangtang) were set; differential trapping effort by habitat is reported in table 2.

Species were identified at the Centre de Biologie et Gestion des Populations (J.P. Quéré) using the following references: Corbet (1978); Fen and Zheng (1985); Gromov and Polyakov (1978); Gromov and Erbajeva (1995); Smith and Xie (2008). Apodemus penninsulae, Apodemus draco and Apodemus latronum identifications were confirmed using cytochrome b sequencing. Nomenclature followed Wilson and Reeder (2005).

2.2 Assemblage definition

2.2.1 Statistical model

The response variable, the category (i.e species or empty trap) observed in a given trap-night, was assumed to follow a multinomial distribution (Raoul et al., 2008). Relationships between habitat classes and species distribution were modelled using log linear multinomial regression with a priori selected habitat classes as explanatory variables (McCullag and Nelder, 1989). The three nights per trap and trap type were included as factors in the regression. Within each study site, a preliminary model comparison via AIC indicated no evidence for a night effect, so the factor was removed for further analyses.

2.2.2 Expert-class-merging procedure

Following Raoul et al. (2008), pairs of habitat classes (H_i and H_j) were “merged” by imposing an equality constraint on their regression coefficients (i.e. β _Hi = β_Hj). Iterative application of this constraint to all habitat class pairs lead to K new models which were compared via the difference in AICc (ΔAICc_{i j}) between each new model and the original (unconstrained) one. The model/merge providing the largest ΔAICc_{i j} identified the most redundant habitat class distinction and the two corresponding classes were fused into a single super-class. The process was iterated until no further evidence of class redundancy was observed i.e. once ΔAICc_{i j} < 2 (Burnham and Anderson, 1998). Finally, we computed the Simpson diversity index of each resulting assemblage. All statistical algorithms were implemented in R (R Development Core Team, 2008). Multinomial models were fitted using the multinom function of the nnet package.

2.3 Assemblage habitat modelling

2.3.1 Environmental descriptors

The environment at trapline locations was described using remotely sensed data layers corresponding to: spectral responses of Landsat Enhanced Thematic Mapper (ETM) bands; elevation; slope; and sun exposure. A (July 2005) multi-spectral ETM image from Landsat 7 was obtained from the U.S. Geological Survey ( landsat.usgs.gov). ETM bands 3, 4 and 7, corresponding to red, near-infrared and middle infrared respectively, each with a 30 meters resolution, were used for the analyses. Other ETM bands were omitted from further analysis due to strong correlations with the selected bands. Using the ETM image, the Normalized Difference Vegetation Index (NDVI) and Enhanced Vegetation Index (EVI) were computed (Huette et al., 1999). NDVI quantifies the difference between photosynthetic activity related absorption in the visible range and reflectance in the near-infrared which is related to electro-magnetic emission by plants. NDVI is thus correlated to vegetation biomass. However, the NDVI is known to suffer from saturation when vegetative biomass is high and to be sensitive to canopy background in open forested areas (Huette et al., 2002). Therefore, we computed EVI, defined as

$$\mathit{EVI}=\frac{G\times (\mathit{NIR}-\mathit{RED})}{L+\mathit{NIR}+C_1\times \mathit{RED}-C_2\times \mathit{BLUE}}$$

where L is the canopy background and snow correction, C1 and C2 are coefficients of aerosol “resistance” terms and G the gain factor with L = 1, C₁ = 6, C₂ = 7.7 and G = 2.5.

A digital elevation model (DEM) was obtained from the SRTM program ( http://srtm.usgs.gov/). Slope, aspect and elevation were derived from the DEM in GRASS GIS ( http://grass.itc.it/). The sun index (SI), which provides a proxy for net incident solar radiation, was estimated as (Gibson et al., 2004):

$$SI=cos(\mathit{aspect})\times tan(\mathit{slope})\times 100.$$

In general traplines were not confined within the bounds of single pixels. In order to construct the data matrix the mean of each variable was estimated from 10 points regularly spaced along each trapline. This was performed using spgrass6, the R/GRASS interface available at http://r-spatial.sourceforge.net/xtra/xtra.RHnw.html.

2.3.2 Discriminant models

We explored if the set of environmental descriptors could: explain small mammal assemblage distributions locally, i.e. within each study area; and discriminate between the two study areas using data from trapline locations, a regional level analysis. Essentially this entailed discrimination of previously identified assemblages/traplines in the environmental space and thus presents a supervised classification problem. Model performances of two currently popular methods were compared: Discriminant Analysis (DA) and Logistic Multiple Regression (LMR). Both techniques were tested: in linear form, Linear Discriminant Analysis (LDA) (Fisher, 1936) and multinomial Generalized Linear Model (GLM); and in non-linear form, Mixture Discriminant Analysis (MDA) and Multiple Adaptive Regression Splines (MARS).

MARS

Multiple Adaptive Regression Splines (Friedman, 1991) enable modelling multiple categorical responses with weak assumptions on the shape of the response. A set of pairwise basis functions provide a set of nonlinear transformations on covariates enabling regression modelling in an enlarged space defined by the set of basis functions and their products and thus enabling identification of complex non-linear responses (Hastie et al., 2001, 1994). In the context of species distribution modelling, MARS incorporated within GLMs has been shown to outperform other non-parametric and non-linear modelling techniques on real (Leathwick et al., 2006) and simulated (Moisen and Frescino, 2002) data sets. Here we test performance of MARS incorporated into a multinomial GLM.

MDA

Non-linear decision boundaries in classification problems can also be modelled indirectly, i.e. without specifying and parameterising the form of the non-linear decision boundary. Mixture Discriminant Analysis is such an approach, generalising the linear decision boundaries of LDA by incorporating mixtures of multivariate Gaussians to discriminate a single class (Hastie and Tibshirani, 1993). MDA divides a given class into multiple subclasses each following a multivariate normal distribution with unique mean vector and a common covariance matrix. As far as we know, this method has been rarely tested in the context of niche spatial modelling except by Ter Braak et al. (2003). Here, maximum likelihood based parameter estimation was achieved using the expectation maximisation (EM) algorithm (cf. Appendix 1). Starting values for the EM algorithm were obtained by the Learning Vector Quantisation clustering algorithm (Hastie and Tibshirani, 1993).

All computations were performed in R (R Development Core Team, 2008). LDA was computed using the lda function of the “MASS” package. MARS and MDA were computed using the mars and mda functions of the mda package.

2.3.3 Evaluation and comparison of modelling techniques’ performances

In order to compare modelling techniques on the basis of their statistical properties, we only compared models of similar structure in their explanatory components, i.e. including all available explanatory variables (Segurado and Araujo, 2004; Potts and Elith, 2006).

Evaluation criteria

Following Pearce and Ferrier (2000), models were evaluated on their ability to i) provide reliable predictions (as soft classifiers) and ii) discriminate between occupied and unoccupied sites (as hard classifiers). Prediction reliability was quantified using residual deviance (RD) (Pearce and Ferrier, 2000; Leathwick et al., 2006) equivalent to minus twice the log likelihood of the fitted probabilities. i.e. for N observations

$$RD=-2\times \sum _{i=1}^N\mathit{log}Pr({\widehat{y}}_i-y_i).$$

Discriminative performance (ii) is composed of omission (true positive fraction) and commission (false positive fraction) error (Pearce and Ferrier, 2000; Anderson et al., 2003). Here, predicted assemblages were mutually exclusive, i.e the commission error of one assemblage corresponded to the omission error of another. Consequently, discriminative performance was assessed by omission error only using the true presence misclassification error rate (Segurado and Araujo, 2004).

Model validation

Predictive ability was assessed using the above mentioned criteria on independently re-sampled testing data sets using the bootstrap 632+ (Efron and Tibshirani, 1995) which provides the least biased and variant model re-sampling evaluation method (Hastie et al., 2001). Bootstrap 632+ was developed to reduce optimistic error estimation that arises with the original bootstrap due to commonality between the observations of training and testing data sets. Originally used to estimate error rates of per-subject prediction rule (e.g. misclassification error rate) it has recently and successfully been applied to evaluate predictive models of species or disease distribution (Steyerberg et al., 2001; Leathwick et al., 2006; Potts and Elith, 2006). We computed the bootstrap 632+ in R (R Development Core Team, 2008), using the bootpred function of the boostrap package and the errorest function of the ipred package. For each criteria the mean and standard deviation across 1000 bootstrap samples was calculated.

2.3.4 Effects of environmental descriptors on assemblage distributions

To simplify the assessment of effect size we selected the classification methods that provided the lowest bootstraped misclassification error rate and residual deviance.

Effect Size

Multicollinearity between factors is known to inflate the variance of regression coefficients, alter model predictive performance and complicates identification of real effects of factors on data variability (Legendre and Legendre, 1998). Hierarchical partitioning (MacNally, 2000, 2002), widely used in explanatory modelling (Gibson et al., 2004; Greaves et al., 2006; Olivier et al., 2000), permits to partition the variance explained by a model in order to isolate the independent versus joint contributions of each variable. We used this method to estimate the independent effects of each variable on the log-likelihood. Significance of these independent effects was assessed using a permutation test. The independent effect was re-estimated using 100 random permutations of the covariates, the mean and standard deviation of the resulting distribution permitting a z-test of the original independent effect.

The effect size of each environmental descriptor on the probability of observing each assemblage were assessed. All possible additive combinations of variables were fitted. For each combination we calculated the mean predicted probability of each assemblage at sites where that assemblage was observed. The difference in predicted probabilities

$$\mathrm{\Delta }{\mu }_{j10}={\mu }_{j1}-{\mu }_{j0}$$

were computed, where μ_j1 and μ_j0 represent the mean predicted probabilities across models which included and excluded the j^th variable respectively. Means and 95% quantile intervals were estimated over 200 cross-validation iterations. Predictive effects were considered for further analysis if the lower 95% quantile was greater than zero.

Response shape along environmental gradients

The shape of assemblage responses were visualised by plotting predicted probabilities with respect to each relevant environmental variable (Elith et al., 2005). Predictions of assemblage occurrence probabilities were made across the range of the variable of interest whilst all other variables were fixed to their mean value among sites corresponding to the assemblage in question.

All computations were made in R (R Development Core Team, 2008). Independent effects were estimated using the combos and partition functions of the hier.part package. The z.test was adapted from the rand.hp function of the same package.

3 Results

3.1 Trapping success: small mammal data

A total of 173 small mammals were trapped in Rangtang (90) and Maerkang (83) including 10 rodent, 1 lagomorph and 4 insectivore species (table 1). Four species were trapped in both areas: Ochotona cansus, Eozapus setchuanus, Apodemus peninsulae, and Microtus irene.

Table 1.

Sampling success for each species (number of trapped individuals) obtained in each study area. The order of each species is indicated: Rodent (R), Insectivore (I) or Lagomorph (L).

		Location
	Order	Maerkang	Rangtang
Empty traps		4516	3396
Apodemus draco (Apda)	R	17	0
Apodemus latronum (Apla)	R	14	0
Apodemus peninsulae (Appe)	R	3	68
Eospalax fontanirerf (Eofo)	R	1	0
Eozapus setchuanus (Eose)	R	1	1
Microtus irene (Miir)	R	1	1
Microtus limnophilus (Mili)	R	0	13
Micromys minutus (Mimi)	R	6	0
Niviventer confucianus (Nico)	R	19	0
Sicista concolor (Sico)	R	1	0
Chodsigoa hypsibia (Chhy)	I	10	0
Sorex cylindricauda (Socy)	I	1	0
Sorex thibetanus (Soth)	I	2	0
Uropsilus soricipes (Urso)	I	2	0
Ochotona cansus (Occa)	L	5	7

3.2 Assemblage definition

Maerkang

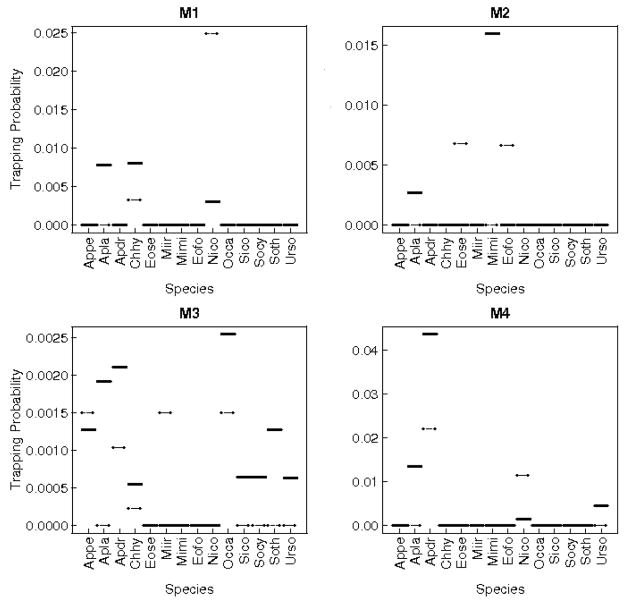
Four assemblages were identified (M1 to M4) (table 2, Appendix 3. a). Assemblage M1, which included seven habitats subjected to human influences, was dominated by the rat Niviventer confucianus. M2, the Culture habitat, was not merged with other classes and was dominated by Micromys minutus which was specific to that habitat. M3 included forest and bush was the richest (n = 11) and most diversified (7.86) assemblage. Trapping probabilities were an order of magnitude lower in M3 than in other assemblages and nothing was trapped in Forest Oak and Stream bushes. M4 grouped white and red birch forests and had the lowest diversity. Trapping frequencies of Apodemus draco in M4 were greater than for any other species in any other assemblage.

Rangtang

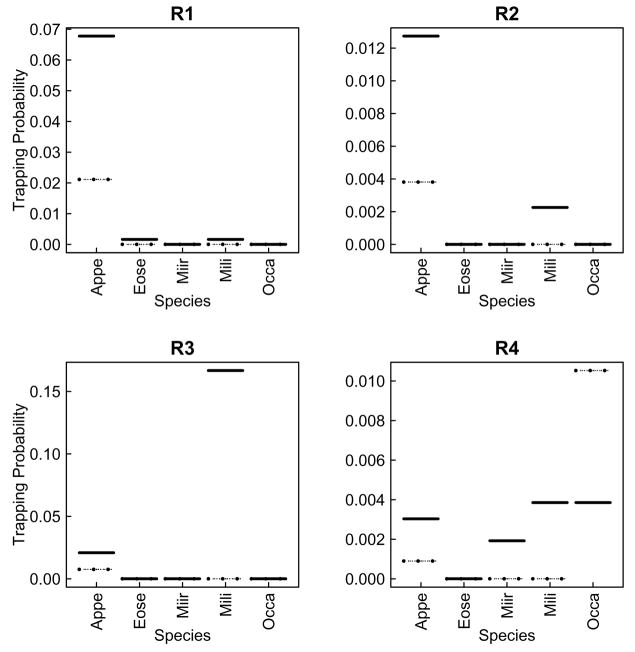
Four assemblages were identified (R1 to R4) (table 2, Appendix 3. b). R1, which included habitats in close vicinity to culture, was dominated by Apodemus peninsulae and provided the lowest diversity among all assemblages. In R2, which included valley bottom bushes, Forest coniferous/willow bushes and Village garden, Apodemus peninsulae was dominant but trapped with lower probability than in R1. R3 corresponded to the Fenced grassland class which was not merged with other classes. Only two species were found: Microtus limnophilus which was trapped at highest probability in R3, and Apodemus peninsulae. R4 grouped Forest rhododendron/coniferous with Slope and Stream bushes. Diversity was highest in this assemblage and Ochotona cansus was specific to it.

Details of AICc and Δ AICc evolution according to the number of the expert-class-merging procedure iterations, for Maerkang and Rangtang study areas, are available in the Appendix 2.

3.3 Assemblage habitat modelling

Modelling techniques were applied to discriminate all assemblages previously defined except assemblage R3 since it included only 2 traplines (table 2).

3.3.1 Modelling techniques performances (table 3)

Table 3.

Residual deviance (RD) and misclassification error rates (Error) obtained for each modelling procedure (Linear Discriminant Analysis (LDA), Mixture Discriminant Analysis (MDA), Multinomial logistic regression (MN) and Multiple Adaptive Regression Spline (MARS)), for each study case, on training (Train) and testing (Boot) data sets. For the test data set, means (Boot mean) and standard deviances (Boot sd), estimated over 1000 bootstrap 632+ iterations, are indicated.

		LDA		MDA		MN		MARS
		RD	Error	RD	Error	RD	Error	RD	Error
Maerkang
	Train	86.645	0.212	55.251	0.121	70.886	0.197	0.001	0.000
	Boot mean	111.322	0.270	105.491	0.258	107.589	0.313	53.585	0.221
	Boot sd	0.092	0.001	0.109	0.001	0.084	0.001	0.049	0.000
Rangtang
	Train	46.815	0.182	71.922	0.073	13.060	0.055	0.000	0.000
	Boot mean	67.082	0.308	65.095	0.265	44.391	0.253	41.144	0.232
	Boot sd	0.092	0.001	0.069	0.001	0.129	0.001	0.046	0.001
Study sites
	Train	51.693	0.106	17.506	0.033	41.230	0.081	0.000	0.000
	Boot mean	56.292	0.111	46.620	0.073	57.401	0.101	16.927	0.029
	Boot sd	0.001	0.000	0.012	0.000	0.027	0.000	16.927	0.029

Discriminant Analysis

For discriminant analysis of Maerkang assemblages and study sites, bootstrapped RD and error rate of MDA were approximately twice the RD and error estimated on training data. MDA was a more discriminant and reliable predictor than LDA in terms of lower bootstrapped error rates (Δ Error(Maerkang)_LDA−MDA = 0.012; Δ Error(Region)_LDA−MDA = 0.038) and RD (Δ RD(Maerkang)_LDA−MDA = 5.831; Δ RD(Region)_LDA−MDA = 9.672). In Rangtang, training data based estimates indicated MDA gave a more deviant fit than LDA although again bootstrapped RD (Δ RD(Rangtang)_LDA−MDA = 1.99) and error (Δ Error(Rangtang)_LDA−MDA = 0.043) were lower than for LDA.

Mixture Discriminant Analysis was also a more discriminatory and reliable model than the multinomial GLM in the Maerkang (Δ Error(Maerkang)_MN−MDA = 0.055; Δ RD(Maerkang)_MN−MDA = 2.089) and regional level (Δ Error(Region)_MN−MDA = 0.028; Δ RD(Region)_MN−MDA = 10.781) analysis. However, in Rangtang, MN outperformed MDA (Δ Error(Rangtang)_MDA−MN = 0.012; Δ RD(Rangtang)_MDA−MN = 20.704).

Finally, in each of the three analysis, MARS perfectly fitted the training data (RD_MARS,train = 0.00; Error_MARS,train = 0.00). Despite this overfitting, MARS was the most reliable and discriminatory model in the prediction test, providing bootstrap predictor errors 0.037, 0.021 and 0.044 lower than the next most discriminant predictor of Maerkang assemblages, Rangtang assemblages and study sites respectively.

3.3.2 Effects of environmental descriptors on assemblage distributions

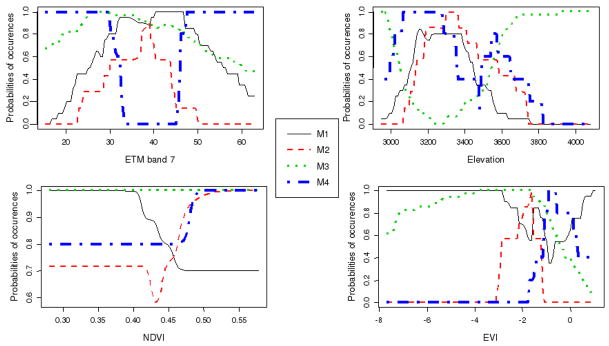
Maerkang

Significant independent contributions to model goodness-of-fit were observed for elevation and ETM band 7 (table 4). Among all variables, elevation provided the largest independent contribution (I%= 39.7). It increased predicted probabilities for all assemblages bar M2 on training and bootstrapped data sets (table 5). A threshold was observed at about 3600 meters altitude above which M1 was seldom observed, the probability of M2 and M4 dropped rapidly and M3 became predominant (figure 2). Enhanced Thematic Mapper band 7 consistently discriminated all assemblages. The probability of M2 (cultures) reached a distinct peak at intermediate values (40) where the probability of M4 approached zero.

Table 4.

Percentage of the independent contribution over all independent effects (I %) and total contributions (Total) in model goodness of fit estimated for each variable and for each study case. The statistical significance (sig.) of the Z.score based on upper 0.95 confidence limit is indicated by (*)

	ETM7	Elevation	Slope	SI	NDVI	EVI
Maerkang
I%	20.912	39.196	11.461	2.208	11.068	15.156
Z.score	2.13	9.36	0.17	−0.15	−0.03	0.52
sig.	*	*	ns	ns	ns	ns
Total	23.096	39.691	15.099	3.601	11.091	16.627
Rangtang
I %	16.410	23.313	21.160	2.263	29.058	7.790
Z.score	1.9	5.88	4.13	−1.1	2.92	−0.27
sig.	*	*	*	ns	*	ns
Total	17.251	18.888	9.694	2.369	26.061	5.812
Region
I %	26.842	37.132	8.529	0.316	21.024	6.156
Z.score	12.68	16.4	3.79	0.19	7.35	2.74
sig.	*	*	*	ns	*	*
Total	31.888	58.427	16.210	−0.549	39.418	13.850

Table 5.

Contributions of each variable to change in the mean predicted probabilities of each assemblage at sites where the given assemblage was observed. Estimates based on training data (Mean Train) and cross validation means (Mean CV P1-P0) and confidence intervals (qt0.05 CV P1-P0) are shown. Grey cells correspond to variable effects which lower 95% quantile was greater than zero.

		Maerkang				Rangtang
		M1	M2	M3	M4	R1	R2	R4
ETM 7	Mean Train	0.158	0.254	0.096	0.255	0.101	0.113	0.098
	Mean CV P1-P0	0.107	0.143	0.049	0.212	0.030	0.003	0.015
	qt0.05 CV P1-P0	0.079	0.068	0.021	0.133	0.008	−0.017	0.000
	qt0.95 CV P1-P0	0140	0.234	0.073	0.293	0.053	0.018	0.029
elevation	Mean Train	0.363	0.133	0.278	0.433	0.161	0.128	0.123
	Mean CV P1-P0	0.250	0.060	0.329	0.283	0.207	0.073	0.127
	qt0.05 CV P1-P0	0.212	−0.007	0.290	0.160	0.178	0.038	0.078
	qt0.95 CV P1-P0	0.278	0.121	0.357	0.364	0.237	0.102	0.163
slope	Mean Train	0.076	0.092	0.038	0.197	0.150	0.228	0.071
	Mean CV P1-P0	0.018	0.028	−0.021	0.036	0.190	0.307	0.052
	qt0.05 CV P1-P0	−0.012	−0.050	−0.044	−0.046	0.159	0.271	0.028
	qt0.95 CV P1-P0	0.049	0.075	0.003	0.096	0.222	0.342	0.079
SI	Mean Train	0.005	−0.003	0.003	−0.012	−0.002	0.007	0.008
	Mean CV P1-P0	−0.016	−0.042	−0.009	−0.030	−0.009	−0.006	−0.011
	qt0.05 CV P1-P0	−0.032	−0.195	−0.019	−0.058	−0.011	−0.009	−0.017
	qt0.95 CV P1-P0	−0.002	0.017	−0.001	−0.001	−0.007	−0.004	−0.008
NDVI	Mean Train	0.087	0.106	0.045	0.140	0.084	0.195	0.300
	Mean CV P1-P0	0.034	0.011	−0.003	0.043	0.041	0.084	0.218
	qt0.05 CVP1-P0	0.008	−0.030	−0.019	−0.006	0.014	0.057	0.186
	qt0.95 CV P1-P0	0.063	0.066	0.014	0.092	0.069	0.111	0.245
EVI	Mean Train	0.104	0.237	0.055	0.180	0.043	0.042	0.058
	Mean CV P1-P0	0.029	0.104	0.000	0.093	−0.014	−0.014	−0.010
	qt0.05 CV P1-P0	−0.008	0.037	−0.019	0.035	−0.024	−0.021	−0.016
	qt0.95 CV P1-P0	0.063	0.179	0.022	0.169	−0.005	−0.006	−0.004

Figure 2.

Responses (predicted probabilities) of Maerkang assemblages along those continuous gradients for which predictive power for at least one assemblage was identified (table 5).

Despite the non-significance of their independent contributions, vegetation indices influenced mean predicted probabilities (table 4, table 5). On average, inclusion of NDVI increased predicted probabilities of M1 by 0.087. A change was observed at NDVI = 0.45 with M1 being more probable than M2 or M4 below and less probably than other assemblages above this point respectively (figure 2). Inclusion of EVI significantly increased the probability to predict M2 and M4 whose bootstrapped means increased by 0.104 and 0.093 respectively. The range of EVI corresponding to M2 occurrence being lower than that of M4 (birch forests). Finally, slope and SI had no predictive power.

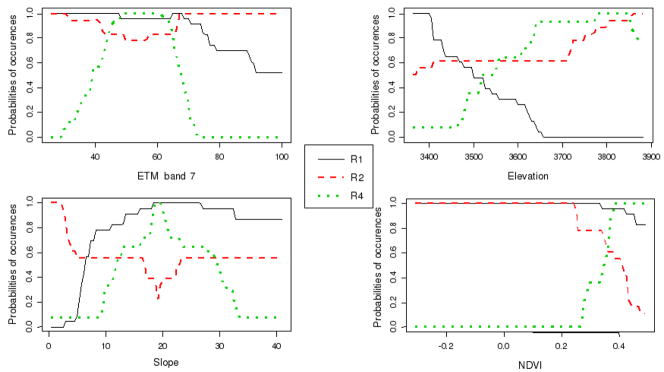
Rangtang

Independent effects of NDVI, elevation, ETM band 7 and slope were all significant (table 4). NDVI provided the highest independent contribution (I%=29.058) and significantly improved mean predicted probabilities for all assemblages, this improvement being greatest for R4 (Forest rhododendron/coniferous and Slope bushes) (0.30) which was not observed when NDVI < 0.25 (table 5, figure 3). By contrast, above this threshold, the probability of R2, and to a lesser extent R1, dropped considerably.

Figure 3.

Responses (predicted probabilities) of Rangtang assemblages along those continuous gradients for which predictive power for at least one assemblage was identified (table 5).

Elevation increased predicted probabilities for all assemblages, the size of the effect being greatest for R1 (fields and bushes) which was predominant at lower altitudes and did not occur above 3650 meters. Above this level, the probability of R4 reached a plateau and the probability of R2 also increased. Inclusion of ETM band 7 significantly increased prediction accuracy for R1 and R4. Band 7 values greater than 70 corresponded to predominant and subordinant predicted probabilities of R2 and R4 respectively, the latter being optimally distributed in the range 50–65. Inclusion of slope significantly increased predictive probabilities at R2, R1 and R4 sites (ordered by decreasing effect size). R2 was the predominant assemblage in flat areas and R1 became predominant when slopes became steeper than 10 °. Finally, SI and EVI had no predictive effects.

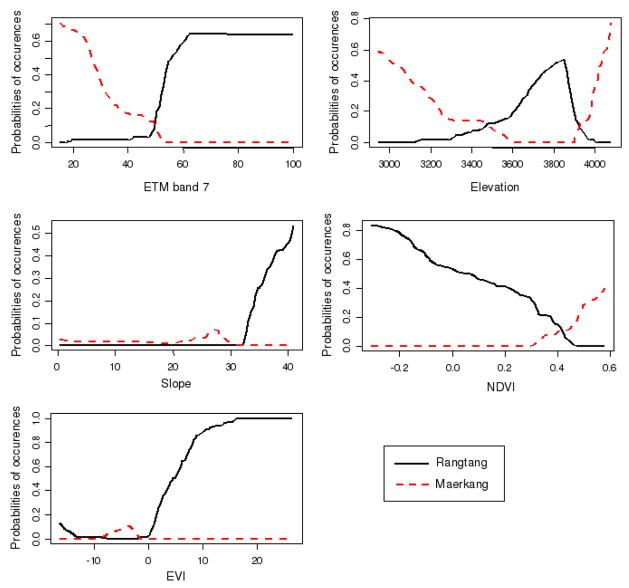
Between study sites

All variables had significant and independent contributions in model goodness-of-fit except SI which had a negative contribution in the model likelihood (table 4). Rangtang was associated with ETM band 7 > 50, steep slopes, EVI > 0, NDVI < 0.4 and elevations in the range 3600–3900 meters. Maerkang was associated with ETM band 7 < 50, NDVI > 0.4 and elevations below and above 3500m and 3900m respectively (figure 4).

Figure 4.

Responses (predicted probabilities) of the two study areas along those continuous gradients for which predictive power for at least one assemblage was identified.

4 Discussion

4.1 Assemblages as mixtures of species distributions

The ability of the expert-class-merging procedure to cluster observations from a large number of habitats into a small number of super-classes highlights that apparently different habitats in fact provide approximately equivalent habitat quality for many small mammals species. However, the influence of a species in the assemblage definition is directly related to trapping frequency, the definition being dominated by those species trapped in largest number (e.g. Apodemus peninsulae), whilst rare or shy species trapped in low numbers (e.g. Eozapus setchuanus) play a relatively small role in the assemblage definition. It is well known that spatial distributions of small mammals can be driven by population dynamics (Giraudoux et al., 1997, 2007). The assemblages defined in the present study constituted a spatio-temporal snapshot of a process of complex interactions between multi-species metapopulations (Guisan and Thuiller, 2005). The current data set, with its lack of a temporal component, thus limits analyses to the description of “potential habitats” for the identified small mammal assemblages (Guisan and Thuiller, 2005; Araujo and Guisan, 2006; Guisan et al., 2006).

4.2 Assemblage habitat distribution in environmental space

Linear or non-linear Discriminant Analysis for small sample size problems?

Linear Discriminant Analysis is said to perform well when sample size is small because of the simple boundaries it provides between classes (Hastie et al., 1997). However, our analyses showed prediction reliability and class discrimination were consistently lower for MDA than for LDA. MDA’s discrimination of assemblages in several sub-classes, permitting identification of non-linear boundaries, clearly helped capture important extra within class variability. This result re-enforces the need to use non-linear models in community modelling even when sample size is small (Munoz and Felicisimo, 2004).

MDA allows multi-modal representation of an assemblage in environmental space. By contrast, MN assumes assemblage responses can be represented as simple linear combinations of variables rescaled to the 0–1 range via a link function. Despite a larger number of parameters, MDA was more discriminant and less deviant than MN for discrimination of Maerkang assemblages and site environments. This result highlights the importance of modelling sub-class clusters in those case studies. By contrast, Rangtang assemblages were better discriminated by MN than by MDA suggesting a more homogeneous distribution of those assemblages in environmental space. MN was also a more performant predictor of Rangtang data than LDA despite the two models sharing the same logit regression form (Hastie et al., 2001). Regardless of linearity/non-linearity assumptions, discriminant analysis was not the most appropriate method for modelling the distribution of Rangtang assemblages for which sample sizes were smallest.

Parametric or non-parametric non-linear modelling of assemblage distributions?

Multiple Adaptive Regression Splines advantageously extends the logistic response of multinomial GLMs to include multi-modal variation of the linear predictor with respect to a given variable. MARS has previously been shown to be a more appropriate mapping technique for Fagus species than Logistic Multiple Regression (Munoz and Felicisimo, 2004) although more generally there has been difficulty to demonstrate better performance of MARS over linear models on real data sets (Moisen and Frescino, 2002). Here, MARS consistently provided more discriminatory and reliable predictions than LDA, MDA and GLM in all three of our cases studies. The Non-linear structures in class distributions were more accurately captured by a model which didn’t rely on parametric assumptions regarding assemblage distribution in environmental space. These promising prediction results of MARS were obtained despite strong evidence of overfitting (i.e. selection of an excessive number of basis functions) the training data. This observation is encouraging since the superior predictive performance of MARS could clearly be improved via the increased parsimony obtainable with model selection procedures such as step-wise pruning (Friedman, 1991).

Assuming each a priori habitat was representable as a single cluster in environmental space, a mixture representation of an assemblage (i.e. super-class), including the diversity of species responses, and thus the requirement of non-linear decision boundaries for assemblage discrimination, becomes natural. This complexity arises in part from the fact that most of the variables in question were, at best, indirectly related to small mammal dynamic processes. Guisan and Zimmerman (2000) suggested that the use of direct environmental variables provides a physiologically mechanistic character to a model that is not apparent when indirectly related variables are used. We further suggest that the use of indirect variables in fact complicates response curves. Multi-modal responses in the space of indirect variables might correspond to relatively homogeneous responses among variables directly related to processes.

4.3 Explanatory and predictive power of environmental descriptors

Within versus between study area discrimination

The observed between site differences in small mammal fauna, environmental conditions and pertinence of environmental variables provided strong evidence that two distinct biogeographical zones had been identified. The degree of abruptness/smoothness in the transition between these zones was not identifiable given the scale of the sampling design and clearly further work is required before the process of small mammal communities on the fringes of the Tibetan plateau are fully elucidated.

The discrimination between Maerkang and Rangtang at high and low NDVI values respectively suggests greater productivity in terms of vegetative biomass in Maerkang. This corresponds with our a priori land cover classification since forested habitats were more widespread and diversified in Maerkang than in Rangtang. By contrast, within study sites, NDVI and EVI were useful discriminators of different assemblages. In Maerkang, NDVI significantly improved predictions of M1 (bushes, grassland an oak forests near villages), while EVI helped discriminate birch forests (M4) and culture (M2). In Rangtang, NDVI discriminated forest (R4), valley-bottom vegetation (R2) and non-forested bush (R1), whereas EVI displayed no discriminative ability. The fact that NDVI was less useful in Maerkang, where nine in eighteen habitats were forested, than in Rangtang, where only two in twelve habitats were forested habitats, probably reflects the saturation problem, i.e. NDVI’s limited ability to discriminate among forest types (Huette et al., 1999).

Variables such as elevation, ETM band 7 and slope had descriptive and predictive power but their indirect relation to small mammal resources renders interpretation of their effects difficult (regardless of the mixture problem outlined above). Moreover, these variables are subjected to the law of relative site constancy (Guisan and Zimmerman, 2000; Randin et al., 2006) which complicates the comparison of assemblage distributions between the two study areas along these gradients.

The discriminatory power of environmental variables differed according to the study area (Maerkang versus Rangtang) and to the spatial extent of the training area (local versus regional analysis). For predictive mapping purposes, one should be aware of such variation in order to select a set of environmental variables appropriate for the required extent, resolution and location of the map (Guisan and Thuiller, 2005).

Improving habitat definition

Numerous improvements to the current habitat descriptions can be envisaged. Firstly, numerous species have been shown to respond to landscape level effects whereby densities respond to composition or structure of landscape in a surrounding neighbourhood. Examples include Tetrao urogallus (Graf et al., 2005), Echinococcus multilocularis (Giraudoux et al., 2003), Arvicola terrestris (Fichet-Calvet et al., 2000; Giraudoux et al., 2007; Morilhat et al., 2007) and Microtus arvalis (Delattre et al., 1999, 2006; Duhamel et al., 2000), the latter two being small mammal species of the sub-family Arvicolinae. Here effects of composition and structure in buffers surrounding traplines were not considered, largely due to identifiability issues associated with the required increased level of data mining and the small sample size.

Secondly, trapline locations were often observed to lie within mixed pixels where numerous habitat types contribute to the observed spectral response. Improved predictive performance might therefore be achievable by addressing the mixed pixel problem for which fuzzy set approaches (Foody, 2000) and super-resolution techniques (Tatem et al., 2002) exist.

Thirdly, descriptors of structure and composition of the first vegetative strata, being more directly related to small mammal resources would be pertinent (Catling and Coops, 1999; Pearce et al., 2001; Gibson et al., 2004). This move to direct variables would be of particular relevance in a predictive modelling setting since indirect variables limit model transferability across large areas (Guisan and Thuiller, 2005; Randin et al., 2006). Understory modelling with very high resolution satellite remotely sensed data has recently been applied in sparse forests (Jianxi et al., 2007). Further, helicopter-borne laser scanner data has been used to provide high resolution DEMs from which understory structural and textural characteristics are easily extracted (Hirata et al., 2003). Further research is needed before remotely sensed indices of understory structure can be incorporated into small mammal species distribution models.

Toward building a process based models

As outlined above, statistical models can help resolve some theoretical hypotheses on species/environment relationships (e.g. shape of the response curves, selection of influent environmental factors) and thus provide basis for the development of process based models. Inversely, process based models can serve statistical modelling and an iterative procedure incorporating both approaches had been advocated (Austin, 2007). Here, prediction precision might be increased once a deeper understanding of the ecological processes driving small mammal distributions on the fringes of the Tibetan plateau is achieved. It would be helpful to investigate landscape composition effects on small mammal communities in time and space. For this purpose, there is need to develop process based landscape metrics of direct relevance to small mammal resources. Ultimately, such relationships could be incorporated into a Structural Equation Modelling framework (Guisan et al., 2006; Austin, 2007).

4.4 Conclusion and perspectives

Our results showed mixtures of Gaussians provided better descriptions of the environmental space occupied be small mammal assemblages than single cluster model. However, the Gaussian mixture model was in turn outperformed by MARS with its flexible ability to detect non-linearity. ETM band 7, vegetation indices, elevation and slope all helped discriminate assemblages. Their predictive effects varied according to the location and spatial scale of the training area. However, predictive performance might be improved given further investigation of methodological issues and a deeper understanding of underlying ecological processes. i.e. given: a deeper knowledge of the responses of multiple-species to environmental variation; a closer match between spectrally derived variables and small-mammal resources; or, an improved data set characteristics (sampling protocol). In our study, MARS was prone to over-fitting, thus its transferability and superior performance over other techniques should be assessed cautiously prior to extrapolation beyond the sampling area (Randin et al., 2006). Moreover, because it is a classifier (i.e assumes the pre-defined groups exist), used here to model assemblage responses jointly, prediction of new (i.e. untrained) assemblages in space and time was not possible. Two distinct biogeographical areas regarding small mammal assemblages and environmental conditions were identified here, but the current sampling design does not permit elucidation of the transition between the two areas. Mapping small mammal assemblages in the area between Rangtang and Maerkang would require a sampling design spanning the ranges of each species within both the geographical and environmental space separating the two areas (Murphy, 2007).

4.5.1 Appendix 1: MDA algorithm

The algorithm computes the mixture density for each class j divided in R_j subclasses each defined by their own mean μ(j,r) and a common covariance matrix Σ, such as:

$$m_{j(x)}=P(X=x\mid G=j)=\mid {(2\pi )}^d\mathrm{\sum }{\mid }^{-1/2}\sum _{r=1}^{R_j}{\pi }_{jr}{e}^{-D_{(x{\mu }_{jr})}/2}$$

where D(x,y) is the Mahalanobis distance between x and the y and the mixing probability π_jr are unknown model parameters. Then, the conditional log-likelihood for the data l^mix is computed and maximised by the EM (Expectation Maximisation) algorithm with:

$$l^{\mathit{mix}}({\mu }_{rj},\mathrm{\sum },{\pi }_{jr})=\sum _{i=1}^{N}log{m}_{gi}(x_i)$$

Expectation Maximisation (EM) algorithm is an iterative two-step procedure: first, it estimates the mixing probabilities for each subclass and class and then, it conditionally optimises the mean and covariance for each subclasses.

4.5.2 Appendix 2: Expert-class-merging procedure

Appendix 2.

Redundancy reduction of the expert-class-merging procedure for (a) Maerkang and (b) Rangtang data sets illustrated by decreasing AICc and increasing Δ AICc w.r.t. to the number of iterations of the procedure.

4.5.3 Appendix 3: Species predicted probability distributions in Maerkang and Rangtang assemblages

Appendix 3.a.

Species trapping joint probabilities predicted by the multinomial model for each assemblage (M1 to M4), in Maerkang. Dashes and full lines correspond to small and big traps respectively. Correspondence between species names and their abbreviations is available in table 2.

Appendix 3.b.

Species trapping joint probabilities predicted by the multinomial model for each assemblage (R1 to R4), Rangtang. Dashes and full lines correspond to small and big traps respectively. Correspondence between species names and their abbreviations is available in table 2.