Abstract
Experimental investigations for anatomic variation in the magnitude and anisotropy of elastic constants in human femoral cortical bone tissue have typically focused on a limited number of convenient sites near the mid-diaphysis. However, the proximal and distal ends of the diaphysis are more clinically relevant to common orthopaedic procedures and interesting mechanobiology. Therefore, the objective of this study was to measure anatomic variation in the elastic anisotropy and inhomogeneity of human cortical bone tissue along the entire length (15-85% of the total femur length) and around the periphery (anterior, medial, posterior and lateral quadrants) of the femoral diaphysis using ultrasonic wave propagation in the three orthogonal specimen axes. The elastic symmetry of tissue in the distal and extreme proximal portions of the diaphysis (15-45% and 75-85% of the total femur length, respectively) was, at most, orthotropic. In contrast, the elastic symmetry of tissue near the mid- and proximal mid-diaphysis (50-70% of the total femur length) was reasonably approximated as transversely isotropic. The magnitudes of elastic constants generally reached maxima near the mid- and proximal mid-diaphysis in the lateral and medial quadrants, and decreased toward the epiphyses, as well as the posterior and anterior quadrants. The elastic anisotropy ratio in the longitudinal and radial anatomic axes showed the opposite trends. These variations were significantly correlated with the apparent tissue density, as expected. In summary, the human femur exhibited statistically significant anatomic variation in elastic anisotropy, which may have important implications for whole bone numerical models and mechanobiology.
Keywords: Anisotropy, Compact Bone, Cortical Bone, Elastic Constants, Femur, Orthotropy, Stiffness Coefficients, Transverse Isotropy, Ultrasound
1. Introduction
The mechanical properties of cortical bone tissue are known to be both inhomogeneous and anisotropic. Relationships for variation in key mechanical properties due to changes in structure are needed in whole bone numerical models used in the design of orthopaedic implants and the study of adaptive bone remodeling. Elastic inhomogeneity is customarily accounted for using well-established power-law scaling relationships with the apparent tissue density, porosity or ash fraction (Hernandez, et al., 2001; Keller, et al., 1990; Martin, et al., 1998; Orr, et al., 1990; Rho, et al., 1993, 1995; Schaffler and Burr, 1988). In contrast, the elastic anisotropy of cortical bone tissue has only recently begun to be incorporated into numerical models (Bagge, 2000; Doblaré and Garcia, 2001; Jacobs, et al., 1997; Taylor, et al., 2003) and experimentally correlated to structural and anatomic features (Dong and Guo, 2004; Skedros, et al., 2006; Takano, et al., 1999).
Early investigations of the elastic inhomogeneity (Amtmann, 1968; Evans and LeBow, 1951; Reilly and Burstein, 1974) and anisotropy (Dempster and Liddicoat, 1952; Reilly and Burstein, 1974, 1975) of cortical bone tissue utilized destructive tests in uniaxial tension, uniaxial compression or bending. Pope and Outwater (1974) appear to be the first to have simultaneously investigated elastic inhomogeneity and anisotropy, utilizing specimens from the diaphysis of a bovine tibia. Elastic anisotropy was greatest at the mid-diaphysis and decreased to near isotropy toward the epiphyses, though no error bars were reported and the test methods were likely suspect (Reilly and Burstein, 1975). Although destructive tests have continued to be used in recent investigations (Dong and Guo, 2004), results from all destructive tests are inherently limited by specimen size constraints and the inability to measure all the requisite elastic constants from one test specimen.
Nondestructive testing using ultrasonic wave propagation enabled the measurement of all requisite elastic constants on a single specimen. Early investigations assumed transverse isotropy in the plane normal to the longitudinal bone axis (Bonfield and Grynpas, 1977; Lang, 1970; Lappi et al., 1979; Yoon and Katz, 1976a, 1976b). Van Buskirk et al. (1981) measured the nine orthotropic stiffness coefficients in cortical bone tissue from a bovine femur and showed statistically significant differences between all terms along the tensor diagonal with C33 > C22 > C11 > C44 > C55 > C66, where the indices 1, 2 and 3 denote the radial, circumferential and longitudinal anatomic directions, respectively. Orthotropy was subsequently corroborated in human tissue (Ashman, et al., 1984; Hoffmeister, et al., 2000; Rho, 1996). However, Katz et al., (1984) argued that an orthotropic versus transversely isotropic symmetry was dependent on whether the tissue exhibited a predominately laminar or Haversian microstructure, respectively. More recently, an “anisotropy ratio,” defined as the ratio of the longitudinal and circumferential stiffness coefficients, was used to quantify the degree of elastic anisotropy for comparison between tissue from a variety of different species, bones and preparations (Hasegawa, et al., 1994; Takano, et al., 1996; Turner, et al., 1995).
Ultrasound also enabled the use of small specimens, on the order of millimeters, which could be sampled with respect anatomic locations along the length and around the periphery of long bones. Ashman et al. (1984) reported that the longitudinal stiffness coefficient, C33, in human femoral cortical bone tissue was greater in the medial and lateral anatomic quadrants than in the posterior quadrant and that no significant differences existed with respect to sites along the diaphysis within 30-70% of the total femur length. Anatomic variation in the longitudinal stiffness coefficient was shown to follow similar patterns to the tissue density. Bensamoun et al. (2004) used an acoustic microscope to map spatial variation in the longitudinal stiffness coefficient on thin cross-sections of a whole human femur, which revealed maxima near the medial and lateral quadrants and minima in the posterior quadrant. A host of other studies concluded that no trends were either apparent or statistically significant along the length or around the periphery of the diaphysis of human tibiae (Hoffmeister, et al., 2000; Rho, 1996), human femora (Hunt, et al., 1998) and bovine femora (Van Buskirk, et al., 1981; Yamato, et al., 2006). Two noteworthy animal models using canine radii (Takano, et al., 1999) and cervine calcanei (Skedros, et al., 2006) showed that the anisotropy ratio was higher in anatomic quadrants that experienced tensile compared to compressive strain in vivo. Otherwise, no studies have examined anatomic variation in the elastic anisotropy or symmetry, though the data may have been available to do so, and correlations might be expected (Cowin and Mehrabadi, 1989; Katz and Meunier, 1990).
Many recent investigations of elastic anisotropy and inhomogeneity in cortical bone have tended to focus on probing the tissue at finer length scales using acoustic microscopy (Bensamoun, et al., 2004; Hofmann, et al., 2006) and nanoindentation (Fan, et al., 2002; Rho, et al., 1999a, 1999b, 2002; Swadener, et al., 2001; Zysset, et al., 1999) with a resolution on the order of ten μm and one nm, respectively. These techniques have enabled characterization of osteonal versus interstitial bone and even individual lamellae. However, in order to obtain meaningful tissue level properties, these measurements must be extrapolated using micromechanical models or statistical correlations.
In summary, experimental investigations for anatomic variation in the magnitude and anisotropy of elastic constants in cortical bone tissue have typically focused on a limited number of convenient sites near the mid-diaphysis. However, the proximal and distal ends of the diaphysis are more clinically relevant to common orthopaedic procedures and interesting mechanobiology. Furthermore, recent scientific interest has focused on the use of new techniques to measure at finer length scales, while relatively little work has continued to consider anatomic variation of the apparent tissue properties across whole bones. Therefore, the objective of this study was to measure anatomic variation in the elastic anisotropy and inhomogeneity of human cortical bone tissue along the entire femoral diaphysis with considerable spatial variation at the tissue level.
2. Materials and Methods
2.1. Specimen Preparation
A whole femur was harvested from the right lower extremity of a 78 year old male donor, presenting no toxicology or bone-related pathology. The cause of death was ischemic cardiomiopathy. After dissection, the femur was stored in a freezer at −20°C wrapped with gauze soaked in phosphate buffered saline. Dual-energy x-ray absorptiometry (DEXA) (Hologic QDR 4500A, Hologic, Waltham, MA) was used to measure the areal bone mineral density (BMD) on the proximal whole femur, which was classified as osteopenic by standard clinical practices.
Sixty parallelepiped cortical bone specimens were prepared from each anatomic quadrant along the entire length of the femoral diaphysis (Fig. 1). The femur was initially sectioned into 5% length segments, from 15% to 85% of the total femur length using a wet band saw (Fig. 1a). The total femur length was measured parallel to the longitudinal bone axis as the distance from the medial knee condyle to the femoral head. Parallelepiped specimens were sectioned from each anatomic quadrant of the annular femur segments using a low speed diamond wafer saw (ISOMET, Buehler Ltd., Lake Bluff, IL) (Fig. 1b). The nominal specimen size was 5 × 5 × 5 mm; however, at the extreme distal and proximal diaphysis, the specimen thickness (radial bone axis) was maximized within the available cortical thickness. An orthogonal curvilinear coordinate system (Cowin and Mehrabadi, 1989) with radial (1), circumferential (2), and longitudinal (3) axes was defined by the anatomic shape of the femoral diaphysis (Fig. 1b). Specimens were identified by position along the length of the femoral diaphysis, e.g., 25% of the total femur length, and the anatomic quadrant, e.g., anterior (A), medial (M), posterior (P) and lateral (L). Specimens were stored at -20°C in a solution of 50% ethanol and 50% phosphate buffered saline during all interim periods, and kept fully hydrated for ultrasonic characterization.
Figure 1.
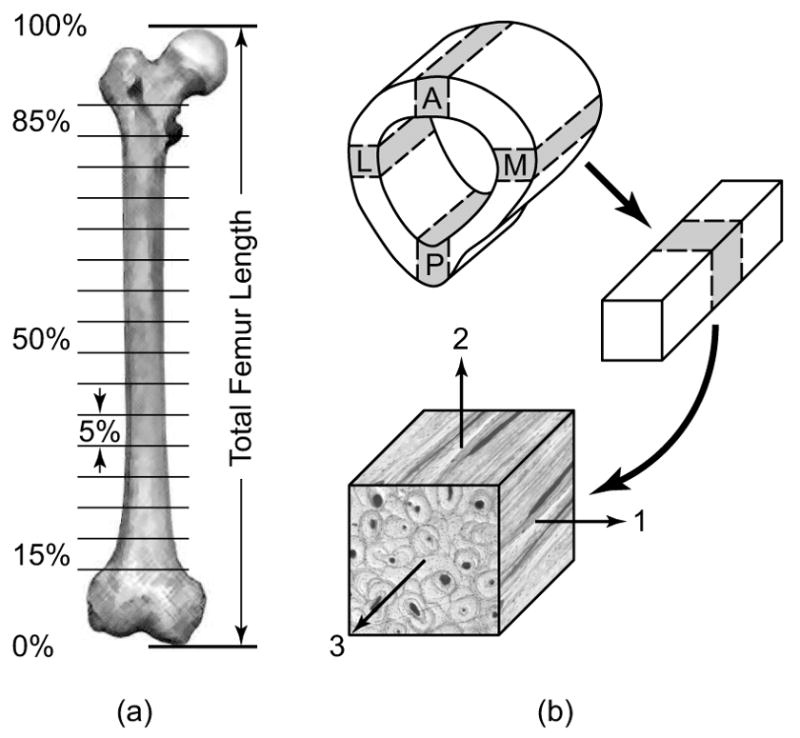
Schematic diagram showing cortical bone specimen preparation from the diaphysis of a whole human femur. (a) The femoral diaphysis was sectioned into 5% length segments from 15 to 85% of the total femur length. (b) Each segment of the diaphysis was subsequently sectioned into parallelepiped specimens (nominally 5 × 5 × 5 mm) from each anatomic quadrant (A = anterior, M = medial, P = posterior and L = lateral) with an orientation defined by the axes of an anatomically based orthogonal curvilinear coordinate system (1 = radial, 2 = circumferential, 3 = longitudinal).
2.2. Ultrasonic Characterization
Stiffness coefficients were determined from measurements of the ultrasonic wave velocity and apparent tissue density under ambient conditions while hydrated in de-ionized water. Longitudinal (or dilational) waves were used to measure the first three terms from the main diagonal of the reduced fourth-order stiffness tensor, Cii, corresponding to the three mutually orthogonal specimen axes. Longitudinal stiffness coefficients were calculated as,
| (1) |
where ρ is the apparent tissue density and vii is the longitudinal wave velocity in the i-th specimen direction (Fig. 1b). Shear (or transverse) waves were used to measure the last three terms from the main diagonal of the stiffness tensor, C44, C55 and C66. Shear stiffness coefficients were calculated as,
| (2a) |
| (2b) |
| (2c) |
where ρ is the apparent tissue density and vij is the shear wave velocity in the i-j specimen plane (Fig. 1b). The two wave velocities measured for each shear stiffness coefficient were not statistically different (p = 0.83, paired t-test) and were therefore averaged. The apparent tissue density of each specimen was measured in the wet state using Archimedes' principle as,
| (3) |
where M is the specimen mass measured while completely saturated with de-ionized water, S is the specimen mass measured while submerged in de-ionized water, and ρw is the density of de-ionized water (Ashman, et al., 1984; ASTM, 1999). The coefficient of variation was 0.25% for ten repeated measurements of the apparent density on a single specimen.
The ultrasonic wave velocity was measured using the pulse transmission method (Lang, 1970; Lappi et al., 1979; Van Buskirk, et al., 1981; Yoon and Katz, 1976b). Pulsed longitudinal and shear waves were generated at 50 μJ and 500 Hz using an ultrasonic pulser/receiver, and were transmitted to and received from the specimen using 2.25 MHz, 12.7 mm diameter longitudinal and shear transducers, respectively (Models 5800, V106RM and V154RM, Panametrics, Inc., Waltham, MA). The transmitted wave velocity was calculated as vij = di/Δt where di is the specimen dimension and Δt is the time delay for wave transmission and displacement in the i-th and j-th specimen directions, respectively. Note that the directions for wave transmission and displacement are coincident for longitudinal waves (i = j) but orthogonal for shear waves (i ≠ j). The time delay, Δt, for wave transmission through the specimen was measured using an oscilloscope (TDS 2012, Tektronix Inc., Beaverton, OR) as the shift in the relative position of the received ultrasonic pulses with and without the specimen inserted between the transducers. All specimen dimensions were measured using digital calipers accurate to ±0.01 mm. Consistent alignment and contact of the transducers to the specimen was facilitated by a spring-loaded parallel sliding mount (Ashman, et al., 1984). De-ionized water and honey were used as coupling agents to aid signal transmission between longitudinal and shear transducers, respectively, and the specimen. A 5 mm steel gauge block was used to verify the system accuracy before and after measurements on bone specimens. Repeatability was verified by taking five measurements of the longitudinal wave velocity on a single specimen after sequentially sectioning the specimen to six different thicknesses ranging from 8 to 3 mm. The overall coefficient of variation was 1.3% (n = 30) and the effect of the specimen thickness on the repeated measures was not statistically significant (p > 0.54, ANOVA).
The degree of elastic anisotropy was calculated as the ratio of longitudinal elastic constants, C33/C11, C33/C22 and C11/C22, which are hereafter termed the anisotropy ratios. Note that for an orthotropic symmetry, the lowest symmetry considered here, only two anisotropy ratios are not redundant. For transverse isotropy, the highest symmetry considered here, only one anisotropy ratio is not redundant.
2.3. Statistical Methods
Experimental data were reported and grouped by anatomic location along the length (% of the total femur length) and around the periphery (anatomic quadrants) of the femoral diaphysis. All measurements for groups were reported as the mean ± one standard deviation. Groups were compared using one-way analysis of variance (ANOVA) (JMP 5.1, SAS Institute, Inc., Cary, NC). Post hoc comparisons were performed using an unpaired Student's t-test with a level of significance of 0.05. Linear least squares regression was used to correlate the elastic constants and anisotropy ratios to the apparent tissue density.
3. Results
The elastic constants for the main diagonal of the reduced fourth-order stiffness tensor, Cii (i = 1-6), anisotropy ratios and apparent tissue density were measured for all specimens and tabulated by anatomic location along the length and around the periphery of the femoral diaphysis. The full data set is available in Electronic Annex 1 in the online version of this article. The mean stiffness coefficients for all specimens (Table 1) exhibited orthotropy with C33 > C22 > C11 > C44 > C55 > C66 (p < 0.0001, ANOVA). However, the magnitude and anisotropy of stiffness coefficients varied significantly by anatomic location.
Table 1.
Stiffness coefficients for the main diagonal of the reduced fourth-order stiffness tensor, Cii (GPa), and the apparent density, ρ (g/cm3), for cortical bone specimens grouped along the length of the femoral diaphysis showing the mean (± one standard deviation).
| % Length | C11 | C22 | C33 | C44 | C55 | C66 | ρ |
|---|---|---|---|---|---|---|---|
| 85 | 12.2 (1.7) | 18.0 (1.8) | 24.6 (1.9) | 5.6 (0.5) | 4.4 (0.5) | 3.8 (0.2) | 1.80 (0.08) |
| 80 | 16.6 (3.8) | 19.2 (2.9) | 26.5 (2.5) | 5.9 (0.5) | 5.6 (0.6) | 4.3 (0.8) | 1.88 (0.10) |
| 75 | 19.4 (1.8) | 21.2 (1.2) | 29.0 (1.4) | 6.3 (0.3) | 6.1 (0.3) | 4.8 (0.4) | 1.96 (0.04) |
| 70 | 18.4 (2.6) | 20.2 (2.4) | 27.6 (2.0) | 6.1 (0.6) | 6.1 (0.2) | 4.7 (0.4) | 1.94 (0.07) |
| 65 | 19.5 (2.5) | 19.9 (2.5) | 28.4 (2.0) | 6.1 (0.4) | 6.1 (0.6) | 4.8 (0.6) | 1.96 (0.05) |
| 60 | 18.0 (3.0) | 19.3 (2.9) | 27.5 (2.1) | 6.3 (0.0) | 5.9 (0.6) | 4.7 (0.5) | 1.92 (0.06) |
| 55 | 19.0 (3.6) | 18.9 (2.5) | 27.3 (2.4) | 6.2 (0.3) | 6.0 (0.5) | 4.8 (0.7) | 1.91 (0.09) |
| 50 | 18.9 (2.7) | 19.3 (2.0) | 27.8 (2.1) | 6.0 (0.3) | 5.9 (0.2) | 4.6 (0.4) | 1.93 (0.05) |
| 45 | 18.1 (1.8) | 20.5 (1.0) | 28.2 (1.2) | 6.2 (0.2) | 5.9 (0.7) | 4.3 (1.1) | 1.94 (0.03) |
| 40 | 17.2 (2.0) | 19.1 (1.3) | 26.7 (1.6) | 6.3 (0.2) | 5.8 (0.6) | 4.7 (0.4) | 1.94 (0.00) |
| 35 | 16.9 (1.7) | 20.3 (0.9) | 27.6 (0.8) | 6.3 (0.3) | 5.9 (0.6) | 4.7 (0.6) | 1.90 (0.07) |
| 30 | 15.9 (1.8) | 19.9 (1.1) | 27.5 (0.6) | 6.3 (0.3) | 5.9 (0.5) | 4.9 (0.9) | 1.90 (0.04) |
| 25 | 16.1 (0.7) | 20.7 (2.7) | 29.6 (0.9) | 6.4 (0.5) | 5.5 (0.7) | 4.1 (0.5) | 1.92 (0.06) |
| 20 | 13.6 (2.1) | 18.8 (4.0) | 27.2 (2.0) | 6.2 (0.5) | 4.8 (0.9) | 3.8 (0.8) | 1.85 (0.09) |
| 15 | 11.6 (2.2) | 19.5 (2.2) | 24.5 (1.0) | 6.2 (0.3) | 4.8 (1.3) | 4.1 (1.0) | 1.80 (0.03) |
| All | 16.8 (2.3) | 19.7 (2.1) | 27.3 (1.6) | 6.2 (0.4) | 5.6 (0.8) | 4.5 (0.7) | 1.90 (0.07) |
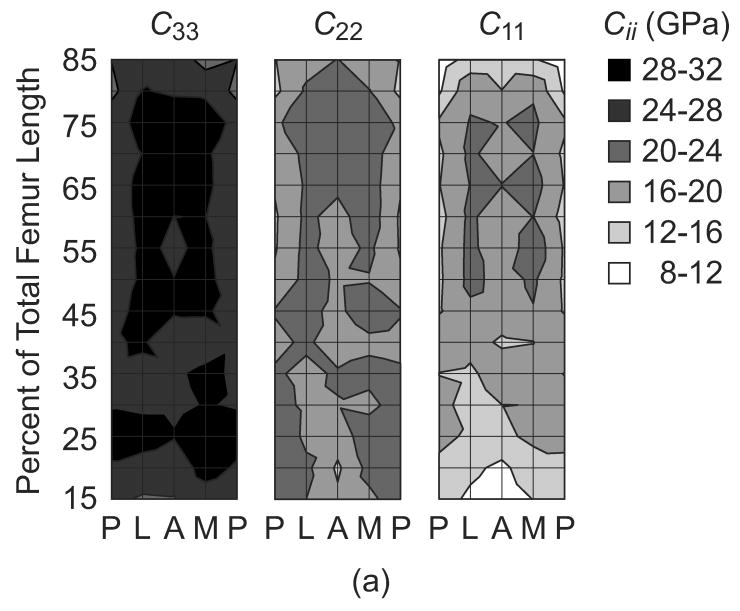
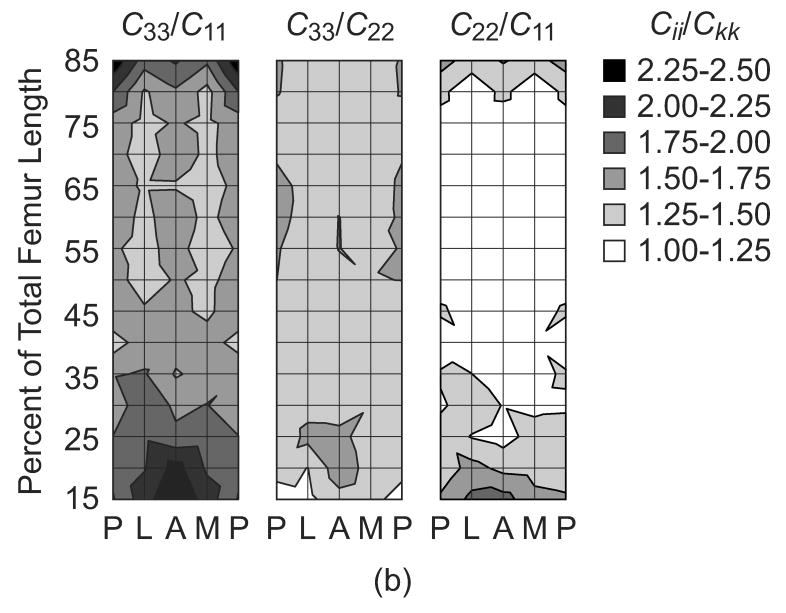
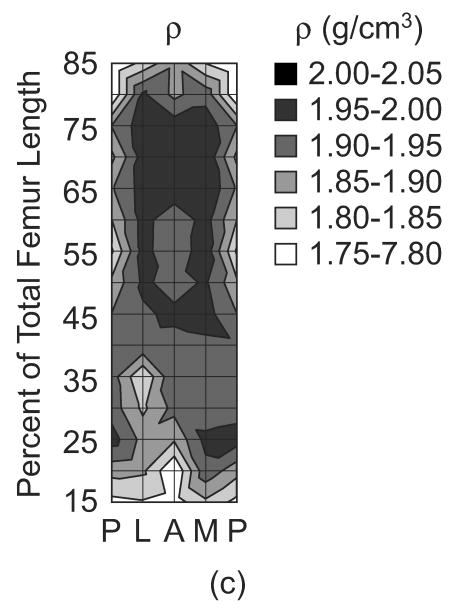
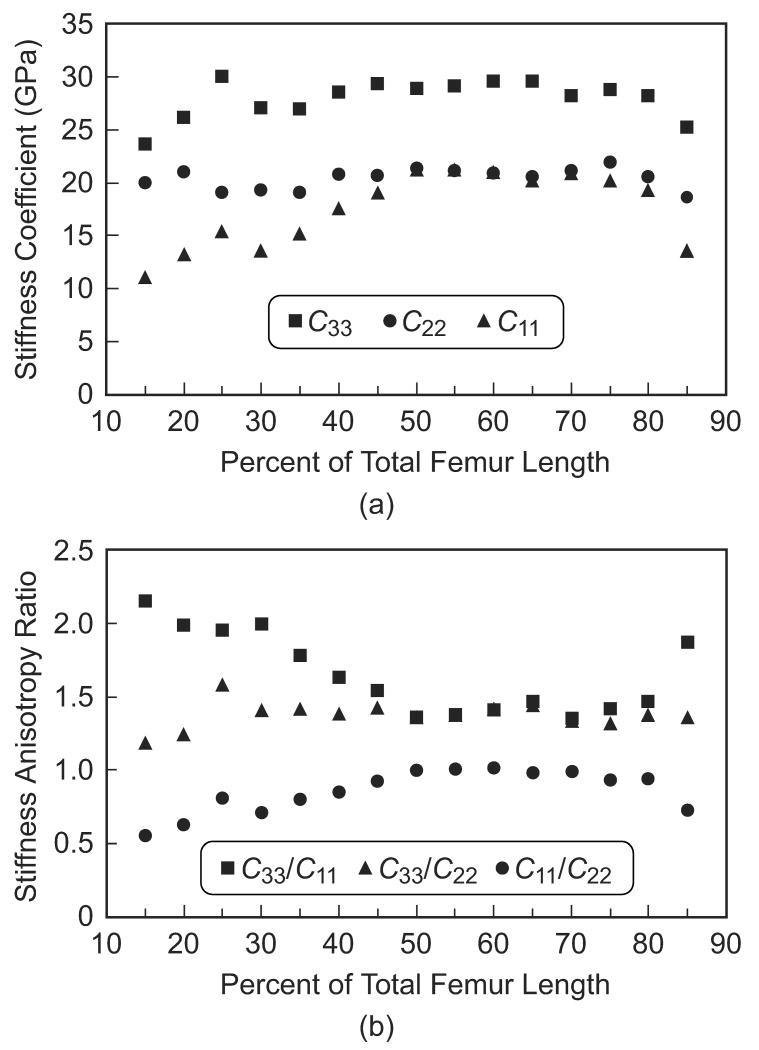
The magnitude of the elastic constants in the three mutually orthogonal specimen axes, (C33, C22 and C11), anisotropy ratios (C33/C11, C33/C22, and C11/C22) and apparent tissue density (ρ) were each mapped on a surface in terms of anatomic location along the length and around the periphery of the femoral diaphysis (Fig. 2). The magnitude of each elastic constant generally reached maxima from approximately 50-75% of the total femur length in the lateral and medial quadrants, and decreased toward the epiphyses and the posterior quadrant. These trends were consistent and significantly correlated with the apparent tissue density, as expected (Fig. 2, Table 2). The elastic anisotropy ratio in the longitudinal and radial anatomic axes (C33/C11) reached minima from approximately 50-75% of the total femur length in the lateral and medial quadrants, and increased toward the epiphyses, as well as the posterior and anterior quadrants (Fig. 2). Note that these trends were similar but inversely related to those observed for the radial stiffness coefficient (C11). In contrast, the elastic anisotropy ratio in the longitudinal and circumferential anatomic axes (C33/C22) was generally lower in magnitude and more uniform with anatomic location. C33/C11 and C11/C22 were significantly correlated with the apparent tissue density, but C33/C22 was not (Table 2). Finally, since it is difficult to appreciate on the contour maps, the observed trends along the length of the femoral diaphysis were smooth and consistent for each anatomic quadrant (e.g., lateral, Fig. 3).
Figure 2.
The (a) magnitude of the elastic constants in the three mutually orthogonal specimen axes, (C33, C22 and C11), (b) anisotropy ratios (C33/C11, C33/C22 and C22/C11) and (c) apparent tissue density (ρ) mapped by anatomic location along the length and around the periphery of the femoral diaphysis. Each surface represents an unrolled cylindrical surface showing the anterior (A), medial (M), posterior (P) and lateral (L) anatomic quadrants on the x-axis. Note that contours were plotted using linear interpolation for equal values between nodes on the surface. Also, C22/C11 was plotted in this figure instead of C11/C22 in order to maintain a consistent scale in the contours for each anisotropy ratio.
Table 2.
Linear least squares linear regression of the elastic constants, C33, C22 and C11 (GPa), and anisotropy ratios, C33/C11 and C33/C22, in the three mutually orthogonal specimen axes with the apparent tissue density (ρg/cm3). Note that correlations for shear stiffness coefficients, C44, C55 and C66, were not statistically significant.
| Parameter | Intercept | Slope | p | R2 |
|---|---|---|---|---|
| C11 | -56.5 | 38.5 | <0.0001 | 0.78 |
| C22 | -18.1 | 19.9 | <0.0001 | 0.53 |
| C33 | -15.5 | 22.5 | <0.0001 | 0.67 |
| C33/C11 | 7.30 | -2.95 | <0.0001 | 0.61 |
| C33/C22 | 2.04 | -0.34 | 0.06 | 0.06 |
| C11/C22 | -1.31 | 1.13 | <0.0001 | 0.42 |
Figure 3.
(a) Stiffness coefficients and (b) anisotropy ratios in the three specimen axes measured along the length of the femoral diaphysis for the lateral anatomic quadrant, representing the similar trends observed in each quadrant.
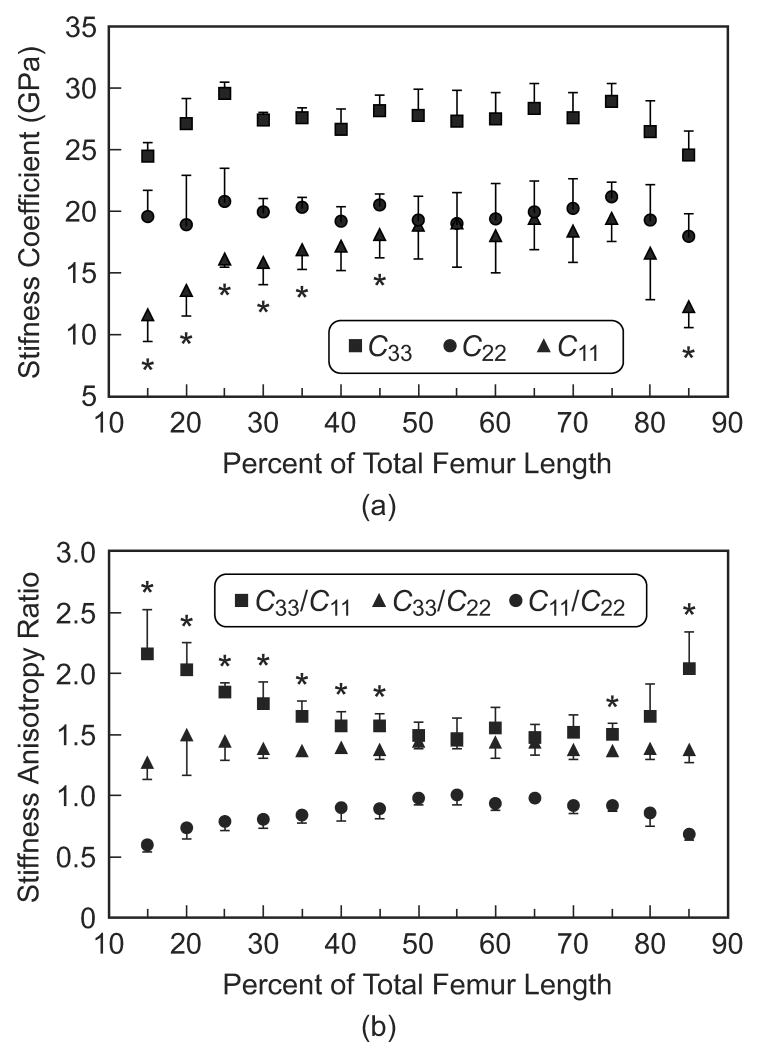
Specimens were grouped by location along the length of the femoral diaphysis in order to statistically examine anatomic variation in the magnitude and anisotropy of elastic constants (Table 1, Fig. 4a). The longitudinal stiffness coefficient (C33) was significantly greater than both transverse stiffness coefficients (C22 and C11) at each location along the entire length (p < 0.01, t-test). The circumferential stiffness coefficient (C22) was significantly greater than the radial stiffness coefficient (C11) at locations less than 50% or greater than 80% of the total femur length (p < 0.05, t-test), but not significantly different over 50-80% of the total femur length. Pair-wise statistical comparisons for a given stiffness coefficient at locations along the length of the femoral diaphysis were too numerous to show; however, the trends were clearly apparent and verified statistically. The radial stiffness coefficient (C11) decreased toward the epiphyses, gradually distally and sharply at extreme proximal locations. The circumferential stiffness coefficient (C22) was relatively constant along the entire length of the diaphysis. Finally, the longitudinal stiffness coefficient (C33) decreased toward the epiphyses only at the extreme distal and proximal locations.
Figure 4.
Mean (a) stiffness coefficients and (b) anisotropy ratios in the three specimen axes measured along the length of the femoral diaphysis. Error bars span one standard deviation. Asterisks denote statistically significant differences between (a) C11 and C22, and (b) C33/C11 and C33/C22 at locations along the length of the femoral diaphysis (p < 0.05, t-test). Statistically significant differences existed between (a) C33, and (b) C11/C22, and other groups at all locations along the length of the femoral diaphysis (p < 0.01, t-test).
Anatomic variation in the elastic anisotropy was even more apparent when examining the anisotropy ratios grouped by location along the length of the femoral diaphysis (Fig. 4b). The elastic anisotropy ratio in the longitudinal and radial anatomic axes (C33/C11) was significantly greater than in the longitudinal and circumferential anatomic axes (C33/C22) at locations less than 50% or greater than 70% of the total femur length (p < 0.05, t-test), but not significantly different over 50-70% of the total femur length. Note that the elastic anisotropy ratio in the radial and circumferential anatomic axes (C11/C22) is redundant with respect to symmetry, but is shown for reference. Again, pair-wise statistical comparisons for a given anisotropy ratio at locations along the length of the femoral diaphysis were too numerous to show; however, the trends were clearly apparent and verified statistically. The elastic anisotropy ratio in the longitudinal and radial anatomic axes (C33/C11) increased toward the epiphyses, gradually distally and sharply at extreme proximal locations. The elastic anisotropy ratio in the longitudinal and circumferential anatomic axes (C33/C22) was relatively constant along the entire length of the diaphysis. Finally, the elastic anisotropy ratio in the radial and circumferential anatomic axes (C11/C22) gradually decreased toward the epiphyses both distally and proximally.
Specimens were also grouped by anatomic quadrant in order to examine anatomic variation in the magnitude and anisotropy of stiffness coefficients around the periphery of the femoral diaphysis. In order to make meaningful statistical comparisons given the above observations, specimens were first divided into two groups: those generally exhibiting (15-45 and 75-85% of the total femur length) and not exhibiting (50-70% of the total femur length) statistically significant anisotropy in the transverse plane (1-2). Specimens located at 15-45 and 75-85% of the total femur length exhibited no statistically significant differences between anatomic quadrants for all measured elastic constants and anisotropy ratios (p > 0.40, ANOVA). Specimens located at 50-70% of the total femur length exhibited lower elastic constants (C33, C22 and C11) in the posterior quadrant and less anisotropy (C33/C11 and C33/C22) in the medial and lateral quadrants (p < 0.05, t-test).
4. Discussion
The elastic anisotropy of cortical bone tissue in a human femur was shown to be highly dependant on anatomic location (Fig. 2). Elastic constants in the transverse plane (C11 and C22) or anisotropy ratios (C33/C11 and C33/C22) were not significantly different near the mid- and proximal mid-diaphysis (approximately 50-70% of the total femur length), but were significantly divergent toward the epiphyses (approximately <50% and >70% of the total femur length). Therefore, the elastic symmetry of human cortical bone tissue in the distal (<50% of the total femur length) and extreme proximal (>70% of the total femur length) portions of the femoral diaphysis was, at most, orthotropic. In contrast, the elastic symmetry of tissue near the mid- and proximal mid-diaphysis (50-70% of the total femur length) was reasonably approximated as transversely isotropic.
This study was the first to explicitly report anatomic variation in the elastic anisotropy of human femoral cortical bone tissue, though the necessary data may have been available in previous studies. Moreover, the results of this study may help explain discrepancies in the elastic symmetry reported in previous studies. Cortical thickness is typically greatest in the mid- and proximal mid-diaphysis, making this region most convenient and practical for preparing specimens. Those previous studies that reported or assumed a transverse isotropy prepared specimens from a limited number of locations within this region of the human femoral diaphysis (Hunt, et al., 1998; Katz, et al., 1984; Lappi, et al., 1979; Reilly and Burstein, 1975; Yoon and Katz, 1976a, 1976b). In contrast, those studies that included specimens taken from locations over a larger range of the diaphysis (typically 30-70% of the total length) reported orthotropic symmetry for cortical bone tissue in the human femur (Ashman, et al., 1984), human tibia (Hoffmeister, et al., 2000; Rho, 1996) and bovine femur (Van Buskirk, et al., 1981; Yamato, et al., 2006). Note that this study also extended the region of investigation to 15-85% of the total femur length.
The overall mean value of each elastic constant measured in this study was not statistically different than those previously reported for human femora using similar methods (Ashman, et al., 1984), except for C11 (p < 0.005, t-test). The difference in C11 was due to a significant decrease at extreme distal and proximal locations (Fig. 4a), which were not included in the study by Ashman et al. (1984). The magnitude of anisotropy ratios (C33/C11 and C33/C22) were similar on average but exhibited a greater range compared with previous studies for human femoral cortical bone (Dong and Guo, 2004; Hasegawa, et al., 1994; Takano, et al., 1996). However, these studies reported only C33/C22 with an explicit or implied assumption of axisymmetry, and sampled tissue from a relatively restricted number of anatomic sites. Therefore, the results of this study suggest that a pair of elastic constants or a single anisotropy ratio, especially the relatively insensitive C33/C22, is inadequate to characterize the elastic symmetry of cortical bone tissue, particularly if considering a whole bone or various anatomic sites.
A limitation of this study was that only elastic constants for the main diagonal of the reduced fourth-order stiffness tensor, Cii (i = 1-6), were measured. This prevented conversion of the elastic stiffness coefficients (or compliances) into engineering coefficients (Young's moduli, shear moduli and Poisson's ratios). However, this restriction enabled specimens to be prepared from the widest possible range of anatomic locations and was sufficient to establish the elastic symmetry. Anatomic variation in the elastic anisotropy was verified statistically using only the longitudinal elastic constants. Note that in all cases shear elastic constants exhibited similar trends in magnitude and anisotropy as those reported for the longitudinal elastic constants. For example, when C11 ≈ C22 < C33, C44 ≈ C55 > C66, as would be expected. However, the statistical power for comparisons of shear coefficients was less than for longitudinal coefficients, despite similar variability, due to relatively smaller differences in magnitude, which was to be expected. Another limitation of this study was the use of a single donor. This limitation was a necessary trade-off in order to sample a relatively large number of anatomic locations. Future studies might consider specific anatomic locations from a greater number of donors.
The results of this study beg the question: which hierarchical structural feature(s) in the tissue were responsible for the measured anatomic variation in elastic symmetry along the length of the femoral diaphysis? While this question was beyond the objective of the present study, several possible explanations are worthy of discussion and investigation in future studies. Whatever feature(s) are responsible, it is clear that they had a significant effect in the radial direction, but little or no effect in the circumferential direction (Figs. 2 and 4). At the microstructural level, Katz et al. (1984) reported that Haversian tissue could reasonably be approximated as transversely isotropic, but that laminar (or plexiform) tissue was orthotropic. A typical cross-section of a healthy adult human femur, reveals mostly secondary Haversian tissue, but also primary circumferential lamellar tissue around the periosteal surface (Martin, et al., 1998). Thus, distal and extreme proximal locations in the femur may have exhibited orthotropy and an increased degree of anisotropy (for C33/C11 but not C33/C22) compared to locations near the mid- and proximal mid-diaphysis, due to decreased cortical thickness with a corresponding increased proportion of circumferential lamellar to Haversian tissue. However, the histology of specimens sampled from all four anatomic quadrants at 20, 50 and 85% of the total femur length revealed no significant differences (p = 0.36, ANOVA) in the fraction of Haversian tissue and little or no presence of circumferential lamellar tissue (Fig. 5). On the other hand, the apparent tissue density, which is inversely related to the porosity, was positively correlated with C33, C22 and C11, as well as negatively correlated with C33/C11 (Table 2), similar to the results of Dong and Guo (2004). The correlation was relatively strong for C11 (or C33/C11) and relatively weak for C22 (or C33/C22), which suggests that variations in porosity in the radial direction accounted for significant variation in radial stiffness and thus anisotropy. Variations in porosity (Fig. 5) might include Haversian canals and resorption cavities with an elongated rather than circular cross-section, and/or the number or size of Volkmann's canals and canaliculi, which tend to be oriented radially relative to the whole bone and lamellae, respectively (Martin, et al., 1998). Finally, at the nano-scale, the anisotropy of cortical bone tissue was previously shown to be due to the mineral phase, not collagen fibrils (Hasegawa, et al., 1994; Takano, et al., 1996; Turner, et al., 1995). Therefore, variations in the degree of crystallographic alignment of apatite crystals might account for variation not explained by porosity (Deuerling, et al., 2008; Yue and Roeder, 2006; Yue, et al., 2006). Further investigation of the above mechanisms is needed.
Figure 5.

Optical micrographs of the specimen surface normal to the longitudinal anatomic direction showing representative regions of tissue from the medial quadrant at (a) 20% and (b) 50% of the total femur length. Note that each image was taken nearest the periosteal specimen surface, which is located to the right.
Finally, the data reported in this study may be useful for numerical models of the human femur to 1) incorporate anisotropic and inhomogeneous tissue properties, or 2) validate models for adaptive bone remodeling. First, recent efforts to include tissue anisotropy in numerical models assumed that elastic constant ratios (herein described as anisotropy ratios) were constant throughout the femur and acknowledged that this assumption could be problematic when considering cortical versus trabecular bone (Taylor, et al., 2003). The results of this study show that this assumption is not valid even within cortical bone (Figs. 2 and 4), but that anisotropy ratios may be able to be correlated with apparent tissue density (Table 2). Second, general variation in the apparent tissue density and magnitude of elastic constants along the length of the femoral diaphysis was somewhat similar to trends in maximum principal strains calculated by numerical models, with maxima near the mid- or proximal mid-diaphysis and decreasing magnitude toward the ephipyses (Duda, et al., 1998; Speirs, et al., 2007). Relationships around the periphery of the femoral diaphysis and for the anisotropy ratios were not clear. However, the increase in C11 and decrease in C33/C11 in the mid-proximal lateral and medial quadrants may reflect muscle attachment sites (Viceconti, et al., 2003). Anatomic quadrants experiencing tensile strain due to bending in vivo were reported to correlate with increased elastic anisotropy for canine radii (Takano, et al., 1999) and cervine calcanei (Skedros, et al., 2006). In this study, elastic anisotropy increased toward the epiphyses and in the anterior and posterior quadrants of the femur, which corresponds to decreased tensile strains calculated by numerical models (Duda, et al., 1998; Speirs, et al., 2007). The difference may lie in the fact that, in distinction from the cited animal models, overall compression dominates the more complex loading of the human femur (Duda, et al., 1997). Nonetheless, the results of this study support the concept that mechanobiology (van der Meulen and Huiskes, 2002) governs at least the distribution of apparent tissue density (or porosity), which in turn governs the magnitude of elastic constants and, though perhaps less directly, the elastic anisotropy.
Acknowledgments
This research was partially supported by the Indiana 21st Century Research and Technology Fund, National Institutes of Health (AR049598) and Department of Defense (F33615-98-D-3210). The authors thank the Indiana University Medical School Anatomical Donations Program for providing the femur used in this study, and Dr. Charles H. Turner at the Indiana University Medical Center for use of DEXA.
Funding Sources: Indiana 21st Century Research and Technology Fund, National Institutes of Health (AR049598), DARPA AFRL F33615-98-D-3210
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Amtmann E. The distribution of breaking strength in the human femur shaft. J Biomechanics. 1968;1:271–277. doi: 10.1016/0021-9290(68)90022-5. [DOI] [PubMed] [Google Scholar]
- Ashman RB, Cowin SC, Van Buskirk WC, Rice JC. A continuous wave technique for the measurement of the elastic properties of cortical bone. J Biomechanics. 1984;17:349–361. doi: 10.1016/0021-9290(84)90029-0. [DOI] [PubMed] [Google Scholar]
- ASTM Standard C373-88. Standard Test Method for Water Absorption, Bulk Density, Apparent Density and the Apparent Specific Gravity of Fired Whiteware Products. American Society for Testing Materials; West Conshohocken, PA: 1999. [Google Scholar]
- Bagge M. A model of bone adaptation as an optimization process. J Biomechanics. 2000;33:1349–1357. doi: 10.1016/s0021-9290(00)00124-x. [DOI] [PubMed] [Google Scholar]
- Bensamoun S, Ho Ba Tho MC, Luu S, Gherbezza JM, de Belleval JF. Spatial distribution of acoustic and elastic properties of femoral human cortical bone. J Biomechanics. 2004;37:503–510. doi: 10.1016/j.jbiomech.2003.09.013. [DOI] [PubMed] [Google Scholar]
- Bonfield W, Grynpas MD. Anisotropy in the Young's modulus of bone. Nature. 1977;270:453–454. doi: 10.1038/270453a0. [DOI] [PubMed] [Google Scholar]
- Cowin SC, Mehrabadi MM. Identification of the elastic symmetry of bone and other materials. J Biomechanics. 1989;22:503–512. doi: 10.1016/0021-9290(89)90001-8. [DOI] [PubMed] [Google Scholar]
- Dempster WT, Liddicoat RT. Compact bone as a non-isotropic material. Am J Anat. 1952;91:331–362. doi: 10.1002/aja.1000910302. [DOI] [PubMed] [Google Scholar]
- Deuerling JM, Yue W, Espinoza Orías AA, Roeder RK. Specimen-specific multiscale model for the anisotropic elastic constants of human cortical bone. J Biomechanics. 2008 doi: 10.1016/j.jbiomech.2009.06.002. submitted. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Doblaré M, Garcia JM. Application of an anisotropic bone-remodelling model based on a damage-repair theory to the analysis of the proximal femur before and after total hip replacement. J Biomechanics. 2001;34:1157–1170. doi: 10.1016/s0021-9290(01)00069-0. [DOI] [PubMed] [Google Scholar]
- Dong XN, Guo XE. The dependence of transversely isotropic elasticity of human femoral cortical bone on porosity. J Biomechanics. 2004;37:1281–1287. doi: 10.1016/j.jbiomech.2003.12.011. [DOI] [PubMed] [Google Scholar]
- Duda GN, Schneider E, Chao EYS. Internal forces and moments in the femur during walking. J Biomechanics. 1997;30:933–941. doi: 10.1016/s0021-9290(97)00057-2. [DOI] [PubMed] [Google Scholar]
- Duda GN, Heller M, Albinger J, Schulz O, Schneider E, Claes L. Influence of muscle forces on femoral strain distribution. J Biomechanics. 1998;31:841–846. doi: 10.1016/s0021-9290(98)00080-3. [DOI] [PubMed] [Google Scholar]
- Evans FG, Lebow M. Regional differences in some physical properties of the human femur. J Appl Physiol. 1951;3:563–572. doi: 10.1152/jappl.1951.3.9.563. [DOI] [PubMed] [Google Scholar]
- Fan Z, Swadener JG, Rho JY, Roy ME, Pharr GM. Anisotropic properties of human tibial cortical bone as measured by nanoindentation. J Orthop Res. 2002;20:806–810. doi: 10.1016/S0736-0266(01)00186-3. [DOI] [PubMed] [Google Scholar]
- Hasegawa K, Turner CH, Burr DB. Contribution of collagen and mineral to the elastic anisotropy of bone. Calcif Tissue Int. 1994;55:381–386. doi: 10.1007/BF00299319. [DOI] [PubMed] [Google Scholar]
- Hernandez CJ, Beaupré GS, Keller TS, Carter DR. The influence of bone volume fraction and ash fraction on bone strength and modulus. Bone. 2001;29:74–78. doi: 10.1016/s8756-3282(01)00467-7. [DOI] [PubMed] [Google Scholar]
- Hoffmeister BK, Smith SR, Handley SM, Rho JY. Anisotropy of Young's modulus of human tibial cortical bone. Med Biol Eng Comput. 2000;38:333–338. doi: 10.1007/BF02347055. [DOI] [PubMed] [Google Scholar]
- Hofmann T, Heyroth F, Meinhard H, Franzel W, Raum K. Assessment of composition and anisotropic elastic properties of secondary osteon lamellae. J Biomechanics. 2006;39:2282–2294. doi: 10.1016/j.jbiomech.2005.07.009. [DOI] [PubMed] [Google Scholar]
- Hunt KD, O'Loughlin VD, Fitting DW, Adler L. Ultrasonic determination of the elastic modulus of human cortical bone. Med Biol Eng Comput. 1998;36:51–56. doi: 10.1007/BF02522857. [DOI] [PubMed] [Google Scholar]
- Jacobs CR, Simo JC, Beaupré GS, Carter DR. Adaptive bone remodeling incorporating simultaneous density and anisotropy considerations. J Biomechanics. 1997;30:603–613. doi: 10.1016/s0021-9290(96)00189-3. [DOI] [PubMed] [Google Scholar]
- Katz JL, Yoon HS, Lipson S, Maharidge R, Meunier A, Christel P. The Effects of remodeling on the elastic properties of bone. Calcif Tissue Int. 1984;36:S31–S36. doi: 10.1007/BF02406131. [DOI] [PubMed] [Google Scholar]
- Katz JL, Meunier A. A generalized method for characterizing elastic anisotropy in solid living tissues. J Mater Sci: Mater Med. 1990;1:1–8. [Google Scholar]
- Keller TS, Mao Z, Spengler DM. Young's modulus, bending strength, and tissue physical properties of human compact bone. J Orthop Res. 1990;8:592–603. doi: 10.1002/jor.1100080416. [DOI] [PubMed] [Google Scholar]
- Lang SB. Ultrasonic method for measuring elastic coefficients of bone and results on fresh and dried bones. IEEE Trans Biomed Eng. 1970;17:101–105. doi: 10.1109/tbme.1970.4502706. [DOI] [PubMed] [Google Scholar]
- Lappi VG, King MS, LeMay I. Determination of elastic constants for human femurs. J Biomech Eng. 1979;101:193–197. [Google Scholar]
- Martin RB, Burr DB, Sharkey NA. Skeletal Tissue Mechanics. Springer Verlag; New York: 1998. pp. 32–48.pp. 143–172. [Google Scholar]
- Orr TE, Beaupré GS, Carter DR, Schurman DJ. Computer predictions of bone remodeling around porous-coated implants. J Arthroplasty. 1990;5:191–200. doi: 10.1016/s0883-5403(08)80074-5. [DOI] [PubMed] [Google Scholar]
- Pope MH, Outwater JO. Mechanical properties of bone as a function of position and orientation. J Biomechanics. 1974;7:61–66. doi: 10.1016/0021-9290(74)90070-0. [DOI] [PubMed] [Google Scholar]
- Reilly DT, Burstein AH. The mechanical properties of cortical bone. J Bone Joint Surg Am. 1974;56A:1001–1022. [PubMed] [Google Scholar]
- Reilly DT, Burstein AH. The elastic and ultimate properties of compact bone tissue. J Biomechanics. 1975;8:393–405. doi: 10.1016/0021-9290(75)90075-5. [DOI] [PubMed] [Google Scholar]
- Rho JY, Ashman RB, Turner CH. Young's modulus of trabecular and cortical bone material: Ultrasonic and microtensile measurements. J Biomechanics. 1993;26:111–119. doi: 10.1016/0021-9290(93)90042-d. [DOI] [PubMed] [Google Scholar]
- Rho JY, Hobatho MC, Ashman RB. Relations of mechanical properties to density and CT numbers in human bone. Med Eng Phys. 1995;17:347–355. doi: 10.1016/1350-4533(95)97314-f. [DOI] [PubMed] [Google Scholar]
- Rho JY. An ultrasonic method for measuring the elastic properties of human tibial cortical and cancellous bone. Ultrasonics. 1996;34:777–783. doi: 10.1016/s0041-624x(96)00078-9. [DOI] [PubMed] [Google Scholar]
- Rho JY, Roy ME, Tsui TY, Pharr GM. Elastic properties of microstructural components of human bone tissue as measured by nanoindentation. J Biomed Mater Res. 1999a;45:48–54. doi: 10.1002/(sici)1097-4636(199904)45:1<48::aid-jbm7>3.0.co;2-5. [DOI] [PubMed] [Google Scholar]
- Rho JY, Zioupos P, Currey JD, Pharr GM. Variations in the individual thick lamellar properties within osteons by nanoindentation. Bone. 1999b;25:295–300. doi: 10.1016/s8756-3282(99)00163-5. [DOI] [PubMed] [Google Scholar]
- Rho JY, Zioupos P, Currey JD, Pharr GM. Microstructural elasticity and regional heterogeneity in human femoral bone of various ages examined by nano-indentation. J Biomechanics. 2002;35:189–198. doi: 10.1016/s0021-9290(01)00199-3. [DOI] [PubMed] [Google Scholar]
- Schaffler MB, Burr DB. Stiffness of compact bone: Effects of porosity and density. J Biomechanics. 1988;21:13–16. doi: 10.1016/0021-9290(88)90186-8. [DOI] [PubMed] [Google Scholar]
- Skedros JG, Sorenson SM, Takano Y, Turner CH. Dissociation of mineral and collagen orientations may differentially adapt compact bone for regional loading environments: Results from acoustic velocity measurements in deer calcanei. Bone. 2006;39:143–151. doi: 10.1016/j.bone.2005.12.007. [DOI] [PubMed] [Google Scholar]
- Speirs AD, Heller MO, Duda GN, Taylor WR. Physiologically based boundary conditions in finite element modeling. J Biomechanics. 2007;40:2318–2323. doi: 10.1016/j.jbiomech.2006.10.038. [DOI] [PubMed] [Google Scholar]
- Swadener JG, Rho JY, Pharr GM. Effects of anisotropy on elastic moduli measured by nanoindentation in human tibial cortical bone. J Biomed Mater Res. 2001;57:108–112. doi: 10.1002/1097-4636(200110)57:1<108::aid-jbm1148>3.0.co;2-6. [DOI] [PubMed] [Google Scholar]
- Takano Y, Turner CH, Burr DB. Mineral anisotropy in mineralized tissues is similar among species and mineral growth occurs independently of collagen orientation in rats: results from acoustic velocity measurements. J Bone Miner Res. 1996;11:1292–1301. doi: 10.1002/jbmr.5650110914. [DOI] [PubMed] [Google Scholar]
- Takano Y, Turner CH, Owan I, Martin RB, Lau ST, Forwood MR, Burr DB. Elastic anisotropy and collagen orientation of osteonal bone are dependent on the mechanical strain distribution. J Orthop Res. 1999;17:59–66. doi: 10.1002/jor.1100170110. [DOI] [PubMed] [Google Scholar]
- Taylor WR, Roland E, Ploeg H, Hertig D, Klabunde R, Warner MD, Hobatho MC, Rakotomana L, Clift SE. Determination of orthotropic bone elastic constants using FEA and modal analysis. J Biomechanics. 2002;35:767–773. doi: 10.1016/s0021-9290(02)00022-2. [DOI] [PubMed] [Google Scholar]
- Turner CH, Chandran A, Pidaparti RMV. The anisotropy of osteonal bone and its ultrastructural implications. Bone. 1995;17:85–89. doi: 10.1016/8756-3282(95)00148-7. [DOI] [PubMed] [Google Scholar]
- Van Buskirk WC, Cowin SC, Ward RN. Ultrasonic measurement of orthotropic elastic constants of bovine femoral bone. J Biomech Eng. 1981;103:67–72. doi: 10.1115/1.3138262. [DOI] [PubMed] [Google Scholar]
- Van der Meulen MCH, Huiskes R. Why mechanobiology? A survey article. J Biomechanics. 2002;35:401–414. doi: 10.1016/s0021-9290(01)00184-1. [DOI] [PubMed] [Google Scholar]
- Viceconti M, Ansaloni M, Baleani M, Toni A. The muscle standardized femur: A step forward in the replication of numerical studies in biomechanics. Proc Inst Mech Eng, Part H, J Eng Med. 2003;217:105–110. doi: 10.1243/09544110360579312. [DOI] [PubMed] [Google Scholar]
- Yamato Y, Matsukawa M, Otani T, Yamazaki K, Nagano A. Distribution of longitudinal wave velocities in bovine cortical bone in vitro. Ultrasonics. 2006;44:e233–e237. doi: 10.1016/j.ultras.2006.06.055. [DOI] [PubMed] [Google Scholar]
- Yoon HS, Katz JL. Ultrasonic wave propagation in human cortical bone—I. Theoretical considerations for hexagonal symmetry. J Biomechanics. 1976a;9:407–412. doi: 10.1016/0021-9290(76)90118-4. [DOI] [PubMed] [Google Scholar]
- Yoon HS, Katz JL. Ultrasonic wave propagation in human cortical bone—II. Measurements of elastic properties and microhardness. J Biomechanics. 1976b;9:459–464. doi: 10.1016/0021-9290(76)90089-0. [DOI] [PubMed] [Google Scholar]
- Yue W, Roeder RK. Micromechanical model for hydroxyapatite whisker reinforced polymer biocomposites. J Mater Res. 2006;21:2136–2145. [Google Scholar]
- Yue W, Espinoza Orías AA, Renaud JE, Roeder RK. Correlation of anatomic variation in the elastic anisotropy of human cortical bone with the bone mineral orientation distribution. Proc. 2006 ASME Summer Bioengineering Conference; Amelia Island, FL. 2006. 151775. [Google Scholar]
- Zysset PK, Guo XE, Hoffler CE, Moore KE, Goldstein SA. Elastic modulus and hardness of cortical and trabecular bone lamellae measured by nanoindentation in the human femur. J Biomechanics. 1999;32:1005–1012. doi: 10.1016/s0021-9290(99)00111-6. [DOI] [PubMed] [Google Scholar]