Abstract
Spectral counting is a strategy to quantitate relative protein concentrations in pre-digested protein mixtures analyzed by liquid chromatography online with tandem mass spectrometry. In this work we used combinations of normalization and statistical (feature selection) methods on spectral counting data to verify whether we could pinpoint which and how many proteins were differentially expressed when comparing complex protein mixtures. These combinations were evaluated on real, but controlled, experiments (protein markers were spiked into yeast lysates in different concentrations to simulate differences), which are therefore verifiable. The following normalization methods were applied: total signal, Z-normalization, hybrid normalization, and log preprocessing. The feature selection methods were: Golub's index, Student's t-test, a strategy based on the weighting used in a support vector machine model (SVM-F), and support vector machine recursive feature elimination. The results showed that Z-normalization combined with SVM-F correctly identified which and how many protein markers were added to the yeast lysates for all different concentrations. The software we used is available at http://pcarvalho.com/patternlab.
Keywords: MudPIT, feature selection, SVM, spectral counting, feature ranking
1. Introduction
A goal of proteomics is to distinguish between various states of a system to identify protein expression differences (Jessani et al. 2005). The first strategies used two-dimensional gel electrophoresis (2-DGE) for comparing the migration of proteins according to their molecular weight and isoelectric point. In 2002, alternative approaches emerged to compare biological samples from different states. Mass spectrometry (MS) analysis was performed on enriched proteins that were fractionated on the surface of a mass spectrometry plate. By correlating the peptide mass to charge (m/z) values obtained from SELDI-TOF MS (Surface Enhanced Laser Desorption Ionization – Time of Flight Mass Spectrometry) with peptide abundance, Petricoin et al. used machine learning over a SELDI-TOF dataset acquired from SELDI-TOF MS of serum from control subjects and ovarian cancer patients. As a second step, unknown spectra were classified as belonging to the patient or control subject class (Petricoin et al. 2002;Unlu et al. 1997). A variety of feature selection / classification methods have since then been described as being used for this purpose, including genetic algorithms (Shan S C. and Kusiak A 2004), Fisher criterion scores (Kolakowska and Malina 2005), beam search (Badr and Oommen 2006;Carlson et al. 2006), branch-and-bound (Polisetty et al. 2006) Pearson correlation coefficients (Mattie et al. 2006), and Support Vector Machines recursive feature elimination (Carvalho et al. 2007).
The need for high sensitivity when analyzing samples of greater complexity led to the use of liquid chromatography coupled with electrospray mass spectrometry (LC-MS) to profile digested protein mixtures. Elimination of the data-dependent tandem mass spectrometry process enhances the detection of ions, since the instrument spends less time acquiring tandem mass spectra and the lack of alternating MS and MS/MS scans improves the ability to compare analyses. Becker et al. used ion chromatograms from an LC-MS system to identify differences between samples including complex mixtures such as digested serum with reasonable variation in the analyses (Wang et al. 2003). Wiener et al. used replicate LC-MS analyses to develop statistically significant differential displays of peptides (Wiener et al. 2004). These approaches divide the comparison and identification processes into first identifying chromatographic and ion differences and then identifying the peptides responsible for the differences. To reduce comparison errors and ambiguities between samples, chromatographic peak alignment is increasingly used (Bylund et al. 2002;Wong et al. 2005;Katajamaa et al. 2006;Katajamaa and Oresic 2005;Zhang et al. 2005;Maynard et al. 2004;Wiener et al. 2004).
By using the numbers of tandem mass spectra obtained for each protein or “spectral counting” as a surrogate for protein abundance in a mixture, Liu et al demonstrated that “spectral counts” correlated linearly with protein abundance in a mixture within over two orders of magnitude (Liu et al. 2004). Because of the more complex nature of the LC/LC method and the alternating acquisition of mass spectra and tandem mass spectra, chromatographic alignment is far more complicated than using LC-MS and therefore data are most often analyzed from the perspective of tandem mass spectra and identified proteins. Two issues with the use of LC/LC/MS/MS analyses to compare samples are the normalization of spectral counting data and the identification of differences between samples.
In this work we analyze how well selected univariate and multivariate statistical / pattern recognition approaches can pinpoint protein markers, added at different concentrations into complex protein mixtures (yeast lysates), using spectral counting data. Different combinations of normalization / feature selection methods were applied and the combination that performed best on our dataset was identified by means of two approaches. The first ranked each protein by a statistical score according to which spiked markers were expected to rank highest. The second method relied on the support vector machine (SVM) leave-one-out (LOO) cross-validation and the Vapnik-Chervonenkis (VC) confidence; briefly, these are quantifiers that allow the estimation of how well a classifier is to categorize unseen samples (Vapnik VN 1995).
2. Experimental
2.1 MudPIT spectral count acquisition from yeast lysate with spiked proteins
Four aliquots of 400 μg of a soluble yeast total cell lysate were mixed with Bio-Rad SDS-PAGE low range weight standards containing phosphorylase b, serum albumin, ovalbumin, lysozyme, carbonic anhydrase, and trypsin inhibitor at relative levels of 25%, 2.5%, 1.25%, and 0.25% of the final mixtures' total weight, respectively. Each sample was sequentially digested, under the same conditions, with Endoproteinase Lys-C and trypsin (Washburn et al. 2001). Approximately 70 μg of the digested peptide mixture were loaded onto a biphasic (strong cation exchange/reversed phase) capillary column and washed with a buffer containing 5% acetonitrile, 0.1% formic acid diluted in DDI water. The two-dimensional liquid chromatography (LC/LC) separation and tandem mass spectrometry (MS/MS) conditions were as described by Washburn et al. (Washburn et al. 2001). The flow rate at the tip of the biphasic column was 300 nL/min when the mobile phase composition was 95% H2O, 5% acetonitrile, and 0.1% formic acid. The ion trap mass spectrometer, Finnigan LCQ Deca (Thermo Electron, Woburn, MA), was set to the data-dependent acquisition mode with dynamic exclusion turned on. One MS survey scan was followed by four MS/MS scans. Each aliquot of the digested yeast cell lysate was analyzed 3 times. The data sets were searched using a modified version of the Pep_Prob algorithm (Sadygov and Yates, III 2003) against a database combining yeast and human protein sequences, and the results were post-processed by DTASelect (Tabb et al. 2002). The sequences of the spiked markers and some common protein contaminants (e.g., keratin) were added to the database.
2.2 Generation of the 3 testing conditions
All computations in this work were performed using PatternLab for proteomics, available at http://pcarvalho.com/patternlab for academic use; its source code is also available upon request.
Firstly, PatternLab generated an index file listing all the proteins (features) identified in all the MudPIT assays. This index assigns a unique Protein Index Number (PIN) to each feature. Secondly, all experimental data from the DTASelect files were combined into a single sparse matrix; this format is more suitable for feature selection. Each row of this matrix is relative to one MudPIT assay and gives the spectral count identified for each PIN in that assay. So, for example, the row “1:3 2:5 3:6” specifies an assay having spectral count values of 3, 5, and 6 for PINs 1, 2, and 3 respectively; all other PINs are understood to have value 0. The sparse matrix generated for this study had 15 rows, obtained from 15 MudPIT runs with different percentages of protein markers spiked in the yeast lysate (4 runs with spiked markers representing 25% of the total protein content, 4 with 2.5%, 3 with 1.25%, and 4 with 0.25%). We note that each row had approximately 1200 PINs and a total of 2181 PINs were detected among all 15 rows, showing that many proteins were not identified in all runs.
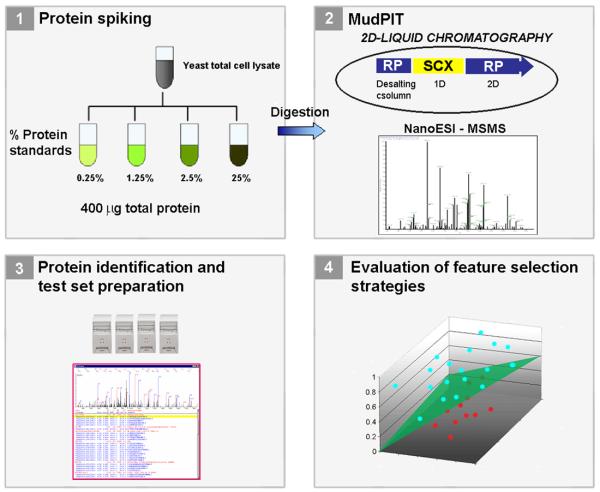
Three testing datasets were then generated using the matrix, each one being identical to all others except for a class label introduced before each row. In the first test set (TSet1), the rows originating from the 25% protein spiking were labeled as +1 (positive) and all the others −1 (negative). In the second test set (TSet2), the 25% and the 2.5% matrix rows were labeled as +1 and the rest as −1. In the third (TSet3), the rows resulting from the 0.25% spiking were labeled as −1, the others as +1. The aim of such class labeling was to create 3 testing conditions for us to later compare the positively and negatively labeled rows in each testing dataset and verify whether the spiked proteins having different concentrations could be pinpointed. Figure 1 summarizes our methodology.
Figure 1.
Protein markers were spiked at different concentrations in 15 yeast total cell lysate samples. Each lysate was analyzed by MudPIT (1.2) and protein identification carried out by Pep_Prob (1.3) and post-processed by DTASelect. Three different test sets were then generated. Combinations of normalization / feature selection methods were used to search for the spiked protein markers with different concentrations in each test set (1.4).
3. Calculation
3.1 Normalization methods evaluated in this work
For this study, we evaluated the following normalization strategies: total signal (TS), Z normalization (Z), a hybrid normalization obtained by TS followed by Z (TS→Z), and log preprocessing.
3.1.1 Normalization by total spectral counting (total signal or TS)
Let SCji be the spectral count associated with PIN i in row j. The total spectral count of row j is
| (1) |
The normalization by TS of row j is obtained by performing
| (2) |
for all i.
3.1.2 Z normalization
The Z normalization has been widely adopted in microarray studies (Cheadle et al. 2003). For PIN i, let μi be the mean SCji over all j, and similarly σi the standard deviation. Normalization is achieved by performing
| (3) |
for all j. The mean of the resulting SCji over all j is then zero and the standard deviation is 1. We note that Z is carried out over each matrix column while TS is performed on each matrix row.
3.1.3 Hybrid normalization (TS→Z)
This is obtained by TS followed by Z.
3.1.4 Log preprocessing
Taking the logarithm of the spectral count data was also evaluated as a preprocessing step before the above normalization steps:
| (4) |
Our aim was to increase the signal of the PINs with low spectral counts with respect to the “highly abundant” PINs.
3.2 Feature selection / ranking methods evaluated in this work
For this study, we evaluated Golub's correlation coefficient (GI), Student's t-test, a method we call forward-SVM (SVM-F), and SVM recursive feature elimination (SVM-RFE). All computations were carried out using PatternLab.
3.2.1 Golub's index (GI)
For PIN i, Golub's index (Golub et al. 1999) is defined by
| (5) |
where , , , and are the means and standard deviations of the data in column i restricted to the positive (+) or negative (−) class. The larger a positive GIi the stronger the PIN's correlation with the positive class, whereas the smaller a negative GIi the stronger the correlation with the negative class. For our goal of feature ranking, we simply took absolute values.
3.2.2 Student's t-test
The score used for Student's t-test is given by
| (6) |
where each ni is of the number of samples restricted to column i and to the positive (+) or negative (−) class, and each si is the corresponding variance. For our goal of feature ranking, we simply took absolute values.
3.2.3 Support vector machine (SVM)
SVMs constitute a supervised learning method based on statistical learning theory and the principle of structural risk minimization (Vapnik 1995). SVMs have been successfully used in a number of bioinformatics applications, including the prediction of protein folds (Saha and Raghava 2006), siRNA functionality (Teramoto et al. 2005), rRNA, DNA and DNA-binding proteins (Yu et al. 2006), and the prediction of personalized genetic marker panels (Carvalho et al. 2006). An SVM model is evaluated using the most informative patterns in the data (the so-called support vectors) and is capable of separating two classes by finding an optimal hyperplane of maximum margin between the corresponding data.
Briefly, in the linearly separable case the SVM approach consists of finding a vector w in the feature space and a scalar b such that the hyperplane 〈w, x〉 + b can be used to decide the class, + or −, of input vector x (respectively if 〈w, x〉 + b ≥ 0 or 〈w, x〉 + b < 0). During the training phase, the model's compromise between the empirical risk and its own complexity (related to its generalization capacity) is controlled by a penalty parameter C, a positive constant. We refer the reader to Vapnik's book for further details of the SVM approach, including how to obtain w and b from the training dataset (Vapnik VN 1995). To carry out SVM modeling, PatternLab makes use of SVMlight (Joachims T 1999).
3.2.4 SVM-F
SVM-F feature ranking is performed on the SVM model of the whole training set. If w is the corresponding vector in the feature space and wi is the coordinate of w that corresponds to PIN i, then SVM-F ranks features in nonincreasing order of . Clearly, the lowest ranking PINs influence the hyperplane the least. SVM-F's output consists of the PINs ordered and listed side by side with their ranking scores.
3.2.5 SVM-RFE
SVM-RFE consists of recursively applying SVM-F on a succession of SVM models. The first of these corresponds to the whole training set; for k > 1, the kth SVM model corresponds to the previously used training set after the removal of all entries that refer to the least-ranking PIN (according to SVM-F). The SVM models are then built on successively lower-dimensional spaces. Termination occurs when a desired dimensionality is reached or some other criterion is met. Since features are removed one at a time, an importance ranking can also be established.
3.3 Evaluation of combined normalization and feature-ranking methods
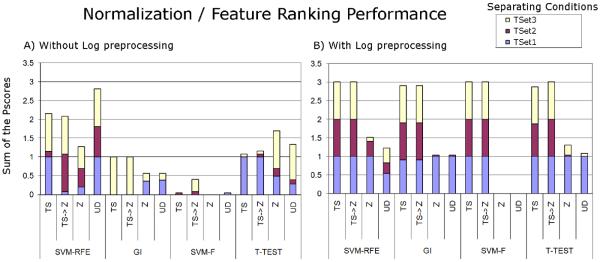
Combinations of the methods described were used to verify whether the spiked proteins could be pinpointed when comparing mixtures having markers spiked with different concentrations. In the ideal case, the four spiked proteins should achieve the top feature ranks. The ranks of the spiked proteins are listed in Tables I and II for the various method combinations and concentration comparisons. We used C = 100 for SVM training, following Guyon et al. (Guyon et al. 2002). The tables also show, in each case, a penalty score (Pscore) used to evaluate each method. This score plus one is the logarithm to the base 10 of the summed ranks of the four markers. Clearly, the ideal ranks yield a (minimum) Pscore of 0. Figure 2 plots the performance of each combination of normalization and feature ranking strategy.
Figure 2.
Sum of Pscores calculated for each combination of normalization / feature selection method when comparing the different spiked concentrations (legend), with (B) and without (A) Log preprocessing. Lower bars indicate better performance. The bar heights were limited to 4. We recall that the Pscore is calculated by obtaining the Log10 of the sum of the ranks and subtracting 1. Note that SVM-F with and without log preprocessing obtains at least one perfect score. UD stands for “unnormalized” data.
3.4 Evaluation of the normalization methods
By using only the spectral counts of the spiked proteins, SVM models were also calculated varying the C parameter from 2 to 100 with a step of 2 for all normalization methods. The C's that achieved a minimum LOO error or VC confidence were recorded. In either case, the LOO error, the VC confidence, and the number of support vectors of the model were also recorded (Table III). We note that LOO error and VC confidence, are respectively, ways of measuring a model's empirical risk (the error within the dataset) and how much may be added to that risk as the model is applied on a new dataset (generalization capacity).
The LOO technique consists of removing one example from the training set, computing the decision function with the remaining training data and then testing it on the removed example. In this fashion one tests all examples of the training data and measures the fraction of errors over the total number of training examples.
The model's VC confidence has roots in statistical learning theory (Vapnik VN 1995) and is given by
| (6) |
were h is the VC dimension of the model's feature space, l is the number of training samples and 1-η is the probability that the VC confidence is indeed the maximum additional error to the empirical risk as new datasets are presented to the model. We used η = 0.05 throughout. We recall that, given an SVM model, the VC dimension is a function of the separating margin between classes and the smallest radius of the hypersphere that encompasses all input vectors.
3.5 Predicting how many proteins were spiked
Feature ranking can be combined with methods that predict how many features are significant. Here, predicting the number of features is equivalent to estimating how many proteins were spiked. All feature ranking methods we used output a two-column list having features (PINs) ordered by their ranks in the first column and the method's score for each PIN in the second column. The number of spiked proteins was estimated by locating, in this output list, the two consecutive rows that presented the greatest difference in score values. The number of features was then computed by counting how many features have scores above or equal to this gap's upper limit.
4. Results and discussion
4.1 Evaluation of the feature selection / ranking methods
An efficient feature ranking criterion should select the features that best contribute to a learning machine's ability to “separate” data, reduce pattern recognition costs, and make the model less prone to overfitting. Translational studies usually possess a limited number of samples and have high dimensionality (many features), making feature selection and evaluation of the generalization capacity imperative steps. By spiking proteins within yeast lysates and detecting them, we perform a proof of principle of the potential of using spectral counts and SVMs to identify differences and perform classification in proteomic profiles.
In our hands, for the yeast MudPIT spectral count dataset, both Z normalization, with and without Log preprocessing, and the use of “unnormalized” data with Log preprocessing followed by SVM-F achieved a perfect score, pinpointing all spiked proteins for all configurations over the 102 dynamic range tested. These results are shown in Tables I, II, and Figure 2.
Overall, the greatest difficulties were in locating the spiked markers in TSet1. We hypothesize that this originates from limitations in both the feature selection methods and the experimental procedure used. From the machine learning perspective, according to Cover and Van Campenhout, no non-exhaustive sequential feature selection procedure is guaranteed to find the optimal feature subset or list the ordering of the error probabilities (T.M.Cover and J.M.Van Campenhout 1977). We do not use exhaustive feature searching, since the number of subset possibilities grows exponentially with the number of features; this method quickly becomes unfeasible, even for a moderate number of features. Less abundant proteins are not identified for every MudPIT analysis, generating a bias toward the acquisition of the more abundant peptide ions. Thus, less abundant proteins are identified by fewer peptides and their identifications can sometimes be suppressed by peptides from more abundant proteins. Liu et al. addressed the randomness of protein identification by MudPIT for complex mixtures (Liu et al. 2004). The rows originating from TSet1 show that fewer PINs were identified during these runs (∼800), contrasting with the ∼1200 PINs from the other runs. This lack of PINs may have driven the SVM-RFE toward an “undesired direction” while recursively eliminating the features. During the RFE computation and before narrowing down to ∼600 features, the weights of the normal vector (w) still included the spiked proteins among the most important features.
Although we have successfully identified the spiked proteins, we believe our methods could evolve to variants that might perform better for datasets of a different nature. The methods we employed are deterministic, in the sense that they quickly narrow down to what may be only locally optimal solutions. The quest for the global optimum in high-dimensional feature spaces still remains a challenge for pattern recognition. Distributed computing, coupled with algorithms that can efficiently rake the feature space (genetic algorithms (Shan S C. and Kusiak A 2004;Link et al. 1999), swarms (Guo et al. 2004), etc.), holds promises for proteomics of mining datasets more complex than the ones we addressed.
4.2 Evaluation of the normalization methods regarding dataset “separability”
Given that more than one method is able to select the spiked proteins, which one is best? Since spiked markers exist in different concentrations in each class and that spectral counts correlate with protein abundance, there should be a linear function capable of separating the input vectors containing only the spectral count information of the spiked proteins. To further evaluate the generalization capacity of the model, we used the VC confidence.
Both Z and Log preprocessed data allowed SVM-F to correctly select the spiked proteins and yielded a 0% LOO error for all spiking configurations (Table III). VC confidence shows that TSet1 and TSet2 normalized by Z led to a greater capacity than TSet3, thus here the lower concentrations made it harder for Z preprocessing. On the other hand, the Log preprocessed data separated better in the lower concentrations, probably because of the nature of the log function which discriminates lower values better than larger values.
In our results, the feature selection methods applied to “unnormalized” data achieved good Pscores. We hypothesize that this happened because the datasets were similar in the sense that the background proteins were technical replicates (thus easily reproducible). Had the yeast proteins had more variability, then it is possible that the normalization methods would become critically important. Further work is needed on this.
4.3 Predicting the number of spiked proteins
Overall, according to our benchmarking strategy, Z normalization followed by SVM-F was the method that obtained a perfect score for the yeast MudPIT dataset. The method used to predict the number of spiked markers described in Section 3.5 was applied to the Z/SVM-F results and it correctly identified the number of spiked markers as being 4 for all three possibilities of spiked-marker separation (TSet1 through 3).
5. Conclusions
In this study we set out to address the question of whether the data from spectral counts can be normalized and then classified using pattern recognition techniques. The above results indicate that Z followed by SVM-F applied on the yeast MudPIT spectral count dataset is an effective method for finding differences in this type of data. The methodology described was also capable of correctly identifying how many markers were spiked in the lysate. It is expected that the presented method should perform satisfactorily for other experiments where data are similarly acquired.
The identification of trustworthy marker proteins is not an easy task, since mass spectrometry based proteomics is still in development and spectral counting effectiveness can vary on the experimental setup, including mass spectrometry type and data-dependent analysis configuration. Here, combinations of normalization and feature selection strategies were validated on a controlled (spike-in) but realistic (yeast lysate) experiment, which is therefore verifiable. Our results indicate that even in “simple” scenarios where the spiked concentrations can be considered relatively high, the data can still play tricks on well founded feature selection methods. This is due to the dataset's high dimensionality, sparseness, and lack of a known a priori probability distribution. For even more complex scenarios, the searched markers could be present in extremely low concentrations when compared to the absolute concentrations. One of the existing strategies to reduce complexity is to isolate sub-proteomes; however, these separations are many times not straightforward to be carried out while disturbing protein content only minimally and remain a challenge.
We have also demonstrated the importance of evaluating computational strategies for proteomics studies to verify which one best suits the experiment at hand before drawing conclusions when dealing with complex datasets. As shown by our results, the application of SVM-RFE on our spectral count yeast dataset could lead to false conclusions. This shows that pattern recognition methods can perform differently on datasets of distinct natures, strengthening the idea that there is no “one suits all” method.
6. Acknowledgments
This work was supported by funds from the National Institutes of Health (P41 RR11823-10, 5R01 MH067880, and U19 AI063603-02), CNPq, CAPES, a FAPERJ BBP grant, and the Genesis Molecular Biology Laboratory. The authors thank Dr. Hongbin Liu for sharing MudPIT data (Liu et al. 2004).
7. Reference List
- Badr G, Oommen BJ. On optimizing syntactic pattern recognition using tries and AI-based heuristic-search strategies. IEEE Trans Syst.Man Cybern.B Cybern. 2006;36:611–622. doi: 10.1109/tsmcb.2005.861860. [DOI] [PubMed] [Google Scholar]
- Bylund D, Danielsson R, Malmquist G, Markides KE. Chromatographic alignment by warping and dynamic programming as a pre-processing tool for PARAFAC modelling of liquid chromatography-mass spectrometry data. J Chromatogr.A. 2002;961:237–244. doi: 10.1016/s0021-9673(02)00588-5. [DOI] [PubMed] [Google Scholar]
- Carlson JM, Chakravarty A, Gross RH. BEAM: a beam search algorithm for the identification of cis-regulatory elements in groups of genes. J Comput.Biol. 2006;13:686–701. doi: 10.1089/cmb.2006.13.686. [DOI] [PubMed] [Google Scholar]
- Carvalho PC, Carvalho MGC, Degrave W, Lilla S, De Nucci G, Fonseca R, Spector N, Musacchio J, Domont GB. Differential protein expression patterns obtained by mass spectrometry can aid in the diagnosis of Hodgkin's disease. J.Exp.Ther.Oncol. 2007;6:137–145. [PubMed] [Google Scholar]
- Carvalho PC, Freitas SS, Lima AB, Barros M, Bittencourt I, Degrave W, Cordovil I, Fonseca R, Carvalho MGC, Moura Neto RS, Cabello PH. Personalized diagnosis by cached solutions with hypertension as a study model. Genet.Mol.Res. 2006;5:856–867. [PubMed] [Google Scholar]
- Cheadle C, Vawter MP, Freed WJ, Becker KG. Analysis of microarray data using Z score transformation. J Mol.Diagn. 2003;5:73–81. doi: 10.1016/S1525-1578(10)60455-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Golub TR, Slonim DK, Tamayo P, Huard C, Gaasenbeek M, Mesirov JP, Coller H, Loh ML, Downing JR, Caligiuri MA, Bloomfield CD, Lander ES. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286:531–537. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- Guo CX, Hu JS, Ye B, Cao YJ. Swarm intelligence for mixed-variable design optimization. J Zhejiang.Univ Sci. 2004;5:851–860. doi: 10.1631/jzus.2004.0851. [DOI] [PubMed] [Google Scholar]
- Guyon I, Weston J, Barnhill S, Vapnik V. Gene Selection for Cancer Classification using Support Vector Machines. Mach Learn. 2002;46:389–422. [Google Scholar]
- Jessani N, Niessen S, Wei BQ, Nicolau M, Humphrey M, Ji Y, Han W, Noh DY, Yates JR, III, Jeffrey SS, Cravatt BF. A streamlined platform for high-content functional proteomics of primary human specimens. Nat.Methods. 2005;2:691–697. doi: 10.1038/nmeth778. [DOI] [PubMed] [Google Scholar]
- Joachims T. Making large-Scale SVM Learning Practical. Advances in Kernel Methods - Support Vector Learning. MIT-Press; 1999. [Google Scholar]
- Katajamaa M, Miettinen J, Oresic M. MZmine: toolbox for processing and visualization of mass spectrometry based molecular profile data. Bioinformatics. 2006;22:634–636. doi: 10.1093/bioinformatics/btk039. [DOI] [PubMed] [Google Scholar]
- Katajamaa M, Oresic M. Processing methods for differential analysis of LC/MS profile data. BMC Bioinformatics. 2005;6:179. doi: 10.1186/1471-2105-6-179. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolakowska A, Malina W. Fisher sequential classifiers. IEEE Trans Syst.Man Cybern.B Cybern. 2005;35:988–998. doi: 10.1109/tsmcb.2005.848493. [DOI] [PubMed] [Google Scholar]
- Link AJ, Eng J, Schieltz DM, Carmack E, Mize GJ, Morris DR, Garvik BM, Yates JR., III Direct analysis of protein complexes using mass spectrometry. Nat.Biotechnol. 1999;17:676–682. doi: 10.1038/10890. [DOI] [PubMed] [Google Scholar]
- Liu H, Sadygov RG, Yates JR., III A model for random sampling and estimation of relative protein abundance in shotgun proteomics. Anal.Chem. 2004;76:4193–4201. doi: 10.1021/ac0498563. [DOI] [PubMed] [Google Scholar]
- Mattie MD, Benz CC, Bowers J, Sensinger K, Wong L, Scott GK, Fedele V, Ginzinger DG, Getts RC, Haqq CM. Optimized high-throughput microRNA expression profiling provides novel biomarker assessment of clinical prostate and breast cancer biopsies. Mol.Cancer. 2006;5:24. doi: 10.1186/1476-4598-5-24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard DM, Masuda J, Yang X, Kowalak JA, Markey SP. Characterizing complex peptide mixtures using a multi-dimensional liquid chromatography-mass spectrometry system: Saccharomyces cerevisiae as a model system. J Chromatogr.B Analyt.Technol.Biomed.Life Sci. 2004;810:69–76. doi: 10.1016/j.jchromb.2004.07.015. [DOI] [PubMed] [Google Scholar]
- Petricoin EF, Ardekani AM, Hitt BA, Levine PJ, Fusaro VA, Steinberg SM, Mills GB, Simone C, Fishman DA, Kohn EC, Liotta LA. Use of proteomic patterns in serum to identify ovarian cancer. Lancet. 2002;359:572–577. doi: 10.1016/S0140-6736(02)07746-2. [DOI] [PubMed] [Google Scholar]
- Polisetty PK, Voit EO, Gatzke EP. Identification of metabolic system parameters using global optimization methods. Theor.Biol Med Model. 2006;3:4. doi: 10.1186/1742-4682-3-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sadygov RG, Yates JR., III A hypergeometric probability model for protein identification and validation using tandem mass spectral data and protein sequence databases. Anal.Chem. 2003;75:3792–3798. doi: 10.1021/ac034157w. [DOI] [PubMed] [Google Scholar]
- Saha S, Raghava GP. VICMpred: an SVM-based method for the prediction of functional proteins of Gram-negative bacteria using amino acid patterns and composition. Genomics Proteomics.Bioinformatics. 2006;4:42–47. doi: 10.1016/S1672-0229(06)60015-6. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shan SC, Kusiak A. Data mining and genetic algorithm based gene/SNP selection. Artificial Intelligence in Medicine. 2004;31:183–196. doi: 10.1016/j.artmed.2004.04.002. [DOI] [PubMed] [Google Scholar]
- Cover TM, Van Campenhout JM. On the possible orderings in the measurement selection problem. 1977:657–661. [Google Scholar]
- Tabb DL, McDonald WH, Yates JR., III DTASelect and Contrast: tools for assembling and comparing protein identifications from shotgun proteomics. J Proteome.Res. 2002;1:21–26. doi: 10.1021/pr015504q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teramoto R, Aoki M, Kimura T, Kanaoka M. Prediction of siRNA functionality using generalized string kernel and support vector machine. FEBS Lett. 2005;579:2878–2882. doi: 10.1016/j.febslet.2005.04.045. [DOI] [PubMed] [Google Scholar]
- Unlu M, Morgan ME, Minden JS. Difference gel electrophoresis: a single gel method for detecting changes in protein extracts. Electrophoresis. 1997;18:2071–2077. doi: 10.1002/elps.1150181133. [DOI] [PubMed] [Google Scholar]
- Vapnik VN. The nature of statistical learning theory. Springer-Verlag; New York, Inc.: 1995. [Google Scholar]
- Wang W, Zhou H, Lin H, Roy S, Shaler TA, Hill LR, Norton S, Kumar P, Anderle M, Becker CH. Quantification of proteins and metabolites by mass spectrometry without isotopic labeling or spiked standards. Anal.Chem. 2003;75:4818–4826. doi: 10.1021/ac026468x. [DOI] [PubMed] [Google Scholar]
- Washburn MP, Wolters D, Yates JR., III Large-scale analysis of the yeast proteome by multidimensional protein identification technology. Nat.Biotechnol. 2001;19:242–247. doi: 10.1038/85686. [DOI] [PubMed] [Google Scholar]
- Wiener MC, Sachs JR, Deyanova EG, Yates JR., III Differential mass spectrometry: a label-free LC-MS method for finding significant differences in complex peptide and protein mixtures. Anal.Chem. 2004;76:6085–6096. doi: 10.1021/ac0493875. [DOI] [PubMed] [Google Scholar]
- Wong JW, Cagney G, Cartwright HM. SpecAlign--processing and alignment of mass spectra datasets. Bioinformatics. 2005;21:2088–2090. doi: 10.1093/bioinformatics/bti300. [DOI] [PubMed] [Google Scholar]
- Yu X, Cao J, Cai Y, Shi T, Li Y. Predicting rRNA-, RNA-, and DNA-binding proteins from primary structure with support vector machines. J Theor.Biol. 2006;240:175–184. doi: 10.1016/j.jtbi.2005.09.018. [DOI] [PubMed] [Google Scholar]
- Zhang X, Asara JM, Adamec J, Ouzzani M, Elmagarmid AK. Data pre-processing in liquid chromatography-mass spectrometry-based proteomics. Bioinformatics. 2005;21:4054–4059. doi: 10.1093/bioinformatics/bti660. [DOI] [PubMed] [Google Scholar]