Abstract
Purpose
To propose a new measure of target underdose that can be used in the evaluation and optimization of radiotherapy dose distributions.
Methods and Materials
We compare various formulations of the equivalent uniform dose (EUD) and introduce a modification of existing EUD definitions, which we call tail EUD. Tail EUD is a measure of “cold spots” below the prescription dose in the target dose distribution. It has units of Gy. We investigate the mathematical properties of various target EUD concepts, including tail EUD. We apply the tail EUD measure retrospectively to intensity modulated radiation therapy (IMRT) treatment plans from our plan database. We also use tail EUD as an optimization objective in the optimization of prostate, pancreas, and head&neck plans.
Results
Tail EUD has desirable mathematical properties. In particular, it is convex and it leads to convex level sets (i.e., no local minima) if the EUD from which it is derived is concave. The tail EUD value is correlated with the subjective degree of target coverage. Constraining tail EUDs to a certain level in plan optimization leads to comparable target coverage in different plans and treatment sites.
Conclusions
The newly introduced concept of tail EUD appears to be useful both for plan evaluation and optimization. In addition, it can potentially be applied in the design of new clinical protocols.
Keywords: radiation therapy, IMRT, optimization, equivalent uniform dose, tumor coverage
1 Introduction
The evaluation of the clinical significance of dose cold spots in the tumor target volume, and the tradeoff of cold spots with potential hot spots in nearby critical structures, are unsolved problems in radiation therapy planning. Various schemes to evaluate, optimize, and report target doses and their variations have been proposed, and are in clinical use. The international commission on radiation units and measurements (ICRU) recommends to report the minimum and maximum dose in the planning target volume (PTV), and to keep those values between -5% and +7% of the reference (prescribed) dose (ICRU report 50 [12], repeated in report 62 [13]). Especially in intensity modulated radiation therapy (IMRT), these recommendations are difficult to comply with. There are no generally agreed-upon guidelines how the sometimes unavoidable deviations from the ICRU recommendations should be handled. In particular, it is unclear how much of the target volume can get how far below 95% of the prescription dose level. Many articles have shown that underdosing even small fractions of the target volume can lead to a drastic reduction of the tumor control probability (see, for example, [9, 14, 18, 24]). Hence, the common practice to prescribe dose to the D95%, i.e., the dose value at the 95% volume level in the dose volume histogram (DVH), is problematic, unless the dose tail below the D95% is somehow limited [22].
Others have recommended to report the mean target dose and its variance, based on the finding that, for small variances, the mean dose often correlates well with outcome [4]. The use of quadratic dose objectives in IMRT optimization is in line with this approach. However, one can easily construct cases in which the mean dose is not a good predictor of outcome, even when the dose variance is small [18].
More recently, the use of the equivalent uniform dose (EUD) concept [19, 20] has increased significantly for dose reporting and optimization. EUD is a very useful descriptor that boils down the 3 dimensional dose distribution into a single number, which is easily interpretable since it is expressed in units of Gy, and it is correlated with outcome for some critical structures. However, difficulties arise when EUD is used for target volumes. EUD does not per se lead to a clinically desirable level of dose uniformity in the target. One way around this problem is to define the target volume as both target and critical structure, with two corresponding EUDs [26]. Even then, the use of dose-volume objectives or constraints may be desirable to further improve the dose homogeneity [25, 1]. This is because EUD does not give one a good handle to control specific aspects of a dose distributions, such as specific regions in a DVH.
We were motivated to perform this study because the fact that there is no obvious way to evaluate dose cold spots in the target volume is a problem in every day clinical treatment planning. In particular, we need a measure of dose cold spots for our work on multi-objective treatment planning [15, 6]. We will focus on cold spots but keep in mind that target dose hot spots are, of course, another concern in treatment planning. However, first, this is somewhat less of a clinical problem than cold spots and, secondly, the measures proposed in this paper can easily be adapted to control hot spots in targets as well as critical structures.
The goal of this paper is to develop a method to evaluate and optimize target dose distributions, which has some of the EUD qualities such as easy interpretability, and which also has local “tweaking” features like DVH constraints.
2 Theoretical methods
2.1 Definition of EUD
The EUD has been defined as a generalized mean dose:
| (2.1) |
where Di is the dose in voxel i, and N is the number of voxels in a given structure. For target volumes, values a < 0 are used, with a = −10 being a typical value, while for critical structures, values a ≥ 1 are used, with the magnitude of this parameter depending on the serial or parallel nature of the structure (see [20, 21]). Note that this EUD definition falls into the framework of a generalized f-mean (see [11]):
| (2.2) |
with
| (2.3) |
An alternative way of defining EUD for target volumes is by use of biological motivated exponential cell kill models. In particular, [19, 18] introduced this definition by equating the tumor control probability (TCP) for an inhomogeneous dose distribution to that for a homogeneous dose distribution and solving for the corresponding homogeneous dose. Under a single-hit (linear) model of cell kill, this leads to
| (2.4) |
(see also [23]). Under the most common linear-quadratic model of cell kill that, conservatively, assumes complete recovery of injured cells between fractions, we have
| (2.5) |
where n is the number of fractions used for treatment.
For the purpose of treatment planning, it is highly desirable if the EUD, equation 2.2, is concave as a function of the dose distribution delivered to the patient when used for controlling cold spots in target volumes, i.e., when large values of the EUD are preferable to lower values. It is well-known that the EUD based on the power-law or the single-hit model are indeed concave (see [5, 23]). In appendix A.1 we will show that the LQ EUD measure is also concave provided that , which is fulfilled in all practically relevant cases.
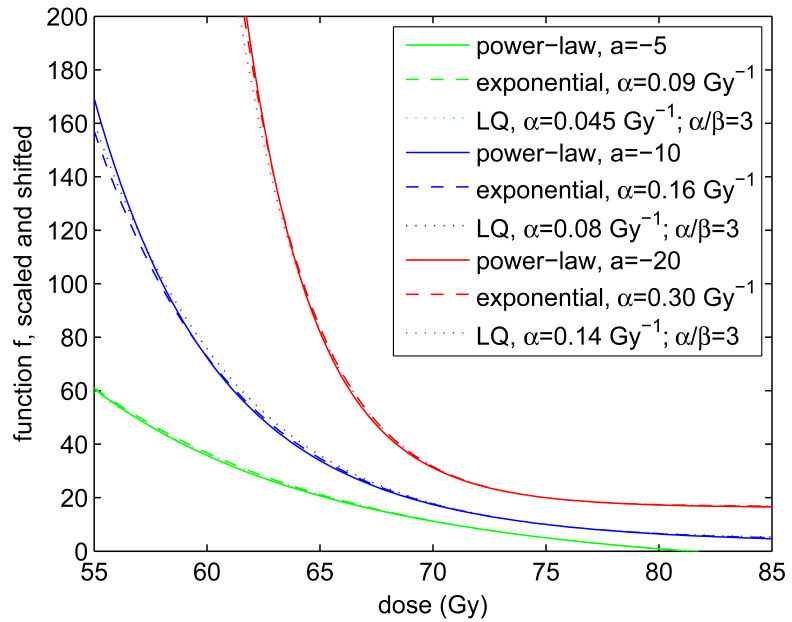
Even though the functions f in equations (2.3) (with a < 0) and (2.4) and (2.5) appear to be very different, their graphs become quite similar when appropriately scaled and shifted. Note that scaling and shifting of f is allowed because any linear transformation of f will leave the EUD untouched. This is one reason why the EUD is somewhat insensitive to the choice of the underlying f functions. Figure 1 compares power-law and exponential versions of f for various a values and their corresponding α values. The often used a = −10 corresponds with a biologically motivated parameter of α = 0.16 Gy−1, which is an entirely realistic value (see [14, 18]). However, α = 0.09 Gy−1 and α = 0.30 Gy−1, corresponding with a = −5 and a = −20, respectively, are also possible. In the linear-quadratic (LQ) case we assumed a low α/β ratio of 3, in order to accentuate differences from the mono-exponential (β = 0) case. Differences are still very small.
Figure 1.
This graph shows a comparison of power-law (equation 2.3) and biologically motivated exponential and LQ (equations 2.4 and 2.5) f functions for various a and α parameters. All functions were normalized such that they have a slope of −1 at an arbitrarily chosen reference dose of D̂ = 75 Gy. Further, the f functions were shifted to have values of 5, 10, and 20 for a = −5, −10, and −20, respectively. The α values yielding exponential functions that are similar in shape to corresponding power-law functions were found by trial and error. In the linear-quadratic (LQ) case we assumed n = 40 fractions.
The rather surprising close agreement between power-law and exponential f functions suggests that it does not matter very much whether one defines the EUD for target volumes using power-law or exponential functions. In the sequel, we will focus on the more common power-law definition. It does matter, however, which a parameter one chooses. We will come back to this issue. See also [18, 19].
2.2 Tail EUD
The main purpose of this paper is to introduce and study a new measure for controlling cold spots in targets, which we will call tailEUD. In particular, we wish to define the tailEUD as a measure of how much the EUD is affected by dose cold spots below the prescription dose, say D̂. One way to do this is to define tail EUD as the difference between the “true” EUD and the EUD of the truncated dose distribution without the tail, in which all dose values below D̂ are set to D̂ However, with this definition, the tail EUD would generally depend not only on the dose values in the tail, but also on all other dose values. Instead, we define the tailEUD through the following definition of fD̂, in which dose values above D̂ are truncated:
| (2.6) |
This definition of fD̂ can be applied to all variants of f mentioned above, as well as to others, and it lends itself to an EUD according to equation 2.2, simply by replacing f with fD̂. In appendix A.2 we show that the EUD resulting from the truncated function, fD̂, is a concave function if the EUD of the original function, f, is concave.
To facilitate the assessment of target volume underdosing independently of the value of the prescription dose, we define the tailEUD as an associated shortfall measure, i.e., we define tailEUD as the prescription dose D̂ minus the EUD of the dose distribution truncated above D̂:
| (2.7) |
Note that since the generalized mean term on the right is concave, as discussed above, the tailEUD is a (positive) convex function.
In words, the tail EUD of equation (2.7) can be defined as follows: If the tail EUD of an underdose tail is z Gy, it means that adding this tail to an otherwise homogeneous dose distribution at the prescribed dose level is equivalent to reducing the prescribed dose uniformly by z Gy.
The use of a tailEUD as defined above (i.e., truncated at D̂) can be motivated by the fact that, for two reasons, dose values above D̂ contribute little to the EUD: first, in treatment planning one generally strives to limit dose tails above D̂. Secondly, the f function (equation 2.2) gives a relatively small weight to higher dose values. The use of dose values in the tail only for the definition of tailEUD can be further motivated as follows. In clinical practice, one tries to keep the difference between EUD and D̂ small. Hence, we can linearize f−1(y) of equations 2.2 and 2.3 around y0 = f(D̂) using a Taylor expansion:
| (2.8) |
For the power-law f function, this yields
| (2.9) |
| (2.10) |
Note that the approximation above is a lower bound (i.e., a conservative estimate) of the “real” target EUD (with negative a).
In this approximation, the difference between EUD and D̂ is due to the sum of contributions from individual voxels i. To get the tailEUD, it is now clear that we should include the voxels in the tail only:
| (2.11) |
Now let us assume that, in addition to EUD being close to D̂, every Di < D̂ is close to D̂. Then we can linearize , and obtain:
| (2.12) |
Incidentally, this approximation of the tailEUD can also be derived by first order Taylor expansion of the tailEUD (2.7) around the point Di = D̂, ∀i.
Equation 2.12 indicates that, for very good target dose homogeneities (small cold spots), the tailEUD is independent of the “biological” parameter, a. Here the tailEUD is basically a sum of “underdose ramps”, similar to those used in one of our previous papers [10], see also [8]. This first order approximation of the tail EUD (equation 2.12) is in fact completely independent of the choice of f. Incidentally, unlike most other underdose measures that have been used as planning objectives, tailEUD has a non-zero slope at Di = D̂. It remains to be seen, how well the approximations (2.11, 2.12) agree with the exact tail EUD from equation 2.7.
3 Application to clinical cases
3.1 Application of tail EUDs to clinical target DVHs
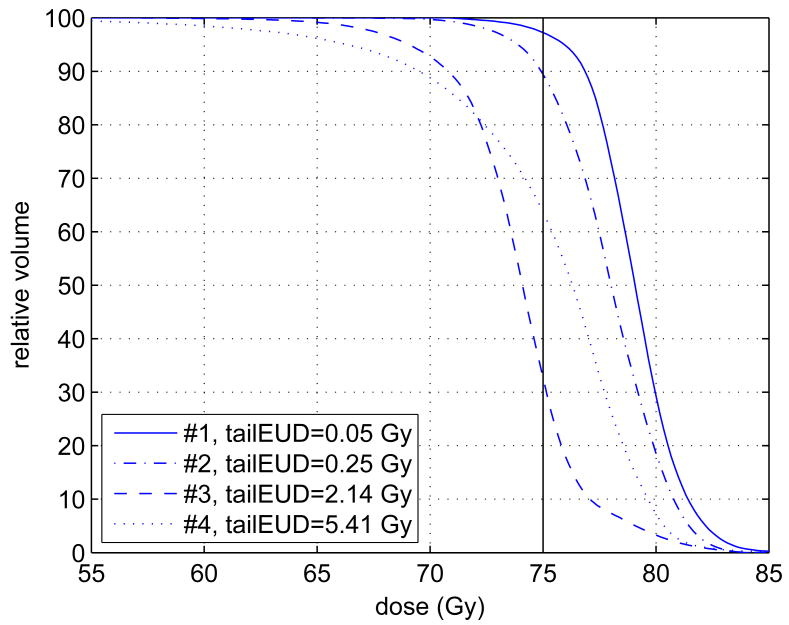
We investigated more than 40 treatment plans from our IMRT plan data base of CMS1 plans. All plans were normalized to a nominal prescription dose of 75 Gy, for comparability. Four representative DVHs of the planning target volume (PTV) were selected and are shown in figure 2. In terms of target coverage, the plans span the range from very good (#1), not so good (#2), bad (#3), to borderline acceptable (#4). It turns out that, for plans that are considered to have good target coverage, the tail EUD is generally below 0.1 Gy. The tail EUDs calculated with the various calculation models described above are summarized in table 1. Note that equation (2.7) provides the “true” tail EUD value. Its approximations (equations 2.11 and 2.12) can lead to artifacts (e.g., the large entry in the table for Plan #4 and a = −20). Table 1 also shows commonly used alternative measures such as standard EUD and D95 (dose value at the 95% volume level in the DVH). The latter cannot directly serve as indicators of cold spots.
Figure 2.
This graph shows four target (PTV) dose-volume histograms taken from our database. They span the range from very good coverage (#1) to very bad coverage (#4). The tail EUDs were calculated with equation 2.7 using the power-law EUD with a = −10. The four dose-volume histograms stem from various treatment sites with different prescription doses. For purposes of illustration and comparability the doses were normalized such that the prescribed dose is D̂ = 75 Gy in each case.
Table 1.
Comparison of tail EUDs in Gy for the four cases from figure 2 using the various calculation models discussed in the text. Equation (2.7) gives the “true” value of the tail EUD (underlined) for various values of the a parameter. The approximation (equation 2.11) consistently overestimates the tail EUD. The approximation is valid unless the underdose becomes too severe (as in Plan # 4) and one uses a large negative value for a, such as -20. The linear approximation (equation 2.12), on the other hand, consistently underestimates tail EUD. In either case, tail EUD can be used as an indicator of dose cold spots, and their severeness: tail EUD is positive if and only if such dose cold spots (below the prescribed dose) exist. Other measures such as standard EUD and D95 do not have this property. Their values can be above the prescribed dose (75 Gy in this case) even when cold spots exist.
| Model | Plan #1 | Plan #2 | Plan #3 | Plan #4 |
|---|---|---|---|---|
| tail EUD (Gy) | ||||
| power-law, a = −5, eq (2.7) | 0.04 | 0.20 | 1.87 | 2.59 |
| power-law, a = −5, eq (2.11) | 0.04 | 0.20 | 2.02 | 2.88 |
| exponential, α = 0.09 Gy−1 | 0.04 | 0.20 | 1.89 | 2.54 |
| power-law, a = −10, eq (2.7) | 0.05 | 0.25 | 2.14 | 5.41 |
| power-law, a = −10, eq (2.11) | 0.05 | 0.25 | 2.52 | 8.37 |
| exponential, α = 0.16 Gy−1 | 0.05 | 0.24 | 2.15 | 4.25 |
| power-law, a = −20, eq (2.7) | 0.06 | 1.07 | 3.13 | 20.16 |
| power-law, a = −20, eq (2.11) | 0.06 | 1.25 | 5.06 | 1959.70 |
| exponential, α = 0.30 Gy−1 | 0.06 | 0.65 | 3.04 | 12.38 |
| linear approximation, eq (2.12) | 0.04 | 0.17 | 1.64 | 1.64 |
| EUD (Gy) (power-law, a = −10) | 78.7 | 77.3 | 73.2 | 70.2 |
| D95 (Gy) | 75.8 | 73.8 | 69.0 | 66.3 |
3.2 Use of tail EUDs in plan optimization
Since tailEUD is a convex function, we can formulate and solve IMRT optimization problems using it either as a minimization objective or a constraint (e.g. tailEUD ≤ 0.2 Gy). We use MOSEK2, which is a leading nonlinear convex constraint solver, and possibly the only one that can handle constraints of the form for large scale problems. A constraint on the tailEUD, using the power-law formulation, can be written in this form because of the equivalence of the following set of inequalities:
| (3.1) |
| (3.2) |
| (3.3) |
where we have assumed that f is a decreasing function. This is consistent with the fact that, as per section 2.2, we focus on evaluating cold spots in targets. The min(Di, D̂) term can be handled by introducing an auxiliary variable, a standard trick from linear optimization modeling. For optimizations, we use the value a = −10.
Mosek uses a barrier method, and is thus capable of solving convex optimizations to any desired degree of optimality. The barrier method is an efficient interior point method originally designed for solving linear programs, but generalized thereafter to solve constrained convex optimization problems [3].
For three cases, a prostate, a pancreas, and a parotid tumor, we run several optimizations on a 64 bit linux machine with an Intel Pentium 4 processor, 16 Gbyte memory. Number of beamlets and voxels, and run times are given in table 2. Each case is formulated as a multi-objective IMRT optimization problem [7] where target coverage is constrained via the tailEUD and the organ at risks (OARs) are objectives. Different plans shown for each tailEUD constraint level arise from different importance weights put on the various OARs in the objective function. The results (figures 3-5) indicate that while the plans themselves are diverse, the target coverage is preserved, especially as the tailEUD is more tightly constrained. Another observation here is that tailEUDs of dose distributions that are clinically judged to exhibit “good” tumor coverage are generally quite small (below about 0.25% of the prescribed dose). Note that each figure contains DVH plots of 3 (figures 3 and 5) or 4 (figure 4) different plans with different priorities for the sparing of critical structures, but for the same patient.
Table 2.
Optimization information for the three cases solved with tailEUD constraints.
| Case | Prostate | Pancreas | Parotid |
|---|---|---|---|
| Total # voxels | 77,287 | 40,256 | 24,781 |
| Target # voxels | 11,527 | 5084 | 10,780 |
| # beamlets | 550 | 683 | 1852 |
| Typical run time | 5 minutes | 1 minute | 7 hours |
Figure 3.
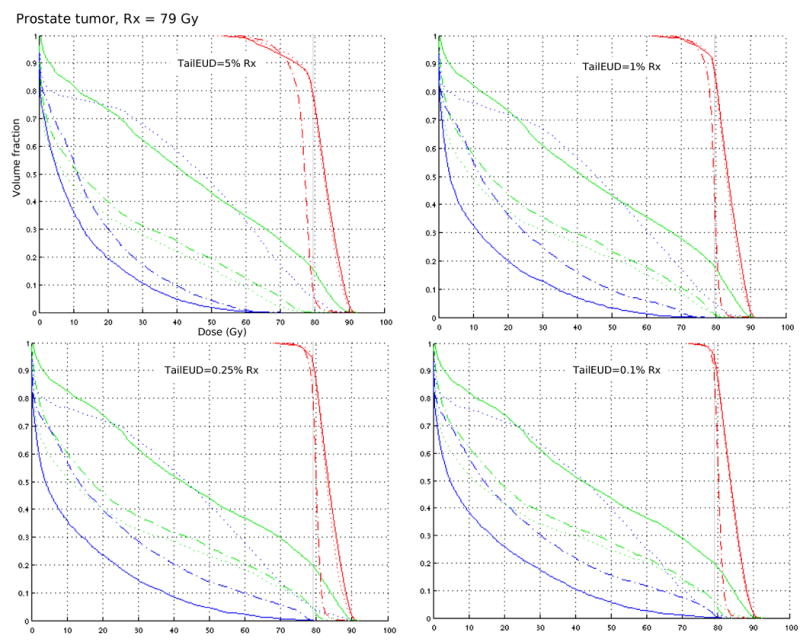
Each DVH plot contains three plans (shown with solid, dotted, and dash-dotted lines) from a multi-objective solution database for a clinical prostate case, with posterior rectum (blue) and bladder (green) DVHs included. Target coverage is fixed by constraining the tailEUD to ≤ 5% Rx, 1% Rx, 0.25% Rx, and 0.1% Rx.
Figure 5.
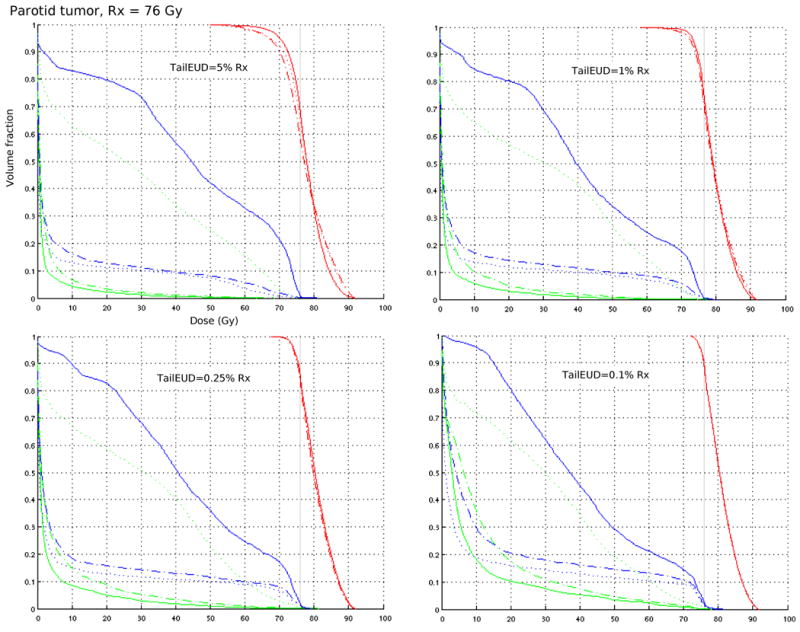
Each DVH plot contains three plans (shown with solid, dotted, and dash-dotted lines) from a multi-objective solution database for a clinical parotid case, with mandible (blue) and brain stem (green) DVHs included. Target coverage is fixed by constraining the tailEUD to ≤ 5% Rx, 1% Rx, 0.25% Rx, and 0.1% Rx.
Figure 4.
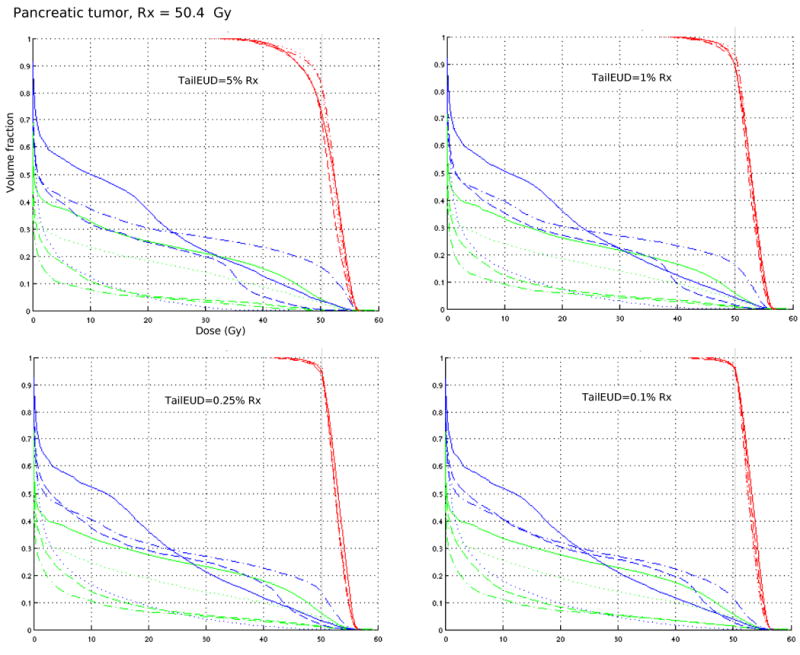
Each DVH plot contains four plans (shown with solid, dotted, dashed, and dash-dotted lines) from a multi-objective solution database for a clinical pancreas case, with stomach (blue) and liver (green) DVHs included. Target coverage is fixed by constraining the tailEUD to ≤ 5% Rx, 1% Rx, 0.25% Rx, and 0.1% Rx.
In figure 6 we compare the tailEUD formulation with the piecewise linear approximation given in equation 2.12, for the prostate case. For tailEUD less than or equal to 0.25% and 0.1%, the approximation gives almost identical results. The discrepancy is much more noticeable for the constraint levels 1% and 5%. Run times are comparable for the two formulations. The advantage of the piecewise linear approximation is that it can be solved with linear programming.
Figure 6.
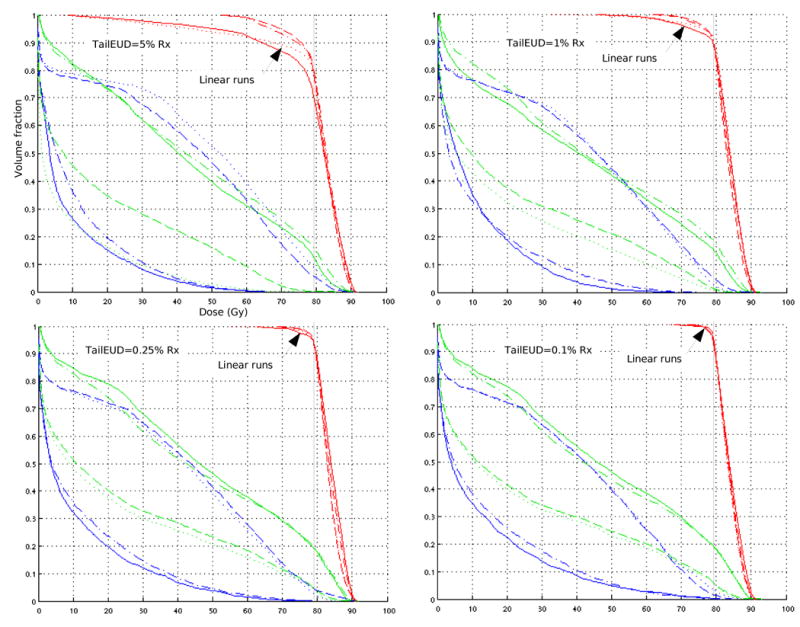
Each DVH plot contains four prostate plans: two are optimized by constraining the tailEUD (equation 2.7), and shown by the dashed and dash-dotted lines. The other two are optimized by constraining the linear approximation (equation 2.12), and shown by the dotted and solid lines. For the 0.1% plot, the plans regarding target DVH are almost indistinguishable. Posterior rectum (blue) and bladder (green) DVHs are included.
4 Discussion
Clinical radiotherapy treatment planning often involves a human iteration loop [16] in which the planner, with input from the clinician, tweaks plan parameters until a satisfactory plan is found. Dose and dose-volume based objectives and constraints (such as D95 – the dose value corresponding with the 95% volume level in the DVH) are used in these tweaking steps because they permit a direct control of specific characteristics of the dose distribution, for example cold and hot dose spots in the target volumes. However, the clinical/biological relevance of the dosimetric tuning parameters is often not known. It has been shown that underdosing a small portion of the target can lead to drastic reductions of the TCP, according to commonly used mathematical TCP models [9, 24]. In other words, a large value of D95 close to the prescribed dose is no guarantee for a good plan.
EUD based objectives, on the other hand, are biologically motivated but they are by definition an overall measure of the dose in all voxels in the respective organ. Therefore, they are not as suitable for controlling specific regions in a dose volume histogram. One might argue that tweaking is unnecessary since an EUD or, ultimately, TCP/NTCP based plan is already optimal. However, because of uncertainties in the models, one does not fully rely on their predictions. More fundamentally, physicians use the notion of a prescription dose to target volumes. As long as this is the case, deviations from the prescription, especially regions of underdose, will have to be quantified. Neither the standard EUD nor D95 are well suited for this purpose because they are not an indicator of dose cold spots: their value can be above the prescribed dose level even when underdose is present (see figure 2 and the caption of table 1).
We believe that tailEUD combines some of the advantages of the classic dosimetric and volumetric measures of target cold spots, and EUD as an intuitive biologically motivated measure. On top of that, tail EUD is an indicator of dose cold spots: it is positive if and only if at least one volume element is underdosed (below prescription level). We have also shown that tailEUD has the right mathematical features to be used as an objective or constraint in an optimization algorithm. The idea of tailEUDs, especially the approximation of equation 2.11, can easily be generalized to more complex functionally based dose prescriptions [17, 2].
Moreover, in figures 3-5 it has been shown that a given value of tail EUD uniquely represents a certain level of target underdose that is comparable for different treatment plans per patient, and across different clinical cases. As such, tailEUD could be a useful parameter in controlled clinical trials such as those organized by the Radiation Therapy Oncology Group (RTOG).
Mathematically, a key difference between tailEUD and most other measures of target dose homogeneity is the following: tailEUD starts out linearly from the prescription dose level D̂, as evidenced by equation 2.12, whereas other measures have zero slope at D̂. Therefore tailEUD yields a greater “incentive” to push dose values to the prescription level, even for small deviations from D̂.
It is not always easy to say which value of the tail EUD one should aspire to. As mentioned above, DVHs that are considered to exhibit good target coverage generally have a low corresponding tail EUD value, on the order of 0.25% of the prescribed dose, or about 0.2 Gy. On the other hand, a tail EUD value on the order of 2 Gy would be considered undesirable because it means that an entire standard treatment fraction is “lost” due to target cold spots. A more concrete answer could be obtained if the slope of the dose-response curve is known.
We have not yet discussed the question about the differing importance of cold spots in the gross tumor volume (GTV), the clinical target volume (CTV), and the planning target volume (PTV) [12, 13]. This is a difficult question, and we can provide no further insights than those discussed in [24], with which we concur.
5 Conclusions
We have introduced a new type of EUD specifically designed to quantify tumor underdosing, the tailEUD. This function is built from a generalized mean (like the standard EUD), and under reasonable assumptions it is convex, which is highly desireable from an optimization perspective. We utilize the tailEUD by applying it to historical plans and by using it in IMRT treatment plan optimization to constrain target coverage. The main advantages of using tail EUD in clinical treatment planning are:
Tail EUD can be biologically motivated.
It is an indicator of target cold spots, i.e., it is non-zero if and only if at least one volume element in the target is underdosed, i.e., below the prescribed dose level.
The value of tail EUD corresponds with a subjective level of severity of target underdose.
Tail EUD's desirable mathematical properties make it suitable for use in treatment plan optimization algorithms.
When used in plan optimization, tail EUD provides a greater “incentive” to push dose values towards the prescribed dose level, thanks to its nonzero slope.
Acknowledgments
We wish to thank Dr. David Herrup (MGH) for providing some of the clinical data used for this study. We also thank Dr. Andrzej Niemierko (MGH) for thoughtful feedback on the manuscript.
A Appendix
We will use the following result from [11]:
Theorem A.1
Let f be a continuous function that is
positive, i.e., f(x) > 0 for all x > 0;
decreasing, i.e., f′(x) < 0 for all x > 0;
convex, i.e., f″(x) > 0 for all x > 0.
In addition, assume that f″″ (x) exists for all x > 0. Then EUD is a concave function of D if and only if
| (A.1) |
or, equivalently,
| (A.2) |
A.1 LQ model
Under the LQ model (equation 2.5) we have
| (A.3) |
| (A.4) |
where n, α, β > 0. It is easy to verify that f satisfies conditions (i) and (ii) in Theorem A.1. Moreover, the function f″ is positive whenever
| (A.5) |
so that f is convex for x > 0 (and thus condition (iii) in Theorem A.1 is satisfied) as long as
| (A.6) |
Now note that
| (A.7) |
To determine whether this function is concave, we define the function
| (A.8) |
so that
| (A.9) |
It is easy to see that f′/f″ is concave for x > 0 if g is convex for v > α. The first two derivatives of the function g are:
| (A.10) |
| (A.11) |
Thus, g is convex for v > α if v2 − 2β/n ≥ 0, which means that f′/f″ is concave if (α + 2βx/n)2 − 2β/n > 0, which precisely corresponds to the condition for convexity of f above, see equation (A.6). Theorem A.1 thus implies that EUD is a concave function of D as long as
| (A.12) |
We will next study whether the condition for concavity in (A.12) is realistic from a clinical point of view. Let SF(x) denote the surviving fraction of clonogens when the target is irradiated to x/n Gy in each of n fractions, for a total dose of x Gy. The LQ model then says that
| (A.13) |
which clearly depends on the number of fractions n. Note in passing that our definition of f(x) (equation 2.5) equals this surviving fraction. The surviving fraction of clonogens after a single fraction of 2 Gy is, according to this model, equal to
| (A.14) |
To simplify the notation we will assume that all dose values are given in units of Gy.
The literature often mentions values for the ratio α/β that are estimated or deemed reasonable for various types of targets. Clearly, this ratio does not uniquely determine the values of the individual parameters, and therefore it cannot be used to assess whether the condition can be expected to hold in practice. However, note that we can determine α and β if both SF2 and the ratio α/β are known:
| (A.15) |
| (A.16) |
We can now express the condition in terms of the ratio α/β as follows:
| (A.17) |
or, in terms of that ratio as well as SF2:
| (A.18) |
| (A.19) |
or
| (A.20) |
For example, with a dose rate of 2 Gy per fraction and n = 35 fractions:
If α/β = 3, this means that we need 3β = α > 0.019 (by equation A.17) and SF2 < 93.8% (by equation A.20). This corresponds to a surviving fraction of clonogens after 35 fractions of 2 Gy of no more than 0.93835 ≈ 11%.
If α/β = 10, this means that we need 10β = α > 0.0057 (by equation A.17) and SF2 < 98.6% (by equation A.20). This corresponds to a surviving fraction of clonogens after 35 fractions of 2 Gy of no more than 0.98635 ≈ 61%.
A.2 Tail EUD
For convenience, we represent the EUD by
| (A.21) |
We assume that F is concave, as per the derivation above. The tailEUD can be represented as
| (A.22) |
Letting 0 < λ < 1 and and be two (nonnegative) dose distributions, we have
| (A.23) |
| (A.24) |
where (A.23) follows since F is nondecreasing in the voxel doses, while (A.24) follows by the concavity of F. This implies that tailEUD is a convex function of the dose distribution.
Footnotes
Short title: Target cold spots and tail EUDs
This study was supported by grant CA103904 “Multi-Criteria IMRT Optimization” from the National Cancer Institute and by grant DMI-0457394 from the National Science Foundation.
Conflict of Interest Notification: There are no conflicts of interest of any kind associated with this manuscript by any of the authors. No commercial products are described or endorsed by the authors. The authors have no relationship with organizations that would influence the results reported in this manuscript.
Computerized Medical Systems Inc., St. Louis, MO, USA
MOSEK ApS, Copenhagen, Denmark
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- 1.Amols HI, Ling CC. EUD but not QED. Int J Radiat Oncol Biol Phys. 2002;52(1):1–2. doi: 10.1016/s0360-3016(01)02586-x. [DOI] [PubMed] [Google Scholar]
- 2.Bentzen SM. Theragnostic imaging for radiation oncology: dose-painting by numbers. Lancet Oncol. 2005;6(2):112–7. doi: 10.1016/S1470-2045(05)01737-7. [DOI] [PubMed] [Google Scholar]
- 3.Bertsimas D, Tsitsiklis J. Introduction to linear optimization. Athena Scientific; 1997. [Google Scholar]
- 4.Brahme A. Dosimetric precision requirements in radiation therapy. Acta Radiol Oncol. 1984;23(5):379. doi: 10.3109/02841868409136037. [DOI] [PubMed] [Google Scholar]
- 5.Choi B, Deasy JO. The generalized equivalent uniform dose function as a basis for intensity-modulated treatment planning. Phys Med Biol. 2002;47:3579–3589. doi: 10.1088/0031-9155/47/20/302. [DOI] [PubMed] [Google Scholar]
- 6.Craft DL, Halabi TF, Shih HA, Bortfeld TR. Approximating convex pareto surfaces in multiobjective radiotherapy planning. Med Phys. 2006;33(9):3399–407. doi: 10.1118/1.2335486. [DOI] [PubMed] [Google Scholar]
- 7.Craft DL, Halabi TF, Shih HA, Bortfeld T. An Approach for Practical Multiobjective IMRT Treatment Planning. Int J Radiat Oncol Biol Phys. 2007;69(5):1600–1607. doi: 10.1016/j.ijrobp.2007.08.019. [DOI] [PubMed] [Google Scholar]
- 8.Ferris MC, Einarsson R, Jiang Z, Shepard D. Sampling issues for optimization in radiotherapy. 2006 http://pages.cs.wisc.edu/ferris/papers/annor-sampling.pdf.
- 9.Goitein M, Niemierko A. Intensity modulated therapy and inhomogeneous dose to the tumor: a note of caution. Int J Radiat Oncol Biol Phys. 1996;36(2):519–22. doi: 10.1016/s0360-3016(96)00348-3. [DOI] [PubMed] [Google Scholar]
- 10.Halabi T, Craft D, Bortfeld T. Dose-volume objectives in multi-criteria optimization. Phys Med Biol. 2006;51(15):3809–3818. doi: 10.1088/0031-9155/51/15/014. [DOI] [PubMed] [Google Scholar]
- 11.Hardy GH, Littlewood JE, Pólya G. Inequalities. Cambridge University Press; Cambridge, U.K.: 1952. [Google Scholar]
- 12.ICRU. Report 50. Prescribing, recording, and reporting photon beam therapy. International Commission on Radiation Units and Measurements; Bethesda: 1993. [Google Scholar]
- 13.ICRU. Report 62. Prescribing, recording, and reporting photon beam therapy (Supplement to ICRU report 50) International Commission on Radiation Units and Measurements; Bethesda: 1999. [Google Scholar]
- 14.King CR, DiPetrillo TA, Wazer DE. Optimal radiotherapy for prostate cancer: predictions for conventional external beam, IMRT, and brachytherapy from radiobiologic models. Int J Radiat Oncol Biol Phys. 2000;46(1):165–72. doi: 10.1016/s0360-3016(99)00406-x. [DOI] [PubMed] [Google Scholar]
- 15.Küfer KH, Scherrer A, Monz M, Alonso F, Trinkaus H, Bortfeld T, Thieke C. Intensity modulated radiotherapy - a large scale multi-criteria programming problem. OR Spectrum. 2003;25:223–249. [Google Scholar]
- 16.Langer M. What is different about imrt. In: Palta JR, Mackie TR, editors. Intensity-modulated radiation therapy - the state of the art. Medical Physics Publishing; Madison, Wisconsin: 2003. pp. 200–219. [Google Scholar]
- 17.Ling CC, Humm J, Larson S, Amols H, Fuks Z, Leibel S, Koutcher JA. Towards multidimensional radiotherapy (md-crt): biological imaging and biological conformality. Int J Radiat Oncol Biol Phys. 2000;47(3):551–60. doi: 10.1016/s0360-3016(00)00467-3. [DOI] [PubMed] [Google Scholar]
- 18.McGary JE, Grant W, Woo SY. Applying the equivalent uniform dose formulation based on the linear-quadratic model to inhomogeneous tumor dose distributions: Caution for analyzing and reporting. J Appl Clin Med Phys. 2000;1(4):126–37. doi: 10.1120/jacmp.v1i4.2634. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Niemierko A. Reporting and analyzing dose distributions: a concept of equivalent uniform dose. Med Phys. 1997;24(1):103–10. doi: 10.1118/1.598063. [DOI] [PubMed] [Google Scholar]
- 20.Niemierko A. A generalized concept of equivalent uniform dose (EUD) (abstract) Medical Physics. 26(6):1100, 1999. [Google Scholar]
- 21.Niemierko A. Biological optimization. In: Bortfeld T, Schmidt-Ullrich R, De Neve W, Wazer DE, editors. Image-Guided IMRT. Springer Verlag; Berlin Heidelberg: 2006. pp. 199–216. [Google Scholar]
- 22.Romeijn HE, Ahuja RK, Dempsey JF, Kumar A, Li JG. A novel linear programming approach to fluence map optimization for intensity modulated radiation therapy treatment planning. Phys Med Biol. 2003;48(21):3521–42. doi: 10.1088/0031-9155/48/21/005. [DOI] [PubMed] [Google Scholar]
- 23.Romeijn HE, Dempsey JF, Li JG. A unifying framework for multi-criteria fluence map optimization models. Phys Med Biol. 2004;49(10):1991–2013. doi: 10.1088/0031-9155/49/10/011. [DOI] [PubMed] [Google Scholar]
- 24.Tome WA, Fowler JF. On cold spots in tumor subvolumes. Med Phys. 2002;29(7):1590–8. doi: 10.1118/1.1485060. [DOI] [PubMed] [Google Scholar]
- 25.Wu Q, Djajaputra D, Wu Y, Zhou J, Liu HH, Mohan R. Intensity-modulated radiotherapy optimization with gEUD-guided dose-volume objectives. Phys Med Biol. 2003;48(3):279–91. doi: 10.1088/0031-9155/48/3/301. [DOI] [PubMed] [Google Scholar]
- 26.Wu Q, Mohan R, Niemierko A, Schmidt-Ullrich R. Optimization of intensity-modulated radiotherapy plans based on the equivalent uniform dose. Int J Radiat Oncol Biol Phys. 2002;52(1):224–35. doi: 10.1016/s0360-3016(01)02585-8. [DOI] [PubMed] [Google Scholar]