Unit-cell determination from randomly oriented electron-diffraction patterns

An algorithm is described that calculates the most likely primitive unit cell given a set of randomly oriented electron-diffraction patterns with unknown angular relationships.

Abstract

Unit-cell determination is the first step towards the structure solution of an unknown crystal form. Standard procedures for unit-cell determination cannot cope with data collections that consist of single diffraction patterns of multiple crystals, each with an unknown orientation. However, for beam-sensitive nanocrystals these are often the only data that can be obtained. An algorithm for unit-cell determination that uses randomly oriented electron-diffraction patterns with unknown angular relationships is presented here. The algorithm determined the unit cells of mineral, pharmaceutical and protein nanocrystals in orthorhombic high- and low-symmetry space groups, allowing (well oriented) patterns to be indexed.

1. Introduction

Elastic diffraction provides the information for atomic structure determination. However, the majority of electrons or X-­rays impinging on a sample scatter inelastically and these inelastically scattered quanta induce radiation damage. Relative to the total elastic diffraction, high-energy (300 keV) electrons deposit approximately 1000 times less energy in thin biological samples than X-rays and hence induce less radiation damage after normalizing for the elastically diffracted quanta. In theory, electrons should therefore be more suited for structure determination if radiation damage is the limiting factor (Henderson, 1995 ▶). However, practical problems in data collection and data processing prevent the use of electrons for the three-dimensional crystallographic structure determination of organic molecules such as proteins and pharmaceuticals. Here, we address one of these practical problems: the determination of an unknown unit cell from random diffraction patterns.

In electron crystallography, the unit cell is determined from electron diffraction tilt series. For this purpose, three-dimensional diffraction data are collected by tilting a crystal about a selected crystallographic axis and recording a set of oriented diffraction patterns (a tilt series) at various (preferably main) crystallographic zones. Vainshtein (1964 ▶) proposed a simple two-dimensional lattice-reconstruction method based on tilt series, in which the d* values for the non-tilt axis were plotted against the tilt angle.

Recently, a method of unit-cell parameter determination based on a tomography tilt series of diffraction patterns has been presented (Kolb et al., 2008 ▶).

A different algorithm is implemented in the program TRICE (Zou et al., 2004 ▶), which determines the unit cell in two steps. Firstly, the position and the intensities of each diffraction reflection in the individual electron diffraction patterns from the tilt series are determined and refined. For this purpose, any three reflections that do not lie in the same line are selected and are assigned a two-dimensional index, assuming a primitive cell. The positions of diffraction spots and the angles between the diffraction patterns are then used to identify the shortest three-dimensional vectors defining the unit-cell parameters and the crystal orientation. The angle θ between two electron diffraction patterns of a single crystal, oriented with a double-tilt holder at the angles (α₁, β₁) and (α₂, β₂), is given by

The concept of the Niggli cell and the cell-reduction technique are well established algorithms in electron crystallography. A crystal lattice can be characterized by the choice of ‘reduced’ cell. There are 44 primitive reduced (Niggli) cells corresponding to 14 Bravais lattices. The determination of the unit cell is performed by first determining the reduced direct primitive cell and then transforming it to a conventional cell. The recognition and interpretation of the reduced form are often difficult and are aggravated by errors in the cell parameters or rounding errors in calculations. Thus, procedures aimed at reducing these errors need to be performed. An approach suggested by Clegg (1981 ▶) to minimize the errors implies the generation of a list of lattice vectors sorted on length, together with angles between pairs of them. In addition to the conventional algorithms, Grosse-Kunstleve et al. (2004 ▶) implemented two numerically stable algorithms to generate the reduced cell.

However, all these methods require the collection of at least two diffraction patterns from one single crystal, each collected at precisely known angles. This is not always possible. For instance, in the case of three-dimensional organic crystals of proteins and pharmaceuticals, the high beam-sensitivity of the materials often does not allow the collection of a tilt series from a single nanocrystal. So far, this has limited the application of electron diffraction to the study of beam-sensitive molecules.

Here, we present an algorithm for unit-cell determination from randomly oriented electron diffraction patterns of different but similar crystals. These diffraction patterns may be noisy, their centre may be poorly defined and their low-resolution reflections (which are of prime importance for unit-cell determination) may be obscured by a beam stop or be out­shone by the central beam. To deal with these problems, we first calculate the autocorrelation pattern of the diffractograms. Because of the low curvature of the Ewald sphere, the spots of the diffractogram overlap with all spots of the autocorrelation pattern (but not vice versa; see also Fig. 1 ▶). Furthermore, autocorrelation patterns have an inversion centre, whereas the beam centre of a diffractogram may be unknown. Identifying the peak positions in the autocorrelation pattern is similar to the approach taken by the indexing program REFIX (Kabsch, 1993 ▶), which calculates the low-resolution spacings between observed spots.

Figure 1.

(a) Electron diffraction pattern of lysozyme (electron energy 300 keV). (b) Diffraction pattern after removing the central beam and subtracting the radial background. (c) Autocorrelation pattern of (b). The diffractogram in (a) shows a regular point-symmetrical pattern. The flatness of the Ewald sphere (the wavelength of 300 keV electrons is approximately 0.019 Å) causes this regularity.

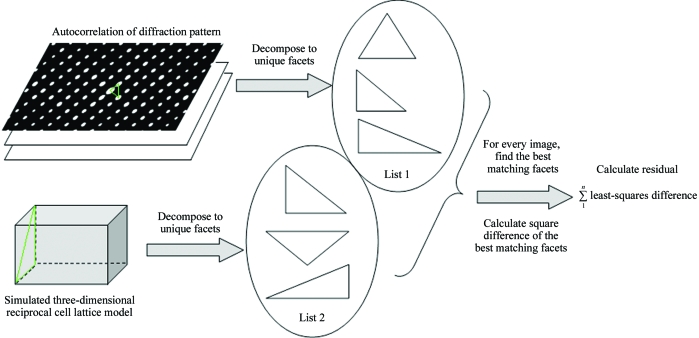
The low-resolution peaks in the autocorrelation pattern form a two-dimensional lattice (Fig. 1 ▶) which is defined by a pair of independent vectors. From this vector pair we construct a facet which is characterized by three numbers: the lengths of the two basis vectors and the angle between them. A facet is a rotation-invariant feature of a two-dimensional lattice. Each planar intersection of a three-dimensional lattice along a principal zone also generates a two-dimensional lattice and hence defines a corresponding facet. Our algorithm is based on matching the observed crystal facets to model facets extracted from a simulated three-dimensional lattice. Briefly, our procedure involves the following steps (see also Fig. 2 ▶).

• (1) For each observed electron diffraction pattern, we determine its crystal facet by

  • (i) removing the central beam and overall background of the image;
  • (ii) calculating the autocorrelation pattern of each corrected diffraction pattern;
  • (iii) identifying the principal facet of the autocorrelation pattern and adding it to list 1.
• (2) For each potential unit cell, we determine its fit to the experimental data by

  • (i) calculating all unique low-resolution model facets that can be extracted from the corresponding simulated three-dimensional lattice and storing these in list 2;
  • (ii) for each crystal facet of list 1, selecting the best-matching model facet from list 2 and calculating a residual and accumulating the residuals.

• (3) Finally, we select the potential unit cell with the lowest accumulated residual.

The algorithm was tested with electron diffraction data from random orientations of protein (lysozyme), organic (potassium penicillin G and sodium oxacillin) and inorganic (mayenite) nanocrystals.

Figure 2.

For a given unit cell, a three-dimensional reflection lattice can be calculated. For each characteristic facet from the experimental diffraction pattern, the corresponding facet in the three-dimensional reflection lattice which fits best is identified. The squared distance differences between calculated and experimentally found facets are accumulated in a penalty function.

2. Methods

2.1. Data collection

Potassium penicillin G and sodium oxacillin were available as white crystalline powders. To obtain thin crystals suitable for electron-microscopy studies, the powder was crushed in a mortar. A small amount of the sample was placed on a 300 mesh holey carbon electron-microscopy grid. Crystals suitable for electron diffraction studies (in terms of size, thickness and crystallinity) were selected. Diffraction experiments were performed under cryogenic conditions to increase the stability of the sample in the beam. Diffraction patterns were collected from randomly oriented crystals with a CM30T LaB6 microscope operating at 300 keV in microdiffraction mode. A con­denser aperture (C2) of 30 µm and spot size 8 were used (the diameter of the beam on the crystal was approximately 1 µm). The data were recorded at a camera length of 420 mm on DITABIS image plates and digitalized at a resolution of 0.025 mm per pixel with the DITABIS Micron imaging-plate read-out system.

2.2. Data preprocessing and determining the crystal facets

Firstly, the digitized diffraction patterns were processed. The approximate centre of the diffraction patterns was found, the central beam or backstop shadow was removed, the resolution-dependent background was subtracted, the autocorrelation patterns were determined and the beam centre was refined. Peak positions were automatically extracted from the autocorrelation patterns using the automated particle-picking tool of the Cyclops software suite (Plaisier et al., 2007 ▶). At low resolution, the peak positions of the diffractogram coincide with those of the autocorrelation pattern (see Fig. 1 ▶). From these peak positions, we calculated a low-resolution facet for each diffraction pattern and stored these in list 1.

In the absence of a beam stop, the centre of a diffraction pattern was found by a search for the most intense connected spot using an adaptation of a standard peak search. When a beam stop occluded the direct beam, the centre was located by cross-correlating the autocorrelation pattern of the diffractogram with the diffractogram itself and by making use of the point symmetry of the low-resolution reflections (the point symmetry is caused by the low curvature of the Ewald sphere).

The crystal facet describing the lattice of the autocorrelation pattern was determined by locating the two peaks close to the centre, ensuring that the angle they defined together with the centre was between π/2 and π/3. These two peaks can be located interactively or automatically in our algorithm. Visual inspection ensured that the facet indeed correlated to the two-dimensional lattice of the autocorrelation pattern and that it did not correspond to low-resolution noise peaks.

2.3. Simulating a three-dimensional reflection lattice and extracting low-resolution model facets

Six cell parameters (axes a, b and c, and angles α, β and γ) define a primitive cell. Using these six parameters, a systematic set of possible unit cells can be simulated in a grid search of axes and angles. Good guesses for the dimensions of the parameters and the step size can be made on the basis of the observed spacings and angles in the experimentally determined crystal facets, but we also allow the user to select the search range and step size.

From a set of cell parameters, a reciprocal cell matrix C can be constructed. The crystal orientation can be defined by a rotation matrix R and from these matrices R and C a matrix M = CR is constructed. The position of any reflection point p of the three-dimensional reflection lattice in Fourier space for a given unit cell and crystal orientation can be calculated using the equation

Here h = (h, k, l) is an index vector containing the integral indices of p. M is defined by the unit-cell parameters and the crystal orientation. The indices that satisfy p for a chosen resolution range can be found by imposing the boundary conditions

where d _min is the lower boundary of the resolution range and d _max is the upper boundary resolution. Given these equations and boundary conditions, we implemented an algorithm to quickly generate all possible positions of reflection spots in three-dimensional Fourier space. From this collection of simulated three-dimensional spot positions, we generated a list of all unique model facets, i.e. model facets differing from all others by less than a specified tolerance.

2.4. Calculating residuals

In the ideal case, all facets from the experimental data exactly match the facets of one specific model unit cell. In practice, however, the limited accuracy of determining the centroids of autocorrelation peaks, small variations in unit-cell parameters of different crystals and the uncertainty of the crystal orientation prevent such ideal fits. Therefore, function approximation needs to be performed, in which a function is selected that matches a target function as closely as possible.

The ‘squared difference function’ is used to calculate the least-squares error of fitting two facets. If we assume that p ₀ and p ₁ define the two-dimensional vector pair of the observed facet and q ₀ and q ₁ define the simulated facet, then the square error is defined as

where R is the rotation matrix that minimizes r. This function can be solved analytically for R, thus speeding up its computation. In order to improve accuracy, but at the expense of computational speed, multiple vectors of the autocorrelation image can also be matched.

However, it is not sufficient to accumulate the residual defined in (3) for all observed facets. We need to take into account that by choosing an arbitrarily large unit cell (resulting in a very dense modelled reciprocal lattice) this residual can be decreased at will. We tested several weighting schemes and found that the one which most consistently produces good unit cells was

where the weighting factors h _q0 and h _q1 are the integral indices of the vectors (h, k, l) of q ₀ and q ₁ of the simulated facet. For instance, the indices q ₀ and q ₁ of a facet might be {[0, 1, 1], [1, 0, 0]}, in which case |h _q0|² would be 2 and |h _q1|² would be 1. If a simulated dense lattice oversamples the observed lattice N times, the r value in (3) is statistically 1/N ² smaller, whereas the length of the indices vector of the fitted facet is N times larger, so the weighting factor of the square of indices length in (4) corrects the overfitting problem of oversampling.

3. Results

3.1. Unit-cell determination of mayenite from electron diffraction data

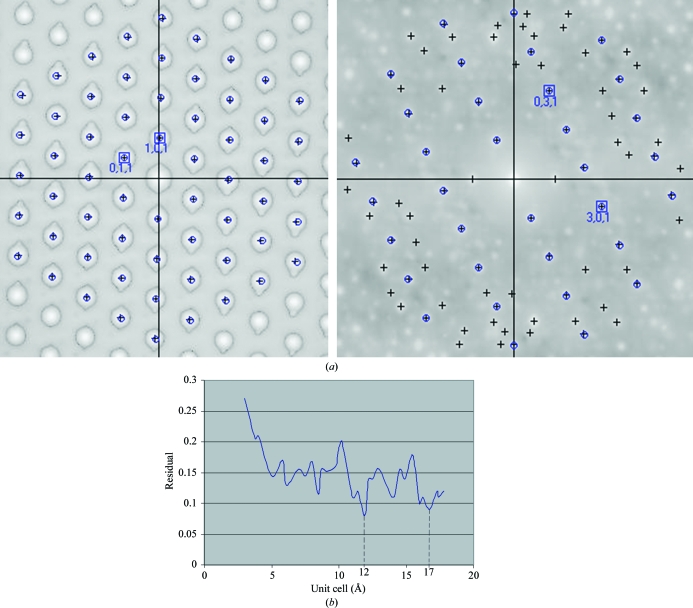
The algorithm was tested on randomly oriented electron diffraction data from mayenite (Ca₁₂Al₁₄O₃₃), a cubic in­organic mineral (Fig. 3 ▶). Our algorithm suggested a unit-cell parameter of 11.9 Å, which is in line with a reported value from the literature of 11.98 Å (Boysen et al., 2007 ▶). We could index the diffraction patterns of certain zones satisfactory (Fig. 3 ▶), with r.m.s.d.s between observed and predicted spot positions of about 0.5%. We considered data from eight diffractograms in this analysis. In order to test the accuracy of our method and the potential for false minima, we performed a fine-grid search (Fig. 3 ▶ b). Here, we found a broader second minimum around 17 Å. This is, within a few percent, a factor of 2^1/2 times larger than the known unit cell of about 12 Å and hence represents an oversampling of exactly the same lattice.

Figure 3.

(a) Examples of autocorrelation patterns from experimental electron diffractograms of mayenite. Crosses indicate the centroids of the peaks of the autocorrelation image used for the calculation and circles indicate the peak positions of the simulated diffraction pattern. The extra peaks in the second autocorrelation pattern were caused by low-intensity extra lattices in the original diffractogram (not shown). (b) Fine grid search of the unit cell (based on eight images). The ‘Residual’ value on the vertical axis is defined as the square root of the average weighted residual in (4).

3.2. Unit-cell determination of potassium penicillin G and sodium oxacillin from electron diffraction data

Electron diffraction data of potassium penicillin G (C₁₆H₁₇KN₂O₄S) and sodium oxacillin (C₁₉H₁₈N₃NaO₅S.H₂O) were analysed using our new algorithm. The unit-cell parameters that our algorithm suggested are given in Table 1 ▶, together with X-ray diffraction data taken from the literature (Dexter & van der Veen, 1978 ▶; Gibon et al., 1988 ▶). On the basis of these unit cells, we could index two main zones (001) and (011) in the case of potassium penicillin G using the program PhIDO (Calidris, Solentuna, Sweden; http://www.calidris-em.com; see Fig. 4 ▶). We considered data from 13 diffractograms for potassium penicillin G and 11 for sodium oxacillin in the analysis.

Table 1. Unit-cell parameters of potassium penicillin G determined by single-crystal X-ray diffraction and electron diffraction of single nanocrystals from a powder sample using our algorithm.

Sample	Method	a (Å)	b (Å)	c (Å)	α = β = γ (°)
Potassium penicillin G	X-ray diffraction (literature)	6.342	9.303	30.015	90
Potassium penicillin G	Electron diffraction	6.4	9.3	31	90
Sodium oxacillin	X-ray diffraction (literature)	7.342	10.303	26.7	90
Sodium oxacillin	Electron diffraction	7.3	10.1	27	90

Figure 4.

(a) Crystals of potassium penicillin G (scale bar: 2 µm). (b–e) Electron diffraction patterns and corresponding autocorrelation patterns of potassium penicillin G from two main crystallographic zones. Crosses indicate the centroids of peaks in the autocorrelation image; circles indicate the predicted peak positions. The root-mean-square deviation (r.m.s.d.) of the experimental and simulated patterns for the different zones (diffraction patterns) is between 0.6% and 1.7%.

3.3. Unit-cell determination of orthogonal lysozyme

In the case of orthogonal nanocrystals of hen egg-white lysozyme, our algorithm did not produce a unit cell that was known from the literature (Saijo et al., 2005 ▶; Biswal et al., 2000 ▶; see Fig. 1 ▶ for an example of a diffractogram and corresponding autocorrelation pattern and Table 2 ▶ for reported unit cells and the unit cell determined by our algorithm). For this calculation we used 19 different crystals. The crystals adopt preferred orientations on the EM grid and hence we also collected diffractograms at various random tilt angles to obtain more samplings of spacings that preferred to point in the direction normal to the EM grid. Overweighting crystals with such rare orientations made the cell determination more robust, but in general very similar results were obtained if we did not include this weighting. We do not exclude the possibility that the nanocrystals of lysozyme correspond to a new polymorph, but it may also be that the algorithm for some reason produces a large error of up to around 4% for large unit cells. Table 2 ▶ gives an overview of the unit cells of some known polymorphs of lysozyme, together with the unit cell produced by our new algorithm.

Table 2. Representative unit-cell parameters of orthorhombic hen egg-white lysozyme determined by single X-ray diffraction (first three entries) and electron diffraction of single nanocrystals from a powder sample using the new algorithm.

Method	a (Å)	b (Å)	c (Å)	α = β = γ (°)
X-ray diffraction 1 (PDB code 1wtm)	30.43	56.44	73.73	90
X-ray diffraction 2 (PDB code 1jj1)	30.56	58.99	68.26	90
X-ray diffraction 3 (PDB code 1f10)	30.58	55.86	68.58	90
Electron diffraction	31.5	52.5	89	90

4. Discussion and conclusions

Our new algorithm for unit-cell determination is independent of knowledge about the angular relationship between experimentally determined diffraction patterns. It does assume that all diffraction patterns share a similar three-dimensional lattice. Because it can deal with a limited number of outliers, it is fairly robust. Because our algorithm uses autocorrelation patterns rather than the original data, precise knowledge of the position of the beam centre is not required, as autocorrelation patterns are always centred by definition. Using autocorrelation patterns for unit-cell determination would fail at higher diffraction angles, but since the wavelength of the electrons used (approximately 0.013 Å) was two to three orders of magnitude smaller than the highest resolutions we used for our analyses (between 1 and 4 Å), this did not impose any serious problems in practice.

For the small-molecule crystals, which belonged to ortho­rhombic or cubic space groups and hence had three or less degrees of freedom in their unit-cell parameters, the algorithm performed well, reproducing literature values within a few percent. We do not expect a higher level of accuracy, as the method is based on the low-resolution spacings. In a subsequent indexing and unit-cell refinement step, which will use the original diffraction pattern, we assume that these small errors can be reduced.

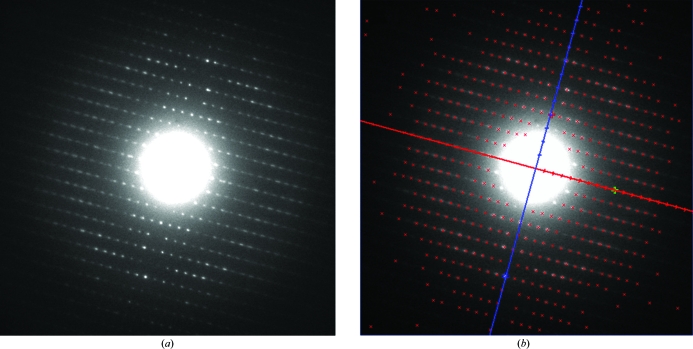
Somewhat surprising was the unit cell we found for orthorhombic lysozyme, which had a significantly shorter b axis and a significantly longer c axis than the unit cells reported in the literature. The unit-cell volume of the largest known orthorhombic polymorph of hen egg-white lysozyme was about 13% smaller than that of our nanocrystals (Table 2 ▶). Unfortunately, our nanocrystals could not be grown to a larger size. Hence, we could not corroborate the new unit cell by X-­ray analysis and in the absence of independent proof we cannot exclude the possibility that our algorithm failed to identify the correct unit cell of nanocrystalline lysozyme. It may be that the combination of randomly oriented diffraction patterns, a relatively large unit cell and a potentially anisotropic rocking curve frustrates our algorithm and we are further investigating potential improvements. However, using the large unit cell, we were able to index well aligned diffraction patterns using the program ELD (Zou et al., 1993 ▶), yet we failed to index these patterns if we used the unit cells of known orthorhombic polymorphs of hen egg-white lysozyme (Fig. 5 ▶). Furthermore, all the known unit cells of lysozyme gave considerably worse residuals as defined by (4) and therefore were not supported by our experimental data. In this light, we propose that the nanocrystals are a new polymorph of lysozyme that was induced by the heterogeneous nucleation on human hair as described in Georgieva et al. (2007 ▶).

Figure 5.

(a) Diffraction pattern from a lysozyme nanocrystal. (b) Lattice indexing performed with ELD, using the unit-cell parameters for lysozyme obtained using the algorithm described here. The directions of the shortest reciprocal spacings, given in blue and red [corresponding to the (100) and (011) axes, respectively] are indicated.

How many diffractograms are needed to estimate the unit cell? There is not a straightforward answer to this question, but in general it is better to include as many data in the analysis as possible. If the crystals have a favoured orientation on the grid (as the lysozyme crystals did), then it is important to collect tilted data, as otherwise the possibility exists that one of the spacings is not observed. However, there are also other issues that influence the robustness of our algorithm, for instance the symmetry of the unit cell (higher symmetry gives better results) or peculiarities of a specific combination of unit-cell parameters: if, for instance, in an orthorhombic unit cell the (100) and (021) directions have similar lengths, indexing may become confused.

With our new algorithm we have made progress in enabling structure determination by electron diffraction of beam-sensitive three-dimensional nanocrystals. Subsequent steps involve testing our algorithm on lower symmetry space groups (monoclinic and triclinic), refining the unit-cell parameters, indexing the electron diffraction patterns, integrating the diffraction intensities, merging the data and phasing. How­ever, these subsequent steps crucially depend on knowledge of the unit cell and in many cases we can use algorithms and programs developed for X-ray crystallography.