This paper describes procedures for obtaining confidence intervals for coordinate locations resulting from the fitting of atomic models into low-resolution densities.
Keywords: confidence intervals, fitting to low-resolution densities, electron microscopy
Abstract
The fitting of high-resolution structures into low-resolution densities obtained from techniques such as electron microscopy or small-angle X-ray scattering can yield powerful new insights. While several algorithms for achieving optimal fits have recently been developed, relatively little effort has been devoted to developing objective measures for judging the quality of the resulting fits, in particular with regard to the danger of overfitting. Here, a general method is presented for obtaining confidence intervals for atomic coordinates resulting from fitting of atomic resolution domain structures into low-resolution densities using well established statistical tools. It is demonstrated that the resulting confidence intervals are sufficiently accurate to allow meaningful statistical tests and to provide tools for detecting potential overfitting.
1. Introduction
While performing their functions, proteins and other biological macromolecules often form large macromolecular assemblies. To date, only a relatively small number of these assemblies have been accessible to the atomic resolution techniques X-ray crystallography and NMR. Because of the requirement to generate suitably diffracting crystals for crystallography and because of the upper size limit for NMR, this fact is not likely to change dramatically in the near future. Electron microscopy in conjunction with image reconstruction has now matured into a powerful approach for revealing the structures of such macromolecular complexes, occasionally, at least in the presence of symmetry, even reaching near-atomic resolution (Henderson et al., 1990 ▶; Kühlbrandt et al., 1994 ▶; Nogales et al., 1998 ▶; de Groot et al., 2001 ▶; Holm et al., 2006 ▶; Zhang et al., 2008 ▶). However, for most biological specimens the achievable resolution is limited to 10–20 Å, thus precluding atomic modeling directly from the data. Atomic models can often be generated by combining high-resolution structures or homology models of individual components in a macromolecular complex with a low-resolution structure of the entire assembly.
Owing to the relatively low resolution of most density maps from electron microscopy, objective fitting of atomic models into these maps is difficult. In the early days, this task was achieved by manually placing atomic models within the density to optimize the visual fit, sometimes followed by computational rigid-body refinement (reviewed in Baker & Johnson, 1996 ▶). By the end of the millennium, the first fully automatic programs for rigid-body docking had been introduced (Wriggers et al., 1999 ▶; Volkmann & Hanein, 1999 ▶), eliminating the inherent subjectivity of the manual fitting approach. The interactions between components or interactions with other cofactors often result in dramatic conformational changes in the components themselves. The first attempt to address this issue was to break up the components into smaller domains or ‘modules’ and to dock these independently as rigid bodies into the density (Volkmann & Hanein, 1999 ▶; Volkmann et al., 2000 ▶). Later on, many methods were developed that allowed even higher degrees of flexibility in the fitting process. These methods were designed to refine a predefined starting model and sacrifice the global character of the rigid-body searches. In essence, all available flexible-fitting methods try to mold a starting model into the density by balancing force fields that optimize the density fit with force fields that ensure proper stereochemistry in one way or another. Examples include the use of normal modes (Tama et al., 2004 ▶; Hinsen et al., 2004 ▶), full fledged molecular dynamics (Trabuco et al., 2008 ▶) and a real-space refinement technique (Chen et al., 2001 ▶; Gao et al., 2003 ▶) originally developed for X-ray crystallography (Chapman, 1995 ▶).
While flexible-fitting approaches generally perform quite well with test data where the correct answer is known, there is currently no method available that allows the judgement of performance with experimental data when the answer is unknown. This is especially critical with regard to overfitting. If too much flexibility is introduced into the fitting process, then eventually noise will be fitted. In X-ray crystallography, this problem is traditionally solved by using the free R factor, a cross-validated measure of fit in Fourier space (Brünger, 1992 ▶). Because the free R factor relies on the independence of the Fourier terms, as is the case in crystallography, it is not applicable in the same form in electron microscopy, where the Fourier terms are strongly correlated. It may be possible to remove some of this correlation in an analogous way to treating noncrystallographic symmetry (Fabiola et al., 2006 ▶), but the resulting measure would still be more or less heuristic without any clearly defined limits.
An alternative strategy is to determine whether the additional degrees of freedom introduced by allowing flexibility significantly improve the fit in comparison to the fit achieved with less flexibility. If the inevitably resulting improvement in the scoring function is not statistically significant, it can be regarded as spurious and the more conservative fit should be chosen. This strategy can only be applied if confidence intervals for the scores can be derived. Previously, we introduced the use of Fisher’s z-transformation (Fisher, 1921 ▶) to obtain confidence intervals for rigid-body fitting of modules into low-resolution densities (Volkmann & Hanein, 2003 ▶). The technique allows the determination of whether a particular fit is significantly different from the globally best fit by testing whether its associated correlation coefficient score falls within the confidence interval at the desired confidence level. This leads to a set of fits which are regarded as statistically equivalent solutions for the fitting problem at hand. Here, we demonstrate that the z-transformation approach is applicable even when its exact theoretical underpinnings are not fulfilled. We also show that the use of flexible-fitting protocols can significantly decrease accuracy if compared with modular rigid-body docking.
2. Methods
Firstly, we will outline the underlying statistical framework of the approach. We will then describe how synthetic data were generated to test various aspects of the method. This will be followed by a description of the fitting procedure. Finally, we will describe the handling of the experimental data used in this study.
2.1. Fisher’s z-transformation
In a typical fitting experiment, an atomic structure is fitted into the low-resolution density by optimizing some scoring function. However, because the data carry measurement errors, many alternative data sets could be realised by repeating the experiments, all leading to different scores (Fig. 1 ▶). If we knew this score distribution, we could deduce its statistical properties such as an estimate of the expectation value of the score (the mean) or, more importantly in this context, confidence intervals for the scores that would allow us to deduce whether one fit is significantly different from another at a given confidence level. Unfortunately, three-dimensional reconstructions are difficult to obtain and independent reconstructions of the same structure are rarely available.
Figure 1.
Schematic representation of the statistical underpinnings of fitting coordinates into density data. Because the data carry measurement errors, many different data sets (Datan) can be realised. As a consequence, different correlation coefficients (CCn) arise if the score is calculated between the coordinates and the various density maps. Knowledge of this CC distribution would allow the calculation of its statistical properties, including a confidence interval (CI) for the CC.
One of the more popular and successful scoring functions in this context is the correlation coefficient. As an added benefit, confidence intervals for the correlation coefficient can be obtained even in the absence of the actual score distribution, relieving us of the need for multiple data sets if we want to deduce confidence intervals. The correlation coefficient is defined as
where the sum is over all voxels in the experimental target density t and the density d calculated from the coordinates of the fitted structure using electronic scattering factors. The overbar denotes an average. Unfortunately, the distribution of the CC tends to be rather complex. Fisher’s z-transformation (Fisher, 1921 ▶) can be used to simplify things. The transformation has the form
If the joint distribution of the two densities (t, d) is bivariate normal, z approximately follows a Gaussian distribution where the standard deviation of z depends only on the independent pieces of information N in the system (Fisher, 1921 ▶),
Once σ(z) has been determined, we can use the normality of the z distribution for hypothesis testing. For example, a particular CCi is significantly different from the global maximum CCmax at a given confidence level CL if
where z i is the z-transformed CCi and erfc denotes the complementary error function. Even though we know that all CCs to be tested at this stage will be smaller than CCmax, we use a two-sided test rather than a one-sided test here. The reason is that an arbitrary solution for the docking problem could generate a CC that is higher than CCmax if, for example, flexibility is introduced into the docking process. As we shall see, the two-sided testing framework allows us to test the results of flexible fitting in the light of rigid-body fitting.
For the docking problem discussed here, the choice for N in (3) is not obvious because of the correlation between voxels in the reconstructions and because the exact spatial resolution in these types of reconstructions is generally not well defined. If multiple independent data sets are available, σ(z) can be estimated from the data (Volkmann & Hanein, 2003 ▶) but, as mentioned previously, additional data sets are rarely available. In addition, deviations of the joint (t, d) distribution from the assumption of bivariate normality, as may be suspected for experimental data, may render the estimate of the confidence interval inaccurate even if a good estimate for σ(z) is available.
2.2. Synthetic test data
To test the applicability of the z-transformation method outlined above, we used Monte Carlo simulations to gain direct access to the CC and z-distributions of well defined docking problems with known solutions. The availability of these distributions allows us to assess the accuracy of the estimated confidence intervals under various conditions. Test target densities were calculated for four different structures. Their Protein Data Bank (PDB) identifiers and other properties are listed in Table 1 ▶. For each structure a density was generated on a 2 Å grid using sums of three Gaussians approximating the electronic scattering factors of the atoms. Each of these densities was perturbed with different types of noise.
Table 1. Docking summary.
For each entry, the data appearing in the columns are the PDB identifier of the target structure, the PDB identifier of the search structure, the resolution of the target map, the number of domains used as modules, the number of residues, the sequence identity between target and search structures and the root-mean-square deviation between Cα atoms of the search and target structures after least-squares fitting of the modules, after modular rigid-body docking of the same modules and after using flexible-fitting protocols. The values for the last column were taken from Trabuco et al. (2008 ▶), Jolley et al. (2008 ▶), Topf et al. (2008 ▶), Topf et al. (2008 ▶) and this study, respectively. The target map resolution used in Jolley et al. (2008 ▶) was 14 Å and that used in Topf et al. (2008 ▶) was 10 Å. ρEM denotes experimental density extracted from an electron-microscopy reconstruction of human rhinovirus with bound Fab fragment (Smith et al., 1993 ▶).
| Target | Search | Resolution (Å) | Modules | Residues | Identity (%) | R.m.s.d.lsq (Å) | R.m.s.d.mod (Å) | R.m.s.d.flex (Å) |
|---|---|---|---|---|---|---|---|---|
| 1oao chain C | 1oao chain D | 15 | 3 | 729 | 100 | 0.92 | 1.11 | 2.01 |
| 1lfh | 1lfg | 15 | 3 | 691 | 100 | 0.94 | 0.98 | 1.89 |
| 1hwz | 1hrd | 15 | 2 | 491 | 28 | 2.58 | 2.98 | 4.90 |
| 1blb | 1a45 | 10 | 2 | 172 | 35 | 1.57 | 2.03 | 11.50 |
| ρEM | 1for | 28 | 1 | 229 | 100 | 0.97 | 2.25 | 3.60 |
The bivariate normality assumption would be most accurately fulfilled if the errors in the densities were uncorrelated Gaussian. To emulate different degrees of deviation from this assumption and generate more realistic experiment-like density maps, we mixed in impulse noise (using a Laplacian distribution) and allowed various degrees of correlations between the voxels. The noise level was adjusted to give a specific target resolution as measured by the 0.5 cutoff of the Fourier shell correlation, a common resolution measure in electron microscopy (Böttcher et al., 1997 ▶). The corresponding noise parameters and the target resolutions are listed in Table 2 ▶ and central slices of some of the densities are shown as insets in Fig. 2 ▶. For each condition, 500 maps with different random seeds were generated. These 500 density maps (Datan) were used to calculate the CC distribution and its associated statistical properties, in analogy to Fig. 1 ▶, using the docked search structures (see below) as coordinates.
Table 2. Summary of test data and quality of σ(z) estimation.
For each entry, the data appearing in the columns are the Protein Data Bank identifier of the target structure, the resolution of the target map, the standard deviation of the actual z-statistics, the estimate of the standard deviation of the z-statistics calculated according to (5), an accuracy measure for this estimate, the mean correlation coefficient between target map and search structure, the mixing factor between Gaussian noise and Laplacian impulse noise (1.0 corresponds to Gaussian only, 0.0 to Laplacian only) and a measure of the extent of voxel correlation (the relative weight for neighboring voxels in respect to the central voxel).
| PDB code | Resolution (Å) | σ(z)true | σ(z)est | Accuracy | CC | Mix | Weight |
|---|---|---|---|---|---|---|---|
| 1oao | 6 | 0.00753 | 0.00771 | 0.0922 | 0.8693 | 0.5 | 0.08 |
| 15 | 0.01087 | 0.01219 | 0.4097 | 0.9419 | 0.8 | 0.12 | |
| 25 | 0.02498 | 0.01644 | 1.1337 | 0.8649 | 0.7 | 0.17 | |
| 1lfh | 15 | 0.00959 | 0.00964 | 0.0207 | 0.9883 | 0.5 | 0.08 |
| 20 | 0.01239 | 0.01112 | 0.3889 | 0.9435 | 0.8 | 0.13 | |
| 20† | 0.01066 | 0.01112 | 0.1620 | 0.9108 | 0.8 | 0.13 | |
| 1hwz | 10 | 0.00978 | 0.01261 | 0.7970 | 0.9390 | 0.5 | 0.20 |
| 15 | 0.01071 | 0.01489 | 0.9653 | 0.8243 | 0.9 | 0.14 | |
| 20 | 0.02124 | 0.01735 | 0.6655 | 0.6450 | 0.6 | 0.07 | |
| 1blb | 10 | 0.01567 | 0.01967 | 0.7307 | 0.6239 | 0.6 | 0.25 |
| 12 | 0.02191 | 0.02155 | 0.0652 | 0.5619 | 0.3 | 0.08 | |
| 15 | 0.03031 | 0.02409 | 0.7366 | 0.4842 | 0.8 | 0.13 |
Rigid-body docking with the entire unmodified search structure was used.
Figure 2.
Normal probability plots of z-transformed correlation coefficients. For normally distributed variables, the data points lie approximately on the identity line. The insets show central slices through representative densities used to calculate the underlying correlation coefficients. The noise parameters used to generate the maps are listed in Table 2 ▶. (a) Maps were calculated at 6 Å resolution from PDB entry 1oao chain C. (b) Maps were calculated at 15 Å resolution from PDB entry 1lfh. (c) Maps were calculated at 12 Å resolution from PDB entry 1blb. (d) Maps were calculated at 20 Å resolution from PDB entry 1hwz.
2.3. Docking procedure for synthetic data
For each of the four target structures, modular rigid-body docking using a homologous search structure in a different conformation was performed. The PDB identifiers for both are listed in Table 1 ▶ together with the resolution of the target map, the number of modules used in the procedure, the number of residues and the sequence identity between the target and search structures. All target search pairs exhibit large-scale conformational changes. The root-mean-square deviations between the Cα atoms of the structures (r.m.s.d.) after least-squares fitting (Kabsch, 1976 ▶) of the individual search modules to the corresponding regions in the target structure are listed in the r.m.s.d.lsq column of Table 1 ▶. R.m.s.d.lsq is the best possible r.m.s.d. value for the given modularization if only rigid-body movements are allowed.
The target maps were calculated as described in the previous section. The resolution was then reduced by applying a Butterworth-shaped Fourier space filter at the target resolution. These maps were then divided into density modules using the watershed transform (Volkmann, 2002b ▶). The search structures were divided into domain modules using an algorithm based on comparing the two alternative conformations (Hayward & Berendsen, 1998 ▶). It should be noted that it is not necessary to have access to the atomic structures of the two conformations in order to divide the structure reliably into independently moving domains. Alternatively, normal-mode analysis can be used to make this division (Hinsen et al., 1999 ▶) or the watershed transform can be applied to a low-resolution density calculated from the search model to define the module boundaries.
Once extracted, each domain was docked into the corresponding density segment using the global rigid-body fitting protocol implemented in our docking software (Volkmann & Hanein, 1999 ▶). One important step is to identify the correct correspondence between the target density modules and the search domain modules. In practice, the correspondence between volume and radius of gyration is usually sufficient and was trivial for all test cases except eye lens crystallin (PDB codes 1blb and 1a45). For this case, each domain was docked into both density segments and the correspondence was picked according to the highest correlation coefficient. In practice, a significance test using the technique outlined here can be performed at this stage to decide whether it is adequate in light of the data to choose one configuration over another.
After this initial round of global fitting, an iterative refinement procedure was applied in which a discrepancy map (Volkmann et al., 2000 ▶) was generated for each domain in turn by removing the contribution of the other docked domains from the unsegmented density. The orientation and position of the remaining domain was then refined using this discrepancy map. Once this had been performed for all domains, this discrepancy-mapping–refinement cycle was repeated until no further changes in orientation and position occurred. The purpose of this refinement step is twofold. Firstly, it ensures the removal of bias from sharp edges and inaccuracies introduced by the watershed segmentation. Secondly, it removes bias that might be introduced by erroneous modularization of the search structure. This is not an issue for the tests presented here, but is a valid consideration for experimental cases in which the optimal domain boundaries are unknown. The iterative discrepancy mapping can identify inadequate modularization and allows refinement of the module boundaries. For the test cases presented here, the maximum number of iterations was three. This number tends to be higher for experimental cases, in which inaccuracies are likely to be more pronounced.
As a final step, the docked domains were stitched together and the stereochemistry at the break points was fixed using the idealization approach implemented in REFMAC (Murshudov et al., 1997 ▶). The resulting structures were used to calculate the r.m.s.d. with the Cα atoms of the target structure without any further alignment. These values are given in the r.m.s.d.mod column of Table 1 ▶. The same structures were used without further alignment to calculate the 500 CCs for each test data set described in the previous section using the individual noisy maps. This essentially emulates the situation depicted in Fig. 1 ▶. The resulting standard deviation of the z-distribution, σ(z)true, and the mean CC are listed in Table 2 ▶.
2.4. Estimating the standard deviation of the z-distribution
A critical parameter for the determination of confidence intervals is the standard deviation of the z-transformed CC distribution σ(z). If the underlying parameters follow a bivariate normal distribution, σ(z) only depends on the number of independent pieces of information contributing to the CC. This number is ill-defined for the noisy low-resolution densities obtainable from techniques such as electron microscopy. However, the relevant number should still primarily depend on the molecular volume, properly corrected for the spatial resolution of the target reconstruction. Thus, an estimate for N in (3) should be some function N est = MV/c reso, where c reso is a resolution-dependent correction factor to the molecular volume MV. This resolution correction cannot easily be derived by first principles because it needs to account for short-range and long-range spatial correlations, inaccuracies in the bivariate normality assumption, noise contributions and other factors that may exhibit resolution-dependence.
On top of that, there is some dispute in the field as to how exactly the resolution of a reconstruction should be assessed. One relatively common resolution measure in electron microscopy is the 0.5 cutoff value of the Fourier shell correlation (FC0.5), which is calculated using reconstructions from randomly selected half data sets (Böttcher et al., 1997 ▶). Using the test data described above, we empirically tested the performance of several correction functions f(FC0.5) as correction factors c reso. The one that yielded the most consistent estimates for σ(z) over a large range of conditions (Table 2 ▶) was c reso = uFC0.5, where u is a constant that accounts for the unit system used. If FC0.5 and MV are expressed in angstrom units, u = 1 Å2. Thus, we define the estimate of σ(z) for determining confidence intervals in the docking context as
In practice, we first determine the 0.5 cutoff value of the Fourier shell correlation FC0.5 using two random half sets of the target data. We then determine MV by resampling the target map with the Shannon sampling at resolution FC0.5 and calculating the volume with the resampled volume units that is closest to the volume given by the molecular composition of the target structure. The resampling step significantly increases the accuracy of the estimate, most likely by accounting for grid aliasing effects. For convenient comparison of the estimated and true standard deviations, we define an accuracy measure
This operation maps the accuracy measure into the range between 0 and 1 if N is accurate within a factor of two, which was shown to be tolerable in terms of confidence-interval accuracy (Volkmann & Hanein, 2003 ▶). The wiggle room in N allows substantial flexibility, but gross mis-estimation will render the confidence intervals severely inaccurate. For all our test cases, including the experimental data discussed below, quite acceptable estimates for σ(z) were achieved using this procedure (Table 2 ▶).
2.5. Normality tests
In addition to a reasonably accurate estimate of σ(z), the normality of the z-distribution is essential for the validity of the confidence intervals. We used three well established complementary methods to test the normality of the z-distributions generated by the Monte Carlo simulations. The Anderson–Darling test is based on empirical distribution functions (Anderson & Darling, 1952 ▶), the Shapiro–Wilk test is based on variance analysis (Shapiro & Wilk, 1965 ▶) and the third method is based on probability plot correlations (Filliben, 1975 ▶).
In addition, we calculated and visually inspected normal probability plots for each test data set. Some of these plots are shown in Fig. 2 ▶. Generating the data points in the normal probability plots involved three steps. (i) The z-transformed CCs were normalized to zero mean and standard deviation 1, (ii) the resulting values were ordered from smallest to largest and the percentiles for each value were determined and (iii) the standard score corresponding to the value’s percentile was drawn from the standard normal distribution and was paired with the value to generate a data point. Normality of the tested distribution implies that these data points lie more or less on the identity line. Significant deviations from the identity line indicate that the tested data do not follow a normal distribution. Such deviations can easily be picked up by eye (we essentially employed the time-honored interocular traumatic test here: you know what the data mean if it hits you between the eyes).
2.6. Experimental data
We used a 28 Å resolution map of human rhinovirus complexed with Fab fragments (Smith et al., 1993 ▶) to test the utility of the outlined z-transformation procedure with experimental data. The crystal structure of exactly the same construct was solved to atomic resolution a few years later by X-ray crystallography (Smith et al., 1996 ▶), giving a one-to-one correspondence between the low-resolution density obtained by electron microscopy and the corresponding atomic structure. For the tests performed here, we pretended that only the electron-microscopy reconstruction, the structure of the uncomplexed virion (Rossmann et al., 1985 ▶) and the structure of the unbound Fab fragment (Liu et al., 1994 ▶) were available.
To isolate the Fab density from the reconstruction, we went through the following steps. Firstly, we docked the crystal structure of the uncomplexed virion into the reconstruction. We then removed the contribution of the docked model using discrepancy mapping. One of the symmetry-related densities corresponding to a single Fab fragment was boxed out from the discrepancy map for further analysis. The Fab fragment used to decorate the virion consists of two domains, the so-called variable and constant domains, which are named after their tendencies towards sequence variation. The domains are clearly visible in the reconstruction. However, only the variable domain, which is directly attached to the virion, is ordered in the crystal structure of the complexed virus and thus available for direct atom-to-atom comparison. Application of watershed segmentation to the discrepancy map extracted in the previous step readily yielded two segments. Only the segment closest to the virion was used for subsequent calculations. The corresponding density is shown as a chicken-wire representation in Fig. 3 ▶.
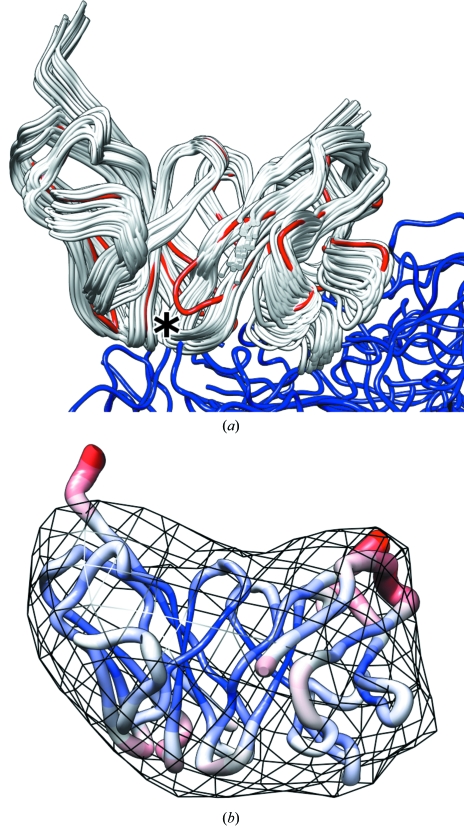
Figure 3.
Docking of Fab fragment into the equivalent density segment derived from an experimental electron-microscopy reconstruction. (a) The correct structure is shown in red (Fab fragment) and blue (virion). A representation of the ensemble of fitted structures with correlation coefficients within the confidence interval (solution set) is shown in white. The asterisk indicates the Fab-fragment loop that locally changes conformation upon binding to the virus. (b) Root-mean-square deviation within the solution set mapped onto the structure with thickness and color. Thinner and blue corresponds to small deviations and thicker and red to large deviations. The 28 Å resolution density map used for the docking experiment is shown as black chicken wire.
This density was used as a target map with the corresponding domain from the structure of the unbound Fab fragment (PDB code 1for) as a search structure using our global rigid-body docking protocol (Volkmann & Hanein, 1999 ▶). The best CC was then extracted and the estimate for σ(z) was calculated according to (5) and used to derive the limits of the CC confidence interval at confidence level 99.99%. Fits that corresponded to CCs within the confidence interval were then extracted from the global list for further analysis. Representations of this solution set are shown in Fig. 3 ▶.
3. Results and discussion
The confidence intervals of correlation coefficients from fitting atomic structures into low-resolution densities are useful tools for judging the quality of the fit and for detecting ambiguities in fitting space (Volkmann & Hanein, 2003 ▶). They allow the extraction of sets of fits that all satisfy the data within its margin of error. These solution sets can in turn be used to extract fitting parameters such as atomic coordinates or interaction distances as well as their error estimates, making them amenable to statistical hypothesis testing. Here, we investigate the applicability of the underlying statistical framework under a wide variety of non-ideal conditions using Monte Carlo methods and demonstrate the utility of the confidence-interval approach to experimental low-resolution data with known corresponding atomic structure. In addition, we tested the performance of modular-docking protocols in terms of achievable accuracy and compared them with various flexible-fitting methods.
3.1. Accuracy of modular rigid-body and flexible fitting
Most observed protein conformational changes involve movements of rigid domains that have their internal structure preserved (Krebs & Gerstein, 2000 ▶; Gerstein & Krebs, 1998 ▶; Hayward, 1999 ▶). Modular fitting of rigid-body domains should be adequate to accurately model those types of changes. Whether fitting methods based on higher degrees of flexibility yield more accurate structures than those based on modular rigid-body fitting is an open question. We chose four cases to test how well the modular-docking approach performs in comparison with various flexible-fitting methods proposed in the literature (Table 1 ▶). It should be noted that these structures had previously been selected by others as adequate test cases for flexible-fitting methods (Trabuco et al., 2008 ▶; Wriggers & Birmanns, 2001 ▶; Jolley et al., 2008 ▶; Topf et al., 2008 ▶).
3.1.1. α-Subunit of acetyl-coenzyme A synthase/carbon monoxide dehydrogenase
The crystal structure of the acetyl-coenzyme A synthase/carbon monoxide dehydrogenase assembly (Darnault et al., 2003 ▶) revealed two significantly different conformations of the α-subunit (PDB entry 1oao, chains C and D). A comparison of the two conformations indicated that this change can be approximated by hinged movements of three rigid domains. We performed the modular-docking protocol outlined in §2 using a 15 Å resolution calculated density map from chain C and the atomic structure of chain D, broken up into these three domains, as a search structure. This resolution was chosen because 15 Å corresponds to a reasonable target resolution for an average single-particle reconstruction project these days. The fit resulting from the modular-docking protocol for this test, with an r.m.s.d. of 1.11 Å, is close to the 0.92 Å achievable by least-squares fitting of the Cα atoms.
The same docking problem was tackled as a test case for molecular-dynamics-based flexible fitting (Trabuco et al., 2008 ▶). The resulting r.m.s.d. at 15 Å resolution using this approach (2.01 Å) is significantly worse than that from modular docking; it is still slightly worse (1.25 Å) if a target map at 10 Å resolution is used. Only if data at 5 Å are available does the flexible-fitting approach surpass the modular rigid-body approach, with an r.m.s.d. of 0.75 Å. This also improves upon the least-squares r.m.s.d., indicating that at this resolution nonrigid conformational changes can be picked up correctly by this flexible-fitting approach. It is worth noting that in three dimensions the amount of information increases by a factor of 3.375 on going from 15 to 10 Å resolution and by a factor of 27 on going from 15 to 5 Å resolution.
3.1.2. Lactoferrin
The iron-binding protein lactoferrin exhibits a large conformational change when iron binds to it (Norris et al., 1991 ▶). Comparison of the conformations suggests three hinged rigid-body domain movements to explain the change. We performed a modular-docking study at 15 Å resolution using apolactoferrin (PDB code 1lfh) as a target and iron-bound lactoferrin (PDB code 1lfg), broken up into three domains, as a search structure. Here, the r.m.s.d. after modular docking (0.98 Å) was almost indistinguishable from the least-squares r.m.s.d. (0.94 Å).
The same docking problem was addressed by two flexible-docking approaches. One used flexible fitting based on vector quantization and molecular-mechanics force fields (Wriggers & Birmanns, 2001 ▶). This study was also performed at 15 Å resolution and the best r.m.s.d. achieved with this approach was 2.72 Å, exhibiting local deviations of up to 9 Å (Volkmann & Hanein, 2003 ▶). The second approach was based on constraint geometric simulations (Jolley et al., 2008 ▶). This study evaluated the r.m.s.d. at various resolutions, the lowest of which was 14 Å. At this resolution the best r.m.s.d. was 1.89 Å. The best overall r.m.s.d. of 1.27 Å was achieved at 3.3 Å target map resolution. Even at near-atomic resolution, this flexible-fitting approach does not provide any advantage over modular rigid-body fitting at 15 Å resolution for this test case.
3.1.3. Glutamate dehydrogenase
This test involved docking the structure of Pyrococcus furiosus glutamate dehydrogenase (Britton et al., 1992 ▶), split into two domains as indicated by comparison of the conformations, into a 15 Å resolution target map calculated from the bovine homologue (Smith et al., 2001 ▶). The sequence identity between the two is 28% and there are several inserts present in the bovine form (PDB code 1hwz) that are not present in the P. furiosus form (PDB code 1hrd). This includes an extended finger-like helix–turn–helix motif of 46 residues. This region was easily identified by watershed segmentation and was deleted from the target map after completing the initial step of the modular-docking procedure but before invoking the iterative refinement. Removal of extra density during refinement is not strictly necessary but does tend to increase the accuracy of the docked structure. In this case, a 0.09 Å improvement in r.m.s.d. can be achieved by deleting the density of the helix–turn–helix motif prior to the iterative refinement. The r.m.s.d. of the final structure (2.98 Å) is again very close to the least-squares-based r.m.s.d. (2.58 Å).
The same fitting task was addressed using a hierarchical flexible-fitting procedure involving Monte Carlo-based refinement of successively smaller structure fragments (Topf et al., 2008 ▶). This study was performed with target maps calculated at 10 Å resolution. Despite the significant increase in information corresponding to the use of higher resolution data, the best r.m.s.d. achieved with this method (4.90 Å) was significantly higher than the r.m.s.d. achieved by modular docking.
3.1.4. Eye lens crystallin
The last test case also involved the fitting of homologous structures; in this case the structure of β-crystallin (Nalini et al., 1994 ▶) was used as a target and γ-crystallin (Norledge et al., 1997 ▶), divided into two domains, was used as a search structure. The sequence identity between the two is 35%. This case was difficult in various ways. (i) This is the smallest structure used in this study; the single domain modules are only ∼80 residues. This fact implies that less information is available for fitting than in the other test cases. (ii) Both modules are highly similar in structure and shape, consisting of relatively symmetrical β-barrels. As a consequence, the assignment of each domain to its corresponding segment is not trivial and after fitting the barrel alignment might be out of register. (iii) The conformational change is large. The centers of masses of the barrels in the extended γ-crystallin (PDB code 1blb) are 43 Å apart, whereas this distance is only 24 Å in the compact β-crystallin structure (PDB code 1a45). This change is primarily achieved by stretching the linker between the two barrels, which makes modeling of the linker regions using the modular-docking approach difficult.
When we used our approach with a target map at 15 Å resolution one of the barrels aligned within 2.5 Å r.m.s.d., whereas the second one was out of register by one β-strand. It appears that at this resolution this configuration is the true correlation maximum because even when using only local refinement and the correct least-squares-based alignment as a starting point the structures would misalign in the same way. Deletion of the linker region in the search structure did not improve the situation. This result has far-reaching consequences for fitting strategies. The hierarchical multi-resolution strategy often employed in registration of volumes derived by MRI or other clinical imaging techniques (Studholme et al., 1996 ▶) is not applicable for docking atomic structures into low-resolution density maps. The test case presented here shows that there is a real danger of getting stuck in the wrong local maximum of the score function. Global searches need to be performed at the highest available resolution.
In order to obtain the correct registration of the β-strand, data up to a minimum of 10 Å resolution need to be included. However, even in this case the radius of convergence of the iterative idealization step is insufficient to mend the ends of the broken linker. The ends first need to be moved manually within ∼10 Å of each other, at which point the idealization is capable of generating a stereochemically sensible conformation of the linker region. The r.m.s.d. of the resulting model with the target structure is 2.03 Å and compares quite favorably with the least-squares-based r.m.s.d. of 1.57 Å. The crystallin docking was also chosen as a test case for the hierarchical approach mentioned in the last paragraph (Topf et al., 2008 ▶). However, this method failed to align the β-barrels correctly even at 10 Å resolution.
3.1.5. Summary
In all four test cases the modular-docking approach yielded r.m.s.d.s within 0.5 Å of what was achievable by least-squares fitting of the Cα coordinates. While quite remarkable, this is not necessarily a surprising result. For each domain or module, only six parameters (three translational and three rotational) need to be fixed. This problem is highly overdetermined for most practical cases. This also makes the method very resilient against random noise, which has little influence on the accuracy of the docking (Volkmann, 2002a ▶). The question is not whether there are enough pieces of independent information in the data to support the degrees of freedom used for fitting (as one would ask for flexible fitting); the question is whether the level of detail in the density is fine enough to nail down the six parameters accurately and uniquely. With the availability of confidence intervals, these questions become testable hypotheses.
The global rigid-body fitting protocol implemented in our docking software (Volkmann & Hanein, 1999 ▶) is fast and the modular-docking experiments described here took only between 1 and 3 min on a standard Linux workstation. Thus, a full global analysis can easily be performed and, together with the z-transformation technique and the associated confidence intervals, ambiguities can be detected and the accuracy (or at least the precision) of the fit can be estimated (Volkmann & Hanein, 2003 ▶). In all tests presented here, flexible-fitting protocols significantly deteriorated the r.m.s.d. (Table 1 ▶), most likely owing to overfitting and inadequate distortions of the search structures. Only at 5 Å resolution, a 27-fold increase in information content over our 15 Å resolution map, did one of the flexible-fitting methods (Trabuco et al., 2008 ▶) appear to pick up conformational changes that cannot be adequately modeled as movements of rigid domains and improved upon the results obtained by modular rigid-body docking at 15 Å resolution.
3.2. Validity of deducing correlation confidence intervals using Fisher’s z-transformation
Reliable confidence intervals for correlation coefficients (CC) obtained from docking atomic structures into low-resolution density maps are an attractive possibility to allow testing of statistical hypotheses, to detect ambiguities in fitting space and to derive precision estimates for the fitting parameters. The approach outlined in §2 relies on the application of Fisher’s z-transformation (Fisher, 1921 ▶) to the measured CC, which then allows the derivation of confidence intervals from the volume and resolution of the experimental reconstruction alone (1)–(5).
There are two major requirements that need to be met in order to derive meaningful confidence intervals using this procedure. (i) The underlying distribution of the z-transformed CC variable must be approximately normal and (ii) the estimate of the standard deviation of this distribution, σ(z), must be sufficiently accurate. The normality of the z-distribution is guaranteed if the two variables used for calculating the CC, here the density values calculated from the search structure and those taken from the experimental map, are drawn from a bivariate normal distribution. While the voxel errors in reconstructions from frozen-hydrated samples appear to be nearly normally distributed, data that were taken in the presence of stain often exhibit significantly heavier tails than the normal distribution (van der Heide et al., 2007 ▶). Correlations between individual voxels and their neighbors can further complicate things.
3.2.1. Normality condition
In order to test whether z-transformed CC values obtained under the clearly non-ideal conditions outlined above still follow a normal distribution, we used Monte Carlo simulations to generate sets of noise-corrupted data that were used to explicitly derive the corresponding CC distributions and to analyze the resulting z-distributions. We used the target maps of the docking experiments described in the previous section as starting points and generated three synthetic data sets for each using different mixes of Gaussian and impulse noise as well as different extents of voxel correlations (summarized in Table 2 ▶). The signal-to-noise ratio for each set was chosen in order to give maps with resolution between 6 and 25 Å as measured by the 0.5 cutoff of the Fourier shell correlation. This resolution estimate was also used to calculate the estimate for σ(z) using (5). The coordinates used to calculate the CCs with these maps were those obtained by modular docking as described in the previous section. In addition, we performed a rigid-body fitting of the entire unmodified iron-bound lactoferrin into the map calculated from apolactoferrin, leading to a docking solution with obvious and severe mismatches. The purpose of this exercise was to evaluate the potential impact of such mismatches on the z-distribution.
We analyzed all 12 z-distributions for normality using three well established complementary tests (Shapiro & Wilk, 1965 ▶; Filliben, 1975 ▶; Anderson & Darling, 1952 ▶). None of the distributions were significantly different from a normal distribution according to any of the tests at the 1% and 5% significance levels. Visual inspection of normal probability plots confirmed that all conditions generated plots in which most data points lie on the identity line as expected for a normal distribution. Four of the plots are shown in Fig. 2 ▶ together with central slices through a representative noisy map used for calculating that particular CC distribution. The plot in Fig. 2 ▶(d) is the one that appears most nonlinear of all the conditions tested. In conclusion, the z-transformed CC values are approximately normally distributed for all tested conditions, regardless of voxel correlation, impulse components, resolution, the size of the underlying structure, mismatches in the docking or the quality of the search structure in relation to the target (i.e. the degree of homology). It appears that the normality of the z-distribution is extremely robust in the context of fitting atomic models into low-resolution densities and that the assumption of normality will be valid under most experimental conditions.
3.2.2. Accuracy of standard deviation estimate
In addition to analyzing the normality, we used the z-distributions to determine the actual standard deviation σ(z)true and compared it with the resolution-based estimate σ(z)est. We have shown previously that mis-estimating the correlated variable N (see equation 3) by a factor of two has very little influence on the size and shape of the corresponding sets of fits with CCs within the corresponding confidence intervals (Volkmann & Hanein, 2003 ▶). We translated this condition into an accuracy measure (equation 6; values listed in Table 2 ▶) of the estimated value compared with σ(z)true. If this accuracy value is between 0 and 1 then the corresponding estimate of N is within the tolerable factor of two. With one exception, the accuracy values of all tests fell well within the desired range. The one case that fell outside the range corresponded to an actual factor of 2.3, which was hardly a dramatic deviation. We conclude that for the most part the volume- and resolution-based estimate of σ(z) is sufficiently accurate to allow the construction of meaningful confidence intervals.
3.3. Application to experimental data
We applied the rigid-body docking procedure and the derivation of the confidence interval to experimental data extracted from a 28 Å resolution electron-microscopy reconstruction of human rhinovirus with bound Fab fragments (Smith et al., 1993 ▶). We docked the unbound structure of the Fab fragment (Liu et al., 1994 ▶) into the corresponding density segment (black chicken wire in Fig. 2 ▶ b) extracted by a combination of discrepancy mapping and watershed segmentation (see §2). The global CC maximum for this docking task was 0.9831. (5) was used to derive a σ(z) estimate of 0.03062, corresponding to 1069 independent pieces of information N.
The corresponding lower limit for the CC confidence interval at the 99.99% confidence level is 0.9764. Representations of the solution set extracted from the global list with this cutoff are shown in Fig. 3 ▶. The correct coordinates extracted from the crystal structure of the rhinovirus with bound Fabs (Smith et al., 1996 ▶) are, with a CC of 0.9769, included in the confidence interval (see also Fig. 3 ▶ a). In fact, only if the confidence level falls below 99.97% does the the correct solution fall outside the confidence-interval limits. This result indicates that the z-transform-based confidence interval can correctly capture the correct solution in experimental densities, even at resolutions as low as 28 Å. The shape of the confidence interval is nontrivial and gives rise to a complex distribution of deviations in the solution set (Fig. 3 ▶ b).
However, the one change between the bound and unbound forms of the Fab fragment that cannot easily be modeled by rigid-body movements (asterisk in Fig. 3 ▶ a) cannot be deduced from that distance distribution. This loop of the correct structure is not covered by the solution set and penetrates out of the coverage of the ensemble. This means that the accuracy estimate deduced from the solution set will not be valid for this loop. The CC of the least-squares-fitted search structure (0.9870) is practically indistinguishable from that of the correct structure. Thus, not surprisingly, there is no way to pick up on this change at 28 Å resolution, at least not with this scoring function.
The r.m.s.d. of the global CC maximum with the structure in the Fab-bound virus is 3.40 Å. We calculated an ensemble average from the solution set by picking the fit that has the minimum joint r.m.s.d. with all other members. The CC of this ensemble average is 0.9813 and the r.m.s.d. with the correct structure is 2.25 Å, a clear improvement over relying on the highest scoring fit only.
Next, we tested whether flexible fitting could improve results in this case or, if not, whether our procedure would detect the corresponding overfitting. We used flexible fitting based on normal-mode analysis (Tama et al., 2004 ▶) to further refine the results from the modular docking described above. We chose the ensemble average as a starting point and the lowest ten nontrivial modes to systematically perturb the structure in order to improve the fitting score. Ten modes appeared to be a reasonable number (supported by visually inspecting the individual modes) to represent conformational changes such as relative movements of the two subdomains or rearrangements of groups of secondary-structure elements without introducing high-resolution motions such as side-chain movements. The resulting model had an improved CC of 0.9865 but a significantly larger r.m.s.d. (3.60 Å). This result clearly indicates that the added degrees of freedom lead to overfitting. When looking at the confidence intervals, the CC of the flexible fit is not significantly different from either the ensemble average or the global rigid-body maximum (at the 99.99% confidence level). Based on this analysis, the improvement in the CC would be regarded as spurious. Thus, in the proposed framework the introduction of additional flexibility would have been correctly rejected.
It should be noted that the introduction of excessive amounts of flexibility will eventually break this test. For example, if 50 normal modes are allowed for the refinement for this test case, which amounts to allowing side-chain movements and excessive loop rearrangements, the CC soars to 0.9982, which is well outside the confidence limits even at the 99.999% confidence level. While this is clearly a significant improvement in the score over the rigid-body fit in the statistical sense, it is also wrong. The key for the test to work as intended is to only allow additions of flexibility that are more or less reasonable at a given resolution.
4. Conclusions
We have described and tested a method for obtaining confidence intervals for correlation coefficients derived from fitting atomic models into low-resolution density maps. Our approach is based on Fisher’s z-transformation and relies on two conditions. (i) The z-transformed correlation coefficients need to be approximately normally distributed and (ii) a reasonably accurate estimate for the standard deviation of this distribution must be available. Using Monte Carlo simulations, we show that both conditions are fulfilled under a large variety of adverse circumstances. We conclude that these conditions are likely to be met for most experimental reconstructions. Our tests on actual experimental data from human rhinovirus corroborate this conclusion. The confidence interval derived from this data incorporates the correct structure and allows the identification of overfitting introduced by allowing flexibility in the fitting. Furthermore, the fitting accuracy of the ensemble average of all the structures inside the confidence interval clearly exceeds the accuracy of the fit with the global score maximum.
In addition, we performed a comparison of modular rigid-body docking with various flexible-fitting methods in the resolution range 10–15 Å. In all these test cases, flexible fitting deteriorated the accuracy obtained by the modular-docking approach considerably. Only at 5 Å resolution did one of the methods exceed the quality of the rigid-body fit at 15 Å resolution. We conclude that flexibility needs to be used with caution. If the conformational changes mostly arise from rigid-body movements, modular rigid-body docking is likely to outperform flexible-fitting approaches in most practical cases. In addition, the speed of the rigid-body routines allows a full global analysis and the extraction of all fits that have scores within the confidence interval for further analysis. Modular rigid-body docking in conjunction with confidence intervals provides an adequate and versatile tool for fitting atomic models into low-resolution densities and for analyzing the results.
Acknowledgments
I would like to thank Drs Tom Smith and Tim Baker for providing the reconstruction of human rhinovirus complexed with Fab fragments. This work was supported by NIH grant GM076503. Software for modular rigid-body docking, watershed segmentation and analysis of confidence intervals can be obtained at http://coan.burnham.org.
References
- Anderson, T. W. & Darling, D. A. (1952). Ann. Math. Stat.23, 193–212.
- Baker, T. S. & Johnson, J. E. (1996). Curr. Opin. Struct. Biol.6, 585–594. [DOI] [PubMed]
- Böttcher, B., Wynne, S. A. & Crowther, R. A. (1997). Nature (London), 386, 88–91. [DOI] [PubMed]
- Britton, K. L., Baker, P. J., Rice, D. W. & Stillman, T. J. (1992). Eur. J. Biochem.209, 851–859. [DOI] [PubMed]
- Brünger, A. T. (1992). Nature (London), 355, 472–475. [DOI] [PubMed]
- Chapman, M. S. (1995). Acta Cryst. A51, 69–80.
- Chen, L. F., Blanc, E., Chapman, M. S. & Taylor, K. A. (2001). J. Struct. Biol.133, 221–232. [DOI] [PubMed]
- Darnault, C., Volbeda, A., Kim, E. J., Legrand, P., Vernede, X., Lindahl, P. A. & Fontecilla-Camps, J. C. (2003). Nature Struct. Biol.10, 271–279. [DOI] [PubMed]
- Fabiola, F., Korostelev, A. & Chapman, M. S. (2006). Acta Cryst. D62, 227–238. [DOI] [PubMed]
- Filliben, J. J. (1975). Technometrics, 17, 111–117.
- Fisher, R. A. (1921). Metron, 1, 1–32.
- Gao, H., Sengupta, J., Valle, M., Korostelev, A., Eswar, N., Stagg, S. M., Van Roey, P., Agrawal, R. K., Harvey, S. C., Sali, A., Chapman, M. S. & Frank, J. (2003). Cell, 113, 789–801. [DOI] [PubMed]
- Gerstein, M. & Krebs, W. (1998). Nucleic Acids Res.26, 4280–4290. [DOI] [PMC free article] [PubMed]
- Groot, B. L. de, Engel, A. & Grubmuller, H. (2001). FEBS Lett.504, 206–211. [DOI] [PubMed]
- Hayward, S. (1999). Proteins, 36, 425–435. [PubMed]
- Hayward, S. & Berendsen, H. J. (1998). Proteins, 30, 144–154. [PubMed]
- Heide, P. van der, Xu, X. P., Marsh, B. J., Hanein, D. & Volkmann, N. (2007). J. Struct. Biol.158, 196–204. [DOI] [PubMed]
- Henderson, R., Baldwin, J. M., Ceska, T. A., Zemlin, F., Beckmann, E. & Downing, K. H. (1990). J. Mol. Biol.213, 899–929. [DOI] [PubMed]
- Hinsen, K., Reuter, N., Navaza, J., Stokes, D. L. & Lacapere, J. J. (2004). Biophys. J.12, 12. [DOI] [PMC free article] [PubMed]
- Hinsen, K., Thomas, A. & Field, M. J. (1999). Proteins, 34, 369–382. [PubMed]
- Holm, P. J., Bhakat, P., Jegerschold, C., Gyobu, N., Mitsuoka, K., Fujiyoshi, Y., Morgenstern, R. & Hebert, H. (2006). J. Mol. Biol.360, 934–945. [DOI] [PubMed]
- Jolley, C. C., Wells, S. A., Fromme, P. & Thorpe, M. F. (2008). Biophys. J.94, 1613–1621. [DOI] [PMC free article] [PubMed]
- Kabsch, W. (1976). Acta Cryst. A32, 922–923.
- Krebs, W. G. & Gerstein, M. (2000). Nucleic Acids Res.28, 1665–1675. [DOI] [PMC free article] [PubMed]
- Kühlbrandt, W., Wang, D. N. & Fujiyoshi, Y. (1994). Nature (London), 367, 614–621. [DOI] [PubMed]
- Liu, H., Smith, T. J., Lee, W. M., Mosser, A. G., Rueckert, R. R., Olson, N. H., Cheng, R. H. & Baker, T. S. (1994). J. Mol. Biol.240, 127–137. [DOI] [PubMed]
- Murshudov, G. N., Vagin, A. A. & Dodson, E. J. (1997). Acta Cryst. D53, 240–255. [DOI] [PubMed]
- Nalini, V., Bax, B., Driessen, H., Moss, D. S., Lindley, P. F. & Slingsby, C. (1994). J. Mol. Biol.236, 1250–1258. [DOI] [PubMed]
- Nogales, E., Wolf, S. G. & Downing, K. H. (1998). Nature (London), 391, 199–203. [DOI] [PubMed]
- Norledge, B. V., Hay, R. E., Bateman, O. A., Slingsby, C. & Driessen, H. P. (1997). Exp. Eye Res.65, 609–630. [DOI] [PubMed]
- Norris, G. E., Anderson, B. F. & Baker, E. N. (1991). Acta Cryst. B47, 998–1004. [DOI] [PubMed]
- Rossmann, M. G., Arnold, E., Erickson, J. W., Frankenberger, E. A., Griffith, J. P., Hecht, H.-J., Johnson, J. E., Kamer, G., Luo, M., Mosser, A. G., Rueckert, R. R., Sherry, B. & Vriend, G. (1985). Nature (London), 317, 145–153. [DOI] [PubMed]
- Shapiro, S. S. & Wilk, M. B. (1965). Biometrika, 52, 591–611.
- Smith, T. J., Chase, E. S., Schmidt, T. J., Olson, N. H. & Baker, T. S. (1996). Nature (London), 383, 350–354. [DOI] [PMC free article] [PubMed]
- Smith, T. J., Olson, N. H., Cheng, R. H., Chase, E. S. & Baker, T. S. (1993). Proc. Natl Acad. Sci. USA, 90, 7015–7018. [DOI] [PMC free article] [PubMed]
- Smith, T. J., Peterson, P. E., Schmidt, T., Fang, J. & Stanley, C. A. (2001). J. Mol. Biol.307, 707–720. [DOI] [PubMed]
- Studholme, C., Hill, D. L. & Hawkes, D. J. (1996). Med. Image Anal.1, 163–175. [DOI] [PubMed]
- Tama, F., Miyashita, O. & Brooks, C. L. III (2004). J. Mol. Biol.337, 985–999. [DOI] [PubMed]
- Topf, M., Lasker, K., Webb, B., Wolfson, H., Chiu, W. & Sali, A. (2008). Structure, 16, 295–307. [DOI] [PMC free article] [PubMed]
- Trabuco, L. G., Villa, E., Mitra, K., Frank, J. & Schulten, K. (2008). Structure, 16, 673–683. [DOI] [PMC free article] [PubMed]
- Volkmann, N. (2002a). Atomic Model of the Cell: Docking in a Tomographic Environment. http://www.biophysics.org/discussions/volkmann-speaker.pdf.
- Volkmann, N. (2002b). J. Struct. Biol.138, 123–129. [DOI] [PubMed]
- Volkmann, N. & Hanein, D. (1999). J. Struct. Biol.125, 176–184. [DOI] [PubMed]
- Volkmann, N. & Hanein, D. (2003). Methods Enzymol.374, 204–225. [DOI] [PubMed]
- Volkmann, N., Hanein, D., Ouyang, G., Trybus, K. M., DeRosier, D. J. & Lowey, S. (2000). Nature Struct. Biol.7, 1147–1155. [DOI] [PubMed]
- Wriggers, W. & Birmanns, S. (2001). J. Struct. Biol.133, 193–202. [DOI] [PubMed]
- Wriggers, W., Milligan, R. A. & McCammon, J. A. (1999). J. Struct. Biol.125, 185–195. [DOI] [PubMed]
- Zhang, X., Settembre, E., Xu, C., Dormitzer, P. R., Bellamy, R., Harrison, S. C. & Grigorieff, N. (2008). Proc. Natl Acad. Sci. USA, 105, 1867–1872. [DOI] [PMC free article] [PubMed]