What can we learn by computing ¹³C^α chemical shifts for X-ray protein models?

The room-temperature X-ray structures of two proteins, solved at 1.8 and 1.9 Å resolution, are used to investigate whether a set of conformations, rather than a single X-ray structure, provides better agreement with both the X-ray data and the observed ¹³C^α chemical shifts in solution.

Abstract

The room-temperature X-ray structures of ubiquitin (PDB code 1ubq) and of the RNA-binding domain of nonstructural protein 1 of influenza A virus (PDB code 1ail) solved at 1.8 and 1.9 Å resolution, respectively, were used to investigate whether a set of conformations rather than a single X-ray structure provides better agreement with both the X-ray data and the observed ¹³C^α chemical shifts in solution. For this purpose, a set of new conformations for each of these proteins was generated by fitting them to the experimental X-ray data deposited in the PDB. For each of the generated structures, which show R and R _free factors similar to those of the deposited X-ray structure, the ¹³C^α chemical shifts of all residues in the sequence were computed at the DFT level of theory. The sets of conformations were then evaluated by their ability to reproduce the observed ¹³C^α chemical shifts by using the conformational average root-mean-square-deviation (ca-r.m.s.d.). For ubiquitin, the computed set of conformations is a better representation of the observed ¹³C^α chemical shifts in terms of the ca-r.m.s.d. than a single X-ray-derived structure. However, for the RNA-binding domain of nonstructural protein 1 of influenza A virus, consideration of an ensemble of conformations does not improve the agreement with the observed ¹³C^α chemical shifts. Whether an ensemble of conformations rather than any single structure is a more accurate representation of a protein structure in the crystal as well as of the observed ¹³C^α chemical shifts is determined by the dispersion of coordinates, in terms of the all-atom r.m.s.d. among the generated models; these generated models satisfy the experimental X-ray data with accuracy as good as the PDB structure. Therefore, generation of an ensemble is a necessary step to determine whether or not a single structure is sufficient for an accurate representation of both experimental X-ray data and observed ¹³C^α chemical shifts in solution.

1. Introduction  

Structural knowledge of biological macromolecules is crucial for a full understanding of their function as well as for a number of practical applications such as protein engineering and drug design. X-ray crystallography and NMR spectroscopy are two major techniques that are used to obtain this information. Based on biophysical principles, these techniques are expected to lead to similar structures, within certain error bounds, of a given protein. However, a recent study of pairs of NMR- and X-ray-determined structures of 148 proteins (Andrec et al., 2007 ▶) showed that statistically significant differences exist between these two types of structures. It was also concluded that at the present time it is not possible to decide whether differences in the methodologies used to solve protein structures from X-ray and NMR data or the difference between the crystal and solution environments are the main source of the structural variation.

Proteins are flexible molecules which exhibit anisotropic motion and exist as a dynamic ensemble of conformations. NMR experiments provide information about protein structure in solution in the form of such an ensemble. Although protein flexibility in the crystalline state is reduced (compared with that in solution) as a result of crystal packing, some dynamics and heterogeneity still remain (Ringe & Petsko, 1986 ▶; DePristo et al., 2004 ▶) because of the high solvent content of most protein crystals (Jensen, 1997 ▶). Nevertheless, when differences between NMR- and X-ray-derived models are discussed, protein structures solved by X-ray diffraction are traditionally represented by a single conformation. Crystallo­graphic temperature (B) factors, which contain information about atomic displacements arising from the combined effects of dynamics and static and lattice disorder within the crystal lattice, provide an important indication of protein motions in the crystalline state. Clore & Schwieters (2006 ▶), who carried out ensemble refinement of the third immunoglobulin-binding domain of streptococcal protein G by using a combination of residual dipolar coupling and ¹⁵N relaxation data with B factors from a high-resolution room-temperature crystal structure, came to the conclusion that all these data are consistent with one another and reflect the same type of motion. The use of explicit B-factor restraint terms by Clore and Schwieters may not be fully justified because temperature factors not only contain information about protein dynamics but are also influenced by lattice disorder and systematic errors. Nevertheless, consideration of an ensemble of protein conformations generated using B-factor values as a guide may potentially improve the agreement between the NMR- and X-­ray-derived protein models in terms of some NMR observables, such as ¹³C^α chemical shifts.

It has recently been shown (Vila, Villegas et al., 2007 ▶) that ¹³C^α chemical shifts can be used as a metric to assess the quality of experimental protein models. This analysis was carried out by using a self-consistent quantum-chemical-based methodology to compute ¹³C^α chemical shifts in proteins of any class or size accurately (Vila, Villegas et al., 2007 ▶). The methodology has also been applied to validate (Vila, Villegas et al., 2007 ▶), refine (Vila & Scheraga, 2008 ▶) and determine (Vila, Ripoll et al., 2007 ▶; Vila et al., 2008 ▶) protein structures at a high-quality level without relying on any knowledge-based information. Using this methodology, we demonstrated that an ensemble of ten NMR-derived conformations (PDB code 1d3z) of ubiquitin (Cornilescu et al., 1998 ▶) is a better representation of the ¹³C^α chemical shifts in solution than a single conformation solved by X-ray diffraction at 1.8 Å resolution (Vijay-Kumar et al., 1987 ▶) for the same protein.

However, this previous analysis was carried out using the standard ECEPP/3 residue geometry (Némethy et al., 1992 ▶), in which bond lengths and bond angles are fixed (rigid-geometry approximation), for both the ten NMR-derived conformations and the single conformation solved by X-ray diffraction at 1.8 Å resolution. This standard geometry was adopted because quantum-chemical calculations are very sensitive to bond length and bond angle (de Dios et al., 1993 ▶) and hence the use of this geometry was a necessary condition for consistent comparison of protein structures.

The goal of this communication is to investigate whether by fitting the X-ray diffraction data it is possible to generate a set of conformations which provides a better representation, in terms of ca-r.m.s.d., of the observed ¹³C^α chemical shifts than a single X-ray structure. Since protein dynamics in solution is reflected to a certain extent in the observed ¹³C^α chemical shifts, it is reasonable to suggest that consideration of protein dynamics remaining in the crystalline state (Ringe & Petsko, 1986 ▶), as indicated by the dispersion of conformations fitting the electron-density distribution with similar accuracy, may improve the agreement between the observed ¹³C^α chemical shifts and those computed for X-ray-derived models. In contrast to all our earlier work (Vila, Villegas et al., 2007 ▶; Vila, Ripoll et al., 2007 ▶; Vila et al., 2008 ▶, 2009 ▶), we did not use standard (rigid) geometry in model refinement in this paper because it may not lead to protein conformations with accuracy comparable to that of the X-­ray PDB structures.

To accomplish this goal, two proteins were selected, namely ubiquitin (α/β, 76 residues; from here on called UBQ) and the RNA-binding domain of nonstructural protein 1 of influenza A virus (α-­helical, 70 residues; from here on called AIL). The structures of both of these proteins (shown in Fig. 1 ▶) were solved by X-ray [PDB code 1ubq (Vijay-Kumar et al., 1987 ▶) and PDB code 1ail (Liu et al., 1997 ▶), respectively] and NMR [PDB code 1d3z (Cornilescu et al., 1998 ▶) and PDB code 1ns1 (Chien et al., 1997 ▶), respectively] methods, with the latter providing the available ¹³C^α chemical shifts.

Figure 1.

Ribbon diagrams of protein 1ubq (a) and protein 1ail (b). Segments colored yellow and red designate sequences of residues in α-helices, cyan those in β-sheets and grey those residues which do not pertain to any regular secondary structure.

2. Method  

2.1. Model generation and refinement  

The atomic structures and structure factors of 1ubq and 1ail were obtained from the PDB.

Initial models for UBQ and AIL were generated by carrying out a search with the Monte Carlo-with-Minimization (MCM) method (Li & Scheraga, 1998 ▶), starting from the corresponding regularized experimental X-ray structure, i.e. that with the bond lengths and bond angles of all residues set to the standard ECEPP/3 values (Némethy et al., 1992 ▶) and kept fixed (rigid geometry approximation). This rigid geo­metry was used only in the MCM conformational search, not in the refinement against the X-ray data. During the search, variations of the (ϕ, ψ, χ) torsional angles were allowed for all the residues in the sequence. The reported B factors were used to estimate the upper limit of the torsional angle variation (Λ). Thus, a tolerance range of Λ = ±10° was adopted. This range of angular variation leads to a temperature factor of up to 45 Ų per residue, which is close to the largest B factors reported for either the 1ubq (Vijay-Kumar et al., 1987 ▶) or 1ail (Liu et al., 1997 ▶) structures (36 and 39 Ų, respectively). The temperature factors were computed as (8π²)〈u _j〉, with 〈u _j〉 representing the mean-square displacement of all atoms of residue j, other than H atoms, from their mean positions.

Conformations with an all-atom r.m.s.d. of <2 Å from the deposited PDB structure were selected and clustered using the minimal spanning tree method (Kruskal, 1956 ▶) and by assuming a specific r.m.s.d. cutoff of 0.2 Å for all heavy atoms and no cutoff in energy. The resulting 18 and 11 conformations of UBQ and AIL, respectively, were chosen for further analysis.

Structure-refinement and R-factor calculations for the models were performed using the Crystallography and NMR System (CNS) program (Brünger et al., 1998 ▶; Brunger, 2007 ▶) with a maximum-likelihood function and Babinet bulk-solvent correction (Hodel et al., 1992 ▶). New free sets of structure factors including 10% of the reflections were generated to compute R _free for both UBQ and AIL. The free sets were excluded from all refinement and map calculations. B factors were reset to 20 Ų for backbone and 30 Ų for side-chain atoms at the beginning of the structure refinement to eliminate bias towards the PDB structure. Water molecules were taken directly from the PDB to ensure that an equivalent number of atoms was modeled. Water atoms were allowed to move during refinement.

The generated initial structures of UBQ (18) and AIL (11) were poor models of the corresponding diffraction data, with R and R _free factors of 45–52%. Refinement of these initial structures with CNS was carried out using the procedure described by Adams et al. (1997 ▶). Initial simulated-annealing refinements were repeated six times with different initial velocities. Structures with values of R < 24% and R _free < 26% (five and three for UBQ and AIL, respectively) were selected. Simulated-annealing OMIT electron-density maps for these structures were calculated with CNS using the Babinet bulk-solvent correction. The maps and the corresponding models were displayed with the molecular-graphics application Coot (Emsley & Cowtan, 2004 ▶). Whenever it was necessary, the conformations of the side chains were corrected manually to improve the fit to the electron-density distribution. Final structure refinements for each of these remaining conformations were carried out by simulated annealing, repeated ten times with different initial velocities followed by B-factor refinement.

The ensemble R and R _free factors were calculated by including all the final models (five and three for UBQ and AIL, respectively) generated for each protein using the procedure described above in a single asymmetric unit and assigning the atomic occupancies to 0.20 and 0.33 for UBQ and AIL, respectively.

Since the deposited PDB structures (1ubq and 1ail) were solved and refined using software and parameters that differed from those employed in this work, reference conformations were obtained by one round of simulated annealing [simulated-annealing refined (SAR) structures], starting from the original PDB structures. This refinement of the PDB structures is also a necessary step for consistent comparison between the chemical shifts of the generated models and the PDB structure, because ¹³C^α chemical shifts are very sensitive to small differences in bond lengths and bond angles (deDios et al., 1993 ▶).

To assess the stereochemical quality of the models, measures such as the r.m.s.d. of bond lengths and bond angles, the ϕ/ψ compatibility with the Ramachandran plot (Lovell et al., 2003 ▶) and the number of unfavorable contacts were employed. Ramachandran outliers were calculated with PROCHECK (Laskowski et al., 1993 ▶).

2.2. Calculation of ¹³C^α chemical shifts  

The ¹³C^α chemical shifts were computed using the method­ology described in a recently published paper (Vila, Villegas et al., 2007 ▶) and hence only the most essential information is provided here.

The ¹³C^α chemical shifts for each conformation were computed with the following approximations: (i) each amino-acid residue X in the protein sequence was treated as a terminally blocked tripeptide with sequence Ac-GXG-NMe, with X in the conformation of the protein structure, and (ii) the ¹³C^α isotropic shielding values (σ) for each amino-acid residue X were computed at the OB98/6–311+G(2d,p) level of theory (Vila et al., 2009 ▶) with the Gaussian03 package (Frisch et al., 2004 ▶). The remaining residues in each tripeptide were treated at the OB98/3-21G level of theory, i.e. by using the locally dense basis set approach (Chesnut & Moore, 1989 ▶). All ionizable residues were considered to be neutral during the quantum-chemical calculations (Vila & Scheraga, 2008 ▶).

2.3. Computation of the ca-r.m.s.d.  

For each amino-acid residue μ in the sequence, the ¹³C^α conformational average chemical shift, 〈¹³C^α _computed〉_μ, is com­puted as 〈¹³C^α _computed〉_μ = (1/ Ω) ¹³C^α _μ,i, where ¹³C^α _μ,i is the DFT-computed chemical shift for residue μ in conformation i out of Ω conformations, 1 ≤ μ ≤ N, with N being the total number of residues in the sequence, e.g. 76, and Ω is the total number of conformations obtained, viz. five for ubiquitin. The 〈¹³C^α _computed〉_μ for each residue μ in the sequence is used to compute the ca-r.m.s.d. (Vila, Villegas et al., 2007 ▶) as follows:

If Ω = 1, as for the X-ray structure or any single conformation, then ca-r.m.s.d. ≅ r.m.s.d.

2.4. CPU-time requirements  

Calculation of the ¹³C^α chemical shifts represents the highest computational cost of this work. The average com­putational time for this step can be estimated as the average over the total number (N) of residues in a single conformation,

where T _i represent the total CPU time (in seconds) for residue i, as reported by the Gaussian03 suite of programs (Frisch et al., 2004 ▶). All DFT calculations were carried out on a system (i.e. Pople) of 768 cores with a floating-point capability of 5.1 Tflops located at the Pittsburgh Supercomputing Center. The CPU time necessary to compute all of the ¹³C^α chemical shifts for conformation 1 of ubiquitin, averaged over 76 residues, was 1634 s per residue using a cluster of 76 processors with one processor per residue. Thus, computation of the ¹³C^α chemical shifts for five conformations of ubiquitin was accomplished in ∼2 h.

3. Results and discussion  

3.1. Ubiquitin  

Details of the five final X-ray models generated for ubiquitin are provided in Table 1 ▶. These models are quite different among themselves and from the corresponding SAR PDB structure (Fig. 2 ▶), with an all-atom r.m.s.d. of 0.36–1.13 Å; the R and R _free factors of the models are equivalent to or better than those of the refined PDB structure (columns 3 and 4 in Table 1 ▶).

Table 1. Results of the refinement against the X-ray data for UBQ.

Models	R.m.s.d.† ()	R (%)	R free (%)	R.m.s.d. bond lengths ()	R.m.s.d. bond angles ()	Allowed /‡ (%)	No. of bad contacts
PDB§		19.1 (17.6)¶	20.1	0.014	1.71	100.0	1
1	1.125	17.9	19.7	0.016	1.89	100.0	0
2	1.056	18.0	19.7	0.014	1.79	98.5††	2
3	1.018	18.3	20.1	0.015	1.80	98.5††	1
4	1.082	18.1	20.2	0.015	1.83	98.5††	2
5	0.358	17.8	19.0	0.016	1.85	100.0	0
Ensemble‡‡		17.9	20.4

^†Compared with the SAR PDB structure.

^‡Including core and allowed regions of the Ramachandran plot (PROCHECK).

^§Following one round of simulated-annealing refinement of the PDB structure (1ubq).

^¶ R factor reported in the original publication. It may differ from the SAR value owing to the use of different parameters and approximations for the R-factor calculations and the bulk-solvent correction.

^††The remaining 1.5% belongs to the generously allowed region of the Ramachandran plot.

^‡‡The ensemble consists of models 15.

Figure 2.

Overlay of the SAR PDB structure (red) with the five alternative models (blue) of ubiquitin.

As shown in Table 1 ▶, measures of the local correctness, such as r.m.s.d. in bond lengths and bond angles, ϕ/ψ compatibility with the Ramachandran plot (Lovell et al., 2003 ▶) and the number of unfavorable contacts, are also similar to those of the SAR PDB structure. For all five models, no residues were in disallowed regions of the Ramachandran plot (Laskowski et al., 1993 ▶). All unfavorable contacts occurred between the atoms from the last five residues in the sequence which were not visible in the electron-density map.

B-factor distributions are almost identical among the alternative and SAR PDB structures, with correlation coefficients of 0.91–0.99 over the average residue B factors (Fig. 3 ▶ a). Figs. 3 ▶(b) and 3 ▶(c) show all-atom and backbone-atom r.m.s.d.s from the SAR PDB structure. The most significant variability of the generated models was found for the C-­terminal region, including amino-acid residues 71–76 which were disordered and not visible in the electron-density map. The rest of the sequence is also quite flexible, with a backbone r.m.s.d. of up to 0.5 Å. The atomic positions of side chains are highly variable, as reflected by the larger all-atom r.m.s.d. (Fig. 3b ▶).

Figure 3.

B factors and r.m.s.d. per residue for ubiquitin. (a) B factors of the PDB structure (1ubq; dotted line) and the five alternative models (averaged over five models; solid line). (b) All-atom and (c) backbone r.m.s.d. from the SAR PDB structure for each residue averaged over the five alternative models.

Considering the overall quality of the new conformations obtained for ubiquitin, we conclude that these structures are equivalent solutions for the contents of the protein crystal.

For ubiquitin, the ensemble R _free factor is slightly worse than any individual model (Table 1 ▶) and ∼0.7% higher than the average R _free of the models, presumably owing to the simplicity of our ensemble structure-factor calculations, which did not include simulated-annealing refinement of the ensemble. Moreover, the ensemble R _free factor is only slightly higher (0.3%) than the R _free of the refined PDB structure.

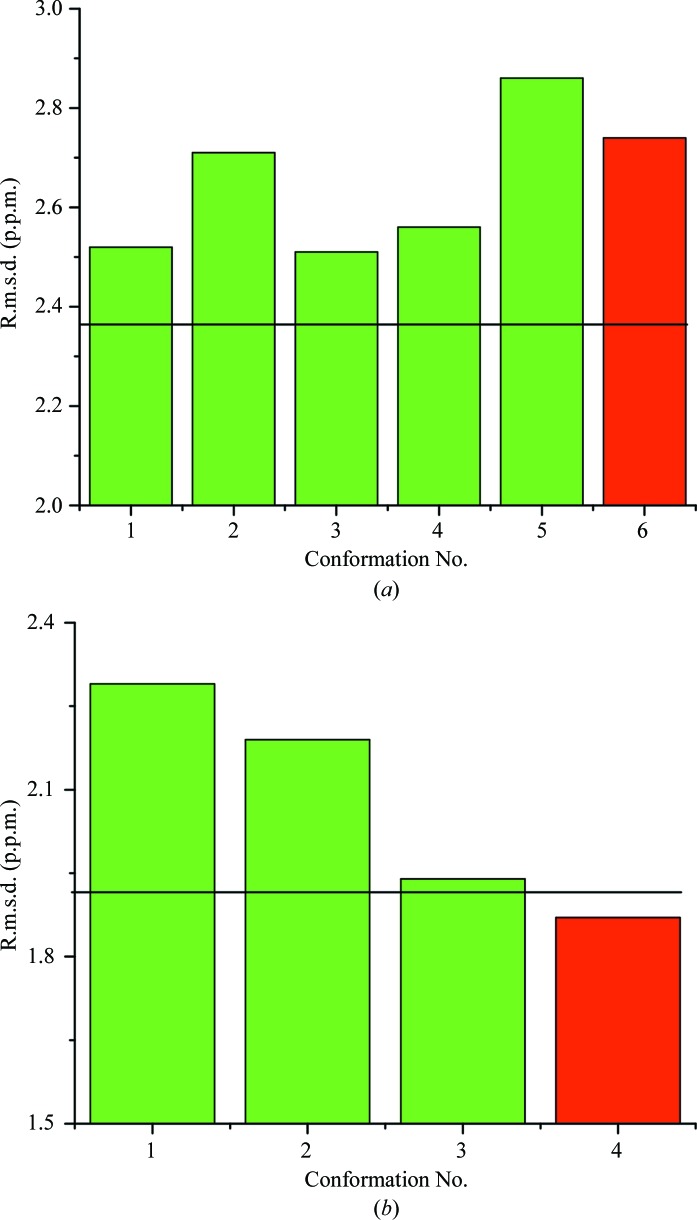
Fig. 4 ▶(a) shows the r.m.s.d. values between the observed and computed ¹³C^α chemical shifts obtained for the five generated conformations (green bars) and the SAR PDB structure (red bar). The ca-r.m.s.d. computed for the ensemble of the five generated conformations (green-filled bars) is shown as a horizontal solid line in Fig. 4 ▶(a). The ca-r.m.s.d. (2.36 p.p.m., shown in Fig. 4 ▶ a) is lower than the value for the SAR PDB structure (2.74 p.p.m.) or for any of the new models. These results obtained for ubiquitin demonstrate that consideration of an ensemble of five conformations derived from the refined PDB structure leads to better agreement with the observed ¹³C^α chemical shifts than does a single conformation (the SAR PDB structure).

Figure 4.

Bar diagram of the r.m.s.d. (p.p.m.) between computed and observed ¹³C^α chemical shifts for (a) ubiquitin and (b) the RNA-binding domain of nonstructural protein 1 of influenza A virus. Red bars represent the SAR PDB models. Green bars represent the r.m.s.d. for each conformation from the UBQ and AIL ensembles generated in this work; the black solid horizontal lines represent the ca-r.m.s.d. for each ensemble (2.36 and 1.92 p.p.m. for UBQ and AIL, respectively).

3.2. The RNA-binding domain of nonstructural protein 1 of influenza A virus  

This protein was solved at 1.9 Å resolution (Liu et al., 1997 ▶) as a single conformation with isotropic B factors (PDB code 1ail). The R _free values of our three models are 0.1–0.6% higher than those of the SAR PDB structure (Table 2 ▶). The B factors of the SAR PDB structure and the three models listed in Table 2 ▶ are almost identical (see Fig. 5 ▶ a), with a correlation coefficient of ∼0.99 among them.

Table 2. Results of the refinement against the X-ray data for AIL.

Models	R.m.s.d.† ()	R (%)	R free (%)	R.m.s.d. bond lengths ()	R.m.s.d. bond angles ()	Allowed /‡ (%)	No. of bad contacts
PDB§		18.3 (18.2)	22.2	0.017	1.45	100.0	0
1	0.675	19.2	22.7	0.016	1.44	100.0	0
2	0.224	18.1	22.3	0.016	1.48	100.0	0
3	0.187	18.2	22.8	0.015	1.47	100.0	0
Ensemble		18.1	21.8

^†Compared with the SAR PDB structure.

^‡Including core and allowed regions of the Ramachandran plot (PROCHECK).

^§Following one round of simulated-annealing refinement of the PDB structure (1ail).

^¶ R factor reported in the original publication. It may differ from the SAR value owing to the use of different parameters and approximations for the R-factor calculations and the bulk-solvent correction.

^††The ensemble consists of models 13.

Figure 5.

B factors and r.m.s.d. per residue for the RNA-binding domain of nonstructural protein 1 of influenza A virus. (a) B factors of the PDB structure (1ail; dotted line) and the three alternative models (solid line). (b) All-atom and (c) backbone r.m.s.d. for each residue of the alternative models compared with the SAR PDB structure.

All three models in Table 2 ▶ as well as the refined PDB structure have very similar stereochemical quality, as seen from their r.m.s.d. in bond lengths and bond angles, ϕ/ψ compatibility with the Ramachandran plot and the number of unfavorable contacts (Table 2 ▶). All the models have no residues in disallowed regions of the Ramachandran plot and can be considered as equivalent solutions for the content of the protein crystal.

The alternative conformations exhibited little variance from the PDB structure or among themselves (Fig. 6 ▶). Thus, the all-atom r.m.s.d. of the new models from the SAR PDB structure is 0.19–0.68 Å (Table 2 ▶), which is almost two times lower than the corresponding values for ubiquitin (Table 1 ▶). The RNA-binding domain of nonstructural protein 1 of influenza A virus exhibits a lower degree of both side-chain and backbone variability in our models (Figs. 5 ▶ b and 5 ▶ c) than ubiquitin. The backbone conformation is essentially the same in all models (backbone r.m.s.d. of ∼0.1 Å). The side chains are somewhat more variable (all-atom r.m.s.d. of up to 0.4 Å) than the backbone, with ∼10% of the side chains in different conformations.

Figure 6.

Overlay of the SAR PDB structure (red) with the three alternative models (blue) of the RNA-binding domain of nonstructural protein 1 of influenza A virus.

The lower variability of the models produced for this protein can be explained by the presence of an unusually high percentage (80%) of residues in repetitive secondary structure (α-­helix) compared with the average percentage of residues in regular secondary structure in proteins of about 40% (Xu & Case, 2001 ▶), which makes them more ‘rigid’ compared with those of ubiquitin.

For AIL, the ensemble R _free factor is better than that of any individual model, the SAR PDB structure or the average R _free of the models (Table 2 ▶).

Figure 4 ▶(b) shows the ¹³C^α chemical shift r.m.s.d. versus the protein conformation number for three models of AIL (green bars) plus the SAR PDB structure (red bar). It can be seen from Fig. 4 ▶(b) that the SAR PDB structure (r.m.s.d. = 1.87 p.p.m.) is a better representation of the observed ¹³C^α chemical shifts than any one of the three derived conformations or their ensemble described by the ca-r.m.s.d. (1.92 p.p.m., as shown by a black horizontal line in Fig. 4 ▶ b).

Considering the significant similarity of the generated models among themselves and to the SAR PDB structure as well as the results of ¹³C^α chemical-shift calculations, a single PDB structure of AIL appears to be a suitable representation of the X-ray and ¹³C^α chemical-shift data. This result is in contrast to that obtained for ubiquitin, for which the ensemble of derived conformations was found to be a better representation of the ¹³C^α chemical shifts than the SAR PDB structure (see Fig. 4 ▶ a).

3.3. In summary  

The results obtained for UBQ and AIL represent two different examples for a number of reasons. Firstly, the number of X-ray-derived conformations for each of them is different and shows a different dispersion of all-atom (and backbone) r.m.s.d. between the models (Tables 1 ▶ and 2 ▶, and Figs. 3 ▶ and 5 ▶). Thus, three models of AIL possess almost identical backbone conformations. The dispersion of all-atom (and backbone) r.m.s.d. between the UBQ models remains almost two times greater than the corresponding dispersion for AIL, even after removal of the most flexible C-terminal residues from the r.m.s.d. calculations for both proteins (results not shown). Secondly, the ca-r.m.s.d. of the UBQ ensemble is lower than that for any individual model, including the SAR PDB structure. On the other hand, the SAR PDB structure of AIL exhibits a better ¹³C^α chemical-shift r.m.s.d. than either the ensemble or any generated model. These results may indicate different dynamics of these two proteins in both solution and crystal. The origin of this difference may lie in the flexibility of these two proteins resulting from the significantly different number of residues in secondary structure, namely 80% and 57% for 1ail and 1ubq, respectively. It should be mentioned that crystal structures of both proteins were solved at the same temperature and have very similar solvent content (∼33%). From this point of view, AIL seems to be more rigid than UBQ and therefore a single SAR PDB structure of AIL is a suitable representation of the observed ¹³C^α chemical shifts in solution.

4. Conclusions  

Recent work on X-ray protein structure determination (DePristo et al., 2004 ▶; Furnham et al., 2006 ▶) suggested that an ensemble of conformations is a more suitable representation of a protein crystal structure than a single model. The results of our analysis of the observed and computed ¹³C^α chemical shifts for different X-ray-derived models of UBQ are in agreement with this suggestion. However, if the ensemble of derived models is very tight, as for AIL, a single model would be a suitable representation of the observed ¹³C^α chemical shifts in solution and the experimental X-ray data.

In the absence of observed ¹³C^α chemical shifts, the formulation of accurate criteria to decide whether an ensemble or a single conformation should be reported as a solution for the X-ray diffraction data will require further analysis of a larger number of X-ray-derived proteins displaying a variety of secondary-structure contents, three-dimensional motifs and crystal packings. Analysis of these criteria will be a topic of future work.