Abstract
Freezing of biological tissue is emerging in various biomedical applications. The success of these applications requires precise control of the tissue functionality, which is closely associated with the microstructure of the extracellular matrix (ECM). In the present study, the spatiotemporal effects of freezing on the ECM were experimentally and theoretically investigated by approximating biological tissue as a poroelastic material saturated with interstitial fluid. The experiments with type I collagen gel showed that its matrix underwent two distinct levels of structural changes due to freezing : enlarged pore structure of the matrix and increased collagen fibril diameters. The extent of these changes was augmented as the freezing temperature was lowered. The theoretical model suggested that the interstitial fluid might be transported toward the unfrozen region from the phase change interface due to the volumetric expansion associated with the water-ice phase change, and the transported fluid could interact with the matrix and enlarge its pore structure. The model also illustrated the effects of matrix structural properties on this interaction including initial porosity, hydraulic conductivity and elastic modulus. These results imply that an identical macroscopic freezing protocol may result in different microstructural alterations of poroelastic materials depending on the structural properties of the matrix. This may be relevant to understanding the tissue-type dependent outcomes of cryomedicine applications and be useful in designing cryomedicine applications for a wide variety of tissues.
Keywords: Poroelastic material, Freezing, Fluid-matrix interaction, Matrix Structure
INTRODUCTION
Freezing of biological tissue is emerging in biomedical applications to treat diseased tissues (i.e., cryotherapy) or to preserve tissues (i.e., cryopreservation). Cryotherapies are minimally invasive surgical techniques to destroy malignant tissues by freezing while sparing surrounding normal tissues. These include cryosurgery of cancer in several organs [1], cryoplasty for restenosis of coronary arteries [2, 3], and cryoablation for cardiac arrhythmia [4, 5]. To the contrary, cryopreservation employs freezing to preserve native and engineered tissues for an extended period of time [6, 7]. This can provide a prolonged time window for transplantation and implantation surgery, and ultimately “off-the-shelf” availability of engineered tissues [8, 9]. In spite of its success in several tissue systems, the utilization of cryomedicine in different tissue systems is still significantly challenging since its outcomes are highly tissue-type dependent [10]. Moreover, the success of these applications requires precise control of both viability and functionality of tissues, which makes the problem even more challenging. In particular, post-thaw functionality is critical to the prognosis and recovery of cryo-treated tissues, and the physiology of cryopreserved tissues. The control of post-thaw functionality becomes more important as freezing-based technologies begin to be applied to larger and more complex tissues.
In order to control and predict the outcomes of these applications, the effects of freezing on the extracellular matrix (ECM) should be understood as well as those on the cellular viability [11-14], since the microstructure of the ECM is closely associated to and often determines various functional properties of tissues including mechanical and transport properties. Besides providing structural support and determining the functional properties, the ECM plays significant roles in tissue physiology through interaction with cells and interstitial fluid transport. These roles include regulating cell morphology and growth [15, 16], and intercellular signaling [17]. The ECM can also be reconfigured by cells during tissue remodeling and wound healing [18-20]. In spite of its significance, the effects of freezing/thawing-induced biophysical phenomena on post-thaw cell-ECM interaction and cellular physiology are not well understood. Thus, preserving the ECM microstructure during freezing/thawing is a key for cryopreservation of functional tissues.
Although the formation of ice in the extracellular space is thought to induce damage on the ECM microstructure, the extent of extracellular ice formation (EIF) and subsequent damage on the ECM microstructure are not well understood nor quantified. When tissue undergoes a freezing process, spatiotemporal fluid-matrix interaction may occur, as illustrated in Figure 1. These are - 1) volume expansion during water-ice phase change; 2) interstitial fluid transport at the freezing interface; and 3) deformation of the unfrozen ECM to accommodate the interstitial fluid. Though not shown in Figure 1, the cells will also actively participate in the fluid-matrix interaction through osmotic pressure-driven water transport, exerting mechanical force on the matrix, and even acting as a granular matrix.
Figure 1.
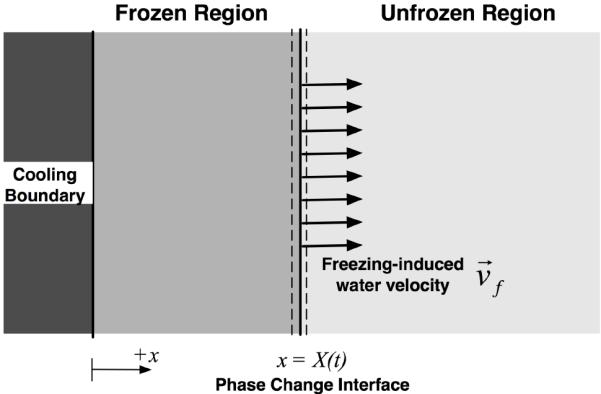
Schematic of freezing induced interstitial fluid transport. Due to the volumetric expansion associated with freezing of water, the interstitial fluid is expected to transport from the phase change interface to the unfrozen region.
Among these tissue-level biophysical phenomena during freezing, osmotic pressure-driven water transport between the intracellular and extracellular spaces has mainly been studied and analyzed using similar principles as in cell suspensions. Several experimental techniques have been used to quantify the water transport including cryomicroscopy [21, 22], a “two-step freezing” technique [23], and differential scanning calorimetry [24, 25]. The morphology of EIF in several tissues has also been investigated and correlated to freezing/thawing parameters including cooling rates and end temperatures [23, 26-28]. Although these studies implied that the EIF was affected by the freezing-induced biophysical phenomena, many of the studies have been performed with small tissue samples or have been analyzed based on compartment models, where the temporal aspects of the biophysical phenomena were dominant. A theoretical study on these temporal effects on non-biological poroelastic material was performed by Coussy [29]. However, a recent study [30] reported that noticeable microstructural alteration, which was highly spatially varying, was observed after engineered tissue equivalents were frozen and thawed. This suggests that the spatial aspects of the EIF and subsequent damage of the ECM may become important during freezing of larger and more complex tissues. Thus, the understanding of freezing-induced spatiotemporal fluid-matrix interaction is highly desired for successful cryomedicine applications to various tissue systems.
In the present study, the spatiotemporal effects of freezing on the ECM were experimentally and theoretically investigated by approximating biological tissue as a poroelastic material saturated with interstitial fluid. For the experiment, collagen gel was prepared and the freezing-induced microstructural changes of collagen matrix were investigated using a quantitative microscopy technique. For the analysis, a theoretical model was developed to analyze the freezing-induced interaction of interstitial fluid and matrix, and predict the alteration of the matrix microstructure. With the poroelastic approximation, one-dimensional freezing process was numerically simulated considering energy conservation with phase change, freezing-induced interstitial fluid transport through porous matrix, balance of stress-strain-interstitial fluid pressure (IFP), and swelling of the elastic matrix. The effects of matrix structural properties including initial porosity, hydraulic conductance and elastic modulus were also investigated.
MATERIALS AND METHODS
Collagen Gel Preparation
As a model poroelastic material, collagen gel was prepared by a similar protocol used in [30]. Briefly, to prepare a 2 mL gel with a final collagen concentration of 3 mg/mL, 138 μL of sterile, ice cold 0.1 M NaOH (Sigma-Aldrich, St. Louis, MO) was added to 200 μL of warm 10X MEM (Invitrogen, Carlsbad, CA). Next, 1062 μL of sterile distilled water was added, and the contents were mixed. Then, 600 μL of collagen (Collagen Type I High Protein Rat Tail, BD Bioscience, Franklin Lakes, NJ) with an initial concentration of 10 mg/mL was added to the solution and mixed. Finally, the solution was placed in a one-well chamber slide (Nunc Lab-Tek II Chamber Slide System, Fisher Scientific, Pittsburgh, PA) and polymerized for 1 hour at 37 °C and 5% CO2 environment. After polymerization, 2 mL of 1xPBS was added and the gel was incubated for 24 hours before the freezing procedures.
Directional freezing of collagen gels
The gels were frozen on a directional solidification stage [31] from 4 °C to either -20 or -40 °C at the rate of 5 °C/min. The directional solidification stage consisted of two constant temperature reservoirs, which are at different temperatures and separated by an adjustable gap. The first reservoir was held at 4.0 ± 0.2 °C and the temperature of the other reservoir was set at either -20.0 ± 0.2 °C or -40.0 ± 0.2 °C. The chamber slide was moved from the high temperature reservoir to the low temperature one over the gap at a precisely controlled velocity. By appropriately setting the chamberslide velocity, gap size, and reservoir temperatures, nominally constant cooling rates and precise end temperatures could be imposed on the gels. Half of each gel was frozen, leaving a frozen and unfrozen section of the same sample. The samples were passively thawed at room temperature after freezing, and then characterized using scanning electron microscopy (SEM).
Microscopy and image analysis for freezing-induced microstructural change
To assess the morphological and fibril level changes of the collagen matrix, scanning electron microscopy (SEM) was employed. After thawing, the gels were divided in four column sections as noted in Figure 2 (i.e., F1, F2, UF3 and UF4). F1 and F2 were obtained by dividing the frozen region into a half, and UF3 and UF4 were obtained by dividing the unfrozen region into a half. Then, the sample columns were fixed by the osmium tetroxide vapor fixation technique [32]. After vapor fixation, three plugs were cut out from each column section and then dehydrated in ethanol series for 72 hours. After dehydration, the plugs were critical point dried and sputter-coated with gold-palladium. The plugs were then observed and imaged using a scanning electron microscope (JEOL JSM-35C, JEOL Ltd., Tokyo, Japan) operating at 1500X magnification.
Figure 2.

Top view of collagen gel after freezing/thawing on a directional solidification stage. The unfrozen portion (i.e., UF3 and UF4) is translucent, but the frozen portion (F1 and F2) is transparent.
The SEM micrographs were quantitatively analyzed using NIH ImageJ for collagen fibril diameter and mean void area (MVA) of collagen matrix. The image processing procedures were developed based on [33], and the detailed procedures were described in [34]. Briefly, after importing an SEM image in ImageJ, at least 5 interrogation windows of 130 × 100 pixels (6.2μm × 4.6μm) were randomly cropped and despeckled. The fibril diameter was determined by measuring the thickness of 10 blindly selected fibrils in each interrogation window, and all the measured diameters were averaged. Then, the images were further processed to quantify the mean void area (MVA), which is the ratio of the void area to the area of the interrogation window. Thus, the MVA can be interpreted as a 2-dimensional porosity. The cropped interrogation windows were binarized and skeletonized to obtain the morphological information of the collagen matrix. Then, the total number of pixels occupied with voids was obtained and normalized to the number of total pixels.
THEORETICAL BACKGROUND
To investigate the freezing-induced fluid-matrix interaction illustrated in Figure 1, freezing of biological tissue was approximated to the one-dimensional freezing of a poroelastic material saturated with water and its deformation is infinitesimal. With the assumptions of constant properties in each frozen and unfrozen region and thermal equilibrium of water and the matrix, the governing equations are reduced to - 1) consolidation equation; 2) energy conservation equation; 3) modified Darcy’s law; 4) pressure-dilatation relation; and 5) dilatation-porosity relation as described in [35]. Besides these governing equations, the boundary conditions at the phase change interface need to be formulated. The interface location is determined by solving the energy conservation equation, and the movement of the phase change interface is used to evaluate the interstitial fluid velocity at the interface by considering mass conservation as below,
| (1) |
where vf is the interstitial fluid velocity, X(t) is the location of the phase change interface, ϕ is the porosity, and ρs and ρl are the density of ice and water, respectively. This interstitial fluid velocity was integrated over time, t, to provide the boundary condition for the consolidation equation of the unfrozen region to evaluate local dilatation (i.e., volume expansion) of the poroelastic matrix as below,
| (2) |
where K is the hydraulic conductivity, E is the elastic modulus, and ν is Poisson’s ratio. The dilatation, e, is related to the interstitial fluid pressure (IFP) through the modified Darcy’s law and the constitutive equation as below,
| (3) |
where p is the IFP. Detailed derivation of Equations (2) and (3) are described in [36]. In addition, the dilatation, e, can be related to the local porosity as below [37]
| (4) |
where ϕi is the initial porosity.
These equations were discretized using an explicit finite difference scheme and solved numerically to calculate the local porosity, dilatation and IFP changes during freezing. For the numerical simulation, the following parameter values were used - the initial temperature was 20 °C, and the cooling boundary (at x = 0) was maintained at -80 °C. The initial porosity was set to 0.9 based on the measured values in previous tissue engineering studies [38, 39]. The transport and mechanical properties of the poroelastic material were adopted from [40]. The thermal properties were estimated by weight-averaging those of water and collagen from [41, 42]. All these properties were summarized in Table 1. Since the interstitial fluid was approximated as water, the phase change occurred at 0 °C. To elucidate the tissue-dependent interaction mechanism, further simulation was performed with varying initial porosity, hydraulic conductivity and elastic modulus.
Table 1.
Material properties used in the numerical simulation
| Parameters | Values | References | |
|---|---|---|---|
| Hydraulic Conductivity (K) | 7×10-11 m2/s-mmHg | [40] | |
| Elastic Modulus (E) | 110 mmHg | [40] | |
| Poisson’s ratio (v) | 0.3 | [40] | |
| Latent Heat | 335 J/g | [42] | |
| Thermal Conductivity | Water | 0.552 W/m-K | [42] |
| Ice | 2.0 W/m-K | [42] | |
| Collagen | 0.207 W/m-K | [41] | |
| Specific Heat | Water | 4200 J/g-K | [42] |
| Ice | 2100 J/g-K | [42] | |
| Collagen | 1883 J/g-K | [41] | |
| Density | Water | 999 kg/m3 | [42] |
| Ice | 990 kg/m3 | [42] | |
| Collagen | 1304.2 kg/m3 | [41] | |
RESULTS
Figure 3 shows representative SEM micrographs of collagen gels frozen to -20 °C and -40 °C with unfrozen gel as control. The collagen matrix of the unfrozen gel (Figure 3 (A)) exhibits very dense and organized fibril network morphology, and relatively uniform fibril diameter. On the contrary, the collagen network of the gel frozen to -20 °C (Figure 3 (B)) shows a sparse and disorganized network morphology and thicker fibril diameter. The gel frozen to -40 °C also shows similar trends, but the extent of the change is augmented (Figure 3 (C)). These structural changes are thought to be associated with the microstructure of ice formed within the matrix, which is determined by freezing conditions including cooling rates and end temperatures [26-28].
Figure 3.
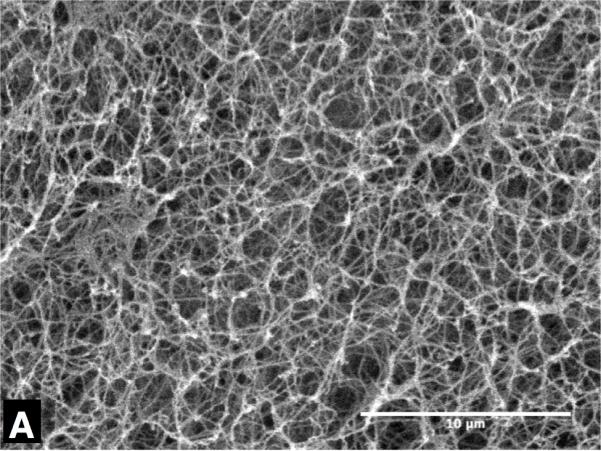
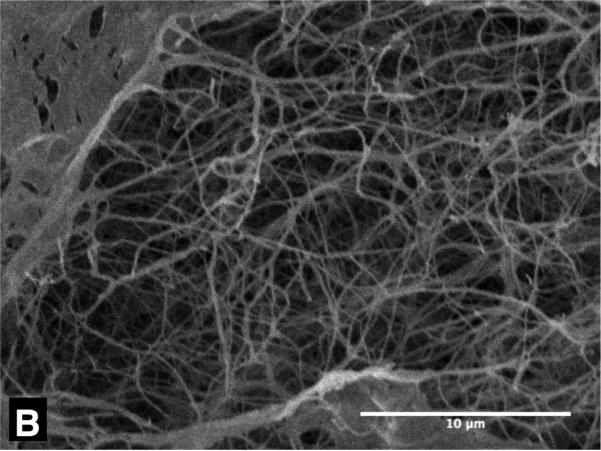

Typical SEM micrographs of collagen gel - (A) unfrozen, (B) frozen to -20 °C and (C) frozen to -40 °C. The unfrozen gel has dense matrix structure of thin collagen fibrils, but the frozen ones have coarse matrix of thick collagen fibrils. The scale bars are 10μm.
The quantified void area ratio of each sample column is shown in Figure 4 (A). As for the gels frozen to -20 °C, the void area ratios of the unfrozen columns, i.e., UF1 and UF2, are 0.893 ± 0.011 and 0.892 ± 0.004 respectively. Across the freezing interface, the void area ratios increase to 0.912 ± 0.006 at F3 and 0.916 ± 0.008 at F4, and these increases are statistically significant (p < 0.01). As for the gels frozen to -40 °C, the void area ratios of the unfrozen columns are 0.883 ± 0.022 and 0.879 ± 0.007 respectively, which are slightly smaller than those of the gels frozen to -20 °C.
Figure 4.
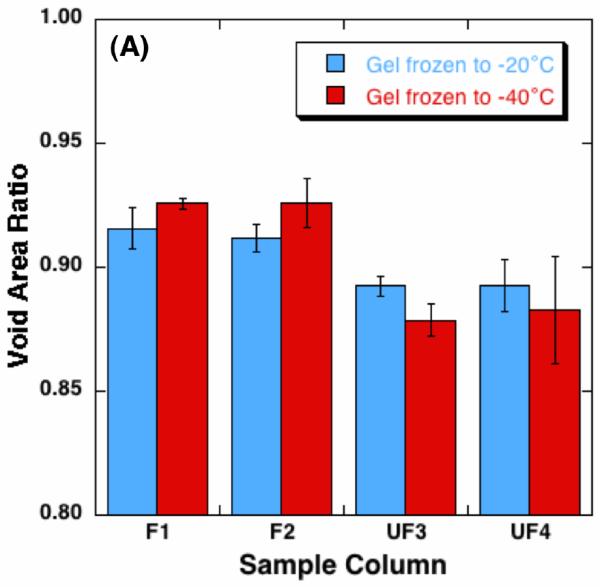
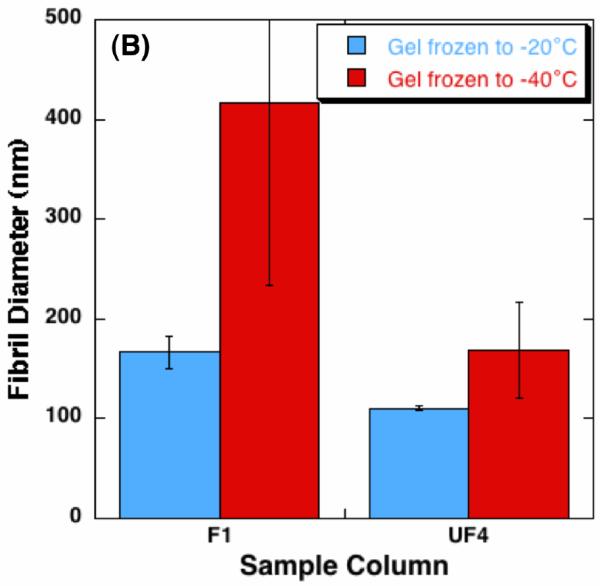
Quantified alteration of collagen gel matrix microstructure after freezing/thawing (n = 3 for each freezing temperature) - (A) void area ratio, and (B) fibril diameter. The void area ratio increases in the frozen region, and the increase of the void area ratio is augmented with lowering the freezing temperature. The fibril diameter also increases after freezing/thawing, whose extent is also augmented with lowering the freezing temperature.
However, the ratios of the frozen columns are 0.926 ± 0.010 at F3 and 0.926 ± 0.002 at F4, which are larger than those of the unfrozen columns (p < 0.01) and even larger than those of the frozen columns in the gels frozen to -20°C (p ≤ 0.05). Measured collagen fibril diameter in column UF1 and F4 are shown in Figure 4 (B). The fibril diameter of the gels frozen to -20 °C increases from 110.4 ± 2.4 nm to 166.7 ± 16.4nm. As for the gels were frozen to -40 °C, the fibril diameter increase is significantly enlarged, i.e., from 168.7 ± 47.6 nm to 417.0 ± 182.4 nm.
Figure 5 shows the results of numerical calculation in terms of the temperature profiles at different times, and the time-dependent interface location and the interstitial fluid velocity at the interface. The calculated temperature profiles agree with well-known moving boundary problem solutions [42]. Due to the volumetric expansion across the water-ice phase change, water transport is induced at the interface with a magnitude of 1∼10 μm/s.
Figure 5.
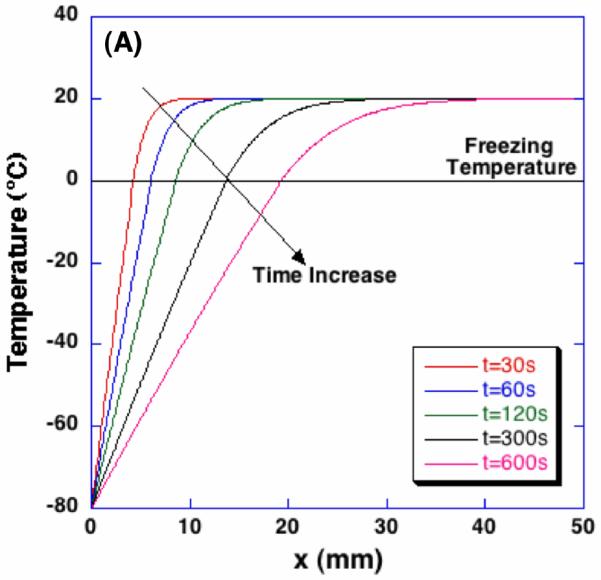
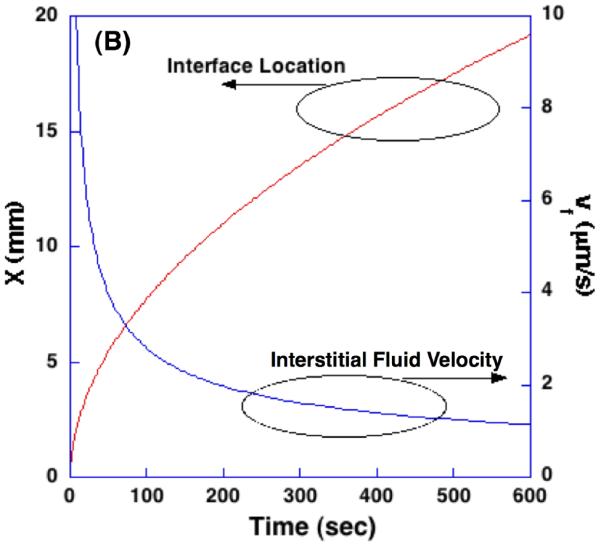
Temperature profiles, the location of phase change interface, and the interstitial fluid velocity at the interface during freezing of poroelastic material.
The profiles of porosity at different time steps are shown in Figure 6. In the frozen region, porosity increases in the x-direction and has a maximum value at the phase change interface. Then, it rapidly decreases to the initial porosity. This increased porosity in the frozen region is attributed to the volumetric expansion of water-ice phase change and the accumulation of the excess water. The increased porosity implies enlarged pores, expansion along and perpendicular to x-direction, and consequent compression of the unfrozen region. The magnitude of these changes is depending on its hydraulic conductivity and elastic modulus, and may ultimately lead to the alteration of the matrix microstructure.
Figure 6.
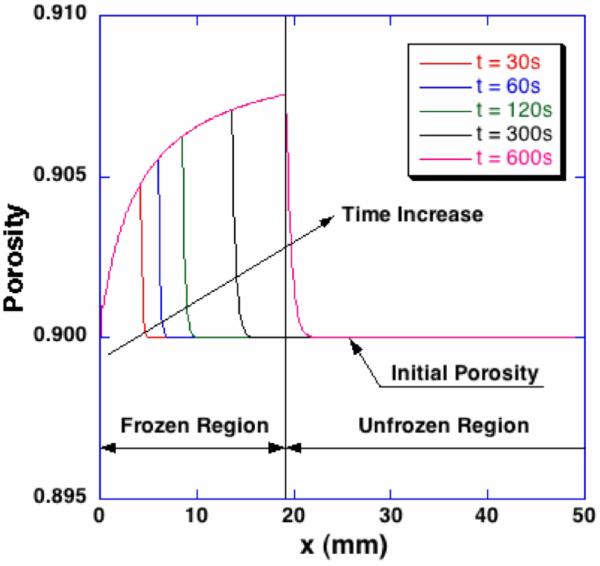
Spatiotemporal porosity profiles during freezing. In the frozen region, the porosity increases along the freezing direction, which indicates the microstructure of collagen matrix swells. Near the phase change interface, a thin layer of the unfrozen region is also dilated due to the excess water from the phase change.
Corresponding dilatation profiles and interstitial fluid pressure distributions are shown in Figure 7. As illustrated with the porosity change, the tissue is dilated in the frozen region. Although the freezing-induced porosity change was very small (i.e., approximately 0.8% of the initial porosity), the dilatation change shows that the volume of the tissue increases by approximately 8% of the initial volume. It is also noted that a drastic volume change is observed in a thin swollen layer of the unfrozen region near the phase change interface. A significant local stress gradient is expected in this layer. In this swollen layer, the maximum IFP is observed and the magnitude of the IFP increases with time. The distributions of the IFP show that the thickness of the swollen layer also increases with time.
Figure 7.
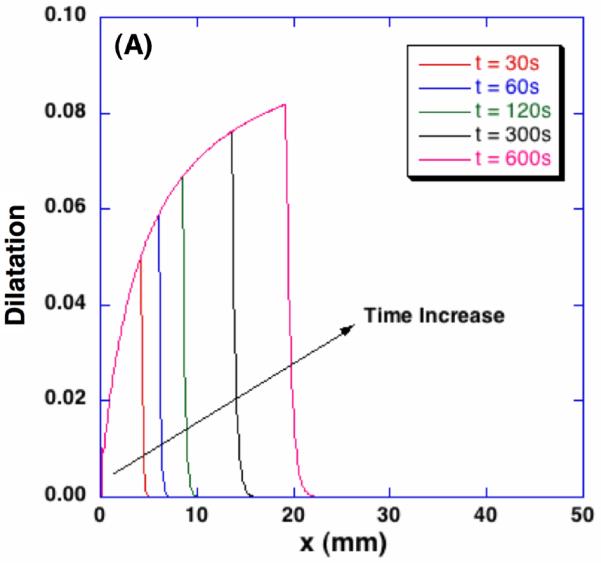
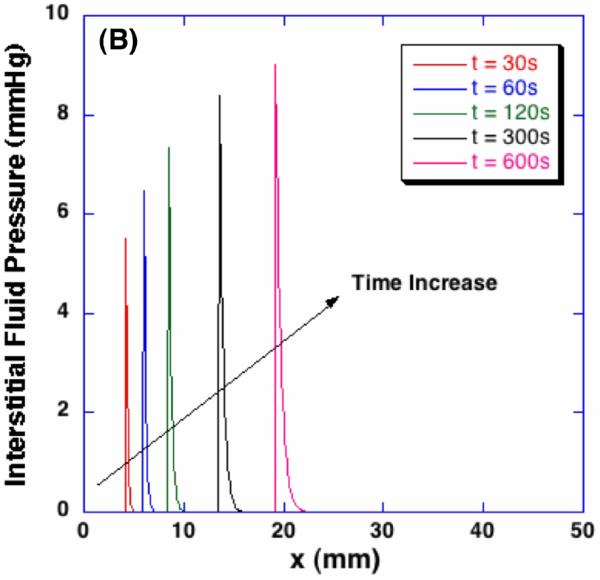
Spatiotemporal dilatation and interstitial fluid pressure profiles during freezing. Corresponding to the freezing-induced porosity change, poroelastic material experiences local dilatation up to 8% and significantly increased interstitial fluid pressure.
The effects of initial porosity on the freezing-induced changes of porosity and dilatation are presented in Figure 8. When the initial porosity is 0.85, a larger porosity increase is observed in the frozen region than in other initial porosity cases. The thickness of the swollen thin layer in the unfrozen region does not vary with the initial porosity. Thus, the largest gradient of porosity change across the swollen layer occurs at the lowest initial porosity.
Figure 8.
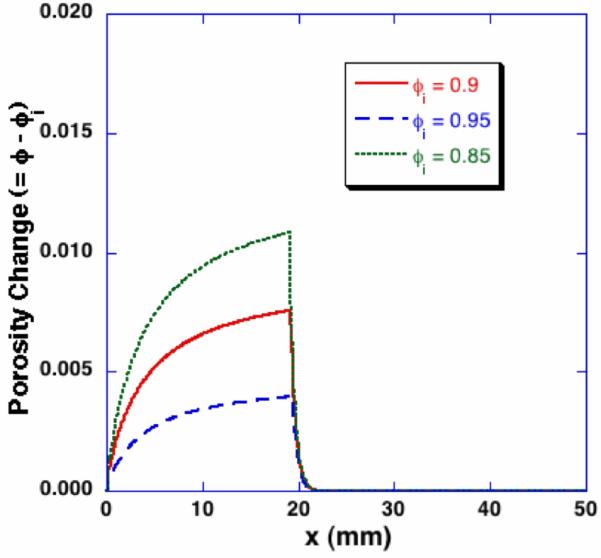
Effects of initial porosity on the freezing-induced porosity change - Porosity profiles at t = 600 sec. By the identical macroscopic freezing condition, poroelastic material with different initial porosity results in different porosity change during freezing.
Figure 9 (A) shows the spatial porosity profiles at t = 600 sec with different values of the product of hydraulic conductivity and elastic modulus. Since the significance of these two parameters on dilatation and porosity are the same as shown in Equation (2), their effects on the freezing-induced structural change are shown by varying the values of EK. As the value of EK decreases, larger porosity increase is observed in the frozen region but the swollen layer in the unfrozen region becomes thinner. This trend may be explained by considering the freezing-induced fluid-matrix interaction. Since the excess water should either enlarge the pores or flow through the unfrozen matrix, as the value of EK decreases, the excess water tends to be more accumulated near the phase change interface and result in larger porosity increase. As the value of EK increases, on the contrary, the excess water tends to flow through the unfrozen matrix rather than accumulating near the interface and enlarging the pores. Their effects on the interstitial fluid pressure (IFP), however, are quite different. As shown in Figure 9 (B), as the hydraulic conductivity increases with a given elastic modulus, the maximum IFP at the interface decreases but the layer of increased IFP becomes thicker, which indicates the interstitial fluid is transported further into the unfrozen region. Contrastingly, as the elastic modulus increases with a given hydraulic conductivity as presented in Figure 9 (C), the maximum IFP is predicted to become larger and the IFP increase is observed further into the unfrozen region. These results imply that an identical macroscopic freezing protocol may result in different microstructural alterations of poroelastic material depending on the matrix structural properties, which may be relevant to understanding the tissue-type dependent outcomes of cryomedicine applications [10].
Figure 9.
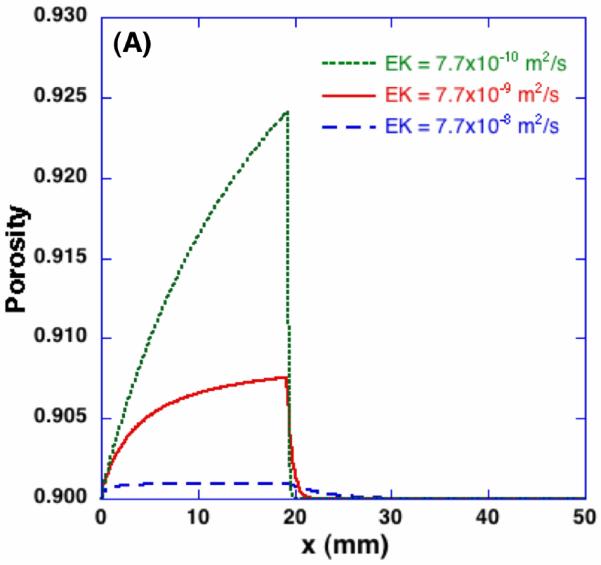
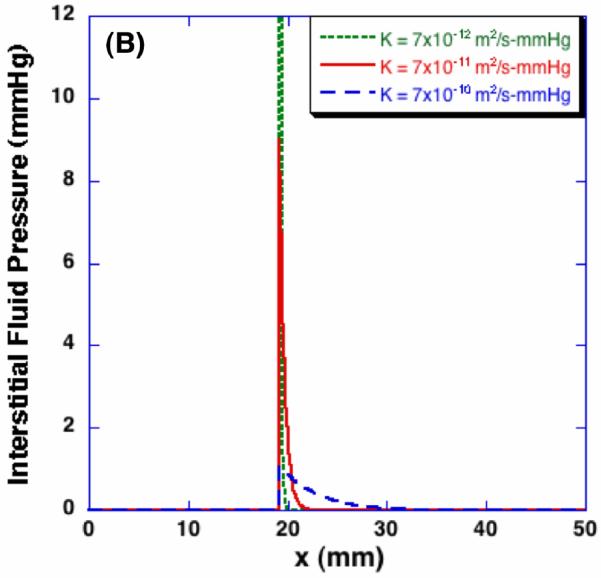
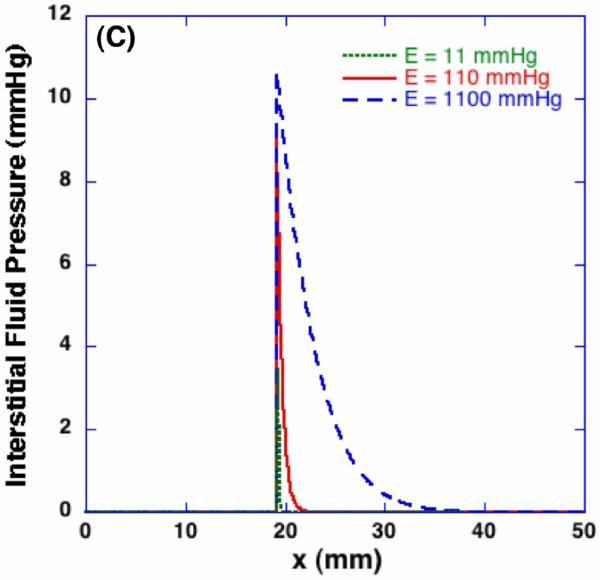
Effects of elastic modulus and hydraulic conductivity on porosity and interstitial fluid pressure - profiles at t = 600 sec. The same macroscopic freezing condition induces different microstructural changes depending on poroelastic material specific properties. The elastic modulus for (B) is 110 mmHg, and the hydraulic conductivity for (C) is 7×10-11 m2/s-mmHg respectively.
DISCUSSION
The present results imply that freezing induces interstitial fluid transport and this fluid transport interacts with the porous matrix, which can lead to the post-thaw alteration of the microstructure of the matrix. A possible sequence of the freezing-induced spatiotemporal events are - 1) phase change of interstitial fluid, 2) volumetric expansion associated with the phase change, 3) transport of excess interstitial fluid, 4) local swelling of the ECM, and 5) increase of the IFP. This increased IFP may suppress the freezing-induced fluid transport by acting as backpressure. As the results of these two-way interactions, the interstitial fluid is redistributed and the ECM microstructure may be altered.
The SEM analysis shows that the collagen matrix experiences two different levels of structural changes during freezing/thawing. These are - 1) morphological change of collagen fibril network level, and 2) diameter change of collagen fibril levels. The network level morphological change is well explained with the proposed fluid-matrix interaction mechanisms, but the fibril level diameter change seems to be induced by different level of interaction mechanisms. These increased fibril diameters, as shown in Figures 3 (C) and 4 (B), are thought to be freezing-induced denaturation or unfolding of hierarchical collagen fibrils [43, 44]. Compared to heat-induced denaturation of collagen, freezing-induced one is significantly less understood. Moreover, since the collagen fibrils experienced elevated IFP and subsequent increased stress, the denaturation kinetics are expected to be much more complex than pure freezing-induced denaturation. However, further research is still warranted to identify the interaction mechanism at this level.
The developed model also illustrates the effects of various matrix structural properties affecting the freezing-induced fluid-matrix interaction including initial porosity, hydraulic conductivity and elastic modulus. The effects of these properties may help to elucidate tissue-type dependent outcomes of various cryomedical applications, where freezing/thawing protocols should be adjusted and verified prior to applying to different types of tissues. For an example, cryopreservation protocol for hard tissue like bone may be designed and improved by considering that freezing of hard tissue might induce smaller dilatation but higher IFP and stress on the ECM during freezing than that of soft tissues.
Although the developed model could provide physical insights on the freezing-induced fluid-matrix interaction, its results should be carefully correlated to the experimental results considering the assumptions employed. Firstly, this poroelastic model, especially Equations (2) and (3), were developed assuming infinitesimal deformation. When the deformation is not infinitesimal, the one-dimensional dilatation should be calculated considering the finite strain as follows,
| (5) |
where u is the displacement in x direction. Considering the typical value of dilatation is less then 0.08 within the range studied as shown in Figure 7 (A), the error due to the infinitesimal deformation assumption is estimated to be less than 4% (= 0.5 × (0.08)2 / 0.08) for the present study. However, the error is expected to increase and the contribution by the finite strain should be considered as the deformation increases.
Secondly, Equation (2) assumed that there was no efflux of the interstitial fluid out of the matrix during freezing. Although it was not quantified, it was observed that the frozen portions of the collagen gels (i.e., F1 and F2 in Figure 2) became thinner when the portions were thawed. Several other experimental studies also reported the decrease in thickness and weight of tissues after freezing/thawing [30, 45]. These decreased thickness and weight suggest that there is the efflux of the interstitial fluid during freezing. Thus, the present model may overestimate the freezing-induced dilatation. Since this efflux is thought to be driven by the freezing-induced IFP increase, its significance would be augmented as the elastic modulus increases and the hydraulic conductivity decreases.
Thirdly, the present model assumed that the matrix of the unfrozen portion was not compressed by the ice in the frozen portion and the mass conservation around the phase change interface was formulated only considering the mass conservation of the interstitial fluid as shown in Equation (1). This assumption presumed that biological tissues are highly porous and the freezing process occurs very slowly so that the ice formed in the frozen portion mainly pushes the interstitial fluid in the unfrozen portion. Although this might be valid for the present study, in order to analyze freezing of dense tissues or rapid freezing, Equation (1) should be modified to address the compression of the unfrozen portion by considering the mass conservation of both interstitial fluid and matrix.
Finally, in order to simulate freezing of biological tissues, the role of the cells in the freezing-induced interaction with the fluid and matrix should considered. As already mentioned, the cells actively interact with the interstitial fluid and/or the matrix during the phase change. Thus, their contribution should be considered for a more realistic model. In addition, other constituents in the interstitial fluid may also affect the phase change characteristics of water including freezing point depression and eutectic phase change as illustrated in [46]. Moreover, it is expected that the presence of other constituents alters the morphology of the phase change interface from a planar to a dendritic one. Even though constant matrix structural properties are assumed in the model, the alteration of the ECM microstructure may lead to the change of these properties during the freezing. In particular, the hydraulic conductivity is known to significantly change even with small deformation [47].
ACKNOWLEDGEMENT
This work is partially supported by National Science Foundation (CBET-0747631), National Institute of Bioengineering and Biomedical Imaging (R01 EB008388), and a REP Award from the University of Texas at Arlington.
REFERENCES
- [1].Rubinsky B. Cryosurgery. Annual Review of Biomedical Engineering. 2000;2:157–187. doi: 10.1146/annurev.bioeng.2.1.157. [DOI] [PubMed] [Google Scholar]
- [2].Kataoka T, Honda Y, Bonneau HN. New Catheter-Based Technology for the Treatment of Restenosis. Journal of Interventional Cardiology. 2002;15(5):371–379. doi: 10.1111/j.1540-8183.2002.tb01070.x. [DOI] [PubMed] [Google Scholar]
- [3].Grassl ED, Bischof JC. In Vitro Model Systems for Evaluation of Smooth Muscle Cell Response to Cryoplasty. Cryobiology. 2005;50(2):162–173. doi: 10.1016/j.cryobiol.2005.01.002. [DOI] [PubMed] [Google Scholar]
- [4].Keane D. New Catheter Ablation Techniques for the Treatment of Cardiac Arrhythmias. Cardiac Electrophysiology Review. 2002;6(4):341–348. doi: 10.1023/a:1021115804352. [DOI] [PubMed] [Google Scholar]
- [5].Skanes AC, Yee R, Krahn AD. Cryoablation of Atrial Arrhythmias. Cardiac Electrophysiology Review. 2002;6(4):383–388. doi: 10.1023/a:1021128207078. [DOI] [PubMed] [Google Scholar]
- [6].Coger R, Toner M. Bioengineering Handbook. CRC Press; 1995. Preservation Techniques for Biomaterials; pp. 1567–1577. [Google Scholar]
- [7].Karlsson JO, Toner M. Principles of Tissue Engineering. Academic Press; 2000. Cryopreservation; pp. 293–307. [Google Scholar]
- [8].Nerem RM. Tissue Engineering: The Hope, the Hype, and the Future. Tissue Engineering. 2006;12(5):1143–1150. doi: 10.1089/ten.2006.12.1143. [DOI] [PubMed] [Google Scholar]
- [9].Pancrazio JJ, Wang F, Kelley CA. Enabling Tools for Tissue Engineering. Biosensors and Bioelectronics. 2007;22(12):2803–2811. doi: 10.1016/j.bios.2006.12.023. [DOI] [PubMed] [Google Scholar]
- [10].Han B, Bischof JC. Engineering Challenges in Tissue Preservation. Cell Preservation Technology. 2004;2:91–112. [Google Scholar]
- [11].Schenke-Layland K, Madershahian N, Riemann I. Impact of Cryopreservation on Extracellular Matrix Structures of Heart Valve Leaflets. The Annals of Thoracic Surgery. 2006;81(3):918–926. doi: 10.1016/j.athoracsur.2005.09.016. [DOI] [PubMed] [Google Scholar]
- [12].Schenke-Layland K, Xie J, Heydarkhan-Hagvall S. Optimized Preservation of Extracellular Matrix in Cardiac Tissues: Implications for Long-Term Graft Durability. The Annals of Thoracic Surgery. 2007;83(5):1641–1650. doi: 10.1016/j.athoracsur.2006.12.005. [DOI] [PubMed] [Google Scholar]
- [13].Narine K, Ing EC, Cornelissen M. Readily Available Porcine Aortic Valve Matrices for use in Tissue Valve Engineering. is Cryopreservation an Option? Cryobiology. 2006;53(2):169–181. doi: 10.1016/j.cryobiol.2006.05.007. [DOI] [PubMed] [Google Scholar]
- [14].Han B. Interaction of Freezing-Induced Water Transport with Extracellular Matrix of Biological Tissues; Proceedings of 2006 ASME Summer Bioengineering Conference; 2006.pp. BIO2006–157692. [Google Scholar]
- [15].Berthiaume F, Moghe PV, Toner M, Yarmush ML. Effect of Extracellular Matrix Topology on Cell Structure, Function, and Physiological Responsiveness: Hepatocytes Cultured in a Sandwich Configuration. The FASEB Journal. 1996;10(13):1471–1484. doi: 10.1096/fasebj.10.13.8940293. [DOI] [PubMed] [Google Scholar]
- [16].Borene ML, Barocas VH, Hubel A. Mechanical and Cellular Changes during Compaction of a Collagen-Sponge-Based Corneal Stromal Equivalent. Annals of Biomedical Engineering. 2004;32(2):274–283. doi: 10.1023/b:abme.0000012747.97620.3a. [DOI] [PubMed] [Google Scholar]
- [17].Meridith J, Fazeli B, Schwarz M. The Extracellular Matrix as a Survivial Factor. Mol.Biol.Cell. 1993;4:953–961. doi: 10.1091/mbc.4.9.953. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [18].Grinnell F. Fibroblast Biology in Three-Dimensional Collagen Matrices. Trends in Cell Biology. 2003;13(5):264–269. doi: 10.1016/s0962-8924(03)00057-6. [DOI] [PubMed] [Google Scholar]
- [19].Tranquillo RT. Self-Organization of Tissue-Equivalents: The Nature and Role of Contact Guidance. Biochemical Society Symposium. 1999;65:27–42. [PubMed] [Google Scholar]
- [20].Petroll WM, Ma L. Direct, Dynamic Assessment of Cell-Matrix Interactions Inside Fibrillar Collagen Lattices. Cell Motility and the Cytoskeleton. 2003;55(4):254–264. doi: 10.1002/cm.10126. [DOI] [PubMed] [Google Scholar]
- [21].de Freitas RC, Diller KR, Lakey JR, Rajotte RV. Osmotic Behavior and Transport Properties of Human Islets in a Dimethyl Sulfoxide Solution. Cryobiology. 1997;35(3):230–239. doi: 10.1006/cryo.1997.2045. [DOI] [PubMed] [Google Scholar]
- [22].Yarmush ML, Toner M, Dunn JC, Rotem A, Hubel A, Tompkins RG. Hepatic Tissue Engineering. Development of Critical Technologies. Annals of the New York Academy of Sciences. 1992;665:238–252. doi: 10.1111/j.1749-6632.1992.tb42588.x. [DOI] [PubMed] [Google Scholar]
- [23].Pazhayannur PV, Bischof JC. Measurement and Simulation of Water Transport during Freezing in Mammalian Liver Tissue. Journal of Biomechanical Engineering. 1997;119(3):269–277. doi: 10.1115/1.2796091. [DOI] [PubMed] [Google Scholar]
- [24].Devireddy RV, Raha D, Bischof JC. Measurement of Water Transport during Freezing in Cell Suspensions using a Differential Scanning Calorimeter. Cryobiology. 1998;36(2):124–155. doi: 10.1006/cryo.1997.2071. [DOI] [PubMed] [Google Scholar]
- [25].Devireddy RV, Smith DJ, Bischof JC. Mass Transfer during Freezing in Rat Prostate Tumor Tissue. AICHE J. 1999;45:639–654. [Google Scholar]
- [26].Bischof J, Hunt CJ, Rubinsky B, Burgess A, Pegg DE. Effects of Cooling Rate and Glycerol Concentration on the Structure of the Frozen Kidney: Assessment by Cryo-Scanning Electron Microscopy. Cryobiology. 1990;27(3):301–310. doi: 10.1016/0011-2240(90)90029-4. [DOI] [PubMed] [Google Scholar]
- [27].Hong JS, Rubinsky B. Patterns of Ice Formation in Normal and Malignant Breast Tissue. Cryobiology. 1994;31(2):109–120. doi: 10.1006/cryo.1994.1015. [DOI] [PubMed] [Google Scholar]
- [28].Muldrew K, Novak K, Yang H, Zernicke R, Schacher NS, McGann LE. Cryobiology of Articular Cartilage: Ice Morphology and Recovery of Chondrocytes. Cryobiology. 2000;40(2):102–109. doi: 10.1006/cryo.2000.2236. [DOI] [PubMed] [Google Scholar]
- [29].Coussy O. Poromechanics of Freezing Materials. Journal of the Mechanics and Physics of Solids. 2005;53:1689–1718. [Google Scholar]
- [30].Han B, Grassl ED, Barocas VH, Coad J, Bischof JC. A Cryoinjury Model using Engineered Tissue Equivalents for Cryosurgical Applications. Annals of Biomedical Engineering. 2005;33(7):972–982. doi: 10.1007/s10439-005-3478-z. [DOI] [PubMed] [Google Scholar]
- [31].Rubinsky B, Ikeda M. A Cryomicroscope using Directional Solidification for the Controlled Freezing of Biological Material. Cryobiology. 1985;22:55–68. [Google Scholar]
- [32].Coetzee SH, Jordaan A, Mpuchane SF. Low Pressure Mode Combined with OsO4 Vapor Fixation and Sputter-Coating for the Preservation of Delicate Aerial Hyphae and Conidia in the ESEM. Microscopy Research and Technique. 2005;67(5):265–270. doi: 10.1002/jemt.20209. [DOI] [PubMed] [Google Scholar]
- [33].Zaman MH, Trapani LM, Sieminski AL, Mackellar D, Gong H, Kamm RD, Wells A, Lauffenburger DA, Matsudaira P. Migration of Tumor Cells in 3D Matrices is Governed by Matrix Stiffness Along with Cell-Matrix Adhesion and Proteolysis. Proceedings of the National Academy of Sciences of the United States of America. 2006;103(29):10889–10894. doi: 10.1073/pnas.0604460103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [34].Miller JD. Master Thesis. University of Texas at Arlington; Arlington, TX: 2006. Freezing-Induced Microstructural Change of Collagen Scaffolds. [Google Scholar]
- [35].Han B. Freezing-Induced Fluid-Matrix Interaction in Biological Tissue; Proceedings of 18th International Symposium on Transport Phenomena; 2007.pp. ISTP18–331. [Google Scholar]
- [36].Truskey GA, Yuan F, Katz DF. Transport Phenomena in Biological System. Pearson Prentice Hall; 2004. pp. 419–421. [Google Scholar]
- [37].Lai WM, Hou JS, Mow VC. A Triphasic Theory for the Swelling and Deformation Behaviors of Articular Cartilage. Journal of Biomechanical Engineering. 1991;113(3):245–258. doi: 10.1115/1.2894880. [DOI] [PubMed] [Google Scholar]
- [38].Chen G, Ushida T, Tatishi T. A Biodegradable Hybrid Sponge Nested with Collagen Microsponges. J. Biomed Mater Res. 2000;51:273–279. doi: 10.1002/(sici)1097-4636(200008)51:2<273::aid-jbm16>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- [39].Mauck RL, Hung CT, Ateshian GA. Modeling of Neutral Solute Transport in a Dynamically Loaded Porous Permeable Gel: Implications for Articular Cartilage Biosynthesis and Tissue Engineering. Journal of Biomechanical Engineering. 2003;125:602–614. doi: 10.1115/1.1611512. [DOI] [PMC free article] [PubMed] [Google Scholar]
- [40].Swartz MA, Kaipainen A, Netti PA, Brekken C, Boucher Y, Grodzinsky AJ, Jain RK. Mechanics of Interstitial-Lymphatic Fluid Transport: Theoretical Foundation and Experimental Validation. Journal of Biomechanics. 1999;32(12):1297–1307. doi: 10.1016/s0021-9290(99)00125-6. [DOI] [PubMed] [Google Scholar]
- [41].Shitzer A, Becker B, Fricke B. ASHRAE Handbook: Refrigeration. 2006. Thermal Property of Foods; pp. 9.1–9.31. [Google Scholar]
- [42].Alexiades V, Solomon AD. Mathematical Modeling of Melting and Freezing Processes. Hemisphere Publishing; 1993. pp. 59–77. [Google Scholar]
- [43].Whitten ST, Kurtz AJ, Pometun MS. Revealing the Nature of the Native State Ensemble through Cold Denaturation. Biochemistry. 2006;45(34):10163–10174. doi: 10.1021/bi060855+. [DOI] [PubMed] [Google Scholar]
- [44].Babu CR, Hilser VJ, Wand AJ. Direct Access to the Cooperative Substructure of Proteins and the Protein Ensemble Via Cold Denaturation. Nature Structural and Molecular Biology. 2004;11(4):352–357. doi: 10.1038/nsmb739. [DOI] [PubMed] [Google Scholar]
- [45].Venkatasubramanian RT, Grassl ED, Barocas VH, Lafontaine D, Bischof JC. Effects of Freezing and Cryopreservation on the Mechanical Properties of Arteries. Annals of Biomedical Engineering. 2006;34(5):823–832. doi: 10.1007/s10439-005-9044-x. [DOI] [PubMed] [Google Scholar]
- [46].Han B, Bischof JC. Thermodynamic Nonequilibrium Phase Change Behavior and Thermal Properties of Biological Solutions for Cryobiology Applications. Journal of Biomechanical Engineering. 2004;126(2):196–203. doi: 10.1115/1.1688778. [DOI] [PubMed] [Google Scholar]
- [47].Zhang XY, Luck J, Dewhirst MW, Yuan F. Interstitial Hydraulic Conductivity in a Fibrosarcoma. American Journal of Physiology: Heart and Circulatory Physiology. 2000;279(6):H2726–34. doi: 10.1152/ajpheart.2000.279.6.H2726. [DOI] [PubMed] [Google Scholar]


