X-ray cross correlation analysis uncovers hidden local symmetries in disordered matter

Abstract

We explore the different local symmetries in colloidal glasses beyond the standard pair correlation analysis. Using our newly developed X-ray cross correlation analysis (XCCA) concept together with brilliant coherent X-ray sources, we have been able to access and classify the otherwise hidden local order within disorder. The emerging local symmetries are coupled to distinct momentum transfer (Q) values, which do not coincide with the maxima of the amorphous structure factor. Four-, 6-, 10- and, most prevalently, 5-fold symmetries are observed. The observation of dynamical evolution of these symmetries forms a connection to dynamical heterogeneities in glasses, which is far beyond conventional diffraction analysis. The XCCA concept opens up a fascinating view into the world of disorder and will definitely allow, with the advent of free electron X-ray lasers, an accurate and systematic experimental characterization of the structure of the liquid and glass states.

Disordered matter, such as glasses and liquids, does not exhibit translational symmetry and in turn is able to accommodate different local symmetries in the same system, among them the icosahedral local order, which belongs to the forbidden motifs in periodic structures. This mysterious and so far experimentally inaccessible localized order within disorder has been fascinating scientists for many decades (1–5), because it is held responsible for the undercooling of liquids and the existence of the glass state. Similarly, nonperiodic materials have always attracted the attention of materials scientists, because they do carry—through these structural degrees of freedom—a unique potential to display novel smart functions (6–8).

The microscopic understanding of the structure and properties of crystals has advanced rapidly during the last decades. The translational invariance of the crystalline state allowed the introduction of the Brillouin Zone concept, thus enabling an elegant and powerful theoretical description of the thermal, electronic and magnetic properties. At the same time, crystal diffraction has continuously been developed to such a fine art that even complex biological structures can be solved today with atomic resolution (when forced to form a crystal). In severe contrast to this, the local microscopic structure of disordered matter has remained a challenge and a mystery (1–3). Our lack of knowledge on the local order within disorder constrains the development of a better understanding of the properties of liquids and glasses (9). In turn, the open question of how the structure of the liquid and amorphous states can be accessed experimentally has become one of the holy grails in condensed matter science (10).

The fundamental limits of conventional (X-ray, neutron, electron) diffraction from disordered materials are accountable for this situation, because such techniques only allow to extract the pair distribution function g(r) = n₀⁻²〈ρ(0)ρ(r)〉 of the single particle density ρ(r) = Σ_mδ(r − R_m) averaged over the illuminated sample area. Here, and in the rest of the article, R_m denotes the positions of the particles, n₀ the average particle density and r the interparticle distance. The associated structure factor 〈S(Q)〉 = 1 + n₀∫(g(r) − 1) e^iQrdr, which gives the scattering intensity I(Q), depends on the momentum transfer Q. 〈S(Q)〉 shows rather similar features for all disordered structures (see Fig. 1B), thus carrying a quite limited information, i.e., the probability to find another atom in a certain distance from a given “average atom.” In particular, 〈S(Q)〉 provides no direct answer on the local symmetries in the system (11), which are intimately related to the local bonding and to bonding angles.

Fig. 1.

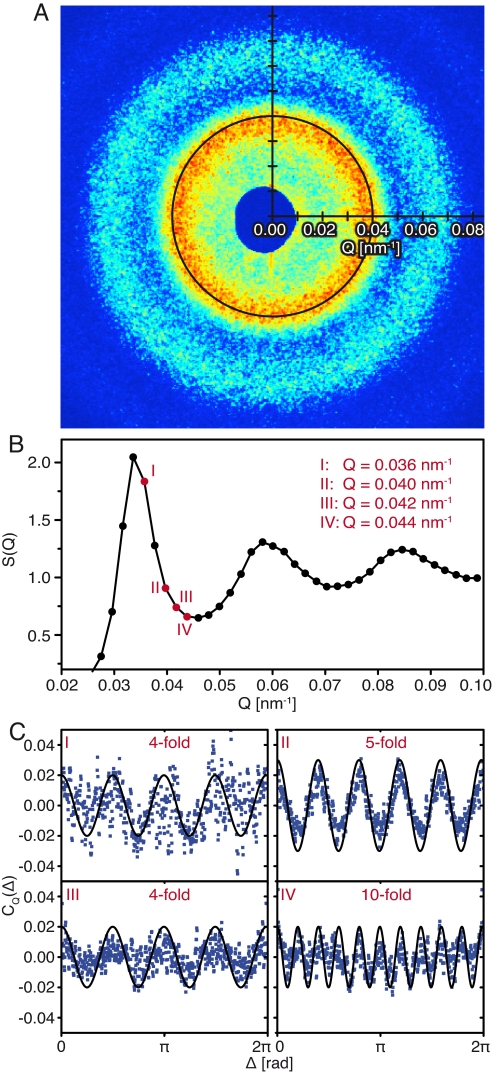
Experimental data and XCCA results. (A) CCD image showing a typical intensity spectrum with speckle structure. (B) Angular averaged structure factor of the image in A, which is the standard radial intensity distribution. (C) Experimental results after applying the cross-correlator C_Q(Δ) to the data in A at different Q values. Solid lines are guide to the eyes.

Our experimental and theoretical approach to solve this age-old problem has followed the guiding principle that the intrinsic spatial (and temporal) averaging mechanism performed in conventional (i.e., partially coherent) diffraction has to be eliminated experimentally. Then, a properly defined higher-order angular correlation function has to be devised and applied to data in order to disclose the hidden local symmetries of disordered matter. The first results obtained from different colloidal glasses deliver a new realm of structural details, which already shed a fascinating new light on the origin of glasses and on the glass forming mechanism.

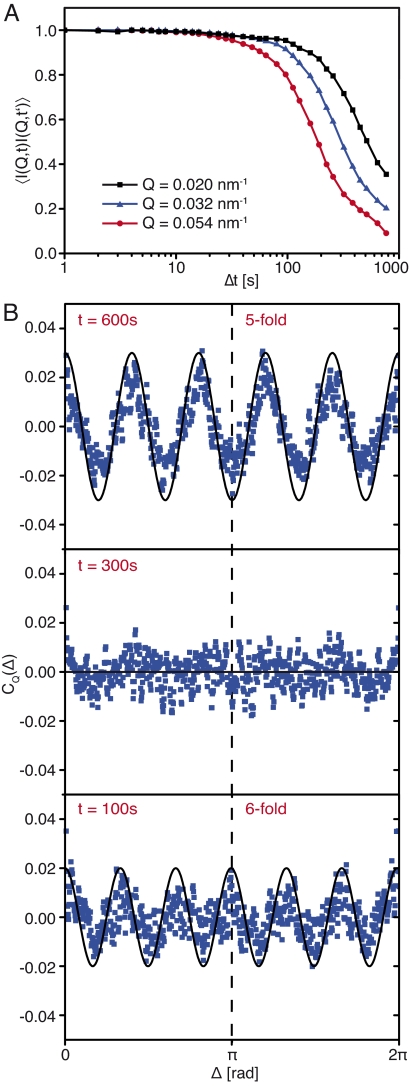
Configurational averaging can be avoided if the coherence volume of a partially coherent X-ray beam is equal to the illuminated sample volume (12, 13). In case of extreme forward scattering only the transverse coherence is relevant (14). Additionally, temporal averaging can be neglected for exposure times shorter than the onset time for speckle dynamics (15). Modern high-brilliance synchrotron radiation facilities and—in the future, even more so—free electron X-ray laser facilities deliver sufficient coherent X-ray flux for carrying out (nonaveraging) coherent diffraction experiments from disordered matter that produce the well-known laser speckle patterns on a 2D-detector (14–16) (see Fig. 1A). By applying a temporal correlator to one selected speckle spot associated with a fixed Q-vector, the Q-dependent temporal relaxation behavior of colloidal glasses has been extracted (14) [X-ray photon correlation spectroscopy (XPCS)] (see for example Fig. 2A).

Fig. 2.

Temporal relaxation behavior of C_Q(Δ) and 〈I(Q,t)I(Q,t′)〉. (A) Normalized temporal intensity autocorrelation function 〈I(Q,t)I(Q,t′)〉 for different Q values (black squares: Q = 0.020 nm⁻¹; blue triangles: Q = 0.032 nm⁻¹; red dots: Q = 0.054 nm⁻¹), Δt = t′ − t. Solid lines are guide to the eyes. (B) The cross-correlation function C_Q(Δ) at Q = 0.04 nm⁻¹ evolves from an initially 6-fold to a 5-fold symmetry. The curves at 600 s and 300 s are averaged over the subsequent 100-s interval; the one at 100 s is averaged over a 50-s interval.

Results and Discussion

Colloidal glasses can be studied with commercially available 2D-detectors, whereas suitable 2D-detectors, which cover the Q-range required to study molecular or metallic glasses yet have to be developed. Here, we use a similar experimental setup as for XPCS (Fig. 3A): The coherent X-ray beam prepared at station ID10A of the European Synchrotron Radiation Facility (ESRF) hits a colloidal glass sample and produces a full 2π speckle pattern at the 2D-detector covering a Q-range up to 0.2 nm⁻¹. A typical dataset displays the expected isotropic granular “intensity rings” that are mediated by the random local order within the system (Fig. 1A). The deduced angular averaged structure factor shows the standard radial intensity distribution (Fig. 1B).

Fig. 3.

XCCA setup and principle. (A) A 10-μm partially coherent X-ray beam with a wavelength of 0.154 nm was defined by a collimating aperture. The colloidal sample is kept at a distance of ≈ 20 cm in the near field region of the pinhole. Speckle patterns are recorded by a charge coupled device camera with 20-μm pixel size in 2,265-mm distance. Series of 1,000 CCD images were taken with exposure time of 0.15 s and for a diluted sample with 0.4 s. An additional 50 dark images were recorded. Including CCD readout the time interval between consecutive images was 1 s. (B) Schematic intensity distribution with instructional guide for the construction of C_Q(Δ).

To transcend this information, we must unravel correlations in the angular distribution of the X-ray speckles. At first sight this is not evident at all, because the angular variation of the intensity exhibits an isotropic distribution as anticipated for amorphous systems (Fig. 1A). However, as we shall show, this is possible by considering the generic intensity-intensity cross correlation

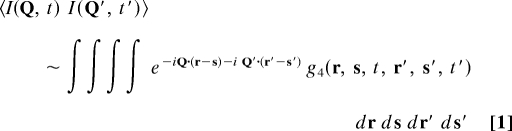and the associated 4-point correlation function.

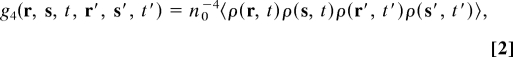where 〈…〉 means a statistical average.

Angular Cross Correlation Function.

Here, we introduce a first simple subset of these new types of higher-order correlations, i.e., the instantaneous local angular correlations with respect to a given azimuth Δ.* They are found by performing the average in Eq. 1 over ϕ with the vectors Q and Q′ separated by Δ on the intensity ring with modulus Q (see Fig. 3B) and t = t′. We define the normalized angular 4-point cross-correlation function C_Q(Δ),

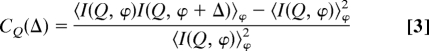with

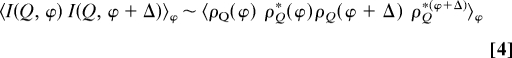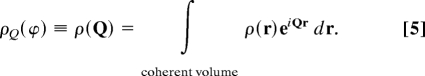Fig. 1C shows the result after applying C_Q(Δ) (Eq. 3) to data in Fig. 1A for selected Q values. Most fascinating is that C_Q(Δ) clearly reveals a very pronounced anisotropy with 5-fold symmetry specifically for the intensity ring associated with |Q| = 0.04 nm⁻¹ (marked in black in Fig. 1A), which points to a so far hidden local symmetry in the colloidal system. The other Q values shown in Fig. 1C present a C_Q(Δ), which most closely resembles 4-fold and 10-fold symmetry; and 6-fold symmetry can also be found (Fig. 2B). The fluctuations of the data points are (mostly) due to its speckle origin and not due to counting statistics (see numerical simulation results below). The solid lines are only guides to the eye to point out the dominant symmetry in C_Q(Δ).

Encouraged by this discovery, we have systematically evaluated the speckle patterns of many different colloidal systems, which all produced pronounced features in C_Q(Δ). We focus in this report on a hard sphere polymethylmethacrylate (PMMA) system with radius of 117 nm. Details on the sample preparation can be found in Materials and Method.

We have made several systematic observations in all colloidal glass systems. The emerging local symmetries are coupled to distinct Q values, which do not coincide with the maxima of the amorphous structure factor. The most prevailing symmetry is 5-fold.^† For a basic understanding of these observations we assume our sample to consist of locally-favored structures with icosahedral symmetry embedded randomly in disordered regions (19). Then, C_Q(Δ) (Eq. 3) has the simple form

with ρ_Qⁱ(ϕ) as the structure amplitude of the ith LFS. Eq. 6 shows that C_Q(Δ) is a superposition of the angular intensity-autocorrelation function of individual local structures, each contributing an intensity pattern |ρ_Qⁱ(ϕ)|² as the one in Fig. 4B. In the coherent speckle pattern produced by the random ensemble of such clusters, this pattern becomes completely obscured. Only the application of XCCA recovers its symmetries. In the SI we present a straightforward discussion of the Q-dependent behavior of C_Q(Δ) based on an analytical derivation of the structure factor of icosahedral clusters (20–22). We note that angular correlations between local clusters, so called medium-range correlations, are also accessible by XCCA. This requires a different 4-point correlator in Eq. (3), which takes Q-vectors with |Q′| ≠ |Q| into account.

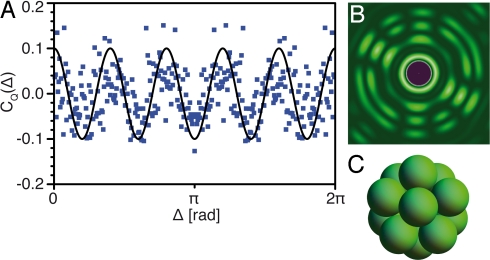
Fig. 4.

Numerical simulation of C_Q(Δ). (A) Calculated cross-correlation pattern for a close-packed random ensemble of 8,000 icosahedra made of 12 spheres with radius 100 nm on a simple cubic lattice. For this specific Q value, C_Q(Δ) shows 5-fold symmetry. (B) Intensity distribution of a single icosahedron. (C) Icosahedral cluster with its 5-fold symmetry axis.

We have performed calculations of the full expression (Eq. 3) for 8000 randomly oriented icosahedra (Fig. 4C) on a cubic lattice. The resulting correlation patterns confirm very nicely the local angular symmetries of our experiment (Fig. 4A) and show that the sprinkle of the data points is due to the coherent scattering process (speckles).

Dynamical Heterogeneity.

A further most fascinating observation is associated with the temporal relaxation behavior of C_Q(Δ) (Fig. 2B). Our new 4-point correlator unveils a continuous change of the locally-favored structures within the first 600 s from initially 6-fold symmetry to 5-fold symmetry, with no obvious symmetry in between. Apparently, icosahedral clusters reorganize in different orientations, form either out of local nanocrystals (hexagonal/fcc) or disorder, all of which involves a breaking and forming of bonds. Such behavior is known from molecular dynamics simulations as “dynamical heterogeneity” (19). Within the observed time frame, the temporal autocorrelation drops below 30% (see Fig. 2A). This new X-ray cross-correlation analysis concept reveals now that the processes, which are responsible for these relaxations, are accompanied by distinct changes of the local structure. These cooperative processes are the β-relaxation at shorter and α-relaxation at longer time scales (23), where the β-relaxation describes the rattling of individual particles trapped in transient cages formed by their neighbors and the α-relaxation the structural rearrangement of these cages (24). In future, this technique can be used to interrogate the time dependence of the local structures in glassy and supercooled states and new local structural motifs in strong and fragile glass formers by employing even more sophisticated cross-correlators between intensities at different times.

Conclusions

We have introduced and applied a particularly simple 4-point cross correlator that enables us to unveil otherwise hidden symmetries in a colloidal glass. Our approach is general enough to accommodate many more complex cross correlators derived from Eq. 1. In particular, the orientational pair–pair correlations will allow access to midrange order. Preliminary yet promising calculations employing a mode-coupling ansatz and an appropriate atomic potential (25) show a dominant instability for 6- and 5-fold symmetry (associated with close-packed structures) and a multitude of incommensurate wave vector instabilities (associated with random arrangements). This should enable to extract in the future the relevant interaction potentials from experimental datasets.

The availability of short-pulse XFEL radiation in the 0.1-nm regime and with 100-fs pulse length will open up the fascinating option to analyze the local structure of liquids (in particular also water) by applying the new concept of X-ray cross correlation analysis (XCCA) to single laser shot speckle diffraction pattern. The combination of short-pulse XFEL radiation and large 2D-detector arrays will also open up the window for the study of nano-powders and transient complex molecular structures in solution.

Materials and Methods

Samples.

The colloidal particles were synthesized via a polymerization method for preparing lattices of polymethylmethacrylate (PMMA) with a covalently surface linked stabilizer of poly(12-hydroxy-stearic-acid) (PHSA) following the method of Antl et al. (26). These fluorescent PMMA particles are obtained by copolymerization of methyl methacrylate, methacrylic acid and the fluorescent monomer, 7-nitrobenzo-2-oxa-1,3-diazole-methyl methacrylate (NBD-dyed) (27). To obtain highly concentrated, glassy systems, particle suspensions of ≈20–30% in volume were filled into quartz-glass capillaries of 1 mm and centrifuged at 1,360 × g for ≈2 days. The supernatant decalin has been removed and the capillaries sealed.

Data Treatment.

The dark images were averaged and subtracted from the data. The colloidal form factor f_S(Q) has been obtained from a diluted PMMA sample. The form factor allowed to deduce the static structure factor S(Q) of the concentrated sample presented in this work. A multispeckle temporal intensity autocorrelation analysis yielded the dynamic correlation function of the sample. The dynamical correlation function, which relates to the diffusive motion of the colloidal particles, shows no decay within the first 100 s. Therefore, for the XCCA analysis we averaged 50–100 CCD images. Rings of intensity with constant Q and 1- to 2-pixel widths have been extracted and an unbiased cross correlation function according to Eq. 3 has been calculated.

Note also that a diffraction pattern obtained via a 2D detector (i.e., mapping an Ewald sphere) will not satisfy Friedel's law at higher momentum transfers (see SI).