Abstract
Supervised learning of microarray data is receiving much attention in recent years. Multiclass cancer diagnosis, based on selected gene profiles, are used as adjunct of clinical diagnosis. However, supervised diagnosis may hinder patient care, add expense or confound a result. To avoid this misleading, a multiclass cancer diagnosis with class-selective rejection is proposed. It rejects some patients from one, some, or all classes in order to ensure a higher reliability while reducing time and expense costs. Moreover, this classifier takes into account asymmetric penalties dependant on each class and on each wrong or partially correct decision. It is based on ν-1-SVM coupled with its regularization path and minimizes a general loss function defined in the class-selective rejection scheme. The state of art multiclass algorithms can be considered as a particular case of the proposed algorithm where the number of decisions is given by the classes and the loss function is defined by the Bayesian risk. Two experiments are carried out in the Bayesian and the class selective rejection frameworks. Five genes selected datasets are used to assess the performance of the proposed method. Results are discussed and accuracies are compared with those computed by the Naive Bayes, Nearest Neighbor, Linear Perceptron, Multilayer Perceptron, and Support Vector Machines classifiers.
1. Introduction
Cancer diagnosis, based on gene expression profiling, have improved over the past 40 years. Many microarray technologies studies were developed to analyze the gene expression. These genes are later used to categorize cancer classes. Two different classification approaches can be used: class discovery and class prediction. The first is an unsupervised learning approach that allows to separate samples into clusters based on similarities in gene expression, without prior knowledge of sample identity. The second is a supervised approach which predicts the category of an already defined sample using its gene expression profiles. Since these classification problems are described by a large number of genes and a small number of samples, it is crucial to perform genes selection before the classification step. One way to identify informative genes pointed in [1] is the test statistics.
Researches show that the performance of supervised decisions based on selected gene expression can be comparable to the clinical decisions. However, no classification strategy is absolutely accurate. First, many factors may effectively decrease the predictive power of a multiclass problem. For example, findings of [2] imply that information useful for multiclass tumor classification is encoded in a complex gene expression and cannot be given by a simple one. Second, it is not possible to find an optimal classification method for all kinds of multiclass problems. Thus, supervised diagnosis are always considered as an important adjunct of traditional diagnostics and never like its substitute.
Unfortunately, supervised diagnosis can be misleading. They may hinder patient care (wrong decision on a sick patient), add expense (wrong decision on a healthy patient) or confound the results of cancer categories. To overcome these limitations, a multi-SVM [3] classifier with class-selective rejection [4–7] is proposed. Class-selective rejection consists of rejecting some patients from one, some, or all classes in order to ensure a higher reliability while reducing time and expense costs. Moreover, any of the existing multiclass [8–10] algorithms have taken into consideration asymmetric penalties on wrong decisions. For example, in a binary cancer problem, a wrong decision on a sick patient must cost more than a wrong decision on a healthy patient. The proposed classifier handles this kind of problems. It minimizes a general loss function that takes into account asymmetric penalties dependant on each class and on each wrong or partially correct decision.
The proposed method divides the multiple class problem into several unary classification problems and train one ν-1-SVM [11–13] coupled with its regularization path [14, 15] for each class. The winning class or subset of classes is determined using a prediction function that takes into consideration the costs asymmetry. The parameters of all the ν-1-SVMs are optimized jointly in order to minimize a loss function. Taking advantage of the regularization path method, the entire parameters searching space is considered. Since the searching space is widely extended, the selected decision rule is more likely to be the optimal one. The state-of-art multiclass algorithms [8–10] can be considered as a particular case of the proposed algorithm where the number of decisions is given by the existing classes and the loss function is defined by the Bayesian risk.
Two experiments are reported in order to assess the performance of the proposed approach. The first one considers the proposed algorithm in the Bayesian framework and uses the selected microarray genes to make results comparable with existing ones. Performances are compared with those assessed using Naive Bayes, Nearest Neighbor, Linear Perceptron, Multilayer Perceptron, and Support Vector Machines classifiers, invoked in [1]. The second one shows the ability of the proposed algorithm solving multiclass cancer diagnosis in the class-selective rejection scheme. It minimizes an asymmetric loss function. Experimental results show that, a cascade of class-selective classifiers with class-selective rejections can be considered as an improved supervised diagnosis rule.
This paper is outlined as follows. Section 2 presents a description of the model as a gene selection task. It introduces the multiclass cancer diagnosis problem in the class-selective rejection scheme. It also proposes a supervised training algorithm based on ν-1-SVM coupled with its regularization path. The two experiments are carried out in Section 3, results are reported, compared and discussed. Finally, a conclusion is presented in Section 4.
2. Models and Methods
This section describes the multiclass cancer diagnosis based on microarray data. Feature selection is evoked as a first process in a gene-based cancer diagnosis. Test statistics are used as a possible way for informative genes identification [1]. Once genes selection is processed, a classification problem should be solved. The multiclass cancer diagnosis problem, formulated in the general framework of class-selective rejection, is introduced. A solution based on ν-1-SVM [11–13] is proposed. First a brief description of ν-1-SVM and the derivation of its regularization path [14, 15] is presented. Second, the proposed algorithm [3] is explained. It allows to determine a multiclass cancer diagnosis that minimizes an asymmetric loss function in the class-selective rejection scheme.
2.1. Genes Selection Using Test Statistics
Gene profiles are successfully applied to supervised cancer diagnosis. Since cancer diagnosis problems are usually described by a small set of samples with a large number of genes, feature or gene selection is an important issue in analyzing multiclass microarray data. Given a microarray data with N tumor classes, n tumor samples and g genes per sample, one should identify a small subset of informative genes that contribute most to the prediction task. Various feature selection methods exist in literature. One way pointed in [1] is to use test statistics for the equality of the class means. Authors of [1] formulate first the expression levels of a given gene by a one-way analysis of variance model. Second, the power of genes in discriminating between tumor types is determined by a test statistic. The discrimination power is the value of the test evaluated at the expression level of the gene. The higher the discrimination power is, the more powerful the gene is in discriminating between tumor types. Thus, genes with higher power of discrimination are considered as informative genes.
Let Yjp be the expression level from the pth sample of the jth class, the following general model is considered:
| (1) |
In the model μj represents the mean expression level of the gene in class wj, ϵjp are independent random variables and E(ϵjp) = 0, V(ϵjp) = σj2 < ∞ for j = 1,…, N; p = 1,…, nj.
For the case of homogeneity of variances, the ANOVA F or F test [16] is the optimal one testing the means equality hypothesis. With heterogeneity of variances, the task is challenging. However, it is known that, with a large number of genes present, usually in thousands, no practical test is available to locate the best set of genes. Thus, the authors of [1] studied six different statistics.
- ANOVA F test statistic, the definition of this test is
where and , . For simplicity, ∑ is used to indicate the sum taken over the index j. Under means equality hypothesis and assuming variance homogeneity, this test has a distribution of FN−1,n−N [16].(2) - Brown-Forsythe test statistic [17], given by
Under means equality hypothesis, B is distributed approximately as FN−1,τ where(3) (4) - Welch test statistic [18], defined as
with ωj = nj/sj2 and hj = ωj/∑ωj. Under means equality hypothesis, W has an approximate distribution of FN−1,τω where(5) (6) - Adjusted Welch test statistic [19]. It is similar to Welch statistic and defined to be
where ωj* = nj/(Φjsj2) with Φj chosen such that 1 ≤ Φj ≤ (nj − 1)/(nj − 3) and hj* = ωj*/∑ωj*. Under means equality hypothesis, W* has an approximate distribution of FN−1,τω* where(7) (8) - Cochran test statistic [20]. This test statistic is simply the quantity appearing in the numerator of the Welch test statistic W, that is,
Under means equality hypothesis, C has an approximate distribution of χN−12.(9) - Kruskal-Wallis test statistic. This is the well-known nonparametric test given by
where Rj is the rank sum for the jth class. The ranks assigned to Yjp are those obtained from ranking the entire set of Yjp. Assuming each nj ≥ 5, then under means equality hypothesis, H has an approximate distribution of χN−12 [21].(10)
These tests performances are evaluated and compared over different supervised learning methods applied to publicly available microarray datasets. Experimental results show that the model for gene expression values without assuming equal variances is more appropriate than that assuming equal variances. Besides, under heterogeneity of variances, Brown-Forsythe test statistic, Welch test statistic, adjusted Welch test statistic, and Cochran test statistic, perform much better than ANOVA F test statistic and Kruskal-Wallis test statistic.
2.2. Multitumor Classes with Selective Rejection
Once gene selection is processed, the classification problem should be solved. Let us define this diagnosis problem in the class-selective rejection scheme. Assuming that the multiclass cancer problem deals with N tumor classes noted w1 … wN and that any patient or sample x belongs to one tumor class and has d informative genes, a decision rule consists in a partition Z of ℜd in I sets Zi corresponding to the different decision options. In the simple classification scheme, the options are defined by the N tumor classes. In the class-selective rejection scheme, the options are defined by the N tumor classes and the subsets of tumor classes (i.e. assigning patient x to the subset of tumor classes {w1, w3} means that x is assigned to cancer categories w1 and w3 with ambiguity).
The problem consists in finding the decision rule Z* that minimizes a given loss function c(Z) defined by
| (11) |
where cij is the cost of assigning a patient x to the ith decision option when it belongs to the tumor class wj. The values of cij being relative since the aim is to minimize c(Z), the values can be defined in the interval [0;1] without loss of generality. Pj is the a priori probability of tumor class wj and P(Di/wj) is the probability that patients of the tumor class wj are assigned to the ith option.
2.3. μ-1-SVM
To solve the multiclass diagnosis problem, an approach based on ν-1-SVM is proposed. Considering a set of m samples of a given tumor classes X = {x1, x2,…, xm} drawn from an input space 𝒳, ν-1-SVM computes a decision function fXλ(·) and a real number bλ in order to determine the region ℛλ in 𝒳 such that fXλ(x) − bλ ≥ 0 if the sample x ∈ ℛλ and fXλ(x) − bλ < 0 otherwise. The decision function fXλ(·) is parameterized by λ = νm (with 0 ≤ ν < 1) to control the number of outliers. It is designed by minimizing the volume of ℛλ under the constraint that all the samples of X, except the fraction ν of outliers, must lie in ℛλ. In order to determine ℛλ, the space of possible functions fXλ(·) is reduced to a Reproducing Kernel Hilbert Space (RKHS) with kernel function K(·, ·). Let Φ : 𝒳 → ℋ be the mapping defined over the input space 𝒳. Let 〈·, ·〉ℋ be a dot product defined in ℋ. The kernel K(·, ·) over 𝒳 × 𝒳 is defined by:
| (12) |
Without loss of generality, K(·, ·) is supposed normalized such that for any x ∈ 𝒳, K(x, x) = 1. Thus, all the mapped vectors Φ(xp), p = 1,…, m are in a subset of a hypersphere with radius one and center O. Provided K(·, ·) is always positive and Φ(X) is a subset of the positive orthant of the hypersphere. A common choice of K(·, ·) is the Gaussian RBF kernel K(xp, xq) = exp[−1/2σ2||xp − xq||𝒳2] with σ the parameter of the Gaussian RBF kernel. ν-1-SVM consists of separating the mapped samples in ℋ from the center O with a hyperplane 𝒲λ. Finding the hyperplane 𝒲λ is equivalent to find the decision function fXλ(·) such that fXλ(x) − bλ = 〈wλ, Φ(x)〉ℋ − bλ ≥ 0 for the (1 − ν)m mapped samples while 𝒲λ is the hyperplane with maximum margin bλ/||wλ||ℋ with wλ the normal vector of 𝒲λ.
This yields fXλ(·) as the solution of the following convex quadratic optimization problem:
| (13) |
where ξp are the slack variables. This optimization problem is solved by introducing lagrange multipliers αp. As a consequence to Kuhn-Tücker conditions, wλ is given by
| (14) |
which results in
| (15) |
The dual formulation of (13) is obtained by introducing Lagrange multipliers as
| (16) |
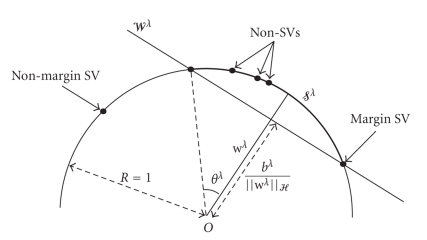
A geometrical interpretation of the solution in the RKHS is given by Figure 1. fXλ(·) and bλ define a hyperplane 𝒲λ orthogonal to fXλ(·). The hyperplane 𝒲λ separates the Φ(xp)s from the sphere center, while having bλ/||wλ||ℋ maximum which is equivalent to minimize the portion 𝒮λ of the hypersphere bounded by 𝒲λ that contains the set {Φ(x) s.t. x ∈ ℛλ}.
Tuning ν or equivalently λ is a crucial point since it enables to control the margin error. It is obvious that changing λ leads to solve the optimization problem formulated in (16) in order to find the new region ℛλ. To obtain great computational savings and extend the search space of λ, we proposed to use ν-1-SVM regularization path [14, 15]. Regularization path was first introduced by Hastie et al. [14] for a binary SVM. Later, Rakotomamojy and Davy [15] developed the entire regularization path for a ν-1-SVM. The basic idea of the ν-1-SVM regularization path is that the parameter vector of a ν-1-SVM is a piecewise linear function of λ. Thus the principle of the method is to start with large λ, (i.e., λ = m − ϵ) and decrease it towards zero, keeping track of breaks that occur as λ varies.
As λ decreases, ||wλ||ℋ increases and hence the distance between the sphere center and 𝒲λ decreases. Samples move from being outside (non-margin SVs with αpλ = 1 in Figure 1) to inside the portion 𝒮λ (non-SVs with αpλ = 0). By continuity, patients must linger on the hyperplane 𝒲λ (margin SVs with 0 < αpλ < 1) while their αpλs decrease from 1 to 0. αpλs are piecewise-linear in λ. Break points occur when a point moves from a position to another one. Since αpλ is piecewise-linear in λ, fλ(·) and bλ are also piecewise-linear in λ. Thus, after initializing the regularization path (computing αpλ by solving (16) for λ = m − ϵ), almost all the αpλs are computed by solving linear systems. Only for some few integer values of λ smaller than m, αpλs are computed by solving (16) according to [15].
Using simple linear interpolation, this algorithm enables to determine very rapidly the ν-1-SVM corresponding to any value of λ.
2.4. Multiclass SVM Based on μ-1-SVM
Given N classes and N trained ν-1-SVMs, one should design a supervised decision rule Z, moving from unary to multiclass classifier by assigning samples to a decision option. To determine the decision rule, first a prediction function should decide the winning option. A distance measure between x and the training class set wj, using the ν-1-SVM parameterized by λj, is defined as follows:
| (17) |
where θλj is the angle delimited by wλj and the support vector as shown in Figure 1. cos(θλj) is a normalizing factor which is used to make all the djλ (x) comparable.
Figure 1.
Training data mapped into the feature space on a portion 𝒮λ of a hypersphere.
Using ||Φ(x)|| = 1 in (17) leads to the following:
| (18) |
Since the αpλj are obtained by the regularization path for any value of λj, computing dλj is considered as an easy-fast task. The distance measure dλj(x) is inspired from [22]. When data are distributed in a unimodal form, the dλj(x) is a decreasing function with respect to the distance between a sample x and the data mean. The probability density function is also a decreasing function with respect to the distance from the mean. Thus, dλj(x) preserves distribution order relations. In such case, and under optimality of the ν-1-SVM classifier, the use of dλj(x) should reach the same performances as the one obtained using the distribution.
In the simplest case of multiclass problems where the loss function is defined as the error probability, a patient x is assigned to the tumor class maximizing dλj(x).
To extend the multiclass prediction process to the class-selective scheme, a weighted form of the distance measure is proposed. The weight βj is associated to dλj. βj reflects an adjusted value of the distance dλj according to the penalty associated with the tumor class wj. Thus, introducing weights leads to treat differently each tumor class and helps solving problems with different costs cij on the classification decisions.
Finally, in the general case where the loss function is considered in the class-selective rejection scheme, the prediction process can be defined as follows: a blinded sample x is assigned to the ith option if and only if
| (19) |
Thus, in contrast to previous multiclass SVMs, which construct the maximum margin between classes and locate the decision hyperplane in the middle of the margin, the proposed approach resembles more to the robust Bayesian classifier. The distribution of each tumor class is considered and the optimal decision is slightly deviated toward the class with the smaller variance.
The proposed decision rule depends on σ, ν and β vectors of σj, νj and βj for j = 1,…, N. Tuning νj is the most time expensive task since changing νj leads to solve the optimization problem formulated in (16). Moreover, tuning νj is a crucial point, it enables to control the margin error. In fact, it was shown in [11] that this regularization parameter is an upper bound on the fraction of outliers and a lower bound on the fraction of the SVs. In [9, 23] a smooth grid search was supplied in order to choose the optimal values of ν. The N values νjs were chosen equal to reduce the computational costs. However, this assumption reduces the search space of parameters too. To avoid this restriction, the proposed approach optimizes all the νj with j = 1,…, N corresponding to the Nν-1-SVMs using regularization path and consequently explores the entire parameters space. Thus the tuned νj are most likely to be the optimal ones. The parameter σ are set equals σ1 = σ2 = ⋯ = σN.
The optimal vector of σj, λj and βj, j = 1,…, N, is the one which minimizes an estimator of c(Z) using a validation set. Since the problem is described by a sample set, an estimator of c(Z) given by (11) is used:
| (20) |
where and are the empirical estimators of Pj and P(Di/wj), respectively.
The optimal rule is obtained by tuning λj, βj and σj so that the estimated loss computed on a validation set is minimum. This is accomplished by employing a global search for λj and βj and an iterative search over the kernel parameter. For each given value σ of the parameter kernels, ν-1-SVMs are trained using the regularization path method on a training set. Then the minimization of over a validation set is sought by solving an alternate optimization problem over λj and βj which is easy since all ν-1-SVM solutions are easily interpolated from the regularization path. σ is chosen from a previously defined set of real numbers [σ0,…, σs] with s ∈ ℵ. Algorithm 1 elucidates the proposed approach.
Algorithm 1.
Multiclass SVM minimizing an asymmetric loss function.
3. Experimental Results
In this section, two experiments are reported in order to assess the performance of the proposed approach. First, the cancer diagnosis problem is considered in the traditional Bayesian framework. Five gene expression datasets and five supervised algorithms are considered. Each gene dataset was selected using the six test statistics of [1]. The decisions are given by the possible set of tumor classes and the loss function is defined as the probability of error to make results comparable with those of [1]. Second, in order to show the advantages of considering the multiclass cancer diagnosis in class-selective rejection scheme, one gene dataset is considered and studied with an asymmetric loss function. A cascade of classifiers with rejection options is used to ensure a reliable diagnosis. For both experiments, the loss function was minimized by determining the optimal parameters βj and λj for j = 1,…, N for a given kernel parameter σ and by testing different values of σ in the set [2−3, 2−2, 2−1, 20, 21, 22]. Finally, the decision rule which minimizes the loss function is selected.
3.1. Bayesian Framework
Five multiclass gene expression datasets leukemia72 [24], ovarian [25], NCI [26, 27], lung cancer [28] and lymphoma [29] were considered. Table 1 describes the five genes datasets. For each dataset, the six test statistics F, B, W, W*, C, and H were used to select informative genes.
Table 1.
Multiclass gene expression datasets.
| Dataset | Leukemia72 | Ovarian | NCI | Lung cancer | Lymphoma |
|---|---|---|---|---|---|
| No. of gene | 6817 | 7129 | 9703 | 918 | 4026 |
| No. of sample | 72 | 39 | 60 | 73 | 96 |
| No. of class | 3 | 3 | 9 | 7 | 9 |
The cancer diagnosis problem was considered in the traditional Bayesian framework. Decisions were given by the set of possible classes and loss function was defined by the error risk. This means that in (20) cij are defined according to the Table 2. The performance of the proposed method was measured by evaluating its accuracy rate and it was compared to results obtained by the five predictors evoked in [1]: Naive Bayes, Nearest Neighbor, Linear Perceptron, Multilayer Perceptron Neural Network with five nodes in the middle layer, and Support Vector Machines with second-order polynomial kernel.
Table 2.
Loss function cost matrix in the Bayesian framework.
| Patient class | ||||||
| 1 | 2 | . | . | N | ||
| 1 | 0 | 1 | · | · | 1 | |
| 2 | 1 | 0 | 1 | · | ||
| Prediction | · | · | · | · | · | · |
| · | · | · | · | 1 | ||
| N | 1 | · | · | 1 | 0 | |
To compute the generalization accuracy of the proposed classifier, Leave One Out (LOO) resampling method is used to divide a gene dataset of n patients into two sets, a set of n − 1 patients and a test set of 1 blinded patient. This method involves n separate runs. For each run, the first set of n − 1 samples is divided using 5 Cross-validation (5-CV) into a training set and a validation set. Nν-1-SVMs are trained using the training set for all values of νj. The decision is obtained by tuning the parameters βj, λj and σj for j = 1,…, N so that the loss function computed on the validation set is minimum. Optimal parameters are then used to build the decision rule using the whole n − 1 samples. The blinded test set is classified according to this rule. The overall prediction error is the sum of the patients misclassified on all n runs.
Table 3 reports errors of the proposed algorithm, the average value and the median value of the 5 classifiers prediction errors reported in [1] when 50 informative genes are used. Table 4 reports values when 100 informative genes are used. F, B, W, W*, C, and H represent the six test statistics.
Table 3.
Prediction errors of the proposed classifier, mean and median values of the 5 classifiers prediction errors according to [1] with 50 informative selected genes.
| F | B | W | W* | C | H | ||
|---|---|---|---|---|---|---|---|
| Leukemia | Proposed algorithm | 4 | 3 | 5 | 5 | 3 | 2 |
| Mean | 3.4 | 2.4 | 2.8 | 2.8 | 3.2 | 3.0 | |
| Median | 3 | 2 | 3 | 3 | 3 | 3 | |
| Ovarian | Proposed algorithm | 0 | 0 | 0 | 0 | 0 | 0 |
| Mean | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Median | 0 | 0 | 0 | 0 | 0 | 0 | |
| NCI | Proposed algorithm | 31 | 26 | 27 | 27 | 27 | 33 |
| Mean | 36.0 | 32.0 | 27.4 | 26.0 | 27.0 | 35.4 | |
| Median | 35 | 29 | 27 | 27 | 27 | 35 | |
| Lung cancer | Proposed algorithm | 14 | 16 | 16 | 16 | 16 | 15 |
| Mean | 17.6 | 17.0 | 17.6 | 17.6 | 18.0 | 18.0 | |
| Median | 17 | 17 | 18 | 18 | 18 | 18 | |
| Lymphoma | Proposed algorithm | 18 | 16 | 9 | 10 | 9 | 15 |
| Mean | 23.8 | 19.8 | 14.0 | 14.0 | 12.8 | 22.0 | |
| Median | 23 | 19 | 12 | 12 | 13 | 20 |
Table 4.
Prediction errors of the proposed classifier, mean and median values of the 5 classifiers prediction errors according to [1] with 100 informative selected genes.
| F | B | W | W* | C | H | ||
|---|---|---|---|---|---|---|---|
| Leukemia | Proposed algorithm | 5 | 2 | 3 | 3 | 4 | 6 |
| Mean | 3.4 | 3.0 | 3.0 | 3.0 | 3.2 | 3.0 | |
| Median | 3 | 3 | 4 | 3 | 3 | 3 | |
| Ovarian | Proposed algorithm | 0 | 0 | 0 | 0 | 0 | 0 |
| Mean | 0.2 | 0.0 | 0.0 | 0.0 | 0.0 | 0.0 | |
| Median | 0 | 0 | 0 | 0 | 0 | 0 | |
| NCI | Proposed algorithm | 33 | 21 | 26 | 25 | 26 | 36 |
| Mean | 33.0 | 22.6 | 23.8 | 25.2 | 25.2 | 31.6 | |
| Median | 33 | 22 | 25 | 26 | 26 | 31 | |
| Lung cancer | Proposed algorithm | 11 | 10 | 11 | 11 | 11 | 13 |
| Mean | 12.2 | 12.2 | 11.4 | 12.2 | 12.2 | 15.8 | |
| Median | 12 | 12 | 11 | 11 | 11 | 14 | |
| Lymphoma | Proposed algorithm | 16 | 16 | 11 | 10 | 11 | 17 |
| Mean | 21.8 | 19.2 | 13.0 | 13.8 | 14.4 | 18.2 | |
| Median | 17 | 16 | 12 | 12 | 12 | 18 |
Experimental results show that, for ovarian, NCI, lung cancer and lymphoma multiclass genes problems, the proposed approach achieves competitive performances compared to the 5 classifiers reported in [1]. For these datasets, prediction errors of the proposed approach are less than the mean and median values of the 5 classifiers prediction errors reported in [1]. However, for leukemia72, the proposed algorithm performances are almost in the same range of those provided by the 5 classifiers reported in [1]. The proposed approach prediction error is equal, or in the worst case, slightly higher than the mean and median errors.
Moreover, we can note that focussing on the test statistics comparison, experimental results confirm those of [1]. B, W and W* can be the most performing tests under variances heterogeneity assumptions.
3.2. Class-Selective Rejection Framework
In the following, we present the study of lung cancer problem in the class-selective rejection scheme. Lung cancer diagnosis problem is determined by the gene expression profiles of 67 lung tumors and 6 normal lung specimens from patients whose clinical course was followed for up to 5 years. The tumors comprised 41 Adenocarcinomas (ACs), 16 squamous cell carcinomas (SCCs); 5 cell lung cancers (LCLCs) and 5 small cell lung cancers (SCLCs). ACs are subdivided into three subgroups 21 AC of group 1 tumors, 7 AC of group 2 tumors and 13 AC of group 3 tumors. Thus, the multiclass diagnosis cancer consists of 7 classes.
Authors in [28] observed that AC of group 3 tumors shared strong expression of genes with LCLC and SCC tumors. Thus, poorly differentiated AC is difficult to distinguish from LCLC or SCC. Confusion matrices (Tables 5 and 6) computed in the Bayesian framework, with 50 W* and 50 H prove well these claims. It can be noticed that 8 of the 16 misclassified 50 W* patients and 8 of the 15 misclassified 50 H patients correspond to confusion between these three subcategories. Therefore, one may define a new decision option as a subset of these three classes to reduce error.
Table 5.
Confusion matrix of 50 W* lung cancer dataset. Total of misclassified is equal to 16.
| Patient class | ||||||||
| Normal | SCLC | LCLC | SCC | AC2 | AC3 | AC1 | ||
| Predicted decision | Normal | 6 | 0 | 0 | 0 | 0 | 0 | 0 |
| SCLC | 0 | 4 | 0 | 0 | 0 | 1 | 0 | |
| LCLC | 0 | 0 | 3 | 0 | 0 | 4 | 1 | |
| SCC | 0 | 0 | 0 | 16 | 0 | 3 | 0 | |
| AC2 | 0 | 0 | 0 | 0 | 4 | 0 | 0 | |
| AC3 | 0 | 1 | 1 | 0 | 1 | 4 | 0 | |
| AC1 | 0 | 0 | 1 | 0 | 2 | 1 | 20 | |
Table 6.
Confusion Matrix of 50 H lung cancer dataset. Total of misclassified is equal to 15.
| Patient class | ||||||||
| Normal | SCLC | LCLC | SCC | AC2 | AC3 | AC1 | ||
| Predicted decision | Normal | 5 | 0 | 0 | 0 | 0 | 0 | 0 |
| SCLC | 0 | 4 | 0 | 0 | 0 | 0 | 0 | |
| LCLC | 0 | 0 | 1 | 1 | 0 | 2 | 2 | |
| SCC | 0 | 0 | 2 | 14 | 0 | 1 | 0 | |
| AC2 | 0 | 0 | 0 | 0 | 7 | 0 | 0 | |
| AC3 | 0 | 0 | 2 | 1 | 0 | 8 | 0 | |
| AC1 | 1 | 1 | 0 | 0 | 0 | 2 | 19 | |
Moreover, same researches affirm that distinction between patients with nonsmall cell lung tumors (SCC, AC and LCLC) and those with small cell tumors or SCLC is extremely important, since they are treated very differently. Thus, a confusion or wrong decision among patients of nonsmall cell lung tumors should cost less than a confusion between nonsmall and small lung cells tumors. Besides, one may provide an extra decision option that includes all the subcategories of tumors to avoid this kind of confusion. Finally, another natural decision option can be the set of all classes, which means that the classifier has totally withhold taking a solution.
Given all these information, the loss function can be empirically defined according to the asymmetric cost matrix given in Table 7. Solving 50 W* lung cancer problem in this scheme leads to the confusion matrix presented in Table 8. As a comparison with Table 5, one may mainly note that the number of misclassified patients decreases from 16 to 10 and 8 withhold decisions or rejected patients. This partial rejection contributes to avoid confusion between nonsmall and small lung cells tumors and reduces errors due to indistinctness among LCLC, SCC and AC3. Besides, according to the example under study, no patient is totally rejected. It is an expected result since initially (Table 5) there was no confusion between normal and tumor samples.
Table 7.
Asymmetric cost matrix of the loss function.
| Patient class | ||||||||
| Normal | SCLC | LCLC | SCC | AC2 | AC3 | AC1 | ||
| Normal | 0 | 1 | 1 | 1 | 1 | 1 | 1 | |
| SCLC | 1 | 0 | 1 | 1 | 1 | 1 | 1 | |
| LCLC | 1 | 1 | 0 | 0.9 | 0.9 | 1 | 1 | |
| SCC | 1 | 1 | 0.9 | 0 | 0.9 | 1 | 0.9 | |
| AC2 | 1 | 1 | 0.9 | 0.9 | 0 | 0.9 | 0.9 | |
| Predicted decision | AC3 | 1 | 1 | 0.9 | 0.9 | 0.9 | 0 | 0.9 |
| AC1 | 1 | 1 | 0.9 | 0.9 | 0.9 | 0.9 | 0 | |
| {LCLC, SCC, AC3} | 1 | 1 | 0.6 | 0.6 | 0.9 | 0.2 | 0.9 | |
| All tumors | 1 | 0.2 | 0.6 | 0.6 | 0.2 | 0.2 | 0.5 | |
| All classes | 0.6 | 0.2 | 0.6 | 0.6 | 0.2 | 0.6 | 0.6 | |
Table 8.
Confusion matrix of the 50 W* lung cancer problem with class-selective rejection using cost matrix defined in Table 7. Total of misclassified is equal to 10, total of partially and totally rejected samples is equal to 8.
| Patient class | ||||||||
| Normal | SCLC | LCLC | SCC | AC2 | AC3 | AC1 | ||
| Normal | 6 | 0 | 0 | 0 | 0 | 0 | 0 | |
| SCLC | 0 | 3 | 0 | 0 | 0 | 0 | 0 | |
| LCLC | 0 | 0 | 3 | 0 | 0 | 4 | 0 | |
| SCC | 0 | 0 | 0 | 16 | 0 | 2 | 0 | |
| Predicted decision | AC2 | 0 | 0 | 0 | 0 | 4 | 0 | 0 |
| AC3 | 0 | 0 | 0 | 0 | 1 | 3 | 0 | |
| AC1 | 0 | 0 | 1 | 0 | 1 | 1 | 20 | |
| {LCLC, SCC, AC3} | 0 | 0 | 1 | 0 | 0 | 2 | 0 | |
| All tumors | 0 | 2 | 0 | 0 | 1 | 1 | 1 | |
| All classes | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
To take a decision concerning the rejected patients, we may refer to clinical analysis. It is worth to note that for partially rejected patients, clinical analysis will be less expensive in terms of time and money than those on completely blinded patients. Moreover, a supervised solution can be also proposed. It aims to use genes selected from another test statistic in order to assign rejected patients to one of the possible classes. According to Tables 3 and 4, prediction errors computed on same patients using genes selected by different test statistics may decrease since errors of two different test statistics do not occur on the same patients. Thus, we chose 50 H lung cancer dataset to reclassify the 8 rejected patients of Table 8. Five of them were correctly classified while three remained misclassified. Results are reported in Table 9. The number of misclassified patients decreases to 13 which is less than all the prediction errors obtained with 50 informative genes (lung cancer problem prediction errors of Table 3). In fact, many factors play an important role in the cascade classifiers system such as the asymmetric costs matrix which has been chosen empirically, the choice of test statistics, the number of classifiers in a cascade system,…. Such concerns are under study.
Table 9.
Confusion matrix of the cascade classifier (50 W* with rejection and 50 H classifier). Total of misclassified is equal to 13.
| Patient class | ||||||||
| Normal | SCLC | LCLC | SCC | AC2 | AC3 | AC1 | ||
| Predicted decision | Normal | 6 | 0 | 0 | 0 | 0 | 0 | 0 |
| SCLC | 0 | 4 | 0 | 0 | 0 | 0 | 0 | |
| LCLC | 0 | 0 | 3 | 0 | 0 | 4 | 1 | |
| SCC | 0 | 0 | 0 | 16 | 0 | 2 | 0 | |
| AC2 | 0 | 0 | 0 | 0 | 5 | 0 | 0 | |
| AC3 | 0 | 1 | 1 | 0 | 1 | 6 | 0 | |
| AC1 | 0 | 0 | 1 | 0 | 1 | 1 | 20 | |
4. Conclusion
Cancer diagnosis using genes involve a gene selection task and a supervised classification procedure. This paper tackles the classification step. It considers the problem of gene-based multiclass cancer diagnosis in the general framework of class-selective rejection. It gives a general formulation of the problem and proposes a possible solution based on ν-1-SVM coupled with its regularization path. The proposed classifier minimizes any asymmetric loss function. Experimental results show that, in the particular case where decisions are given by the possible classes and the loss function is set equal to the error rate, the proposed algorithm, compared with the state of art multiclass algorithms, can be considered as a competitive one. In the class-selective rejection, the proposed classifier ensures higher reliability and reduces time and expense costs by introducing partial and total rejection. Furthermore, results prove that a cascade of classifiers with class-selective rejections can be considered as a good way to get improved supervised diagnosis. To get the most reliable diagnosis, the confusion matrix defining the loss function should be carefully chosen. Finding the optimal loss function according to performance constraints is an promising approach [30] which is actually under investigation.
Acknowledgments
The authors thank Dr. Dechang Chen of the Uniformed Services University of the Health Sciences for providing the gene selected data of leukemia72, ovarian, NCI, lung cancer and lymphoma using six test statistics ANOVA F, Brown-Forsythe test, Welch test, Adjusted Welch test, Cochran test and Kruskal-Wallis test. This work was supported by the “Conseil Régional Champagne Ardenne” and the “Fonds Social Européen”.
References
- 1.Chen D, Liu Z, Ma X, Hua D. Selecting genes by test statistics. Journal of Biomedicine and Biotechnology. 2005;2005(2):132–138. doi: 10.1155/JBB.2005.132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Ramaswamy S, Tamayo P, Rifkin R, et al. Multiclass cancer diagnosis using tumor gene expression signatures. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(26):15149–15154. doi: 10.1073/pnas.211566398. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Jrad N, Grail-Maës E, Beauseroy P. A supervised decision rule for multiclass problems minimizing a loss function. In: Proceedings of the 7th International Conference on Machine Learning and Applications (ICMLA '08); December 2008; San Diego, Calif, USA. pp. 48–53. [Google Scholar]
- 4.Ha TM. The optimum class-selective rejection rule. IEEE Transactions on Pattern Analysis and Machine Intelligence. 1997;19(6):608–615. doi: 10.1109/TPAMI.2008.239. [DOI] [PubMed] [Google Scholar]
- 5.Horiuchi T. Class-selective rejection rule to minimize the maximum distance between selected classes. Pattern Recognition. 1998;31(10):1579–1588. [Google Scholar]
- 6.Grall-Maës E, Beauseroy P, Bounsiar A. Multilabel classification rule with performance constraints. In: Proceedings of IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP '06), vol. 3; May 2006; Toulouse, France. pp. 784–787. [Google Scholar]
- 7.Jrad N, Grall-Maës E, Beauseroy P. Gaussian mixture models for multiclass problems with performance constraints. In: Proceedings of the 17th European Symposium on Artificial Neural Networks (ESANN '09); April 2009; Bruges, Belgium. [Google Scholar]
- 8.Bottou L, Cortes C, Denker J, et al. Comparison of classifier methods: a case study in handwritten digit recognition. In: Proceedings of the 12th IAPR International Conference on Pattern Recognition (ICPR '94), vol. 2; October 1994; Jerusalem, Israel. pp. 77–82. [Google Scholar]
- 9.Yang X, Liu J, Zhang M, Niu K. A new multiclass SVM algorithm based on one-class SVM. In: Proceedings of International Conference on Computational Science (ICCS '07); May 2007; Beijing, China. pp. 677–684. [Google Scholar]
- 10.Hao P-Y, Lin Y-H. A new multi-class support vector machine with multi-sphere in the feature space. In: Proceedings of the 20th International Conference on Industrial, Engineering and Other Applications of Applied Intelligent Systems (IEA/AIE '07), vol. 4570; June 2007; Kyoto, Japan. pp. 756–765. Lecture Notes in Computer Science. [Google Scholar]
- 11.Schölkopf B, Platt JC, Shawe-Taylor J, Smola AJ, Williamson RC. Estimating the support of a high-dimensional distribution. Neural Computation. 2001;13(7):1443–1471. doi: 10.1162/089976601750264965. [DOI] [PubMed] [Google Scholar]
- 12.Tax D. One-class classification: concept learning in the absence of counter-examples. Delft, The Netherlands: Technische Universiteit Delft; 2001. Ph.D. thesis. [Google Scholar]
- 13.Schölkopf B, Smola AJ. Learning with Kernels: Support Vector Machines, Regularization, Optimization, and Beyond. Cambridge, Mass, USA: MIT Press; 2001. [Google Scholar]
- 14.Hastie T, Rosset S, Tibshirani R, Zhu J. The entire regularization path for the support vector machine. The Journal of Machine Learning Research. 2004;5:1391–1415. [Google Scholar]
- 15.Rakotomamojy A, Davy M. One-class SVM regularization path and comparison with alpha seeding. In: Proceedings of the 15th European Symposium on Artificial Neural Networks (ESANN '07); April 2007; Bruges, Belgium. pp. 271–276. [Google Scholar]
- 16.Kutner MH, Nachtsheim CJ, Neter J, Li W. Applied Linear Statistical Models. 5th edition. New York, NY, USA: McGraw-Hill; 2005. [Google Scholar]
- 17.Brown MB, Forsythe AB. The small sample behavior of some statistics which test the equality of several means. Technometrics. 1974;16(1):129–132. [Google Scholar]
- 18.Welch BL. On the comparison of several mean values: an alternative approach. Biometrika. 1951;38(3-4):330–336. [Google Scholar]
- 19.Hartung J, Argaç D, Makambi KH. Small sample properties of tests on homogeneity in one-way Anova and meta-analysis. Statistical Papers. 2002;43(2):197–235. [Google Scholar]
- 20.Cochran WG. Problems arising in the analysis of a series of similar experiments. Journal of the Royal Statistical Society. 1937;4:102–118. [Google Scholar]
- 21.Daniel W. Biostatistics: A Foundation for Analysis in the Health Sciences. New York, NY, USA: John Wiley & Sons; 1999. [Google Scholar]
- 22.Davy M, Desobry F, Gretton A, Doncarli C. An online support vector machine for abnormal events detection. Signal Processing. 2006;86(8):2009–2025. [Google Scholar]
- 23.Hsu C-W, Lin C-J. A comparison of methods for multiclass support vector machines. IEEE Transactions on Neural Networks. 2002;13(2):415–425. doi: 10.1109/72.991427. [DOI] [PubMed] [Google Scholar]
- 24.Golub TR, Slonim DK, Tamayo P, et al. Molecular classification of cancer: class discovery and class prediction by gene expression monitoring. Science. 1999;286(5439):531–527. doi: 10.1126/science.286.5439.531. [DOI] [PubMed] [Google Scholar]
- 25.Welsh JB, Zarrinkar PP, Sapinoso LM, et al. Analysis of gene expression profiles in normal and neoplastic ovarian tissue samples identifies candidate molecular markers of epithelial ovarian cancer. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(3):1176–1181. doi: 10.1073/pnas.98.3.1176. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Ross DT, Scherf U, Eisen MB, et al. Systematic variation in gene expression patterns in human cancer cell lines. Nature Genetics. 2000;24(3):227–235. doi: 10.1038/73432. [DOI] [PubMed] [Google Scholar]
- 27.Scherf U, Ross DT, Waltham M, et al. A gene expression database for the molecular pharmacology of cancer. Nature Genetics. 2000;24(3):236–244. doi: 10.1038/73439. [DOI] [PubMed] [Google Scholar]
- 28.Garber ME, Troyanskaya OG, Schluens K, et al. Diversity of gene expression in adenocarcinoma of the lung. Proceedings of the National Academy of Sciences of the United States of America. 2001;98(24):13784–13789. doi: 10.1073/pnas.241500798. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Alizadeh AA, Elsen MB, Davis RE, et al. Distinct types of diffuse large B-cell lymphoma identified by gene expression profiling. Nature. 2000;403(6769):503–511. doi: 10.1038/35000501. [DOI] [PubMed] [Google Scholar]
- 30.Grall-Maës E, Beauseroy P. Optimal decision rule with class-selective rejection and performance constraints. IEEE Transactions on Pattern Analysis and Machine Intelligence. 2009;99(1) doi: 10.1109/TPAMI.2008.239. [DOI] [PubMed] [Google Scholar]