IC₅₀-to-K_i: a web-based tool for converting IC₅₀ to K_i values for inhibitors of enzyme activity and ligand binding

Abstract

A new web-server tool estimates K_i values from experimentally determined IC₅₀ values for inhibitors of enzymes and of binding reactions between macromolecules (e.g. proteins, polynucleic acids) and ligands. This converter was developed to enable end users to help gauge the quality of the underlying assumptions used in these calculations which depend on the type of mechanism of inhibitor action and the concentrations of the interacting molecular species. Additional calculations are performed for nonclassical, tightly bound inhibitors of enzyme-substrate or of macromolecule-ligand systems in which free, rather than total concentrations of the reacting species are required. Required user-defined input values include the total enzyme (or another target molecule) and substrate (or ligand) concentrations, the K_m of the enzyme-substrate (or the K_d of the target-ligand) reaction, and the IC₅₀ value. Assumptions and caveats for these calculations are discussed along with examples taken from the literature. The host database for this converter contains kinetic constants and other data for inhibitors of the proteolytic clostridial neurotoxins (http://botdb.abcc.ncifcrf.gov/toxin/kiConverter.jsp).

INTRODUCTION

Some analyses of networks, pathways and metagenomics focus on identifying key proteins or polynucleic acids as targets for inhibitory compounds. Typically, high-throughput screening assays are initially used to compare and down-select potential inhibitors of enzymatic activity or macromolecule-ligand binding. Many functional assays seek a total inhibitor concentration that reduces these activities by 50% (IC₅₀). However, the IC₅₀ value depends on concentrations of the enzyme (or target molecule), the inhibitor, and the substrate (or ligand) along with other experimental conditions. What is required is an accurate determination of the K_i value, an intrinsic, thermo-dynamic quantity that is independent of the substrate (ligand) but depends on the enzyme (target) and inhibitor. Thus, comparisons can be more readily made among different laboratories to characterize the inhibitors. While these more time-consuming assays are usually done with the most promising candidates, accurate, initial estimates of K_i values for more of the candidates would be beneficial. A much discussed problem in the literature (1–8) is converting IC₅₀ to K_i values because even the simplest types of inhibitory mechanisms (e.g. competitive, uncompetitive and noncompetitive) will influence the calculation.

To help address this problem, our web-server tool calculates K_i values from IC₅₀ values using equations for enzyme-substrate and target-ligand interactions by different inhibitory mechanisms (http://botdb.abcc.ncifcrf.gov/toxin/kiConverter.jsp). Additional calculations are performed for tightly bound inhibitors of enzyme-substrate reactions in which free, rather than total, concentrations of the molecular species are calculated for nonclassic Michaelis–Menten kinetics. Similar calculations can be performed for target molecule-ligand systems. User-defined input values include total concentrations of the enzyme (or target molecule) and substrate (or ligand), the K_m of the enzyme-substrate (or the K_d of the target-ligand) reaction and the IC₅₀ value. The outputs include tabulations of the K_i values under different kinetic schemes, extensive tabulations of the results, summary histograms and the corresponding equations. Help buttons are available for Background, Assumptions, Literature, Links and Equations along with examples taken from the host database-server that contains kinetic information on neurotoxin inhibitors. An example calculation is included here for a tight-binding inhibitor of an enzyme–substrate reaction, while other enzyme inhibitor and protein–ligand–inhibitor examples are also provided. Our rationale for creating this converter is to enable end users to judge the quality of the underlying assumptions for these calculations and to help facilitate research and the development of potential therapeutic products.

METHODS

Reactions and equations

The website cited in (9) served as an initial design template for our IC₅₀-to-K_i converter. Equations (1–4) were adapted from refs. (3), (6) and (9) whereas we derived Equation (5) for this study. The analytic expressions for K_i that are shown below were verified numerically by methods used in a previous kinetic analysis (10).

The derivations for converting IC₅₀ to K_i values published by Brandt et al. (3) include three types of classic inhibitor mechanisms in which different relations may exist between S and K_m. For tightly bound inhibitors, the equation for K_i by Copeland et al. (6) is used to take into account the larger amounts of inhibitor bound species, thus making the Michaelis–Menten assumption of the total enzyme concentration being equal invalid (5). These equations are also relevant for protein–ligand–inhibitor (P–L–I) interactions that also adhere to the above assumptions.

Enzyme–substrate–inhibitor reactions

For competitive inhibition

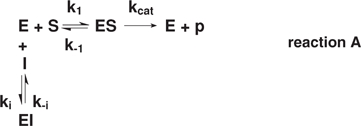where K_d = k_–1/k₁ and K_i = k_−i/k_i, the classic expression is

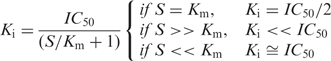1a

and for tightly bound inhibitors (5,6)

1b

For uncompetitive inhibition

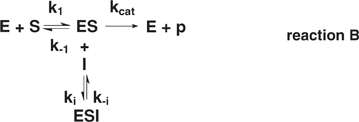the classic expression is:

2a

and for tightly bound inhibitors (5,6)

2b

For noncompetitive inhibition (2)

where K_ia = k_–ia/k_ia and K_ib = k_–ib/k_ib, the classic expression is:

3a

and for tightly bound inhibitors (5,6)

3b

This noncompetitive reaction also assumes that the inhibitor dissociation constants are equal: K_ia = K_ib = K_i. Mixed inhibition, where K_ia < > K_ib, is not considered here.

P–L–I reactions

For total concentrations, E is replaced by P and S is replaced by L. Additional reaction schemes are located at this tool's website. As in classic enzyme–substrate systems the relation of K_i and IC₅₀ in competitive inhibition is:

4a

For protein–ligand experiments with tight-binding inhibitors, the free rather than the total concentrations of the reactants need to be used as modified from ref. 9

4b

where I₅₀ and L₅₀ are the free concentrations of the inhibitor and ligand, respectively, at 50% inhibition, and P₀ is the free concentration of the protein in the absence of inhibitor. The concentration of the free inhibitor species is given by

4c

where P₀ = –((K_d + L–P) + [(K_d + L–P)² + 4PK_d]^1/2)/2, PL₀ = P–P₀, PL₅₀ = PL₀/2, L₀ = L–PL₀ and L₅₀ = L–PL₅₀.

For this study, we derived a corresponding value of K_i for uncompetitive inhibition

5

in which the variables are the same as in Equation (4) except that L₅₀ = – ((P–L) + [(P–L)² + 4(PL₀K_d/2)]^1/2)/2. Although in this study we use the term K_d to quantify an antagonist's effect, the pharmacology-derived EC₅₀ value is more appropriate when functional experiments are performed (11).

General assumptions and caveats

It is assumed that all of the substrate- and inhibitor-binding reactions are reversible and that they all have a one-to-one stoichiometry, i.e. no multiple binding of inhibitor molecules or any form of cooperativity, or other complex mechanisms of inhibition such as partial or mixed types (3). It is also assumed that in the enzymatic reactions enzyme autocleavage did not occur and that when substrates for fluorescence resonance energy transfer were used, appropriate corrections for inner filter effects were performed. Comparison of K_m or IC₅₀ values for a set of inhibitor candidates is only assumed to be valid when they are evaluated under identical experimental conditions. In most experimental studies of enzyme kinetics, the total concentrations of substrate and inhibitor used are in excess of the enzyme concentration to make their free and total concentrations essentially the same (1). Under the conditions of some ligand-receptor (e.g. protein)-binding studies, the free concentrations also become sufficiently important to require modifications of these equations (1, 2), and (9).

Description of the web server

The IC₅₀-to-K_i tool is implemented as a web resource using an Oracle database (Oracle9i Enterprise Edition Release 9.2.0.4.0), Java (JDK 1.5.0) and Apache web server components including Tomcat 4.1. Information on candidate inhibitors of the botulinum neurotoxins was collected by mining the biomedical literature including searches with botXminer (12) using the National Library of Medicine's MEDLINE®/PubMed® (13). Experimental data (IC₅₀ values) and accompanying assay information were manually extracted from primary literature results and other relevant databases: JCVI-Pathema-Clostridium (13), Brenda (14) and Protein Data Bank (15).

USAGE

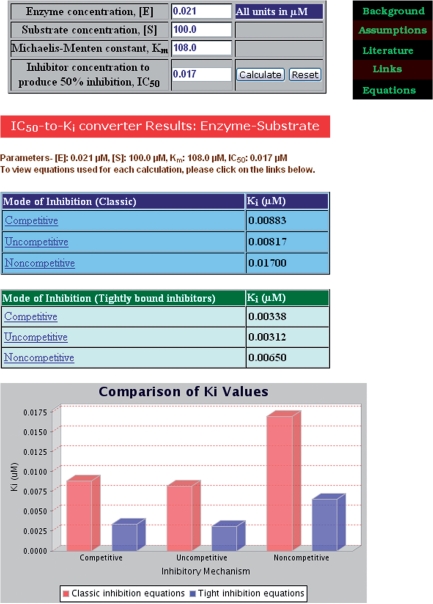
An internal link to the user-accessible converter is also located on the left side of the BotDB home page. The four required inputs for E, S, K_m and IC₅₀ are indicated with default settings for several examples. After submitting these values by using the ‘calculate’ button, these input data are returned along with the K_i results for the example cases.

An illustration is provided for a tight-binding inhibitor of an enzyme–substrate (E–S) reaction (Figure 1). The values for this example are from data using cimoxatone, a tight-binding inhibitor of monoamine oxidase (16). The four inputs for E, S, K_m and IC₅₀ are 0.021, 100, 108 and 0.017, respectively, in micromolar units. The K_i results for three modes of inhibition are returned on a new page. The top block of results corresponds to the solutions for a classic inhibitor (i.e. Michaelis–Menten kinetics). The second block represents the corrections made to the first set of equations [Equations (1b–3b)] for tightly bound inhibitors when there is substantial inhibitor depletion (5,6). Equations can be viewed by clicking on a label for a mode of inhibition. Below these two tables, histograms plotting the six results are shown for a visual comparison. In this example, the results from the classic and corrected equations are quite different. This difference in K_i values enables the user to conclude that not all of the assumptions underlying classic Michaelis–Menten equations are being obeyed and that the data are consistent with the kinetics of a tight-binding inhibitor.

Figure 1.

Results page from the IC₅₀-to-K_i web tool for a tight-binding inhibitor of monoamine oxidase. The top table contains sample input data obtained from ref. 16. The middle table contains the results for a classic inhibitor that follows Michaelis–Menten kinetic Equations (1a–3a) for three kinetic reactions. The bottom table contains the results for nonclassic, tight-binding inhibitor uses Equations (1b–3b) for the same three reactions. The histograms summarize these results. Equations for each displayed mode of inhibition can be viewed by clicking on its label. A help list located on the upper right side is available for more detailed information about this tool.

Two other examples of enzyme inhibitors are also available for users to examine at the IC₅₀-to-K_i tool website. For classic inhibition, data values using a candidate inhibitor of botulinum neurotoxin type A (17) are used as inputs: E, S, K_m and IC₅₀ (in micromolar units) 0.0067, 300, 1300 and 3.2, respectively. In contrast to the tight-binding inhibitor example, the returned values for K_i are similar for classic and tight-binding kinetics indicating that this data set is consistent with classical kinetics.

In another example of a potentially cooperative inhibitor of CYP3A4 (18), the input data for E, S, K_m and IC₅₀, in micromolar units, are 0.1, 50, 51 and 0.05, respectively. This example returns an error message from the converter that states that the 1:1 stoichiometry assumption may have been violated and requests the user to enter different values.

Finally, Equations (4) and (5) are used to calculate K_i values for reactions involving inhibitors of P–L-binding reactions. For this case, a user interface similar to the enzyme–substrate page is produced (see website). The values for a tight-binding inhibitor of an apoptosis-related protein from ref. 9 are used as an example calculation. The inputs are labeled P, L, K_d and IC₅₀. In this case, only the competitive and uncompetitive modes of inhibition are considered. The tabulated output includes the free concentrations of protein and ligand species in the absence of an inhibitor (P₀ and L₀, respectively). The free concentrations at 50% inhibition are also returned for the protein, ligand, inhibitor, protein–ligand complex and P–L–I complex (P₅₀, L₅₀, etc.). As with the tight-binding enzyme inhibitor calculations, the summary histograms again indicate that these data are consistent with the kinetics of a tight-binding inhibitor.

It is our intent for this general tool to provide results for classic and tight-binding inhibitors of enzyme activity and ligand-binding reactions that are assumed to follow relatively simple kinetic schemes. These different sets of kinetic results will allow investigators to decide whether additional experiments are required to understand better the kinetic behaviors of their candidate inhibitors for further research or therapeutic product development.

FUNDING

The Defense Threat Reduction Agency Joint Science and Technology Office-Chemical Biological Defense (project 3.10043_07_RD_B to F.J.L.); and by the National Cancer Institute, National Institutes of Health (contract No. HHSN261200800001E). Funding for open access charge: Defense Threat Reduction Agency.

Conflict of interest statement. None declared.