ProSMoS server: a pattern-based search using interaction matrix representation of protein structures

Abstract

Assessing structural similarity and defining common regions through comparison of protein spatial structures is an important task in functional and evolutionary studies of proteins. There are many servers that compare structures and define sub-structures in common between proteins through superposition and closeness of either coordinates or contacts. However, a natural way to analyze a structure for experts working on structure classification is to look for specific three-dimensional (3D) motifs and patterns instead of finding common features in two proteins. Such motifs can be described by the architecture and topology of major secondary structural elements (SSEs) without consideration of subtle differences in 3D coordinates. Despite the importance of motif-based structure searches, currently there is a shortage of servers to perform this task. Widely known TOPS does not fully address this problem, as it finds only topological match but does not take into account other important spatial properties, such as interactions and chirality. Here, we implemented our approach to protein structure pattern search (ProSMoS) as a web-server. ProSMoS converts 3D structure into an interaction matrix representation including the SSE types, handednesses of connections between SSEs, coordinates of SSE starts and ends, types of interactions between SSEs and β-sheet definitions. For a user-defined structure pattern, ProSMoS lists all structures from a database that contain this pattern. ProSMoS server will be of interest to structural biologists who would like to analyze very general and distant structural similarities. The ProSMoS web server is available at: http://prodata.swmed.edu/ProSMoS/.

INTRODUCTION

Comparative methods advance our understanding of the relationship between structure and function in proteins (1). In comparative structure analysis, the most important and difficult task is the detection of structural similarity, especially the discovery of remote but biologically meaningful connections between protein structures (2–4). Most of the structure comparison approaches assess the structure similarity by using superposition and closeness of either spatial coordinates or inter-residue contacts and find sub-structures in common between protein structures (5,6). However, for the purpose of fold classification it is more natural to look for specific 3D motifs or patterns instead of finding common features in two proteins (7,8). Protein folds are defined by similarities in 3D packing of major SSEs, their spatial arrangement and topological connections, but without consideration of subtle differences in 3D coordinates(7). It is desirable to have a server that finds protein similarities using this definition. Pattern search, instead of a general structure similarity search, is more suited for this task. Namely, given a pattern of secondary structures with defined topology and mutual arrangement in 3D, we would like to find all structures matching this pattern. Recently, we developed a program, Protein Structure Motif search (ProSMoS) to address this question (9). ProSMoS is not sensitive to finer structure details, but finds proteins matching user-defined structure pattern. Here, we describe a server based on ProSMoS. We convert 3D structure from each PDB file into 2D meta-matrix, which stores the type and length of SSEs and interactions between them. We offer a set of rules for users to define the structure motif of interest by specifying query meta-matrix in which SSEs type, length, interaction type, handedness and information about β-sheets are customized by user. ProSMoS server carries out the pattern search for the query against a database [PDB or SCOP (10)] and reports structures matching the pattern.

Despite the importance of motif-based searches, this task is not widely addressed (11,12). Another web server, TOPS, aims to find topology matches directly based on the user defined structure pattern (13). However, TOPS does not take into account other important spatial properties of motifs, such as interactions and chirality. The only other similar web servers are SSM (14) and TableauSearch (15). Although SSM is based on the secondary structure matching, it is a structure similarity search rather than a pattern search program. We compared the performance of ProSMoS, TOPS and SSM previously (9), and the results indicate that our method finds more matches than other two programs. The detection of potentially similar, but at the same time quite distant structures is important in a structure classification project, which should not miss meaningful hits. TableauSearch developed by the Lesk group is a web server that finds proteins with similar folding patterns. TableauSearch represents the interaction and topology information between SSEs by tableau representation. Several methods were attempted to compare a query structure against tableaux databases, such as Tableau hashing for searching identical and closely-related folding patterns and the quadratic integer programming and integer linear programming for extracting maximally-similar subtableaux. The practical rapid method they developed is TableauSearch, which implements dynamic programming to compare SSE strings of two proteins based on a derived scoring function (15,16). Presently (February 2009), TableauSearch is still under maintenance, and is not available. The authors of TableauSearch described its comparison with ProSMoS using the example of beta-grasp motif (15). TableauSearch did not recognize some very distant beta-grasp containing proteins found by ProSMoS. Moreover, the query of TableauSearch is a protein structure not a user-defined pattern as in ProSMoS. Therefore, ProSMoS server is different from all other servers: it finds exact structure patterns in proteins while not being very sensitive to the details of packing and orientation of SSEs, thus detecting very distant possible connections between protein structures. We hope that ProSMoS server will be helpful for structural and computational biologists who are interested in 3D motif searches and would like to analyze very general and distant structural similarities.

PROCESSING METHOD

Secondary structure element delineation

We pre-process each structure in PDB and SCOP databases to generate SSEs. We use PALSSE (17) to define SSEs. PALSSE is robust to coordinate errors and structural deviations, thus giving longer SSEs and better residue coverage for inclusion in SSEs. The assignment of SSE by PALSSE covers an average of 85% of the protein chain and is in agreement with the expert judgment (17). We consider only three secondary structures: helix (H), which includes all types of helices (α, 3₁₀, π), β-strand (E) and Linker (L) defined as a stretch of a polypeptide chain between two consecutive parallel β-strands if there are no H and E elements between them.

Meta-matrix construction

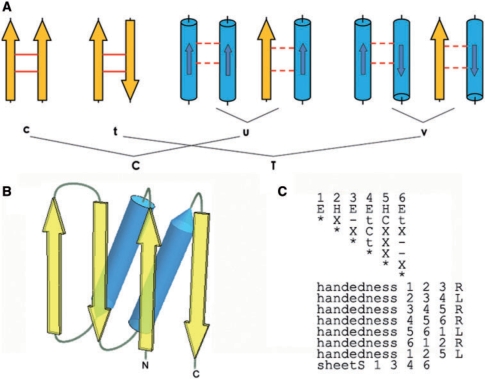
For each protein in PDB or SCOP, we convert the 3D structure into a 2D matrix. The interactions between SSEs are defined in the upper triangle of a (symmetric) matrix (Figure 1). Each SSE is represented by a vector (9,18), and interaction types between SSEs are computed. We define six interaction types: c, t, u, v, N and –. Symbols c and t denote hydrogen-bonded parallel and antiparallel β-strands, respectively. In contrast, the interaction type between non-hydrogen-bonded β-strands in the same β-sheet is recorded as symbol–(no interaction), even if some side-chains in non-H-bonded β-strands in the same sheet may come close to each other. This is an idealization having its goal to treat β-sheets as 2D rather than 3D objects. For all other SSE pairs, we use distance and overlap between the two elements to determine existence of an interaction. Here, the distance is defined as the shortest distance between Cα on the two elements (default <11 Å) and the overlap is defined as the intersection of projections of the two vectors representing SSEs on the line passing through the midpoint of vectors’ starts and the midpoints of vectors’ ends (default >2.5 Å) (9). If the distance and overlap criteria are met (distance <11 Å, overlap >2.5 Å), the angle φ between SSE vectors is calculated leading to three interaction types: symbols u, v and N stand for the presence of interaction with 0 ≤ φ < 85°, 95° ≤ φ < 180°, and 85° ≤ φ < 95°, respectively. Otherwise, the absence of interaction is recorded as –. These matrices are stored as a database for the ProSMoS server.

Figure 1.

(A) Interaction types used to define a query matrix. Yellow arrows and blue cylinders denote β-strands and α-helices, respectively. Smaller arrow inside each cylinder indicates the direction of a helix. Solid line between two strands shows H-bonding. Dashed line between SSEs means interaction other than H-bonding. ‘c’ and ‘t’ refer to the presence of interaction between hydrogen-bonded parallel and antiparallel β-strands, respectively. ‘u’ and ‘v’ mean there is an interaction between parallel helix-helix or helix-strand pair and the angle between the pair is 0 ≤ φ < 85° and 95° ≤ φ < 180°, respectively. ‘C’ is a union of {c, u}, i.e. interaction present whether through H-bond or not, but the angle between elements is 0 ≤ φ < 85°. ‘T’ is a union of {t, v}, i.e. interaction present whether through H-bonds or not, but the angle between elements is 95 ≤ φ < 180°. ‘−’ is used to indicate the absence of any interaction. ‘N’ means that there is an interaction between two SSEs, but the angle between them is 85° ≤ φ < 95°. ‘X’ means any relationship, i.e. interaction present or absent: a union of {C,T,N, −}. ‘x’ means any interaction, i.e. a union {C,T,N}. (B) Ferredoxin-like fold diagram. Ferredoxin fold is an α + β t-lawoyer sandwich with the secondary structure order βαββαβ. Four strands form an antiparallel β-sheet, which is covered by two α-helices on one side. (C) Query meta-matrix for the ferredoxin-like fold pattern.

In order to have a more flexible representation for a query pattern, we introduce four more interaction types: X, which matches all six symbols of the database meta-matrix, and x, which matches five symbols with no interaction (–) being a mismatch. T and C match {v,t} and {u,c}, respectively. Other than interactions, handedness is a major structure constraint in proteins. Handedness for each triplet of SSEs can be defined with the following symbols: R, right; L, left and N, no handedness (planar arrangement). Users can additionally specify which strands should or should not be in the same β-sheet, and define the length ranges for each SSE. Handedness, sheet information and length restrictions together with the interaction matrix constitute a query meta-matrix.

Database search and ranking of hits

ProSMoS searches all proteins of the target database for user-defined structure pattern, i.e. query meta-matrix, which has m SSEs. ProSMoS searches for query within a protein structure represented as a meta-matrix. SSEs (1, …, m) of the query are matched to the SSEs of the structure that form a strictly increasing subsequence, and consecutive SSEs in a motif hit need not have consecutive index numbers in the structure but are in increasing order. The extraction of subsequence, i.e. path finding, is implemented by our forward sequence enumeration with pruning algorithm. We define a forward sequence as a strictly increasing sequence of SSEs in a given protein structure and its length is defined as the number of SSEs in the sequence. In our algorithm, for all SSEs in a given chain that match the first SSE (in type and length) of the query, all feasible forward sequences of length m are enumerated subject to pruning. The options specified in query, such as SSE type, SSE length, sheet information, interactions, chain information (default setting is search pattern within a chain), are enforced on the partial sequences to prune out infeasible ones. The partial sequence is increased by one and the current searching pointer is moved to the newly joined member. For example, starting from the first SSE in query, we find two partial sequence (#2, #3) and (#3, #5) in structure match the first two SSEs in query, then the path finding is continued on #3 and #5 to find the matches of the third SSE in query. For all successfully enumerated sequences of length m, the chiralities specified in the query are enforced to eliminate the ones that do not conform. The sequences that remain are real hits; they are listed and are mapped to SCOP database on all SCOP hierarchy levels (class, fold, superfamily, family and domain). Moreover, ProSMoS provides PyMOL (http://pymol.sourceforge.net/) script files to visualize the results on the fly.

Being a structure pattern search program, ProSMoS is not aimed at detecting homologs by structure similarity. All the found hits contain the user-defined structure pattern as exact matches, while all other proteins do not contain submatrix matching the query. Thus the results of ProSMoS are deterministic and binary: either a structure contains the pattern or it does not. However, ranking of hits is always beneficial for the users in order to focus on the most relevant results. Therefore, we developed a new but simple score function to rank hits. Our structure analysis experience indicates that motifs perceived as ‘good’ by experts are compact, with regular and closely interacting SSEs, and SSE lengths are being close to their average values found in proteins. Hence, the scoring function is based on the distance and overlap between SSE pairs and SSE lengths, a total of three components.

Distance score (D)

First, we plotted the distance between SSE pairs for all proteins of PDB database and found that the average closest distance between adjacent β-strands is 4.5 Å for parallel β-strands and 4.2 Å for antiparallel β-strands, and the reasonable distance between neighboring β-strand–helix or helix–helix pair is 7.3 Å for parallel SSEs and 7 Å for antiparallel SSEs. Those values are set as the ‘ideal’ distance between SSE pair. Second, we calculate the distance of each pair of SSE in motif hits if corresponding interaction has been specified in query matrix. Third, we sum over the squares of the differences between the observed distances and the ideal distances. The score is divided by the number of specified interactions plus one, and its square root is taken.

Overlap score (V)

Considering the overlap definition described in the matrix construction section above, perfect overlap is equal to the vector length of the smaller SSE in a pair. First, we calculate the overlap for each SSE pair if interaction between them is defined in the query matrix. Then, we sum over the squares of the differences between overlap lengths and vector lengths of smaller SSEs. The score is also divided by the number of specified interactions plus one, and its square root is taken.

Length score (L)

We define the length of SSE as the length of SSE vector in Å, rather than the number of residues of SSE. This makes all the three scores (D, V and L) comparable and measured in Å. First, we computed all the lengths for β-strands and helices for the motif hits. Then, we calculate the median of β-strand length and the median of helix length. The median of SSE length represents the length tendency of SSE of the query structure pattern. Second, we sum over the squares of differences between observed SSE lengths and their median lengths. The score is divided by the number of SSEs in the query matrix plus one, and its square root is taken.

We combine the three scores in the following function:

Here, the weights W_D and W_V were set as 4.5 and 2.5, respectively to balance the three scores giving the best performance in our test. Apparently, when all the sums of deviations from ideal values are close to 0, the score is close to 1 (maximum score). When the distances deviate from ideal, the score decreases to 0.

ProSMoS WEB SERVER

Target database

Databases used in ProSMoS server are: PDB, PDB90 (identity ≤ 90%), PDB70 (identity ≤ 70%), SCOP, SCOP40 (representative PDB structures with no more than 40% sequence identity) and SCOP95 (identity ≤ 95%). We pre-calculated SSE assignment for each entry in these spatial structure databases and converted 3D structures into 2D meta-matrix databases to be queried by the ProSMoS server.

Input

ProSMoS server runs in two modes: (i) motif search starting from a user-defined interaction matrix; and (ii) motif search with an atomic coordinate file for a protein structure. In the first mode, the input query matrix should be designed by a user based on the set of rules described above. In the second mode, user can input PDB ID, SCOP ID or upload a structure file in PDB format. The server will generate the interaction matrix from the structure.

In the first mode, user supplies a query matrix. Format of the matrix is checked by ProSMoS for usability. After the initial check, the search with the query matrix is performed against the target database selected by user. The first mode is more flexible and yields the best results if the user has a clear understanding of the structure pattern of interest, and specifies the essential structure constraints while omitting minor details. Such supervised query matrix construction generates high-quality results.

The second mode is more suitable for users who are not confident in manual meta-matrix definition. After the meta-matrix is automatically produced by the server from the input coordinate file, an options is given to refine the matrix by (i) specifying the length restrictions on SSEs (e.g. in order to remove short unessential elements), and by (ii) setting the distance cutoff for filtering out unessential interaction between SSEs. While the matrix generated after this step can be used ‘as is’ to initiate searches, the option is provided to edit the matrix manually. It is recommended that this step is taken. Automatically constructed matrix may be too constrained on the query PDB file and will include some SSEs not essential for the fold (insertions to the common core). Search results with such matrix will be too restrictive. Therefore, it is beneficial to refine the query matrix by removing non-essential SSEs, revising the β-sheet and handedness information, or editing interactions between SSEs.

Output

Output is the list of proteins in PDB or SCOP matching the query matrix. All structure motifs matching the query are comprehensively listed and ranked by the ProSMoS score. For each motif, the corresponding PDB ID, protein name, SCOP domain ID, description of domain and the ranges of residue numbers that define motif SSEs are provided. Each motif can be visualized on the fly with PyMOL. The PyMOL script displays the Cα trace of a structure with the backbone colored in gray, each motif SSE colored in red, the first residue in the first SSE in the motif colored in green, and first residues of all other motif SSEs colored in purple. In addition, we provide the lists of SCOP superfamilies and folds for the found motifs.

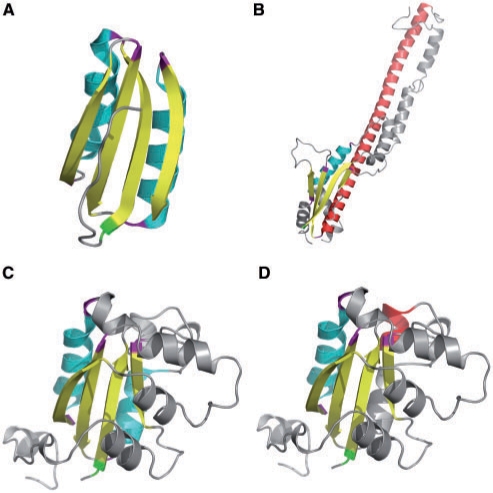
Here, we use the ferredoxin-like fold (10,19) to illustrate the output of the ProSMoS Server. Ferrodoxin-like fold is a wide-spread α + β two-layer sandwich with the SSEs order βαββαβ. Four β-strands form an antiparallel β-sheet and two α-helices pack against one side of this sheet (Figure 1B). The query meta-matrix for the ferredoxin-like fold is shown on Figure 1C. This query is very permissive, as the goal is to find all possible candidates. In the interaction matrix, other than the interactions between the β-strands in the same β-sheet, we only required that the first helix and the second helix should have interactions with the fourth strand and the first strand respectively. All other interactions are not specified (X symbol). Additionally, we did not set the SSE length limitation. A search of this query matrix against the PDB (26 January 2009, 53 305 entries) found 2291 PDB hits containing 8299 matched motifs (the results are available at: http://prodata.swmed.edu/ProSMoS/compattern/plait.htmlresult/index.html). In SCOP, these PDBs are attributed to 46 folds and 100 superfamilies, showing that this is a very common pattern in protein structures. It is interesting to see that about 50 different SCOP folds have a ferredoxin-like motif in their structures. Figure 2A shows the first hit (pdbid 1sc6, SCOP domain d1sc6d3 ferredoxin-like SCOP fold). This is a very typical and structurally compact ferredoxin motif with ideal SSE lengths and good SSE packing. In contrast, Figure 2B shows the hit #8299 (pdbid 3b8m, not classified in SCOP, bacterial polysaccharide co-polymerases which is located in the inner membrane and plays important role in the control of the chain length distribution of complex polysaccharides). In this motif, the second helix is very long (colored red in Figure 2B). Between the third strand and the last strand, there is a long α helical hairpin which comprises the long helix (the second helix in motif, red) extending about 100 Å into the periplasm and three additional helices folding back (20). This hit, although undoubtedly containing ferredoxin-like pattern, are not scored very high by ProSMoS due to the long helix. Similarly, Figure 2C (rank #482) and Figure 2D (rank #4750) show a pair of two overlapping motifs found in the same protein domain (pdb id 2az1, motifs located in the range of SCOP domain 2az1e1, ferredoxin-like fold). It is clear that #482 is a better match to ferredoxin-like fold than #4750, as the second helix is too short in the latter.

Figure 2.

Representative ferredoxin-like motif hits. β-Strands shown in yellow and α-helices shown in cyan. The first residue of the motif is colored green and the first residue of each SSE is colored purple. (A) The best-scoring motif hit, pdb id 1sc6, chain D, D-3-phosphoglycerate dehydrogenase, residue ranges 337–346, 347–362, 364–373, 375–384, 386–400, 402–410. (B) The weakest-scoring motif hit (#8299), pdb id 3b8m, chain B, bacterial polysaccharide co-polymerase, residue ranges 64–74, 99–114, 152–157, 171–179, 180–251, 320–324. (C) The hit #482, pdb id 2az1, chain E, nucleoside diphosphate kinase, residue ranges 6–13, 20–33, 34–43, 73–81, 83–93, 117–121. (D) The hit #4750. This motif overlaps with #482 (C) over 5 SSEs, 6–13, 20–33, 34–43, 73–81, 104–110, 117–121, with the second helix being distinct (residue range 104–110, colored red). Since this helix is shorter than in (C), this motif scores worse. (C) and (D) illustrate the possibility of overlapping motifs being found by the server.

The speed of complete PDB database search

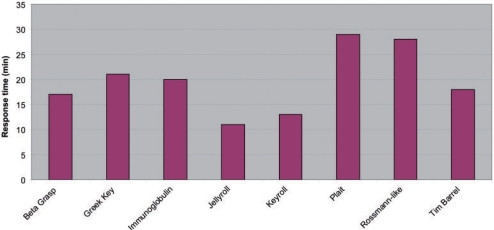
ProSMoS server completely enumerates all candidate motif hits for a user-defined query, thus the search is time-demanding. Moreover, running time may vary among different queries, as it largely depends on query complexity and abundance. To illustrate the speed of ProSMoS Server, we carried out the searches for eight wide-spread structure patterns against the target database built on complete PDB (the largest database to use), and recorded the response time for each job. The response times are shown in Figure 3 with the average response time being about 20 min, which we find acceptable for this time-demanding task. The results for the eight structure patterns are available at: http://prodata.swmed.edu/ProSMoS/prepattern.html

Figure 3.

Response time of ProSMoS Server for eight wide-spread structure patterns in complete PDB database. The response time (min) is recorded from the submission of a job to the receipt of result for each structure pattern.

Comparison between ProSMoS and Dali

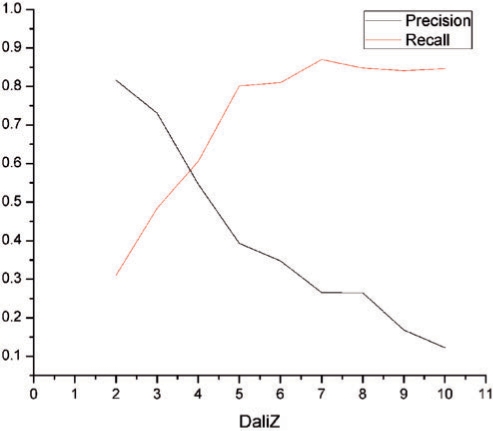
ProSMoS find structures matching a user-defined pattern. DALI (6) finds structures sharing contact similarity with the query. Although these two approaches are quite different, comparison of the two programs is instructive because the majority of structural biologists are well-familiar with DALI. We compared ProSMoS and DALI on eight common structure patterns (http://prodata.swmed.edu/ProSMoS/comparetest/) in terms of precision = TP/(TP + FP) and recall = TP/(TP + FN), where TP, FP and FN are true positives, false positives and false negatives, respectively. Experiments were done with varying DALI Z-score cutoffs on SCOP40 database (9479 domains). Coordinates of the first motif found by ProSMoS were used as a DALI query. Structures found by DALI above the given cutoff (Z-score higher than the cutoff) were considered ‘true’, below the cutoff were considered ‘false’. DALI found 1408 domains (15% of total domains) in all eight families above Z-score of 2. ProsMoS found motifs in 2947 domains (31% of total domains). The results, averaged for eight patterns, are shown in Figure 4. Precision and recall values are about the same for DALI Z-score cutoff 4. When DALI Z-score is lower, many DALI hits do not have the pattern and similarity between structures resides elsewhere, for instance in a long α-helix, thus ProSMoS recall is low. When Z-score is above 7, most DALI hits contain the motif (recall is high and relatively constant) and thus are found by ProSMoS, however, many proteins with the motif are not found by DALI due to lower structural similarity, thus precision is low.

Figure 4.

Comparison between ProSMoS and Dali. The red curve is the average precision of ProSMoS searches of eight common structure patterns. The dark blue curve is the average recall. The x-axis is the Dali Z-score used to define ‘true’ matches.

FUNDING

National Institutes of Health (GM67165); Welch foundation (I1505) to NVG. Funding for open access charge: Howard Hughes Medical Institute.

Conflict of interest statement. None declared.