Post-Treatment Hemodynamics of a Basilar Aneurysm and Bifurcation

Abstract

To investigate whether or not a successful aneurysm treatment procedure can subject a parent artery to harmful hemodynamic stresses, computational fluid dynamics simulations are performed on a patient-specific basilar aneurysm and bifurcation before and after a virtual endovascular treatment. Prior to treatment, the aneurysm at systole is filled with a periodic train of vortex tubes, which form at the aneurysm neck and advect upwards into the dome. Following the treatment procedure however, the motion of the vortex train is inhibited by the aneurysm filling material, which confines the vortex tubes to the region beneath the aneurysm neck. Analysis of the post-treatment flow field indicates that the impingement of the basilar artery flow upon the treated aneurysm neck and the close proximity of a vortex tube to the parent artery wall increase the maximum wall shear stresses to values approximately equal to 50 Pa at systole. Calculation of the time-averaged wall shear stresses indicates that there is a 1.4 × 9 10⁻⁷ m² area on the parent artery exposed to wall shear stresses greater than 37.9 Pa, a value shown by Fry [Circ. Res. 22(2):165–197, 1968] to cause severe damage to the endothelial cells that line the artery wall. The results of this study demonstrate that it is possible for a treatment procedure, which successfully isolates the aneurysm from the circulation and leaves no aneurysm neck remnant, to elevate the hemodynamic stresses to levels that are injurious to the artery wall.

INTRODUCTION

Patients diagnosed with a cerebral aneurysm receive treatment by means of either endovascular coiling or surgical clipping. Despite their widespread use, these two treatment techniques are not always successful in eliminating the risk for subsequent aneurysm rupture and subarachnoid hemorrhage (SAH). For the coiling technique, one of the primary failure mechanisms leading to aneurysm re-growth, re-canalization, and re-bleeding is coil compaction.^10,31 A dense packing of coils is necessary to promote blood stasis and subsequent isolation of the aneurysm from the vascular system. Yet, even in the best cases, the coiling material accounts for less than 50% of the total treated aneurysm volume.^26,29 Consequently, coil compaction can occur and is especially problematic for giant aneurysms, large aneurysms containing thrombus, and aneurysms that project along the direction of blood flow in the parent artery. In addition, a loose packing of coils can lead to coil unraveling and migration into the parent artery and subsequent aneurysm re-growth. As a result, about 14% of the cases that are considered “successfully” treated at the time of coiling unexpectedly exhibit aneurysm recurrence.¹⁰ Overall, the hemorrhage or re-hemorrhage rate after aneurysm coiling is roughly estimated to be 0.79% per patient-year,³¹ although this may be higher for incompletely treated aneurysms. For surgical clipping, the risk of re-growth for a completely clipped aneurysm is about 0.26–0.52% annually, while that for de novo aneurysm formation is about 0.89–1.8%.^12,52 To reduce the number of these failed clipping procedures, clinicians have narrowed the definition of what constitutes an acceptable residual aneurysm neck during intra-operative angiography; 1–2 mm residual necks, which were once considered to be insignificant, are now eliminated when surgically feasible by placing the clip as flush as possible with the long axis of the aneurysm neck.³⁵ Despite these measures, aneurysm remnants, de novo aneurysms, re-growth, and rupture sometimes unexpectedly occur following procedures that were initially considered to be successful due to a perfect clip placement at the time of surgery and post-operative angiography.⁵¹ In some cases, the treatment failure can be attributed to clip slippage or to a faulty clip¹⁷; however, there are other cases in which the clip functioned properly and complete aneurysm obliteration was initially achieved.^6,57

While these latter types of failure may be due, in part, to pathological factors, such as congenital defects, hypertension, atherosclerosis, and thrombosis, hemodynamics may also play an important role in the post-treatment pathogenesis of aneurysms.^44,57 It is well documented in the literature that extreme hemodynamic stresses can have a detrimental effect upon the integrity of arteries.^13,21,28,53 In regions where the wall shear stress (WSS) is low and the wall shear stress gradient (WSSG) is high, such as that at points of flow separation and reattachment, the endothelial cells have high cell division rates and a low cell density, which can lead to the influx of low density lipoproteins and subsequent changes to the structural integrity of the artery wall.⁵⁶ In some cases, elevated WSSs can completely scour off the endothelial cells, thereby exposing the internal elastic lamina, or, in other cases, produce “cellular ulcers,” consisting of cell membrane loss and of a thin layer of underlying cytoplasm.²⁸ Fry measured the acute critical yield stress of endothelial cells to be 37.9 ± 8.5 Pa.²¹ When exposed to time-averaged WSSs of this value, the endothelial cells underwent the greatest rate of change from normal to abnormal cellular forms through processes that Fry described as “yielding,” “melting,” “dissolving,” or “changing chemically,” all of which led to a distinct deterioration of the endothelial surface. And, by utilizing computational replicas of cerebral vessels, Hassan et al. found a correlation between the aneurysm rupture locations and regions of high WSS.²⁴

If a treatment procedure either produces or does not eliminate these harmful hemodynamic stresses, it would not be too surprising that arterial wall damage and subsequent SAH could occur following what was originally deemed a successful treatment. Consequently, a better understanding of post-treatment hemodynamic flow patterns and stresses within the vicinity of a treated aneurysm may not only highlight some of the possible mechanisms leading to these failed treatments, but may also guide medical device manufacturers in designing novel treatment techniques that could potentially reduce the risk for recurring SAH. To help provide this understanding, we investigate the pre- and post-treatment hemodynamics of a patient-specific, basilar tip aneurysm using computational fluid dynamics (CFD) simulations.

A similar computational approach has been taken in a number of recent studies, in which aneurysms were virtually treated with devices that were modeled with varying degrees of complexity. For example, Byun and Rhee⁵ employed a simplified representation of a Guglielmi detachable coil (GDC) mass by treating it as a solid sphere that had a diameter of 75% of the lateral aneurysm long axis. The resulting simulations demonstrated that the WSSs and the flow into the aneurysm were sensitive to the location of the post-treatment coil mass. Groden et al.²³ modeled GDCs and post-treatment thrombosis within a simplified basilar tip aneurysm by randomly blocking off a percentage of the computational cells across the aneurysm neck and throughout the aneurysm dome, respectively. To reduce the pulsatile flow into the aneurysm, they determined that it was necessary to block off at least 20% of the computational cells at the aneurysm neck. Cha et al.⁸ and Mitsos et al.³⁸ utilized a different approach by modeling GDCs as a porous media that had minimum porosities of 70 and 73.5%, respectively. Although the hemodynamic forces on the modeled GDCs were only a weak function of the permeability of the porous media, Cha et al.⁸ observed significant changes in the intra-aneurysmal flow patterns as the permeability was decreased. To capture the complex shapes of treatment devices, Cebral and Löhner⁷ used an adaptive grid embedding technique, which enabled the simulation of flow through patient-specific aneurysms treated with geometrically realistic stents and GDCs. Virtual post-treatment angiograms performed on a cerebral aneurysm demonstrated that the simulated GDCs increased the fluid residence time within the aneurysm. And, using refined unstructured grids, Kim et al.³³ modeled the post-treatment hemodynamics of a patient-specific, wide-necked basilar trunk aneurysm that was virtually treated with multiple commercial stents. This study showed that the stenting procedures reduced both the complex flow patterns and the WSSs within the aneurysm, though reductions in these quantities were found to depend upon the particular stent design.

Unlike these previous CFD studies, we assume that the aneurysm is completely isolated from the circulation following the virtual endovascular treatment procedure. In particular, we investigate the following questions in this study: what types of flow patterns arise following the treatment procedure? How do these post-treatment flow patterns affect the hemodynamic stresses on the parent artery wall? And, is it possible for a successful aneurysm treatment to either produce or fail to eliminate potentially harmful hemodynamic stresses?

SETUP

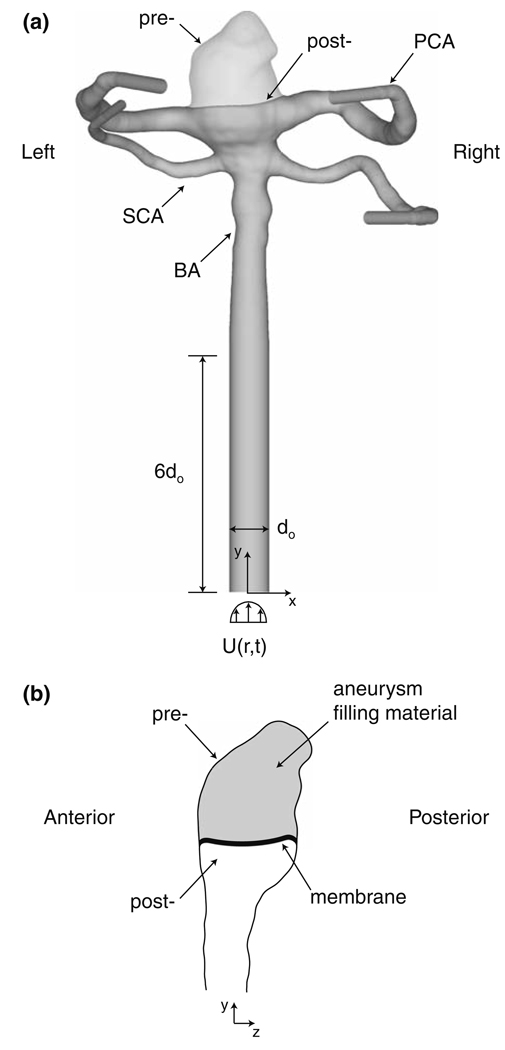
To address these questions, a virtual endovascular treatment is performed on a 44-year-old patient who underwent computed tomography angiography (CTA) for evaluation of a basilar tip aneurysm, which had a volume of 3.3 × 10⁻⁷ m³ and neck area of 5.5 × 10⁻⁵ m². CAD software (Maya 6.0) is used to “treat” the aneurysm geometry (Fig. 1a and 1b) obtained from the CT scan data. We assume that the aneurysm is completely isolated from the parent artery and that a membrane covers the entire surface of the filling material at the aneurysm neck. Thus, only the flow within the parent artery lumen is modeled following the “treatment” procedure. Such a post-treatment aneurysm neck geometry has been observed within several previous investigations. Murayama et al.^39,40 showed that the necks of model aneurysms treated with biologically active GDCs became covered with a well-organized fibrous tissue membrane, which both excluded the aneurysm from the circulation and presented the parent artery flow with a smooth post-treatment surface. Similar findings have been made in a patient study of aneurysms treated with biologically active GDCs.⁵⁰ In another patient study,³ the neck of an aneurysm treated with traditional GDCs was seen to be covered with an endothelial-lined membrane, indicating that the aneurysm had been totally isolated from the circulation. Lastly, Stiver et al.⁴⁹ observed a membrane across the neck of an aneurysm that had been filled with traditional GDCs only 36 h earlier.

FIGURE 1.

Pre- and post-treatment computational domains and geometries of the basilar aneurysm and bifurcation.

Defining the specific shape of the filling material at the aneurysm neck is somewhat subjective. Even though the virtual treatment procedure completely fills the aneurysm and leaves no “dog ears” around the periphery of the aneurysm neck, any number of shapes at the aneurysm neck could have been selected, leading to slight variations in the surface curvature of the aneurysm filling material or in the location of the intersection between the filling material and the artery wall. To ensure that the resulting post-treatment lumen shape is representative of that seen in a typical treatment, an interventional neuroradiologist (J. Hartman) subsequently inspected this geometry and deemed it to be a successful “endovascular treatment” of the basilar aneurysm.

To properly apply the CFD boundary conditions needed to model the pre- and post-treatment flow patterns and stresses, we loft circular, cylindrical extensions from the basilar artery (BA), the two posterior cerebral arteries (PCA), and the two superior cerebellar arteries (SCA). We also assume that the aneurysm and artery walls are rigid. Ferguson²⁰ compared the elasticity of aneurysms to that of major intrancranial arteries and observed that aneurysms are relatively indistensible, indicating a loss of elastin within their walls. The in vitro experiments of Steiger et al.⁴⁸ on lateral, saccular aneurysms demonstrated that the flow within an aneurysm is much more sensitive to the pulsatile nature of the cardiac waveform than to the effects of vessel wall deformation. Additionally, others^18,60 showed that although wall elasticity slightly decreases the magnitude of the WSS, the overall flow and stress patterns within the vessel remain unchanged.

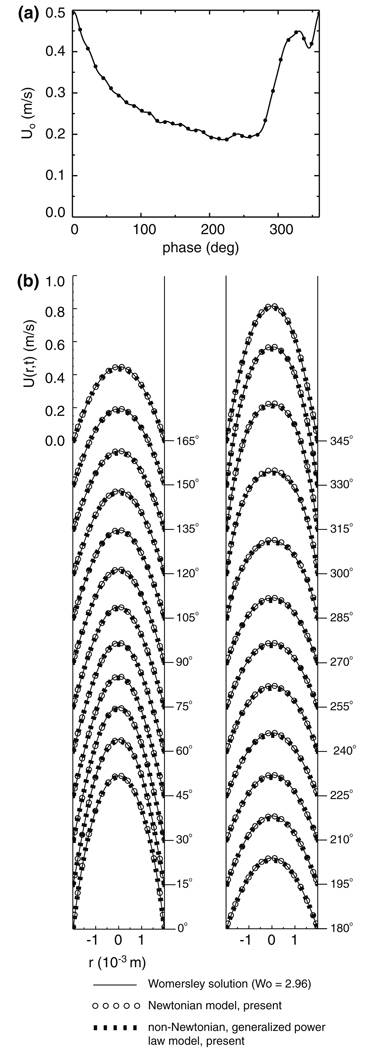
A pulsatile velocity boundary condition is specified at the inlet to the basilar artery. Since in vivo velocity data is not available for this particular patient (as it is not possible to obtain this data from CTA), we use the cardiac waveform of Kato et al.,³² who measured the mean velocity within a basilar artery using a contrast-enhanced 2D cine phase MR angiographic technique. With this in vivo data (Fig. 2a), we employ the Womersley solution method⁵⁸ to compute the pulsatile velocity profile, U(r,t), that is applied to the inlet (Fig. 1a), where r is the radial distance from the centerline of the inlet and t is time. Since the in vivo data presented by Kato et al.³² does not include a measured heart rate, we choose a typical resting pulse frequency of f = 1.17 Hz (70 beats/min), yielding a Womersley number, $Wo=0.5d_0\sqrt{2\pi f\rho /{\mu }_0}$, of 2.96, where d₀ = 3.97 × 10⁻³ m is the diameter of the inlet circular cylinder to the basilar artery, μ₀ = 0.0035 Pa s is the characteristic viscosity of blood, and ρ = 1060 kg/m³is the characteristic density of blood.⁵⁸ At systole, which is taken to be the phase (2°) of the maximum of the mean velocity over the cardiac cycle, the mean velocity, U₀, is 0.496 m/s, while at diastole, which is likewise taken to be the phase (219°) of the minimum of the mean velocity, the mean velocity is 0.187 m/s. Over the entire cardiac cycle, the time-averaged mean velocity, U̅₀; is 0.289 m/s, which corresponds to a time-averaged basilar artery flowrate of 3.58 × 10⁻⁶ m³/s (214.8 cc/min). The corresponding maximum, minimum, and mean Reynolds numbers, Re = ρU₀d₀/μ₀, are 596, 225, and 347, respectively.

FIGURE 2.

(a) Mean velocity through a basilar artery as measured in vivo by Kato et al.³² (b) Velocity profiles for the Womersley solution, the present Newtonian CFD simulations, and the present non-Newtonian² CFD simulations for fully-developed, pulsatile flow in a circular cylinder of diameter, d₀ = 3.97 × 10⁻³ m.

The viscosity of blood within the computational domain is modeled using a generalized power law,²,

$$\mu =\lambda |\gamma {|}^{n-1}$$ (1)

where γ is the fluid shear rate,

$$\gamma =\sqrt{2S_{\mathit{ij}}{S}_{\mathit{ji},}}$$ (2)

S_ij = (u_i,j + u_i,j)/2 is the symmetric portion of the velocity gradient tensor, u_i,j,

$$\lambda (\gamma )={\mu }_0+\mathrm{\Delta }\mu \text{exp}\left[-\left(1+\frac{|\gamma |}{a}\right)\text{exp}\left(\frac{-b}{|\gamma |}\right)\right],$$ (3)

$$n(\gamma )=n_0-\mathrm{\Delta }n\text{exp}\left[-\left(1+\frac{|\gamma |}{c}\right)\text{exp}\left(\frac{-d}{|\gamma |}\right)\right],$$ (4)

n₀ = 1.0, Δμ = 0.025 Pa s, Δn = 0.45, a = 50, b = 3, c = 50, and d = 4.

This viscosity model closely agrees with the Carreau model⁹ for low to mid-range shear and is effectively Newtonian for mid-range to high shear rates. The subsequent simulations of the pre- and post-treatment bifurcations indicate spatial and temporal variations of the blood viscosity over the cardiac cycle. For example at systole, the average viscosity within the pre-treatment aneurysm is 3.51 × 10⁻³ Pa s, while at diastole, it increases to 3.90 × 10⁻³ Pa s. For both the pre- and post-treatment bifurcations, local maxima of viscosity are observed to arise within recirculation zones and other regions of the flow field characterized by relatively low shear rates.

We anticipate that the Womersley velocity profile, U(r,t), which is computed analytically for a Newtonian fluid with a constant viscosity, μ₀, will require a finite entrance length in order to become fully developed within the non-Newtonian fluid. To properly model the flow within the pre- and post-treatment basilar bifurcations, the length of the inlet circular cylinder extension must be greater than this entrance length, y_e, which, for a pulsatile flow, is defined to be the distance along the pipe where the difference between the centerline velocity and its fully developed value is less than one percent of its time-averaged fully developed value²⁵:

$$\frac{u(\infty ,r=0,t)-u(y_{\mathrm{e}},r=0,t)}{\frac{1}{T}{\displaystyle {\int }_0^{T}u(\infty ,r=0,t)}dt}=0.01$$ (5)

where T is the period (6/7 s) of the cardiac cycle. Rather than use the entire computational domain of the basilar bifurcation and aneurysm to determine the necessary entrance length, an iterative exercise that would require an excessive amount of CPU time for these unsteady simulations, we utilize a domain comprised of a circular cylinder of diameter, d₀, and length, l = 43d₀. The Womersley velocity profile is prescribed at the inlet to the cylinder and a no-slip boundary condition is specified along the cylinder wall. A zero gradient boundary condition is specified at the cylinder outlet, such that the variables at the outlet nodes are extrapolated from the values at the interior nodes. The unsteady Navier-Stokes equations³⁴ are solved within this computational domain for a non-Newtonian fluid with a generalized power law viscosity model for blood.² The simulation is run for one cardiac cycle to eliminate the initial transients and the pulsatile entrance length is subsequently computed over the second cardiac cycle. The maximum pulsatile entrance length, which occurs at a phase of 318°, is found to be 5.4d₀. Subsequent refinement of the grid and doubling of the pipe length results in negligible changes (0.3 and 0.5%, respectively) to the pulsatile entrance length. The fully developed, non-Newtonian velocity profile (Fig. 2b) closely resembles the Newtonian velocity profile in the region of high shear near the cylinder wall, though in the region of low shear at the cylinder center, the non-Newtonian velocity profile is ever so slightly more plug-like in appearance. With the results of this exercise in mind, we specify the length of the inlet circular cylinder extension to be 6d₀, thus allowing the pulsatile velocity profile to become fully developed before entering the basilar artery of the patient.

To complete the specification of the boundary conditions, fractional outlet flowrates must be assigned to the two PCAs and two SCAs. Amin-Hanjani et al.¹ made in vivo flowrate measurements on fifty healthy patients and observed that 72 ± 22 and 68 ± 18 cc/min of the 190 ± 40 cc/min basilar artery inflow exits through the left and right PCAs, respectively. Like-wise, in a comparative study of patients with and without preeclampsia, Zeeman et al.⁵⁹ measured the left and right PCA flowrates within the healthy patients to be nearly equal. However, neither study presents data for the flowrates through the left and right SCAs. Thus, for the sake of the present investigation, we assume that the exiting flow is equally divided between the left and rights sides of the basilar bifurcation. Furthermore, we assume that 38.5% (82.7 cc/min) of the basilar artery inflow exits through each of the PCAs, a value about equal to the PCA flowrate fraction measured by Amin-Hanjani et al.¹ and Enzmann et al.,¹⁹ and, by conservation of mass, that 11.5% (24.7 cc/min) of the remaining basilar artery inflow exits through each of the SCAs. At the outlet boundaries of the PCAs and SCAs, the variables are computed by an upstream extrapolation, assuming a zero gradient along the direction of a line joining the near-boundary cell center to the boundary face center. The velocities at the outlets are then adjusted in order to yield the specified fractional outlet flowrates.

The velocity, pressure, and viscosity fields are computed within the pre- and post-treatment bifurcations using a finite-volume CFD code, STAR-CD.⁴⁷ The spatial fluxes within the Navier-Stokes equations are discretized with a second-order monotone advection and reconstruction scheme (MARS),⁴⁷ while the temporal derivatives are discretized by blending a second-order Crank-Nicholson scheme with a first-order implicit scheme, which reduces the over- and under-shooting of computed variables commonly observed with higher order schemes. The resulting order of this blended scheme is 1.8. A time step of 4 × 10⁻⁵ s is chosen, resulting in a mean (both spatial and temporal) Courant number that is of order 1 over all of the cells within the computational domain. The finite volume equations are solved using an implicit predictor-corrector PISO method,²⁷ which utilizes operator splitting to temporarily decouple the flow equations from one another, allowing them to be solved sequentially with an algebraic multigrid (AMG) approach.⁴³ At each time step, the residuals are reduced by at least three orders of magnitude. The velocity, pressure, and viscosity fields are initialized by running a steady state simulation with an inlet velocity profile of U(r,t = 0) for a few thousand iterations. The transient simulation is then initialized with this “steady state” solution and run for three cardiac cycles to eliminate the initial transients in the flow field. Data sampling is then made over two additional cardiac cycles.

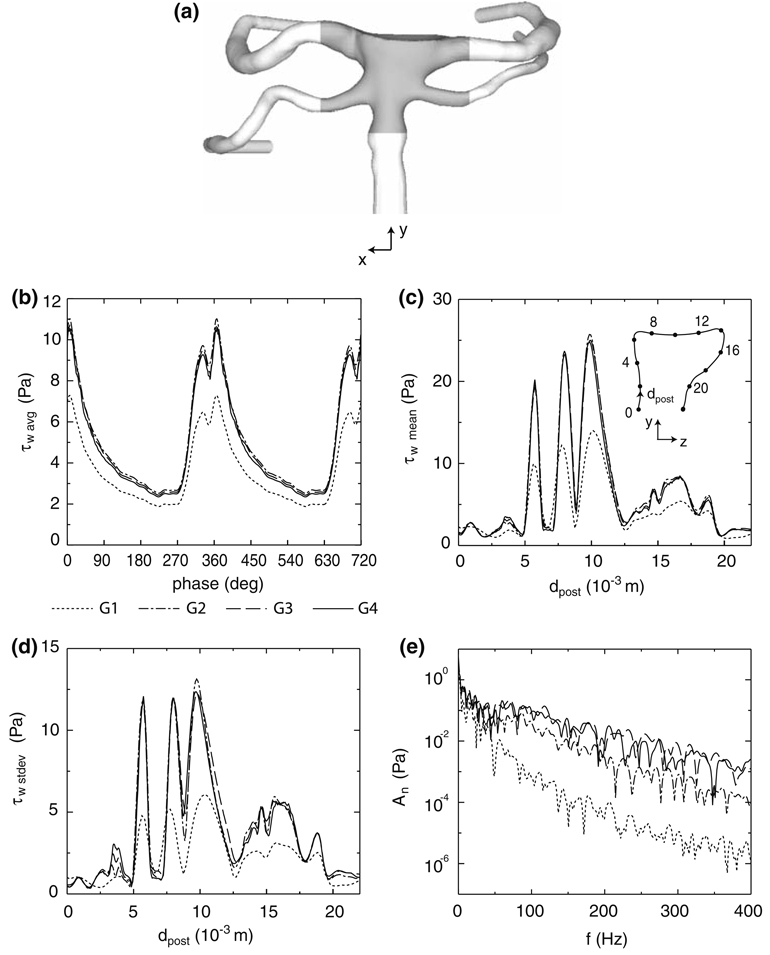
In order to ensure that the computed results are not dependent upon grid resolution, the simulations of the post-treatment bifurcation are repeated on four unstructured, trimmed cell grids⁴⁷ having sizes of 1.1 × 10⁵ (G1), 4.0 × 10⁵ (G2), 2.0 × 10⁶ (G3), and 4.0 × 10⁶ (G4) cells. Each trimmed cell grid is comprised of a Cartesian core mesh and several layers of prismatic cells extruded from the no-slip walls of the computational domain. Between these two grids are transitional, polyhedral cells. This meshing technique reduces the number of highly skewed or warped elements next to no-slip surfaces and increases the number of perfectly orthogonal cells throughout the computational domain.

The spatial average of the WSS in the area immediately surrounding the treated aneurysm neck (Fig. 3a and 3b) exhibits grid independence for the three finest grids, as do the time-average and standard deviation (Fig. 3c and 3d) of the WSS through a slice (x = 0) of the bifurcation. However, only the two largest grids adequately capture the unsteady WSS signal, while the two coarser grids damp out the higher frequency content (Fig. 3e). For this reason, the subsequent simulations of the post-treatment bifurcation are performed on the grid, G3, which has a 2.0 × 10⁻⁴ m thick extrusion layer and a near-wall prism cell thickness of 1.5 × 10⁻⁵ m. The simulation of the pre-treatment bifurcation employs a grid with a comparable spatial resolution. Due to the significant computational time needed to obtain grid-independent solutions, the pre- and post-treatment simulations in the present study are conducted only on this particular basilar bifurcation. (For example, the calculation of the transient solution on the finest, post-treatment grid, G4, required 36 days of computing time on 128 2.4 GHz AMD Opteron CPUs.)

FIGURE 3.

(a) Interrogation area (shaded region) for computing the spatial mean of the WSS across the bifurcation. (b) Spatial mean of the WSS across the interrogation area over two cardiac cycles, (c) average and (d) standard deviation of the WSS along x = 0 of the post-treatment bifurcation, and (e) the fast Fourier transform of the unsteady, post-treatment WSS at x = 0, d_post = 15 × 10⁻³ m for four different mesh resolutions (G1, G2, G3, G4).

RESULTS

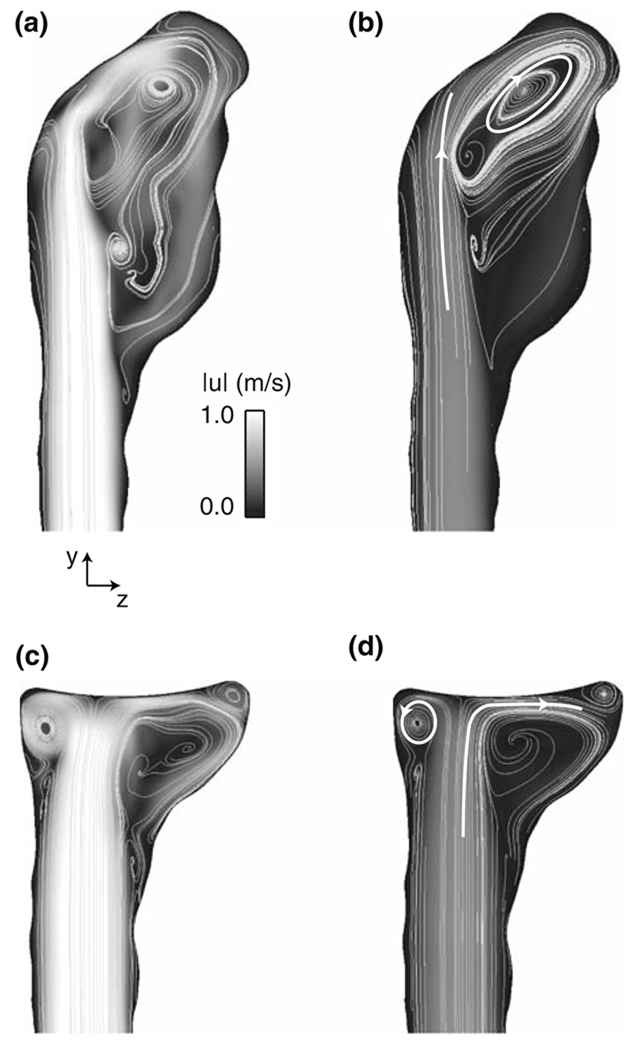
The most apparent change to occur to the bifurcation flow field as a result of the treatment procedure is the elimination of a confined jet that is produced by the basilar artery flow issuing through the pre-treatment aneurysm neck. This jet, which spans nearly the entire length of the aneurysm and is present throughout the cardiac cycle, impinges upon the aneurysm wall in a skewed fashion, forming a large recirculation zone on the posterior side of the aneurysm as the jet reverses direction and exits through the aneurysm neck (Fig. 4a and 4b). Following the treatment procedure, however, the basilar artery flow impinges instead upon the membrane that lines the filling material and produces a much smaller recirculation zone and a concentrated region of swirling flow on the anterior side of the bifurcation. Both of these flow patterns persist over the entire post-treatment cardiac cycle (Fig. 4c and 4d).

FIGURE 4.

Velocity magnitude and streamlines at (a,c) systole (phase = 2°) and (b,d) diastole (phase = 219°) for the (a,b) pre- and (c,d) post-treatment bifurcations at x = 0. The white lines and arrowheads highlight the general flow directions.

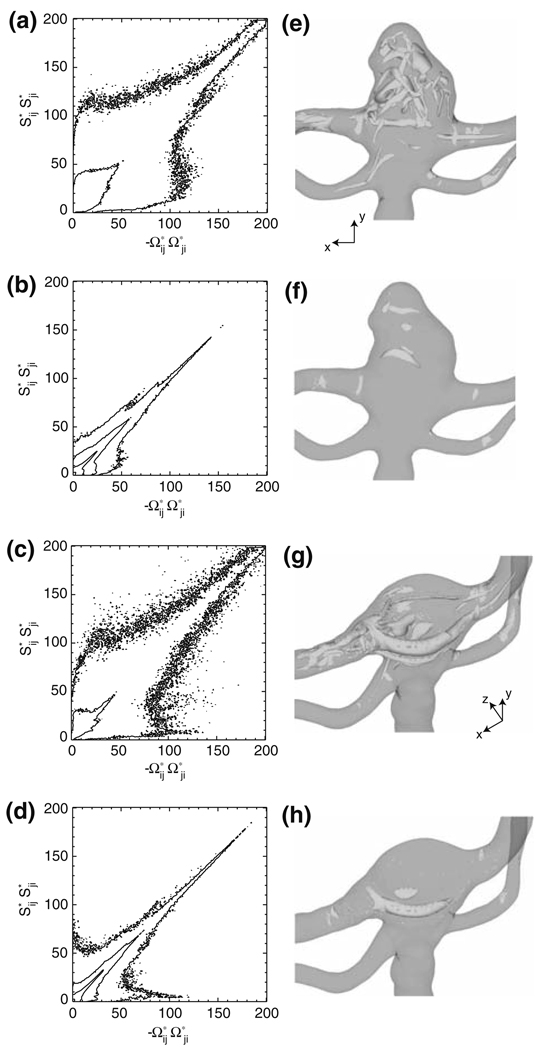
A comprehensive understanding of these flow field changes can be obtained by examining the velocity gradient tensor, u_i,j, an approach which has proven to be successful in identifying the coherent structures present in such flows as those through mechanical heart valves,¹¹ aneurysms,¹⁴ and stenotic arteries.⁴⁵ In particular, the straining, S_ij, and rotational, Ω_ij, components of u_i,j are computed within the volume bound by the shaded area in Fig. 3a, where Ω_ij = (u_i,j − u_j,i)/2 is the skew-symmetric portion of u_i,j. For the pre-treatment bifurcation, this shaded area also encompasses the aneurysm. The quantities, S_ij and Ω_ij, are interpolated onto a three-dimensional Cartesian mesh with a spacing of Δ_x = Δ_y = Δ_z = 6 × 10⁻⁵ m, thus providing a uniform distribution of points from which probability statistics may be obtained. The joint probability density plots^4,46 of $S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*}\text{and}-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}$ (Fig. 5a–5d) for the pre- and post-treatment bifurcations highlight the underlying flow structures by comparing the relative importance of the straining and rotational components of the velocity gradient tensor, where the plotted quantities $S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*}\text{and}-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}$ are the values of S_ijS_ji and −Ω_ijΩ_ji non-dimensionalized by (U̅₀=d₀)². Points near the $S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*}$-axis are characterized by straining motion, while those near the $-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}$-axis by solid-body rotation; those points lying along the line $S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*}=-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}$ have nearly equal straining and rotational motions.⁴ A more thorough discussion of this plotting technique can be found in Perry and Chong⁴¹ and Soria et al.⁴⁶ At both systole and diastole, the majority of the fluid within the pre- and post-treatment bifurcations exhibits nearly equal straining and rotational motions, indicating a predominantly “vortex sheet-like” or shearing flow.⁴⁶ Though at diastole, it is evident that the treatment procedure increases the probability of both pure straining and pure rotational motions. At systole, there is a slight decrease in the amount of pure straining motion and a slight increase in the amount of rotational motion.

FIGURE 5.

Joint probability density plots of $S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*}\text{and}-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}$ for the (a,b) pre- and (c,d) post-treatment bifurcations at (a,c) systole (phase = 2°) and (b,d) diastole (phase = 219°). Iso-surfaces of Q^* for the (e,f) pre- and (g,h) post-treatment bifurcations at (e,g) systole (Q^* = 40) and (f,h) diastole (Q^* = 10).

The flow structures corresponding to these probability distributions are visualized by plotting iso-surfaces of the second invariant of the velocity gradient tensor, $Q*=\frac{1}{2}(-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}-S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*})$ (for incompressible flow), which is equivalent to a 45 degree line with a y-intercept of −2Q^* in Figs. 5a–5d.⁴ Clearly, it follows that where Q^* is large and positive, the flow field is rotationally dominant $(-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}\gg S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*})$; where Q^* is large and negative, it is straining dominant $(-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}\ll S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*})$; and where Q^* = 0, rotation and strain are equal to one another $S_{\mathit{ij}}^{*}{S}_{\mathit{ji}}^{*}=-{\mathrm{\Omega }}_{\mathit{ij}}^{*}{\mathrm{\Omega }}_{\mathit{ji}}^{*}$. At systole, iso-surfaces of Q^* = 40 indicate the presence of vortex tubes in the bifurcation (Fig. 5e and 5g). At diastole, the vortex tubes are visible at a smaller value of Q^*, which in Fig. 5f and 5h is chosen to equal 10. Prior to treatment, the aneurysm at systole is filled with a periodic train of these tubes (Fig. 5e), which form at the aneurysm neck and advect upwards into the dome. During the diastole phase (Fig. 5f), this train of vortex tubes vanishes, leaving behind a few isolated pockets of rotationally dominant flow. The treatment procedure, however, alters this behavior. At systole, the upward motion of the vortex train is inhibited by the membrane lining the filling material, which confines the vortex tubes to the junction of the artery wall and the membrane. An example of this is plainly evident on the anterior side of the bifurcation (Fig. 5g), in which a large vortex tube, corresponding to the concentrated swirling flow region in Fig. 4c, spans the entire bifurcation and extends downstream into the left PCA. At diastole, the treatment procedure causes this vortex tube to appear at the same location (Fig. 5h). Iso-surfaces of Q^* = −40 and −10 (not shown) at systole and diastole, respectively, reveal that regions of the large straining motion arise at the stagnation zones of the basilar artery flow upon either the aneurysm wall (pre-treatment) or the membrane lining the filling material (post-treatment). Upstream of the bifurcation, no iso-surfaces of Q^* = ±40 or ±10 are present at systole or diastole, respectively. This is expected since the basilar artery flow in this region does not significantly deviate from the inlet Womersley velocity profile, which is characterized, in general, by a shearing motion with nearly equivalent magnitudes of fluid strain and rotation.

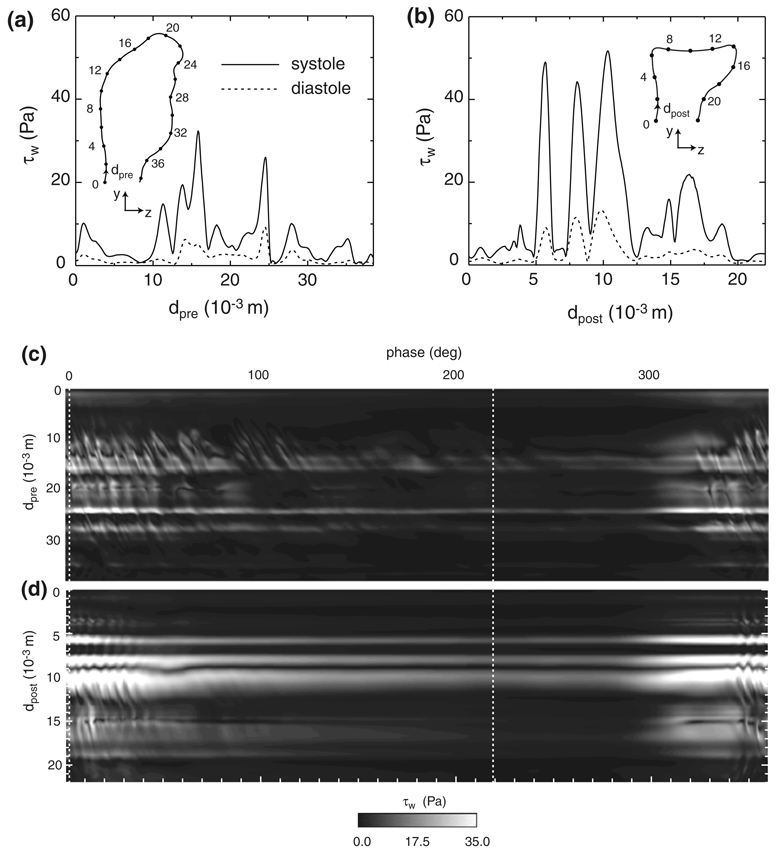
Prior to treatment, the WSS over the aneurysm wall exhibits two distinct local maxima along the x = 0 cross-section (Fig. 6a). The first (d_pre ≈ 14 × 10⁻³ at diastole; d_pre ≈ 16 × 10⁻³ m at systole) is due to the skewed impingement of the confined jet, while the second (d_pre ≈ 24 × 10⁻³ m at diastole and systole) occurs when the recirculating flow within the aneurysm glances upon a convex protuberance. By removing the cavity previously formed by the aneurysm, the treatment procedure forces the basilar artery flow to impinge in a nearly perpendicular manner upon the membrane lining the filling material and to change direction over a much smaller volume, which, in turn, produces larger WSSs at diastole and especially at systole (Fig. 6b). The local maximum in the post-treatment WSS at d_post ≈ 6 × 10⁻³ m is caused by the adjacent vortex tube on the anterior side of the bifurcation. A qualitatively similar local increase in the WSS was shown by Walker ⁵⁵ for a vortex placed in close proximity to a wall. On the other hand, the pair of maxima at d_post ≈ 8 × 10⁻³ m and 10 × 10⁻³ m are due to the stagnation of the basilar artery flow upon the membrane lining the filling material. The appearance of this pair of closely spaced peaks in WSS separated by a distinct local minimum (d_post ≈ 9 × 10⁻³ m) is qualitatively similar to the WSS distribution resulting from the impingement of an axi-symmetric jet upon a plane.^15,42 (Note that the minimum in WSS at d_post ≈ 9 × 10⁻³ m does not equal zero since the x = 0 cross section shown in Fig. 6b does not coincide with the stagnation point at diastole and systole.) At systole, a secondary impingement (d_post ≈ 15 × 10⁻³ m, see also Fig. 4c) of the basilar artery flow also generates two closely spaced local maxima in WSS separated by a distinct local minimum, though the peak values of WSS are significantly less than those of the primary impingement.

FIGURE 6.

WSS at x = 0 for the (a) pre- and (b) post-treatment bifurcations at systole (phase = 2°, solid line) and diastole (phase = 219°, dashed line). Spatial-temporal plot of the WSS at x = 0 for the (c) pre- and (d) post-treatment bifurcations over one cardiac cycle. The vertical dashed lines denote the phase locations of systole and diastole.

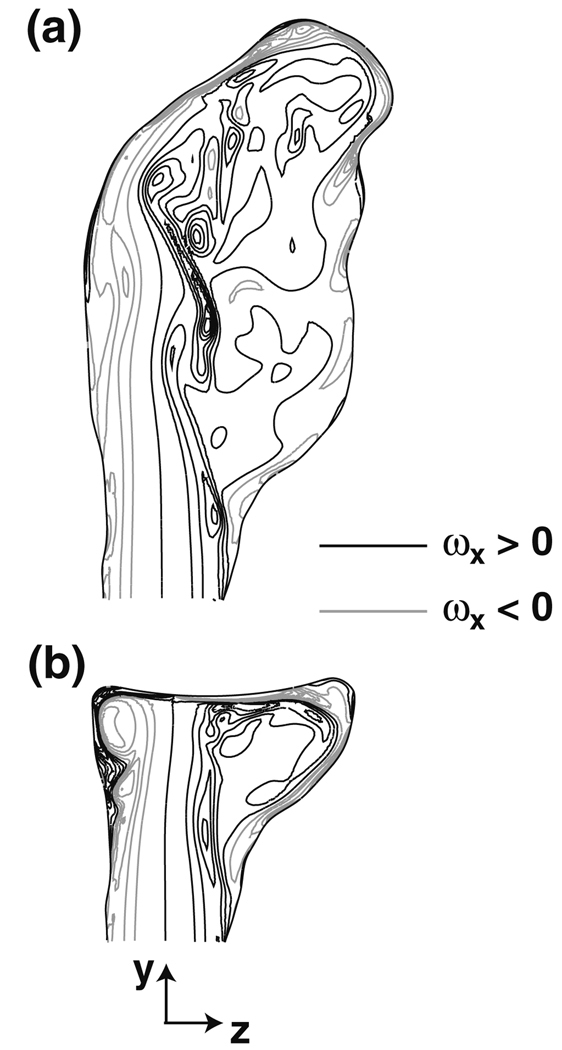
In addition to altering the spatial distribution of the WSS, the treatment procedure also affects its transient evolution. Prior to treatment, the most apparent temporal features in the WSS are those from the confined jet impingement and the recirculating flow that glances upon the convex protuberance (Fig. 6c). These signatures are marked by a considerable amount of unsteadiness, which is evident by the periodically spaced, angled streaks at the beginning and ending phases of the cardiac cycle. These streaks are caused by the passage of the vortex tubes, whose transient presence is the result of a shear layer instability that develops on the confined jet (Fig. 7a). The frequency at which the vortices pass over the aneurysm wall is found from the phase spacing of the streaks to be approximately 50 to 130 Hz from 0° < phase < 40°. This large range of frequencies is a result of the non-linear interactions between the newly formed vortex tubes at the aneurysm neck and those tubes already recirculating within the aneurysm. From the nominal slope of these WSS streaks, the convective velocity of the vortex tubes over the aneurysm wall is found to range from about 9 × 10⁻⁴ to 14 × 10⁻⁴ m/deg, or equivalently 0.4 to 0.6 m/s. Since the recirculating flow rotates clockwise within the aneurysm (when viewed from the left side of the patient), the streaks are sloped in one direction. Following the treatment procedure, the WSS streaks are still evident on the bifurcation wall, though they do not persist to the extent seen prior to treatment (Fig. 6d). This indicates that the removal of the aneurysm cavity suppresses the shear layer instability over portions of the cardiac cycle, which now has a more temporally uniform WSS distribution (100° < phase < 300°) that is distinguished mainly by the signatures of the basilar artery flow impingement (7 × 10⁻³ m < d_post < 12 × 10⁻³ m) and the anterior vortex tube (5 × 10⁻³ m < d_post < 6 × 10⁻³ m). Over those phases in which the shear layer instability persists (Fig. 7b), the vortex passage frequency ranges from about 75 to 100 Hz, as determined from the nominal phase spacing of the post-treatment WSS streaks from 0° < phase < 40°.

FIGURE 7.

Shear layer instability within the (a) pre- and (b) post-treatment bifurcations at systole (phase = 2°) as high-lighted by contours of the x-component of vorticity, 2:21 PM 4/11/2009003C9;_x, at x = 0 (ω_x <0, gray contours; ω_x >0, black contours), where ω = ∇ × u.

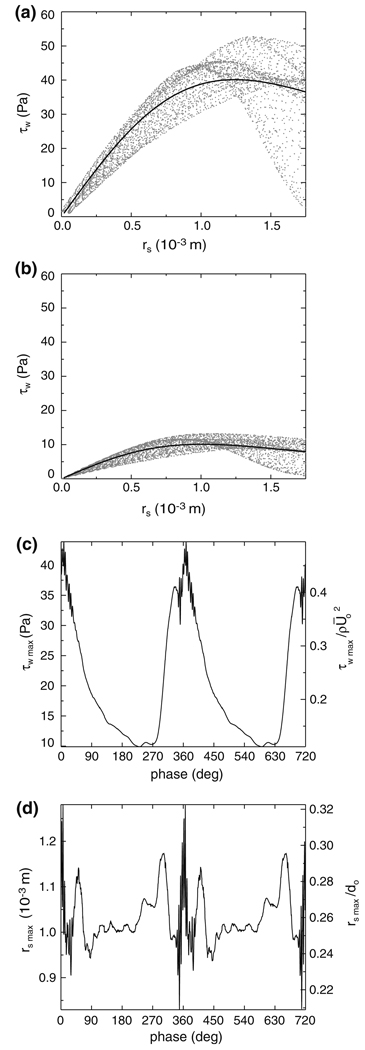
Across the entire surface of the post-treatment bifurcation, it is evident that the magnitude of WSS is dominated by the signatures of the confined vortex tube and the basilar artery flow impingement at both systole and diastole (Fig. 8a and 8b). The WSS signature from the vortex tube has a quasi-2D appearance in the form of a narrow band that spans a region beneath the treated aneurysm. Near the center of this band (x = 0 m, d_post = 5.7 × 10⁻³ m, see the inset of Fig. 6b for the definition of d_post), the magnitude of WSS varies over the cardiac cycle from a maximum of 51 Pa $(0.58\rho {\overline{U}}_0^2)$ at a phase of 1° to a minimum of 8.7 Pa $(0.098\rho {\overline{U}}_0^2)$ at a phase of 230° (Fig. 8c). The WSS signature from the impinging basilar artery flow has a roughly axisymmetric distribution centered on the flow stagnation point (Fig. 8a and 8b), which is the location of a local minimum in the WSS. The transient location of this stagnation point is obtained by fitting the surrounding WSS data with a fifth-order polynomial surface and computing the location of the minimum value of WSS on this surface, thereby yielding sub-mesh resolution accuracy of the stagnation point at each cardiac phase. Over the course of the cardiac cycle, it is apparent that the stagnation point traverses a tortuous circuit that is fairly repeatable from one cycle to the next (Fig. 8d). At both systole and diastole, plots of the WSS as a function of the radial distance, r_s, from the stagnation point demonstrate that the WSS increases from the stagnation point to a local maximum and then decreases at larger radial distances (Fig. 9a and 9b). To determine the transient changes in the magnitude and spatial extent of this WSS distribution over the entire cardiac cycle, the WSS plots at each time step are fit in the vicinity (0 ≤ r_s ≤ 1.75 × 10⁻³ m) of the stagnation point with an empirical relationship,

$${\tau }_{\mathrm{w}}(r_{\mathrm{s}},t)=\frac{a_0(t)}{r_{\mathrm{s}}}(1-e^{-r_{\mathrm{s}}^2/a_1{(t)}^2})$$ (6)

that captures the overall features of the WSS distribution, where the fitting coeffcients a₀(t) and a₁(t) are related to the maximum WSS of the curve fit by

$${\tau }_{{\mathrm{w}}_{\text{max}}}(t)=0.638\frac{a_0(t)}{a_1(t)}$$ (7)

and to its radial location, r_smax, by 1.12a₁(t). It is evident τ_smax(t) varies from a maximum value of 44 Pa $(0.50\rho {\overline{U}}_0^2)$ at a phase of 8° to a minimum of 10 Pa $(0.11\rho {\overline{U}}_0^2)$ at a phase of 230° to (Fig. 9c) and displays a time-dependent behavior that is similar to that of the WSS due to the anterior vortex tube (see Fig. 8c). Furthermore, the radial location of the maximum WSS remains within 1.3 × 10⁻³ m (0.33d₀) of the migrating stagnation point over the entire cardiac cycle (Fig. 9d).

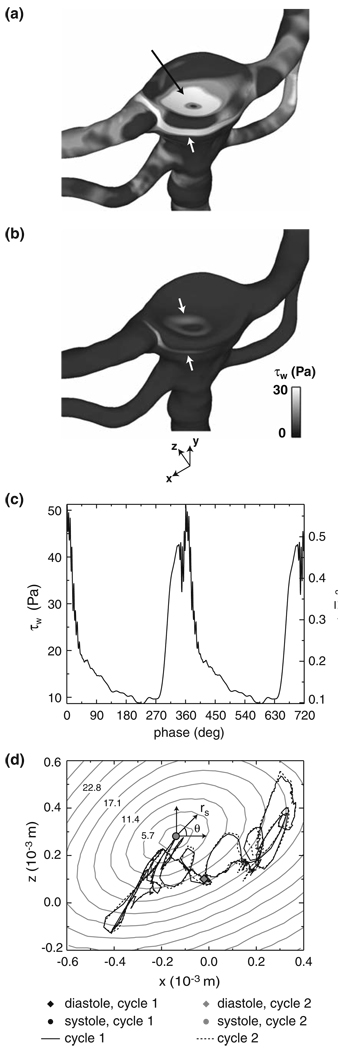
FIGURE 8.

WSS across the post-treatment bifurcation at (a) systole (phase = 2°) and (b) diastole (phase = 219°). The upper and lower arrows in each figure highlight the WSS signatures of the impinging basilar artery flow and the vortex tube adjacent to the artery wall, respectively. (c) Post-treatment WSS at x = 0, d_post = 5.7 × 10⁻³ m (see Fig. 6b for the definition of d_post) due to the vortex tube adjacent to the artery wall. (d) Transient location of the stagnation point arising from the impinging basilar artery flow upon the membrane that covers the aneurysm filling material. The gray contours, labeled in the unit of Pa, indicate the magnitude of the WSS surrounding the stagnation point at systole.

FIGURE 9.

Radial distribution of the post-treatment WSS in the vicinity of the basilar artery flow stagnation point at (a) systole (phase = 2°) and (b) diastole (phase = 219°). The solid lines denote the WSS curve fit defined in Eq. (6). (c) Maximum WSS, τ_wmax, and its (d) radial location, r_smax, from the curve fit (see Fig. 8d for the definition of r_s).

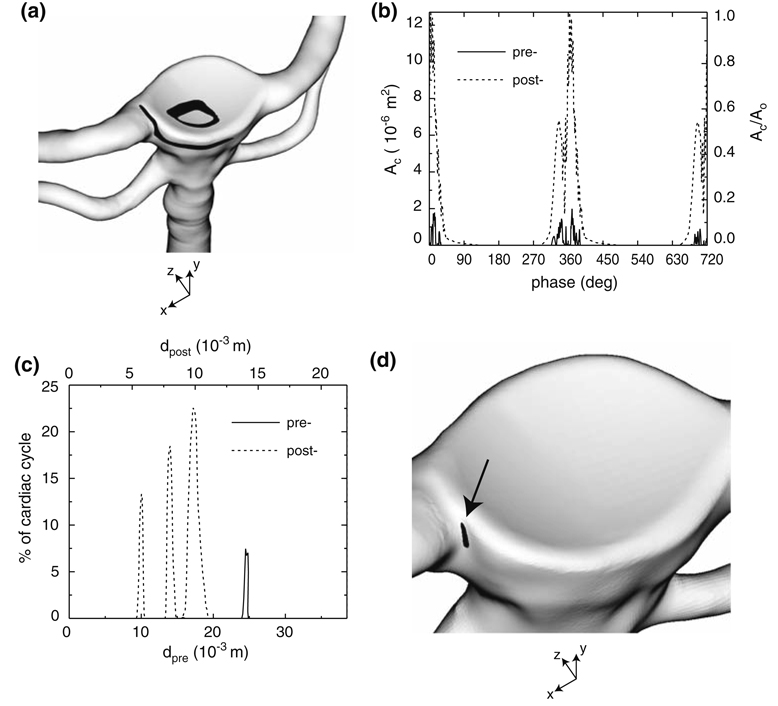
It is clearly evident that the treatment procedure produces a marked increase in the WSS to levels that are greater than Fry’s acute critical yield stress (37.9 Pa).²¹ This is especially true at systole where the maximum WSSs due to the close proximity of the vortex tube to the artery wall and the impingement of the basilar artery flow upon the membrane that lines the aneurysm filling material are approximately 50 Pa (see Fig. 8c and Fig. 9a). At systole, the total area, A_c, exposed to a WSS greater than 37.9 Pa is 1.0 × 10⁻⁵ m², a surface area which is equal to 81% of the characteristic area, $A_0=\frac{\pi }{4}{d}_0^2$, of the inlet basilar artery (Fig. 10a). Throughout the cardiac cycle (0° ≤ phase ≤ 360°), A_c fluctuates from a maximum of 1.3 × 10⁻⁵ m² (1.1A₀) at a phase of 4° to a minimum of zero over phases 131° to 288° (Fig. 10b). This is quite an increase in surface area when compared to the pre-treatment bifurcation, in which A_c is at most 1.8 × 10⁻⁶ m² (0.14A₀) (over 0° ≤ phase ≤ 360°) at a phase of 13° and is comprised of the regions where the confined jet impinges upon the aneurysm wall at d_pre ≈ 15 × 10⁻³ m and where the recirculating flow within the aneurysm glances upon the convex protuberance at d_pre ≈ 24 × 10⁻³ m (see Fig. 6a). The treatment procedure also increases the fraction of time over the cardiac cycle in which the WSS exceeds the acute critical yield stress (Fig. 10c). When time-averaged over the cardiac cycle, the WSS across the pre-treatment bifurcation remains less than 37.9 Pa. However for the post-treatment case, there is an area of 1.4 × 10⁻⁷ m² (0.01A₀) on the basilar artery wall at the junction of the right PCA (Fig. 10d) that is exposed to a time-averaged WSS greater than 37.9 Pa.

FIGURE 10.

(a) Contour of the area, A_c (black), in which the post-treatment WSS is greater than 37.9 Pa at systole (phase = 2°). (b) A_c as a function cardiac phase for the pre- (solid line) and post-treatment (dashed line) bifurcations. (c) Fraction of time over two cardiac cycles in which the pre- and post-treatment WSS at x = 0 is greater than 37.9 Pa (see Figs. 6a and 6b for the definitions of d_pre and d_post). (d) Contour of the area, A_c (black), in which the time-averaged, post-treatment WSS is greater than 37.9 Pa.

DISCUSSION

In major arteries throughout the human body, the nominal WSS ranges from about 0.2–2 Pa.¹⁶ Near arterial branches and regions of sharp wall curvature, the WSS increases as shown in the simulations of Valencia et al.,⁵⁴ in which the maximum WSS of a non-Newtonian blood flow through a generic healthy basilar bifurcation is of order 25 Pa. Yet, the present computational results demonstrate that the treatment procedure produces WSSs that are several times greater than these nominal values. Based upon the histological data of Fry,²¹ the area of the post-treatment artery wall exposed to time-averaged WSSs greater than 37.9 Pa would subsequently undergo endothelial cytoplasmic swelling and cell deformation and disintegration.

The elevated WSSs could also lead to long-term arterial wall remodeling in the vicinity of the treated aneurysm neck. Other studies^22,30 have shown that arteries exposed to increased WSSs remodel by expanding in diameter until the WSS returns to a nominal value. Recently, Meng et al.,³⁷ observed two types of vessel remodeling within arterial bifurcations that were examined either two weeks or two months following their initial surgical generation. The first was an intimal pad that formed where the parent artery flow impinged upon the apex of the bifurcation in a manner similar to that of the present post-treatment geometry. Within this pad, the intima was thicker due to additional collagen and elastin layers. The second type of remodeling, located immediately adjacent to the intimal pad, differed in that it was injurious in nature and resulted in severe degradation to the arterial wall structure. In five of the six bifurcations Meng et al.³⁷ investigated, a groove developed on the thinned media in this region, possibly indicating the early stages of aneurysm formation. Notably, the corresponding CFD simulations demonstrated that this groove was exposed to substantially increased WSSs, which exhibited a spatial distribution qualitatively similar to that of Eq. (6) with values of r_smax approximately equal to 0.002–0.003 m. For values of r_s ranging from about 0.2 × 10⁻³ m to r_smax, the artery wall demonstrated destructive remodeling, which was characterized by internal elastic lamina disruption and loss of endothelial cells, smooth muscle cells, and fibronectin.

Such vessel remodeling could potentially occur within the post-treatment bifurcation in the present study. Perhaps, the endothelial cell and arterial wall damage due to the extreme values of WSS in the 1.4 × 10⁻⁷ m² area of the basilar artery wall could be so severe that the artery degrades in a manner similar to that of Meng et al.,³⁷ possibly resulting in aneurysm re-growth. On the other hand, in the area adjacent to the vortex tube, the endothelial cells that survive outside the region of increased WSS could lead to local vessel dilatation, which may reduce the velocity gradients, thus returning the WSSs to nominal levels and ensuring the long-term success of the treatment procedure. Regardless, without in vivo data for this post-treatment geometry, it is difficult to determine exactly how vessel remodeling might proceed.

There are also several other matters that remain to be determined at the present time. First, one of the assumptions we make in this study is that a membrane forms across the surface of the aneurysm filling material, thus completely isolating the aneurysm from the circulation. While such a treatment outcome has been observed within several previous investigations, there are numerous others in which aneurysms, completely filled with traditional GDCs, do not develop this membrane. This raises a few questions as to how such a neck geometry would influence the post-treatment hemodynamics observed within this study: would the exposed aneurysm filling material diffuse the impinging basilar artery flow and subsequently reduce the WSSs in the vicinity of the stagnation zone? Would the rough surface of the aneurysm filling material break apart the structure of the vortex tubes, possibly enlarging their radial sizes and decreasing the WSS signatures to levels less than the acute critical yield stress? Or, would such disintegration of the vortex tubes produce smaller scale flow structures that would increase the high frequency fluctuations of the WSSs across the filling material and the post-treatment parent artery? Another assumption is made to neglect the compliance of the aneurysm and artery walls. Although other studies have shown that this effect has a negligible influence upon the overall flow and WSS patterns of a solitary artery, perhaps small differences in the elasticity between the parent artery, aneurysm, and filling material can turn a successful aneurysm treatment into a failed one by causing the filling material to shift relative to the aneurysm wall, thus promoting compaction and subsequent aneurysm re-canalization or re-growth. Lastly, lacking patient-specific, in vivo flowrate data, we make an assumption that the unsteady basilar artery flowrate and fractional PCA and SCA outlet flowrates obtained from multiple studies can be applied to the present basilar bifurcation, an approach that raises several questions: would the region of the artery wall exposed to time-averaged WSSs greater than the acute critical yield stress grow or shrink in size had we applied an inlet boundary condition specific to this patient? Do the fractional outlet flowrates remain constant over the cardiac cycle as we assume or do they vary as a result of asymmetries in the downstream vessel networks? If so, to what extent do such variations affect the post-treatment hemodynamics observed within this study? And, by how much do the WSSs increase for an exercise condition, in which the basilar artery flowrate is elevated above that employed in this study by an increase in both the cardiac frequency and the stroke volume of the heart? Clearly, the answers to these questions are beyond the scope of the present study. However, in future computational, clinical, experimental, and animal model studies, we will have the opportunity to determine the effects of these assumptions and thereby provide improved correlations between the post-treatment hemodynamics and the long-term outcome of treated aneurysms.

CONCLUSIONS

By performing a virtual endovascular procedure, we have investigated the post-treatment hemodynamics of a basilar aneurysm and bifurcation. The Womersley solution, computed from in vivo flowrate data, is specified at the inlet boundary to the basilar artery, thereby supplying a physiological flow to the bifurcation. Throughout the computational domain, the non-Newtonian viscosity of blood is modeled using a generalized power law. Prior to treatment, the velocity field within the aneurysm is comprised of a confined jet that is produced by the basilar artery flow issuing from the aneurysm neck. At systole, this jet undergoes an instability, in which the shear layers roll up into a periodic train of discrete vortex tubes. However, following the treatment procedure, in which the aneurysm is occluded, the basilar artery flow impinges instead upon a membrane lining the base of the aneurysm filling material, forming a stagnation zone and trapping a vortex tube along the anterior junction of the filling material and the basilar artery wall. The resulting WSS signatures produced by the flow stagnation and the vortex tube have magnitudes that are significantly greater than those present on the pre-treatment artery and aneurysm walls. In fact, when time-averaged over the cardiac cycle, the WSS at the junction of the basilar artery and one of the PCAs has a magnitude that is greater than that shown by a previous in vivo study to cause severe damage to endothelial cells. Whether or not this increase in post-treatment hemodynamic stress is a common occurrence that leads to long-term aneurysm re-growth or rupture is beyond the scope of the present study and, therefore, remains to be determined in subsequent studies. However, what is indicated by the present study is that the treatment procedure, while successful in occluding the aneurysm and leaving no neck remnant, elevates the WSSs to levels that are in theory injurious to the adjacent arterial wall.

The significant increase in WSS predicted by these simulations is a necessary consequence that results from occluding the aneurysm. Unfortunately, current endovascular treatment techniques do not offer the flexibility nor the fidelity to make small changes to the post-treatment lumen shape, which could possibly mitigate these extreme levels of WSS. However, there are other treatment techniques currently under development that may allow the WSSs to be tailored in the vicinity of the occluded aneurysm neck. An example of such a technique that could potentially be applied in this manner is one that utilizes a thermally-actuated shape memory polymer (SMP) foam that is delivered through a catheter to an aneurysm.³⁶ Since the shape into which the SMP foam is cut can be pre-determined, not only can patient-specific shapes be produced from pre-operation CT or MRI scans of the aneurysm, but optimized shapes that reduce the WSSs due to the vortex tubes and the impinging parent artery flow can also be machined into the SMP foam.

ABBREVIATIONS

BA

Basilar artery

CFD

Computational fluid dynamics

CTA

Computed tomography angiography

GDC

Guglielmi detachable coil

PCA

Posterior cerebral artery

SAH

Subarachnoid hemorrhage

SCA

Superior cerebellar artery

SMP

Shape memory polymer

WSS

Wall shear stress

WSSG

Wall shear stress gradient