Evaluation and Comparison of Computational Models

Abstract

Computational models are powerful tools that can enhance the understanding of scientific phenomena. The enterprise of modeling is most productive when the reasons underlying the adequacy of a model, and possibly its superiority to other models, are understood. This chapter begins with an overview of the main criteria that must be considered in model evaluation and selection, in particular explaining why generalizability is the preferred criterion for model selection. This is followed by a review of measures of generalizability. The final section demonstrates the use of five versatile and easy-to-use selection methods for choosing between two mathematical models of protein folding.

1. Introduction

How does one evaluate the quality of a computational model of enzyme kinetics? The answer to this question is important and complicated. It is important because mathematics makes it possible to formalize the reaction, providing a precise description of how the factors affecting it interact. Study of the model can lead to significant understanding of the reaction, so much so that the model can serve not merely as a description of the reaction, but can contribute to explaining its role in metabolism. Model evaluation is complicated because it involves subjectivity, which can be difficult to quantify.

This chapter begins with a conceptual overview of some of the central issues in model evaluation and selection, with an emphasis on those pertinent to the comparison of two or more models. This is followed by a selective survey of model comparison methods and then an application example that demonstrates the use of five simple yet informative model comparison methods.

Criteria on which models are evaluated can be grouped into those that are difficult to quantify and those for which it is easier to do so (Jacobs and Grainger, 1994). Criteria such as explanatory adequacy (whether the theoretical account of the model helps make sense of observed data) and interpretability (whether the components of the model, especially its parameters, are understandable and are linked to known processes) rely on the knowledge, experience, and preferences of the modeler. Although the use of these criteria may favor one model over another, they do not lend themselves to quantification because of their complexity and qualitative properties. Model evaluation criteria for which there are quantitative measures include descriptive adequacy (whether the model fits observed data), complexity or simplicity (whether the model’s description of observed data is achieved in the simplest possible manner), and generalizability (whether the model provides a good predictor of future observations). Although each criterion identifies a property of a model that can be evaluated on its own, in practice they are rarely independent of one another. Consideration of all three simultaneously is necessary to assess fully the adequacy of a model.

2. Conceptual Overview of Model Evaluation and Comparison

Before discussing the three quantitative criteria in more depth, we highlight some of the key challenges of modeling. Models are mathematical representations of the phenomenon under study. They are meant to capture patterns or regularities in empirical data by altering parameters that correspond to variables that are thought to affect the phenomenon. Model specification is difficult because our knowledge about the phenomenon being modeled is rarely complete. That is, empirical data obtained from studying the phenomenon are limited, providing only partial information (i.e., snapshots) about its properties and the variables that influence to it. With limited information, it is next to impossible to construct the “true” model. Furthermore, with only partial information, it is likely that multiple models are plausible; more than one model can provide a good account of data. Given this situation, it is most productive to view models as approximations, which one seeks to improve through repeated testing.

Another reason models can be only approximations is that data are inherently noisy. There is always measurement error, however small, and there may also be other sources of uncontrolled variation introduced during the data collection process that amplifies this error. Error clouds the regularity in data, increasing the difficulty of modeling. Because noise cannot be removed from data, the researcher must be careful that the model is capturing the meaningful trends in data and not error variation. As explained later, one reason why generalizability has become the preferred method of model comparison is how it tackles the problem of noise in data.

The descriptive adequacy of a model is assessed by measuring how well it fits a set of empirical data. A number of goodness-of-fit (GOF) measures are in use, including sum of squared errors (SSE), percent variance accounted for, and maximum likelihood (ML; e.g., Myung, 2003). Although their origins differ, they measure the discrepancy between empirical data and the ability of a model to reproduce those data. GOF measures are popular because they are relatively easy to compute and the measures are versatile, being applicable to many types of models and types of data. Perhaps most of all, a good fit is an almost irresistible piece of evidence in favor of the adequacy of a model. The model appears to do just what one wants it to—mimic the process that generated data. This reasoning is often taken a step further by suggesting that the better the fit, the more accurate the model. When comparing competing models, then, the one that provides the best fit should be preferred.

Goodness of fit would be suitable for model evaluation and comparison if it were not for the fact that data are noisy. As described earlier, a data set contains the regularity that is presumed to reflect the phenomenon of interest plus noise. GOF does not distinguish between the two, providing a single measure of a model’s fit to both (i.e., GOF = fit to regularity + fit to noise). As this conceptual equation shows, a good fit can be achieved for the wrong reasons, by fitting noise well instead of the regularity. In fact, the better a model is at fitting noise, the more likely it will provide a superior fit than a competing model, possibly resulting in the selection of a model that in actuality bears little resemblance to the process being modeled. GOF alone is a poor criterion for model selection because of the potential to yield misleading information.

This is not to say that GOF should be abandoned. On the contrary, a model’s fit to data is a crucial piece of information. Data are the only link to the process being modeled, and a good fit can indicate that the model mimics the process well. Rather, what is a needed is a means of ensuring that a model does not provide a good fit for the wrong reason.

What allows a model to fit noisy data better than its competitors is that it is the most complex. Complexity refers to the inherent flexibility of a model that allows it to fit diverse data patterns (Myung and Pitt, 1997). By varying the values of its parameters, a model will produce different data patterns. What distinguishes a simple model from a complex one is the sensitivity of the model to parameter variation. For a simple model, parameter variation will produce small and gradual changes in model performance. For a complex model, small parameter changes can result in dramatically different data patterns. It is this flexibility in producing a wide range of data patterns that makes a model complex. For example, the cubic model y = ax² + bx + c is more complex than the linear model y = ax + b. As shown in the next section, model selection methods such as AIC and BIC include terms that penalize model complexity, thereby neutralizing complexity differences among models.

Underlying the introduction of these more sophisticated methods is an important conceptual shift in the goal of model selection. Instead of choosing the model that provides the best fit to a single set of data, choose the model that, with its parameters held constant, provides the best fit to data if the experiment were repeated again and again. That is, choose the model that generalizes best to replications of the same experiment. Across replications, the noise in data will change, but the regularity of interest should not. The more noise that the model captures when fit to the first data set, the poorer its measure of fit will be when fitting data in replications of that experiment because the noise will have changed. If a model captures mostly the regularity, then its fits will be consistently good across replications. The problem of distinguishing regularity from noise is solved by focusing on generalizability. A model is of questionable worth if it does not have good predictive accuracy in the same experimental setting. Generalizability evaluates exactly this, and it is why many consider generalizability to be the best criterion on which models should be compared (Grunwald et al., 2005).

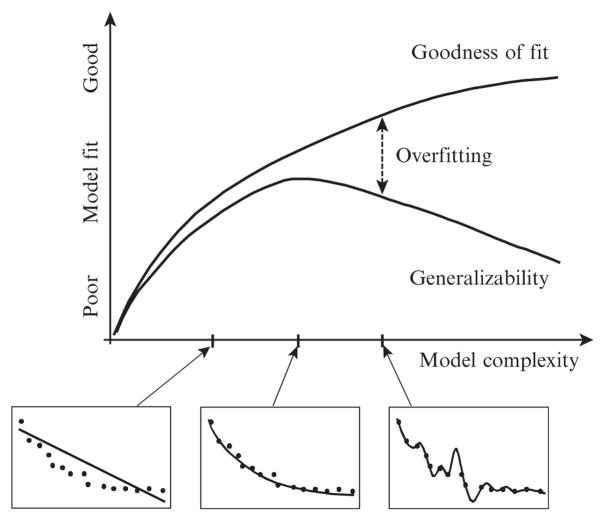
The graphs in Fig. 11.1 summarize the relationship among the three quantitative criteria of model evaluation and selection: GOF, complexity, and generalizability. Model complexity is along the x axis and model fit along the y axis. GOF and generalizability are represented as curves whose performance can be compared as a function of complexity. The three smaller graphs contain the same data set (dots) and the fits to these data by increasingly more complex models (lines). The left-most model in Fig. 11.1 underfits data. Data are curvilinear, whereas the model is linear. In this case, GOF and generalizability produce similar outcomes because the model is not complex enough to capture the bowed shape of data. The model in the middle graph of Fig. 11.1 is a bit more complex and does a good job of fitting only the regularity in data. Because of this, the GOF and generalizability measures are higher and also similar. Where the two functions diverge is when the model is more complex than is necessary to capture the main trend. The model in the right-most graph of Fig. 11.1 captures the experiment-specific noise, fitting every data point perfectly. GOF rewards this behavior by yielding an even higher fit score, whereas generalizability does just the opposite, penalizing the model for its excess complexity.

Figure 11.1.

An illustration of the relationship between goodness of fit and generalizability as a function of model complexity. The y axis represents any fit index, where a larger value indicates a better fit (e.g., maximum likelihood). The three smaller graphs provide a concrete example of how fit improves as complexity increases. In the left graph, the model (line) is not complex enough to match the complexity of data (dots). The two are well matched in complexity in the middle graph, which is why this occurs at the peak of the generalizability function. In the right graph, the model is more complex than data, capturing microvariation due to random error. Reprinted from Pitt and Myung (2002).

The problem of overfitting is the scourge of GOF. It is easy to see when overfitting occurs in Fig. 11.1, but in practice it is difficult to know when and by how much a model overfits a data set, which is why generalizability is the preferred means of model evaluation and comparison. By using generalizability, we evaluate a model based on how well it predicts the statistics of future samples from the same underlying processes that generated an observed data sample.

3. Model Comparison Methods

This section reviews measures of generalizability currently in use, touching on their theoretical foundations and discussing the advantages and disadvantages of their implementation. Readers interested in more detailed presentations are directed to Myung et al. (2000) and Wagenmakers and Waldorp (2006).

3.1. Akaike Information Criterion and Bayesian Information Criterion

As illustrated in Fig. 11.1, good generalizability is achieved by trading off GOF with model complexity. This idea can be formalized to derive model comparison criteria. That is, one way of estimating the generalizability of a model is by appropriately discounting the model’s goodness of fit relative to its complexity. In so doing, the aim is to identify the model that is sufficiently complex to capture the underlying regularities in data but not unnecessarily complex to capitalize on random noise in data, thereby formalizing the principle of Occam’s razor.

The Akaike information criterion (AIC; Akaike, 1973; Bozdogan, 2000), its variation called the second-order AIC (AICc; Burnham and Anderson, 2002; Sugiura, 1978), and the Bayesian information criterion (BIC; Schwartz, 1978) exemplify this approach and are defined as

$$\begin{array}{l}\mathit{AIC}=-2lnf(y\mid w^{\ast })+2k\\ \mathit{AICc}=-2lnf(y\mid w^{\ast })+2k+\frac{2k(k+1)}{n-k-1}\\ \mathit{BIC}=-2lnf(y\mid w^{\ast })+kln(n)\end{array}$$ (11.1)

where y denotes the observed data vector, ln f(y|w*) is the natural logarithm of the model’s maximized likelihood calculated at the parameter vector w*, k is the number of parameters of the model, and n is the sample size. The first term of each comparison criterion represents a model’s lack of fit measure (i.e., inverse GOF), with the remaining terms representing the model’s complexity measure. Combined, they estimate the model’s generalizability such that the lower the criterion value, the better the model is expected to generalize.

The AIC is derived as an asymptotic (i.e., large sample size) approximation to an information theoretic distance between two probability distributions, one representing the model under consideration and the other representing the “true” model (i.e., data-generating model). As such, the smaller the AIC value, the closer the model is to the “truth.” AICc represents a small sample size version of AIC and is recommended for data with relatively small n with respect to k, say n/k < 40 (Burnham and Anderson, 2002). BIC, which is a Bayesian criterion, as the name implies, is derived as an asymptotic expression of the minus two log marginal likelihood, which is described later in this chapter.

The aforementioned three criteria differ from one another in how model complexity is conceptualized and measured. The complexity term in AIC depends on only the number of parameters, k, whereas both AICc and BIC consider the sample size (n) as well, although in different ways. These two dimensions of a model are not the only ones relevant to complexity, however. Functional form, which refers to the way the parameters are entered in a model’s equation, is another dimension of complexity that can also affect the fitting capability of a model (Myung and Pitt, 1997). For example, two models, y = ax^b + e and y = ax + b + e, with a normal error e of constant variance, are likely to differ in complexity, despite the fact that they both assume the same number of parameters. For models such as these, the aforementioned criteria are not recommended because they are insensitive to the functional form dimension of complexity. Instead, we recommend the use of the comparison methods, described next, which are sensitive to all three dimensions of complexity.

3.2. Cross-Validation and Accumulative Prediction Error

Cross-validation (CV; Browne, 2000; Stone, 1974) and accumulative prediction error (APE: Dawid, 1984; Wagenmakers, Grunwald and Steyvers, 2006) are sampling-based methods for estimating generalizability from data, without relying on explicit, complexity-based penalty terms as in AIC and BIC. This is done by simulating the data collection and prediction steps artificially using observed data in the experiment.

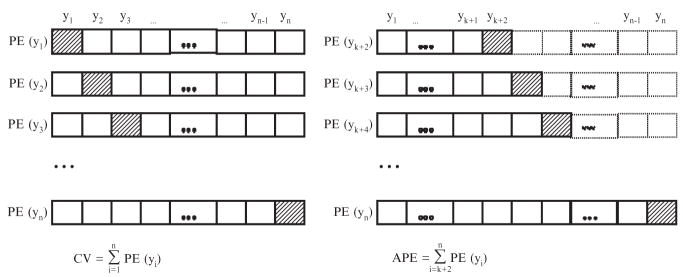
Cross-validation and APE are applied by following a three-step procedure: (1) divide observed data into two subsamples, the calibration sample, y_cal, simulating the “current” observations and the validation sample, y_val, simulating “future” observations; (2) fit the model to y_cal and obtain the best-fitting parameter values, denoted by w*(y_cal); and (3) with the parameter values fixed, the model is fitted to y_val. The resulting prediction error is taken as the model’s generalizability estimate.

The two comparison methods differ from each other in how data are divided into calibration and validation samples. In CV, each set of n − 1 observations in a data set serves as the calibration sample, with the remaining observation treated as the validation sample on which the prediction error is calculated. Generalizability is estimated as the average of n such prediction errors, each calculated according to the aforementioned three-step procedure. This particular method of splitting data into calibration and validation samples is known as the leave-one-out CV in statistics. Other methods of splitting data into two subsamples can also be used. For example, data can be split into two equal halves or into two subsamples of different sizes. In the remainder of this chapter, CV refers to the leave-one-out cross validation procedure.

In contrast to CV, in APE the size of the calibration sample increases successively by one observation at a time for each calculation of prediction error. To illustrate, consider a model with k parameters. We would use the first k + 1 observations as the calibration sample so as to make the model identifiable, and the (k + 2)-th observation as the validation sample, with the remaining observations not being used. The prediction error for the validation sample is then calculated following the three-step procedure. This process is then repeated by expanding the calibration sample to include the (k + 2)-th observation, with the validation sample now being the (k + 3)-th observation, and so on. Generalizability is estimated as the average prediction error over the (n − k − 1) validation samples. Time series data are naturally arranged in an ordered list, but for data that have no natural order, APE can be estimated as the mean over all orders (in theory), or over a few randomly selected orders (in practice). Figure 11.2 illustrates how CV and APE are estimated.

Figure 11.2.

The difference between the two sampling-based methods of model comparison, cross-validation (CV) and accumulative prediction error (APE), is illustrated. Each chain of boxes represents a data set with each data point represented by a box. The slant-lined box is a validation sample, and plain boxes with the bold outline represent the calibration sample. Plain boxes with the dotted outline in the right panel are not being used as part of the calibration or validation sample. The symbol PE(y_i), i = 1, 2, … n, stands for the prediction error for the ith validation data point.

Formally, CV and APE are defined as

$$\begin{array}{l}CV=-\sum _{i=1}^{n}lnf(y_i\mid w^{\ast }(y\ne i))\\ \mathit{APE}=-\sum _{i=k+2}^{n}lnf(y_i(w^{\ast }(y_{1,2,\dots ,i-1})).\end{array}$$ (11.2)

In the aforementioned equation for CV, −ln f(y_i | w* (y _{≠ i})), is the minus log likelihood for the calibration sample y_i evaluated at the best-fitting parameter values w*(y _≠i), obtained from the validation sample y _≠i. The subscript signifies “all observations except for the ith observation.” APE is defined similarly. Both methods prescribe that the model with the smallest value of the given criterion should be preferred.

The attractions of CV and APE are the intuitive appeal of the procedures and the computational ease of their implementation. Further, unlike AIC and BIC, both methods consider, albeit implicitly, all three factors that affect model complexity: functional form, number of parameters, and sample size. Accordingly, CV and APE should perform better than AIC and BIC, in particular when comparing models with the same number of parameters. Interestingly, theoretical connections exit between AIC and CV, and BIC and APE. Stone (1977) showed that under certain regularity conditions, model choice under CV is asymptotically equivalent to that under AIC. Likewise, Barron and colleagues (1998) showed that APE is asymptotically equivalent to BIC.

3.3. Bayesian Model Selection and Stochastic Complexity

Bayesian model selection (BMS; Kass and Raftery, 1995; Wasserman, 2000) and stochastic complexity (SC; Grunwald et al., 2005; Myung et al., 2006 Rissanen, 1996, 2001) are the current state-of-the-art methods of model comparison. Both methods are rooted on firm theoretical foundations; are nonasymptotic in that they can be used for data of all sample sizes, small or large; and, finally, are sensitive to all dimensions of complexity. The price to pay for this generality is computational cost. Implementation of the methods can be nontrivial because they usually involve evaluating high-dimensional integrals numerically.

Bayesian model selection and SC are defined as

$$\begin{array}{l}\mathit{BMS}=-ln\int f(y\mid w)\pi (w)dw\\ SC=-lnf(y\mid w^{\ast })+ln\int f(z\mid w^{\ast }(z))dz.\end{array}$$ (11.3)

Bayesian model selection is defined as the minus logarithm of the marginal likelihood, which is nothing but the mean likelihood of data averaged across parameters and weighted by the parameter prior π(w). The first term of SC is the minus log maximized likelihood of observed data y. It is a lack of fit measure, as in AIC. The second term is a complexity measure, with the symbol z denoting potential data that could be observed in an experiment, not actually observed data. Both methods prescribe that the model that minimizes the given criterion value is to be chosen.

Bayesian model selection is related to the Bayes factor, the gold standard of model comparison in Bayesian statistics, such that the Bayes factor is a ratio of two marginal likelihoods between a pair of models. BMS does not yield an explicit measure of complexity but complexity is taken into account implicitly through the integral and thus avoids overfitting. To see this, an asymptotic expansion of BMS under Jeffrey’s prior for π(w) yields the following large sample approximation (Balasubramanian, 1997)

$$\mathit{BMS}\approx -lnf(y\mid w^{\ast })+\frac{k}{2}ln\left(\frac{n}{2\pi }\right)=\int \sqrt{det(I(w))}dw,$$ (11.4)

where I(w) is the Fisher information matrix of sample size 1 (e.g., Schervish, 1995). The second and third terms on the right-hand side of the expression represent a complexity measure. It is through the Fisher information in the third term that BMS reflects the functional form dimension of model complexity. For instance, the two models mentioned earlier, y = ax^b + e and y = ax + b + e, would have different values of the Fisher information, although they both have the same number of parameters. The Fisher information term is independent of sample size n, with its relative contribution to that of the second term becoming negligible for large n. Under this condition, the aforementioned expression reduces to another asymptotic expression, which is essentially one-half of BIC in Eq. (11.1).

Stochastic complexity is a formal implementation of the principle of minimum description length that is rooted in algorithmic coding theory in computer science. According to the principle, a model is viewed as a code with which data can be compressed, and the best model is the one that provides maximal compression of the data. The idea behind this principle is that regularities in data necessarily imply the presence of statistical redundancy, which a model is designed to capture, and therefore, the model can be used to compress data. That is, data are reexpressed, with the help of the model, in a coded format that provides a shorter description than when data are expressed in an uncompressed format. The SC criterion value in Eq. (11.3) represents the overall description length in bits of maximally compressed data and the model itself, derived for parametric model classes under certain statistical regularity conditions (Rissanen, 2001).

The second (complexity) term of SC deserves special attention because it provides a unique conceptualization of model complexity. In this formulation, complexity is defined as the logarithm of the sum of maximized likelihoods that the model yields collectively for all potential data sets that could be observed in an experiment. This formalization captures nicely our intuitive notion of complexity. A model that fits a wide range of data patterns well, actual or hypothetical, should be more complex than a model that fits only a few data patterns well, but does poorly otherwise. A serious drawback of this complexity measure is that it can be highly nontrivial to compute the quantity because it entails numerically integrating the maximized likelihood over the entire data space. This integration in SC is even more difficult than in BMS because the data space is generally of much higher dimension than the parameter space.

Interestingly, a large-sample approximation of SC yields Eq. (11.4) (Rissanen, 1996), which itself is an approximation of BMS. More specifically, under Jeffrey’s prior, SC and BMS become asymptotically equivalent. Obviously, this equivalence does not extend to other priors and does not hold if the sample size is not large enough to justify the asymptotic expression.

4. Model Comparison at Work: Choosing between Protein Folding Models

This section applies five model comparison methods to discriminating two proteinfolding models.

In the modern theory of protein folding, the biochemical processes responsible for the unfolding of helical peptides are of interest to researchers. The Zimm–Bragg theory provides a general framework under which one can quantify the helix–coil transition behavior of polymer chains (Zimm and Bragg, 1959). Scholtz and colleagues (1995) applied the theory “to examine how the α-helix to random coil transition depends on urea molarity for a homologous series of peptides” (p. 185). The theory predicts that the observed mean residue ellipticity q as a function of the length of a peptide chain and the urea molarity is given by

$$q=f_H·(g_H-g_C)+g_C.$$ (11.5)

In Eq. (1), f_H is the fractional helicity and g_H and g_C are the mean residue ellipticities for helix and coil, respectively, defined as

$$\begin{array}{l}{f}_H=\frac{rs}{{(s-1)}^3}\left(\frac{n·s^{n+2}-(n+2)s^{n+1}+(n+2)s-n}{n\left(1+[rs/{(s-1)}^2][s^{n+1}+n-(n+1)s]\right)}\right)\\ g_H=H_0\left(1-\frac{2.5}{n}\right)+H_U·[\mathit{urea}]\\ g_C=C_0+C_U·[\mathit{urea}],\end{array}$$ (11.6)

where r is the helix nucleation parameter, s is the propagation parameter, n is the number of amide groups in the peptide, H₀ and C₀ are the ellipticities of the helix and coil, respectively, at 0° in the absence of urea, and finally, H_U and C_U are the coefficients that represent the urea dependency of the ellipticities of the helix and coil (Greenfield, 2004; Scholtz et al., 1995).

We consider two statistical models for urea-induced protein denaturation that determine the urea dependency of the propagation parameter s. One is the linear extrapolation method model (LEM; Pace and Vanderburg, 1979) and the other is called the binding-site model (BIND; Pace, 1986). Each expresses the propagation parameter s in the following form

$$\begin{array}{l}\text{LEM}:lns=ln{s}_0-\frac{m·[\mathit{urea}]}{R·T}\\ \text{BIND}:lns=ln{s}_0-d·ln(1+\text{k}·(0.9815·[\mathit{urea}]-0.02978·{[\mathit{urea}]}^2\\ +0.00308·{[\mathit{urea}]}^3))\end{array}$$ (11.7)

where s₀ is the s value for the homopolymer in the absence of urea, m is the change in the Gibbs energy of helix propagation per residue, R = 1.987 cal mol⁻¹ K⁻¹, T is the absolute temperature, d is the parameter characterizing the difference in the number of binding sites between the coil and helix forms of a residue, and k is the binding constant for urea.

Both models share four parameters: H₀, C₀, H_U, and C_U. LEM has two parameters of its own (s₀, m), yielding a total of six parameters to be estimated from data. BIND has three unique parameters (s₀, d, and k). Both models are designed to predict the mean residue ellipticity denoted q in terms of the chain length n and the urea molarity [urea]. The helix nucleation parameter r is assumed to be fixed to the previously determined value of 0.0030 (Scholtz et al., 1991).

Figure 11.3 shows simulated data (symbols) and best-fit curves for the two models (LEM in solid lines and BIND in dotted lines). Data were generated from LEM for a set of parameter values with normal random noise of zero mean and 1 standard deviation added to the ellipticity prediction in Eq. (5)(see the figure legend for details). Note how closely both models fit data. By visual inspection, one cannot tell which of the two models generated data. As a matter of fact, BIND, with one extra parameter than LEM, provides a better fit to data than LEM (SSE = 12.59 vs 14.83), even though LEM generated data. This outcome is an example of the overfitting that can emerge with complex models, as depicted in Fig. 11.1. To filter out the noise-capturing effect of overly complex models appropriately, thereby putting both models on an equal footing, we need the help of statistical model comparison methods that neutralize complexity differences.

Figure 11.3.

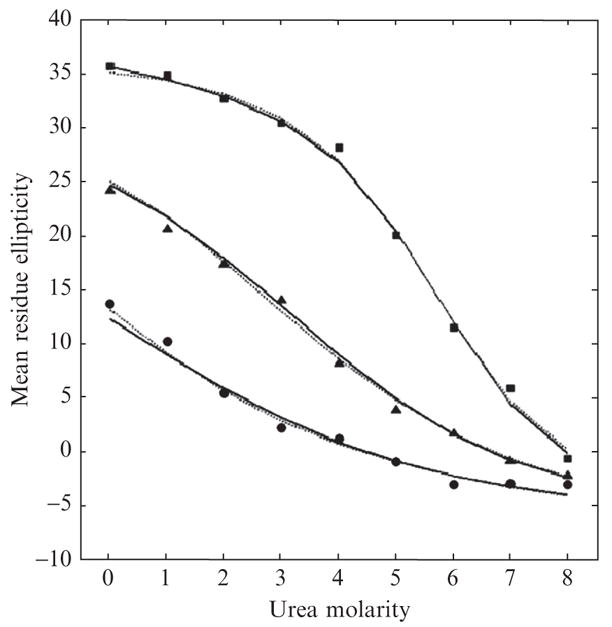
Best fits of LEM (solid lines) and BIND (dotted lines) models to data generated from LEM using the nine points of urea molarity (0,1,2, ….,8) for three different chain lengths of n = 13 (•), 20 (▲), and 50 (■). Data fitting was done first by deriving model predictions using Eqs. (5)–(7) based on the parameter values of H₀ = −44,000, C₀ = 4400, H_U = 320, C_U = 340, s₀ = 1.34, and m = 23.0 reported in Scholtz et al. (1995). See text for further details.

We conducted a model recovery simulation to demonstrate the relative performance of five model comparison methods (AIC, AICc, BIC, CV, and APE) in choosing between the two models. BMS and SC were not included because of the difficulty in computing them for these models. A thousand data sets of 27 observations each were generated from each of the two models, using same nine points of urea molarity (0, 1, 2, …, 8) for three different chain lengths of n = 13, 20, and 50. The parameter values used to generate simulated data were taken from Scholtz et al. (1995) and were as follows: H₀ = −44,000, C₀ = 4400, H_U = 320, C_U = 340, s₀ = 1.34, m = 23.0 and temperature T = 273.15 for LEM and H₀ = −42,500, C₀ = 5090, H_U = −620, C_U = 280, s₀ = 1.39, d = 0.52, k = 0.14 for BIND. Normal random errors of zero mean and standard deviation of 1 were added to the ellipticity prediction in Eq. (11.5).

The five model comparison methods were compared on their ability to recover the model that generated data. A good method should be able to identify the true model (i.e., the one that generated data) 100% of the time. Deviations from perfect recovery reveal a bias in the selection method. (The MatLab code that implements the simulations can be obtained from the first author.)

The simulation results are reported in Table 11.1. Values in the cells represent the percentage of samples in which a particular model (e.g., LEM) fitted best data sets generated by one of the models (LEM or BIND). A perfect selection method would yield values of 100% along the diagonal. The top 2 × 2 matrix shows model recovery performance under ML, a purely goodness-of-fit measure. It is included as a reference against which to compare performance when measures of model complexity are included in the selection method. How much does model recovery improve when the number of parameters, sample size, and functional form are taken into account?

Table 11.1.

Model recovery performance of five model comparison methods

		Data generated from
Model comparison method	Model fitted	LEM	BIND
ML	LEM	47	4
	BIND	53	96
AIC	LEM	81	16
	BIND	19	84
AICc	LEM	93	32
	BIND	7	68
BIC	LEM	91	28
	BIND	9	72
CV	LEM	77	26
	BIND	23	74
APE	LEM	75	45
	BIND	25	55

Note: The two models, LEM and BIND, are defined in Eq. (7). APE was estimated after randomly ordering the 27 data points of each data set.

With ML, there is a strong bias toward BIND. The result in the first column of the matrix shows that BIND was chosen more often than the true data-generating model, LEM (53% vs 47%). This bias is not surprising given that BIND, with one more parameter than LEM, can capture random noise better than LEM. Consequently, BIND tends to be selected more often than LEM under a goodness-of-fit selection method such as ML, which ignores complexity differences. Results from using AIC show that when the difference in complexity due to the number of parameters is taken into account, the bias is largely corrected (19% vs 81%), and even more so under AICc and BIC, both of which consider sample size as well (7% vs 93% and 9% vs 91%, respectively). When CV and APE were used, which are supposed to be sensitive to all dimensions of complexity, results show that the bias was also corrected, although the recovery rate under these criteria was about equal to or slightly lower than that under AIC. When data were generated from BIND (right column of values), the data-generating model was selected more often than the competing model under all selection methods, including ML.

To summarize, the aforementioned simulation results demonstrate the importance of considering model complexity in model comparison. All five model selection methods performed reasonably well by compensating for differences in complexity between models, thus identifying the data-generating model. It is interesting to note that Scholtz and colleagues (1995) evaluated the viability of the same two models plus a third, seven-parameter model, using goodness of fit, and found that all three models provided nearly identical fits to their empirical data. Had they compared the models using one of the selection methods discussed in this chapter, it might have been possible to obtain a more definitive answer.

We conclude this section with the following cautionary note regarding the performance of the five selection methods in Table 11.1: The better model recovery performance of AIC, AICc, and BIC over CV and APE should not be taken as indicative of how the methods will generally perform in other settings (Myung and Pitt, 2004). There are very likely other situations in which the relative performance of the selection methods reverses.

5. Conclusions

This chapter began by discussing several issues a modeler should be aware of when evaluating computational models. They include the notion of model complexity, the triangular relationship among goodness of fit, complexity and generalizability, and generalizability as the ultimate yardstick of model comparison. It then introduced several model comparison methods that can be used to determine the “best-generalizing” model among a set of competing models, discussing the advantages and disadvantages of each method. Finally, the chapter demonstrated the application of some of the comparison methods using simulated data for the problem of choosing between biochemical models of protein folding.

Measures of generalizability are not without their own drawbacks, however. One is that they can be applied only to statistical models defined as a parametric family of probability distributions. This restriction leaves one with few options when wanting to compare nonstatistical models, such as verbal models and computer simulation models. Often times, researchers are interested in testing qualitative (e.g., ordinal) relations in data (e.g., condition A < condition B) and comparing models on their ability to predict qualitative patterns of data, but not quantitative ones.

Another limitation of measures of generalizability is that they summarize the potentially intricate relationships between model and data into a single real number. After applying CV or BMS, the results can sometimes raise more questions than answers. For example, what aspects of a model’s formulation make it superior to its competitors? How representative is a particular data pattern of a model’s performance? If it is typical, the model provides a much more satisfying account of the process than if the pattern is generated by the model using a small range of unusual parameter settings. Answers to these questions also contribute to the evaluation of model quality.

We have begun developing methods to address questions such as these. The most well-developed method thus far is a global qualitative model analysis technique dubbed parameter space partitioning (PSP; Pitt et al., 2006, 2007). In PSP, a model’s parameter space is partitioned into disjoint regions, each of which corresponds to a qualitatively different data pattern. Among other things, using PSP, one can use PSP to identify all data patterns a model can generate by varying its parameter values. With information such as this in hand, one can learn a great deal about the relationship between the model and its behavior, including understanding the reason for the ability or inability of the model to account for empirical data.

In closing, statistical techniques, when applied with discretion, can be useful for identifying sensible models for further consideration, thereby aiding the scientific inference process (Myung and Pitt, 1997). We cannot overemphasize the importance of using nonstatistical criteria such as explanatory adequacy, interpretability, and plausibility of the models under consideration, although they have yet to be formalized in quantitative terms and subsequently incorporated into the model evaluation and comparison methods. Blind reliance on statistical means is a mistake. On this point we agree with Browne and Cudeck (1992), who said “Fit indices [statistical model evaluation criteria] should not be regarded as a measure of usefulness of a model…they should not be used in a mechanical decision process for selecting a model. Model selection has to be a subjective process involving the use of judgement” (p. 253).