A model for individual and collective cell movement in Dictyostelium discoideum

Abstract

The cellular slime mold Dictyostelium discoideum is a widely used model system for studying a variety of basic processes in development, including cell–cell signaling, signal transduction, pattern formation, cell motility, and the movement of tissue-like aggregates of cells. Many aspects of cell motion are poorly understood, including how individual cell behavior produces the collective motion of cells observed within the mound and slug. Herein, we describe a biologically realistic model for motile D. discoideum cells that can generate active forces, that interact via surface molecules, and that can detect and respond to chemotactic signals. We model the cells as deformable viscoelastic ellipsoids and incorporate signal transduction and cell–cell signaling by using a previously developed model. The shape constraint restricts the admissible deformations but makes the simulation of a large number of interacting cells feasible. Because the model is based on known processes, the parameters can be estimated or measured experimentally. We show that this model can reproduce the observations on the chemotactic behavior of single cells, streaming during aggregation, and the collective motion of an aggregate of cells driven by a small group of pacemakers. The model predicts that the motion of two-dimensional slugs [Bonner, J. T. (1998) Proc. Natl. Acad. Sci. USA 95, 9355–9359] results from the same behaviors that are exhibited by individual cells; it is not necessary to invoke different mechanisms or behaviors. Our computational experiments also suggest previously uncharacterized phenomena that may be experimentally observable.

Cell and tissue movement plays a vital role throughout the life span of many organisms. Individual cells such as bacteria find food by a combination of taxis and kinesis, and macrophages and neutrophils use these same processes to find bacteria and cellular debris. Coordinated movements of cells and tissues that lead to either large-scale tissue rearrangements or translocation occur throughout early embryonic development, and special terminology such as convergent extension, gastrulation, and invagination is used to describe these processes. Thus, it is important to develop a better understanding of cell movement, both in the low-density, noninteracting limit where cells move individually, and at “tissue-level” densities where cells interact strongly and move collectively. Understanding the collective motion of Dictyostelium discoideum (Dd hereafter), both in the free-ranging state and in dense aggregates, will shed light on how cells in developing systems respond to short-range surface interactions with other cells and long-range chemotactic stimuli and how these factors affect the collective movement of an aggregate.

The social amoeba Dd uses cAMP as a messenger for signaling to control cell movement in various stages of development (1, 2). The production and relay of cAMP pulses by excitable cells, coupled with chemotactic movement toward the cAMP signaling center (a pacemaker region or the center of a spiral), facilitate the organization of large territories (3, 4). In early aggregation the cells move autonomously, but in late aggregation they form connected streams that migrate toward the aggregation center. These streams converge in a loose mound of cells that usually topples over to form a cigar-shaped mass called the slug (1), which contains up to 10⁵ cells. cAMP waves are thought to organize the transformation of hemispherical mounds into slug-shaped structures, the migration of slugs over the substratum, and their culmination into fruiting bodies. Certain cells in the slug secrete a slime sheath of cellulose and protein through which the slug migrates over the substrate, sometimes in a pulsatile fashion (5).

In this article, we focus on how the motile behavior of individual cells leads to the collective motion of an aggregate of cells. The biochemical and biophysical aspects of cell movement have been reviewed elsewhere (6–8), and we simply summarize the salient aspects that most cells share. The forces that act on a motile cell are 2-fold. First, there are internal forces, which comprise active and passive forces in the cytoskeleton, hydrostatic and osmotic pressures, and stresses that stem from the motion of the cytoplasm. Second, there are external forces that stem from cell–cell and cell–substrate interactions such as adhesion and resistance to deformation, the active locomotive force that a cell applies either to a neighbor cell or to the substrate, and the drag exerted by the extracellular fluid. In suspension a cell is spherical; when resting on a surface it is flattened; and when it moves, it elongates in the direction of movement (9). When subjected to a force, a cell initially resists deformation and thus has elastic properties, but under sustained force, the actin network in the cytoskeleton can break and reform, producing a viscous response (10, 11). Cell motion in Dd consists of the alternating extension of pseudopods and retraction of trailing parts of the cell (12, 13). Not all extensions are persistent, in that they must anchor to the substrate or to another cell, at least temporarily, in order for the remainder of the cell to follow (13).

Much of the present research on tissue movement is aimed at identifying the molecules involved in cell–cell and cell–substrate interactions. However, earlier work by Steinberg and coworkers (14–16) focused on tissue-level properties, in particular, their rheological properties. Their work shows that embryonic tissue masses behave like solids under brief stresses, in that they respond elastically without changes in relative cell positions but that they flow under long-term sustained stress. They characterize these tissues as elasticoviscous liquids, by which they mean that the tissue is a viscous liquid composed of elastic subunits. Applied stresses lead to a bimodal response, consisting of a rapid elastic response and a slower viscous flow, but the authors do not estimate rheological parameters. In Dd, cells in the aggregation streams move faster and more continuously than free-ranging individuals (17), but the rheology of Dd aggregates has not been studied.

Several different theoretical approaches have been used to model cell sorting and the collective motion of the cells in aggregation streams and later stages.

1.

One is a cellular automata approach (18, 19), in which formal rules for cell–cell interactions and for the reactions of the cells to their chemical environment are postulated, without consideration of the forces involved in cell–cell interactions. Simulations of such models show patterns that resemble experimental observations but produce limited insight, because the models do not incorporate the physics of cell–cell interactions and cell–cell signaling.

2.

Another approach uses models based on Steinberg's theory of adhesion-driven sorting (20–25). The dynamics are governed either by formal rules for cell interchanges or by minimization of a surface free energy. Active movement by cells is not considered in this approach; cells deform passively because of surface effects. Although adhesive forces are an important component of the interaction between cells, active propulsion is equally important in the dynamics. A cell-based approach that incorporates active forces was proposed by Jacobson and Gordon (26) and has been used by others (27) in a different context.

3.

Yet another approach uses continuum models: either two-dimensional (2D) models of cell aggregation (28, 29) or models of slug movement as developed by Odell and Bonner (30) and by Vasiev et al. (31). In the Odell–Bonner model, cells respond to cAMP chemotactically, and the active component of the propulsive force enters as a contribution to the stress tensor. Active stresses derive from an active relative velocity field set up at the cell surface. Vasiev et al. (31) also include cAMP dynamics into a continuum model of movement in Dd. They begin with the Navier–Stokes equations and add forces intended to model those arising from chemotaxis. Although their equations can produce solutions that resemble aggregation, the authors do not include an elastic response, and it is difficult to connect the forces postulated with experimentally measurable quantities such as the force exerted by a single cell.

Description of the Model

The basic units in the model are individual cells, each of which is characterized by its location and orientation within the aggregate, its state of stress, and the active forces it can exert in response to the local microenvironment. Knowing this information for each cell, the movement of all cells and hence the movement of an aggregate of cells can be calculated. Below, we describe how the present state of a cell is determined, how the forces it can exert are computed, and the algorithm for time-stepping the equations of motion.

The viscoelastic properties of single cells are incorporated as follows. We assume that cells are deformable ellipsoids having axes of length a, b, and c, each of which contains a nonlinear spring in parallel with a Maxwell element (10, 32). Any external force acting on the cell is resolved into forces on the three axis, which deform the cell under the constraint of constant volume. The spatial location and orientation of a cell is given by its center of mass coordinates and by the orientation and length of the principal axes, which we denote by the vectors a, b, and c.

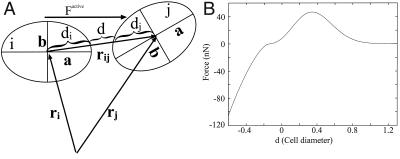
In vivo, a cell's response to a chemotactic signal is to orient toward the signal and polarize, extend a pseudopod, attach it either to another cell or to the substrate, and move the cell body into the pseudopod (9); these behaviors are incorporated in the model. Cell movement has both a random component and a directed component in response to a chemotactic signal, and in the former case, the direction is chosen randomly. In response to a chemotactic signal, it moves in the direction of the chemotactic gradient but is perturbed with a small amount of noise. When cell i “decides” to move, it must generate an active force in the chosen direction. This force is achieved by determining the axis most closely aligned with the chosen direction, reorienting or turning (by internally “rearranging” its structure) such that the new major axis (now relabeled as a_i) coincides with the chosen direction, and extending a pseudopod in that direction. If the pseudopod is sufficiently close to the substrate, it attaches to the substrate; otherwise, it attaches to the neighbor cell j that has the smallest angle between the vector r_ij, which connects the centers of i and j, and the direction a_i (Fig. 1A).§ This attachment of the pseudopod is assumed to be strong enough to withstand the active locomotive force that the cell applies to initiate movement.

Figure 1.

(A) A schematic of how the distance d between the surfaces of two cells is determined. F^active is the tactic force that the cell applies. (B) The dependence of the force between cells, which is the result of the adhesive forces and the resistance to deformation, on the separation d.

When a cell attaches a pseudopod to the substrate on which it is moving, the active locomotive force is applied directly to the substrate, and the force on the moving cell is the reaction force that pulls the cell forward. However, when the pseudopod attaches to a neighbor cell, the active force pulls the neighbor cell toward the first cell, and the opposing reaction force pulls the first cell forward. Thus, the active force enters into the equation of motion for the second cell and the reaction force enters into the equation of motion for the first cell. These internal forces will cancel and produce no net force on interior cells unless some of the active force can be transmitted to the substrate via a connected chain of cells, one or more of which is contact with the substrate.

The magnitude of the active chemotactic force generated depends not only on the average local cAMP concentration but also on whether the cell is attaching to other cells, to the surface, or to the slime sheath. Table 1 gives typical measured values for the force, and in the simulations, we set the active chemotactic force to be a constant at the average value ≈5 × 10⁻³ dynes (1 dyne = 10 mN) whenever the chemical concentration exceeds a threshold, because the dependence of the force on the local cAMP concentration is not known. The active random force was set to be about 20% of the chemotactic force.

Table 1.

Typical values of the model parameters

Parameter	Typical range	Experimental source
Active force, Fact	2 × 10−3 to 10 × 10−3 dyne	3 × 10−3 to 8 × 10−3 Leukocytes (42) and Dd (43)
Cell stiffness, κ	0.3 × 10−3 to 1.0 × 10−3 dyne/μm	10−3 to 0.6 × 10−3 dyne/μm (44) red blood cells—fibroblasts
Normalized viscosity, μs	8 × 10−3 to 20 × 10−3 dyne per s/μm	Estimated from active force and 20 μm/min cell velocity (3)
Cell adhesion, ad	0 × 10−3 to 10 × 10−3 dyne	Estimated from surface tension measurements

The component forces that comprise the net force in Fig. 1B stem primarily from adhesive and elastic interactions with neighboring cells and are based on qualitative assumptions about the force, similar to the work of Evans (refs. 11 and 33; see also ref. 34). The adhesion force between two cells is attracting, and the magnitude depends on their proximity, because it determines how many adhesion molecules can bind. There is also a repulsive force that arises from a cell's resistance to deformation. Estimates of the magnitude of the adhesive and repulsive forces between cells are given in refs. 14, 15, 35, and 36.

Electron micrographs of multicellular tissues, for example of a Dd slug (37), show that there is little free space between cells: they deform so as to occupy it and as a result have a larger contact area than if they were restricted to ellipsoidal shapes as they are in the model. To compensate for this difference, the distance d between the surfaces of the two ellipsoidal cells at which the adhesive and repulsive forces balance is slightly negative. In light of this fact, d does not represent the actual distance between two adhering cell membranes, which is estimated to be ≈0.5 nm (38), but instead provides an estimate of how much surface area the cells have in common.

In addition to the active forces and the static passive forces, there are dynamic forces between cells or between a cell and the substrate. As cells move past one another, their contact area and the force caused by the breaking and reforming of bonds changes in time, and this nonequilibrium contribution is described as an apparent viscous drag force F_i^D per unit mass on the ith cell that depends on the relative velocity and common surface area between cells or between cell and substrate.

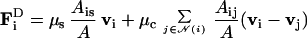1

Here, A_is or A_ij is the common surface area between cell i and the substrate or cell j, respectively; μ_s and μ_c are viscosity coefficients; 𝒩(i) denotes the neighbors of i; and A is the surface area of a spherical cell of the given volume.

Because cell movement is slow (the speed of a cell within a slug is only about 20 μm/min) and extracellular viscous forces are significant, we can ignore acceleration. As a result, the active, elastic, and adhesive forces are balanced by the drag force F^D, and the equations of motion have the following form.

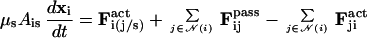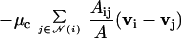2

Here, F_i(j/s) is the reactive force caused by the active force cell i applies to cell j or to the surface, and F_ij^pass and F_ji^act are the adhesive, elastic, and active forces from neighbor cells on cell i. The time-stepping algorithm is as follows. Assume we have a solution [x(t)_i,ẋ(t)_i]; to compute the position and velocity at (t + Δt), either we can use Eq. 2 to define a fixed-point iteration, or we can define an iterative procedure that updates the velocities as we sweep through the array of cells. We use the latter, and for any Δt, we do just one iterative step. Before each new time step, the cell order that is used in the sweep is randomized, which has been shown to minimize spurious results in cell automata models (39).

To describe the evolution of cAMP during aggregation, we use a model of the cAMP signal transduction and relay system that has been used previously to study other aspects of Dd aggregation (40, 47). The reaction-diffusion equation that governs the evolution of extracellular cAMP is solved on a regular grid over which the cells move. Cells are not restricted to grid points; therefore, cAMP is interpolated from the grid to each cell; the internal dynamics are updated to produce the cell's response to a given signal; and the cAMP released is transferred to the grid to produce the cAMP distribution for the next step. Details of the procedure are described in ref. 40. We can summarize the steps of the algorithm for moving the cells and updating cAMP as follows.

Step 1.

Locate all cells that are within a given distance of cell i.

Step 2.

Determine whether the cAMP levels are above threshold in cell i's neighborhood, and if so, find the direction of the highest cAMP concentration.

Step 3.

If necessary, orient the cell in the direction of the highest cAMP concentration.

Step 4.

Find the net forces that act on the cell because of interactions with the neighbor cells found in step 1; deform the three axes of the ellipsoid; and move the cell according to Eq. 2.

Step 5.

Repeat steps 1–4 for all of the cells.

Step 6.

Update the cAMP concentration and increment time.

In our model, the parameter values were chosen to lie within the observed ranges (see Table 1). Because these parameters are based on experimental measurements, changes made in the model parameters reflect a specific biological mechanism or property. Therefore, the model allows us to explore the effect these mechanisms have on the slug movement and how sensitive the system is to variations in the parameters.

Results

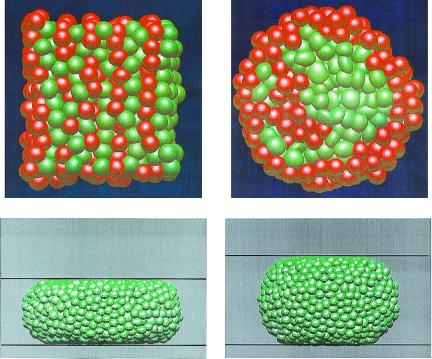
The model was first tested by simulating cell movement in the absence of chemotactic signaling by using two distinct protocols. In the first experiment, we studied sorting of two cell types in an aggregate on which no external forces are imposed. Here, the net force arises from differences in adhesive forces between the two cell types and from the random force. Fig. 2 Upper shows a typical sorting experiment. The green cells are more adhesive and therefore sort to the center by displacing the less adhesive red cells to the surface. Fig. 2 Upper Right shows the configuration after 200 min, which can be compared with sorting experiments reported in ref. 45. This result shows that the expected sorting occurs on a time scale comparable to that observed experimentally. We also investigated the effects of random movement of cells and cell stiffness on sorting. When the cells were made stiffer or the random force was reduced, the sorting time increased, and above some threshold, no sorting occurred. These experiments demonstrate the importance of cell deformability for cell sorting.

Figure 2.

(Upper) Cross section of an aggregate of 1,000 cells after 10 min and 200 min in the cell-sorting simulations. The self-adhesion between green cells is greater than that between red cells, and the latter are eventually displaced to the periphery. (Lower) The final configurations in simulations of 3,500 cells in an aggregate that is compressed between two parallel plates separated by a distance H of 65 μm (Left) and 90 μm (Right).

In the second protocol, we investigated the equilibrium shape of an aggregate of identical cells confined between parallel plates. The purpose of this investigation was to determine the force required to keep the plates separated by a fixed distance H and from this force, to determine the surface tension of the cellular mass. Fig. 2 Lower shows the final configurations in those simulations for two different values of H. The surface tension was then calculated from the geometric shape of the aggregate and the applied force on the plate (16). Even though the force on the plates differed in these two simulations (F = 420 nN and F = 1,300 nN for H = 90 μm and H = 65 μm, respectively) the calculated surface tension of 40 ± 10 dyne/cm in the two experiments was similar and lies within the range of the results reported earlier (36, 45, 46). These results and others to be reported elsewhere show that the multicellular aggregate has the properties of a viscoelastic fluid and can be compared with previous measurements by Steinberg and coworkers (36, 45, 46) by using the same configuration. The close agreement between the results of computational experiments and laboratory findings suggests that the model can reproduce the essential properties of multicellular systems and therefore can be used to investigate other aspects of cell movement in tissue-like aggregates. In the remainder of this article, we apply the model to chemotactic aggregation and slug movement in Dd.

We first investigated the aggregation of cells that are widely dispersed initially. In the following simulations, a few cells in the center of the field (shown in red in Fig. 3) are pacemakers. These pacemaker cells periodically initiate outward propagating cAMP waves that trigger relay of the cAMP signal and chemotaxis in the remainder of the aggregation territory. A rotating spiral cAMP wave can also organize aggregation; however, because pacemakers are easier to initiate and both types have been observed (3, 4), we chose to use pacemakers. Later, we shall study the effects of pacemaker and spiral signaling centers on cell movement, especially during the mound and slug stage. Fig. 3 shows the time series of a simulation of the aggregation. In this simulation, the number of computational “cells” is 2,500, but the cAMP output of each computational cell represents that of 16 real cells (see ref. 40 for details). This “stacking” is an approximation, but a similar simulation with 10,000 cells in which each cell is weighed by a factor of 4 produces similar results. Ideally, one would simulate each cell; and because we can do simulations with 10,000 cells and mounds can be made with far fewer cells, such a simulation is certainly feasible at later stages. However, to study stream formation in early aggregation in a larger territory at densities comparable to those used in laboratory conditions, we weighted the cells by a factor of 4 or 16. The animation of the computational results¶ shows both the evolution of streams during aggregation and how the pacemaker cells are lifted up by the inward motion of the other cells.

Figure 3.

Time snapshots of the aggregation of Dd cells in response to cAMP signaling from pacemaker cells that are located in the center (red cells). The time for the frames is 0 (Upper Left), 80 (Upper Right), 160 (Lower Left), and 320 min (Lower Right). The total number of cells is 2,500, but the cAMP output of each cell is weighted by 16.

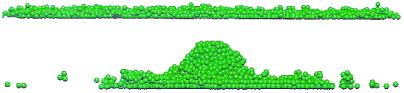
In these simulations, we assume that the cAMP distribution varies only in two space dimensions, and we maintain it uniform in the z direction. This assumption is sufficient during early aggregation, because the cell distribution is essentially 2D, but for mound formation and slug movement, a 3D model of cAMP diffusion between cells is needed. However, we found that mound formation can occur without any 3D chemotaxis and that cells at the center are pushed upward by the movement of the outer cells toward the center (Fig. 4).

Figure 4.

Cross sections of the aggregation field at t = 80 min (Upper) and t = 320 min (Lower).

We also studied the movement of a 2D slug to simulate recent experiments. Bonner (41) has created an essentially 2D slug experimentally by forcing slugs to move between a glass plate and a layer of mineral oil. His results show that many of the characteristic patterns of movement that are observed in 3D aggregates, such as rotary motion, also occur in 2D. To simulate this configuration, we placed cells in a single layer between two plates a cell diameter apart. The cell interactions with the plates were the same above and below, a result that differs from the experimental conditions. However, the results show that this difference is apparently not very significant. Initially the cells were arranged in a regular array, and a few pacemaker cells were placed at one edge of the array. As before, these cells initiate cAMP waves that are relayed throughout the slug, which begins to elongate and move forward. In the movie of this simulation,‖ one can clearly see the cells move forward in response to the cAMP wave emanating from the pacemakers, and this movement gives rise to a pulsatile motion of the slug.

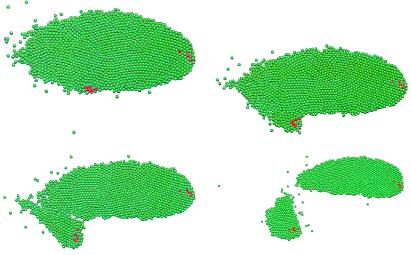
In the simulation shown in Fig. 5, we grafted another group of pacemaker cells onto one side of the slug after 50 min of migration. These pacemakers begin to send out cAMP signals and thus compete with the pacemakers at the anterior end. The animation shows a very strong rotary motion near the grafted pacemaker. Eventually, the signals from the grafted pacemaker dominate the signals from the anterior pacemaker, with the result that the slug splits up into two smaller slugs, each one controlled by its own pacemaker. Such splitting is common in grafting experiments with 3D slugs, but recently it has also been observed in 2D slugs (41). If the cell–cell adhesion is too strong, the slug does not split up, but instead, after some period of tug of war, one of the pacemaker centers eventually entrains the other, and the rest of the slug moves toward that center (results not shown).

Figure 5.

Movement of a slug with 2,500 cells organized by a few pacemaker cells at the front (red cells) at t = 60 (Upper Left), 80 (Upper Right), 100 (Lower Left), and 150 (Lower Right) min. Another pacemaker (also red) was introduced at the lower side at 50 min.

Often when a slug is moving straight ahead, the trajectories of all cells are straight (Fig. 6 Upper). However, when the active chemotactic force that a cell applies is increased, which usually increases their speed in the slug, the random cell movement can shift the pacemakers off center. This displacement causes the slug to turn, because the cAMP wave begins to curve, and the cells follow the wave. In such cases, the posterior cell tracks are straight, whereas the anterior cells often move in a more irregular fashion (Fig. 6 Lower). When the slug turns, the cells at the front begin to rotate around the pacemakers, and this rotation is much more than what is required for simple turning. This result demonstrates that rotational cell movement is possible even in response to a simple wave initiated by a pacemaker.

Figure 6.

Cell tracks corresponding to Fig. 5 Lower Right (Upper) and to a slug in which the active force is 150% of that shown in Upper (Lower)

One explanation for this result is that the lateral shift in the pacemaker position displaces the point of origin of the cAMP wave to one side of the slug. Consequently, cells on the side of the slug distal to the pacemaker move laterally and forward, thereby reinforcing the lateral shift, whereas those on the proximal side continue to move forward. Because the slug is held together by adhesion forces, this asymmetry causes the slug to turn and results in cell rotation around the pacemakers. This rotational “instability” is triggered by the axial asymmetry in cell movements; however, it usually dies out, and eventually the cells stop rotating. This explanation could be tested in the 2D slugs by using Bonner's experimental protocol as follows. It is believed that oxygen increases cell activity (48), and therefore, by changing the oxygen concentration on one side of the slug, one may be able to shift the pacemaker position laterally and determine whether this shift induces rotary motion at the tip. Alternatively, one may be able to mechanically displace the pacemakers at the tip with a micropipette.

Differences in the motive force exerted by cells may also play a role in turning the slug in vivo. In the preceding simulations, all cells have identical properties, and the observation that the cell tracks are often straight when the active force is at the normal level is not inconsistent with observations of more irregular cell movement that is seen at the tip in 2D slugs. In those slugs, the anterior cells move faster than posterior cells, and this difference may give rise to the irregular cell movement at the front, as has been suggested by Bonner (41).

To test this idea, we did simulations of a 2D slug comprised of two cell types, one of which exerts an active force that is 50% larger than the other. Initially these cell types were uniformly distributed in the slug. We discovered that even though the more powerful cells have a tendency to move toward the front, most of them had not sorted to the front at the end of 4 hours. In early aggregation, the result is quite different, because there the more powerful cells move about 50% faster and quickly move ahead of the wild-type cells. In these simulations, the adhesive forces were identical for both cell types, suggesting that when the cells interact strongly, as they do in the slug, simply exerting more force is not enough to produce rapid sorting. However, preliminary results suggest the sorting of the powerful cells to the front occurs much faster when the cells are more easily deformable. These results suggest that sorting of prespore and prestalk cells may be due more to adhesive differences and perhaps a higher cell deformability than used here, and less to differences in the motive forces exerted by each cell type.

Discussion

We have presented a model of cell movement and cell–cell interactions in multicellular systems and have applied it to cell movements in early aggregation and 2D slug movement in Dd. We have shown that the observed collective, coordinated motion of cells in Dd, from aggregation to slug movements, follows directly from the behavior of individual cells; no additional assumptions or mechanisms, such as the squeeze–pull mechanism (49), are necessary to produce motion of an aggregate. We are able to simulate large numbers of interacting cells, accounting for both the passive interactions caused by adhesion and the active locomotory forces, and we allow a restricted class of deformations of individual cells. Because the cells have realistic sizes, we can study the effects of cell size and cell deformability on cell sorting and motility, and we demonstrated how important cell deformability is for both chemotactic- and adhesion-driven cell sorting. When cells in the interior of a multicellular aggregate attempt to move, they can do so only by transmitting forces to the substrate through a connected set of cells, some of which are attached to the substrate. Because all of the forces are incorporated in our model, we can use it to understand the differences between movement in the interior of an aggregate and crawling on a substrate.

The cAMP signal in these simulations was restricted to 2D, but we found nonetheless that mound formation does occur, driven by the inward motion of the cells toward the pacemaker. It remains to be seen whether a more realistic treatment of the cAMP distribution in 3D has a significant effect on the pattern of movement of cells in the early mound. Certainly, the present model cannot account for the spiral patterns of movement observed in the mound.

Even though the wave pattern guiding the 2D slug motion was a spatially localized pacemaker, we could still observe irregular cell movements, such as the slug turning and the cells rotating around the pacemaker. These irregular cell movements became more pronounced when the cells moved at higher speeds. These simulations show that a simple wave may give rise to complex cell tracks because of the complex interaction between the cells.

We also did a number of simulations of the aggregation and slug stages in which we changed the cell adhesion and cell speed. We discovered that cell–cell adhesion affects stream formation rather dramatically. If cell adhesion is increased, the streams become wider, and localized small aggregation centers that become isolated from the cAMP signaling center often form. The increased adhesion also reduces the time it takes to form the mound. When there is no adhesion, the cells still aggregate and form a mound, but it is very loose and prone to “disassembling.” Adhesion also affects the cell movements in the 2D slug, in that the lower the cell adhesion the longer the slug becomes. When adhesion is very high, the slug becomes more rounded and when a second pacemaker is grafted to the side a second slug does not necessarily split off; rather, after some period of tug-of-war, one group of pacemakers wins, and the rest of the slug follows. These observations may be testable by using cells that overexpress or underexpress genes encoding for cell adhesion molecules.

When the active locomotive force that the cells apply is increased, the cell speed increases as well, and this increase affects the overall pattern and cell movements. When cell speed is high, streams do not form well, because cells tend to move directly toward the center, rather than joining into streams. In the 2D slug, a higher cell speed increases the likelihood of slug turning and rotary cell movements. Our simulations suggest that the turning of the 2D slug is due to a lateral shift in the pacemaker location and that this shift may occur naturally when cell speeds are high because of the random component of cell motion. This random shift in the pacemaker location might be one of the mechanisms responsible for the observed vertical pulsatile motion of the slug tip in a 3D slug.

We are grateful to D. Bottino and N. Wang for helpful discussions at various stages of the model development. This work was supported in part by National Institutes of Health Grant GM 29123 and National Science Foundation Grant DMS9805494.

Abbreviations

Dd

Dictyostelium discoideum

2D and 3D

two- and three-dimensional