Abstract
Resequencing genomic DNA from pools of individuals is an effective strategy to detect new variants in targeted regions and compare them between cases and controls. There are numerous ways to assign individuals to the pools on which they are to be sequenced. The naïve, disjoint pooling scheme (many individuals to one pool) in predominant use today offers insight into allele frequencies, but does not offer the identity of an allele carrier. We present a framework for overlapping pool design, where each individual sample is resequenced in several pools (many individuals to many pools). Upon discovering a variant, the set of pools where this variant is observed reveals the identity of its carrier. We formalize the mathematical framework for such pool designs and list the requirements from such designs. We specifically address three practical concerns for pooled resequencing designs: (1) false-positives due to errors introduced during amplification and sequencing; (2) false-negatives due to undersampling particular alleles aggravated by nonuniform coverage; and consequently, (3) ambiguous identification of individual carriers in the presence of errors. We build on theory of error-correcting codes to design pools that overcome these pitfalls. We show that in practical parameters of resequencing studies, our designs guarantee high probability of unambiguous singleton carrier identification while maintaining the features of naïve pools in terms of sensitivity, specificity, and the ability to estimate allele frequencies. We demonstrate the ability of our designs in extracting rare variations using short read data from the 1000 Genomes Pilot 3 project.
DNA sequencing is being revolutionized by new technologies, replacing the methods of the past decade. “Second Generation” sequencing currently offers several orders of magnitude better throughput at the same cost by massively parallel reading of short ends of genomic fragments (Mardis 2008). This enables addressing new questions in genomics, but poses novel technical challenges. Specifically, it is now feasible to obtain reliable genomic sequence along a considerable fraction of the human genome, from multiple individual samples. Such high-throughput resequencing experiments hold the promise of shifting the paradigm of human variation analysis and are the focus of this study.
Connections between genetic and phenotypic variation have traditionally been studied by determining the genotype of prescribed markers. This cost-effective strategy for large-scale analysis has recently led to multiple successes in detecting trait-associated alleles in humans (Wang et al. 1998; Risch 2000). However, genotyping technologies have two fundamental drawbacks: First, they are limited to a subset of segregating variants that are predetermined and prioritized for typing; second, this subset requires the variant to have been previously discovered in the small number of individuals sequenced to date. Both of these limitations are biased toward typing of common alleles, present in at least 5% of the population. Such alleles have been well characterized by the Human Haplotype Map (The International HapMap Project 2003) and have been associated with multiple phenotypes. On the other hand, rare alleles are both underprioritized for association studies, and a large fraction of them remain undiscovered (Reich et al. 2003; Brenner 2007; Levy et al. 2007).
Resequencing can fill in the last pieces of the puzzle by allowing us to discover these rare variants and type them. Particularly, regions around loci that have previously been established or suspected for involvement in disease can be resequenced across a large population to seek variation. However, finding rare variation requires the resequencing of hundreds of individuals: something considered infeasible until now. With the arrival of low-cost, high-fidelity, and high-throughput resequencing technology, however, this search is feasible, albeit expensive. Illumina's Genome Analyzer (Gunderson et al. 2004), ABI's SOLiD sequencer (Fu et al. 2008), 454 Life Sciences' (Roche) Genome Sequencer FLX (Margulies et al. 2005), to name a few, are the current primary technology providers offering throughputs on the order of giga base pairs in a single run (Mardis 2008).
Resequencing is typically done on targeted regions rather than the whole genome, making throughput requirements to sequence an individual much less than what is provided by a single run. A costly option is to utilize one run per individual, but in a study population of hundreds or thousands, such an approach is prohibitively expensive. In such cases, “pooled” sequence runs may be used.
The central idea of pooling is to assay DNA from several individuals together on a single sequence run. Pooled Genotyping has been used to quantify previously identified variations and study allele frequency distributions (Shaw et al. 1998; Ito et al. 2003; Zeng and Lin 2005) in populations. Given an observed number of alleles and an estimate of the number of times an allelic region was sampled in the pool, it is possible to infer the frequency of the allele in the pooled individuals being studied. Pooled resequencing can be used to reach similar ends, with the added advantage of being able to identify new alleles. At least one recent work has analyzed the efficacy of pooled resequencing for complete sequence reconstruction (Hajirasouliha et al. 2008). The investigators of that work studied the problem of reconstructing multiple disjoint regions of a single genome while minimizing overlap between regions. Our work addresses the problem of identifying rare variations contained within a single region across multiple individuals.
Historically, the primary trade-off of a pooled approach has been the inability to pinpoint the variant carrier from among the individuals sequenced in a pool. Retracing an observed variant back to its carrier required additional sequencing (or genotyping) of all of these individuals, one at a time. Barcoding is an upcoming experimental method that involves ligating a “signature” nucleotide string (∼5 bp) to the start of all reads belonging to an individual. These nucleotides serve as the barcode that identifies which individual a given sequenced read came from. If/when established, barcoding technology may essentially offer a more complex assay for a wetlab solution to the same problem we address through computational means.
The central idea behind our overlapping pool design is that while sequencing DNA from several individuals on a single pool, we also sequence DNA from a single individual on several pools. Individuals are assigned to pools in a manner so as to create a code: a unique set of pools for each individual. This set of pools on which an individual is sequenced defines a code word, or pool signature. If a variation is observed on the signature pools of one individual and on no other, then we identify the carrier of the variation. For example, consider a study where a single proband X is part of a cohort of one hundred individuals being resequenced for the same genomic region. Out of 15 pools used by the study, assume that Xs DNA is sequenced on pools 1, 3, and 7, such that no other individual in the cohort has been sequenced on the same three pools. A variation uniquely recorded on these three pools is likely to be carried by X, and only by X. Code-based pool assays like this have been studied before. In particular, we extend and apply principles developed in other contexts of pooling, such as genotyping (Pe'er and Beckmann 2003; Beckman et al. 2006) and de-novo sequencing (Cai et al. 2001; Csuros et al. 2003).
The balance of this work is organized as follows: In the Methods section, we first introduce a generic mathematical model that can be used to represent the pooled resequencing process. We develop figures of merit to evaluate a pool design's robustness to error, and coverage under given budgetary constraints. We then propose two algorithms for pool design: logarithmic signature designs and error-correcting designs. In the Results section we compare the efficacies of our designs against each other and against current practices using synthetic data as well as real short-read data from the 1000 Genomes Pilot 3 project (www.1000genomes.org), where we quantify the abilities and trade-offs of the designs. A significant part of our analysis deals with the errors and noise introduced at various stages in the pooled resequencing process. We summarize our contributions in the Discussion section.
Methods
Terminology
A resequencing experiment is characterized by the target region and a cohort. We consider a cohort I = {i1,…,iN} of N diploid individuals. These individuals are to be sequenced for a target region of L base pairs using R pools (or sequence runs) labeled P = {P1,… ,PR}. Each pool offers a sequencing throughput of T base pairs mapped to the reference sequence. A key factor in such an experiment is the mean expected coverage of diploid individuals in the cohort. This is the number of reads Ĉ in which each haploid nucleotide of that individual is expected to be observed, summed over all pools, and averaged over all individuals and sites. Mean expected coverage is given by:
We introduce notation for a pool design as an R × N binary matrix, D
We further define notation for column and row sums of the design matrix: For each pool p we denote the number n(p) ≡ ∑iDp,i of individuals in that pool; for each individual i we denote the number k(i) ≡ ∑pDp,i of pools with that individual. Whenever n(p) and k(i) are constant, as will be evident from context, we shall omit the parameters p and i, respectively.
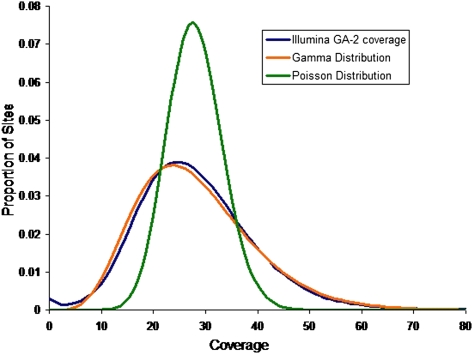
This setup facilitates a discussion of expected coverages of sites across several parameters. The actual coverage, or number of reads that observe a particular nucleotide x on a single haplotype of individual i in a pool p, is a random variable Cp,ix with mean 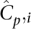 across all sites x ∈ L. The distribution of this random variable around its mean may be technology specific. We demonstrated elsewhere (Sarin et al. 2008) that Cp,ix for Illumina's short read alignments mirror the Gamma distribution (see Fig. 5, below).
across all sites x ∈ L. The distribution of this random variable around its mean may be technology specific. We demonstrated elsewhere (Sarin et al. 2008) that Cp,ix for Illumina's short read alignments mirror the Gamma distribution (see Fig. 5, below).
Figure 5.
Observed distribution of coverage of Illumina's Genome Analyzer-2 with a mean coverage 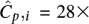 over a 4-Mbp region of C. elegans. The distribution best fits a Gamma distribution Γ(α,β) with shape parameters α = 6.3 and
over a 4-Mbp region of C. elegans. The distribution best fits a Gamma distribution Γ(α,β) with shape parameters α = 6.3 and 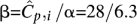 . A Poisson distribution is also shown in the figure to compare fits. These results have also been reported by the authors in Sarin et al. (2008).
. A Poisson distribution is also shown in the figure to compare fits. These results have also been reported by the authors in Sarin et al. (2008).
The mean expected coverage of each haplotype of the diploid individual i in a particular pool p is
 |
Using Equation 3, we normalize the binary entries of D (presence or absence of a site on pool p) to formulate D′ (expected coverage of a site on pool p):
Summing over a column of D′, we get the expected coverage of a site from an individual accumulated over all pools as 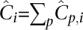 . Likewise, summing across a row gives the expected coverage of a site across all individuals on the pool
. Likewise, summing across a row gives the expected coverage of a site across all individuals on the pool 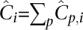 . Finally, the expected cumulative coverage of a site across the whole populations in the pooled arrangement,
. Finally, the expected cumulative coverage of a site across the whole populations in the pooled arrangement, 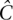 satisfies
satisfies
 |
Next, we model the sequence of alleles carried by individuals in I as an N × L matrix M. Each element Mi,x can take on the values {0, 1, 2} to register how many copies of the minor allele are present in the diploid genome of i at site x. M is the ground reality: It is not known to us a priori, but rather is what we wish to ascertain. Reconstructing as much of M as possible is the objective of this work.
Lastly, our expected sequencing results are captured by an R × L matrix E of nonnegative integers. The pool design, ground truth, and expected results are linked by the equation
Each entry Ep,x is a tally of the expected number of minor alleles at site x across all individuals in pool p.
Design properties
As a first step toward successfully designing overlapping pools, we focus on engineering D, such that it satisfies the following properties of a good design as best as possible.
Property 1: D retains carrier identity
This property states that D must have unique column vectors. Since unique columns serve as unique pool signatures of each individual in the cohort, matching the occurrence pattern of a variant in E to a column vector in D suggests that the variant is carried by the individual associated with that column. Therefore, the design matrix D needs to have at least N unique columns.
Pool signatures for all individuals in the cohort may be defined through a function 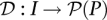 mapping individuals to sets of pools. Here,
mapping individuals to sets of pools. Here,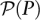 denotes the power set (set of all subsets) of P, while the pool signature of individual i is denoted
denotes the power set (set of all subsets) of P, while the pool signature of individual i is denoted 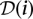 . Formally, the pool signature is defined as the set:
. Formally, the pool signature is defined as the set: 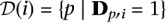 .
.
Property 2: D achieves an equitable allocation of sequencing throughput
All else being equal, there is an equal probability of observing a rare variant carried by any individual in the cohort. It can therefore be shown that any unequal allocation of throughput (coverage) to certain individuals increases the overall probability of missing a variant in the population (see Appendix). While there may often be biological motivation to focus on certain sites (for example, where variation is known or expected to be functional), current technological limitations restrict selective allocation of coverage within the region of interest.
Additionally, the goal of resequencing includes discovery of rare variants, rather than investigating sites that are already known to be polymorphic. We therefore assume no such deliberate preferential coverage, and our aim is to cover all 2L sites in each of N diploid individuals as equally as possible using the P pools at our disposal.
One direct way to achieve equitability would be for the throughput of each pool to be divided equally by the individuals sequenced on it, and the number of pools assigned per individual is constant. In other words, ∀i, k(i)=k and ∀p, n(p)=n Summing coverage assigned to an individual over all of the pools it is sequenced in, we then get
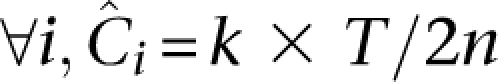 |
Property 3: D is error tolerant
Modeling the empirical errors introduced into pooled resequencing requires review of the different experimental stages and their associated sources of error. The first step in targeted resequencing experiments is typically pulldown of the target genomic region by standard direct PCR with primers for each amplicon, or by tiling oligonucleotide probes and universal amplification. For pooled resequencing, we assume that the entire pool is amplified in a single reaction. The region of interest is then randomly sheared into short library fragments, which are then single-molecule amplified and end-sequenced. Such sequencing protocols provide millions of single or paired-end reads, which are computationally mapped against the reference genomic sequence. Errors occur during several stages, depending on the sequencing technology. A good pool design should account for errors introduced at each stage and use the redundancy of information in high-throughput sequencing for robustness against such errors.
Modeling error
We now quantify errors that occur in the sequencing process within the framework of our model. Equation 6 represents an ideal pooling arrangement, where each value Ep,x is an expectation of the number of rare alleles we should observe. In reality, the observed number of alleles at Ep,x is a random variable whose mean is the corresponding expectation. The reason for this randomness is a variety of errors that can cause differences between the expectation and observation. We address three primary sources of error: read error, error due to undersampling, and error during amplification (PCR).
Read error
Sequence read errors that cause consensus mismatches occur anywhere in the range of one per 50–2000 bases (Smith et al. 2008). These are more likely to occur at nonvariant sites, and therefore show up as false-positives, than occur at variant sites, and be observed as false-negatives. Traditionally, sequence assembly methods (Li et al. 2008) have used base-call quality of reads to assess veracity of base calls across multiple reads. However, in the absence of long-established support of the base-call quality used by current technologies, likelihood may still be evaluated by requiring a minimum threshold t of reads that report a variant in order to call it a variant. We assume that this read error occurs at the technology dependent rate of errread per base pair and is uniform across all pools.
Undersampling error
An individual i is said to be undersampled at base x if Cix is too small to confidently call x. Undersampling is intrinsic to all shotgun sequencing, whether pooled or single sample (Lander and Waterman 1988). However, pooled experiments are generally carried out due to cost/throughput constraints with coverage distributions more prone to undersampling than traditional sequencing (Smith et al. 2008). We define a site to be undersampled if it is read less than t times. The distribution of Cix is therefore key for quantifying undersampling. We propose the density of the Gamma distribution (Sarin et al. 2008) at integer values of coverage as an approximation of the distribution of practical coverage (see Fig. 5, below). The shape parameters for this distribution that we use in our analysis are elaborated in the Appendix.
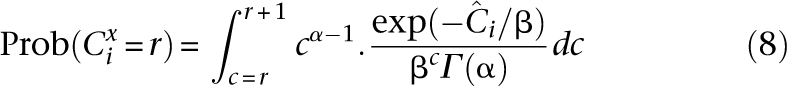 |
The number of undersampled sites is therefore:
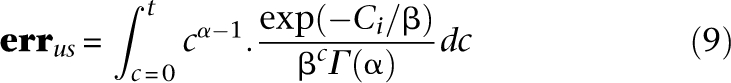 |
Equation 9 applies to pools just as well as to single-sample sequencing: The parameters that determine undersampling remain unchanged. Furthermore, it applies to overlapping pools, with the mean coverage across pools 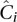 still determining undersampling probability, even if the individual coverage per pool is smaller than naïve pooling.
still determining undersampling probability, even if the individual coverage per pool is smaller than naïve pooling.
These principles are best demonstrated by an example. Consider a naïve pool design that offers 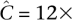 coverage to each pooled individual and recommends an undersampling threshold of t = 3×. In other words, if we observe a variant less than three times, we do not make a confident call. The probability of undersampling a site in this case is relatively small: (Pr[Ci < 3] = 0.3%). However, to accommodate an overlapping pool design within the same resources as a naïve pool design, we would have to distribute total available throughput Ci over the k pools that an individual i occurs in. If our design leads us to sequence each individual of our experiment in k = 3 pools, then our per-pool coverage would be
coverage to each pooled individual and recommends an undersampling threshold of t = 3×. In other words, if we observe a variant less than three times, we do not make a confident call. The probability of undersampling a site in this case is relatively small: (Pr[Ci < 3] = 0.3%). However, to accommodate an overlapping pool design within the same resources as a naïve pool design, we would have to distribute total available throughput Ci over the k pools that an individual i occurs in. If our design leads us to sequence each individual of our experiment in k = 3 pools, then our per-pool coverage would be 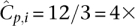 . The chance of undersampling at the given threshold in a specific pool is now high: Pr[Cp,i < 3] ≈ 29%, yet, base calling that is aware of the pool design can distribute the t observations required for calling a new variant across all k pools to formulate a new threshold
. The chance of undersampling at the given threshold in a specific pool is now high: Pr[Cp,i < 3] ≈ 29%, yet, base calling that is aware of the pool design can distribute the t observations required for calling a new variant across all k pools to formulate a new threshold 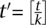 , justifying the same probability of undersampling.
, justifying the same probability of undersampling.
Note that if a variant fails to be observed at all in a particular pool, the signature of its carrier will not be observed accurately, although the presence of the variant will be detected.
Amplification error
These errors occur when PCR chemistries erroneously introduce variants like base substitutions in the replicated DNA (Freeman et al. 1999; Raeymaekers 2000; Huggett et al. 2005). Depending on the enzymes and protocols used, these errors range in frequency from traditional specifications of errpcr = 10−4 errors per base pair to negligible magnitude for high-fidelity chemistries (of the order of errpcr = 10−6 errors per base pair). In pooled resequencing, PCR is most economically pooled as well, and PCR errors may affect multiple reads in that pool. In principle, overlapping pools, each involving separate amplification, are more robust to PCR error, as the error would be introduced to only a small fraction of the independent pools in which a particular individual participates. Empirically, we observe that practical PCR error rates are negligible enough to be ignored compared with other sources of errors.
Pool designs
We now propose a few pool designs in the context of the proposed framework. We demonstrate how our designs quantifiably appease the outlined properties to a greater extent than a naïve pooling strategy.
Logarithmic signatures
The binary representation of numbers {1,…,N} uses bitwords of size log2N. One potential design is to use an encoding function 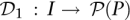 , where each signature
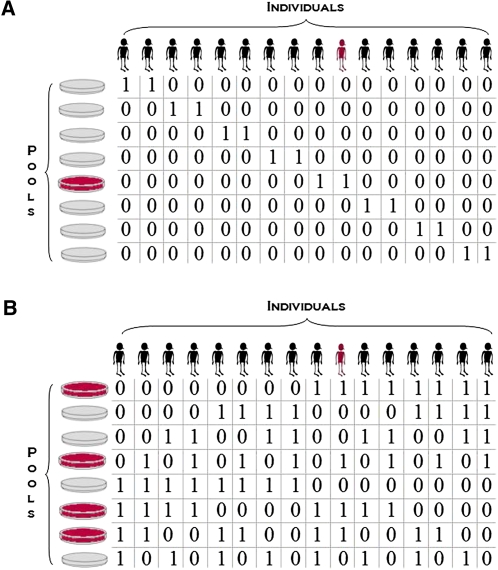
, where each signature 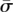 is one of N unique bitwords. For example, a small study cohort of 16 individuals would require log216 = 4 pools to generate unique signatures as shown by the first four rows of Figure 1B. The encoding clearly maintains carrier identity: A variant noticed only in pools {1, 3} points to individual 11, whereas a variant observed on {1, 3, 4} is carried by individual 12, and so on. However, not every individual is sequenced on the same number of pools through this scheme (individual 1 is not on any of the first three pools for that matter).
is one of N unique bitwords. For example, a small study cohort of 16 individuals would require log216 = 4 pools to generate unique signatures as shown by the first four rows of Figure 1B. The encoding clearly maintains carrier identity: A variant noticed only in pools {1, 3} points to individual 11, whereas a variant observed on {1, 3, 4} is carried by individual 12, and so on. However, not every individual is sequenced on the same number of pools through this scheme (individual 1 is not on any of the first three pools for that matter).
Figure 1.
Resequencing with naïve and log pool designs. (A) A total of 16 individuals are divided into groups of two and pooled; (B) 16 distinct pool signatures are created using just eight pools. In both cases, the pools on which the variant appears and the variant carrier are marked in crimson.
We revised the design to satisfy the equitability property by appending the 1's complement of each word to itself, represented by the last three rows of Figure 1B. The resulting signatures require 2 × log2N pools. Observe that each individual in this example is now pooled on exactly four out of eight pools. The ratio of the number of individuals sequenced to the number of pools utilized is given by the code efficiency:
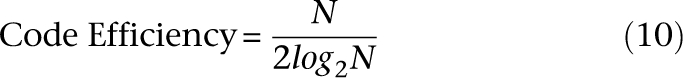 |
which grows with N. This schema is extendible to θ-ary encodings as follows. Each of the N individuals is uniquely indexed base-θ by logθN numerals in the range {0, 1, … , θ − 1}. A base θ numeral is then mapped to its unique binary signature given by its corresponding vector from the standard basis of order θ. In other words, first numeral 0 to first θ-bit basis vector 0…0.001, numeral 1 to vector 0…010, numeral 2 to vector 0…100, and so on. A total of θlogθN pools are required to construct the design. For the general case:
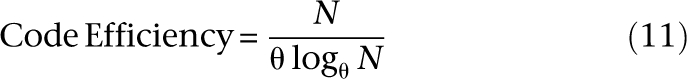 |
The continuous version of this expression maximizes at θ = e, and for natural θ = 3 (ternary encoding). We call this family of encodings “logarithmic signature designs,” because the design uses the order of a logarithmic number of pools in the size of the study cohort.2
Regardless of undersampling, determining allele frequency is no more difficult than with a naïve pool design. The total number of copies of a site x sequenced across all pools is 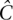 (Equation 5). If m minor alleles are observed cummulatively, then assuming equitable coverage (Property 2), we deduce the maximum likelihood estimate of the allele frequency
(Equation 5). If m minor alleles are observed cummulatively, then assuming equitable coverage (Property 2), we deduce the maximum likelihood estimate of the allele frequency 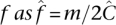 .
.
More often than not, N may not be a perfect power of any integral value θ. In such a case, we may not use the entire spectrum of θ-ary signatures (e.g., in a study of only 14 out of 16 individuals in Fig. 1B). The result is that some pools may sequence fewer individuals than others (i.e., n(p) is not constant), violating the equitable coverage dictum. However, by the nature of the design, this variation of n(p) across pools is restricted to 1. In such a case, allele frequency calculations are normalized as 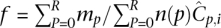 , where ∑pmp = m.
, where ∑pmp = m.
Error-correcting signatures
While economical, logarithmic signatures fail to satisfy Property 3. They are prone to ambiguous carrier identity in the presence of false-negative variant calls. For example, in the design illustrated in Figure 1B, individual 1 is sequenced in pools {5, 6, 7, 8}. Suppose the variant call is a false-negative in pool 8 due to undersampling, but is observed on all others. The resulting “incomplete” signature {5, 6, 7} is not sufficient to unambiguously identify the carrier as individual 1. In fact, it is equally likely that individual 2 undersampled in pool 4 elicited such an observation. In the general case, a false-negative call in a θ-ary signature ambiguates precisely θ individuals as potential carriers.
We now develop error-correcting designs that are able to unambiguously identify the variant carrier, even in the presence of false-negatives. Borrowing from results in coding theory (Sloane and MacWilliams 1977), we formulate a one-to-one mapping 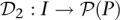 that retains identity in the face of false-positives. Consider an individual I with a pool signature
that retains identity in the face of false-positives. Consider an individual I with a pool signature 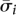 . Intuitively, undersampling error can be identified and corrected if the incomplete signatures resulting from the loss of “1” bits in
. Intuitively, undersampling error can be identified and corrected if the incomplete signatures resulting from the loss of “1” bits in 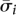 .all continue to point to the same individual i. Rather than associating an individual with a single signature, such a design reserves an entire set of signatures within an “error-space” of
.all continue to point to the same individual i. Rather than associating an individual with a single signature, such a design reserves an entire set of signatures within an “error-space” of 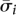 to individual i. This error space is the set of all the signatures {
to individual i. This error space is the set of all the signatures {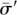 } generatable by converting up to some ∈ < k(i) number of “1”s to “0”s in
} generatable by converting up to some ∈ < k(i) number of “1”s to “0”s in 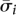 The larger the ∈, the more signatures reserved per individual, and consequently, the fewer individuals we can multiplex into the pool design. This is the trade-off between efficiency and error correction. With a fixed number of pools at its disposal, an error-correcting design has to maximize the number individuals it can identify while maintaining a disjoint error space.
The larger the ∈, the more signatures reserved per individual, and consequently, the fewer individuals we can multiplex into the pool design. This is the trade-off between efficiency and error correction. With a fixed number of pools at its disposal, an error-correcting design has to maximize the number individuals it can identify while maintaining a disjoint error space.
An estimate of the expected coverage of each site Cp,ix also allows us to calculate the expected number of pools on which a site x of i may be undersampled: e = k × Pr[Cp,ix < t′].We may then choose an error-correcting scheme that can handle up to e false-negatives by setting the parameter ∈ ≥ e. By definition then, a variant observed in as few as q = k−∈ out of k pools is sufficient to identify the carrier individual.
A fixed-length block code assigns each individual in a set I = {i1,…,iN} to code words such that each code word is of the same length (but not necessarily the same Hamming weight). Logarithmic signatures are a type of fixed-length block code without error-correction ability. There is an extensive theory regarding such codes that do offer error correction. Extended binary Golay codes (EBGC) are such a type of error-correcting block code. Formally, the EBGC consists of a 12-dimensional subspace of the space 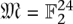 over the binary field
over the binary field 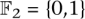 , such that any two elements in
, such that any two elements in 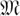 differ in at least eight co-ordinates. The code words of
differ in at least eight co-ordinates. The code words of 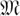 have Hamming weight 0, 8, 12, 16, or 24. To satisfy Property 2, we only use those code words of Hamming weight 8 (i.e., every pool signature assigns its individual to exactly eight pools). These code words of weight 8 are elements of the S(5, 8, 24) Steiner system. The error space of these Hamming weight 8 code words is a hypersphere of radius ε = 3. In other words, all signatures generated by up to three false-negatives of
have Hamming weight 0, 8, 12, 16, or 24. To satisfy Property 2, we only use those code words of Hamming weight 8 (i.e., every pool signature assigns its individual to exactly eight pools). These code words of weight 8 are elements of the S(5, 8, 24) Steiner system. The error space of these Hamming weight 8 code words is a hypersphere of radius ε = 3. In other words, all signatures generated by up to three false-negatives of 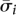 are reserved for the individual i.
are reserved for the individual i.
EBGC has 759 code words of Hamming weight 8. We therefore repeat this coding separately for [N/759] subsets of the individuals. We note that similar to logarithmic signatures, equitable coverage (Property 2) holds for specific values of N, which in this case its values are divisible by 759. For other values, coverage is only approximately equitable, as different pools may accommodate different numbers of individuals.
Results
We assessed the performance of our designs by simulating pools of short read data. We downloaded short read sequences from the 1000 Genomes Pilot 3 project (www.1000genomes.org) that were available on the Short Read Archive (SRA) in January, 2009. The 1000 Genomes Pilot 3 project states that it is a targeted sequencing of the coding region of ∼1000 genes, while the SRA annotates it as sequence from 1000 to 2000 gene regions and conserved elements (5 KB average length), giving an expected total of 5 Mbp sequence. Illumina runs from 12 individuals, sequenced using single-end, 51-bp read-length libraries, were selected. We created a 123.4-Mbp region of interest from the Human Genome, as outlined in the Supplemental material. The individuals show between 4.2 and 5.3 Mb of mapped sequence with ≥3× coverage, with the notable exception of one individual. From the coverage profile, we verified that the exception was due to poor fidelity/low scoring reads for that run, possibly due to experimental error. Merging the coverage of all individuals, we identified 6.41 million unique sites of high significant coverage.
We constructed two simulated pool designs of 12 individuals on eight sequencing lanes by mixing reads from multiple individuals as detailed in the Supplemental material. Reads for individuals and pools were then independently aligned against the same 123.4-Mbp reference using MAQ (Li et al. 2008), and SNPs were called on the alignment. Since available algorithms call alleles under the assumption that they are looking at reads from a single individual (allele frequency 0, 1, or 2), we built our own SNP-calling algorithm for pooled data (refer Supplemental Methods and Analysis). A combined total of 13,022 single nucleotide variants were detected across the 123.4-Mbp region in the identity design (i.e., combining independent calls made on each of 12 data sets), of which 10,668 were detected by log pools and 10,868 by ECC Pools. Both designs demonstrate a high-fidelity allele frequency prediction, as evidenced by data outlined in the Supplemental material.
Based on the pool signature of each detected variant, we associated a distribution over possible carrier individuals. Out of a total of 8618 singletons and doubletons, log pools detected 6270 of these variants, while ECC pools detected 6478 of these variants (refer to the table in Supplement on Allele Detection). In truth, we ascertained (using the 12 data sets) that 5332 of the variants detected by log pooling had a single carrier (either homozygous causing singleton or heterozygous causing doubleton), while 5539 of the variants detected by ECC pools had a single carrier individual.
At each of these sites, our algorithm uses the variants pool signature to output a set of equally likely candidate individuals (uniform distribution) to be the variant carriers. Log pools associated 4798 variants with a candidate carrier distribution, while being unable to assign the rest. Likewise, ECC pools assigned 5060 variants with a distribution. In some cases, the call is ambiguous (multiple individuals are given a uniform probability of being potential carriers), while in other cases, the design identifies a single variant carrier.
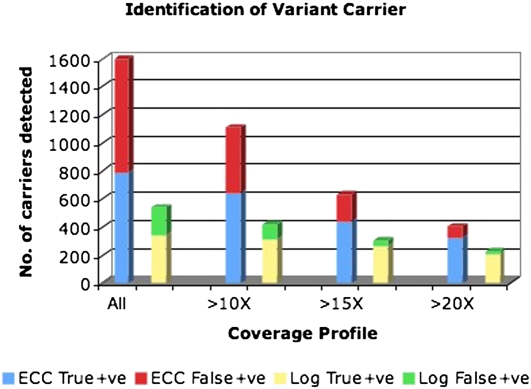
Of these calls, 3130 distributions in log design captured the correct individual as one of the prospective carriers, while 2907 distributions in ECC design captured the same. Some variants strongly identified single individuals as their carriers instead of offering a distribution over multiple prospective individuals. The degree of correctness of these calls show a strong correlation to what coverage the site enjoyed on the carrier individual's data set (and, consequently, on the pools in which the individual was sequenced). Figure 2 shows the relative abilities of ECC and log pools to identify carrier individuals. The results confirm our hypothesis that error-correcting designs enjoy a considerable advantage in terms of numbers of correct calls.
Figure 2.
Identification of carriers. For log pools, 345 out of a total of 539 single carrier identifications were correct across all coverage profiles, 311 out of 421 were correct (≥15× coverage), 266 out of 302 were correct (≥15× coverage), and 206 out of 223 were correct (≥20× coverage). For ECC pools, 783 out of a total of 1597 single carrier identifications were correct across all coverage profiles, 637 out of 1109 were correct (≥10× coverage), 441 out of 633 were correct (≥15× coverage), and 321 out of 405 were correct (≥20× coverage).
In the absence of a suitable paired-end data set, we were unable to assess the ability of our designs to characterize structural variants like indels, copy-number changes, and transposons.
We also assessed the performance of our pool designs on synthetic data. In particular, the logarithmic and error-correcting pool designs were compared against a no-pooling strategy (one individual per pool), and the barcoding strategy. Naïve pooling does not claim to establish carrier identity in the first place, and therefore is irrelevant as a benchmark for these results.
We ran our simulations to identify rare mutations on 500 human individuals, each harboring a targeted region of interest whose size we varied from 300 KB to 3 MB. We pooled these individuals over 24 sequence runs, mirroring eight lanes on three Illumina GA-2 machines. Each sequence run was given a throughput of 0.5-Gbp mapped sequence, resulting in a total throughput offering of 12 Gbp. This translated to a realistic expected per-haplotype coverage range of 40× to 4× per individual for the corresponding RoI sizes.
Recent literature (Levy et al. 2007) suggests that ≈518 K high-confidence variations were found in a newly sequenced genome, which were undocumented in dbSNP, giving a genome-wide approximate new variation incidence rate of 1 in 6.5 Kbp. Assuming most of these variants occur at a 1% allele frequency in the general populace, we approximate the likelihood of a singleton in a 500 individual (1000 chromosome) cohort to be one in 65 Kb. We randomly inserted mutations at this rate to the data set, and further subjected it to PCR and read error. From the resulting noisy observations Eobs, we predicted a reality matrix Mpredict, which we then compared against the ground truth.
The no-pooling scheme was used to sequence 24 individuals chosen at random from the 500 individual cohorts. The EBGC scheme uses 24 pools to generate up to 759 code words as discussed earlier. We used the first 500 of these in lexicographic order. We used a value of θ = 8 for logarithmic designs; consequently, also giving us a total of 8[log8 500] = 24 pools. Barcoding also used 24 pools, albeit, effectively simulating 500 distinct pools from their cumulative throughput. Each individual was offered a pool of T/N = 1 Mbp. Figures 3 and 4 show a summary of the recovery statistics.
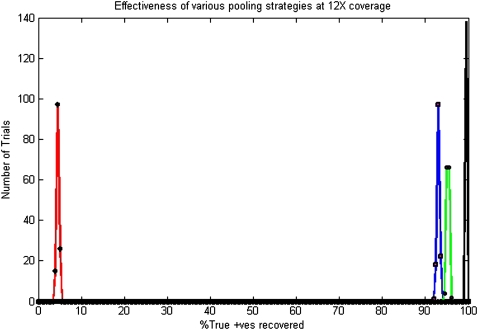
Figure 3.
Distribution of performance at 12×. Color coding indicates red for no pooling, blue for logarithmic designs, green for error-correcting designs, and black for barcoding strategy. Since we are only able to sequence 24 individuals on 24 pools in the absence of a pooling strategy, only ≈5% singleton variants are observed (and consequently recovered). Logarithmic pooling recovers ∼94% singletons, while error-correcting code recovers ∼96% singletons. Barcoding outperforms both pooling strategies, recovering ∼100% singletons in all cases.
Figure 4.
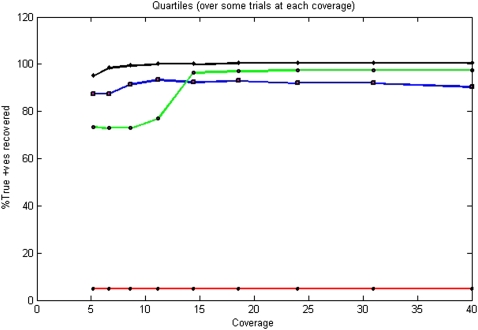
Performance across coverage. Color coding indicates red for no pooling, blue for logarithmic designs, green for error-correcting designs, and black for barcoding strategy. In the absence of a pooling strategy, since we only observe 24 out of 500 individuals, most variations are missed. The base-8 logarithm signatures perform well throughout since total coverage is only distributed among three pools, giving a high mean-per-pool coverage. Golay error-correcting code performs better than logarithmic code at high coverage despite the coverage being divided among eight pools, with error correction offering better response. However, they suffer declining performance toward the lower end of the spectrum when per-pool coverage becomes unsustainable. Barcoding outperforms the designs under most conditions.
Discussion
In this study we tackle the design of resequencing pools, a very current challenge for large-scale analysis of genetic variation. To the best of our knowledge, this is the first attempt to develop a framework for the design of such pools. We were able to represent real experimental error (as observed on Illumina Genome Analyzer-2 runs) within this framework. We introduced a few properties that represent quantitative figures of merit by which any pooling scheme may be judged. Finally, we presented two original design schemes: logarithmic design and error-correcting design. Each scheme demonstrated a unique set of advantages and disadvantages, but both held much promise compared with a naïve pooling strategy. A comparison between our two designs themselves reveals that they are both valid approaches, each suited for a varying set of requirements. Table 1 summarizes the characteristics of the different designs currently available to the experimentalist.
Table 1.
Summary of design characteristics
In fact, logarithmic signatures are appropriate when undersampling is a negligible consideration. If there is a relatively high-per-pool throughput available vis-à-vis the amount of DNA to be sequenced, a scenario that marginalizes considerations of false-negatives, logarithmic designs offer the most promise to find rare variation. Error-correcting designs are best suited for more trying experimental conditions, when large population studies must be done within minimal resources. These designs can effectively identify variant carriers in spite of noisy signals, but concomitantly run the risk of assigning lesser sequencing throughput to other carrier individuals in the cohort.
Our results indicated that both error-correcting designs and logarthmic designs detect most of the variation in the cohort, with fidelity and ability both dropping as a function of coverage. Our algorithms currently do not attempt to determine carrier identity of more common variations that might have higher incidence (doubletons, tripletons, and polytons), and will be the subject of future work.
In conclusion, our proposed framework motivates both analytical and experimental downstream studies. Analytically, this study focused at identification of rare mutation carriers. Information content in the pooled sequences may facilitate such recovery, particularly if samples are known to be related and carry variants identical by descent at the resequenced locus, as demonstrated for genotype pools (Beckman et al. 2006). Our computational contribution is particularly useful for characterizing human variation by enabling pooled resequencing studies to be conducted with overlapping pools.
Acknowledgments
S.P. was supported in part by NSF CCF 0829882; I.P. was supported in part by NIH 5 U54 CA121852. We also acknowledge the 1000 Genomes Pilot 3 project.
Appendix
Equitable distribution
Equitable distribution mandates an equal coverage to all pooled individuals in order to maximize the probability of observing a rare variant and identifying its carrier. This may be seen as follows: Consider a pooling of two individuals a and b, given unequal overall coverages 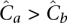 . By Equation 9, we get a total number of FNs for a site as
. By Equation 9, we get a total number of FNs for a site as
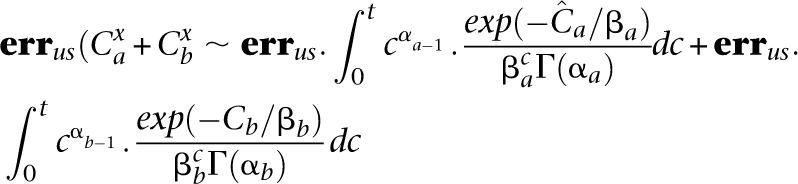 |
where αa = α = 6.3, while βa < βb by Equation 8. Under equitable allocation 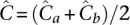 , it may be shown that 2. errus·Cx< errus·(Cax+Cbx). That is,
, it may be shown that 2. errus·Cx< errus·(Cax+Cbx). That is,
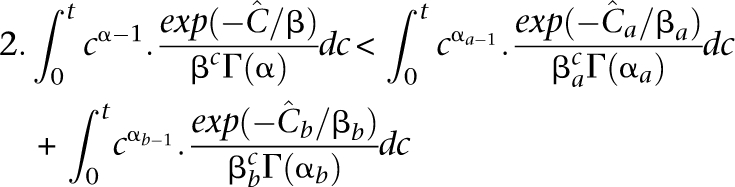 |
For example, if individual a has an overall coverage 8×, while individual b has overall coverage 4×, their independent undersampling rates at threshold 2 are 0.3% and 7.7%, respectively. However, at a mean coverage of 6× across both, the probability of a FN is 1.4%.
Footnotes
We note that as a very broad generalization, R pools could potentially assign unique signatures to 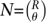 individuals, where each individual is sequenced on θ pools. Choosing one set of signatures over another is often a case specific analysis of the trade-offs involved.
individuals, where each individual is sequenced on θ pools. Choosing one set of signatures over another is often a case specific analysis of the trade-offs involved.
[Supplemental material is available online at www.genome.org.]
Article published online before print. Article and publication date are at http://www.genome.org/cgi/doi/10.1101/gr.088559.108.
References
- Beckman KB, Abel KJ, Braun A, Halperin E. Using DNA pools for genotyping trios. Nucleic Acids Res. 2006;34:e129. doi: 10.1093/nar/gkl700. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brenner SE. Common sense for our genomes. Nature. 2007;449:783–784. doi: 10.1038/449783a. [DOI] [PubMed] [Google Scholar]
- Cai WW, Chen R, Gibbs RA, Bradley A. A clone-array pooled shotgun strategy for sequencing large genomes. Genome Res. 2001;11:1619–1623. doi: 10.1101/gr.198101. [DOI] [PubMed] [Google Scholar]
- Csuros M, Li B, Milosavljevic A. Clone-array pooled shotgun mapping and sequencing: Design and analysis of experiments. Genome Inform. 2003;14:186–195. [PubMed] [Google Scholar]
- Freeman WM, Walker SJ, Vrana KE. Quantitative RT-PCR: Pitfalls and potential. Biotechniques. 1999;26:112–122. doi: 10.2144/99261rv01. [DOI] [PubMed] [Google Scholar]
- Fu Y, Peckham HE, McLaughlin SF, Ni JN, Rhodes MD, Malek JA, McKernan KJ, Blanchard AP. Biology of genomes. Cold Spring Harbor Laboratory Press; Cold Spring Harbor, NY: 2008. SOLiD system sequencing and 2 base encoding. [Google Scholar]
- Gunderson KL, Kruglyak S, Graige MS, Garcia F, Kermani BG, Zhao C, Che D, Dickinson T, Wickham E, Bierle J, et al. Decoding randomly ordered DNA arrays. Genome Res. 2004;14:870–877. doi: 10.1101/gr.2255804. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hajirasouliha I, Hormozdiari F, Sahinalp SC, Birol I. Optimal pooling for genome re-sequencing with ultra-high-throughput short-read technologies. Bioinformatics. 2008;24:32–40. doi: 10.1093/bioinformatics/btn173. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Huggett J, Dheda K, Bustin S, Zumla A. Real-time RT-PCR normalization; strategies and considerations. Genes Immun. 2005;6:279–284. doi: 10.1038/sj.gene.6364190. [DOI] [PubMed] [Google Scholar]
- The International HapMap Project. The International HapMap Consortium. Nature. 2003;426:789–796. doi: 10.1038/02168. [DOI] [PubMed] [Google Scholar]
- Ito T, Chiku S, Inoue E, Tomita M, Morisaki T, Morisaki H, Kamatani N. Estimation of haplotype frequencies, linkage-disequilibrium measures, and combination of haplotype copies in each pool by use of pooled DNA data. Am J Hum Genet. 2003;72:384–398. doi: 10.1086/346116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lander ES, Waterman MS. Genomic mapping by fingerprinting random clones: A mathematical analysis. Genomics. 1988;2:231–239. doi: 10.1016/0888-7543(88)90007-9. [DOI] [PubMed] [Google Scholar]
- Levy S, Sutton G, Ng PC, Feuk L, Halpern AL, Walenz BP, Axelrod N, Huang J, Kirkness EF, Denisov G, et al. The diploid genome sequence of an individual human. PLoS Biol. 2007;5:e254. doi: 10.1371/journal.pbio.0050254. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li H, Ruan J, Durbin R. Mapping short DNA sequencing reads and calling variants using mapping quality scores. Genome Res. 2008;18:1851–1858. doi: 10.1101/gr.078212.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mardis ER. The impact of next-generation sequencing technology on genetics. Trends Genet. 2008;24:133–141. doi: 10.1016/j.tig.2007.12.007. [DOI] [PubMed] [Google Scholar]
- Margulies M, Egholm M, Altman WE, Attiya S, Bader JS, Bemben LA, Berka J, Braverman MS, Chen YJ, Chen Z, et al. Genome sequencing in microfabricated high-density picolitre reactors. Nature. 2005;437:376–380. doi: 10.1038/nature03959. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pe'er I, Beckmann JS. Resolution of haplotypes and haplotype frequencies from SNP genotypes of pooled samples. RECOMB '03: Proceedings of the seventh annual international conference on research in computational molecular biology, Berlin, Germany; NY: Association for Computing Machinery (ACM); 2003. pp. 237–246. [Google Scholar]
- Raeymaekers L. Basic principles of quantitative PCR. Mol Biotechnol. 2000;15:115–122. doi: 10.1385/MB:15:2:115. [DOI] [PubMed] [Google Scholar]
- Reich DE, Gabriel SB, Altshuler D. Quality and completeness of SNP databases. Nat Genet. 2003;33:457–458. doi: 10.1038/ng1133. [DOI] [PubMed] [Google Scholar]
- Risch NJ. Searching for genetic determinants in the new millennium. Nature. 2000;405:847–856. doi: 10.1038/35015718. [DOI] [PubMed] [Google Scholar]
- Sarin S, Prabhu S, O'Meara MM, Pe'er I, Hobert O. Caenorhabditis elegans mutant allele identification by whole-genome sequencing. Nat Methods. 2008;5:865–867. doi: 10.1038/nmeth.1249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw SH, Carrasquillo MM, Kashuk C, Puffenberger EG, Chakravarti A. Allele frequency distributions in pooled DNA samples: Applications to mapping complex disease genes. Genome Res. 1998;8:111–123. doi: 10.1101/gr.8.2.111. [DOI] [PubMed] [Google Scholar]
- Sloane NJA, MacWilliams FJ. The theory of error-correcting codes. North-Holland Mathematical Library; The Netherlands: 1977. [Google Scholar]
- Smith DR, Quinlan AR, Peckham HE, Makowsky K, Tao W, Woolf B, Shen L, Donahue WF, Tusneem N, Stromberg MP, et al. Rapid whole-genome mutational profiling using next-generation sequencing technologies. Genome Res. 2008;18:1638–1642. doi: 10.1101/gr.077776.108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang DG, Fan JB, Siao CJ, Berno A, Young P, Sapolsky R, Ghandour G, Perkins N, Winchester E, Spencer J, et al. Large-scale identification, mapping, and genotyping of single-nucleotide polymorphisms in the human genome. Science. 1998;280:1077–1082. doi: 10.1126/science.280.5366.1077. [DOI] [PubMed] [Google Scholar]
- Zeng D, Lin DY. Estimating haplotype-disease associations with pooled genotype data. Genet Epidemiol. 2005;28:70–82. doi: 10.1002/gepi.20040. [DOI] [PubMed] [Google Scholar]