CO₂ Production as an Indicator of Biofilm Metabolism

Abstract

Biofilms are important in aquatic nutrient cycling and microbial proliferation. In these structures, nutrients like carbon are channeled into the production of extracellular polymeric substances or cell division; both are vital for microbial survival and propagation. The aim of this study was to assess carbon channeling into cellular or noncellular fractions in biofilms. Growing in tubular reactors, biofilms of our model strain Pseudomonas sp. strain CT07 produced cells to the planktonic phase from the early stages of biofilm development, reaching pseudo steady state with a consistent yield of ∼10⁷ cells·cm⁻²·h⁻¹ within 72 h. Total direct counts and image analysis showed that most of the converted carbon occurred in the noncellular fraction, with the released and sessile cells accounting for <10% and <2% of inflowing carbon, respectively. A CO₂ evolution measurement system (CEMS) that monitored CO₂ in the gas phase was developed to perform a complete carbon balance across the biofilm. The measurement system was able to determine whole-biofilm CO₂ production rates in real time and showed that gaseous CO₂ production accounted for 25% of inflowing carbon. In addition, the CEMS made it possible to measure biofilm response to changing environmental conditions; changes in temperature or inflowing carbon concentration were followed by a rapid response in biofilm metabolism and the establishment of new steady-state conditions.

Notable advances have been made in the study of biofilms since the early recognition (for examples, see references 11 and 29) of this form of microbial existence. Following these earlier studies of selective adherence of bacteria to surfaces was the development of continuous flow cells, as well as computer-assisted and scanning confocal laser microscopy that enabled the improved description of bacterial behavior at surfaces (for an example, see reference 23), and we now know that biofilms are organized aggregates of extracellular polymeric substance (EPS)-enclosed cells that differ substantially from suspended cells (47). Observing biofilm phenotypic responses may provide insight to guide researchers in conducting directed experiments to unravel underlying fundamental mechanisms; however, we still lack methods to measure and monitor biofilm function.

Flemming (9) grouped industrial biofilm monitoring systems into the following three categories: (i) systems detecting the increase and decrease of materials accumulating on a surface without differentiating biomass from other components, (ii) those that can distinguish between biotic and abiotic material, and (iii) those that provide detailed chemical information of biofilms. Janknecht and Melo (16) categorized online biofilm monitoring techniques in a similar way when comparing applications in industrial systems but added a category for monitoring metabolic activity (a category that Flemming [9] hinted at with the proposal of a technique that can distinguish between living and dead organisms on a surface).

In brief, a nonexhaustive list of techniques that deal only with online monitoring increase (whether of biotic or abiotic origin) and the decrease of biofilms includes quartz crystal microbalances (48), large area photometry (3, 33), electrical capacitance (31), fiber optical devices (49), differential turbidity measurement devices (20), microfluidic biochips (39), optical coherence tomography (13), pressure drop or friction resistance (24), and heat transfer resistance (28). Techniques that provide information about the physical structure and chemical properties of biofilms are nuclear magnetic resonance (44), attenuated total reflectance-Fourier transform infrared spectroscopy (7), and photoacoustic spectroscopy (43). Some biofilm monitoring techniques provide information about metabolic activity in biofilms, such as those using electrochemical devices like dissolved oxygen and redox probes (25), microbiologically influenced corrosion monitoring (34), nuclear magnetic resonance (56), measurement of substrate consumption (19, 50) or metabolic products (53), bioluminescence assays, and fluorometry (56).

The objective of the study was to develop a real-time monitoring system to measure gaseous CO₂ production as an indicator of biofilm metabolism and to use the system to determine the biofilm response to environmental conditions and to measure carbon channeling in biofilms.

MATERIALS AND METHODS

Culture media and growth conditions.

Pure culture biofilms of Pseudomonas sp. strain CT07 gfp (3) and Pseudomonas aeruginosa PA01 gfp were grown in silicone tubes (42). The silicone tubes were inoculated with 200 to 500 μl from an overnight culture (the same medium was used as that described below except 5 mM of sodium citrate was used instead of 1 mM) with the pump turned off for 30 min to 1 h to allow initial adhesion to the tube walls. Sterile defined growth medium [a final concentration of 1.51 mM (NH₄)₂SO₄, 3.37 mM Na₂HPO₄, 2.20 mM KH₂PO₄, 179 mM NaCl, 0.1 mM MgCl₂·6H₂O, 0.01 mM CaCl₂·2H₂O, 0.001 mM FeCl₃] with either 1 mM sodium citrate or 3 mM glucose as the sole carbon source was continuously supplied by a Watson Marlow 205U peristaltic pump at 15 ml/h (unless specified otherwise). Medium retention time was 12 min for this reactor size and flow rate.

CEMS and measurements.

A carbon dioxide evolution measurement system (CEMS) was constructed, which is essentially a silicone tube biofilm reactor (inside diameter, 0.16 cm; outside diameter, 0.24 cm; length, 150 cm; VWR International, Mississauga, ON, Canada) encased in a sealed Tygon tube (inside diameter, 0.48 cm; outside diameter, 0.79 cm; formulation R-3603; VWR International, Mississauga, ON, Canada) with the annular space being connected to a CO₂ analyzer. Silicone tubing has a relatively high permeability to both CO₂ and O₂ compared to that of Tygon tubing; approximately 50 times and 200 times higher for CO₂ and O₂, respectively, according to permeability coefficients provided by the manufacturer. Given a higher gaseous CO₂ concentration on the inside of the lumen of the silicone tube due to biofilm metabolic activity, it can be assumed that a fraction will cross the silicone tube wall to the annular space where it can be measured. The annular space of the carbon dioxide exchange system (CEMS) was connected to an absolute, nondispersive, infrared LI-820 CO₂ gas analyzer (LI-COR Biosciences, NE), and compressed air was used as the sweeper gas. The steady-state CO₂ concentration in the compressed air was measured and subtracted from the steady-state CO₂ originating from the CEMS. Gas flow rates were determined by volumetric displacement and a thermal gas mass flow meter (Aalborg, NY).

Although the use of silicone for carbon dioxide transfer has been applied to measure microbial metabolic activity in water research and fermentations, such an approach has to our knowledge not been applied in biofilm studies. For example, Visser et al. (54) and Aboka et al. (1) measured the transfer of O₂ and CO₂ across silicone membranes to monitor respiration of Saccharomyces cerevisiae isolates grown in a chemostat, and Dahod (6) used submerged silicone tubes in a fermentor to measure respiration rates of industrial Streptomyces organisms on a pilot plant scale.

Theory.

During development of the CEMS, it was clear that it would be useful to have a mathematical relationship that determines what fraction of CO₂ will cross the silicone membrane under certain experimental conditions. In this way, it would be necessary to measure only the CO₂ concentration on one side while being able to relate it to the CO₂ concentration on the other side of the membrane.

Gas transport across silicone membranes.

Gas mass transfer across a membrane is often described in terms of Fick's law of diffusion (for examples, see references 36 and 15) as follows:

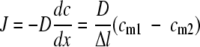(1)

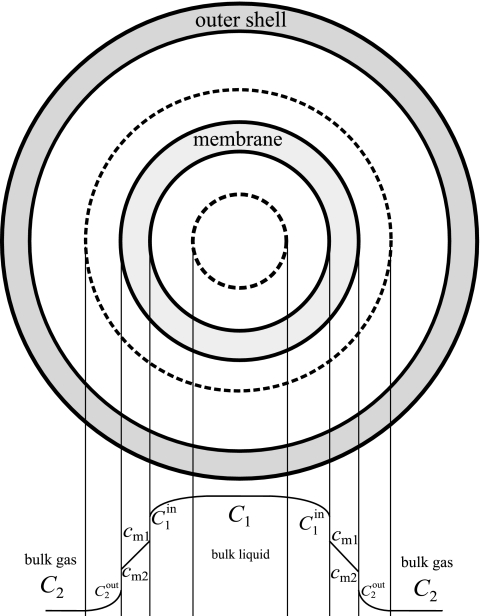
where c describes the concentrations (mol·m⁻³), x is the length (m), J is the flux of the compound crossing the membrane (mol·s⁻¹·m⁻²), D is the diffusion coefficient (m²·s⁻¹), Δl is the thickness of the membrane, and c_m1 and c_m2 (mol·m⁻³) are the concentrations of the species crossing the membrane at the membrane surfaces on either side.

Silicone membranes can be described as nonporous (dense-polymer) membranes like the kind used for pervaporation, perstraction, or gas separations as opposed to porous membranes used in microfiltration or ultrafiltration (36).

In addition to diffusion, the partitioning of the solute between the membrane and adjacent solution plays an important role in the transport. The partitioning of solute between the adjacent solution and the membrane surface is linearly related via a partitioning coefficient analogous to a Henry's law constant of the form σ₁ = c_m(eq)/C₁ⁱⁿ(eq) and σ₂ = c_m(eq)/C₂^out(eq), where σ₁ is the partitioning coefficient (sometimes called a solubility coefficient, but it serves the same purpose of relating the surface membrane concentration to the adjacent phase concentration), and C₁ⁱⁿ is the solute concentration in the adjacent phase in equilibrium (eq) with the solute concentration at the membrane surface (c_m). If the adjacent or bulk solutions are the same (e.g., aqueous), σ₁ = σ₂ = σ and equation 1 can be written as

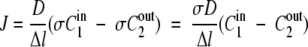(2)

Note that the partitioning coefficient can be written in many forms, depending on the driving force (partial pressure or concentration difference across the membrane). It can be dimensionless or can relate partial pressure to concentration or vice versa, so attention has to be given to the appropriate units. Under certain conditions with specific membrane polymers and permeants, the permeability coefficient, P, can be given as the product of the diffusion constant, D, and the partitioning coefficient, σ. The partition coefficient serves as an indicator of the ability of the membrane to allow transport of certain molecules. Again, the units of P may vary widely depending on the driving force (58).

Depending on the nature (e.g., the size of the molecule) of the solute and membrane properties, diffusion or solubility of the solute in the membrane (σ) will contribute in different amounts to the overall mass transfer. In the case of carbon dioxide transfer through rubber or silicone, solubility plays by far the most important role in gas transport (36).

Gas transport across a silicone tube wall in the CEMS.

The permeability of silicone rubber membranes to O₂ and CO₂ has long been known and is implied in liquid-gas contact applications, such as a membrane gills for submarines and underwater stations (40) or gas exchange in blood (46). However, when the two phases adjacent to the membrane are not the same, equation 2 does not accurately describe the mass transfer anymore. The different phases will pose different mass transfer resistances on either side of the membrane, and the partitioning coefficients may vary (see references 17, 32, and 60 for examples).

If the solutions adjacent to the membrane are not the same (e.g., aqueous and gas) (5), σ₁ ≠ σ₂ and equation 1 becomes as follows:

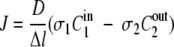(3)

The concentrations for C₁ⁱⁿ and C₂^out are usually not the same as the concentrations in the bulk solutions, C₁ and C₂. For a steady-state flux of solute from bulk solution 1 to bulk solution 2, the fluxes can be expressed as follows: J = k₁(C₁ − C₁ⁱⁿ) = D/Δl(σ₁C₁ⁱⁿ − σ₂C₂^out) = k₂(C₂^out − C₂), where k₁ and k₂ are mass transfer coefficients (m·s⁻¹) (45). The relationship described above can be simplified as follows:

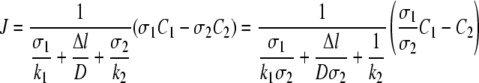(4)

If the bulk solution on side 1 is water and the bulk solution on side 2 is air, based on equation 4, a local transfer coefficient (K_z) can be written as 1/K_z = σ₁/k₁σ₂ + Δl/Dσ₂ + 1/k₂, and equation 4 can be rewritten as follows:

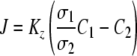(5)

Equation 5 describes the radial transfer from the liquid bulk phase to the gas bulk phase (Fig. 1). To determine the overall transfer coefficient (K_L) of the CEMS, a mass balance can be written across an infinitely thin slice of the CEMS and integrated along the length of the tube, similar to treatment carried out by Dindore et al. (8).

FIG. 1.

Cross section to illustrate radial transfer of CO₂ from the liquid bulk phase to the gas bulk phase in the CEMS. Adapted from reference 8 with permission from Elsevier.

The average flux over the entire length of the tube can be shown by the following equation:

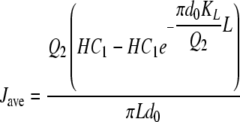(6)

where J_ave is the average flux (mol·m⁻²·s⁻¹), Q₂ is the volumetric flow rate of the gas (m³/s), H is a Henry's law constant relating equilibrium values (σ₁/σ₂), L is the length of the tube (m), and d₀ is the outer diameter of the silicone tube (m). Note that in the derivation of equation 6, it is assumed that the concentration on the liquid side remains constant throughout the length of the reactor tube (see the supplemental material). With equation 6, it is therefore possible to determine the overall transfer coefficient for the CEMS, K_L, with known liquid phase CO₂ concentrations (C₁) by measuring the CO₂ flux appearing in the gas phase. Once calibrated for a particular membrane configuration, the gas phase results can be used to calculate the C₁ for other experimental conditions.

In an experimental configuration where microbes grow in a biofilm on the inside wall of the silicone tube, they will excrete their CO₂ into their surroundings. The CO₂ from microbial respiration is transferred across cell membranes in a dissolved form or aqueous CO₂ (18). Aqueous CO₂ can either be converted to a gaseous form or remain dissolved and even be transformed into bicarbonate and carbonate ions as schematically represented by Zeng (59).

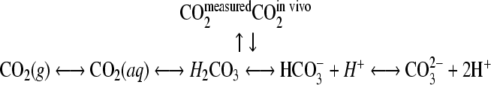(7)

The ratio of the dissolved forms of CO₂ is dependent on pH, temperature, and ion activity (10). At a pH of 4 to 7, the carbonate ion concentration is negligible.

Linearity of dissolved carbon dioxide.

A dilution series of dissolved CO₂ was used to correlate the amount of CO₂ in the liquid phase transferred by the CEMS to the gas phase. A saturated solution of CO₂ in Milli-Q water was made by stirring pieces of “dry ice” (solid CO₂) until the pH stabilized at room temperature. This saturated solution was used to make a dilution series of 1% to 4% (vol/vol) dissolved CO₂ and sealed in serum vials with butyl rubber stoppers. Steady-state CO₂ concentrations in the off-gas were measured with increasingly dissolved CO₂ samples.

Effect of temperature on biofilm respiration/metabolism.

To test the sensitivity of biofilm respiration to temperature changes, the CEMS was submerged in a cooling water bath overnight at 15°C and subsequently subjected to changes in temperature between 27°C and 10°C and CO₂ concentrations in the off-gas measured. To ensure an even distribution of temperature, the carrier gas and growth medium were controlled in the same water bath as the CEMS.

Effect of citrate or glucose concentration.

In each replicate experiment, biofilms were grown for 8 days in the CEMS at citrate and glucose concentrations of 1 mM and 3 mM, respectively, at room temperature before the influent concentrations were randomly varied between 0.125 mM and 5 mM and the CO₂ concentrations were measured in the off-gas. The validity of the biofilm response to different citrate or glucose concentrations in a carbon-limited environment was tested with the following relationship described by Gillooly et al. (12): metabolic rate ∝ (concentration of reactants)(fluxes of reactants)(kinetic energy of the system). For the conditions where only the concentrations of the carbon source were varied, the last two terms can be considered constant.

Determination of cell numbers and carbon in cellular and noncellular fractions.

Cell numbers in the effluent and biofilm were determined by heterotrophic plate counts and total direct cell counts. In brief, cell suspensions were vortexed and diluted in 0.9% saline and stained with 4′,6-diamidino-2-phenylindole (DAPI). The suspension was filtered onto a 0.22-μm black polycarbonate filter, and the cell numbers were determined by epifluorescence microscopy. Images were recorded with a Leica DM5000 B epifluorescence microscope and a Leica DFC350 FX camera, and cell sizes were determined on a PC computer using the Microsoft Windows version of the public domain NIH Image program from the U.S. National Institutes of Health (available at http://rsb.info.nih.gov/nih-image/). Digital image processing was done as described by Massana et al. (30), which involved the application of a series of Gauss, Laplace, and median filters with manual thresholding steps in between. Both cell numbers and cell dimensions could be determined from the processed images. The pseudomonad cells were rod shaped, and cellular volumes were determined by using the following equation: V = [w²(π/4)](l − w) + [w³(π/6)], where w and l are the width and length of the cell, respectively. Values for w and l were determined from the digitally processed images, and the average two-dimensional cell area determined by the equation [(l − w) × w + π(w/2)²] was 0.98 ± 0.12 μm², which is very similar to values of 0.86 ± 0.12 μm² for Pseudomonas fluorescens as determined by Mueller (35). Pseudomonas sp. strain CT07 is closely related to P. fluorescens (3).

Posch et al. (38) described an allometric conversion formula to relate cellular volume to cellular carbon based on images obtained for a specific dye. For DAPI-stained images, the conversion is given by the following equation: cellular carbon = 218 × V^0.86, with the cellular carbon measured in femtograms of carbon and V in micrometers cubed.

Determination of unused citrate exiting the reactor in the liquid phase.

Unused citrate exiting the reactor was determined with an enzymatic analysis kit from Enzytec (Scil Diagnostics GmbH, Germany).

Carbon balance.

For the carbon balance, both effluent liquid samples and off-gas samples were taken at 24-h intervals and measured for carbon content. These discrete concentration values were used together with the flow rates to calculate the cumulative carbon exiting the CEMS. The total carbon in the effluent was measured with a catalytic combustion, nondispersive infrared total carbon analyzer (TOC-V_CSH/CSN; Shimadzu, Kyoto, Japan), while the CO₂ in the off-gas was measured as mentioned above. At the end of the experiment, the organic matter that accumulated in the reactor tube was collected by squeezing out the attached organic matter using a bottle as a rolling pin.

Visual observations revealed that as the biofilms matured, small aggregates would sporadically exit the tube reactor with the effluent. These aggregates are denser than water. Therefore a simple trap consisting of a 1.5-ml Eppendorf tube with the influent line positioned below the effluent line was devised for collecting the aggregate-free liquid phase in a container with sodium azide (final concentration, ∼70 mg/liter) to inhibit further microbial degradation of carbonaceous compounds.

RESULTS

The CEMS was developed for measuring real-time, whole-biofilm CO₂ production rates. This device was used to assess the biofilm response to changing environmental conditions and carbon channeling in biofilms.

Calibration.

When the CEMS was tested with gas phases on both sides of the silicone membrane according to methods described by ASTM standards (2), the gas permeability coefficient was (3.02 ± 0.04) × 10⁻⁶ cm³·mm·s⁻¹·cm⁻²·cm Hg⁻¹ and corresponded well with values from the manufacturer (same order of magnitude).

Milli-Q water with known dissolved CO₂ concentrations (between 0 and 4% saturation) was used to test the CO₂ transfer across the silicone tube wall to the gas phase. The CO₂ measured in the gas phase was highly linear (R² = 0.999) with various dissolved CO₂ concentrations.

Experimental results for biofilm CO₂ production were well within the range tested during the calibration experiments.

Effect of temperature on biofilm metabolism.

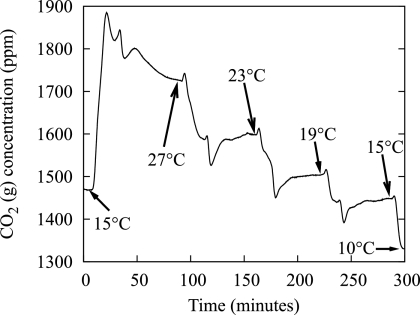
Figure 2 shows an actual output from the CO₂ analyzer. Popular models for describing the dependence of microbial metabolic activity to temperature were used to verify the relationship of steady-state, gaseous CO₂ measurements to variations in temperature. The Arrhenius equation is an exponential function used to model temperature relationships, and the plot of the log of activity (CO₂ measurement) against the inverse of the absolute temperature should be a straight line if the activation energy is constant over the range of measurement (37). Indeed, the results showed an R² value equal to 0.990 and 0.977 for growth on 1 mM citrate and 3 mM glucose, respectively, for Pseudomonas sp. strain CT07 gfp. Another model for relating temperature to microbial activity is a square root relationship used for microbes growing at suboptimal temperatures, which was the case for the strains used in these experiments. A plot of the square root of the activity against the temperature should give a straight line (37), which was the case with an R² value of 0.988 for growth on 1 mM citrate and an R² value of 0.993 for growth on 3 mM glucose for Pseudomonas sp. strain CT07 gfp.

FIG. 2.

Effect of temperature on biofilm metabolism. Output data from the CO₂ analyzer showing the response of a Pseudomonas sp. strain CT07 gfp biofilm and the time to reach new steady-state values with temperature perturbations.

Duplicate experiments provided similar results in terms of both CO₂ measurements and times to reach steady state (results not shown).

Effect of citrate concentration on biofilm metabolism.

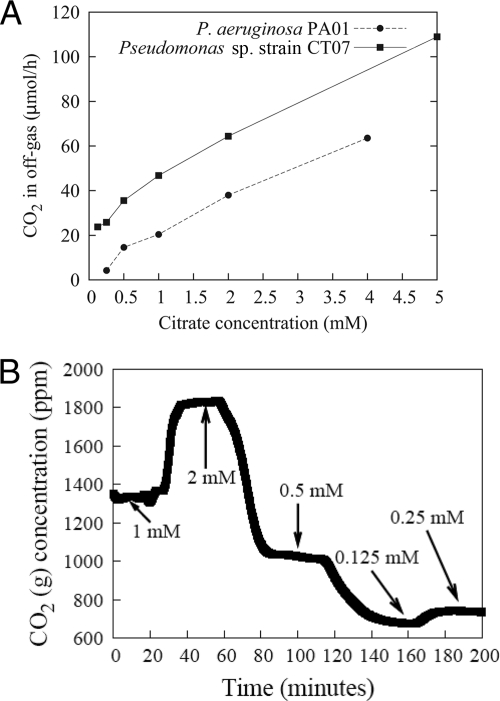
The citrate concentrations in the medium were varied at random (Fig. 3B) while measuring the CO₂ in the off-gas. For citrate concentrations between 0.5 mM and 5 mM, the response in CO₂ evolution was nearly linear (R² = 0.996) for Pseudomonas sp. strain CT07 gfp. Similarly, the response in CO₂ evolution for P. aeruginosa PA01 between 0.5 and 4 mM citrate was also nearly linear, with an R² value of 0.995. Because of its wider range of carbon sources, P. aeruginosa PA01 was also cultivated on glucose, benzoate, and tryptic soy broth with similar linear responses (R² values of 0.996, 0.994, and 0.999, respectively). This metabolic response with various carbon concentrations above the threshold of 0.5 mM (0.3 g/liter in the case of tryptic soy broth) can be explained with the relationship described by Gillooly et al. (12), presented in Materials and Methods. The last two terms in their equation can be considered constant (reasons mentioned below), which leaves the metabolic rate directly proportional to the concentration of reactants (citrate). Microbes have the ability to modulate nutrient uptake and enzyme affinities to ensure high metabolic fluxes even under low-nutrient conditions (with the assumption that fluxes will be kept fairly constant under the conditions of our experiments; i.e., second term) (51). The kinetic energy (third term) of the system is dependent on temperature, which was kept constant during the experiment.

FIG. 3.

CO₂ production rates showing biofilm response to changes in influent citrate concentrations. Biofilm metabolic response showing the linear correlation (an R² value of 0.995 and 0.996 for P. aeruginosa PAO1 and Pseudomonas sp. strain CT07, respectively) (A) with citrate concentration despite the random order (Pseudomonas sp. strain CT07 in this case) (B) in which the concentration was changed, demonstrating the adaptability of biofilms to environmental changes.

Carbon balance.

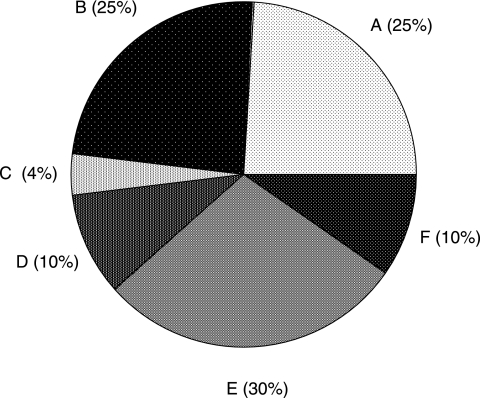
All the carbon exiting the biofilm reactor in the liquid (as suspended materials) and gas phases was compared with the carbon flowing into the reactor over a period of 8 days (Fig. 4). The carbon balance for replicate experiments closed to within 2 and 4%. For the experiment summarized in Fig. 4, carbon that exited the reactor in the liquid phase accounted for 72.4% of the incoming carbon. The cumulative amount of gaseous CO₂ leaving the reactor was 24.9% of the inflowing carbon, while 4.1% of the carbon remained attached to the inner surface of the reactor tube. Components that contributed to the liquid phase carbon fraction that exited the reactor included dissolved CO₂, cellular carbon (biofilm biomass lost, e.g., sloughing, dispersion, and erosion), unused citrate, and EPS. Calibration experiments using known concentrations of dissolved CO₂ and concomitant gas phase measurements showed that at least an amount similar to that of the CO₂ in the gas phase exited the reactor in a dissolved form. Microbial cells in the effluent reached values of ∼10⁶ cells·cm⁻²·h⁻¹ (cells produced per biofilm footprint area per unit of time) within 24 h after inoculation and reached pseudo-steady-state values of ∼10⁷ cells·cm⁻²·h⁻¹ after 3 days. The C fraction leaving the reactor as nonaggregated cells was always less than 10%, as determined by direct microscopy, image analysis, and the conversion formula described in Materials and Methods. Carbon leaving the reactor as aggregates accounted for 30% of the inflowing carbon condensed in less than 1% of the exiting volume. The composition of these aggregates in terms of cell numbers and other contributing constituents has not yet been determined. Unused citrate plateaued at 10% of the growth medium value after 3 days.

FIG. 4.

Carbon balance for a Pseudomonas sp. strain CT07 biofilm over an 8-day cultivation. Shown are cumulative CO₂ exiting in gas phase (A), cumulative CO₂ exiting in liquid phase (B), carbon remaining behind in the biofilm (C), cumulative carbon exiting as cells (D), cumulative carbon exiting as aggregates (less than 1% of vol) (E), and cumulative unused citrate (F). The carbon balance typically closed within 2 to 4%.

DISCUSSION

Lewandowski and Beyenal (26) lamented the divide between the generation of monitoring results and the useful application thereof, due mainly to the inability of mathematical models to accept the monitored parameters even if the monitoring is done with technical excellence. Building the bridge between biofilm monitoring and mathematical models that can successfully implement the data to correlate measured parameters to biofilm function is beyond the scope of this article. However, we hope to demonstrate that simple biofilm monitoring measurements can provide insight into the important biofilm functions of protection (EPS production) and proliferation (releasing progeny into the environment by physiological means and by employing physical means such as erosion, abrasion, and sloughing). Being aware of the phenomenological responses of biofilms may lead to the identification of focus areas for more fundamental research.

Kreft (21) considered the conflict in biofilms for the economical use of limiting resources to channel it toward either a specific growth rate (the rate of biomass increase per time and biomass) or growth yield (biomass formed per amount of resource used), where a high growth yield can be attained only through a decrease in the specific growth rate. In pure culture work, Bester et al. (3) showed that microbes in a biofilm released high numbers of cells into the environment, even at very early stages of biofilm development. EPS production varies with different physical environmental conditions and available nutrients. Xavier et al. (57) simulated competition between microbial strains that differ in their ability to produce EPS. They concluded that polymer production may afford a competitive advantage in mixed-species biofilms under certain conditions by suffocating neighboring nonpolymer producers and exposing later generations to better oxygen conditions. CO₂ production is another important and often neglected sink of carbon in biofilm systems. Liu et al. (27) described an observed growth yield in biofilms that takes channeling of dissolved organic carbon to CO₂ and biomass fractions into account. According to the equation presented by these authors for the observed growth yield it is clear that, given a finite dissolved organic carbon source, an increase in respiration will imply a decrease in biomass as the authors indeed show with data from the literature.

It has been proposed that under conditions of energy limitation, catabolic reactions are tightly coupled to anabolic reactions (41) and diversion of substrate carbon into extracellular products is minimized (14). Our studies show that between 40% and 50% of the inflowing carbon is used for respiration; ∼25% exits during the gas phase, and a similar amount remains dissolved and exits during the liquid phase. Furthermore, around 30% of the carbon leaves as dense aggregates, presumably consisting of cells bound to the EPS. Even if cell density in the aggregates is assumed to be similar to values of the biofilm, it means that roughly 20% of the carbon is converted to EPS and released to the effluent, even though our system may be considered carbon limited (Beyenal et al. [4] considered 5 mM of glucose to be a carbon-limiting condition in P. aeruginosa chemostat cultures). Our focus here is not to elucidate the different EPS fractions; for that, refer to the seminal work by Laspidou and Rittmann (22) who discussed EPS and soluble microbial products with their various subfractions and address the confusion regarding terminology that originated because EPSs have historically been studied from various backgrounds. In brief, a common theme of EPSs (bound and soluble) and soluble microbial products is that they are both organic materials of microbial origins but do not contain any active cells. These authors also reported EPS values as a percentage of influent carbon for continuously stirred tank and batch reactors.

Our data suggest that the measurement of CO₂ in the off-gas is a suitable way of determining biofilm metabolic responses to changes in environmental parameters given the linear relationship to dissolved CO₂ under the conditions used. For changes in citrate concentration, the metabolic responses of Pseudomonas sp. strain CT07 gfp and P. aeruginosa PA01 gfp were nearly linear for values above 0.5 mM, which would suggest a regime of carbon sufficiency for those particular biofilms. For values below 0.5 mM citrate, the response deviated from linearity and can be explained in terms of a threshold level of nutrients required for maintenance. When the level of available substrate carbon is lower than the value required for maintenance, the microbial cell must use carbon from its reserves (52).

The biofilm metabolic response was sensitive even to small changes in temperature. It should be noted that for the measurement of the temperature response, neither the silicone permeability dependence on temperature nor the temperature influence on gas solubility was taken into account. The gas permeability of silicone increases with increasing temperatures according to an Arrhenius-type relationship (36), while the solubility of CO₂ in growth media increases with decreasing temperatures. However, these influences should be negligible over the temperature ranges used in these experiments.

With equation 6, the overall transfer coefficient for the CEMS, K_L, can be determined for known dissolved CO₂ concentrations by measuring the CO₂ flux in the off-gas. We have not yet determined the K_L because of the requirement of the constant dissolved CO₂ concentration, C₁, in the derivation of equation 6. The requirement for constant C₁ could be accomplished by either increasing the dissolved CO₂ concentration and assuming that the CO₂ loss across the membrane is negligible or by shortening the length of the CEMS to minimize the loss of CO₂ along the length of the silicone tube. Once the K_L has been determined, the resulting equation shows a linear relationship between the dissolved CO₂ and the CO₂ measured in the gas phase. Frahm et al. (10) simultaneously solved a set of differential equations to relate carbon dioxide transfer rate measurements (measured in the gas phase) in mammalian suspension cultures to the carbon dioxide production rate. The equations included information about pH changes, buffer, and media composition and CO₂ transfer from the liquid phase to the gas phase. Weissenbacher et al. (55) used a similar approach to calculate the carbon dioxide production rate from the carbon dioxide transfer rate measurements in activated sludge systems by correcting for the dissolved CO₂/bicarbonate equilibrium transformations. Although our method is slightly less sophisticated by considering only a clumped transfer coefficient, it seems that we are still able to predictably relate dissolved CO₂ with CO₂ measured in the gas phase.

In systems considering mass transfer from the gas-to-liquid phase via membranes, liquid and gas flow rates influence the transfer rate. Zhang et al. (61) determined that in the case of physical absorption (when CO₂ does not react with liquid it dissolves into water, and the authors considered CO₂ dissolving into water as a physical process), the CO₂ flux across the membrane increased with liquid velocity while the gas velocity had no effect on the CO₂ flux when the direction of transfer was from gas to liquid. A reason for increased transfer would be an increase in the gradient of the driving force across the membrane. In our system, the liquid phase concentration is assumed to be constant but an increase in the gas flow rate will result in a lower average CO₂ concentration on the gas side, which will increase the driving force gradient for an increased transfer rate. Caution is therefore necessary to ensure constant gas flow rates while using the CEMS during the same experiment.

In conclusion, the CEMS proved to be a useful tool for nondestructive, real-time monitoring of biofilm metabolic activity. Using this approach, it was shown that biofilms responded rapidly to changes in nutrients and temperature. The nondestructive nature of this approach renders it appropriate to accurately and rapidly assess the influence of other environmental conditions on overall biofilm activity, including antimicrobials, nutrient limitation, and microbial community interactions such as predation, competition for a finite substrate, or cooperation to utilize recalcitrant molecules. This approach should therefore not be limited to pure cultures and defined laboratory media; it also provides a measured parameter (CO₂ production as a measure of biofilm activity) with a potential application in mathematical models. In the current research, the CEMS made it possible to determine carbon channeling by biofilm cells, showing that a small fraction (<5%) of the influent carbon is retained in the biofilm, which is a relatively small investment, enabling the biofilm to serve as a catalytic unit to transform carbon from the surrounding environment.