Abstract
Flowering depends upon long-distance transport to supply water for reproductive mechanisms to function. Previous physiological studies suggested that flowers operated uncoupled from stem xylem transport and received water primarily from the phloem. We demonstrate that the water balance of Southern magnolia (Magnolia grandiflora) flowers is regulated in a manner opposite from that of previously examined flowers. We show that flowers of Southern magnolia rely upon relatively efficient xylem hydraulic transport to support high water demand during anthesis. We measured rapid rates of perianth transpiration ranging from twice to 100 times greater than previous studies. We found that relatively efficient xylem pathways existed between the xylem and flower. Perianth hydraulic conductance and the amount of xylem to transpirational surface area ratios of flowers were both approximately one-third those measured for leafy shoots. Furthermore, we observed that perianth tissues underwent significant diurnal depressions in water status during transpiring conditions. Decreases in water potential observed between flowers and vegetative tissues were consistent with water moving from the stem xylem into the flower during anthesis. Xylem hydraulic coupling of flowers to the stem was supported by experiments showing that transpiring flowers were unaffected by bark girdling. With Southern magnolia being a member of a nearly basal evolutionary lineage, our results suggest that flower water balance represents an important functional dimension that influenced early flower evolution.
Sexual reproduction is the primary function of the flower. Most investigations of how flowers orchestrate reproductive processes have focused on developmental biology and biochemical mechanisms operating inside flowers (Franklin-Tong and Franklin, 2003; Glover, 2007). Although such approaches have been successful in understanding the inner workings of flowers, the function of flowers is linked to processes operating in the rest of the plant (Galen, 2005; Lambrecht and Dawson, 2007). As such, the physiological mechanisms that make reproduction possible in the face of environmental stresses are best understood through studies that integrate reproductive and vegetative physiology.
A prime example of where whole plant integration of reproduction is essential concerns how flowers are supplied with the resources necessary for reproduction (Trolinder et al., 1993; Galen, 2005). Like all multicellular plant structures existing in a diffusion-inadequate world, flowers from bud to bloom require continuous supplies of carbohydrates, nutrients, and water that are supplied by long-distance transport vascular systems (Trolinder et al., 1993; Chapotin et al., 2003; De la Barrera and Nobel, 2004; Galen, 2005). In particular, flowers can be water-hungry structures (Blanke and Lovatt, 1993; Galen et al., 1993; Galen, 2005), and a flower's hydraulic needs increase during anthesis due to nectar secretion and when the unfurled perianth, stamens, and stigmatic surfaces become exposed to an evaporative atmosphere (Patino and Grace, 2002; De la Barrera and Nobel, 2004; Galen, 2005).
Considering the diverse roles of water in angiosperm reproduction (Willmer, 1986; Lush et al., 1998; Galen, 2005), it is surprising that so little is understood about how flowers are hydraulically plumbed into the vegetative system. Nonetheless, the few available studies suggest that flowers, unlike leaves, are hydrated by the phloem (Trolinder et al., 1993; Chapotin et al., 2003; De la Barrera and Nobel, 2004; Galen, 2005). A major line of evidence for this comes from differences in water potential (Ψ) and water content (WC) between flowers and the subtending leaves. Flowers of cotton (Gossypium hirsutum) and several dry tropical forest tree species showed Ψ values 0.5 to 1.0 MPa less negative than leaves during transpiring conditions (Trolinder et al., 1993; Chapotin et al., 2003). If flowers were connected to the stem xylem, then transpiring leaves also connected to the stem xylem and operating at lower Ψ should have drained flowers of their water. Yet WCs of flowers remained high (approximately 80%) from day to night amid strong diurnal fluctuations in leaf Ψ (Chapotin et al., 2003). Since the water needed for growth and transpiration (E) of flowers cannot be transported against an uphill ΔΨ if the xylem is the water source, the phloem has been posited as the tissue relaying water from the vegetative system that flowers use (Trolinder et al., 1993; Chapotin et al., 2003).
It remains unclear why phloem should be favored over the xylem for flower hydration (Chapotin et al., 2003). In fact, the xylem could offer advantages over the phloem for supplying water to flowers. For example, hydraulic flow through the xylem can be considerably faster than flow through the phloem due to the far less resistive, nonliving apoplast of the xylem (Van Ieperen et al., 2003). Unlike the phloem-dependent water flow in flowers, which is powered metabolically by the generation of steep osmotic gradients, the motive force for xylem hydraulic flow into flowers would come free of charge in being driven by evaporative water loss. Possible disadvantages of xylem-dependent water use may include the exposure of reproductive organs to more water deficit due to flower E and vascular connectivity to vegetative tissues operating at low Ψ during transpiring conditions.
A few studies have conjectured that some flowers may be hydraulically connected to the stem xylem during anthesis (Hu et al., 1998; He et al., 2006). For example, in detached, minimally transpiring roses (Rosa spp.), Ψ values of petals decreased at the same rate as leaves, while the Ψ values of petals remained higher (about 0.4 MPa) than those of leaves over several days of detachment (Hu et al., 1998). These slow dehydration kinetics were taken as evidence that leaves were able to withdraw water from flowers to prevent leaf wilting. However, the maintenance of such a strong disequilibrium in Ψ between petals and leaves under nontranspiring conditions more likely indicates very high resistance in the vascular connections between leaves and flowers (Melcher et al., 1998). Another line of evidence suggesting a hydraulic role for the xylem during anthesis is the well-known fact in the cut flower industry that petal tissues can be dyed through the transpirational uptake of low-Mr dyes supplied through the cut stem xylem. While dye-uptake observations raise the possibility that stem xylem supplies water to the perianth, such visual-scale patterns of staining are silent on the rates of water supply through the xylem, cannot designate how much water arrives from the phloem versus the xylem, and can be prone to misinterpretation if dyes are transferred between tissues (Bondada et al., 2005). At present, there is no concrete evidence that the xylem participates in the hydration of flower tissues during anthesis for any species.
An interesting system to investigate the diversity of flower water balance is the massive, saucer-like blooms of Southern magnolia (Magnolia grandiflora [Magnoliaceae]; Thien, 1974; Allain et al., 1999). These flowers bloom in the day and remain displayed even under air temperatures up to 38°C. Because of potentially high perianth-to-air vapor pressure deficits, hot air temperatures challenge the maintenance of adequate hydration of essential and drought-sensitive reproductive functions. These functions include the bearing of a nonwilted perianth to attract pollinators and the maintenance of high WC in nectar as well as hydraulic homeostasis of pollen germination, pollen tube growth, fertilization, and embryo nourishment (Willmer, 1986; Trolinder et al., 1993; Lush et al., 1998; Patino and Grace, 2002; Galen, 2005). The flowers of Southern magnolia also differ from previously examined species, which were characterized by low tissue mass investment (less than 2 g fresh weight and with papyraceous perianths), stomata-less perianth parts (tepals), and short life spans of 1 d or less (Trolinder et al., 1993; Galen et al., 1999; Patino and Grace, 2002; Chapotin et al., 2003). In addition to being much larger and longer lived, with 3 to 5 d of lifespan (Thien, 1974; Allain et al., 1999), the tepals of Southern magnolia resemble leaves in having a similar surface area, thickness, and possessing veins and stomata: all traits suggesting significant capabilities for hydraulic flux (Griesel, 1954).
Here, our objectives were 2-fold. First, we examined the water use of Southern magnolia blooms to determine how such large flowers remain displayed in the face of summertime evaporative demand throughout anthesis. We determined the diurnal patterns of flower water vapor exchange and water status in relation to microclimate, developmental stages of anthesis, and the water status of adjacent leaves and stem tissues. We also quantified the drought responses of flowers compared with leaves using pressure-volume analysis and minimum water loss rates on detached shoots and flowers. Second, we identified the nature of the transport processes responsible for flower water balance. We determined the uptake patterns of a xylem-mobile dye during E as well as quantified the allocation patterns of xylem supporting flowers versus leafy shoots. In addition, we undertook comparative whole flower and leaf hydraulic conductance measurements. Lastly, we investigated how flower water balance was affected by girdling the stem bark to manipulate phloem water supplies during anthesis. Because Southern magnolia belongs to a nearly basal evolutionary lineage in angiosperm phylogeny, we discuss the implications of our results on the interactions between vegetative water balance and the reproductive functions during early angiosperm evolution.
RESULTS
Flower Development and Structure
Southern magnolia flowers consisted of three distinct whorls of three tepals. We designated these whorls as first (outermost), second (outer), and third (innermost) whorls. Of the total tepal surface area, the first whorl of tepals contributed 35.5%, the second contributed 40.5%, and the third contributed 23.4% (n = 10 flowers). The tepals surrounded a strobilus with up to 20 carpels and a phalanx of stamens. Our sample of whole flowers averaged 450 ± 20 cm2 (means ± sd; n = 20 flowers) of tepal surface area. First- and 2nd-d flowers did not differ in the amount of perianth surface area (1st-d mean = 450.6 ± 15.8 cm2 versus 2nd-d mean = 450.2 ± 24.35 cm2; n = 10 flowers for each mean; Mann-Whitney U test, not significant). Total fresh masses, sampled at predawn for maximum WC, and total dry masses of flowers averaged 53.35 ± 2.1 g and 11.58 ± 0.6 g, respectively (n = 10 flowers). The mass of the strobilus was approximately 46% of the total flower dry mass (n = 10 flowers).
Tepals from the first and second whorls had vein length density (VD; mm−1) values approximately 73% of those of leaves. However, VD values for the third whorl tepals were about 50% those of leaves (Table I). The veins of tepals appeared to be thinner and more irregularly branched than the minor veins of leaves (data not shown). In contrast to leaves with stomata only on the abaxial surface, we observed that all tepal whorls were amphistomatic. However, stomatal densities for all tepal whorls were lower than those of leaves (Table I). Stomata of tepals were also approximately 9% larger than those of the leaves (Table I).
Table I.
Anatomical and functional traits of Southern magnolia tepals and leaves
Sample sizes are for each organ. Different letters denote significant differences of at least P < 0.05 between the means of the different trait values (Mann-Whitney U test).
| Trait | Mature Leaves | First Whorl Tepals | Second Whorl Tepals | Third Whorl Tepals |
|---|---|---|---|---|
| Abaxial stomatal density (no. mm−2; n = 125) | 288.5 ± 12.2a | 23.8 ± 1.1b | 19.4 ± 3.8c | 11.2 ± 2.2d |
| Adaxial stomatal density (no. mm−2; n = 125) | – | 22.3 ± 3.1a | 24.3 ± 1.7a | 17.9 ± 1.3b |
| Stomatal size (length × width, μm; n = 125) | 30.6 ± 2 × 27.5 ± 1.7a | 31.7 ± 2.2 × 27.8 ± 1.4a,b | 33.3 ± 2.8 × 26.0 ± 2.5b | 32 ± 3.3 × 25.1 ± 3.8a,b |
| Vein length density (mm−1; n = 5) | 7.09 ± 0.5a | 5.18 ± 0.15b | 5.19 ± 0.27b | 3.26 ± 0.94c |
| Leaf mass per area (g cm−2; n = 5) | 0.0137 ± 0.001a | 0.0049 ± 0.0001b | 0.0048 ± 0.0002b | 0.0073 ± 0.002c |
Tepals consisted of less structural biomass than leaves. Leaf mass per area of third whorl tepals was 46% lower than that of leaves, while first and second whorl tepal areas were 65% lower than those of adjacent leaves (Table I). Overall, the first and second whorl tepals were similar in structure and function, including water loss rates, WC dynamics, and drought responses (data not shown). Thus, the functional characteristics of the first and second tepal whorls are not considered separately hereafter.
Gas Exchange, Hydraulic Conductance, Huber Value, Water Loss Rates of Detached Shoots, and Drought Responses
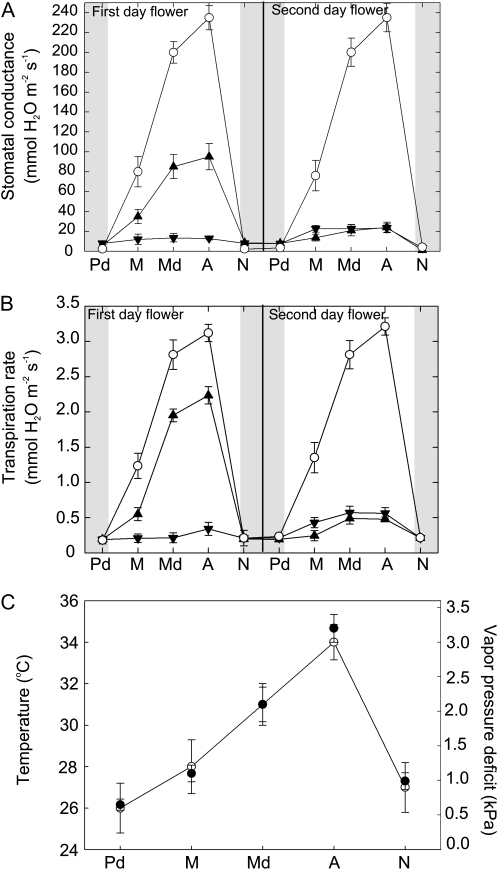
To test for water loss in Southern magnolia flowers, we measured stomatal conductance (gs; mmol m−2 s−1) and E (mmol m−2 s−1) of tepals over the 1st and 2nd d of anthesis (Fig. 1). On the 1st d, first whorl tepals exhibited a significant diurnal response of gs and E. The lowest gs values, at approximately 15 mmol m−2 s−1, occurred at predawn. Stomata then opened in the morning. By the afternoon and under high vapor pressure deficit (VPD), gs and E peaked to nearly 100 and 2.2 mmol m−2 s−1, respectively (Fig. 1, A and B). E of third whorl tepals, however, was approximately 95% lower than that of the first whorl tepals from predawn to nighttime (Fig. 1, A and B).
Figure 1.
Diurnal water vapor gas exchange of Southern magnolia tepals and leaves over 2 d of anthesis and microclimate conditions. A, gs of tepals (first whorl, black triangles; third whorl, black inverted triangles) and leaves (white circles). B, E rates of tepals and leaves (same symbols as in A). C, Microclimatic variables of air temperature (black circles) and air vapor pressure deficit (white circles) averaged over the measurements in A and B. Sample sizes can be found in “Materials and Methods.” Error bars denote sd. Time point abbreviations are as follows: Pd, predawn; M, morning; Md, midday; A, afternoon; N, night.
On the 2nd d of anthesis, diurnal gs patterns of the first whorl tepals were lower throughout the day in comparison with the 1st d (Fig. 1, A and B). The maximum gs measured was approximately 45 mmol m−2 s−1 for the first whorl tepals. Third whorl tepals displayed higher gs than on the 1st d of anthesis.
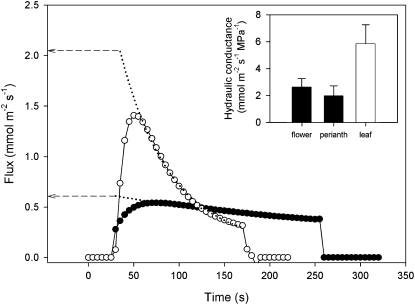
To determine how efficiently the flowers connected to the stem xylem, we measured the hydraulic conductance of detached whole flowers compared with detached leafy shoots (Fig. 2). Using a pressure-relaxation technique, we found that hydraulic conductance of whole flowers expressed on a tepal area basis (KFlower) was approximately 45% of the capacity measured for leafy shoots (Fig. 2; mean KFlower = 2.62 ± 0.64 mmol m−2 s−1 MPa−1 versus mean KLeaf = 5.86 ± 1.41 mmol m−2 s−1 MPa−1; n = 5 each). Although the strobilus tissues contain xylem, the vascular pathways of the tepals contributed more to KFlower (Fig. 2). The average hydraulic conductance of the perianth tissues was 75% of KFlower and 34% of KLeaf (mean KPerianth = 1.98 ± 0.73 mmol m−2 s−1 MPa−1; n = 5).
Figure 2.
Representative flow kinetics after a standard step application of 0.3 MPa hydraulic driving force to an excised leaf (white circles) and flower perianth (black circles). Exponential decay curves (dotted lines) were fitted to the data to allow reconstruction of peak flow at connection (time zero). Hydraulic conductance was calculated by dividing peak flow by the initial pressure gradient. Mean hydraulic conductance (inset) of whole flowers and the perianth only (black bars) was about one-third that of individual leaves (white bar). The drop in flow for each of the samples occurred when the samples were removed from the flow meter. Error bars denote sd.
The mean Huber value (HV) of the receptacle supporting the whole flower perianth was approximately one-third of the mean found for nonflowering shoots (flower mean = 0.31 × 104 ± 0.025 versus leafy shoot mean = 1.02 × 104 ± 0.0909; n = 5 each; P < 0.001 by Mann-Whitney U test). We also found that tracheary element diameters of receptacle xylem were greater than those of the stem wood (receptacle mean = 18.81 ± 1.54 μm versus stem wood mean = 15.43 ± 0.51 μm; n = 50 each; P < 0.05 by Mann-Whitney U test).
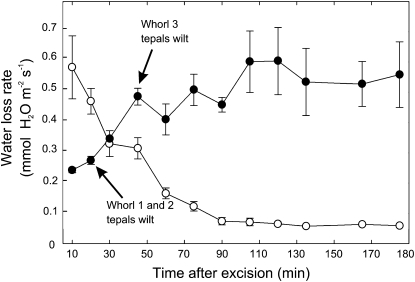
Flowers detached and desiccated under ambient midday to afternoon evaporative conditions (with a variably thick boundary layer) exhibited contrasting time courses of water loss as compared with leafy shoots (Fig. 3). Approximately 70 min after detachment, leafy shoots reduced water loss rates from a maximum of approximately 0.54 mmol m−2 s−1 to about 0.063 mmol m−2 s−1. Leaves on detached shoots did not wilt during the time course. In contrast, water loss rates of detached flowers were approximately 0.27 mmol m−2 s−1 at the wilting point of the outer tepals of the perianth (Fig. 3). After wilting, average water loss rates of flowers increased up to 0.54 mmol m−2 s−1 (Fig. 3). The first and second tepal whorls visibly wilted within 25 min after detachment, while third whorl tepals wilted after 45 min following detachment. The water efflux from flowers was dominated by tepals. Water loss rates from detached strobili from 1st- and 2nd-d flowers, as well as those in the midst of ripening to produce seeds, all lost water at less than 10% of the maximum water loss rates measured for intact flowers (data not shown).
Figure 3.
Time course of water loss rates expressed on an area basis of detached 1st-d flowers (black circles) as compared with leaf-bearing shoots (white circles) after detachment from the plant. Each time course is the average of three flowers (without leaves attached), and three leaf-bearing shoots of a similar surface area constitute the tepal area of flowers. Error bars denote sd. Flowers and shoots were detached at 11:30 am and desiccated under cloud-free ambient field conditions. Ten minutes of the response curve are missing because of transport and preparation of the samples before measurement.
To determine the comparative drought responses of tepals and leaves, we measured their pressure-volume relations. We found that tepals functioned with much lower tolerance to desiccation as compared with leaves. Tepals lost turgor at a significantly higher Ψ than leaves (Table II). The relative WCs at the turgor loss point were significantly higher in tepals than in leaves (Table II).
Table II.
Pressure-volume relations to drying tepals and leaves
Values (n = 8 for each mean) were compared using the Mann-Whitney U test. Asterisks denote P < 0.001.
| Trait | Tepals | Leaves |
|---|---|---|
| Ψ at turgor-loss point (MPa) | −0.701 ± 0.13 | −2.2 ± 0.3* |
| Relative WC at turgor-loss point (%) | 95.5 ± 1.2 | 85 ± 0.8* |
Water Status
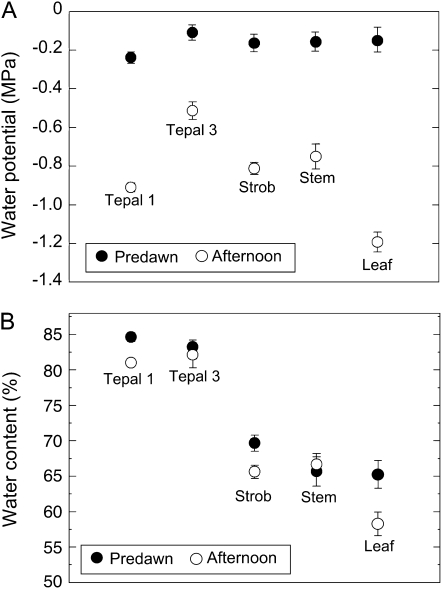
For 1st- and 2nd-d flowers, nearly all parts of Southern magnolia flowers measured in the afternoon decreased in both Ψ and WC from predawn values (Fig. 4). We found that predawn to afternoon differences in Ψ and WC were similar on both days of anthesis (data not shown). Therefore, we pooled the measurements for both days of anthesis. Ψ of the tepals decreased from predawn to afternoon by approximately 0.7 MPa in first whorl tepals and 0.4 MPa in third whorl tepals (Fig. 4A). Ψ of the strobilus decreased from predawn to afternoon by about 0.75 MPa (Fig. 4A). The diurnal variations in Ψ measured for stem and leaf tissues were similar on both days of anthesis, with ranges of approximately 0.5 MPa for stems and 1.1 MPa for leaves (Fig. 5A).
Figure 4.
Changes in Ψ and WC of flower parts in relation to stem and leaves during 2 d of anthesis in Southern magnolia. A, Ψ changes from predawn (black circles) to afternoon (white circles) for 1st-d flower parts, stem, and leaf tissues. B, WC changes from predawn (black circles) to afternoon (white circles). Sample sizes for each point in A and B are as follows for first whorl tepals (Tepal 1; n = 20), third whorl tepals (Tepal 3; n = 20), covered leaves (approximating Ψstem; Stem; n = 20), strobili (Strob; n = 10), and freely transpiring leaves (Leaf; n = 30). Error bars denote sd. Measurements were conducted under the same environmental conditions as presented in Figure 1C.
Figure 5.
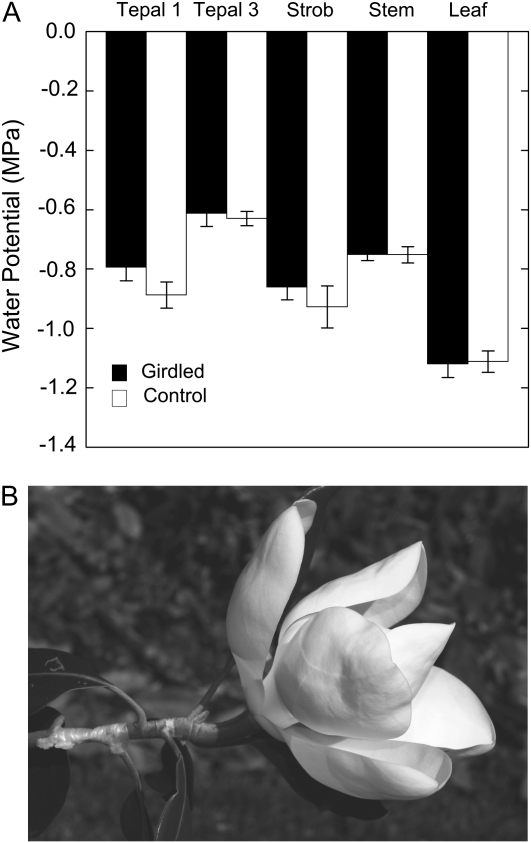
A, The effect of bark girdling on Ψ of 1st-d flowering shoots of Southern magnolia relative to control flowering shoots. Shoots were girdled in the morning (7:00 am) and sampled in the late afternoon (4:00 pm) on the same day. Each bar is the mean of 10 measurements for tepals, stems, and leaves, while five measurements are averaged for the strobilus value. Error bars denote sd. No significant differences were found between organs within treatment comparisons (Mann-Whitney U test). B, Photograph of a 1st-d flower that has been girdled. No wilting of the perianth or adjacent leaves was observed. The flower was photographed at 4:00 pm at an air temperature of 35°C.
Resulting from the predawn to afternoon changes in Ψ, negative Ψ gradients from the first whorl tepals to the stem tissues and from the strobilus tissues to the stem tissues were observed during anthesis (Table III). However, we found the Ψ gradients for third whorl tepals and the stem to be in an opposite (positive) direction during anthesis. The Ψ gradients between leaves and stems during anthesis were approximately four times greater than the Ψ gradients between first whorl tepals and stems (Table III).
Table III.
Afternoon Ψ gradients between flower parts and stem Ψ for flowers during anthesis
Sample sizes denote the number of flower parts sampled from 10 individual flowers, and means ± sd are presented. Since there is only one strobilus per flower, only one strobilus value is reported for each flower sampled. Different letters denote significant differences of at least P < 0.05 between the means of the different trait values (Mann-Whitney U test).
| Sample | Gradient |
|---|---|
| MPa | |
| ΔΨTepal 1 to Stem (n = 20) | −0.112 ± 0.013a |
| ΔΨTepal 3 to Stem (n = 20) | +0.23 ± 0.022b |
| ΔΨStrobilus to Stem (n = 10) | −0.063 ± 0.024c |
| ΔΨLeaf to Stem (n = 20) | −0.40 ± 0.031d |
Maximum predawn WC values of Southern magnolia tepals, at 85% for the first whorl tepals and 83% for the third whorl tepals, were much greater than maximum WC of strobilus, stem wood, and leaf tissues (68%, 65%, and 65%, respectively) during anthesis (Fig. 4B). Consistent with the observation of significant flower E, WC values of first whorl tepals decreased approximately 5% from predawn values (Fig. 4B). However, for third whorl tepals, which transpired less, WC decreased about 3% from the predawn WC value. Strobilus tissues decreased about 5% in WC. Stem WC, at approximately 65%, remained unchanged diurnally. Leaf WC exhibited an approximately 10% decrease (Fig. 4B).
Effect of Girdling and Observations of Dye Accumulation during Flower E
To assess the role of phloem water supplies during anthesis, we girdled the stem bark subtending flowers. We found that in both 1st- and 2nd-d flowers, girdling had no significant effect on Ψ (Fig. 5), WC, or rates of flower water loss (data not shown). Girdling also had no effect on Ψ, WC, and gas exchange of subtending leaves (data not shown).
Safranin fed to transpiring 1st-d flowers produced consistent patterns of staining. All 1st-d flowers exhibited staining of the basal xylem strands of tepal vascular bundles and the xylem veins of first and second whorl tepals. Safranin accumulation occurred in the ring of xylem bundles that supplied the strobilus tissues. However, in all five 1st-d flowers that we measured, no safranin accumulated in the basal vascular bundles or the minor xylem veins of the third whorl tepals. In contrast to 1st-d flowers, detached 2nd-d flowers only weakly took up safranin. We drew this conclusion based on visual observations of less dye loading into the veins of first and second whorl tepals as well as strobilus tissues in 2nd-d flowers. No safranin was evident in the veins of third whorl tepals.
DISCUSSION
Regulation of Flower Water Balance in Southern Magnolia
Previous observations of high, diurnally stable WC and Ψ of flowers juxtaposed with much “drier” tissues and more negative Ψ of transpiring leaves in several species have motivated the hypothesis that flowers were largely uncoupled from the stem xylem and received water entirely from the phloem (Chapotin et al., 2003; De la Barrera and Nobel, 2004; Galen, 2005). We demonstrate here that the water balance of Southern magnolia flowers functions differently from previously examined flowers.
One such water balance difference is that even when leaves subtending flowers were transpiring, most measured parts of Magnolia flowers exhibited Ψ values at or lower than the stem xylem Ψ (Fig. 5). Second, Magnolia flowers underwent significant daytime dehydration (5% decrease in WC and 0.75-MPa decrease in Ψ averaged over the parts of the flower sampled) followed by rehydration at night, albeit at lower magnitudes of decreases in water status than transpiring leaves (Fig. 4; Chapotin et al., 2003). Such diurnal cycling of Ψ in flowers resulted in downhill (negative) Ψ gradients between first whorl tepals to the stem and the strobilus. An exception to this pattern was found in the ΔΨ gradients of the third whorl tepal-to-stem gradients, which were positive. The processes underlying the peculiar water relations of third whorl tepals are discussed below.
Third, maximum E in Magnolia flowers was much higher than rates reported for other species. E from previously measured flowers ranged from 0.0054 to a maximum of 0.431 mmol m−2 s−1 in avocado (Persea spp.) flowers (total of six species; Blanke and Lovatt, 1993; Galen et al., 1999; Patino and Grace, 2002). Magnolia flowers, by contrast, sustained high maximum rates of E at 0.72 mmol m−2 s−1 for first whorl tepals of 1st-d flowers. Consistent with high E relative to other flowers, Southern magnolia tepals possessed abundant stomata (van Doorn, 1997; Patino and Grace, 2002). Unlike petals of other species where the stomata were absent or sparse (0.001–0.05 per mm2) and nonfunctional (van Doorn, 1997; Patino and Grace, 2002), stomata on Southern magnolia tepals were relatively dense. The stomata also responded to light, since minimum gs occurred at predawn and at night (Fig. 1).
A Role for the Xylem in Flower Hydration
Based on the distinct flower water relations we observed from those of previously examined flowers as well as other lines of evidence discussed below, our results demonstrate that flower function of Southern magnolia hinges on xylem hydraulic flow.
The hypothesis that Southern magnolia flowers depend upon on the xylem for water use is supported by our observations that flowers are efficiently connected to the stem xylem (Fig. 2). KPerianth was approximately one-third of the KLeaf value of subtending leaves. Thus, the hydraulic conductance of the perianth falls in the range of maximum KLeaf values found previously for the photosynthetic leaves of ferns and shade-adapted angiosperms that use the xylem for E (Brodribb et al., 2007). The high hydraulic conductance of the flower perianth represents a capacity for water movement that can only be furnished by the nonliving, conduit-based apoplast of the xylem, because the living tissues of the phloem are much more resistant to hydraulic flow (Van Ieperen et al., 2003).
Consistent with the relatively high hydraulic conductance of the flower perianth, we found that the xylem surface area relative to perianth surface area (HV) was nearly one-third of the value found in sun-exposed, nonflowering leafy shoots. The measured HV may underestimate the xylem hydraulic capacity of flower xylem somewhat, given that the conduit diameters were larger in flower xylem as compared with those of the stem. Although no other published values of flower HV were available for comparison, the large (200-cm2 perianth) and likely phloem-hydrated flowers of Hibiscus laevis (Malvaceae; see Trolinder et al. [1993] for another malvaceous example) possess a HV of 0.105 × 104 ± 0.0055 (n = 3), which is only one-third of the HV of Magnolia flowers.
Additionally, anatomical traits of the tepals are consistent with a relatively high hydraulic efficiency of the perianth. For example, the tepal VD values were equivalent to those of ferns as predicted from their fern-like E (Brodribb et al., 2007). However, we found that the relative differences in stomatal density between tepals and leaves were not proportional to the measured differences in maximum gs. This difference was probably due to contrasting stomatal exposure in leaves versus petals. Stomata-bearing surfaces of Southern magnolia leaves are covered in a dense layer of trichomes and sunken stomata, reducing gs relative to pore area (Roth-Nebelsick, 2007). In contrast, tepal stomata are fully exposed to the environment. We also found that the stomata were somewhat larger than leaf stomata, further increasing the pore area available for diffusion (Table I).
The lack of a flower water balance response to stem bark girdling, which severs phloem water delivery (Fishman et al., 2001), is consistent with xylem involvement in flower hydration. Transpiring Magnolia flowers lose relatively large amounts of water, and flowers wilt under much milder water deficits, including both RWC and Ψ, as compared with leaves (Table II). Therefore, if the phloem supported flower E, then we would expect that girdling the bark upstream of the flower would produce rapid wilting of the perianth. Surprisingly, we found that flower water balance remained unchanged by girdling (Fig. 5). Girdling of 1st-d flowers at predawn also did not change the rates observed for any of the phases of flower development, including senescence (data not shown). The only effect of bark girdling we observed was that 1st-d flowers did not secrete nectar in the morning from the stigmatic crests while the control shoots did before significant tension developed in the strobilus (data not shown).
Another line of evidence supporting xylem hydration of Southern magnolia flowers is that xylem hydraulics appear to regulate flower movements. Although physiological mechanisms underpinning flower movements are complex (van Doorn and Van Meeteren, 2003), we found that flowers with an open perianth at midday or with wilted first and second whorl tepals during the afternoon rapidly closed (approximately 5 min) after recutting the stem xylem underwater (data not shown). Thus, we suggest that flower opening and closure in Magnolia is primarily driven by changes in Ψ mediated through the xylem because of the rapid closure response. Flower stems cut in air (thus xylem embolized) and then floated on water did not close, demonstrating that the closure response was not mediated by local humidity (van Doorn and Van Meeteren, 2003).
Finally, we observed that during perianth E, the xylem-mobile dye safranin was strongly taken up by the xylem of first and second whorl tepals as well as the strobilus xylem. Our findings differ from reported anatomical findings on many reproductive structures (including fruits; but see Bondada et al. [2005] and Morandi et al. [2007] for examples of fruits that have open xylem-water pathways during ripening) that demonstrated breaks between vegetative and reproductive xylem strands or highly resistant bottlenecks in the xylem between organs while the phloem remained continuous (Zee and O'Brien, 1970; Creasy et al., 1993; Van Ieperen et al., 2003; Keller et al., 2006; De la Barrera and Nobel, 2004). Such xylem discontinuities or high xylem resistance can explain why the lower Ψ of adjacent leaves or soil did not drain flowers of their water (Chapotin et al., 2003; for a fruit example, see Van Ieperen et al., 2003). In flowers hydrated by the xylem, however, such a possibility cannot be avoided.
However, during anthesis, not all perianth parts of Magnolia appeared to be connected to the stem xylem or the xylem within the flower. For example, third whorl tepals were found to operate at a Ψ of −0.4 MPa, a value more positive than daytime Ψ values of the stem and surrounding flower tissues (Fig. 4). How do third whorl tepals maintain a higher water status despite being bounded by tissues operating at lower Ψ?
Third whorl tepals appeared to be discontinuous from the main xylem system, since safranin never accumulated into the tepal veins on either day of anthesis (data not shown). However, a cryptic phloem supply line hydrating the third whorl tepals cannot explain how water loss was managed, since the water use of third whorl tepals was unaffected by girdling under high VPD (Fig. 5). A plausible mechanism for how the third whorl tepals are hydraulically isolated is through the development of a relatively high xylem resistance between the tepal xylem and the rest of the flower's xylem. A high xylem resistance could result from greater frequency of resistant vessel end walls that could occur between the third whorl tepal base and the strobilus (Van Ieperen et al., 2003).
Certainly, when integrated over the lifetime of reproduction (preanthesis development, including bud initiation and expansion that constructs the flower, and postanthesis, once the tepals are jettisoned and fruit seed maturation occurs), the phloem is the essential supply line for most flower development in Southern magnolia. Unlike what we observed during anthesis, we found that girdling of unopened flower buds resulted in smaller flowers, sometimes flower abortion, and always failures of fruit to develop (data not shown). Along with carbon and nutrients, we suggest that phloem can supply the water necessary for reproductive development during all of these tepal-less stages, since water loss rates of these floral parts are much lower.
CONCLUSION
Our results demonstrate that flowers can be significantly supplied with water from the xylem during anthesis. Efficient xylem pathways are developed in Southern magnolia to support a transient but critical need for high water demand to bear a large perianth for pollinator attraction (Thien, 1974; Allain et al., 1999). Is the involvement of the xylem during flower anthesis related to the unusual evolution of large perianth size (Davis et al., 2008)? Or considering the nearly basal evolutionary position of Southern magnolia in angiosperm phylogeny, is it a mark of an ancestral angiosperm function?
Much more comparative work is needed to address these questions. However, the widespread distribution of phloem-hydrated flowers in derived eudicots (Chapotin et al., 2003; De la Barrera and Nobel, 2004) in conjunction with new measurements of flower water balance in a more basal angiosperm species (Illicium anisatum) suggest that xylem-connected flowers may be an ancestral feature of angiosperms (Feild et al., 2009). Because previously studied eudicots possessed stamen-derived petals (andropetals) whereas Southern magnolia has nonhomologous leaf-like bracteolar tepals (Ronse De Craene, 2008; Soltis et al., 2009), the developmental evolution of true petals may be a major transition in angiosperm reproduction, because petal evolution is correlated with a transition from xylem- to phloem-hydrated flowers that reduce the water costs of flowering (Feild et al., 2009). If xylem-hydrated flowers represent the ancestral condition at the base of the extant phylogeny, then an integrative account for the early evolution of flowers requires an understanding of how flower water use feeds back on flower developmental evolution and pollination biology (Feild et al., 2009).
MATERIALS AND METHODS
Plant Species, Study Site, and Microclimate Observations
We studied three mature trees of Southern magnolia (Magnolia grandiflora [Magnoliaceae]) in Knoxville, Tennessee, from May 30 to June 20, 2008. Southern magnolia is a common evergreen tree in mesic forests across the southeastern United States (Allain et al., 1999). Flowering of Southern magnolia occurs from April and early July. Flower production of Southern magnolia peaked during our sampling period. When unfurled, flowers of Southern magnolia average 20 cm across, and up to 25 cm in our population.
Microclimate observations were made with a data logger (CR 850; Campbell Scientific) fitted with a humidity/temperature sensor (HMP50-L; Vaisala) and a quantum sensor (Li 190SB-L; Li-Cor). Leaf and tepal temperatures were measured with fine thermocouple wire (36 gauge; Omega Engineering) connected to the data logger.
Anatomy and Ecomorphic Traits
For observations of VD (mm of vein length per mm2), we sampled pieces of tissue (2 × 3 mm) from the middle portions of tepals and mature leaves (n = 5 for each). Samples were fixed in 50% ethanol and then cleared using a standard procedure (Ruzin, 1999). Veins were stained in safranin, mounted on slides, and measured using an upright microscope (Axio-Imager; Carl Zeiss). Digital images were captured with an AxioCam camera (Carl Zeiss) and processed using ImageJ 1.40g freeware (NIH Image). For cuticle anatomy, we macerated tepal and leaf tissues using an accepted solution involving 10% hydrogen peroxide and glacial acetic acid (Ruzin, 1999). We stained cuticles in safranin and measured stomatal density and size (length and width) with an upright microscope. Stomatal traits were based on 25 individual measurements per sample. Leaf mass per area of tepals and leaves was determined by scanning the fresh area with a flat-bed scanner at 600 dpi, and the samples were dried at 60°C for 2 d in an oven before weighing on an electronic balance (0.001 g resolution; Denver Instruments).
HV of flowers (xylem area [m2] divided by tepal surface area [m2]) was determined on five flower shoots as compared with leafy shoots of a similar leaf area (approximately 450 cm2) and stem wood thickness (5 mm diameter). For xylem surface area, cross-sections of the xylem in the flower receptacle were used, while the stem cross-section just below the shoot was used for leafy shoots. We sampled fully expanded and undamaged shoots that were exposed to full sun throughout the day. Xylem area was measured using an upright microscope. We determined tepal and leaf surface areas by scanning and analysis with ImageJ. We also measured the xylem conduit diameters of flower and stem xylem using ImageJ on images of free hand sections stained with safranin. Xylem conduit data were based on 10 individual measurements for five samples.
Gas Exchange
We measured water vapor flux of Magnolia tepals and leaves using an infrared gas analyzer equipped with a mixed red-blue light-emitting diode light source (LiCOR 6400XT, Li-Cor). gs and E were measured on flowers and subtending leaves on several blossoming shoots at specific times during the first 2 d of anthesis in Southern magnolia flowers. The 3rd d of anthesis was not measured because flowers senesced in our study population. All gas-exchange parameters were calculated using accepted equations. All gas-exchange measurements were conducted only on clear days to avoid heterogeneities on leaf and flower gas exchange by passing clouds.
First- and 2nd-d flowers as well as subtending leaves on both anthesis days were measured at the following time periods: (1) predawn, 5:30 to 6:30 am; (2) morning, 8:30 to 9:30 am; (3) midday, 11:30 am to 1:00 pm; (4) afternoon, 5:00 to 6:00 pm; and (5) night, 9:30 to 10:30 pm. For each time point, conditions in the cuvette during gas exchange were tuned to ambient conditions. These conditions included (with microclimate variables listed as follows: air temperature, air VPD, and light intensity of photosynthetically active radiation): predawn and nighttime (26°C ± 0.5°C, 0.70 ± 0.1 kPa, 0 μmol m−2 s−1); morning (28°C ± 1.2°C, 1.1 ± 0.15 kPa, 450 μmol m−2 s−1); midday (31°C ± 1.2°C, 2.11 ± 0.21 kPa, 1,500 μmol m−2 s−1); and afternoon (34°C ± 1.2°C, 3.0 ± 0.21 kPa, 1,400 μmol m−2 s−1). Throughout all measurements, we controlled CO2 at 380 μL L−1 with an onboard CO2 mixer (Li-Cor).
For each time period, we sampled two separate flowers. In all, we measured a total of 20 individual flowers for the entire time course of gas exchange. For each flowering shoot sampled per time period, we measured two tepals from each of the three tepal whorls as well as two fully expanded and undamaged leaves. Thus, to construct the 10 time periods over the 2 d of anthesis in Southern magnolia, a total of 120 tepals and 40 leaves were measured.
Because most Southern magnolia branches with flowers occurred high in the canopy (3–6 m), we measured gas exchange on detached branches. We could not measure detached shoots with their cut ends recut underwater because the flowers closed hydopassively upon being recut underwater. Therefore, we developed a specific detachment procedure to avoid introducing xylem embolism artifacts that could affect leaf gas exchange less than 10 min after severing. We severed each flowering branch off of the tree using a pole pruner at a length of approximately 0.85 m. Each selected branch had at least three intervening branch nodes between the flower and the first cut in air. Long branch lengths and multiple nodes ensured that the distance of the first cut was at least two times longer than the length of the rare longest xylem vessel (i.e. approximately 20 cm long). The average length of the longest xylem vessels in the stem wood was determined using low-pressure (0.02 MPa) air injection with a hand pump.
After severing, gas exchange of each flower's tepals and two subtending leaves on each shoot was measured at steady-state fluxes in the cuvette. This required 30 s, and the flux values were recorded every 1 s and averaged over 10 s to give a single sample value. Thus, a measurement for a flowering shoot took about 7 min to sample two leaves and eight tepals. To check that fluxes of detached flowers did not change soon after detachment, we conducted two tests. First, we measured every 20 s how gs of transpiring leaves and first whorl tepals changed in response to detachment. For leaf shoots sampled at midday, stable gs was observed after 7 min of detachment (mean gs at 1 min = 320 ± 10 mmol m−2 s−1 versus mean gs at 7 min = 310 ± 9 mmol m−2 s−1; n = five for each). Approximately 7 min after severing, gs then dropped as the stomata closed. gs of first whorl tepals, however, did not respond to detachment over the 7 min after detachment while in the cuvette chamber (mean gs at 1 min = 75 ± 10 mmol m−2 s−1 versus mean gs at 7 min = 83 ± 8 mmol m−2 s−1; n = five for each). As an additional check, we measured leaf and first whorl tepal water loss rates at midday on a clear day on three attached flowers that were within reach of the gas-exchange system cuvette. We did not observe any significant differences in the fluxes of attached leaves and tepals of flowering shoots as compared with detached ones measured within 7 min after severing (mean gs of leaves attached = 319 ± 10 mmol m−2 s−1 versus mean gs of leaves after 7 min of being severed = 314 ± 9 mmol m−2 s−1; n = five for each). Our measurement order for the tepal types and leaves was randomized.
Water Status
The Ψ of tepals and subtending leaves on a flowering Southern magnolia shoot was determined using a pressure chamber (PMS-1000; Plant Moisture Status Instruments) and a digital pressure gauge (±0.01 MPa; Ashcroft Scientific). To reduce possible dehydration of samples while in the pressure chamber, we wrapped each sample in plastic (Saran Wrap). We determined the balancing pressures of 10 flowering shoots of Southern magnolia at just before sunrise (6:00–7:00 am, when leaf water status was maximal) and late afternoon (3:00–5:00 pm, when leaf water status was lower) on cloud-free days. All blooming shoots that we sampled had a single flower subtended by several leaves. For each shoot, we made an estimate of Ψ of the stem using covered leaves as an estimate of stem Ψ (Melcher et al., 1998). To do so, we individually wrapped two leaves on each shoot in three layers of thin Saran Wrap followed by a layer of reflective aluminum foil and a plastic Whirlpak bag to stop E. During sampling, we cut flowering shoots from trees, and the shoots were placed in humidified bags, protected from sunlight, and transported within 30 s to a laboratory for measurements.
For each of the 10 flowering shoots sampled, we measured the Ψ of two first whorl tepals, two third whorl tepals, one strobilus, two covered leaves to estimate Ψ stem, and three uncovered leaves. We determined strobilus Ψ by equilibrating a single strobilus (with tepals removed) in a tightly sealed and humidified plastic bag that was placed in the dark. After 4 h, the strobilus receptacle was whittled into a length of vascular tissue while inside a humidified bag. Then the cut end was fit through the pressure chamber cap, and the balancing pressure was determined. These procedures were conducted on both 1st- and 2nd-d flowering shoots. Total sample sizes for each time point were 20 first whorl tepals, 20 third whorl tepals, 10 strobili, 20 covered leaves, and 30 freely transpiring leaves.
We determined the percentage of WC (dry mass relative to fresh mass × 100%) for each tissue part measured for Ψ on a separate set of 10 flowering shoots sampled in the morning and afternoon periods. Entire flowers with leaves were rapidly sealed in humid plastic bags in the field and weighed on an electronic balance indoors. Stem WC was determined using a 3-cm-long portion of the wood subtending the flower. The dry mass for each sample was determined as above. Total sample sizes for each time point were the same as for Ψ.
Pressure-Volume Analysis and Water Loss Rates
Ψ isopleths (Ψ versus relative water content [RWC]) of tepals and leaves were determined by repeated measures (four to six observations per organ) of mass and Ψ on the sample using accepted procedures (Sack et al., 2003). Fully expanded tepals and leaves were collected at maximum field hydration before sunrise. Leaf Ψ was greater than −0.05 MPa at the beginning of a pressure-volume curve. Then, alternate measurements of mass and Ψ of leaves and tepals were made as the organs slowly desiccated to below their respective turgor loss points. Fresh masses and dry mass values were used to calculate RWC (Sack et al., 2003). Ψ isopleths were determined on eight leaves and eight tepals taken from eight different blooming shoots. From pressure-volume curves of tepals and leaves, we determined the Ψ and RWC at the turgor loss point using accepted curve-fitting procedures (Schulte and Hinckley, 1985) with a data-analysis program (Sigma-Plot version 8.01; SPSS). We found no significant differences among the pressure-volume relations of the three tepal whorls; therefore, we pooled the data to generate a single pressure-volume relation.
Water loss rates from whole flowers were determined by weighing detached, transpiring, and opened flowers on an electronic balance. For comparison, we measured water loss rates of detached leafy shoots bearing a leaf area roughly equivalent to a whole flower (approximately 450 cm2). Samples were detached at 11:30 am and weighed every 15 min on a typical clear (approximately 1,500 μmol m−2 s−1 photosynthetically active radiation), breezy, hot summer day at a relatively constant relative humidity (45%–55%) and temperature (34°C ± 1.2°C). Water loss rates were expressed as mmol m−2 s−1 after determining the area of sampled flowers and leaves. Time courses presented were averages of three 1st-d flowers and three leafy shoots.
Finally, we measured water loss rates from detached strobili sampled at three developmental stages. These stages were (1) 1st-d strobili with stamens attached, (2) 2nd-d strobili with stamens detached, and (3) ripening strobili that had senesced the tepals. Each stage was represented by three samples, and water loss rates were measured under the same ambient conditions as above.
Flower Hydraulic Conductance
To measure the hydraulic conductance of entire flowers (KFlower) and leaves (KLeaf), we modified the technique of Franks (2006) to measure the kinetics of hydraulic flux relaxation following the application of step changes in the Ψ gradient across the sample. The flow meter measures hydraulic flux into flower or leaves by multiplying the pressure deferential across a PEEK tube of known resistance that is in series with the measured organ (Brodribb and Holbrook, 2006). The pressure of water in the flow meter was determined with a pressure transducer (PX-136; Omega Engineering) monitored with a data logger (CR-10X; Campbell Scientific). Hydraulic flux was expressed on a tepal or leaf area basis (mmol m−2 s−1). The capillary tube was calibrated using a high-resolution electronic balance as described previously (Brodribb and Feild, 2000).
To measure KFlower and KLeaf, five flowers and five leafy shoots were severed during mid morning (9:30–11:00 am). The lengths of the stems with a flower or two to three leaves at the distal end were cut at lengths longer than the longest vessel embolized by the first cut in air (see above). Then, the samples were wrapped in plastic and transported to the laboratory. The ends of the shoots were recut underwater. After recutting, the flower or leaves at the end of the shoot was inserted into a pressure chamber with the stem protruding through the lid of the pressure chamber. The bark was then peeled off the stem wood at a length of 1 cm, and the exposed stem end was shaved with a razor blade. Next, the pressure in the chamber was increased slowly until the balancing point was reached, where the meniscus could be seen at the cut end of the stem using a dissecting microscope. At this point, a tube filled with a degassed, filtered solution of 0.01 m KCl attached to the flow meter was affixed to the hydrated end of the stem. Because sunlight can affect KLeaf (Scoffoni et al., 2008), we made sure that all shoots had been exposed to approximately 1,000 mmol m−2 s−1 outdoor light within 100 s of our measurement.
At the balancing pressure value (0.25–0.4 MPa for all samples), the hydraulic flux measured on the flow meter was zero. After establishing a zero flow steady state (requiring 5 min for flowers and 2 min for leaves), the pressured gas inside the chamber was rapidly vented, creating a driving force equivalent to the balancing pressure. Upon pressure release, the flow meter was used to calculate the hydraulic flux entering the leaf (Brodribb and Holbrook, 2006). Hydraulic conductance (mmol m−2 s−1 MPa−1) was calculated by dividing the theoretical peak hydraulic flux (taken as the zero-time intercept of the exponential decay function fitted to flow after depressurization) by the balancing pressure (MPa) determined before relaxation of the pressure. Hydraulic conductance was normalized to 20°C to normalize the viscosity changes for a 1.3°C to 2.5°C drop in temperature during depressurization. We measured shoot tissues while in the pressure chamber with a thermocouple every 0.5 s with a data logger. Flow was expressed on an area basis. To partition out the hydraulic conductance of the perianth from the rest of the flower (dominated by the strobilus that also contains xylem), we remeasured the hydraulic conductance of the flower again but with the tepals excised. The resulting hydraulic flux was then subtracted from the whole flower flux to calculate KPerianth.
Shoot Girdling
Early in the morning (4:00 am), we removed, by hand, a 4-cm length of bark on the stem that subtended the flower. We covered the exposed xylem with a tight wrapping of Parafilm to prevent further desiccation. We girdled five shoots with 1st-d blooms and left five adjacent shoots with 1st-d blooms as controls. Ψ and WC values of tepal whorls, the strobilus, as well as stem and leaf tissues downstream from the girdled zone were measured as described above. We determined gas exchange for tepals and leaves on girdled and nongirdled shoots as above.
Dye Feeding
A filtered (to 0.5 μm), dilute (1% concentration in water) safranin solution in 0.15 m KCl was fed to transpiring blooms. We severed blooms attached to a length of stem wood twice as long as the longest cut vessel from Southern magnolia trees in the early morning. The blooms were then carefully recut while underwater, and the cut end of the branch and the xylem surface was shaved clean. Finally, the cut ends of the blooms were transferred into the dye solution, and the blooms were held upright under natural full-sun conditions. Dye-fed shoots were sectioned by hand. The distribution of safranin in the flower was assessed with a dissecting microscope.
Acknowledgments
We thank Patrick Hudson, Hubert S. Feild, and Greg Jordan for comments on the manuscript.
This work was supported by the National Science Foundation (grant no. IOB–0714156).
The author responsible for distribution of materials integral to the findings presented in this article in accordance with the policy described in the Instructions for Authors (www.plantphysiol.org) is: Taylor S. Feild (tfeild@utk.edu).
Open Access articles can be viewed online without a subscription.
References
- Allain LK, Zavada MS, Matthews DG (1999) The reproductive biology of Magnolia grandiflora. Rhodora 101 143–162 [Google Scholar]
- Blanke MM, Lovatt CJ (1993) Anatomy and transpiration of the avocado inflorescence. Ann Bot (Lond) 71 543–547 [Google Scholar]
- Bondada BR, Matthews MA, Shackel KA (2005) Functional xylem in the post-veraison grape berry. J Exp Bot 56 2949–2957 [DOI] [PubMed] [Google Scholar]
- Brodribb TJ, Feild TS (2000) Stem hydraulic supply is linked to leaf photosynthetic capacity: evidence from New Caledonian and Tasmanian rainforests. Plant Cell Environ 23 1381–1388 [Google Scholar]
- Brodribb TJ, Feild TS, Jordan GJ (2007) Leaf maximum photosynthetic rate and venation are linked by hydraulics. Plant Physiol 144 1890–1898 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brodribb TJ, Holbrook NM (2006) Declining hydraulic efficiency as transpiring leaves desiccate: two types of response. Plant Cell Environ 29 2205–2215 [DOI] [PubMed] [Google Scholar]
- Chapotin SM, Holbrook NM, Morse SR, Gutierrez MV (2003) Water relations of tropical dry forest flowers: pathways for water entry and the role of extracellular polysaccharides. Plant Cell Environ 26 623–630 [Google Scholar]
- Creasy GL, Price SF, Lombard PB (1993) Evidence for xylem discontinuity in Pinot Noir and Merlot grapes: dye uptake and mineral composition during berry maturation. Am J Enol Vitic 44 187–192 [Google Scholar]
- Davis CC, Endress P, Baum DA (2008) The evolution of floral gigantism. Curr Opin Plant Biol 11 49–57 [DOI] [PubMed] [Google Scholar]
- De la Barrera E, Nobel PS (2004) Nectar: properties, floral aspects, and speculations on origin. Trends Plant Sci 9 65–69 [DOI] [PubMed] [Google Scholar]
- Feild TS, Chatelet DS, Brodribb TJ (2009) Ancestral xerophobia: a hypothesis on the whole plant ecophysiological context for early angiosperm evolution. Geobiology 7: 237–264 [DOI] [PubMed]
- Fishman S, Genard M, Huguet JG (2001) Theoretical analysis of systematic errors introduced by a pedicel-girdling technique used to estimate separately the xylem and phloem flows. J Theor Biol 213 435–446 [DOI] [PubMed] [Google Scholar]
- Franklin-Tong N, Franklin FCH (2003) Gametophytic self-incompatibility inhibits pollen tube growth using different mechanisms. Trends Plant Sci 8 598–605 [DOI] [PubMed] [Google Scholar]
- Franks PJ (2006) Higher rates of leaf gas exchange are associated with higher leaf hydrodynamic pressure gradients. Plant Cell Environ 29 584–592 [DOI] [PubMed] [Google Scholar]
- Galen C (2005) It never rains but then it pours: the diverse effects of water on flower integrity and function. In E Reekie, FA Bazzaz, eds, Reproductive Allocation in Plants. Elsevier Press, San Diego, pp 77–95
- Galen C, Sherry RA, Carrol AB (1999) Are flowers physiological sinks or faucets? Costs and correlates of water use by flowers of Polemonium viscosum. Oecologia 118 461–470 [DOI] [PubMed] [Google Scholar]
- Galen C, Sherry RA, Dawson TE (1993) Carpels as leaves: meeting the carbon cost of reproduction in alpine buttercup. Oecologia 95 187–193 [DOI] [PubMed] [Google Scholar]
- Glover B (2007) Understanding Flowers and Flowering: An Integrated Approach. Oxford University Press, Oxford
- Griesel WO (1954) Cytological changes accompanying abscission of perianth segments of Magnolia grandiflora. Phytomorphology 47 123–132 [Google Scholar]
- He S, Joyce DC, Irving DE (2006) Competition for water between inflorescences and leaves in cut flowering stems of Grevillea ‘Crimson Yul-lo’. J Hortic Sci Biotechnol 81 891–897
- Hu T, Doi M, Imanishi H (1998) Competitive relations between leaves and flower buds of cut roses. J Jpn Soc Hortic Sci 67 532–536 [Google Scholar]
- Keller M, Smith JP, Bondada BR (2006) Ripening grape berries remain hydraulically connected to the shoot. J Exp Bot 57 2577–2587 [DOI] [PubMed] [Google Scholar]
- Lambrecht SC, Dawson TE (2007) Correlated variation of floral and leaf traits along a moisture availability gradient. Oecologia 151 574–583 [DOI] [PubMed] [Google Scholar]
- Lush WM, Grieser F, Wolters-Arts M (1998) Directional guidance of Nicotiana alata pollen tubes in vitro and on the stigma. Plant Physiol 118 733–741 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Melcher PJ, Meinzer FC, Yount DE, Goldstein G, Zimmermann U (1998) Comparative measurements of xylem pressure in transpiring and non-transpiring leaves by means of the pressure chamber and the xylem pressure probe. J Exp Bot 49 1757–1760 [Google Scholar]
- Morandi B, Rieger M, Grappadelli LC (2007) Vascular flows and transpiration affect peach (Prunus persica Batsch.) fruit daily growth. J Exp Bot 58 3941–3947 [DOI] [PubMed] [Google Scholar]
- Patino S, Grace J (2002) The cooling of convolvulaceous flowers in a tropical environment. Plant Cell Environ 25 41–51 [Google Scholar]
- Ronse De Craene L (2008) Homology and evolution of petals in the core eudicots. Syst Bot 33 301–325 [Google Scholar]
- Roth-Nebelsick A (2007) Computer-based studies of diffusion through stomata of different architecture. Ann Bot (Lond) 100 23–32 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ruzin SE (1999) Plant Microtechnique and Microscopy. Oxford University Press, New York
- Sack L, Cowan PD, Jaikumar NJ, Holbrook NM (2003) The ‘hydrology’ of leaves: coordination of structure and function in temperate woody species. Plant Cell Environ 26 1343–1356 [Google Scholar]
- Schulte PJ, Hinckley TM (1985) A comparison of pressure-volume curve data analysis techniques. J Exp Bot 36 1590–1602 [Google Scholar]
- Scoffoni C, Pou A, Aasamaa K, Sack L (2008) The rapid light response of leaf hydraulic conductance: new evidence from two experimental methods. Plant Cell Environ 31 1803–1812 [DOI] [PubMed] [Google Scholar]
- Soltis PS, Brockington SF, Yoo MJ, Piedrahita A, Latvis M, Moore MJ, Chanderbali AS, Soltis DE (2009) Floral variation and floral genetics in basal angiosperms. Am J Bot 96 110–128 [DOI] [PubMed] [Google Scholar]
- Thien LB (1974) Floral biology of Magnolia. Am J Bot 61 1037–1045 [Google Scholar]
- Trolinder NL, McMichael BL, Upchurch DR (1993) Water relations of cotton flower petals and fruit. Plant Cell Environ 16 755–760 [Google Scholar]
- Willmer PG (1986) Foraging patterns and water balance problems of optimization for a xerophilic bee Chalicodoma sicula. J Anim Ecol 55 941–962 [Google Scholar]
- van Doorn WG (1997) Water relations of cut flowers. Hortic Rev (Am Soc Hortic Sci) 18 1–85 [Google Scholar]
- van Doorn WG, Van Meeteren U (2003) Flower opening and closure: a review. J Exp Bot 54 1801–1812 [DOI] [PubMed] [Google Scholar]
- Van Ieperen WV, Volkov VS, Van Meeteren U (2003) Distribution of xylem hydraulic resistance in fruiting truss of tomato influenced by water stress. J Exp Bot 54 317–324 [DOI] [PubMed] [Google Scholar]
- Zee SY, O'Brien TP (1970) A special type of tracheary element associated with ‘xylem discontinuity’ in the floral axis of wheat. J Biol Sci 23 783–791 [Google Scholar]