Defining Functional Areas in Individual Human Brains using Resting Functional Connectivity MRI

Abstract

The cerebral cortex is anatomically organized at many physical scales starting at the level of single neurons and extending up to functional systems. Current functional magnetic resonance imaging (fMRI) studies often focus at the level of areas, networks, and systems. Except in restricted domains, (e.g. topographically-organized sensory regions), it is difficult to determine area boundaries in the human brain using fMRI. The ability to delineate functional areas non-invasively would enhance the quality of many experimental analyses allowing more accurate across-subject comparisons of independently identified functional areas. Correlations in spontaneous BOLD activity, often referred to as resting state functional connectivity (rs-fcMRI), are especially promising as a way to accurately localize differences in patterns of correlated activity across large expanses of cortex. In the current report, we applied a novel set of image analysis tools to explore the utility of rs-fcMRI for defining wide-ranging functional area boundaries. We find that rs-fcMRI patterns show sharp transitions in correlation patterns and that these putative areal boundaries can be reliably detected in individual subjects as well as in group data. Additionally, combining surface-based analysis techniques with image processing algorithms allows automated mapping of putative areal boundaries across large expanses of cortex without the need for prior information about a region’s function or topography. Our approach reliably produces maps of bounded regions appropriate in size and number for putative functional areas. These findings will hopefully stimulate further methodological refinements and validations.

Introduction

In Churchland and Sejnowski’s famous diagram showing the levels of neuroanatomical organization, a level labeled “maps” is interposed between networks (i.e., columns) and systems (Churchland and Sejnowski, 1991). This level was called “maps” because many of the most accurately defined entities at this scale (~ 1 cm) are topographically organized cortical areas. Classic examples include the multiple retinotopic maps of primary and extrastriate visual cortex, where each map constitutes a separate representation of the visual field and contains neurons with a distinctive collection of functional characteristics.

Organization at this scale is not limited to visual cortical regions, nor to topographically organized somatosensory (Clark et al., 1988) or auditory (Langers et al., 2007) maps. Distinct subregions have been reported throughout the cortex, including motor (Strick, 1988), and orbitofrontal (Carmichael and Price, 1994) cortex as well as the complete hemispheric partitioning schemes of Brodmann (Brodmann, 1909) and other classical anatomists. Although topography is not seen in every region, it can be combined with other attributes, as suggested by Passingham and colleagues for frontal and motor regions (Passingham et al., 2002), to provide a distinct “fingerprint” that can be used for the identification of individual regions.

For the remainder of this report, regions that represent separable functional domains of cortex will be referred to as “functional areas”. This is in distinction to a more general term, “region”, or “region of interest”, which may encompass all or part of several functional areas. Because functional areas possess unique combinations of inputs, outputs, and internal structure, each functional area is thought to make a distinct contribution to information processing. Thus, the study of each area’s normal function, developmental trajectory, and modified responses following loss or injury, can be greatly aided by the ability to accurately and reliably define the location and boundaries of functional areas in individual living humans.

Four criteria have been proposed for defining cortical areas, based mainly on studies of non-human primates (Felleman and Van Essen, 1991; Van Essen, 1985): Function (as defined by lesion-behavior or having neurons whose functional properties are distinct from neighboring cortex), Architectonics (having unique arrangements of cells, myelin density, and/or combinations of chemical markers, etc.), Connections (having a different combination of inputs and outputs from neighboring cortex), and Topography (having a topographic map that can be used to define boundaries, for example between primary visual cortex and V2).

Unfortunately, the current ability to define functional areas by these criteria in human cerebral cortex is inadequate. fMRI and lesion studies provide some localization ability, but their precision is relatively low. Historic architectonic partitioning schemes, such as the rendition of areas introduced by Korbinian Brodmann, unfortunately often contain incorrect boundaries and do not address individual variation of location and extent (see (Van Essen and Dierker, 2007)). Promising methodologies such as architectonic measurements in living humans (Scheperjans et al., 2007) and connectional studies using DTI (Klein et al., 2007) are currently still limited to a small set of areas. Mapping of topographic organization is mostly restricted to sensory and motor areas.

Recently, measures of correlation between resting brain regions (so-called resting-state functional connectivity, or rs-fcMRI) have demonstrated promise in describing boundaries between functional areas in limited regions of cortex (Margulies et al., 2007). Resting state functional connectivity is a method for evaluating regional interactions that occur when a subject is not performing an explicit task (Achard et al., 2006; Beckmann et al., 2005; Biswal et al., 1995; Damoiseaux et al., 2006; Dosenbach et al., 2007; Fair et al., 2007a; Fair et al., 2007b; Fox et al., 2005; Greicius et al., 2003; Lowe et al., 1998; Nir et al., 2006; Salvador et al., 2005). It is based on the discovery that low-frequency (< ~0.1 Hz) BOLD fluctuations in distant, but apparently functionally related grey matter regions, show strong correlations at rest (Biswal et al., 1995; Damoiseaux et al., 2006; Lowe et al., 1998; Nir et al., 2006). These low frequency BOLD fluctuations are presumed to relate to spontaneous neural activity (Biswal et al., 1995; Leopold et al., 2003; Nir et al., 2006). Additionally, since rs-fcMRI does not require active engagement in a behavioral task, it unburdens experimental design, subject compliance, and training demands, making it attractive for studies of development, aging, and clinical populations (Bokde et al., 2006; Castellanos et al., 2007; Greicius et al., 2007; Greicius et al., 2004; Rombouts and Scheltens, 2005; Tian et al., 2006; Whalley et al., 2005).

Cross-correlating the time series of a particular brain region (seed region) with all other voxels in the brain can illuminate which voxels are “functionally connected” with the seed region, in that their timecourses are highly correlated. For example, a seed region in the left primary motor cortex shows “functional connections” with the right primary motor cortex as well as supplementary motor area (SMA) (Biswal et al., 1995), and other regions. These voxel-wise correlation maps can be generated for individual subjects (Fox et al., 2006). The specific mechanisms relating neural activity to these very slow (>10 sec.) fluctuations in the BOLD response are not known, but the spatial patterns are similar to those revealed by the signal functional activation data: regions that co-activate tend to have correlated rs-fcMRI signals while regions that become negative when a seed regions activates tend to be negatively correlated with the seed region (Fox et al., 2006; Greicius et al., 2003).

Because “seeds” can be placed in any cortical or subcortical location, development of methods for analyzing these correlation maps could provide a basis for delineating the location and boundaries of a large number of functional areas in single individuals. The analyses presented below provide evidence that rs-fcMRI can aid in the delineation of a large number of functional area boundaries in individual human cortex. They show that: (i) Changes in correlation maps occur abruptly as the seed location moves systematically across the cortical sheet, suggesting the presence of a boundary rather than a smooth gradation. (ii) These transitions occur in many locations in individual subjects. (iii) Customized image processing techniques can be used to identify putative boundaries and bounded regions across large expanses of cortex. (iv) The boundaries appear reliable when assessed with independent measurements. (v) The overall map has the appropriate granularity to reflect area-level cortical parcellation.

Methods

Overview

The aim of the analysis stream presented here is to identify locations on the cortex where the pattern of rs-fcMRI changes rapidly, potentially representing boundaries between functional areas. Our approach utilizes established fcMRI voxel-wise correlation methods, coupled to several novel analysis techniques that are performed on a surface representation of the cortex. These include established edge detection and image segmentation algorithms used in computer vision and image analysis programs. These surface-based operations treat the brain as a 2D sheet, while volume-based analyses treat the brain as a 3D volume.

The flowchart in Figure 1 describes the major steps involved in our analysis stream. Annotations refer to specific parts of the Methods section that describe each portion of our approach and Figures that display the various intermediate steps of the analysis. This methodology can be applied to any set of fcMRI data see (Fair et al., 2007b), but the current analysis involves continuous resting state/relaxed fixation data.

Figure 1.

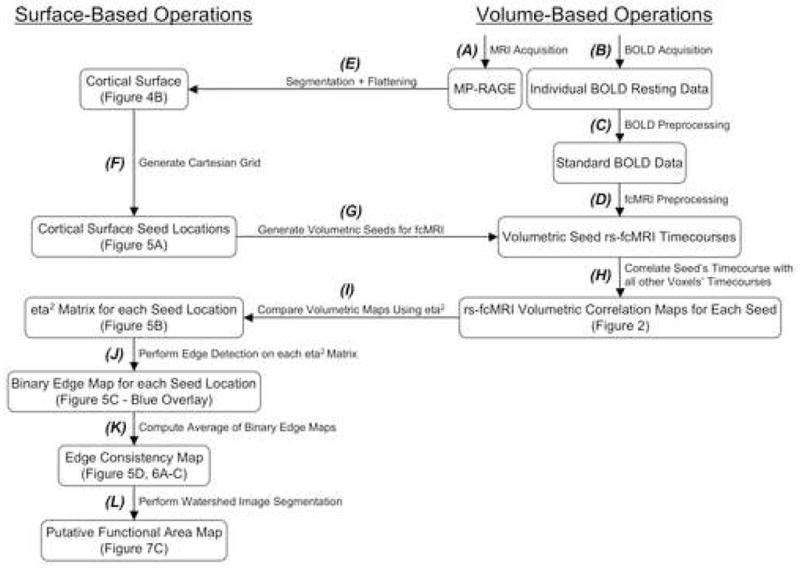
Flowchart outlining the analysis stream presented here and the techniques involved. Bolded letters refer to specific portions of the Methods section that describe each procedural operation. Examples of several steps in the procedure are denoted by the Figure where they can be found.

Data acquisition

fMRI data were acquired on a Siemens 1.5 Tesla MAGNETOM Vision system (Erlangen, Germany). (A) Structural images were obtained using a sagittal magnetization-prepared rapid gradient echo (MP-RAGE) three-dimensional T1-weighted sequence (TE=4 ms, TR=9.7 ms, TI=300 ms, flip angle=12 deg, 128 slices with 1.25 × 1 × 1 mm voxels). (B) Functional images were obtained using an asymmetric spin echo echo-planar sequence sensitive to blood oxygen level-dependent (BOLD) contrast (T2* evolution time=50 ms, α=90°, in-plane resolution 3.75×3.75 mm). Whole brain coverage was obtained with 16 contiguous interleaved 8 mm axial slices acquired parallel to the plane transecting the anterior and posterior commissure (AC-PC plane). Steady state magnetization was assumed after 4 frames (~ 10 s). 128 whole brain images (TR=2.5s) were acquired per BOLD run across 6 runs for our single subject (23yo female). For the population-average analysis, 32 whole brain images (TR=2.5s) were extracted from the rest blocks from a mixed blocked/event-related design per BOLD run across 8 runs for 31 subjects (avg. 24.4yo, 17F).

Data preprocessing

fMRI preprocessing

(C) Functional images were processed to reduce artifacts (Fair et al., 2007b; Miezin et al., 2000). These steps included: (i) removal of a central spike caused by MR signal offset, (ii) correction of odd vs. even slice intensity differences attributable to interleaved acquisition without gaps, (iii) correction for head movement within and across runs and (iv) across-run intensity normalization to a whole brain mode value of 1000.

Several of the temporal nuisance signals that need to be regressed out to examine the resting state signal are related to anatomical structures, such as white matter and the ventricles (see rs-fcMRI preprocessing below). This entails registering the data for each subject to an atlas space, so that common imaging masks and fcMRI seeds can be used to define these nuisance signals in each subject. This transformation of the functional data to atlas space, in this case, 711-2B (Buckner et al., 2004; Talairach and Tournoux, 1988; Ojemann, 1997) was computed for each individual via the MP-RAGE scan. Each run then was resampled in atlas space (Talairach and Tournoux, 1988) on an isotropic grid (3 mm voxels) combining movement correction and atlas transformation in one interpolation (Lancaster et al., 1995; Snyder, 1996). This single interpolation procedure eliminates blurring that would be introduced by multiple interpolations. All subsequent operations were performed on the atlas-transformed volumetric timeseries.

rs-fcMRI preprocessing

(D) Pre-processing for functional connectivity analyses was performed on the fMRI data, as in Fox et. al. (Fox et al., 2005), to optimize the time-series data and remove spurious variance. These steps include removal of the linear trend, temporal band-pass filtering (0.009 Hz < f < 0.08 Hz), spatial smoothing (6 mm full width at half maximum), as well as regression of several “nuisance” signals and their time-based first order derivatives, including six motion parameters, and whole brain, ventricular, and white matter signals.

Surface-based analysis

(E) The structural MRI volume for the single-subject analysis was spatially normalized to the 711-2B volumetric MRI atlas (Lancaster et al., 1995; Snyder, 1996) and resampled to 1 mm³ voxels. Segmentation of the cortical mid-thickness as well as surface reconstruction was done using Caret 5.3 software (Van Essen et al., 2001) (http://brainmap.wustl.edu/caret/). Surface flattening was accomplished by making cuts along five standardized trajectories that help minimize distortions (see figure 2, Van Essen, 2005). This flattened surface was then used to generate a grid of seed points, or patch, which was then used to generate rs-fcMRI correlation maps as described below.

Figure 2.

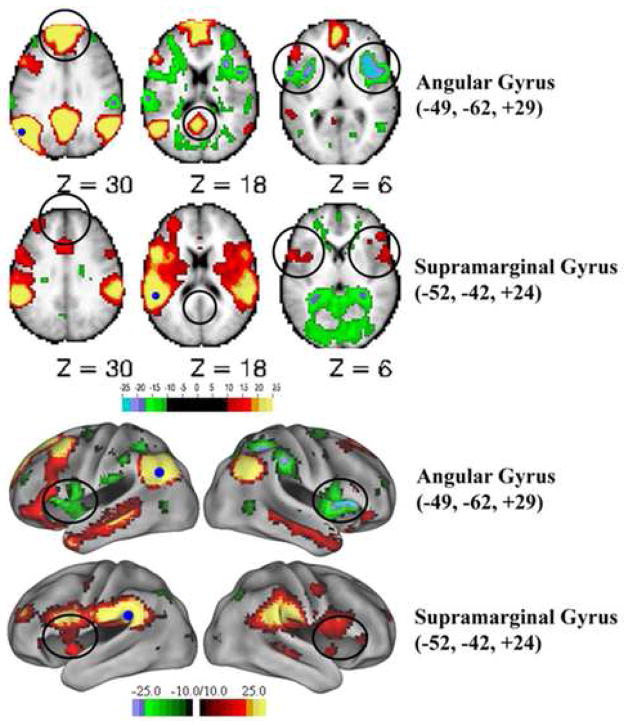
Shown are transverse sections and lateral hemispheric views, mapped to the PALS human cortical atlas (Van Essen, 2005), showing the functional connectivity patterns of regions of interest in the angular (upper slice and lateral view) and supramarginal gyrus (lower slice and lateral view). Highlighted (circles) are a few of the salient differences. Seed regions are indicated with filled dark blue circles. The strength of positive and negative correlations is shown in warm and cool colors respectively.

rs-fcMRI boundary generation

Cortical seed and rs-fcMRI correlation map generation

(F) On the flat map of the subject’s cortex, a Cartesian 3 mm point grid was created using Caret to define a set of seeds representing a patch of the cortical surface that respects cortical folding patterns (as shown in Figure 5A). This allowed us to treat the cortex as a 2D structure and use standard 2D image processing techniques. (G) The corresponding 3D stereotactic coordinates for each Cartesian grid point were used to generate 3 mm diameter spherical regions of interest around each volumetric seed voxel. This sampling density provides a fine-grained map without excessive oversampling of the fMRI data (3 mm voxel size, but with 6 mm FWHM smoothing). While each seed point is 3 mm apart on the flattened representation, the folding pattern of the brain results in some seeds being further than 3mm apart in the underlying volume, while others are closer than 3mm in the underlying volume. (H) For each seed, volumetric correlation maps were generated as in Fox et al. (Fox et al., 2005) and Fair et al. (Fair et al., 2007b) by correlating the timecourse of this region of interest with the timecourses of all other voxels over the entire volume of the brain. This creates a volumetric correlation map for each seed, where the intensity at each voxel is the Fisher Z-transformed correlation (r) between that voxel and the seed region for the volume.

Figure 5.

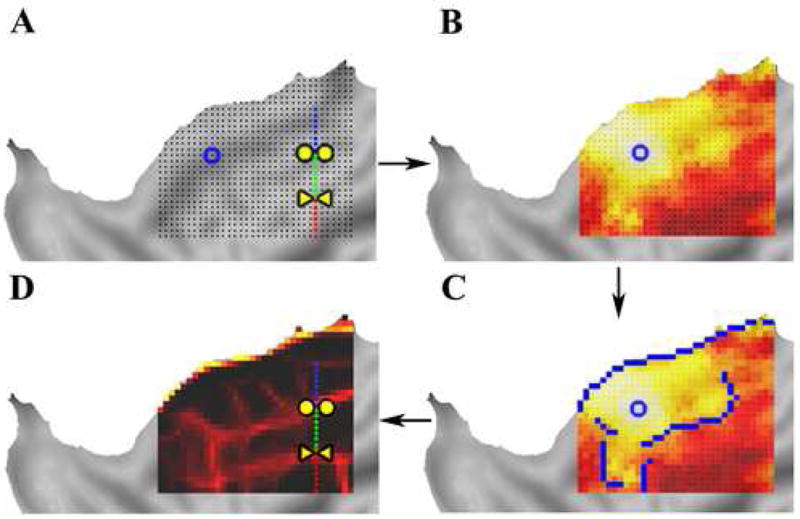
Panel A shows the 2D patch of seed regions on this subject’s flattened cortex (Note: The line of points and boundary locations from Figure 4 are plotted in panels A and D for comparison). The eta² profile for one of the seeds (blue circle) is shown in panel B. Each of these eta² maps are then analyzed with an automated edge-detection algorithm that generates borders, blue overlay in panel C. Averaging all of the detected edge maps (binary blue overlay in panel C) results in the putative edge map shown in panel D, where intensity of each location reflects the fraction of maps in which that location was considered an edge.

eta² matrix creation for each seed

(I) To compute the similarity between seed locations, an eta² coefficient was calculated for every seed pair. eta² is equal to the fraction of the variance in one signal accounted for by variance in a second signal where comparisons are done on a point by point basis. The more similar two signals, or in this case, images, are, the higher the eta² coefficient between them. eta² can vary in value from 0 (no similarity) to 1 (identical). To determine the similarity or difference between the large-scale correlational structure of two seed locations, eta² is calculated between the two volumetric correlation maps (a and b) generated from these two seed locations and equals:

$$et{a}^2=1-\frac{S{S}_{\mathit{Within}}}{S{S}_{\mathit{Total}}}=1-\frac{{\displaystyle \sum _{i=1}^n}\left[{(a_i-m_i)}^2+{(b_i-m_i)}^2\right]}{{\displaystyle \sum _{i=1}^n}\left[{(a_i-\overline{M})}^2+{(b_i-\overline{M})}^2\right]}$$ (1)

where a_i and b_i represent the values at position i in maps a and b respectively. m_i is the mean value of the two images at position i, (a_i+b_i)/2, and M-bar is the grand mean value across the mean image, m, or across all locations in both correlation maps. eta² measures the difference in the values at corresponding points in the two images, not strictly whether the points vary in similar ways, and can detect differences and similarities in the volumetric correlation maps using information from all of the voxels of the entire volume. The eta² coefficients are stored in a series of matrices (the same size and shape as the patch of seeds) such that each seed has a corresponding matrix representing the eta² coefficients of that seed’s volumetric correlation map compared to the volumetric correlation maps of all other seeds in the patch (as shown in Figure 5B).

We use eta² to compare images instead of correlation, r, because our goal is to quantify the similarity of the two images, not the correlational relationship between them. While correlation is often used for similarity description, there are instances where the correlation coefficient between images is unaffected by changes in the two images which make them more or less similar from each other. Two examples where this is readily apparent are scaling and offset; if the value of each voxel in one map is exactly double the value of another, they will have a correlation coefficient of 1, but are still different from one another at every point and will have eta² values that may be much less than unity. Similarly, if the value of each voxel in one map is 100 units greater than another, they will again have a correlation coefficient of 1, even though every voxel is different. In fact, the correlation coefficient will not change from 1 if the scaling factor increases or decreases in the first case, or if the offset factor increases or decreases in the second case. In both cases, however, eta² will measure and detect these differences and will vary as a scaling factor, offset, or another form of variation changes the difference between the two maps. The eta² coefficient will only equal 1 if they are, in fact, identical at every point.

Edge detection algorithms

(J) Since the aforementioned matrix of eta² coefficients (i.e. eta² profile) is a 2D array of values across the cortical surface, it can be treated as flat image data. To find salient edges in these arrays, the Canny edge detection algorithm (Canny, 1986), implemented in the Image Processing Toolbox (v7.2) of the MATLAB software suite, was applied to each seed’s eta² profile ‘image’. The Canny method smoothes the image with a Gaussian filter to reduce noise, and then creates a gradient image that locates regions with high spatial derivatives. High gradient values represent locations where the original image was rapidly changing (i.e. peaks in the first derivative). After eliminating pixels in the 2D array that are not local maxima in the gradient image, the algorithm tracks along the highlighted regions of the image and, using high and low thresholds, categorizes each location as an edge or not. To prevent hysteresis, if the magnitude of the pixel is below the low threshold, it is set to zero, while if the magnitude is above the high threshold, it is considered an edge. If the magnitude of the pixel is between the two thresholds, then the location is only considered an edge if there is a neighboring pixel that itself had a gradient above the high threshold.

Our current implementation uses the default MATLAB algorithm to generate the two thresholds such that the high threshold is calculated to be the lowest value at which no more than 30% of the pixels are detected as edges, and the low threshold is defined as 40% of the high threshold. The use of edge detection here is purely to find the gradient peaks that are spatially stable across short stretches of each of the eta² profile ‘images’. Thus, the specific thresholds for the edge detection algorithm do not have to be manually set each time. The primary goal is to identify and differentiate locations with strong, spatially coherent peaks as being different from locations that are relatively smooth or have incoherent gradient peaks, across some or most of the eta² profiles. The present adaptive threshold algorithm evidently performs this function adequately.

The result of processing the eta² profile set with an edge detection algorithm is a set of binary images representing the locations of rapid changes in each grid point’s eta² profile (blue overlay in Figure 5C).

Putative areal boundary map generation

(K) Since the edge determination is binary, averaging across the entire set of seed matrix images at each location gives the relative likelihood that a particular location was determined to be an edge across the set of seed matrices. This gives a probabilistic or putative edge location map in which the intensity represents how likely a location is actually a functional border (Figure 5D).

Putative functional area identification

(L) Since the intensity of the putative edge map represents the likelihood that a given location is not a member of a functional area, our data can be transformed into regions of interest that represent putative functional areas using the morphology-based watershed transform (Vincent and Soille, 1991). This method treats each low intensity (low probability of edge) region as a ‘valley’ that progressively fills until reaching ambiguous locations between regions (in this case putative edges in the overall edge map) (Figure 7).

Figure 7.

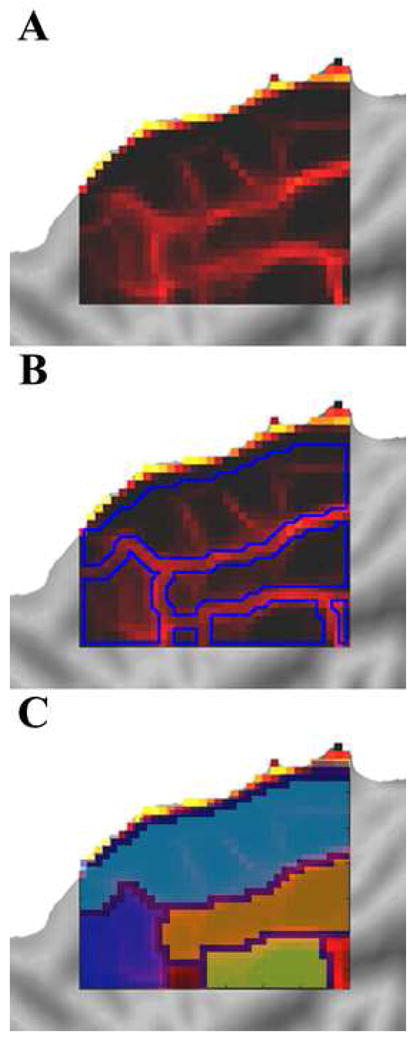
Panel A shows the rs-fcMRI derived boundaries generated above. Applying a watershed image segmentation algorithm parses the patch into contiguous non-overlapping regions least likely to be edges (i.e. most likely to be areas) shown in panel B, which can then be individually identified and labeled for investigation and validation as shown in panel C.

Results

We first demonstrate that rs-fcMRI patterns can be strikingly different in a population-average dataset even when the seed regions are relatively close (2.3cm). We then explore the ramifications of this observation more systematically in single-subject data, expanding on the implications this has for defining functional areas across the cortex.

rs-fcMRI of closely apposed seed regions shows putative areal boundaries where map patterns change abruptly

Voxel-wise correlations were performed on interleaved resting state fMRI data see (Fair et al., 2007b) acquired from 31 healthy adult subjects using functionally defined seed regions (12mm-diameter spheres surrounding the peaks of activation) placed in the nearby supramarginal (−52, −42, +24) and angular (−49, −62, +29) gyri. These regions of interest, whose centers are separated by 2.3 cm (vector distance in 3D), were derived from a study investigating the development of lexical processing that showed these nearby regions to have similar but dissociable developmental profiles for a set of lexical tasks (Church et al., 2006).

The angular and supramarginal gyri seed regions (small blue spheres in left hemispheres in Figure 2) show markedly different functional connectivity profiles, indicating that rs-fcMRI can be remarkably different between nearby functional areas. Regions having positive correlations (warm colors) with the angular gyrus seed (top rows of volume and surface views) show very little overlap with regions showing positive correlations with the supramarginal gyrus seed (bottom rows of volume and surface views). Derived from group data, these results are consistent with previous studies demonstrating that correlation patterns are reliable across subjects and investigators.

Although correlation maps from nearby seeds can be quite different, delineating boundaries necessitates that these differences do not progress smoothly across the brain, but rather show abrupt local changes, similar to those seen in connectional anatomy and functional properties (e.g., Felleman and Van Essen, 1991; Maunsell and Van Essen, 1983). To test for such a transition, a series of spherical seed regions (3 mm diameter) were generated between the centers of the supramarginal and angular gyri regions from group data (Figure 3A and B). The locations for these intermediate regions were delineated on the PALS atlas flat map and projected to the volume via the PALS ‘average fiducial surface’ (Van Essen, 2005).

Figure 3.

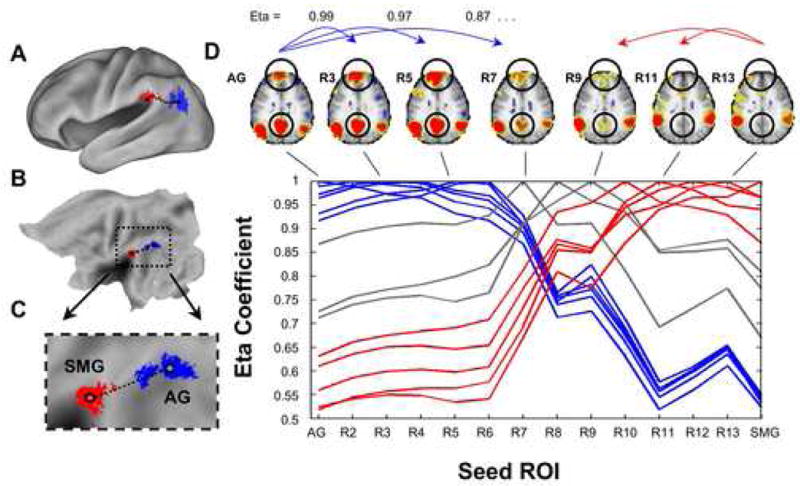
Panels A–C show the locations of the angular (blue) and supramarginal (red) regions. Black dots in C indicate the seed regions used. Panel D (upper panel) shows some of the connectivity maps derived from the series of seed regions. Encircled are particular differences that highlight the changing connectivity patterns. Panel D (lower panel) represents the eta² values derived when comparing the AG map with all other maps (first blue line), the SMG map with all other maps (last red line), and so forth for all maps …

We analyzed the connectivity images for the series of seed regions by visual inspection and by computing the similarity of each connectivity image to each of the other connectivity images using an eta² coefficient. While a correlation coefficient measures the relationship between changes in two images, the eta² coefficient provides a better measure of the overall similarity or difference between images (see Methods for details).

As shown in Figure 3D, the eta² coefficients demonstrate a transition between the locations of seeds R7, R8, and R9, as the profile of eta² coefficients drastically changes within 1cm (3 map-mm separation, Van Essen and Drury, 1997). Thus, the eta² profiles can be divided into three groups: AG-R6 (blue), R10-SMG (red), and an intermediate zone R7-R9 (grey) that is a putative transition region between the other two groups. The transition region found here is wider than typical transition between architectonically defined areas (Zilles et al., 2002), but this may reflect individual variability in the location of areal boundaries in the contributing population.

rs-fcMRI in a single subject can delineate multiple putative areal boundaries simultaneously

Feasibility using single subject data is important, as the group data are inherently blurred by imperfect registration across subjects. Thus, a surface-based “fiducial” representation of the cortical mid-thickness was obtained for a single subject using the SureFit cortical segmentation algorithm available in the CARET software package (Van Essen, 2001). Correlation (volume) maps were generated for a set of 3 mm diameter spherical seed regions along the left cingulate sulcus and adjacent medial cortex (3 map-mm separation along a line on the flat map. For each of the 25 seed locations, its correlation map was compared to the correlation maps for the 24 other seed locations along this line, yielding a profile that peaked at unity for the given seed location.

To objectively separate the eta² profiles into groups, as done in Figure 3, hierarchical clustering analysis was performed on the eta² profiles to find any strong divisions among the set (Cordes et al., 2002; Dosenbach et al., 2007; Salvador et al., 2005). A ‘1-eta²’ calculation was used as a distance measure between the profiles. The commonly chosen UPGMA (Unweighted Paired Group Method with Arithmetic mean) hierarchical clustering method (Eisen et al., 1998; Handl et al., 2005) sorted the eta² profiles for each seed’s correlation map into three main groups (Figure 4C), which recapitulates the anatomical ordering as well as the distinct shape differences seen in Figure 4A (blue curves vs green curves vs red curves). Further inspection of the clusters reveals two abrupt changes in the green curves (triangle and circle locations), which occurred at similar locations for the other curves, indicating functional transitions that are candidates for areal boundaries. While there is a general decrease in eta² coefficient with distance from the comparison point, abrupt changes are concentrated at specific locations along the line regardless of which comparison points are chosen. Thus, rs-fcMRI functional transitions can be derived from individual subject data, and multiple transitions are evident even in this relatively limited view.

Figure 4.

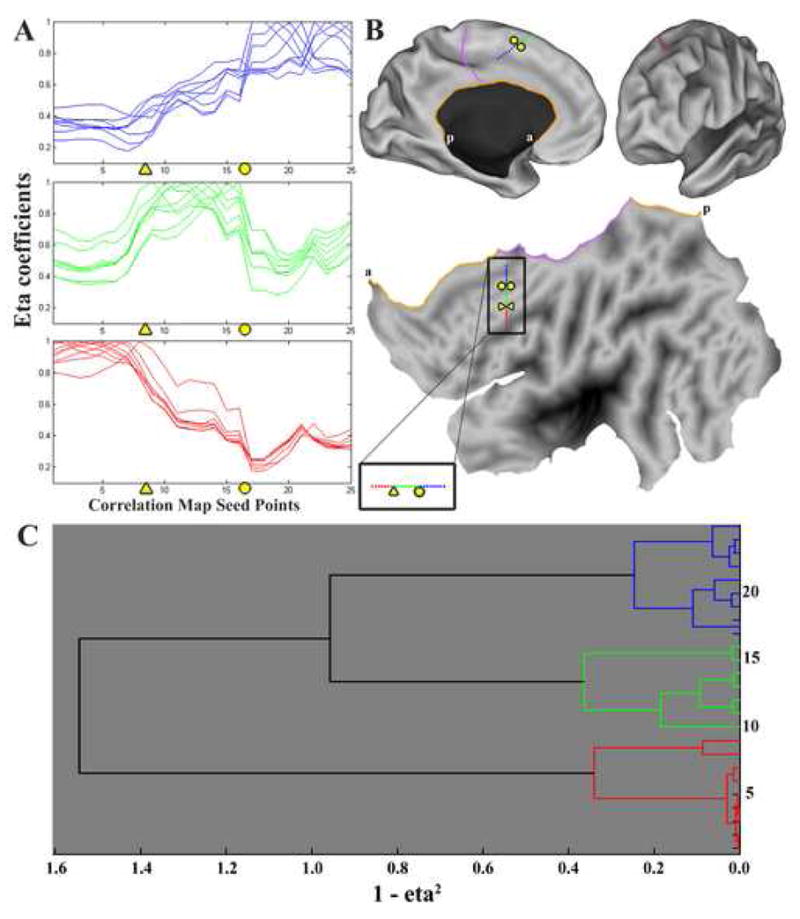
Panel A displays the eta² coefficients between each seed point’s correlation maps, as in Figure 3D. Triangle and circle designate locations of rapid change. Panel B shows the location of the line of seed points on the left hemisphere, as well as the nearby artificial ‘cuts’ created during the process of flattening the cortex. The medial wall hole is shown in orange, with ‘a’ and ‘p’ designating anterior and posterior ends of the anterior medial wall cut. The cingulate cut is shown in purple on both the inflated medial view and the flattened view. Panel C shows the results of hierarchical clustering the eta² profiles shown in Panel A.

Sharp transition zones, or “edges”, can be mapped across the 2D cortical surface using automated image processing techniques

The line-based approach above provides proof of principle that rs-fcMRI measures can delineate putative cortical boundaries in individual subjects. However, mapping functional transitions throughout the cortex using this approach would be highly time-consuming and inefficient. Therefore, it was important to develop a computational approach that takes advantage of the information in rs-fcMRI data more efficiently.

Using a 2D grid of seed regions (i.e. a “patch”) on the cortical surface (Figure 5A), eta² coefficients were computed for all pairs of seed regions within the patch, yielding a 2D eta² profile map for each of the seed regions comprising the patch. Each 2D eta² profile map (Figure 5B) was processed with a Canny edge detection algorithm (Canny, 1986), a method for rapid automated discrimination of strong gradients (edges), creating a binary “edge map” for each seed (Figure 5C, blue overlay). These binary maps were averaged to generate an ‘edge consistency map’ for the grid, where intensity at each location represents the fraction of maps in which that location was considered an edge (Figure 5D). The line-based and edge-detection-based approaches are consistent with one another. The transitions obtained in the line analysis described above (circles and triangles), spatially align with the putative edges determined by the edge consistency analysis, as indicated by the bright red pixels crossing the line of seed points.

As seen in Figure 5D, the set of candidate boundaries derived using this method extend over regions of the flat map that are appropriate in size and trajectory for cortical area boundaries, Thus, processing large portions of the brain can be done much more efficiently using an automated computational approach. In addition, because the analysis is sensitive to gradients in any direction along the cortical sheet, it is inherently more appropriate for systematic identification of cortical area boundaries.

Several putative areas in Figure 5D are only partially enclosed by the presently detected boundaries. This might in part reflect a non-optimal thresholding strategy in the current algorithm but it may also represent a lack of differentiation between functional areas based on resting functional connectivity. If two neighboring functional areas have similar connectivity profiles, the eta² coefficient between maps in the two areas will be high, and such boundaries may not be detected by our current methods. Thus, convergence across methods and a combination of different approaches may be needed to elucidate the entire set of cortical functional areas.

Boundaries generated from adjacent cortical surface patches yield consistent results

Since the edge consistency map is derived from the correlation maps for a particular set of cortical loci, it is conceivable that the resultant pattern is specific to the chosen patch and is unrelated to cortical areal boundaries. We assessed this possibility by analyzing two additional patches, or sets of cortical seed points. First, a patch of dorso-medial cortex adjacent to that used above (blue box, Figure 6A and B), was analyzed to test whether an independent dataset would show continuity with the pattern of edge locations seen previously. Second, an overlapping patch corresponding to half of the original dataset and half of the new independent dataset (green box, Figure 6A and C) was used. The same edge detection analyses were applied to both new sets to find putative edge locations.

Figure 6.

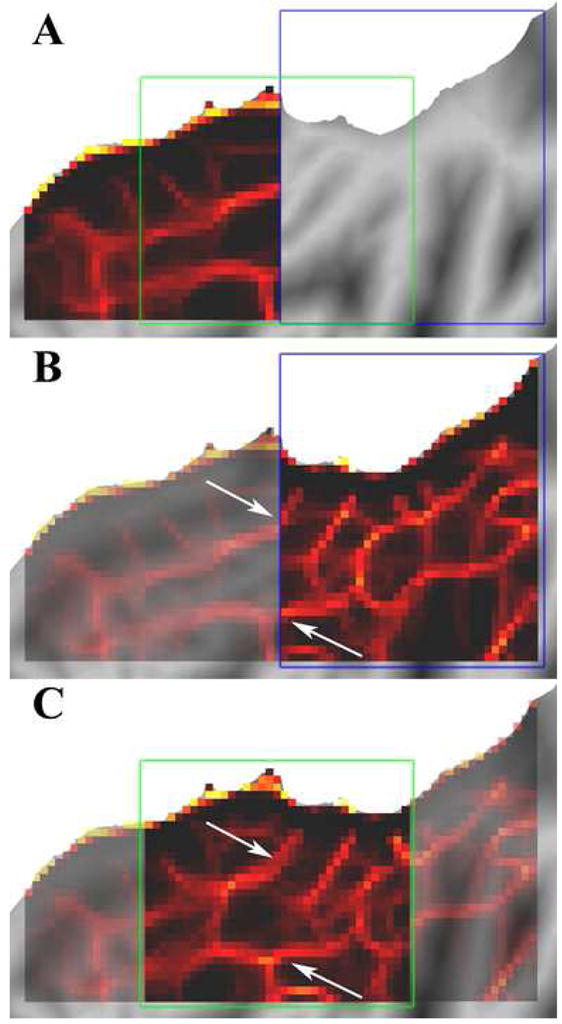
Panel A shows the original patch of the left cingulate cortex shown in Figure 5. Panel B demonstrates that edge locations identified in the neighboring posterior patch align with those in the original patch, even though the two datasets do not share seed points or correlation maps. Panel C shows that the independently analyzed overlapping patch is consistent with the matching regions of A and B.

As seen in Figure 6B, edge consistency maps generated using a completely separate but adjacent set of seed point sets reveal consistent edges that align with one another. When superimposing the edge maps from two independent or overlapping patches onto the same surface, considerable consistency is noted, including the continuous boundaries marked with arrows in Figure 6B and C. These results provide qualitative evidence that our approach can consistently identify boundary contours across the cortex in a single human subject.

Generating boundaries allows automatic definition of putative functional areas

Since the edge consistency maps show continuity across extended regions of cortex, it should be possible to group contiguous seed points surrounded by putative edges into putative functional areas, using existing image segmentation algorithms. A watershed segmentation algorithm (Vincent and Soille, 1991) was applied to the edge consistency map. Figure 7 demonstrates the progression from edges (panel A) to bounded and labeled “areas” (panel C).

Using a putative edge map, a patch of cortex can be segmented into several bounded and partially bounded areas by a watershed algorithm. This suggests that rs-fcMRI derived putative edges and standard imaging segmentation methods should allow parcellation of an individual’s cortical surface into putative functional areas. While these bounded areas may in some cases represent only a part of one or more than one functional area, it allows for the generation of ROIs that can be validated using complementary methods.

Discussion

Imaging and functional areas

Since the mid 1980s, functional neuroimaging has facilitated progress in cognitive neuroscience - the study of neural substrates underlying mental processes and behavior. Typically, functional neuroimaging identifies brain regions that are differentially activated by different task states or affected by specified behavioral events. We use the terms “regions” and “regions of interest” advisedly whenever we are unsure whether functional imaging has identified differential activation in a whole and distinct functional area. We recommend that the term “area” be reserved for “functional areas” and that “region” be used for a collection of voxels or otherwise defined region of interest.

One of the overarching goals of functional neuroimaging is to use differential activity between conditions to identify specific information processing operations reflected in separate functional areas (e.g. Posner et al., 1988). Ascertaining a large-scale collection of functional areas in any mammal, let alone humans, is not straightforward and currently incomplete (Levitt, 2003; Van Essen, 2004a).

A fundamental problem in trying to identify functional areas in humans is that many of the methods used to generate the relatively precise definitions available in nonhuman animals are not available for studies in living humans, as noted above. Recently, the use of areal connections to define areas has been employed in humans. Diffusion tensor imaging (DTI) tractography, which measures the directional diffusion of water within a voxel, can reveal local anisotropic differences in fiber bundles in neighboring regions of cortex in living humans, and was recently used to delineate some human cortical areas (Behrens et al., 2006; Croxson et al., 2005; Johansen-Berg et al., 2004; Johansen-Berg et al., 2005; Klein et al., 2007). The use of probabilistic fiber bundle differences in diffusion tractography is in some respects analogous to the use of blunt dissection to identify major fiber bundles in humans. However, the challenge of accurately dissociating crossing bundles of fibers with DTI speaks to the need for a converging method of areal definition.

Since rs-fcMRI measures correlated activity, it might in principle reflect mainly direct(monosynaptic) anatomical connections. Empirically, though, the linkage between highly correlated regions can evidently be indirect, through one or more intermediate regions or common external input (Vincent et al., 2007). Even if functional connectivity is not directly equivalent to monosynaptic anatomical connections, a functional area’s history of interaction with other areas is likely to be consistent across its extent, and distinct between separate areas. Thus, this method may be well suited for delineating the location and boundaries of a large number of functional areas.

Overcoming individual variation

Individual variation must be considered when comparing functional areas across subjects or populations of subjects (i.e. in cross-sectional development and aging studies, or between patient populations). To address this problem, investigators have implemented neuroimaging approaches that rely upon improved registration techniques (volumetric or surface-based), presuming that alignment of anatomical features will improve the alignment of functional areas. The most advanced registration methods available attempt to compensate for individual variation in brain surface shape, size, and folding pattern (Lyttelton et al., 2007; Van Essen, 2005; Van Essen and Dierker, 2007). However, this approach does not provide an ideal solution because the location and extent of each functional area varies substantially from person to person, irrespective of anatomical landmarks (Amunts et al., 2000; Amunts et al., 1999; Andrews et al., 1997; Uylings et al., 2005; Van Essen et al., 1984). Our current work is performed on a within subject basis, but future across subject comparisons will be made through the PALS B12 atlas (Van Essen and Dierker, 2007) using CARET which can account for more individual differences than volumetric averaging. We hope to then directly examine inter-subject variation of areal location and how this can be used to additionally refine registration.

To overcome the difficulties with regards to individual variability, many studies use a large number of subjects such that, after alignment, the activated brain region common to the majority of subjects will emerge as the active focal point (e.g. Dosenbach et al., 2006). This gives a “best guess” approximation of the centroid of the common activated brain region, presumably located within an actual functional area (Lancaster et al., 1995), but “blurs” the variability in location and extent of areas across individuals.

In some cases, a lack of specificity can lead to regions as far apart as 4 cm in stereotactic space, one quarter the anterior-posterior length of the average brain, being referred to by the same name, and considered as part of the same functional entity (e.g. the application of the name “dorsolateral prefrontal cortex” in Kerns et al. (Kerns, 2006) and Luks et al. (Luks et al., 2007)). However, without the availability of more precise regional definitions, this common practice is unavoidable in order to have a common descriptive language.

Another method utilized to overcome individual variability is to use the average activation of many repetitions of a region-specific “localizer” task in individuals (e.g. Swallow et al., 2003). Analyses can then be performed on a subject-by-subject basis using the activation-delineated peak. However, such localizer tasks exist for relatively few locations in the brain, and the considerable similarity in the functional properties of many neighboring functional areas often makes it difficult to differentiate areas based solely on their activation to a particular task or stimulus set (e.g. Swallow et al., 2003).

Therefore, functional activations and fcMRI seeds are currently most commonly referred to by their stereotactic coordinates or anatomic (gyral and sulcal) locations. The generation of cortex-wide maps of functional areas for individuals would allow for more accurate and functionally meaningful labels to be applied without relying on stereotaxis with its added concerns about individual areal variation.

rs-fcMRI functional area definition

We have demonstrated that rs-fcMRI patterns can abruptly change between putative functional areas and that this signal is strong enough to be detected in individual subjects as well as in group data. Additionally, combining surface-based analysis techniques with image processing algorithms allows for the simultaneous delineation of candidate/putative area borders across expanses of cortex in automated fashion without the need for prior information about a region’s function or topography. We have also shown that putative borders generated from independent data from a separate portion of cortex yield similar and consistent results with our initial dataset. Finally, defining borders with these methods provides usable and biologically plausible putative areas for use as region masks for functional studies or as seeds for use in functional connectivity studies.

Our approach combines several disparate methods that aid the currently used analyses:

(i) Due to the ease of acquisition, rs-fcMRI can be accurately acquired from typical and atypical populations. (ii) The use of widespread surface-equidistant seed regions removes the need for prior stipulations about the location of specific functional areas. Surface-based definition of areas also greatly decreases the amount of processing needed, while still defining salient and meaningful functional boundaries and areas across the cortex. (iii) eta² is a useful similarity index for comparing fcMRI maps, as it captures the difference or similarity between two images as distinct from the correlation between them, (Pearson’s r statistic), and allows for rapid analysis of differences. (iv) The inclusion of automated image processing techniques allows for hypothesis-independent generation of functional areas across wide expanses of cortex in rapid fashion. Specifically, the Canny edge detection algorithm permits the detection of continuous yet near-threshold borders, while excluding spurious noise. (v) Regions identified in individual subjects can be easily labeled and transferred to standard fMRI region generation programs used for analysis of functional data from task paradigms, presumably increasing the signal-to-noise ratio over group-average defined regions. Additionally, the combination of existing methods used in this study can also be extended to other efforts in brain mapping. The methods described here and elsewhere (Margulies et al., 2007), may also provide a basis for comparisons between species (Buckner and Vincent, 2007; Vincent et al., 2007). Clearly, more work remains to refine the methods presented here.

Future directions/caveats

Functional validation

While our rs-fcMRI derived boundaries and areas are within a plausible range in size for known cortical areas (Van Essen and Dierker, 2007) and have a biologically plausible distribution, validation against functional data is essential and is currently in progress. Test-retest validation needs to be performed by scanning the same subjects in different sessions separated by several days or weeks. Since the location of functional areas should not change over time, even if their fcMRI patterns change, we anticipate being able to detect the same borders across multiple scans separated after months or years. The borders generated using rs-fcMRI can be directly compared to functional activations in the same individual for areas where there is topographic organization. For example, the borders of early visual areas can be activated using visual meridia stimuli for retinotopy. Additionally, robust localizers, such as eye-movement for the frontal eye fields (FEF), should generate peaks of activity that localize within putative rs-fcMRI functional areas and not across detected boundaries. Finally, comparison across subjects for the above validations can be performed to determine if the fidelity of detecting borders is variable across subjects.

Method refinement

While we have currently performed our analysis on the cortical surface, these algorithms could potentially be expanded to work in 3 dimensions for parcellation of deep brain nuclei. We focus here on surface-based definition of areas as it greatly decreases the amount of processing needed, while providing salient boundaries and areas across the cortex.

Using flat maps to delineate seed locations is problematic where there are artificial cuts (discontinuities) such as that in the cingulate sulcus (Figure 4B – purple line) or near the natural boundary of the medial wall, which exists even when closed topologies are used. This can be resolved in future analyses using overlapping patches defined on closed topologies (e.g., defined on a spherical or very inflated surface). Also, the watershed algorithm, by design, will always produce closed boundaries, however, as clear from Figure 6, some of these putative areas extend beyond a single patch. Thus, while demonstrated here on a local scale, watershed segmentation should preferably be performed on the entire cortical surface at once.

The methods used in this report describe biologically plausible functional areas, but alternative analysis methods may enhance the robustness of the results. For instance, edge detection on the initial eta² profiles is currently performed by the Canny algorithm, but many other edge detection techniques are also available, including the Roberts-Cross, Prewitt, Sobel, Marr-Hildreth, zero-crossings of the 2^nd derivative method, and the Rothwell method (Lim, 1990; Parker, 1997). Additionally, it may prove advantageous to utilize the entire range of the underlying gradient magnitudes to produce a probabilistic boundary map, retaining much of the information that is discarded when creating binary edge maps of the initial eta² maps for each location. Therefore, methods that do not require edge detection will be explored as well.

Converging methods in the field

In addition to our own efforts at defining areal borders, several other groups are working on converging methods that should allow cross-modality validation and increased confidence in the borders that overlap across methodologies. Johansen-Berg et al. (Johansen-Berg et al., 2004; Johansen-Berg et al., 2005) and Rushworth et. al. (Rushworth et al., 2006) have used DTI to separate specific functional areas based on the underlying tractography. Margulies et. al., (Margulies et al., 2007) have recently shown regional differences in resting state connectivity across large sections of the anterior cingulate gyrus.

The maturation of the above methods (Johansen-Berg et al., 2004; Johansen-Berg et al., 2005; Margulies et al., 2007; Nir et al., 2006) and those used in this manuscript, could radically change the way functional neuroimaging data are analyzed in basic, translational, and clinical settings. If functional areas could be reliably identified within individual subjects, spatially normalizing individual brains using probabilistic atlases could be supplanted by the individual’s own functional area locations as constraints on the registration process. The ability to delineate an individual’s functional areas would greatly improve the utility of fMRI for clinical diagnosis and prognosis. Such capabilities would herald a new era of non-invasive investigation of brain area function.