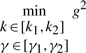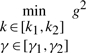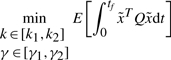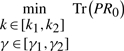Abstract
Motivation: Synthetic biology is to engineer artificial biological systems to investigate natural biological phenomena and for a variety of applications. However, the development of synthetic gene networks is still difficult and most newly created gene networks are non-functioning due to uncertain initial conditions and disturbances of extra-cellular environments on the host cell. At present, how to design a robust synthetic gene network to work properly under these uncertain factors is the most important topic of synthetic biology.
Results: A robust regulation design is proposed for a stochastic synthetic gene network to achieve the prescribed steady states under these uncertain factors from the minimax regulation perspective. This minimax regulation design problem can be transformed to an equivalent stochastic game problem. Since it is not easy to solve the robust regulation design problem of synthetic gene networks by non-linear stochastic game method directly, the Takagi–Sugeno (T–S) fuzzy model is proposed to approximate the non-linear synthetic gene network via the linear matrix inequality (LMI) technique through the Robust Control Toolbox in Matlab. Finally, an in silico example is given to illustrate the design procedure and to confirm the efficiency and efficacy of the proposed robust gene design method.
Availability: http://www.ee.nthu.edu.tw/bschen/SyntheticBioDesign_supplement.pdf
Contact: bschen@ee.nthu.edu.tw
Supplementary information: Supplementary data are available at Bioinformatics online.
1 INTRODUCTION
Synthetic biology will revolutionize how we conceptualize and approach the engineering of biological systems. The vision and applications of this emerging field will influence many other scientific and engineering disciplines, as well as affect various aspects of daily life and society (Andrianantoandro et al., 2006). Synthetic biology builds living machines from the off-the-shelf chemical ingredients, utilizing many of the same strategies that electrical engineers employ to make computer chips (Tucker and Zilinskas, 2006). The main goal of the nascent field of synthetic biology is to design and construct biological systems with the desired behavior (Alon, 2003, 2007; Andrianantoandro et al., 2006; Church, 2005; Endy, 2005; Hasty et al., 2002; Heinemann and Panke, 2006; Kobayashi et al., 2004; Pleiss, 2006; Tucker and Zilinskas, 2006). By a set of powerful techniques for the automated synthesis of DNA molecules and their assembly into genes and microbial genomes, synthetic biology envisions the redesign of natural biological systems for greater efficiency as well as the construction of functional ‘genetic circuit’ and metabolic pathways for practical purposes (Andrianantoandro, et al., 2006; Ferber, 2004; Forster and Church, 2007; Gardner, et al., 2000; Heinemann and Panke, 2006; Isaacs, et al., 2006; Maeda and Sano, 2006; Tucker and Parker, 2000). Synthetic biology is foreseen to have important applications in biotechnology and medicine (Andrianantoandro et al., 2006).
Though the engineering of networks of inter-regulating genes, so-called synthetic gene networks, has demonstrated the feasibility of synthetic biology (Gardner et al., 2000), the design of gene networks is still a difficult problem and most of the newly designed gene networks cannot work properly. These design failures are mainly due to intrinsic perturbations such as gene expression noises, splicing, mutation, uncertain initial states and disturbances such as changing extra-cellular environments, and interactions with cellular context. Therefore, how to design a robust synthetic gene network, which could tolerate uncertain initial conditions, attenuate the effect of all disturbances and function properly on the host cell, will be an important topic for synthetic biology (Alon, 2003, 2007; Andrianantoandro et al., 2006; Batt et al., 2007; Church, 2005; Endy, 2005; Goulian, 2004; Hasty et al., 2002; Heinemann and Panke, 2006; Kaznessis, 2006, 2007; Kitano, 2002, 2004; Kobayashi et al., 2004; Pleiss, 2006; Salis and Kaznessis, 2006; Tucker and Zilinskas, 2006). Previously, sensitivity analysis has been used for analysis of the dynamic properties of gene networks either in qualitative simulations of coarse-grained models or in extensive numerical simulations of non-linear differential equation models or stochastic dynamic models (de Jong, 2002; Szallasi et al., 2006). For applications in synthetic biology, these approaches are not satisfying. The local sensitivity analysis can provide only a partial description of all possible behaviors of a non-linear gene network. In particular, it cannot guarantee that a synthetic gene network behaves as expected for all uncertain initial conditions and disturbances. Moreover, obtaining all convergences of states and parameters by extensive numerical simulations quickly becomes computationally intractable when the size of the synthetic network grows (Batt et al., 2007).
An approach has recently been developed using semidefinite programming to partition the parameter spaces of polynomial differential equation models into so-called feasible and infeasible regions (Kuepfer et al., 2007). Following that, a robustness analysis and tuning approach of synthetic networks was proposed to provide a means to assess the robustness of the expected behavior of a synthetic gene network in spite of parameter variations (Batt et al., 2007). This approach has the capability to search for parameter sets for which a given property is satisfied through a publicly available tool called RoVerGeNe. Several gene circuit design networks have been introduced to implement or delete some circuits from an existing gene network so as to modify its structure for improving its robust stability or filtering ability (Chen and Chen, 2008; Chen and Wu, 2008; Chen et al., 2008b). However, robust synthetic gene network design is a different topic. It needs to design a complete man-made gene network to be inserted into a host cell. Therefore, the synthetic gene networks should be designed with enough robustness to tolerate uncertain initial conditions and to resist all possible disturbances on the host cell so that they can function properly in a desired steady state. This is a so-called robust regulation design that can achieve a desired steady state of synthetic gene networks despite uncertain initial conditions and disturbances on the host cell.
In this study, a robust regulation design of synthetic gene network is proposed to achieve a desired steady state in spite of uncertain initial conditions, parameter variations and disturbances on the host cell. Because most information of these uncertain factors on the host cell is unavailable, in order to attenuate their detrimental effects, their worst-case effect should be considered by the designer in the regulation design procedure from the worst regulation error perspective. The worst-case effect of all possible initial conditions and disturbances on the regulation error to a desired steady state is minimized for the robust synthetic gene networks, i.e. the proposed robust synthetic gene network is designed from the minimax regulation error perspective. The minimax design scheme is a simple robust synthetic gene network design method because we do not need the precise information of the initial conditions, parameter variations and disturbances on the host cell, which are not easy to measure in the design procedure. This minimax regulation design problem for robust synthetic gene networks could be transformed to an equivalent dynamic game problem (Basar and Olsder, 1999; Chen et al., 2002). Dynamic game methods have been widely applied to many fields of robust engineering design problems with external disturbances. Recently, the application of dynamic game theory has been used for robust model matching control of immune systems under environmental disturbances (Chen et al., 2008a). A robust drug administration (control input) is designed to obtain a prescribed immune response under uncertain initial states and environmental disturbances. In this study, the stochastic game theory will be used for robust synthetic gene network design so that the engineered gene network can work properly under uncertain initial conditions and environmental disturbances on the host cell. The uncertain initial states and disturbances are considered as a player doing his best to deteriorate the regulation performance from the worst-case point of view, while the system parameters to be designed are considered as another player optimizing the regulation performance under the worst-case deterioration of a former player. Since the synthetic gene networks are highly non-linear, it is not easy to solve the robust synthetic gene network design problem directly by the non-linear dynamic game method directly. Recently, fuzzy systems have been employed to efficiently approximate non-linear dynamic systems to solve the non-linear control problem (Chen et al., 1999, 2000; Hwang, 2004; Li et al., 2004; Lian et al., 2001; Takagi and Sugeno, 1985). A Takagi–Sugeno (T–S) fuzzy model (Takagi and Sugeno, 1985) is proposed to interpolate several linearized genetic networks at different operating points to approximate the non-linear gene network via some smooth fuzzy membership functions. Then with the help of the fuzzy approximation method, a fuzzy dynamic game scheme (Chen et al., 2002) is developed so that the minimax regulation design of robust synthetic gene networks could be easily solved by the techniques of the linear dynamic game theory, which can be subsequently solved by a constrained optimization scheme via the linear matrix inequality (LMI) technique (Boyd et al., 1994) that can be efficiently solved by the Robust Control Toolbox in Matlab (Balas et al., 2008). Because the fuzzy model can approximate any non-linear system, the proposed robust regulation design method developed from the fuzzy stochastic game theory can be applied to the robust regulation design problem of any synthetic gene network that can be interpolated by a T–S fuzzy model. For comparison, the conventional optimal regulation design method without considering the effect of disturbances is also proposed for the synthetic gene network. Because the effect of disturbances is not attenuated efficiently, the optimal regulation design method of synthetic gene networks is much influenced by the disturbances on the host cell. Finally, an in silico example is given to illustrate the design procedure and to confirm the efficiency and efficacy of the proposed minimax regulation design method for robust synthetic gene networks.
2 SYSTEMS AND METHODS
First, for the convenience of problem description, a simple design example of a four-gene network in Batt et al. (2007) is provided to give an overview of the design problem of robust synthetic gene networks. A more general design problem of robust synthetic gene networks will be given in the sequel. Let us consider a robust regulation design problem of a cascade loop of transcriptional inhibitions built in Escherichia coli. (Hooshangi et al., 2005). The synthetic gene network is represented in Figure 1. It consists of four genes: tetR, lacI, cI and eyfp that code, respectively, three repressor proteins, TetR, LacI and CI, and the fluorescent protein EYFP (enhanced yellow fluorescent protein) (Batt et al., 2007). aTc (anhydrotetracycline) is the input to the system. The fluorescence of the system, due to the protein EYFP, is the measured output. The protein CI inhibits gene eyfp. The protein TetR inhibits gene lacI. The protein LacI inhibits gene cI. The regulatory dynamic equations of the synthetic transcriptional cascade in Figure 1 are given as follows (Batt et al., 2007).
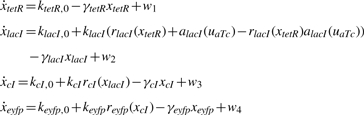 |
(1) |
with the uncertain initial conditions xtetR(0), xlacI(0), xcI(0) and xeyfp(0) in the host cell. ktetR,0, klacI,0, kcI,0 and keyfp,0 are basal production rates of the corresponding proteins, which are assumed to be given constants. klacI, kcI and keyfp are the production rate parameters, while γtetR, γlacI, γcI and γeyfp are decay rate parameters of the corresponding proteins. The regulatory functions rlacI, rcI and reyfp are the Hill functions for repressors and alacI for an activator.
Fig. 1.
Synthetic transcription cascade loop in silico design example. aTc represses TetR, TetR represses lacI, LacI represses cI, CI represses eyfp. aTc is the system input and the fluorescent protein EYFP is the output.
The Hill function can be derived from considering the equilibrium binding of the transcription factor to its site on the promoter region. For a repressor, Hill function is an S-shaped curve which can be described in the form r(x)=βr/(1+(x/Kr)n). βris the maximal expression level of promoter. Kr is the repression coefficient. The Hill coefficient n governs the steepness of the input function. For an activator, Hill function can be described in the form a(x)=βaxn/(Kan + xn). βa is the maximal expression level of promoter. Ka is the activation coefficient. n determines the steepness of the input function (Alon, 2007). w1, w2, w3 and w4 are the disturbances of the synthetic gene network, which denote the total of environmental noises, modeling residuals, intrinsic parameter fluctuations in the host cell. Therefore, wi, i = 1–4 are assumed uncertain but bounded disturbances. The synthetic gene network design is to specify klacI, kcI, keyfp and γtetR, γlacI, γcI, γeyfp such that the system states xtetR, xlacI, xcI and xeyfp can approach the desired states xd1, xd2, xd3 and xd4, respectively, in spite of uncertain initial conditions and disturbances.
If a synthetic gene network consists of n genes, then Equation (1) can be extended to the following n-gene network dynamics.
| (2) |
where the state vector x denotes the concentrations of proteins in the synthetic gene network. k0 denotes the vector of basal production rates of the corresponding proteins. f(x,k,γ) denotes the regulation vector of synthetic gene network, which is the function of production rate parameters k and decay rate parameters γ to be designed. g(u) denotes the input function to the synthetic gene network. w denotes the vector of stochastic disturbances on the host cell, whose statistics may be unavailable. The initial condition x0 is assumed stochastic with unknown covariance. The robust synthetic gene network design is to select parameters k and γ from feasible ranges so that the state vector x can approach a desired state vector xd in spite of uncertain initial condition x(0) and disturbances w on the host cell. i.e. x → xd at the steady state despite uncertain x(0) and w. This is a robust regulation problem of synthetic gene networks, i.e. the state vector x of synthetic gene networks is robustly regulated to xd in the host cell.
Let us denote the regulation error as
| (3) |
Then the regulation error dynamic system is given by
| (4) |
where v=k0+g(u)+w denotes the total uncertain disturbance in the regulation error system because these terms always fluctuate in the host cell and are not easily measured correctly. Because of the uncertainty of v and 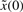 , the minimax regulation design method is an efficient but simple design scheme for robust synthetic gene network. The uncertainty of disturbance v and initial condition
, the minimax regulation design method is an efficient but simple design scheme for robust synthetic gene network. The uncertainty of disturbance v and initial condition 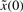 in the following minimax design can be considered as a player maximizing their effects on the regulation error in the following robust design problem of synthetic gene networks (Basar and Olsder, 1999; Chen et al., 2002).
in the following minimax design can be considered as a player maximizing their effects on the regulation error in the following robust design problem of synthetic gene networks (Basar and Olsder, 1999; Chen et al., 2002).
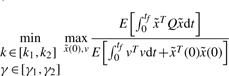 |
(5) |
where Q is the weighting matrix. In general, Q is a diagonal weighting matrix with Q=diag([q11, q22, …, qnn]) to denote the punishment on regulation error. If only the last state xn is required to be regulated to achieve the desired steady state xdn, then we can let qnn = 1 and q11 = q22 =···=qn−1n−1=0. [k1,k2] and [γ1,γ2] denote the allowable ranges of production rate vector k and decay rate vector γ, respectively. The allowable ranges are determined by the engineering biotechnologies of synthetic biology. k and γ to be designed can be considered as another player minimizing the worst-case effect of 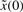 and v on the regulation error. If the disturbances v and initial condition
and v on the regulation error. If the disturbances v and initial condition 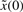 are deterministic, then the expectation operation E[ ] in (5) could be neglected.
are deterministic, then the expectation operation E[ ] in (5) could be neglected.
The physical meaning of (5) is that the worst-case effect of uncertain 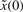 and v on the regulation error
and v on the regulation error 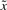 must be minimized from the mean energy perspective by k and γ, which are chosen from the allowable ranges. Therefore, for uncertain
must be minimized from the mean energy perspective by k and γ, which are chosen from the allowable ranges. Therefore, for uncertain 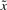 and v, the robust synthetic gene network design is to solve the minimax problem in (5) subject to the regulation error dynamic system in (4). This is the so-called stochastic game problem in the robust synthetic gene network design (Basar and Olsder, 1999).
and v, the robust synthetic gene network design is to solve the minimax problem in (5) subject to the regulation error dynamic system in (4). This is the so-called stochastic game problem in the robust synthetic gene network design (Basar and Olsder, 1999).
In general, it is not easy to solve the non-linear stochastic game problem in (5) subject to (4) directly. It is always solved by a sub-minimax method. First, let the upper bound g2 of (5) (Basar and Olsder, 1999; Chen et al., 2002) be
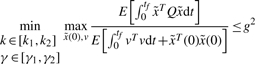 |
(6) |
We will first solve the sub-minimax problem in (6) and then decrease the upper bound g2 as much as possible to approach its minimax solution. In general, the minimax problem in (6) is equivalent to the following minimax problem (Basar and Olsder, 1999; Chen et al., 2002)
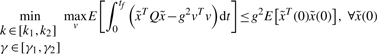 |
(7) |
where g2 is to be minimized because it is the upper bound in (6) and should be as small as possible to approach the minimax solution. Let us denote the cost function as
| (8) |
3 RESULTS
3.1 Sub-minimax design for robust synthetic gene networks
From the above analysis, the dynamic game problem in (6) or (7) is equivalent to finding the worst-case disturbance v* which maximizes J(k, γ, v) and then the minimax k* and γ* which minimize J(k, γ, v*) such that the minimax value J(k*, γ*, v*) is less than 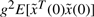 , i.e.
, i.e.
| (9) |
Hence, if there exist k*, γ* and v* such that the minimax design problem in (9) is solved, then they can satisfy the minimax performance of the robust synthetic gene network design in (6) as well. Therefore, the first step of robust synthetic gene network design is to solve the following dynamic game problem:
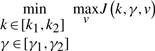 |
(10) |
subject to the error dynamic equation in (4). Since 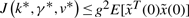 according to (9) and g2 is the upper bound of the game in (6), the sub-minimax has to make g2 as small as possible, too.
according to (9) and g2 is the upper bound of the game in (6), the sub-minimax has to make g2 as small as possible, too.
From the above analysis, we obtain the following sub-minimax result for robust synthetic gene network design.
Proposition 1. —
The sub-minimax synthetic gene network design is equivalent to solving the following constrained optimization for k* and γ*,
(11) subject to the following Hamilton–Jacobi inequality (HJI)
(12) with
and the worst-case disturbance is given by
(13)
Proof. —
see Appendix A in the Supplementary Material.
Remark 1. —
From (6), g2 is the upper bound of the game. In (11), we minimize the upper bound g2 to achieve the sub-minimax solution for robust synthetic gene networks.
The physical meaning of the constrained minimization in (11) and (12) is that we want to specify k* and γ* from the allowable parameter ranges such that the upper bound g2 is as small as possible until no positive solution
of HJI in (12) exists.
At present, there exists no efficient analytic or numerical method to solve the HJI in (12) for non-linear stochastic system control or filtering designs (Zhang and Chen, 2006; Zhang et al., 2005).
3.2 Minimax robust synthetic gene networks via fuzzy interpolation method
Because it is very difficult to solve the non-linear HJI in (12), no simple approach is available for solving the constrained optimization problem in (11) for the minimax robust synthetic gene network design problem. Recently, the T–S fuzzy model has been widely employed (Chen et al., 1999, 2000; Hwang, 2004; Takagi and Sugeno, 1985) to approximate the non-linear system via interpolating several linearized systems at different operating points so that the non-linear Nash stochastic problem could be transformed to a fuzzy stochastic game problem (Chen et al., 2002). By using such approach, the HJI in (12) can be replaced by a set of LMIs. In this situation, the non-linear stochastic game problem in (10) could be easily solved by the fuzzy dynamic method for the robust design of sub-minimax design problem.
Suppose the non-linear system in (4) could be approximated by a T–S fuzzy system (Takagi and Sugeno, 1985). The T–S fuzzy model is a piecewise interpolation of several linearized models through fuzzy membership functions. The fuzzy model is described by fuzzy if-then rules and will be employed to deal with the non-linear stochastic game problem for robust synthetic gene network design under uncertain initial conditions and disturbances. The i-th rule of fuzzy model for non-linear systems in (4) is of the following form (Chen et al., 1999; Takagi and Sugeno, 1985).
Rule i:
If 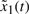 is Fi1 and … and
is Fi1 and … and 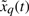 is Fiq,
is Fiq,
| (14) |
where Fij is the fuzzy set. Ai(k,γ) is constant matrix with the elements of k and γ contained in its entries. q is the number of premise variables and  are the premise variables. The fuzzy system is inferred as follows (Chen et al., 1999, 2000; Li et al., 2004; Lian et al., 2001; Takagi and Sugeno, 1985)
are the premise variables. The fuzzy system is inferred as follows (Chen et al., 1999, 2000; Li et al., 2004; Lian et al., 2001; Takagi and Sugeno, 1985)
| (15) |
where 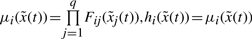
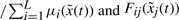 are the grade of membership of
are the grade of membership of 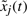 in Fij.
in Fij.
We assume
| (16) |
Therefore, we get the following fuzzy basis functions
| (17) |
The T–S fuzzy model in (15) is to interpolate L linear systems to approximate the non-linear system in (4) via the fuzzy basis functions 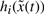 . We could specify system parameter Ai(k,γ) easily so that
. We could specify system parameter Ai(k,γ) easily so that 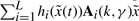 can approximate
can approximate 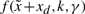 in (4) by the fuzzy identification method (Takagi and Sugeno, 1985).
in (4) by the fuzzy identification method (Takagi and Sugeno, 1985).
After the non-linear system in (4) is approximated by the T–S fuzzy system in (15), the non-linear dynamic game problem in (10) is replaced by solving a dynamic game problem in (6) subject to the fuzzy system (15).
Proposition 2. —
The sub-minimax robust synthetic gene network design is to solve k* and γ* by the following constraint optimization
(18) subject to
(19) and the worst-case disturbance v* is given by
(20)
Proof. —
see Appendix B in the Supplementary Material.
By the fuzzy approximation, the HJI in (12) can be approximated by a set of algebraic inequalities in (19). By Schur complement (Boyd et al., 1994), the constrained optimization problem in (18) and (19) is equivalent to the following LMI-constrained optimization problem
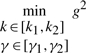 |
(21) |
subject to
 |
(22) |
Remark 2. —
The fuzzy basis functions
in (15) and (17) can be replaced by other interpolation functions, for example, cubic spline functions.
By the fuzzy approximation, the HJI in (12) of non-linear dynamic game problem can be solved by Robust Control Toolbox in Matlab efficiently (Balas et al., 2008). The constrained optimization in (18) and (19) can be solved by decreasing g2 until there is no positive definite solution P > 0 in (22) with k* ∈[k1,k2] and γ* ∈[γ1,γ2].
In the LMI-constrained optimization in (22) for the robust synthetic gene network design, we do not need the statistics of initial conditions and disturbances on the host cell, which are not easy to be measured. Therefore, the proposed method is simple but robust for synthetic gene networks.
Remark 3. —
For comparison, the conventional optimal regulation design is also proposed for synthetic gene networks. If the effect of external disturbances and uncertain initial conditions on the regulation error is not considered as (5) in the design procedure, i.e. only the following optimal regulation design is considered.
(23) subject to (4) then we obtain the following sub-optimal regulation design for synthetic gene networks.
Proposition 3. —
The sub-optimal synthetic gene network design in (23) is to solve the following constrained optimization
(24) subject to
(25)
Proof. —
see Appendix C in the Supplementary Material.
Because it is not easy to solve the above HJI-constrained optimization for the sub-optimal regulation design in (24) and (25), the fuzzy approximation method is needed to simplify the design procedure. If the non-linear error dynamic equation in (4) is represented by the fuzzy interpolation system in (15), then the optimal synthetic gene network design in (23) is equivalent to the following optimal regulation design problem.
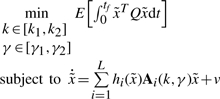 |
(26) |
Proposition 4. —
The sub-optimal regulation design problem in (26) becomes how to solve the following constrained optimization problem
(27) subject to
(28) where R0 denotes the covariance matrix
.
Proof. —
Similar to the proof of Proposition 2.
Since the effect of stochastic disturbances on 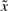 is not considered as (5) in the above sub-optimal synthetic gene network design, the synthesized gene networks will be more sensitive to the external disturbances or other uncertain factors. They will be compared with the sub-minimax robust synthetic gene network in the simulation example.
is not considered as (5) in the above sub-optimal synthetic gene network design, the synthesized gene networks will be more sensitive to the external disturbances or other uncertain factors. They will be compared with the sub-minimax robust synthetic gene network in the simulation example.
Remark 4. —
Since the effect of the disturbance v on the regulation error has not been attenuated efficiently on the design procedure of the sub-optimal regulation in Propositions 3 and 4, the disturbance will have much effect on the sub-optimal regulation design of synthetic gene network. This property will be discussed and compared with the proposed robust synthetic gene network in the design example in the following section.
3.2.1 Design procedure
According to the analyses above, a design procedure is developed for the proposed robust synthetic gene network.
Give feasible parameter ranges [k1,k2] and [γ1,γ2] for production rate parameters k and decay rate parameters γ, respectively, according to the biotechnology ability.
Give the desired steady state xd according to the design purpose and develop a regulation error dynamic (4) for a synthetic gene network.
Construct a T–S fuzzy model in (15) to approximate the regulation error dynamic in (4).
Solve the constrained optimization problem from the ranges k∈[k1,k2] and γ∈[γ1,γ2] in (21) and (22) for the robust synthetic gene network design k* and γ*, respectively according to the sub-minimax scheme or solve the constrained optimization problem in (27) and (28) for the sub-optimal regulation design.
3.3 Design example in silico for the proposed robust design
Consider the man-made synthetic gene network in the dynamic equations (1) (Batt et al., 2007). The synthetic gene network is shown in Figure 1. Where ktetR,0, klacI,0, kcI,0 and keyfp,0 are basal production rates of the corresponding proteins, which are assumed to be 5000, 587, 210 and 3487, respectively (Batt et al., 2007; Hooshangi et al., 2005). klacI, kcI and keyfp are the production rate parameters while γtetR, γlacI, γcI and γeyfp are the decay rate parameters of the corresponding proteins in the host cell (i.e. E. coli.). In the robust synthetic gene network design, we should select the parameters k and γ from feasible ranges so that the state of synthetic gene network xi could approach a desired steady state xd,i for some biotechnical purpose. rlacI, rcI and reyfp are the decreasing Hill functions for regulations of repressors. alacI is an increasing function since aTc is an activator. The Hill function is an S-shaped curve (Alon, 2007). uaTc is the input to the synthetic gene network system. We assume anhydrotetracycline input concentration to be a constant value 10 000 (i.e. uaTc = 10 000). For the convenience of simulation, we assume that extrinsic disturbances w1–w4 are wi = [500n1 10 000n2 100n3 100 000n4]T, where ni, i = 1,2,3,4 are independent Gaussian white noises with zero mean and unit variance.
From the robust synthetic gene network design procedure, we give the feasible parameter ranges of production rate parameters k and decay rate parameters γ as follows (Batt et al., 2007)
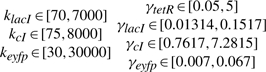 |
(29) |
Then we give the desired steady states of the synthetic gene network are xd,i=[1000, 50 000, 300, 500 000]T, i = tetR, lacI, cI, eyfp. Then the regulation error dynamic equation in (4) is developed for the synthetic gene network. Because it is very difficult to solve the non-linear HJI in (12), no simple approach is available to solve the constrained optimization problem in (11) for robust parameters ki* and γi*. We construct the T–S fuzzy model in (15) to approximate the regulation error dynamic in (4) with the regulation error dynamic system's state variables as the premise variables in the following.
Rule i:
If 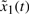 is Fi1 and
is Fi1 and 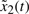 is Fi2 and
is Fi2 and 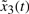 is Fi3 and
is Fi3 and 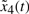 is Fi4,
is Fi4,
where the parameters Ai(k,γ) and the number of fuzzy rules is L=16. To construct the fuzzy model, we need to find the operating points of the regulation error dynamic system. The operating points for 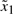 are chosen at
are chosen at 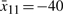 and
and 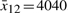 . Similarly, the operating points of
. Similarly, the operating points of 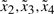 are chosen at
are chosen at 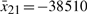 ,
, 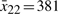 ,
, 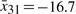 ,
, 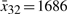 ,
, 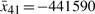 , and
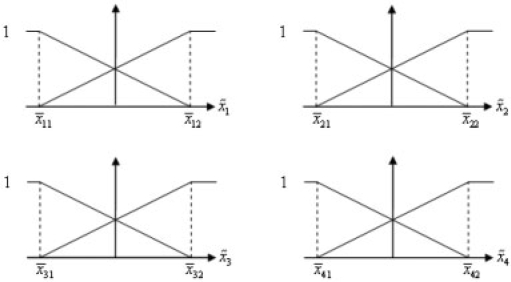
, and 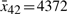 , respectively. For the convenience of design, triangle-type membership functions are taken for Rule 1 through Rule 16. We create two triangle-type membership functions for each state (Fig. 2).
, respectively. For the convenience of design, triangle-type membership functions are taken for Rule 1 through Rule 16. We create two triangle-type membership functions for each state (Fig. 2).
Fig. 2.
Membership functions for four states 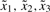 and
and 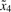 .
.
In order to simplify the non-linear stochastic game problem of the robust synthetic gene network, we just solve only the sub-minimax problem in (6) instead. With the help of fuzzy approximation method and LMI technique, we can easily solve the constrained optimization problem in (21) and (22) instead of the non-linear constrained optimization problem in (11) and (12) for the minimax robust synthetic gene network design. Finally, we obtain the upper bound of the game in (6) g2 = 0.847536 and a common positive definite symmetric matrix P for (22) as follows
 |
with the specified robust production rate parameters klacI*=7000, kcI*=4037.5 and keyfp*=30 000 and robust decay rate parameters γtetR*=5, γlacI*=0.1517, γcI*=4.0216 and γeyfp*=0.067 of the synthetic gene network. With these design parameters, the parameters Ai of fuzzy model are described in Appendix D (Supplementary Material).
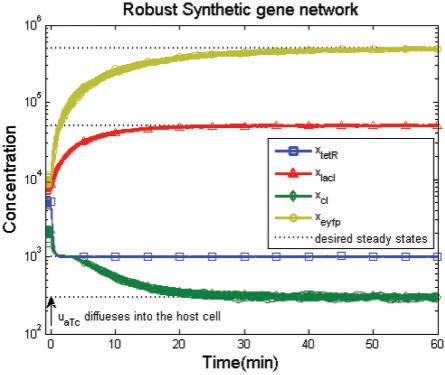
Figure 3 presents the simulation result for robust synthetic gene networks by using Monte Carlo method with 50 rounds and with the uncertain initial values. x1(0)–x4(0) are assumed normal-distributed random numbers with means 5000, 8000, 2000, 10 000 and SDs 500, 800, 200, 1000, respectively. As can be seen, the synthetic gene network has robust regulation ability to achieve the desired steady state (black dashed line) in spite of uncertain initial states and the disturbances on the host cell. Obviously, the robust synthetic gene network by the proposed sub-minimax regulation design method has robust stability to the uncertain initial conditions and enough filtering ability to attenuate the disturbances on the host cell and can approach the desired steady states.
Fig. 3.
The robust synthetic gene network design with uncertain initial values and the desired steady states xd=[1000, 50000, 300, 500000]T. And with specified robust production rate parameters klacI*=7000, kcI*=4037.5 and keyfp*=30000 while the specified robust decay rate parameters are γtetR*=5, γlacI*=0.1517, γcI*=4.0216 and γeyfp*=0.067 of the synthetic gene network. The Monte Carlo simulation method is used with 50 rounds.
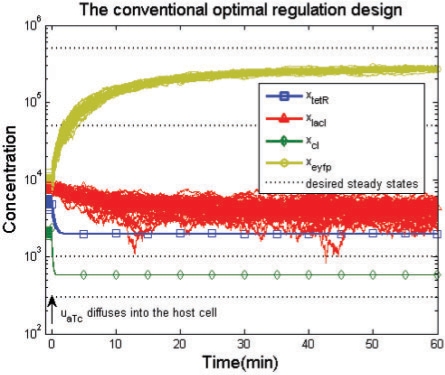
For comparison, we solve the sub-optimal regulation design problem in (27) and (28) for the specified production rate parameters klacI*=70, kcI*=4037.5 and keyfp*=15 015 and decay rate parameters γtetR*=2.525, γlacI*=0.1517, γcI*=7.2815 and γeyfp*=0.067 of the synthetic gene network. The simulation result of conventional optimal regulation design is also shown in Figure 4. As can be seen, the conventional optimal regulation design of the synthetic gene network is more sensitive to the initial conditions and disturbances, and cannot achieve the desired steady state under the uncertain initial conditions and disturbances.
Fig. 4.
The conventional optimal regulation design with uncertain initial values and the desired steady states xd=[1000, 50 000, 300, 500 000]T. And with specified production rate parameters klacI*=70, kcI*=4037.5 and keyfp*=15 015, while the specified decay rate parameters are γtetR*=2.525, γlacI*=0.1517, γcI*=7.2815 and γeyfp*=0.067 of the synthetic gene network. It is seen that the conventional optimal regulation design of the synthetic gene network is sensitive to the initial conditions and disturbances and cannot achieve the desired steady states. The Monte Carlo simulation method is used with 50 rounds.
Remark 5. —
The experimental systems in the above example may not be fully observable. If we want to know whether all state variables can approach to the desired states xd, several fluorescent proteins (red, green and cyan color) should be necessary to observe their protein expressions of all state variables in the experimental design.
4 DISCUSSION
Because the initial conditions and disturbances on the host cell are uncertain, to simplify the design problem, a robust synthetic biology design is formulated as a stochastic game problem in this study. The uncertain initial conditions and disturbances due to intrinsic and extrinsic molecular noises on the host cell are considered as a player maximizing the regulation error and the design parameters are considered as another player minimizing the regulation error. In order to avoid solving HJI in the stochastic game theory-based design problem, a T–S fuzzy interpolation method is introduced to simplify the design procedure of robust synthetic gene networks via only solving a set of LMIs, which can be efficiently solved by Robust Control Toolbox in Matlab.
In our study, we can select the weighting matrix Q=diag([q11, q22, q33, q44]) which denotes the punishment on the corresponding tracking error 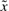 . If we only need to achieve a desired steady state xd4 (EYFP), we just assign a value to the fourth diagonal element q44 of the weighting matrix Q and set q11 = q22 = q33=0. The states x1–x3 will not approach to the given steady state xd1–xd3 because of no any punishment. However, in this case, some infeasible steady states of x1, x2 and x3 may be obtained even an optimal x4 can be achieved. In this study, the desired steady states of x1, x2 and x3 are given because we can avoid obtaining infeasible steady states in x1, x2 and x3 when an optimal x4 is achieved. Further, the undesired steady states of x1, x2 and x3 may also have metabolic toxicity on host cell and should be avoided. Since the steady states of x1–x3 are not that important, the desired steady states xd1–xd3 can be adjusted within feasible ranges, so that the desired steady state xd4 can still achieve some optimization as possible. This kind of design can avoid hampering the optimization of x4 when x1, x2 and x3 achieve some feasible steady states.
. If we only need to achieve a desired steady state xd4 (EYFP), we just assign a value to the fourth diagonal element q44 of the weighting matrix Q and set q11 = q22 = q33=0. The states x1–x3 will not approach to the given steady state xd1–xd3 because of no any punishment. However, in this case, some infeasible steady states of x1, x2 and x3 may be obtained even an optimal x4 can be achieved. In this study, the desired steady states of x1, x2 and x3 are given because we can avoid obtaining infeasible steady states in x1, x2 and x3 when an optimal x4 is achieved. Further, the undesired steady states of x1, x2 and x3 may also have metabolic toxicity on host cell and should be avoided. Since the steady states of x1–x3 are not that important, the desired steady states xd1–xd3 can be adjusted within feasible ranges, so that the desired steady state xd4 can still achieve some optimization as possible. This kind of design can avoid hampering the optimization of x4 when x1, x2 and x3 achieve some feasible steady states.
In our in silico design example, we can design the specified robust production rate parameters ki* and decay rate parameters γi* within the feasible parameter ranges to achieve the desired steady states of the synthetic gene network. As for the biological implementation, we could refer to standard biological parts in biological device datasheets to construct the genetic circuits with the fine-tuned production rate parameters ki* and decay rate parameters γi*. In this way, synthetic biologists can increase efficiency of gene circuit design through registries of biological parts and standard datasheets, which are developed concerned with proper packing and characterizing of ‘modular’ biological activities so that these biological parts or devices with some desired characteristics may be efficiently assembled into gene circuits (Canton, et al., 2008).
Quantitative descriptions of devices in the form of standardized, comprehensive datasheets are widely used in many engineering disciplines. A datasheet is intended to allow an engineer to quickly determine whether the behavior of a device will meet the requirements of a system in which a device might be used (Canton, et al., 2008). Such a determination is based on a set of standard characteristics of device behavior, which are the product of engineering theory and experience. In the datasheets of engineering, the characteristics typically reported are common across a wide range of device types, such as sensors, logic elements and actuators. Recently, biological datasheets have been set as standards for characterization, manufacture and sharing of information about modular biological devices for a more efficient, predictable and design-driven genetic engineering science (Arkin, 2008; Canton, et al., 2008). Because datasheets of biological parts or devices are an embodiment of engineering standard for synthetic biology (Canton, et al., 2008), a good device standard should define sufficient information about biological parts or devices to allow the design of gene circuit systems with the optimal parameters. Datasheets contain a formal set of input–output transfer functions, dynamic behaviors, compatibility, requirements and other details about a particular part or device (Arkin, 2008; Canton, et al., 2008). Since parameters ki are combinations of transcription and translation, they could be measured from the input–output transfer functions and dynamic behaviors of biological parts or devices in biological device datasheets. From properly characterized input–output transfer functions and dynamic behaviors of parts or devices in biological device datasheets, an engineer can estimate the corresponding parameters of biological parts or devices. When the biological parts and devices in datasheets become more complete in future, we can rapidly select from a vast list the parts that will meet our design parameters ki. Therefore, we can ensure that devices selected from datasheets can fit the optimal parameters and systems synthesized from them can satisfy the requirements of design specifications for robust synthetic gene networks.
In order to guarantee the biological feasibility of the calculated optimal parameters, the ranges [k1, k2] and [γ1,γ2] of parameters should be determined by the whole parameters of biological parts repositories (http://partsregistry.org/) so that the optimal parameters selected within these ranges to minimize g2 in Equations (21) and (22) have biological meaning, or equivalently from the whole biological parts in biological device datasheets, we can find a set of biological parts whose parameters can minimize the g2 in Equations (21) and (22) to achieve the robust optimal design of synthetic gene network.
In synthetic gene networks, there is much uncertainty about what affects the behavior of biological circuitry and systems. For example, devices will perturb the cellular functions and there are also likely to be parasitic and unpredictable interactions among components as well as with the host. Since ki is a combination of promoter strength, ribosome binding site and degradation of the transcript, there are some variations or uncertainties on the parameter value ki. These variations or uncertainties of ki can be transformed to an equivalent uncertain disturbance wi in Equation 1 from the viewpoint of mathematic model. The proposed robust minimax synthetic biology design method can predict the most robust value of ki from the perspective of stochastic game. In our robust design method, we do not need the statistics of these parameter uncertainties because the proposed synthetic genetic network not only can achieve the desired steady state but also can tolerate the worst-case effect due to these uncertain parameter variations and external noises on the host cell.
For comparison, a sub-optimal regulation design for synthetic gene network is also developed for synthetic gene network. Because the sub-optimal regulation design cannot efficiently attenuate the effect of uncertain initial conditions and disturbances on the regulation, it is not suitable for robust synthetic gene networks with uncertain initial conditions and disturbances on the host cell. As seen in the example in silico, the proposed robust synthetic gene network can function properly in spite of uncertain initial conditions and disturbances on the host cell. Design of more robust and complex genetic circuits is foreseen to have important applications in biotechnology, medicine and biofuel production, and to revolutionize how we conceptualize and approach the engineering of biological systems (Andrianantoandro et al., 2006). Therefore, it has much potential for the robust synthetic gene network design in the near future.
Funding: National Science Council of Taiwan (Grant no. NSC 97-2627-P-001-002 and NSC 98-2311-B-009-002).
Conflict of Interest: none declared.
REFERENCES
- Alon U. Biological networks: the tinkerer as an engineer. Science. 2003;301:1866–1867. doi: 10.1126/science.1089072. [DOI] [PubMed] [Google Scholar]
- Alon U. An Introduction to Systems Biology: Design Principles of Biological Circuits. Chapman & Hall/CRC; 2007. [Google Scholar]
- Andrianantoandro E, et al. Synthetic biology: new engineering rules for an emerging discipline. Mol. Syst. Biol. 2006;2:1–14. doi: 10.1038/msb4100073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Arkin A. Setting the standard in synthetic biology. Nat. Biotechnol. 2008;26:771–774. doi: 10.1038/nbt0708-771. [DOI] [PubMed] [Google Scholar]
- Balas G, et al. Robust Control Toolbox User's Guide. Natick, MA: The Math Works, Inc.; 2008. [Google Scholar]
- Basar T, Olsder GJ. Society for Industrial and Applied Mathematics. 2. Natick, MA: The Math Works, Inc; 1999. Dynamic Noncooperative Game Theory. [Google Scholar]
- Batt G, et al. Robustness analysis and tuning of synthetic gene networks. Bioinformatics. 2007;23:2415. doi: 10.1093/bioinformatics/btm362. [DOI] [PubMed] [Google Scholar]
- Boyd S, et al. Society for Industrial Mathematics. Philadelphia: Society for Industrial and Applied Mathematics; 1994. Linear Matrix Inequalities in System and Control Theory. [Google Scholar]
- Canton B, et al. Refinement and standardization of synthetic biological parts and devices. Nat. Biotechnol. 2008;26:787–793. doi: 10.1038/nbt1413. [DOI] [PubMed] [Google Scholar]
- Chen BS, Chen PW. Robust engineered circuit design principles for stochastic biochemical networks with parameter uncertainties and disturbances. IEEE Trans. Biomed. Circuits Syst. 2008;2:114–132. doi: 10.1109/TBCAS.2008.926728. [DOI] [PubMed] [Google Scholar]
- Chen BS, Wu WS. Robust filtering circuit design for stochastic gene networks under intrinsic and extrinsic molecular noises. Math. Biosci. 2008;211:342–355. doi: 10.1016/j.mbs.2007.11.002. [DOI] [PubMed] [Google Scholar]
- Chen BS, et al. Robustness design of nonlinear dynamic systems via fuzzy linear control. IEEE Trans. Fuzzy Syst. 1999;7:571–585. [Google Scholar]
- Chen BS, et al. Mixed H2/H∞ fuzzy output feedback control design for nonlinear dynamic systems: an LMI approach. IEEE Trans. Fuzzy Syst. 2000;8:249–265. [Google Scholar]
- Chen BS, et al. Fuzzy differential games for nonlinear stochastic systems: suboptimal approach. IEEE Trans. Fuzzy Syst. 2002;10:222–233. [Google Scholar]
- Chen BS, et al. Robust model matching control of immune systems under environmental disturbances: dynamic game approach. J. Theor. Biol. 2008a;253:824–837. doi: 10.1016/j.jtbi.2008.04.024. [DOI] [PubMed] [Google Scholar]
- Chen BS, et al. Robust H∞ stabilization design in gene networks under stochastic molecular noises: Fuzzy-interpolation approach. IEEE Trans. Syst. Man Cybern. B. 2008b;38:25–42. doi: 10.1109/TSMCB.2007.906975. [DOI] [PubMed] [Google Scholar]
- Church GM. From systems biology to synthetic biology. Mol. Syst. Biol. 2005;1:2005.0032. doi: 10.1038/msb4100007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Jong H. Modeling and simulation of genetic regulatory systems: a literature review. J. Comput. Biol. 2002;9:67–103. doi: 10.1089/10665270252833208. [DOI] [PubMed] [Google Scholar]
- Endy D. Foundations for engineering biology. Nature. 2005;438:449–453. doi: 10.1038/nature04342. [DOI] [PubMed] [Google Scholar]
- Ferber D. Synthetic biology: microbes made to order. Science. 2004;303:158–161. doi: 10.1126/science.303.5655.158. [DOI] [PubMed] [Google Scholar]
- Forster AC, Church GM. Synthetic biology projects in vitro. Genome Res. 2007;17:1–6. doi: 10.1101/gr.5776007. [DOI] [PubMed] [Google Scholar]
- Gardner TS, et al. Construction of a genetic toggle switch in Escherichia coli. Nature. 2000;403:339–342. doi: 10.1038/35002131. [DOI] [PubMed] [Google Scholar]
- Goulian M. Robust control in bacterial regulatory circuits. Curr. Opin. Microbiol. 2004;7:198–202. doi: 10.1016/j.mib.2004.02.002. [DOI] [PubMed] [Google Scholar]
- Hasty J, et al. Engineered gene circuits. Nature. 2002;420:224–230. doi: 10.1038/nature01257. [DOI] [PubMed] [Google Scholar]
- Heinemann M, Panke S. Synthetic biology - putting engineering into biology. Bioinformatics. 2006;22:2790–2799. doi: 10.1093/bioinformatics/btl469. [DOI] [PubMed] [Google Scholar]
- Hooshangi S, et al. Ultrasensitivity and noise propagation in a synthetic transcriptional cascade. Proc. Natl Acad. Sci. USA. 2005;102:3581–3586. doi: 10.1073/pnas.0408507102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hwang CL. A novel Takagi-Sugeno-based robust adaptive fuzzy sliding-mode controller. IEEE Trans. Fuzzy Syst. 2004;12:676–687. [Google Scholar]
- Isaacs FJ, et al. RNA synthetic biology. Nat. Biotechnol. 2006;24:545–554. doi: 10.1038/nbt1208. [DOI] [PubMed] [Google Scholar]
- Kaznessis YN. Multi-scale models for gene network engineering. Chem. Eng. Sci.e. 2006;61:940–953. [Google Scholar]
- Kaznessis YN. Models for synthetic biology. BMC Syst. Biol. 2007;1:47. doi: 10.1186/1752-0509-1-47. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kitano H. Systems biology: a brief overview. Science. 2002;295:1662–1664. doi: 10.1126/science.1069492. [DOI] [PubMed] [Google Scholar]
- Kitano H. Biological robustness. Nat. Rev. Genet. 2004;5:826–837. doi: 10.1038/nrg1471. [DOI] [PubMed] [Google Scholar]
- Kobayashi H, et al. Programmable cells: interfacing natural and engineered gene networks. Proc. Natl Acad. Sci. 2004;101:8414–8419. doi: 10.1073/pnas.0402940101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kuepfer L, et al. Efficient classification of complete parameter regions based on semidefinite programming. BMC Bioinformatics. 2007;8:12. doi: 10.1186/1471-2105-8-12. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li T.HS, et al. Fuzzy target tracking control of autonomous mobile robots by using infrared sensors. IEEE Trans. Fuzzy Syst. 2004;12:491–501. [Google Scholar]
- Lian KY, et al. LMI-based fuzzy chaotic synchronization and communications. IEEE Trans. Fuzzy Syst. 2001;9:539–553. doi: 10.1109/3477.907565. [DOI] [PubMed] [Google Scholar]
- Maeda YT, Sano M. Regulatory dynamics of synthetic gene networks with positive feedback. J. Mol. Biol. 2006;359:1107–1124. doi: 10.1016/j.jmb.2006.03.064. [DOI] [PubMed] [Google Scholar]
- Pleiss J. The promise of synthetic biology. Appl. Microbiol. Biotechnol. 2006;73:735–739. doi: 10.1007/s00253-006-0664-3. [DOI] [PubMed] [Google Scholar]
- Salis H, Kaznessis YN. Computer-aided design of modular protein devices: Boolean AND gene activation. Phys. Biol. 2006;3:295–310. doi: 10.1088/1478-3975/3/4/007. [DOI] [PubMed] [Google Scholar]
- Szallasi Z, et al. System Modeling in Cellular Biology: From Concepts to Nuts and Bolts. Cambridge, MA: The MIT Press; 2006. [Google Scholar]
- Takagi T, Sugeno M. Fuzzy identification of systems and its applications to modeling and control. IEEE Trans.Syst. Man Cybern. 1985;15:116–132. [Google Scholar]
- Tucker JB, Zilinskas RA. The promise and perils of synthetic biology. New Atlantis. 2006;12:25–45. [PubMed] [Google Scholar]
- Tucker M, Parker R. Mechanisms and control of mRNA decapping in Saccharomyces cerevisiae. Ann. Rev. Biochem. 2000;69:571–595. doi: 10.1146/annurev.biochem.69.1.571. [DOI] [PubMed] [Google Scholar]
- Zhang W, Chen BS. State feedback H∞ control for a class of nonlinear stochastic systems. SIAM J. Control Optim. 2006;44:1973–1991. [Google Scholar]
- Zhang W, et al. Robust H∞ filtering for nonlinear stochastic systems. IEEE Trans. Signal Process. 2005;53:589–598. [Google Scholar]