Does water relay play an important role in phosphoryl transfer reactions? Insights from theoretical study of a model reaction in water and tert-butanol

Abstract

To investigate whether water relay plays an important role in phosphoryl transfer reactions, we have used several theoretical approaches to compare key properties of uridine 3’-m-nitrobenzyl phosphate (UNP) in the aqueous and tert-butanol solutions. Previous kinetic experiments found that the isomerization reaction of UNP is abolished in tert-butanol, which was interpreted as the direct evidence that supports the role of water relay in phosphoryl transfer. We have analyzed solute flexibility and solvent structure near the solute using equilibrium molecular dynamics simulations and a combined quantum mechanical/molecular mechanism (QM/MM) potential function for the solute. Snapshots from the simulations are then used in minimum energy path calculations to compare the energetics of direct nucleophilic attack and water-mediated nucleophilic attack pathways. QM/MM simulations are also used to compare the pseudo-rotation barriers for the pentavalent intermediate formed following the nucleophilic attack, another key step for the isomerization reaction. Combined results from these calculations suggest that water relay does not offer any significant energetic advantage over the direct nucleophilic attack. Unfortunately, the lack of isomerization in tert-butanol solution can not be straightforwardly explained based on the results we have obtained here and therefore requires additional analysis. This study, nevertheless, has provided new insights into several most commonly discussed possibilities.

1 Introduction

Phosphoryl transfer reactions are involved in many key biological processes such as energy transduction, signal transduction and protein/nucleic acids synthesis [1]. In additions, some RNA molecules have been found [2] to catalyze phosphoryl transfer reactions as well, and these ribozymes [3] have extended the definition of biological enzymes beyond protein systems, which stimulated the discussion of “RNA world” at the early stage of evolution [4]. The fundamental nature of phosphoryl transfer reactions has triggered an extensive body of experimental and theoretical analyses on their detailed mechanism [5–10]. It has been now established that the reaction pathway, such as being associative vs. dissociative [11–13] in nature, is likely sensitive to a number of factors that include pH, the pK_a values of the nucleophilic group and the leaving group as well as the presence of metal ions.

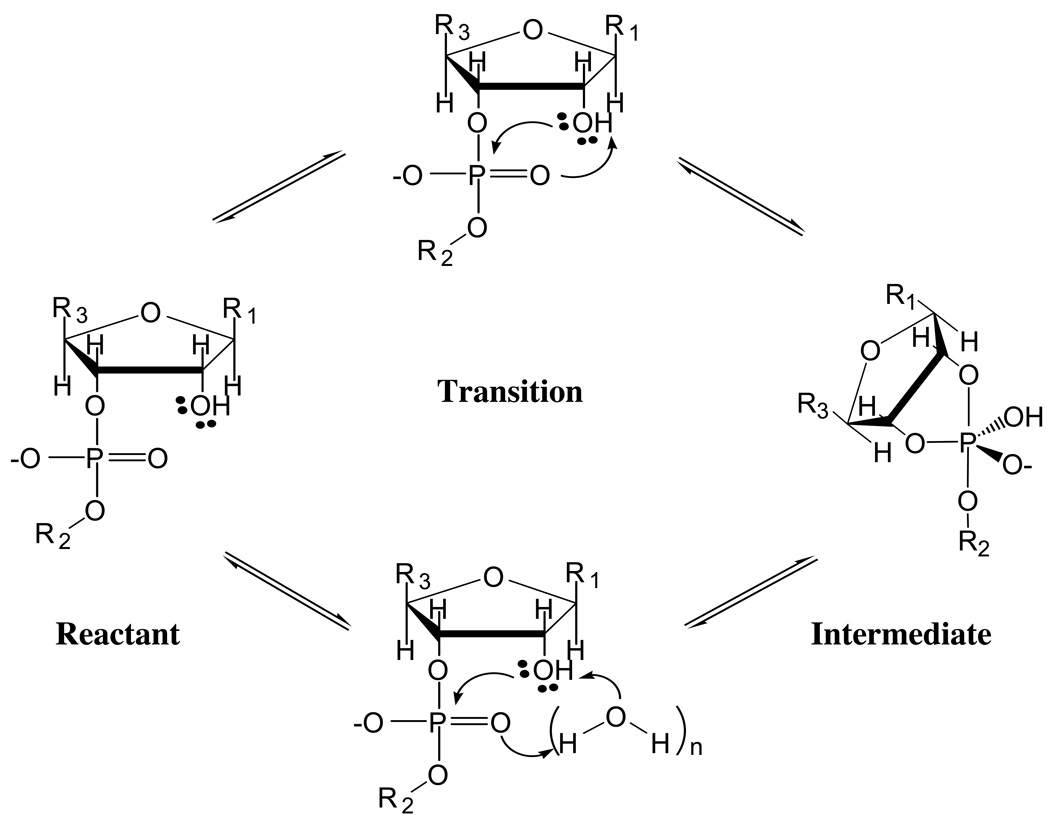
When the nucleophilic attack group has a relatively high pK_a, such as water or the 2’-OH group in RNA, it is commonly assumed that the biological phosphoryl transfer reaction has to be catalyzed by a general base [10]. The identity of the general base is often the question of interest and debate [9, 14–18]. In some cases, no obvious base can be identified and it has been proposed that the phosphate group may act as its own base and accept a proton from the nucleophile. An immediate example that led us to this problem is the hydrolysis of ATP in the molecular motor myosin [19], where the γ phosphate has been proposed to accept one proton from the nucleophilic water; the similar scenario has also been proposed for the hydrolysis of GTP in the signaling protein complex, Ras-GAP [14, 16]. Moreover, as illustrated in Scheme 1, a direct proton transfer from the nucleophile (e.g., water or 2’-OH in RNA) to the phosphate group has been argued to be energetically unfavorable based on stereoelectronic consideration [10]: a four-centered transition state is expected to be high energy in nature. Therefore, it has been proposed that proton transfer proceeds through one or more “relay groups”, which can be water molecule(s) (see Scheme 1) or amino acid sidechain(s), such that a less strained transition state is involved [10]. Specifically for ATP hydrolysis in myosin, high-resolution x-ray structure with the ATP hydrolysis transition state analogue, $\text{ADP}·{\text{VO}}_4^{-}$, indicates that the sidechain of the conserved residue, Ser236, appears to be in an ideal position to relay the proton transfer [20]. However, somewhat surprisingly, mutation of Ser236 to an Alanine does not significantly perturb the hydrolysis activity [21]. Since the interpretation of mutagenesis results is not always straightforward, this result by itself does not imply that proton relay is not important for ATP hydrolysis in myosin; for example, it is possible that a water molecule in the mutant takes the place of the Ser236 sidechain in the WT enzyme, although preliminary calculations (Yang and Cui, work in progress) and recent X-ray crystallographic studies of the Ser236 mutant (Frye and Rayment, manuscript in preparation) do not support this possibility. Clearly, the potential complexity points to the value of analyzing the relevant model systems in solution.

Scheme 1.

Relayed proton transfer through water molecules (or amino acid sidechains in enzymes) in phosphoryl transfer reactions illustrated using RNA as an example.

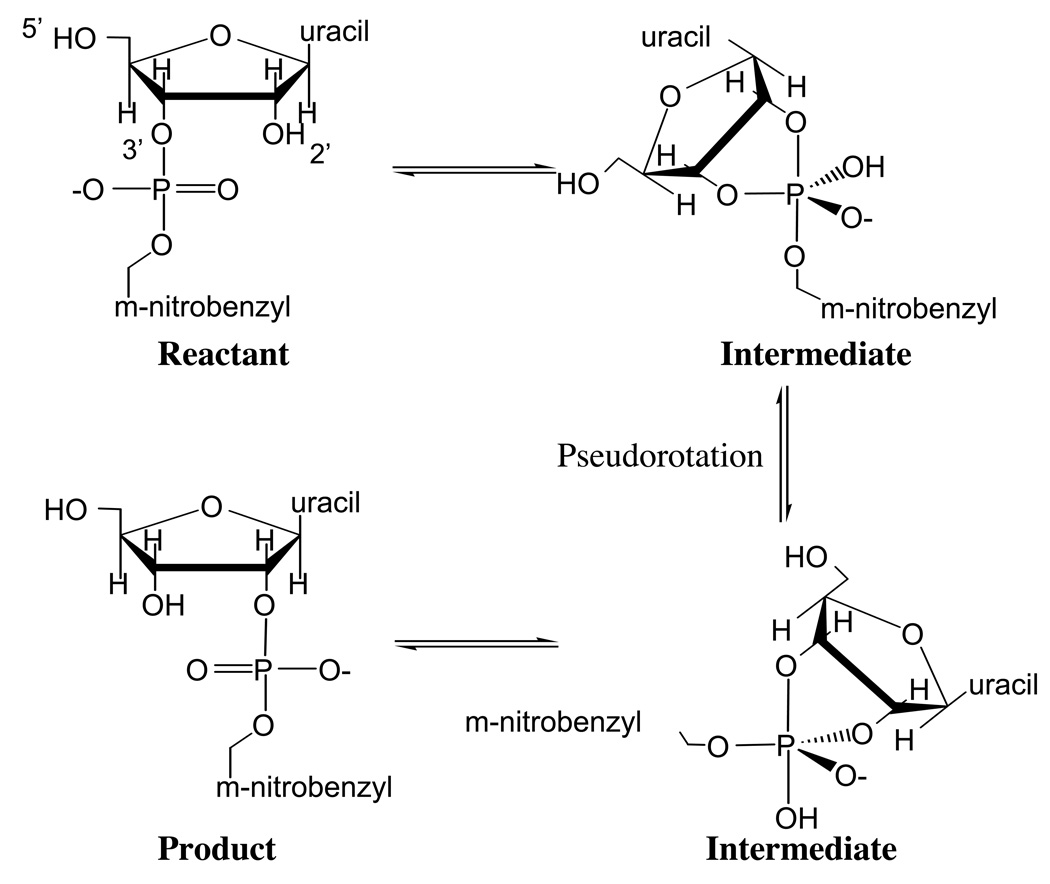
In this context, a highly relevant model system is uridine 3’-m-nitrobenzyl phosphate (UNP), which has been studied in detail by Cleland and co-workers [22] to probe mechanistic issues concerning isomerization and cleavage reactions in RNA. Specifically, they studied the isomerization and cleavage reactions of UNP under different pH conditions in aqueous solution using kinetic isotope effects. It was proposed that under the neutral pH condition the isomerization reaction goes through a phosphorane-like pentavalent intermediate and that for this intermediate to form, water molecules are required to mediate the proton transfer from the 2’-hydroxyl group (proton donor) to the non-bridging oxygen of the phosphate moiety (proton acceptor, see Scheme 2). The proposal was tested by studying the same system in the anhydrous tert-butanol, and it was found that the isomerization reaction was abolished. Their explanation for this observation is that tert-butanol molecules are too bulky to insert between the proton donor and accepter groups, thus proton transfer is abolished, which in turn prevents the formation of the phosphorane-like intermediate and therefore the isomerization reaction. In other words, the difference between the reactivity in aqueous solution and the anhydrous tert-butanol seems to be the most direct evidence to date supporting the importance of proton relay in phosphoryl transfer reactions.

Scheme 2.

The reaction scheme for the isomerization of uridine 3’-m-nitrobenzyl phosphate (UNP).

Theoretically, although relayed proton transfer can be energetically more favorable, the “catalytic” effect of relay can be significantly reduced when the entropic cost associated with constructing the relay pathway is taken into consideration. This is perhaps one of the reasons that the issue of relayed proton transfer in phosphoryl transfer reactions has not been analyzed extensively in previous computational analysis [5, 23–25]. For the hydrolysis of monomethyl monophosphate ester (MMP), Burt et al. [26] did show that water relay plays an important role for the dissociative mechanism although their study did not address the entropic contribution. Moreover, in our recent study of mono/di-methyl monophosphate ester hydrolysis as part of our effort to develop effective approximate QM methods for phosphate chemistry [27], the role of the proton relay was found to be very modest even at the potential energy level for the associative mechanism. Therefore, from the limited number of theoretical analyses, it is not immediately obvious that proton relay is crucial to phosphoryl transfer reactions, and it is worthwhile to reanalyze the UNP reactivity and related problems using state-of-the-art computational methods.

In the current work, we use theoretical approaches to systematically analyze all the elementary steps in the UNP isomerization process. The results are used to evaluate the mechanistic basis behind the different reactivities in aqueous and tert-butanol solutions as observed experimentally [22]. Different simulation techniques are used to analyze the relevant steps individually. Specifically, we apply quantum mechanical/molecular mechanical (QM/MM) [28–30] molecular dynamics (MD) simulations to explore the structural flexibility of the solute and equilibrium solvent structures around the solute in both aqueous and tert-butanol solutions, especially concerning the number of solvent molecules that bridge the proton donor/acceptor groups. Based on the microscopic trajectories, cluster models with different numbers (0, 1) of solvent molecules between the proton donor/acceptor groups are studied using minimum energy path (MEP) calculations with high-level QM methods; the results provide quantitative clues regarding the dependence of proton transfer and phosphoryl transfer energetics on the solvent relay. Finally, pseudo-rotation [10, 31] that links different critical conformations of the phosphorane-like intermediate is also characterized via potential of mean force simulations with a QM/MM potential.

The paper is organized as follows: details of the computational methods and system set-ups are summarized in Sect. 2; the results of simulations are presented in Sect. 3 and discussed in connection with experimental observations in Sect. 4; finally, conclusions are summarized in Sect. 5.

2 Computational Methods

The calculations in this study include both microscopic QM/MM simulations with explicit solvents and MEP calculations using cluster models with implicit solvent models. The QM/MM simulations are made possible by a recently parameterized approximate density functional theory, SCC-DFTBPR [27], which appear to have the proper balance between computational efficiency and accuracy for phosphate chemistry (mainly hydrolysis). These simulations are carried out using a local version of CHARMM [32]. The MEP calculations are done using density functional theory [33] with snapshots from QM/MM trajectories; they are carried out with the Gaussian03 package [34].

2.1 Equilibrium QM/MM simulations

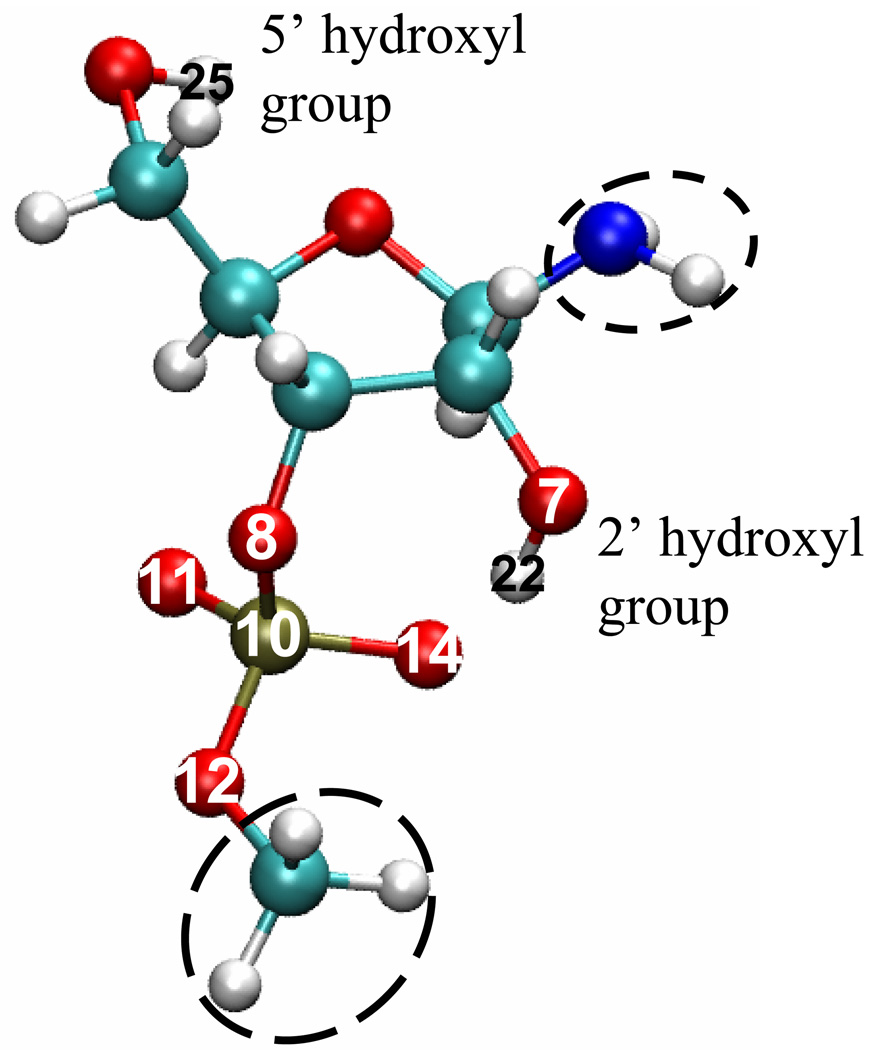
In both aqueous and tert-butanol solutions, the solute molecule, “UNP”, is treated quantum mechanically and all solvent molecules are described using TIP3P for water [35] and a newly developed force field for tert-butanol (see below). For computational efficiency, the solute UNP is simplified by replacing the m-nitrobenzyl group by a hydrogen and replacing the uracil group by NH₂ (see Fig.1); the net charge of the solute is −1, consistent with the pH neutral condition in the experimental study [22]. In the subsequent discussions, we refer the solute simply as UNP for convenience.

Figure 1.

The model structure for uridine 3’-m-nitrobenzyl phosphate (UNP) used in the current simulation study. The simplified moeities compared to the original solute are indicated by the circles. Atoms referred to in the discussions are labeled; the color scheme used for atoms is: oxygen in red, nitrogen in blue, carbon in cyan, hydrogen in white and phosphorus in gold. The figure is generated using VMD [62].

For the aqueous solution simulations, UNP is solvated with a water droplet of 22 Å radius; for the tert-butanol solution simulations, the solute is solvated by a droplet of 25 Å radius. The generalized solvent boundary potential (GSBP) approach [36, 37] is applied as the boundary condition, where the bulk dielectric constant is taken to be 80.0 and 8.22 for water and tert-butanol, respectively. The SHAKE algorithm [38] is used to constrain all bonds involving hydrogen, which makes it possible to use an integration time step of 1 fs. Two independent sets of 300ps simulations are performed for both solutions, and the last 100ps data in each trajectory are used for analysis. Aqueous solution is studied under the room temperature (298K), and the tert-butanol solution is investigated at 330K due to the high melting point of tert-butanol (the normal melting point is 298.8K [39]); we note that the experimental study in Ref. [22] was carried out at 86° for both solutions.

The MM parameters for tert-butanol are based on the most similar molecule (2-propanol) in the CHARMM27 force field [40], with slight variations in partial charges within the CHARMM convention (i.e., replacing the non-polar H in 2-propanol with a methyl group, then adjusting the partial charges on the central carbon such that the net charge of the molecule is zero). As shown in the Supporting Materials, the MM parameters lead to properties for pure tert-butanol, including number density, heat of vaporization and self-diffusion coefficient, in good agreement with available experimental data [39].

To have a reliable description of solute-solvent interactions, van der Waals parameters for five critical oxygen atoms of UNP (O₇, O₈, O₁₁, O₁₂ and O₁₄ as labeled in Fig.1) have been optimized for the SCC-DRTBPR model following the standard protocol [41]. Specifically, 48 gas-phase bimolecular (UNP-water) interaction potential energy curves (273 data points) at the B3LYP [42–44]/6–31+G** [45–48] level are used as reference to optimize the van der Waals parameters using a Genetic Algorithm (micro-GA) approach [49]. The optimized van der Waals parameters (see Supporting Information) give a root-mean-square-error (RMSE) of 1.7 kcal/mol for the B3LYP reference interaction energies.

2.2 Minimum energy path (MEP) analysis for phosphoryl transfer

Since the main goal of this work is to explore the importance of water relay in phosphoryl transfer reactions, MEP calculations have been carried out starting from snapshots from QM/MM trajectories that include either no water between the donor and acceptor groups (“direct-attack” mechanism) or a single water as the potential proton relay (“proton-relay” mechanism). To explore the impact of thermal fluctuations, nine snapshots are taken for the “direct-attack” pathway and seven snapshots are used for the “water-relay” pathway. Longer solvent bridges are deemed less important based on the statistics collected from equilibrium QM/MM simulations (see discussions below in Sect.3.1).

For computational efficiency, the snapshots are first fully optimized at the SCC-DFTBPR level in the gas phase, which are then used as starting points for MEP calculations based on the conjugate peak refinement algorithm implemented in CHARMM [50]. The SCC-DFTBPR results are in turn used as the initial guess for obtaining optimized stationary points (reactant, transition state and intermediate) at the B3LYP/6–31+G* level; frequency calculations are carried out to estimate the zero-point energy and thermal corrections at 298.15K. For better energetics, single point energy calculations are done using the larger 6–311++G** basis set [46, 51], with the solvation effect taken into consideration with the polarizable continuum model (PCM) [52]. To explore the sensitivity of the PCM results to the choice of parameters, the solvation calculations are done with both the United Atom Kohn Sham (UAKS) radii and the Pauling radii that define the solute cavity [53]. The SCC-DFTBPR results are largely consistent with the B3LYP results in the gas-phase, thus only the B3LYP results are discussed below. Regarding the reliability of the B3LYP results, we note that our recent studies [27] have compared B3LYP and MP2 calculations with large basis sets (e.g., those used in the G2/G3 calculations [54, 55]) for very similar phosphoryl transfer reactions, including the possible involvement of water relays. The results at the B3LYP and MP2 levels are very consistent, especially for the mono-anionic systems; for example, the root-mean-square-difference is 2.5 kcal/mol for 37 reaction energies. Further considering that we are focusing on the role of the water relay on the energy barriers, the B3LYP approach ought to be a valid method of choice here.

2.3 Pseudo-rotation potential of mean force (PMF)

To evaluate whether pseudo-rotation in the phosphorane-like intermediate may have significantly different energetics in aqueous and tert-butanol solutions, PMF calculations have been carried out for both cases using the SCC-DFTBPR/MM protocol as described above. The reaction coordinate for characterizing the pseudo-rotation is defined as a linear combination of O₇-O₁₂ and O₈-O₁₁ distances, i.e., d(O₇-O₁₂)-d(O₈-O₁₁). This combination is linearly correlated to the expected pseudo-rotation motion (i.e., O₇-P-O₁₂ angle compresses and O₈-P-O₁₁ angle expands simultaneously, see Fig.S2 in Supporting Information) throughout the umbrella sampling simulations [56], indicating that the reaction coordinate is valid. For the tert-butanol solution, 15 windows are employed with 50 ps simulation for each window; for the aqueous solution, 19 windows are used with also 50 ps sampling for each window. The harmonic force constant for the umbrella potential is 500 kcal/(mol·Å²). To be consistent with the equilibrium simulations, the PMF calculations are done at 330 K and 298 K for the tert-butanol and aqueous solution, respectively. The Weighted Histogram Analysis Method (WHAM) [57] is employed to produce the one-dimensional PMF based on the statistics of the reaction coordinate recorded at each step of the last 20 ps in each window.

3 Results

3.1 Solute flexibility and solvent distribution from equilibrium QM/MM simulations

First, we compare the structural flexibility of the solute (UNP) and solvent distribution in aqueous and tert-butanol solutions based on equilibrium QM/MM simulations.

3.1.1 Aqueous Solution

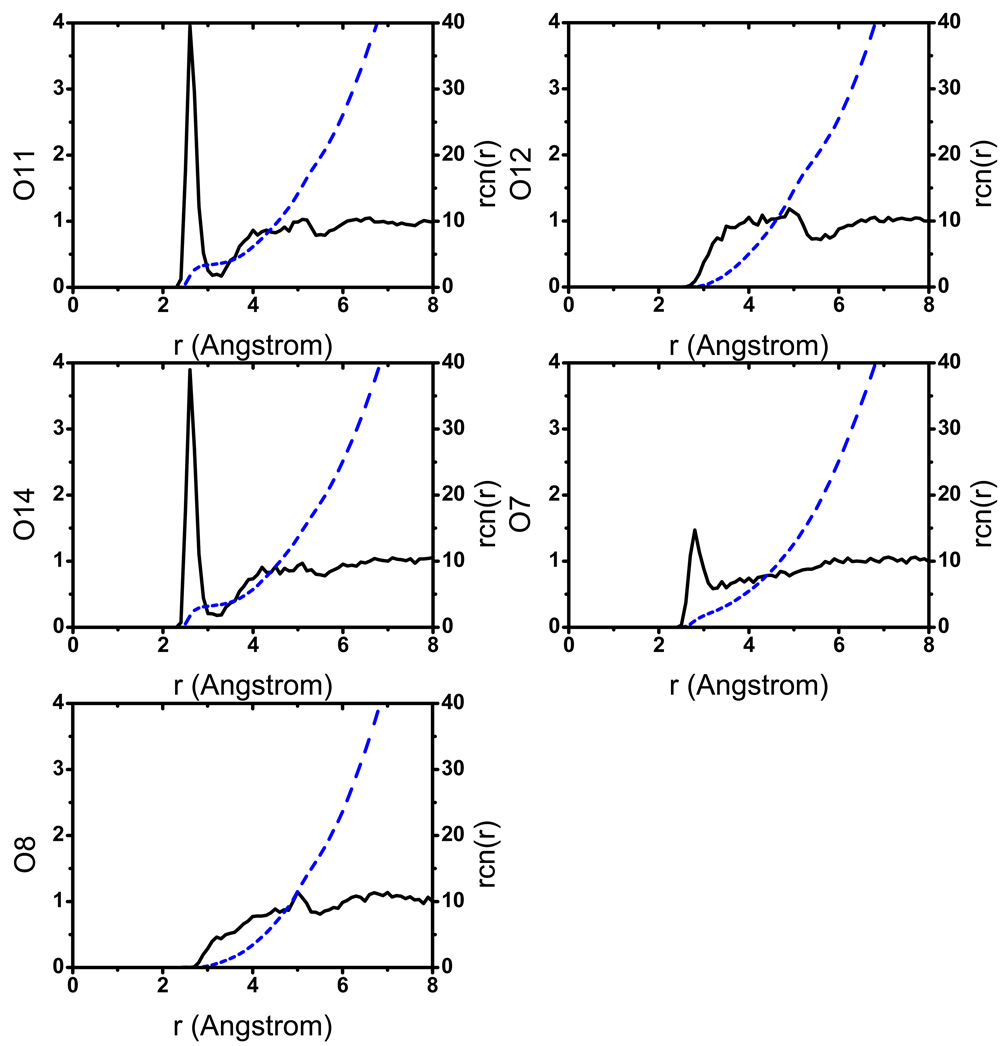
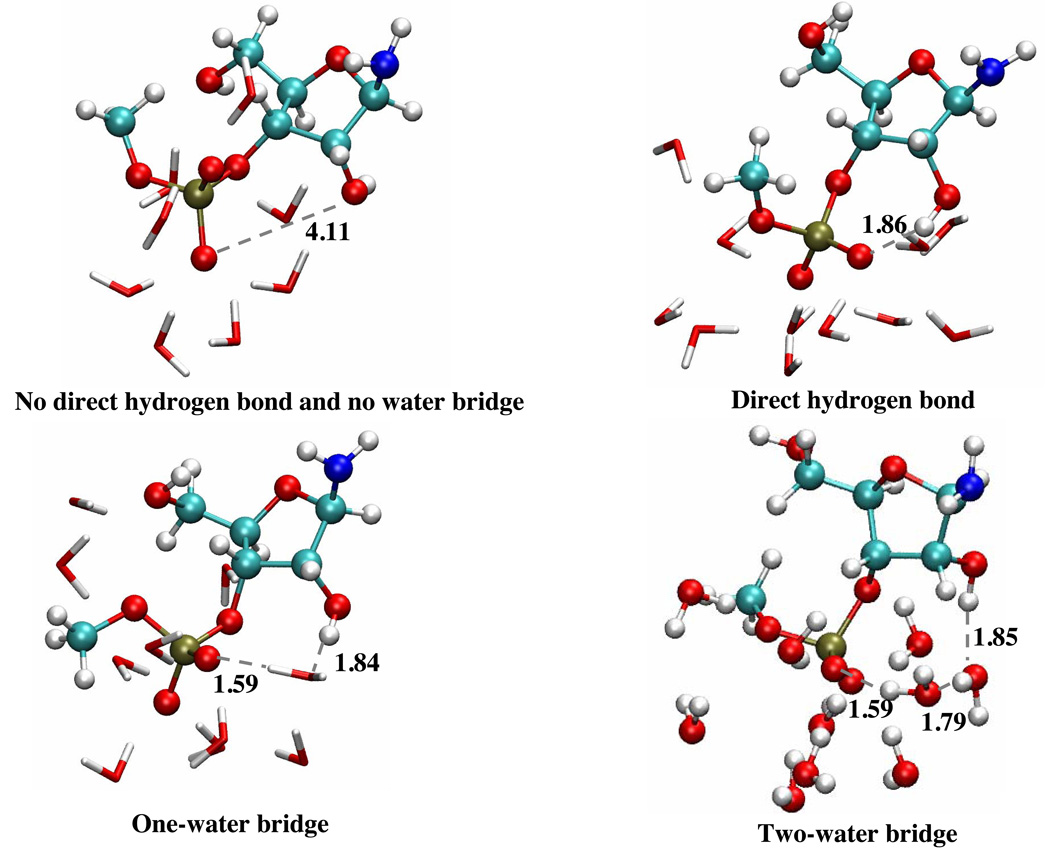
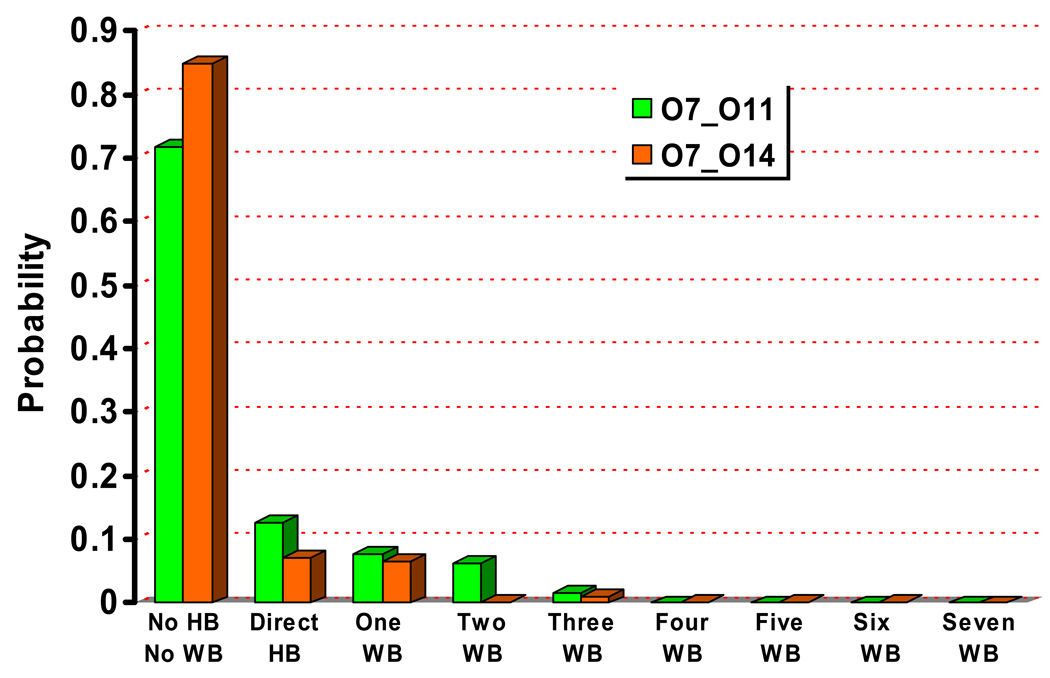
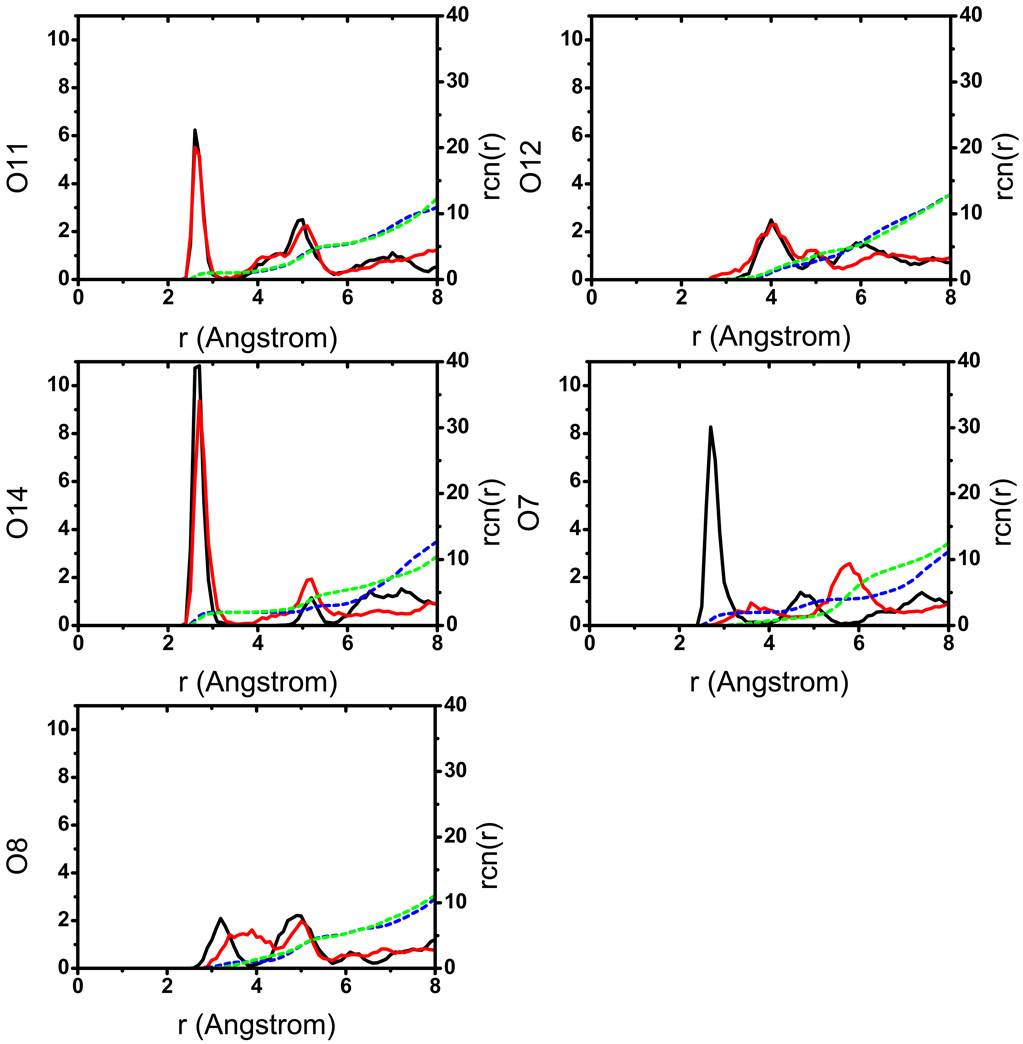
In the aqueous solution, the general observation is that the solute is structurally flexible and may adopt a broad range of conformations that interconvert rapidly at the picosecond time scale. As a result, the solvent distribution around the key oxygen atoms (Fig.2) converges quickly and does not vary much when a different initial structure for the solute is used. The solvent distributions follow the expected trend that the level of solvation is higher around the more negatively charged phosphoryl oxygen atoms (O₁₁, O₁₄, see Fig.1 for notation), which indicates the lack of persistent intra-solute hydrogen bonding (see below for the tert-butanol case). Snapshots from the trajectories (Fig.3) indeed capture very different orientations of the 2’-OH, the 5’-OH and the 3’-phosphate-ester groups. As shown in Fig.4, a few key geometrical parameters of the solute, such as the dihedral angles that characterize the orientation of the 3’-phosphate-ester group and the 5’-OH, undergo significant fluctuations even at the picosecond time scale. The nucleophilic attack distance between O₇ in the 2’-OH and the phosphorus atom fluctuates between 3.0 Å and 4.5 Å, which is likely correlated with the number of solvent molecules that bridge the two groups (see Fig.4 for several scenarios). A more quantitative analysis of the hydrogen bonding pattern between the proton donor (2’-OH) and acceptor (3’-phosphate-ester group) is shown in Fig.5, following the similar protocol used in our analysis of long-range proton transfer in carbonic anhydrase [58, 59]; note that since we are interested in proton transfer from the 2’-OH group, we consider only those hydrogen bonding interactions where the 2’-OH serves as the hydrogen donor. In most cases (>70%), there is actually not any well-defined hydrogen bonding interaction between the donor/acceptor groups, since they are both well solvated by the water molecules and the 2’-OH points away from the phosphate group. In 10% of the trajectory frames, the donor and acceptor groups are involved in a direct hydrogen bond, and there is also similar levels of probability to have one or two water molecules that bridge the donor and acceptor groups; longer water wires occur with extremely low probabilities.

Figure 2.

Radial distribution functions, g(r) (solid lines) and running coordination numbers, rcn (dash lines), of water oxygen around different oxygen atoms of UNP.

Figure 3.

Representative snapshot of the solute and nearby solvent configurations from the aqueous solution simulations. The snapshots illustrate different hydrogen bonding patterns involving the nucleophile (2’-OH), the phosphate group and nearby water molecules. Relevant hydrogen bonding distances (between hydrogen and acceptor atom) are given in Angstroms.

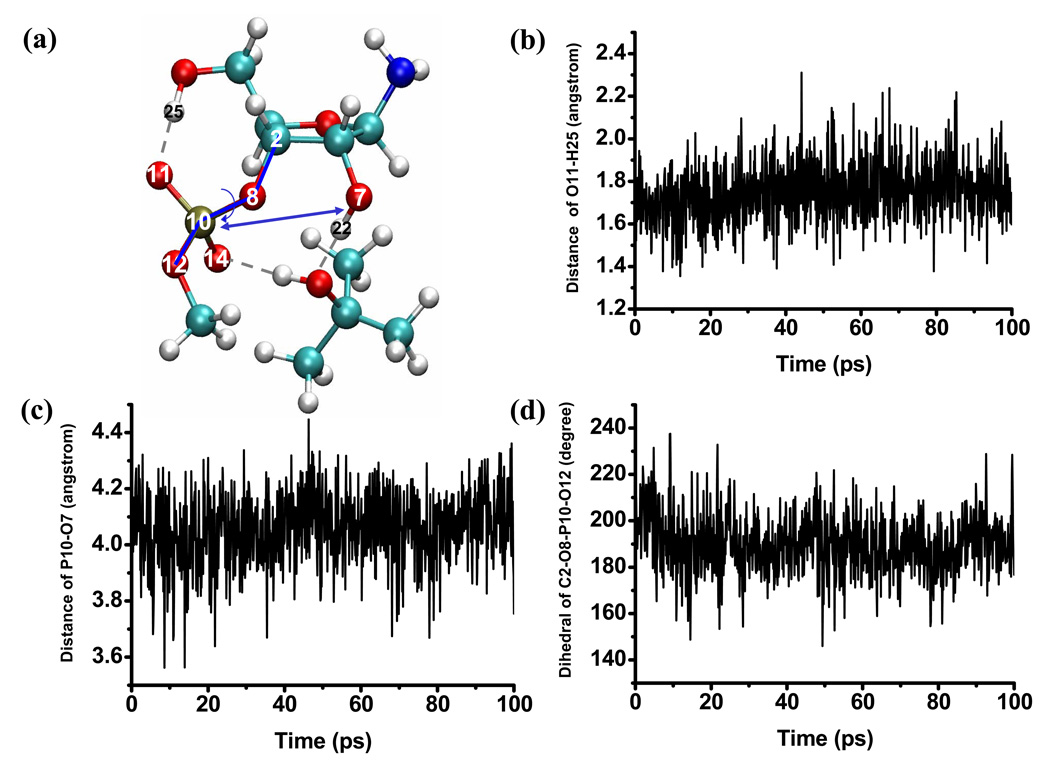
Figure 4.

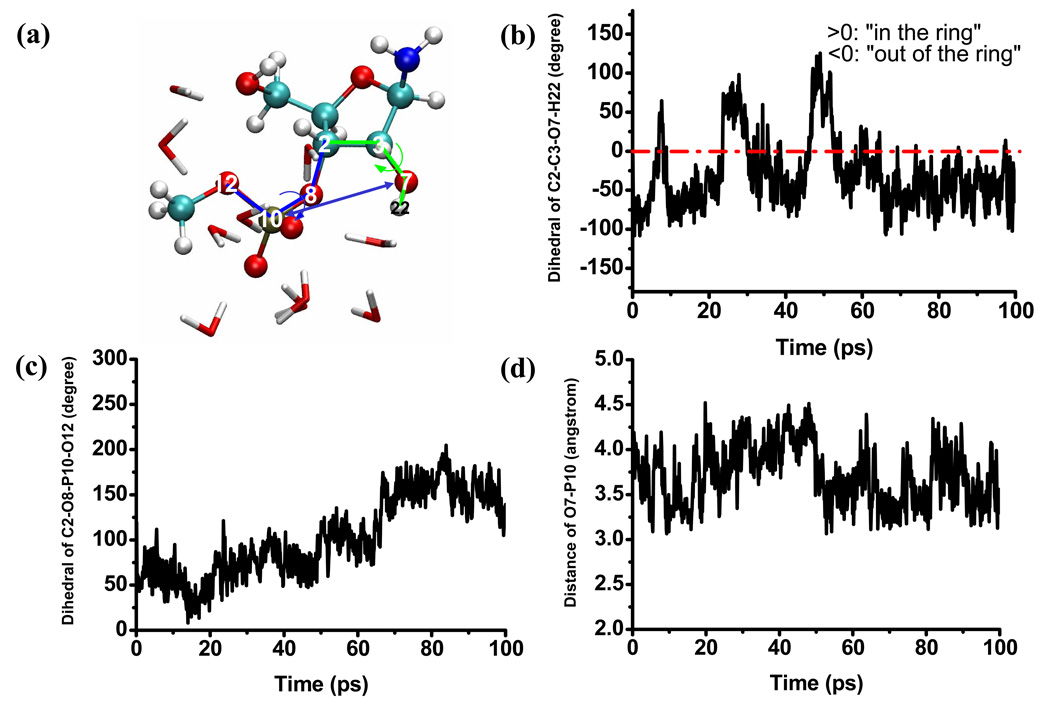
Time dependence of several key geometrical parameters of the solute (indicated in a) during the aqueous solution simulations. These results illustrate the structural flexibility of the solution in the aqueous solution environment.

Figure 5.

Statistical analysis of the hydrogen bonding pattern associated with the nucleophile (2’-OH) and the phosphate group (either O₁₁ or O₁₄, see Fig. 1 for labels) during the aqueous solution simulations. “No HB/No WB” indicates configurations in which the two groups are not engaged in either a direct hydrogen bond or indirect hydrogen bond through water molecules; “Direct HB” indicates a direct hydrogen bonding interaction between the two groups; ”One/Two etc. WB” indicates that the two groups are connected through a specific number of bridging water molecules.

3.1.2 tert-butanol Solution

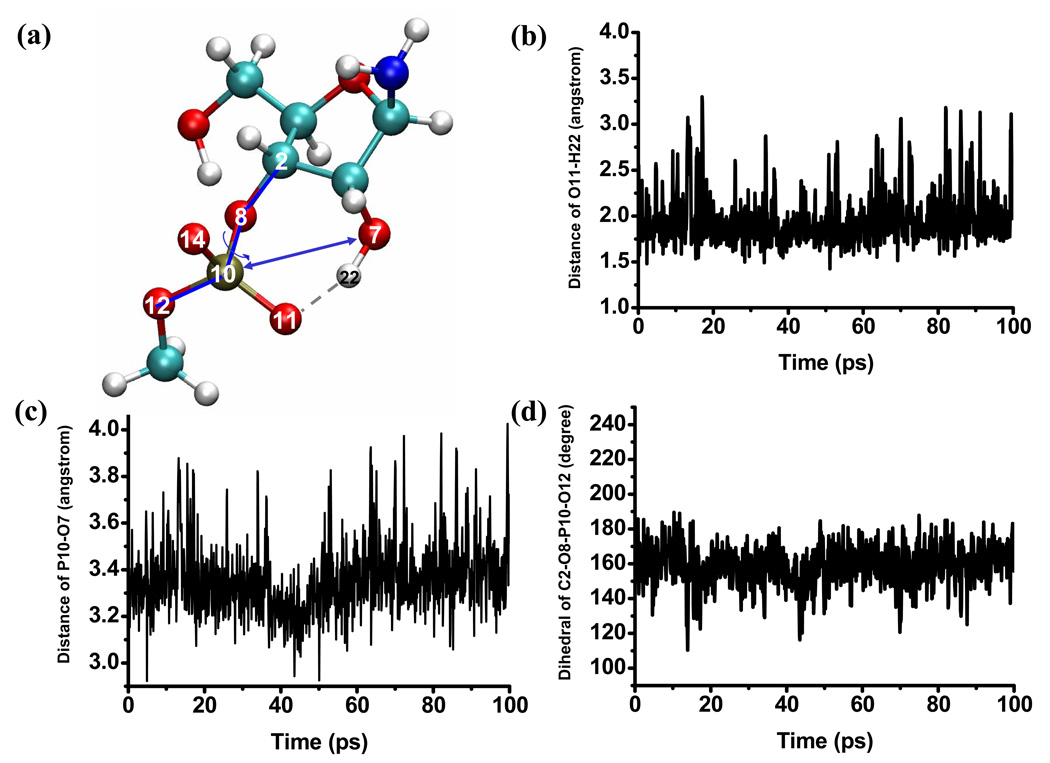
The behavior in the tert-butanol solution is quite different from that in the aqueous solution in that the solute tends to form intra-solute hydrogen bonds and thus is substantially less flexible. As shown in Fig.6, the solvent distributions from two independent simulations differ quite substantially, which indicates rather different solute structures that do not interconvert during the ~300ps simulation time for each trajectory. Indeed, snapshots from these trajectories illustrate different intramolecular hydrogen bonds that persist throughout the simulations. In one trajectory (Fig.7), a stable hydrogen bond is formed between O₁₁ of the phosphate to the 5’-OH; at the same time, a tert-butanol solvent is inserted between the phosphate and the 2’-OH, which is correlated with a long nucleophilic distance that fluctuates between 3.6 to 4.3 Å. In the other trajectory (Fig.8), a direct hydrogen bond is formed between O₁₁ of the phosphate and the 2’-OH, leading to a shorter nucleophilic attack distance that fluctuates around 3.3 Å. In both cases, the fluctuations in the dihedral angle that characterizes the phosphate-ester group orientation are notably smaller than those observed for the aqueous solution (compare Fig.7–Fig.8 to Fig.4). The observation of intra-solute hydrogen bond in the tert-butanol simulations is consistent with the notion that it is a less polar and therefore less stabilizing solvent than water.

Figure 6.

Radial distribution functions, g(r) (solid lines) and running coordination numbers, rcn (dash lines), of tert-butanol oxygen around different oxygen atoms of UNP; black/blue and red/green represent results from two independent simulations.

Figure 7.

Time dependence of several key geometrical parameters of the solute (indicated in a) during the first set of tert-butanol solution simulation; an intramolecular hydrogen bond involving the 5’-OH and the phosphate makes the phosphate and the 2’-OH far separated, allowing a tert-butanol solvent to insert in between. This configuration remains stable at least on the 300 picosecond time scale (data for the last 100 ps are shown).

Figure 8.

Same as Fig.7, but from an independent trajectory starting from a different initial solute configuration. Here a direct hydrogen bond is formed between the nucleophile (2’-OH) and the phosphate and remains stable throughout the 300 ps simulation (data for the last 100ps are shown).

3.2 Barrier of phosphoryl transfer with and without water relay

The equilibrium simulations presented above illustrate that the two most relevant types of configurations for the phosphoryl transfer would involve either a direct hydrogen bonding between the 2’-OH and the phosphate group, or, in the case of aqueous solution, a water that potentially mediates the proton transfer. Although we do observe a tert-butanol solvent bridging the 2’-OH and the phosphate group (see Fig.7), we do not believe it is relevant for the reaction because the nucleophilic distance is too long (average ~ 4Å) due to the bulky size of tert-butanol; for the same reason, we do not consider the two-water-bridging cases despite their similar population as the single-water-bridge configurations (Fig.5). Therefore, we focus on two types of MEP calculations below: a direct nucleophilic attack mechanism without explicitly involving any solvent and the single-water-mediated nucleophilic attack mechanism.

3.2.1 Direct Nucleophilic Attack

As shown in Table 1, although there is notable differences between the overall conformation of the different initial structures (the root-mean-square-difference between different initial structures is about 1.25 Å), there is only small variation in the critical geometrical parameters, including those for the transition state. In the transition state, the distance between the nucleophilic oxygen and phosphorus decreases from ~3.4 Å in the reactant state to ~2.3 Å, and the nucleophilic attack angle is close to be 162°. The proton transfer from the 2’-OH to the phosphate group has essentially completed as indicated by the short distance of ~0.99 Å for the proton/phosphate separation (H₂₂-O_11/14) in the transition state.

Table 1.

Geometrical parameters for the reactant and transition from Minimum Energy Path (MEP) analysis for the phosphoryl transfer reaction of model UNP with different hydrogen-bonding interactions between the nucleophile (2’-OH) and phosphate^a

Geometrical Parametersb	DH	1W
P-O7	3.396 (0.015)/2.270 (0.100)	4.140 (0.042)/2.900 (0.199)
P-O12	1.646 (0.001)/1.670 (0.008)	1.665 (0.014)/1.635 (0.012)
P-O8	1.696 (0.005)/1.665 (0.014)	1.670 (0.017)/1.621 (0.010)
P-O11/14	1.517 (0.004)/1.636 (0.009)	1.515 (0.004)/1.600 (0.005)
H22-O7	0.994 (0.001)/1.742 (0.040)	0.989 (0.001)/1.578 (0.029)
H22-O11/14	1.781 (0.011)/0.989 (0.006)	N/A
∠O7-P-O12	126.5 (0.6)/162.1 (1.3)	124.3 (5.0)/156.0 (4.1)
∠O7-H22-O11/14-P	35.6 (0.5)/−1.2 (2.0)	N/A
H22-OW	N/A	1.867 (0.059)/1.019 (0.007)
HW-OW	N/A	1.000 (0.004)/1.953 (0.075)
HW’-O11/14	N/A	1.727 (0.059)/0.993 (0.001)

^a)The results are averaged over snapshots collected from aqueous solution simulations that include either a direct hydrogen bond (DH) between the nucleophile and phosphate or a single bridging water molecule (1W). The numbers without parentheses are the average values and those with parentheses are standard deviations (9 snapshots for DH and 7 snapshots for 1W). All structures have been optimized at the B3LYP/6–31+G* level in the gas phase. Values before the slash are for the reactant state, and those after the slash are for the transition state.

^b)Distances are in angstrom; angle and dihedral angles are in degrees. For labels of atoms, see Fig. 1; the subscript “W” indicates the bridging water in 1W cases, and O_11/14 means either O₁₁ or O₁₄, whichever acts as the proton acceptor during the nucleophilic attack.

As to the energetics, which are summarized in Table 2, the reaction is highly endothermic in the gas-phase by about 28–29 kcal/mol; including the zero-point and thermal corrections does not change the value significantly. The barrier height is about 30 kcal/mol and decreases by ~ 1 kcal/mol with zero-point and thermal corrections. Including the solvation effect (in water) using the PCM model also leads to only minor changes and the results depend a bit on the set of radii used; with the UAKS radii, the best estimate for the free energy barrier is ~25 kcal/mol, while it is ~27 kcal/mol with the Pauling radii. With a simple transition state theory estimate and assuming that this step is rate limiting, the rate constant is ~2.9×10⁻⁴ s⁻¹ at at 86 °C, which is in fact higher compared to the experimental value of Cleland and co-workers (~ ~6.0×10⁻⁷ s⁻¹) under neutral pH (and 86°) [22].

Table 2.

Results from Minimum Energy Path (MEP) analysis for the phosphoryl transfer reaction of model UNP with different hydrogen-bonding interactions between the nucleophile (2’-OH) and phosphate^a

State	Gas phase 6–31+G* OPTb	Gas phase 6–311++G** SPb	PCM 6–311++G** UAKS SPb	PCM 6–311++G** Pauling SPb
Reactant (DH)	0.0/0.0	0.0/0.0	0.0/0.0	0.0/0.0
TS (DH)	30.0 (1.0) /29.2 (0.5)	29.7 (0.8)/28.9 (0.4)	26.1 (2.5)/24.7 (2.3)	28.0 (1.3)/26.6 (1.2)
INT (DH)	28.6 (0.9)/28.5 (0.7)	29.1 (0.8)/28.9 (0.7)	21.2 (0.6)/20.6 (0.5)	25.5 (0.4)/24.8 (0.2)
Reactant (1W)	0.0/0.0	0.0/0.0	0.0/0.0	0.0/0.0
TS (1W)	28.9 (2.1)/27.4 (1.6)	28.3 (2.0)/26.8 (1.4)	26.1 (2.4)/24.1 (2.4)	26.5 (1.6)/24.5 (1.6)
INT (1W)	28.1 (2.6)/27.1 (1.8)	27.5 (2.4)/26.5 (1.7)	25.6 (2.9)/23.5 (3.0)	25.6 (2.5)/23.6 (2.7)

^c)The energetics are given relative to the respective reactant state in kcal/mol; the values before the slash are potential energies, those after the slash are Gibbs free energies calculated at 300 K using the harmonic-oscillator-rigid-rotor model. The results are averaged over snapshots collected from aqueous solution simulations that include either a direct hydrogen bond (DH) between the nucleophile and phosphate or a single bridging water molecule (1W). The numbers without parentheses are the average values and those with parentheses are standard deviations (9 snapshots for DH and 7 snapshots for 1W).

^d)The structures have been optimized (OPT) at the B3LYP/6–31+G* level; the vibrational contributions are also calculated at this level of theory. Single point (SP) calculations are then carried out with the 6–311+G** basis set in either the gas-phase or solution using the PCM model (either UAKS or Pauling radii).

3.2.2 Single-water-mediated nucleophilic attack

With one water molecule bridging the 2’-OH and the phosphate group, the nucleophilic attack distance is longer in both the reactant and transition state compared to the direct nucleophilic attack mechanism; the values are ~4.1 Å and 2.9 Å in the reactant and transition state, respectively, as compared to the values of ~3.4 Å and ~2.3 Å, respectively, in the direct attack mechanism. The nucleophilic attack angle is also slightly further away from linearity, ~ 156° vs. ~ 162° in the direct attack mechanism, although there is a notable standard deviation of ~4° (Table 1). The relayed proton transfers are also essentially completed in the transition states, as judged by the relevant proton-oxygen distances (Table 1).

Concerning the energetics, it is interesting that involving the water relay has a very minor impact on both the endothermicity and barrier height. For example, the best estimate of the barrier is ~24 kcal/mol with the UAKS radii and ~25 kcal/mol with the Pauling radii; both only differ from the direct attack results by ~ 1–2 kcal/mol. Therefore, the current calculations show that water relay does not have any major energetic impact on the phosphoryl transfer in the (model) UNP system (see further discussions below in Sect.4).

3.3 Energetics of pseudo-rotation of the pentavalent intermediate in water and tert-butanol solutions

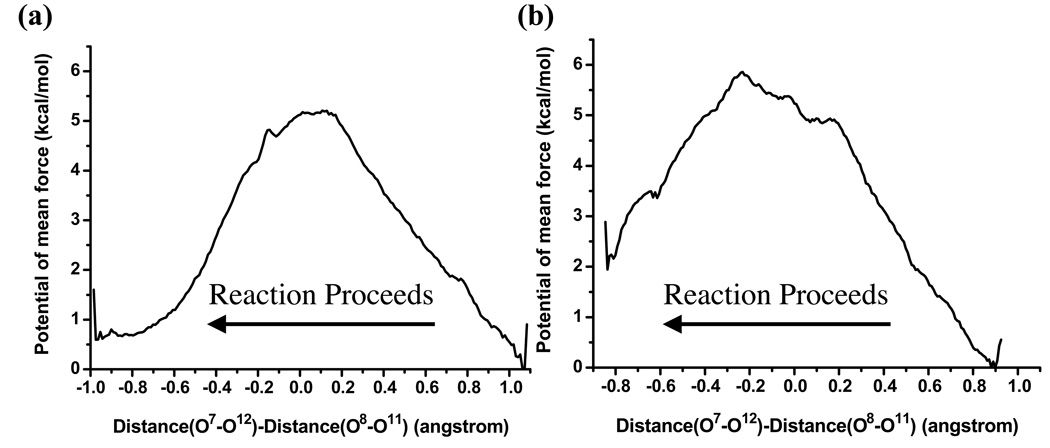
As shown in Fig.9, the pseudo-rotations in water and tert-butanol solution have very similar energetics with a free energy barrier ~ 5–6 kcal/mol; in the transition state, the expansion angle (between O₈-P-O₁₁) and the compression angle (between O₇-P-O₁₂) are also similar for the two cases, with both angles ~150° in water and ~140° in tert-butanol. Apparently, the larger size of tert-butanol does not have a major impact on the pseudo-rotation process, which is consistent with the observation that pseudo-rotation can proceed without any large scale swing of the phosphorus ligands. The barrier of ~5–6 kcal/mol in water is close to implicit solvent calculations of similar phosphate species [60, 61].

Figure 9.

One-dimensional potential of mean force (in kcal/mol) for the pseudo-rotation of the pentavalent intermediate in (a) aqueous solution and in (b) tert-butanol; the antisymmetric stretch defined as d(O₇-O₁₂)-d(O₈-O₁₁) is used as the reaction coordinate (see text and Supporting Information for further discussions regarding the choice of the reaction coordinate).

4 Discussions

In the experimental study of Cleland and coworkers [22], whether water molecules are explicitly involved in the isomerization and cleavage reactions of UNP has been addressed by comparing the reactivity in aqueous and anhydrous tert-butanol solutions. The observation that the isomerization reaction was abolished in the tert-butanol solution was taken as the evidence for supporting the role of water in mediating the proton transfer from the 2’-OH to the phosphate group during the nucleophilic attack. We note that the isomerization from UNP to uridine 2’-m-nitrobenzyl phosphate involves several elementary steps, and, in principle, changes in any one of them could be the reason for abolishing the isomerization reaction in the tert-butanol solution. Therefore, to reach a reliable explanation for the experimental observation, all relevant solute properties and processes should be compared systematically for aqueous and tert-butanol solutions. In the current work, we have attempted to address the problem from a theoretical point of view, which include comparing the following properties in aqueous and tert-butanol solutions: the solute (UNP) flexibility and solute-solvent structure, nucleophilic attack reaction energetics, and pseudo-rotation that links different conformations of the intermediate state.

First, we consider the solute flexibility and solute-solvent structure at equilibrium. Whether a chemical reaction occurs readily is critically dependent on the accessibility (population) of reactant structures that are suitable for reaction. In the aqueous solution, the solute is found very flexible and quickly interconverts among different conformations at the picosecond time scale. Based on two independent ~300 ps simulations, the solute and solute/solvent configurations that satisfy either the direct-attack mechanism or the single-water-mediated mechanism account for more than 20% of the population (Fig.5), which is very significant. In the tert-butanol solution, by contrast, the solute is found to be much more rigid due to the higher tendency of forming intra-solute hydrogen bond(s). With a hydrogen-bond between 5’-OH and the phosphate group, the distance between the 2’-OH and phosphate tends to be too long for an effective nucleophilic attack, especially with a bulky tert-butanol inserted in between (Fig.7). However, an alternative configuration that dominates the other trajectory involves a stable hydrogen bond between 2’-OH and phosphate (Fig.8), which seems ideal for a direct nucleophilic attack. To gain a rough estimate on the relative population of the two sets of solute configurations, we have optimized these two configurations using B3LYP/6–31++G** in the gas phase, followed by PCM single point calculations (ϵ_{tert–butanol}=8.22); with the Pauling radii, the configuration with the 5’-OH-phosphate hydrogen bond is more stable by ~1.5 kcal/mol, which corresponds to ~10 times higher in population. Therefore, the solute configuration that favors the direct-attack mechanism in tert-butanol is likely low (<10%) although this factor by itself is unlikely sufficient for completely abolishing the reactivity.

The observed trends in solute configuration and solvent structure might be able to explain the reactivity difference in aqueous and tert-butanol solutions if one argues that the nucleophilic attack barrier is substantially higher for the direct-attack mechanism than the single-water mediated mechanism; this is because the direct-attack mechanism is expected to be the only relevant pathway in tert-butanol solution, where the nucleophilic attack distance is too longer with a tert-butanol solvent inserted between the 2’-OH and phosphate groups. According to the stereoelectronic argument commonly employed in the literature [10,20], the water-mediate nucleophilic attack is indeed expected to be energetically more favorable than the direct attack mechanism. However, the MEP calculations performed here using different initial starting structures consistently find that there is a very small (<1–2 kcal/mol) energetic difference between the direct-attack and water-mediated pathways, and both barriers correlate well with the experimental rate constants under neutral pH [22]. This result can be explained by the fact that the proton transfer from 2’-OH to the phosphate group has largely completed in the transition state of both pathways, thus the magnitude of unfavorable steric interaction in the direct-attack pathway is unlikely significant at all. Moreover, the nucleophilic attack distance is substantially longer in the water-mediated (~2.9 Å) pathway than in the direct-attack (~2.3 Å) pathway, thus the weaker P-O interaction may have abolished any stereoelectronic advantage of the water-mediated transition state.

Finally, to complete the isomerization reaction from the penta-valent intermediate, the O₈-P bond needs to break. According to Westheimer’s rule [31], the leaving group can only be cleaved at the axial position, which means a pseudo-rotation has to occur prior to P-O cleavage. The rate of pseudo-rotation is affected by various factors that include the degree of esterification, ligand structures (acyclic vs. cyclic), protonation state, solvation, although in general the barrier is expected to be low. For example, the pseudo-rotation barrier between P(O-)(OH)(-O-CH₂CH₂-O-)(OCH₃) and P(O-)(OCH₃)(-O-CH₂CH₂-O-)(OH) is calculated [60, 61] to be 5.3 kcal/mol in the gas phase and ~2.6–2.8 kcal/mol in solution with PCM models. Considering the structural similarity of this molecule to UNP, it is reasonable to expect that the pseudo-rotation barrier in our system is also low, at least in the aqueous solution. In the tert-butanol solution, however, considering the bulky size of the solvent, a higher barrier might be expected, which motivated our PMF simulations with explicit solvents. However, as the PMF calculations (Fig.9) indicate, the pseudo-rotation of the penta-valent intermediate has comparable barriers in the aqueous and tert-butanol solutions, which is consistent with the observation that the pseudo-rotation, in fact, involves fairly modest structural changes in the solute.

In summary, among all the key properties that we or others have speculated to be essential for an efficient phosphoryl transfer reaction, no major trend is observed that can straightforwardly explain the abolishment of UNP isomerization in the anhydrous tert-butanol solution. The solute is structurally much more rigid in tert-butanol due to the fact that the bulky tert-butanol is a worse solvent than water and therefore promotes intra-solute hydrogen bonds. Nevertheless, the 2’-OH and phosphate do not appear to have trouble forming a hydrogen bond that permits a direct nucleophilic attack mechanism. More importantly, unlike commonly assumed [10], the direct nucleophilic attack pathway has very similar energetics compared to a water mediated pathway, thus water relay does not seem to be essential in the phosphoryl transfer studied here. The pseudo-rotation barrier is also similar in the aqueous and tert-butanol solutions. Therefore, we have to conclude that the lack of UNP isomerization in the anhydrous tert-butanol solution alone does not directly support the role of water relay in phosphoryl transfer reactions and some other reason(s) must be responsible for this observation.

5 Conclusions

Phosphoryl transfer reactions are fundamentally important in life processes. Their mechanism in the biological context is complex and therefore solution models are potentially useful for sorting out some mechanistic issues. One issue that has been discussed rather extensively is whether a relay group, which can be a water solvent or an amino acid in the enzyme active site, is required to facilitate the proton transfer from the nucleophilic group to the general base; the latter can be the phosphate group itself. The involvement of the relay group was motivated by stereoelectronic arguments, although an entropic consideration might render it less favorable especially in solution. The most relevant experimental data that we are aware of come from the study of the UNP system [22], where the key finding is that the isomerization reaction of UNP is abolished as the solvent changes from water to anhydrous tert-butanol; this has been interpreted as the direct support for the role of water relay in the phosphoryl transfer. By analyzing several relevant steps of UNP isomerization using a combination of theoretical studies, however, we show that this interpretation is not as straightforward as originally thought. QM/MM simulations show that in both aqueous and tert-butanol solutions, the UNP molecule have a significant population for configurations in which the 2’-OH and the phosphate group are well oriented for a direct nucleophilic attack, while the single-water-mediated configuration is equally likely in the aqueous solution. However, MEP calculations show that both mechanisms have, in fact, very similar energetics; i.e., with an associative nature transition state, water relay does not have any advantage even without invoking entropic considerations. Therefore, the lack of isomerization in UNP alone can not be used as a clear evidence for supporting the role of water relay in phosphoryl transfer reactions. Unfortunately, the precise reason for this interesting experimental observation remains unclear after this study, although we have been able to provide new insights into several most commonly discussed possibilities.

Supplementary Material

1_si_001. Supporting Information.

Benchmark calculations for the MM model for tert-butanol, the van der Waals parameters for the SCC-DFTBPR model of UNP and the performance of SCC-DFTBPR for pseudo-rotation are included.