Nanogranular origin of concrete creep

Abstract

Concrete, the solid that forms at room temperature from mixing Portland cement with water, sand, and aggregates, suffers from time-dependent deformation under load. This creep occurs at a rate that deteriorates the durability and truncates the lifespan of concrete structures. However, despite decades of research, the origin of concrete creep remains unknown. Here, we measure the in situ creep behavior of calcium–silicate–hydrates (C–S–H), the nano-meter sized particles that form the fundamental building block of Portland cement concrete. We show that C–S–H exhibits a logarithmic creep that depends only on the packing of 3 structurally distinct but compositionally similar C–S–H forms: low density, high density, ultra-high density. We demonstrate that the creep rate (≈1/t) is likely due to the rearrangement of nanoscale particles around limit packing densities following the free-volume dynamics theory of granular physics. These findings could lead to a new basis for nanoengineering concrete materials and structures with minimal creep rates monitored by packing density distributions of nanoscale particles, and predicted by nanoscale creep measurements in some minute time, which are as exact as macroscopic creep tests carried out over years.

Concrete is the most-used construction material on earth. The annual worldwide production stands at 20 billion tons and increases per annum by 5%. However, the fundamental causes of concrete creep are still an enigma, and have deceived many decoding attempts from both experimental (1–3) and theoretical sides (4–8). In the United States alone, concrete creep is partly responsible for an estimated 78.8 billion dollars required annually for highway and bridge maintenance. Although it is generally agreed that the complex creep behavior of concrete materials is largely related to the viscoelastic response of the primary hydration product and binding phase of hardened Portland cement paste, the calcium–silicate–hydrate (C–S–H), the creep properties of C–S–H have never been measured directly. C–S–H precipitates when cement and water are mixed, as clusters of nanoscale colloidal particles (9, 10) that cannot be recapitulated ex situ in bulk form suitable for macroscopic testing. Over decades, therefore, concrete creep properties have been probed on the composite scale of mortar and concrete (11), with the conclusion that there are 2 distinct creep phenomena at play (Fig. 1 A and B): a short-term volumetric creep and a long-term creep associated with shear deformation (3, 7, 12, 13), with a creep rate evolving as a power function t⁻ⁿ of exponent n between 0.9 and 1 (14). The assessment of this long-term creep is most critical for the durability of concrete structures, and requires, for a specific concrete composition and structural application, years of expensive macroscopic testing (11, 14). After more than 40 years of research (4–8), basic questions persist regarding the physical origin of this logarithmic creep and its link with microstructure and composition.

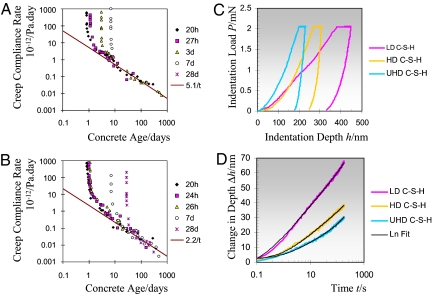
Fig. 1.

Results from creep tests at different scales. (A and B) Macroscopic uniaxial creep compliance rate vs. material age for a normal strength concrete (w/c = 0.5) and a high-strength concrete (w/c = 0.33), loaded in uniaxial compression with a constant load at different material ages (adapted from ref. 3). The long-term creep rate evolves as a power function t⁻ⁿ of exponent n between 0.9 and 1 (14). Macroscopic creep experiments were performed on 16-cm diameter and 1-m long cylindrical concrete samples (47). (C) Characteristic nano-indentation load–indentation depth curves representative of the nano-indentation response of 3 calcium-silicate-hydrate (C–S–H) phases present in cementitious materials (here a cement paste prepared at a w/c = 0.15 mass ratio): low-density (LD) C–S–H; high-density (HD) C–S–H; and ultra-high-density (UHD) C–S–H. After a loading in 10 s, a holding at maximum load for 180 s demonstrates the time-dependent behavior of C–S–H. (D) During the 180-s dwelling time, the change in indentation depth is recorded as a function of time, and fit with a function of the form Δh(t) = x₁1n(x₂t + 1) + x3t + x4. A close inspection of the constants x₁, …,x₄ shows that x₄ = 1.27 ± 1.92 nm and x₃ = 0.02 ± 0.02 nm/s (mean ± SD in >2,000 tests) correct respectively for any inaccuracy in the determination of the beginning of the creep phase, and for the drift of the indentation apparatus (details provided in Materials and Methods). The characteristic time 1/x₂ ≈ 1.66 s is much smaller than the holding time of 180 s, so that the indentation creep compliance rate L̇ = 2a_Uḣ/P_max = 1/(Ct) allows the determination of the contact creep modulus from C = P_max/(2a_Ux1), where P_max is the indentation load kept constant during the holding phase, whereas a_U = $\sqrt{A_c/\pi }$ is the contact radius at the end of the dwelling phase, with A_c the projected area of contact between the indenter and the indented surface determined with the Oliver and Pharr method (22). Here, for the displayed P–h curves, C = 95.0 GPa for LD C–S–H; C = 183.9 GPa for HD C–S–H, and C = 367.6 GPa for UHD C–S–H.

In this study, we investigate the creep properties of C–S–H. This is achieved by means of a statistical nanoindentation technique (SNT), described and validated previously (15–17), which is most suitable for the in situ investigation of mechanical phase properties and microstructure of highly heterogeneous hydrated composite materials. Like the classical indentation technique, an indenter tip (here a 3-sided pyramid Berkovich tip) is pushed orthogonally to the surface of the cement paste, and both the load applied to the tip, and the displacement of the tip with respect to the surface are recorded. By applying continuum-based constitutive models to the resulting load-displacement curve, mechanical properties of the indented material are determined. Applied to heterogeneous and multiphase materials, the SNT then consists of carrying out a large array of such nanoindentation tests, and by applying statistical deconvolution techniques (15, 16) and micromechanical models to link microstructure to phase properties (17–19).

Results

Nine cement pastes of different compositions representative of a large range of real Portland concretes, were tested. They differed by their water-to-cement (w/c) mass ratio ranging from w/c = 0.15 to w/c = 0.40, heat treatment, and mineral additions, including silica fumes and calcareous fillers. The samples were prepared according to a procedure described in a previous study (20). On each sample 2 series of statistical nanoindentation tests were carried out that differ in the loading protocol: the first series assesses the microstructure from indentation hardness and indentation stiffness results; obtained by a trapezoidal load history with a maximum load of P_max = 2 mN, applied in 10 s, kept constant over 5 s and unloaded in 10 s. Following fast loading, the 5-s dwelling time is short enough to ensure that the indentation hardness, H = P_max/A_c (with A_c the projected area of contact between the indenter probe and the indented surface), is representative of the strength content (19, 23, 24). In turn, the unloading is fast enough so that the indentation modulus M, determined from the unloading slope S = (dP/dh)_h=hmax at the end of the holding phase truly relates to the elasticity content of the indented material (25), namely the indentation modulus M = E/(1 − ν²) = S/(2a_U), with E the Young's modulus, ν the Poisson's ratio, and a_U = $\sqrt{A_c/\pi }$ the radius of contact between the indenter probe and the indented surface upon unloading (21, 22, 26). The load protocol of the second series differs from the first in a 180-s long dwelling period, which allows the assessment of the contact creep compliance rate, L̇(t) ≅ 2a_Uḣh/P_max, and the creep compliance, L(t) = 2a_UΔh(t)/P_max + const, from the time-dependent indentation depth rate ḣ(t) and the change in indentation depth Δh(t) = h(t) − h₀ in excess of the indentation depth h₀ ≈ 200 nm ± 45 nm recorded during the 10-s loading to P_max = 2 mN (Fig. 1C). In each series on the 9 samples, 400 nanoindentation tests were performed, of which on-average 282 indentations were identified as indents on C–S–H phases, recognized by an indentation modulus and hardness smaller than the C–S–H particle stiffness and hardness, M < m_s = 63.5 GPa and H < h_s ≈ 3 GPa, determined in previous studies (16, 17, 27).

In all tests on C–S–H phases, after correcting for thermal drift effects of the indenter equipment, a least square fitting of Δh(t) = h(t) − h₀ demonstrates an indentation creep compliance of the C–S–H phases that is logarithmic with regard to time (Fig. 1D), which translates into a rate L̇(t) ∝ t⁻¹. In the >2,000 tests on 9 materials, the average error of the fit was 0.48 nm ± 0.09 nm, which is on the same order as the noise in the depth measurement during the 3-min creep phase of 0.39 nm ± 0.09 nm; that is, within the noise of the measurement, the logarithmic function was in almost perfect agreement with the experimental data (Fig. 1D). The creep rate of the C–S–H phases is thus governed by L̇(t) = (Ct)⁻¹ where C, which has the same dimension as an elastic modulus, is justly termed contact creep modulus (see Materials and Methods).

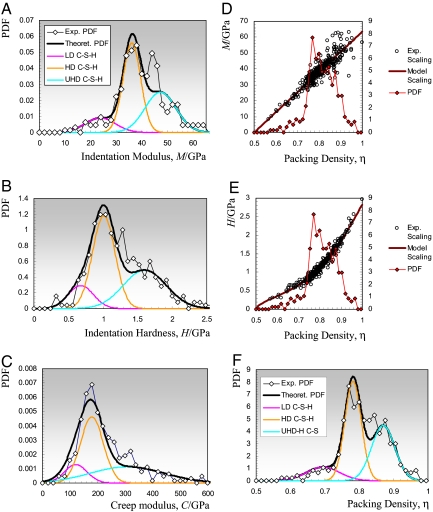
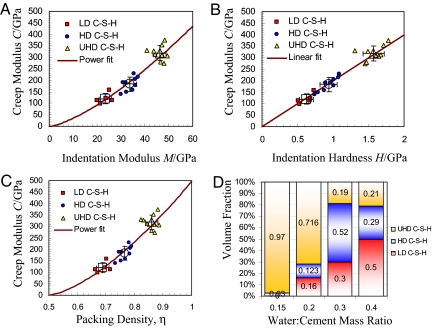
Similar to the indentation modulus and the indentation hardness, this creep modulus shows a large variability from one test to another, as one would expect given the high heterogeneity of the clusters of C–S–H particles in cement paste materials. We, therefore, deconvolute, for each grid of indentations, the obtained indentation hardness, indentation modulus and contact creep modulus with Gaussian distributions (15–17). The deconvolution process demonstrates the existence, in all samples, of 3 significant mechanical phases characterized by their phase properties (Fig. 2 A–C): indentation modulus, indentation hardness, and contact creep modulus. Remarkably, an almost perfect linear scaling of the contact creep modulus with the Berkovich hardness (C = 200.1 H^B, R² = 0.9385) is observed (Fig. 3B), whereas this scaling is nonlinear w.r.t. the indentation modulus (Fig. 3A). We confirmed that these scaling relations equally hold for cube corner indentations (C = 91.4 H^CC, R² = 0/.897) operated to a substantially identical indentation depth h = 260 nm ± 90 nm with a maximum load of P_max = 0.5 mN, that generate another triaxial stress field below the indenter (24); and for depths 10 times as large, h = 2,020 nm ± 440 nm, achieved with a Berkovich probe loaded to P_max = 100 mN (C = 299.1 H^B, R² = 0.984), that sample the composite response of the cement paste (hydration phases and unhydrated cement) (16).

Fig. 2.

Results from statistical indentation analysis. (A–C) Probability density plots (PDF, normalized histogram) and phase deconvolution of the indentation modulus M, the indentation hardness H, and c the contact creep modulus C of a series of 400 nanoindentation tests carried out on a w/c = 0.3 cement paste with 25% of calcareous filler (in weight of cement). The probability density plots (PDF) displayed here, demonstrate the existence of 3 statistically significant C–S–H phases, identified by their mechanical phase properties. Here, in the w/c = 0.3 material, LD C–S–H [M_LD = 23.7 ± 5.9 GPa (mean ± SD), H_LD = 0.68 ± 0.18 GPa and C_LD = 121.0 ± 41.5 GPa] occupies 13.4 Vol% (surface below the Gaussian curve in the PDF); HD C–S–H 48.2 Vol% (M_HD = 36.1 ± 3.4 GPa, H_HD = 1.01 ± 0.16 GPa and C_HD = 179.2 ± 41.6 GPa); and UHD C–S–H 38.1 Vol% (M_UHD = 47.2 ± 6.0 GPa, H_UHD = 1.60 ± 0.31 GPa and C_UHD = 308.1 ± 133.9 GPa). (D and E) Micromechanics-based packing density scaling of indentation modulus M and indentation hardness H (17). Superposed on D and E is the probability distribution (PDF) of the packing density η. (F) A phase deconvolution of the packing density yields 3 characteristic packing densities: η_LD = 0.69 ± 0.05, η_HD = 0.78 ± 0.02 and η_UHD = 0.87 ± 0.03.

Fig. 3.

Scaling of the contact creep modulus C with (A) the indentation modulus M (C = 1.387 (M/Gpa)1.404;R² = 0.8710), (B) the indentation hardness H (C = 200.1H; R² = 0.9385), and c the packing density η for the 9 cement-based materials here investigated. Data points for M, H, and C were obtained from the deconvolution process (Fig. 2 A–C), and identified as the mechanical phase properties of LD C–S–H, HD C–S–H and UHD C–S–H. The large symbols are the mean values and the error bars represent the standard deviation of the phase values of the 9 tested materials. (D) Volume fractions of LD C–S–H, HD C–S–H and UHD C–S–H, as determined from the deconvolution process for a selected number of materials that differ only in the w/c mass ratio.

These scaling relations suggest that the creep rate magnitude (contact creep modulus C) on one hand, and the strength and elasticity content (indentation modulus M and hardness H) on the other hand, are controlled by the same fundamental brick of C–S–H microstructure: the packing of clusters of nanoscale colloidal particles with an associated internal pore system (9, 10).

To further investigate this link, we determined the nanoporosity distribution of the C–S–H phases, respectively its complement, the nano-packing density η (“one minus porosity”), by means of micromechanics-based scaling relations (28), of the indentation modulus, M/m_s = Π_M(η,ν) (16, 17), and indentation hardness, H/h_s = Π_H (η,α) (17, 19), with ν the Poisson's ratio and α the friction coefficient of the solid (Fig. 2 D and E). The variability in shape and size of C–S–H particles leads to a distribution of packing densities that appears more continuous than discrete (Fig. 2F), but in which 3 characteristic packing densities can be identified. Indeed, after deconvolution, the analysis of the short-duration (5-s) dwelling tests for all 9 samples confirms the results in refs. 16–18 and 29–33 that C–S–H exists in 3 structurally distinct but compositionally similar forms, that differ merely in their characteristic packing density (Fig. 2F); that is, for the 9 tested materials: η_LD = 0.66 ± 0.03 for a low-density C–S–H phase; η_HD = 0.75 ± 0.02 for a high-density C–S–H phase; and η_UHD = 0.83 ± 0.05 for an ultra-high-density C–S–H phase. These mean packing densities come remarkably close to limit packing densities of spherical objects, namely the random close-packed limit of 64% (34, 35); the ordered face-centered cubic (fcc) or hexagonal close-packed (hcp) packing of 74% (36), and a 2-scale random packing limit of 1 − (1 − 0.64)² = 87%. Finally, matching η with C for the 3 phases present in all 9 materials, the contact creep modulus is recognized to depend in first order on the specific packing density of each C–S–H phase (Fig. 3C): C_LD = 120.4 ± 226 GPa, C_HD = 183.6 ± 30.5 GPa and C_UHD = 318.6 ± 32.2 GPa (where mean ± SD refer to the phase values of the 9 tested materials).

Discussion

We now need to reconcile the different observations, namely the logarithmic creep of C–S–H (Fig. 1D) and the unique dependence of the creep rate (contact creep modulus C) on the packing density (Fig. 3C). In search for the origin of C–S–H creep, we note that a logarithmic creep is not only observed for metals (37, 38), but also for a wide range of granular materials. It is well known for sands and clays (39) and has been observed in the compaction of vibrated granular media (40, 41). Furthermore, the linear scaling of C with H (Fig. 3B), but not with M (Fig. 3A), suggests that the same mechanisms are at play when C–S–H deforms plastically or creeps. The most likely place for the creep deformation is thus the particle-to-particle contact of nanosized C–S–H particles.

We thus hypothesize that C–S–H creep is due to nano-particle sliding. This sliding leads to a local increase of the packing density toward the jammed state associated with limit packing densities (42), beyond which no particle sliding (i.e., deviatoric creep deformation) is possible without dilation of the granular media. Close below this jammed state, the volume changes are small compared with the limit packing density, and are negligible as regards the mechanical properties of the C–S–H phases. For this case, the free-volume theory of granular physics (40, 42–44) provides a plausible explanation for the observed logarithmic creep (Fig. 1D) and the unique dependence of creep rate and magnitude of C–S–H on their packing density (Fig. 3C). The free-volume model describes the compaction of dry granular media under mild vibrations inducing some form of pseudoBrownian motion. Although the Brownian motion of C–S–H particles is negligible, force distributions within the highly heterogeneous distribution of C–S–H particles are considered to drive void creation and destruction with a stationary distribution of sizes. Following the free-volume theory, we thus assume that the rate decreases exponentially with the excluded volume. To illustrate our purpose, consider N particles per unit volume of same volume w having a packing density η = wN. Let η_lim = wN_lim be the limit packing density at the jammed state. The free volume per particle thus is ν = w (1/η − 1/η_lim), and for small variations around the limit packing density, ν ≈ wx/η_lim where 0 < x = 1 − η/η_lim ≪ 1. Consider then a Poisson's distribution of the pore size distribution around the free volume ν such that the probability to encounter a pore volume greater than the particle size w is P(V^F > w) = exp(−w/v) ≈ exp(−η_lim/x). This probability is assumed to determine the rate of change of packing density, η̇ ∝ exp(−η_lim/x), induced by particle sliding into free nano-pore volume. Retaining in the integration between the initial and current states the dominating exponential term yields t ∝ exp(η_lim/x); and thus η̇ ∝ 1/t.

To test this free-volume creep hypothesis associated with small variations of the packing density, we compare the mean packing density values of the 3 C–S–H phases for the 5-s and the 180-s dwelling period test series. We find indeed, for all 3 C–S–H phases, a densification of the packing due to a prolonged dwelling period: The LD C–S–H packing increases by 0.7%, the HD C–S–H packing increases by 2.8%, and the UHD C–S–H packing increases by 2.0%. Although these changes are small, the general trend supports our suggestion that concrete's logarithmic creep originates from a rearrangement of nanoscale C–S–H particles around limit packing densities of 3 compositionally similar but structurally distinct C–S–H phases: LD C–S–H, HD C–S–H and UHD C–S–H.

These phases are present in concrete materials in different volume proportions (Fig. 3D): LD C–S–H dominates cement-based materials prepared at high w/c mass ratios; HD C–S–H and UHD C–S–H control the microstructure of low w/c ratio materials. Hence, compared with the life span of predominantly used LD C–S–H concretes, the reduced logarithmic creep of HD- and UHD C–S–H promises to raise the life span of creep-sensitive concrete structures by a factor of C_HD/C_LD = 1.5 and C_UHD/C_LD = 2.6. In fact, it is precisely the trend that is observed macroscopically, in the change of the macroscopic creep rate between the normal strength concrete (high w/c = 0.5) (Fig. 1A) and the high performance concrete (low w/c = 0.33) (Fig. 1B), for which the long-term creep modulus increases from C_hs = 1/5.1 TPa = 196 GPa (from Fig. 1A) to C_hs = 1/2.2 TPa = 455 GPa (from Fig. 1B), in close agreement with the values of C_HD and C_UHD. The increase in the macroscopic creep modulus of C_hs/C_ns = 2.3 is recognized to result from the presence of denser C–S–H phases with lower creep rates (higher creep modulus) in the low w/c concrete materials; and it shows that nanoscale creep measurements in some minute time (Fig. 1D) are as exact as macroscopic creep tests carried out over years (Fig. 1 A and B). This illustrates, if need still be, that the insight thus gained into the link between composition (w/c ratio), microstructure (packing density distributions) and C–S–H nano-creep properties has the promise to contribute to the development and implementation of new concrete materials with minimal creep rates monitored through the packing distributions of nanoscale C–S–H building blocks.

In summary, the search for the origin of concrete creep has a long history (1), and progress has been slow because of the difficulty of measuring the creep properties of nanoscale C–S–H particles. The statistical nanoindentation testing technique here proposed allows an in situ probing of C–S–H creep properties. C–S–H phases creep logarithmically with time, which can be explained by and monitored via their nanogranular nature. By probing micrometer-sized volumes of materials, nanoindentation creep experiments provide quantitative results in a 6 orders of magnitude shorter time and on samples 6 orders of magnitude smaller in size than classical macroscopic creep tests. This “length-time equivalence” (large time scales can be accessed by looking at small length scales) may turn out invaluable for the implementation of sustainable concrete materials whose durability will meet the increasing worldwide demand of construction materials for housing, schools, hospitals, energy and transportation infrastructure, and so on.

Materials and Methods

Materials and Preparation.

Cements were mixed at different w/c mass ratios (0.15, 0.20, 0.30, 0.4), and different mineral additions [0.22, 0.24, and 0.32 silica fume/cement mass ratio (sf/c), 0.25 calcareous filler/cement mass ratio (cf/c)] to generate a sufficiently large range of different compositions. Six samples prepared at a 0.15, 0.30 and 0.40 w/c mass ratio, with and without silica fumes or calcareous filler addition, were hydrated at 20 °C for 28 days and stored in sealed conditions until testing. Three samples prepared with a 0.2 and 0.3 w/c mass ratio were subject at a material age of 2 days to a 48-h heat treatment (HT) at 90 °C, representative of a HT protocol used in the field for advanced concrete solutions. This HT protocol at 2 days was also applied to one mix prepared at a 0.2 w/c mass ratio and a 0.24 sf/c mass ratio. All heat treated samples were stored after heat treatment in sealed conditions until testing. The material age at testing was at least 3 months, which can be associated with an asymptotic hydration state. For nanoindentation testing specimens were sliced into 10-mm diameter discs of thickness ≈3 mm, mounted on a stainless steel AFM plate (Ted Pella) with cyanoacrylate as an adhesive, and grinded and polished following a polishing procedure that ensures achievement of as flat a surface as possible, repeatable results, and that minimizes sample disturbance (20).

Nanoindentation Technique.

Nanoindentations (h < 1 μm) were performed with a nanohardness tester enclosed in an environmental chamber, from CSM Instruments SA implemented at MIT. The nanoindentation depth of h₀ ≈ 200 nm ± 45 nm was chosen to assess the phase properties of C–S–H clusters (16), according to the scale separability conditions. That is, the depth of indentation must be much larger than the elementary size of the C–S–H particle [≈5 nm (10, 32)], so that continuum models can be used to extract meaningful mechanical properties; and it must be smaller than the cluster size visible by, e.g., scanning electron microscopy [≈2 μm (46)]. In return, microindentations that probe the properties of the composite material (different C–S–H phases, unhydrated cement), were performed with a MicroTest indenter of Micro Materials Ltd. also available at MIT. Before testing the machines were calibrated, correcting for the machine frame compliance and determining the shape area function of the used indenter probes (Berkovich and Cube Corner).

Determination of Logarithmic Creep of C–S–H.

For each test performed on the hydration products, during the 180-s dwelling time, the change in indentation depth is recorded as a function of time, and fit with a function of the form Δh(t) = x₁ln(x₂t + 1) + x₃t + x₄, where x₁, …,x₄ are 4 constants that are fit with a non linear least-squares solver in Matlab. The average error of this fit is 0.48 nm ± 0.09 nm, which is slightly above (but very close to) the noise level. We then analyze, for all tests (>2,000), the values of x_{1, …,}x₄ and come to the following result: the coefficient x₄ = 1.27 ± 1.92 nm captures any inaccuracy in the determination of the beginning of the creep phase. The coefficient x₃ = 0.02 ± 0.02 nm/s of the linear term has a correlation R ² = 0.0006 with the indentation modulus M, and R² = 0.0050 with the indentation hardness H. From these very low coefficients of correlation we conclude that x₃ is not material-related and is random. The linear term x₃t of the fitting function is thus recognized as drift of the indentation apparatus. Those drift effects are well known for indentation equipments, and need to be corrected when attempting to identify the creep kinetics. The only material-related term in the fitting function is thus the logarithmic one, from where we infer that the creep of C–S–H is logarithmic with regard to time. Finally, an inspection of the characteristic time 1/x₂ of the creep phenomenon shows a weak correlation with the indentation modulus (R² = 0.042) and with the indentation hardness (R² = 0.064). The characteristic time is 1/x₂ = 1.66 s ± 4.76 s. Because 1/x₂ is much smaller than the dwelling time of 180 s, the logarithmic creep rate attributed to C–S–H (after correction of the previously identified drift term) simplifies to ḣ = x₁/t. That is, for the logarithmic time dependence of the creep phenomenon the indentation creep rate is defined by only one parameter of the fitting function, x₁. This parameter x₁ enters the definition of the indentation creep compliance rate L̇ = 2a_Uḣ/P_max = 2a_Ux₁/(P_maxt), where a_U is the contact radius upon unloading [determined with the classical tools of indentation analysis, namely the Oliver and Pharr method (22)], and P_max is the load applied to the indenter during the dwelling time (Fig. 1C). Finally, we condense the pre-(1/t) term of L̇ into the contact creep modulus C = P_max/(2a_Ux₁). Note that we also attempted a power function fit of the form Δh(t) = x₁t^x₂ + x₃t + x₄, with constants x₃ and x₄ still correcting for drift and initialization of the creep phase. Such a fit also provides satisfactory results with a power exponent in >2,000 tests of x₂ = 0.298 ± 0.063, the average error 0.59 nm ± 0.25 nm being only slightly greater than that obtained with the logarithmic fit. In return, this fit requires 2 parameters to determine the creep kinetics, L̇ = 2a_Ux₁x₂t^{x2 − 1}/P_max ∝ t^−0.7.)

Statistical Nanoindentation Analysis.

The statistical indentation analysis is based on a deconvolution process, which consists of fitting a mixture model of multivariate normal components to the experimental dataset (M, H, C, η), using maximum likelihood via the Expectation–Maximization (EM) algorithm implemented in the EMMIX software (46). The rational of using normal (Gaussian) components in the mixture model is that they only involve the first (mean) and second (standard deviation) statistical moments; in contrast to other components (e.g., log-normal distribution) that introduce a bias through higher order moments (e.g., skewness) into the analysis of the phase properties and their volume fraction, and that would not be able to fit the highly heterogeneous datasets of all cement paste materials.