Transmural Myocardial Strain in Mouse: Quantification of High-Resolution MR Tagging using HARP Analysis

Abstract

MR tagging allows noninvasive examination of regional myocardial function with high accuracy and reproducibility. Current tagging method is limited by low tagging resolution for accurate transmural strain quantification. Previously, a SPAMM-based method was proposed to increase the tagging resolution by combining two or more tagged images with different tagging grid positions. However, there has been limited application due to the challenge in image processing of multiple data sets. In the current study, we propose a HARP-based method for automated and fast analysis of high-resolution tagged images. First-order harmonic peaks from low tagging resolution images were combined to generate the composite second-order harmonic peak for strain computation. The combined images reached a tagging resolution of 0.3 mm. The proposed method was applied to the quantification of transmural myocardial wall strain in 7 normal C57BL/6 mice. Principal strains, as well as radial and circumferential strains, were quantified using the current method.

Introduction

Genetically manipulated mouse models are playing an important role in the investigation of human cardiac diseases. The characterization of regional myocardial wall motion in the mouse heart is crucial for the understanding of the biomechanical properties of the heart, as well as the underlying molecular mechanisms of altered ventricular function. MR tagging provides the first noninvasive method for quantitative evaluation of regional myocardial contractile performance. Such methods use either selective spin saturation (1) or spatial modulation (2-4) to generate “tags” in the myocardium. By tracking the displacement of these tags at different phases of the cardiac cycle, accurate quantification of regional myocardial wall motion can be achieved.

One major limitation of current tagging method is the low tagging resolution, as less than three taglines can be placed across the myocardium wall. Such low tagging resolution hampers the quantification of transmural myocardial wall strains. To improve tagging resolution, Stuber et al. proposed and demonstrated in humans a method which allowed doubled tagging resolution through combined SPAMM11 sequence with shifted tagging grids (5). The shift of the tagging grids was accomplished by applying a phase shift to the second RF pulse in a SPAMM11 sequence. By multiplication of two images of the same slice with shifted tagging grids, doubled tagging resolution can be effectively achieved. However, the doubled tagging resolution from two separate data sets presents additional challenge to the post-processing of tagged images. Besides the processing of multiple image sets, tag tracking in the image domain also becomes more difficult as tag lines are more likely to converge at systole with reduced tag spacing. As a result, there has been limited application of this high-resolution tagging method.

Recently, harmonic phase (HARP) analysis has been proposed as a rapid and automated method for strain quantification (6-8). HARP method is based on the fact that tissue motion is directly encoded in the phase images of the offcenter spectral peaks (harmonic peaks) in the Fourier domain of SPAMM tagged images. Method for direct calculation of the 2D Eulerian strains from spatial derivatives of HARP images has been developed and validated in humans and large animals (7, 9, 10). Recently, we also developed method for direct quantification of the 2D Lagrangian strains from HARP images. The accuracy and sensitivity of such quantification were evaluated in a rat model of myocardial infarction (11).

In the present study, we developed a novel HARP-based strain analysis method that allowed fast strain calculation from the high-resolution tagged images. The utility of such method was demonstrated in mouse heart by quantifying the transmural difference of normal and principal strains.

Methods

Animal Preparation and MR Imaging Protocol

A total of seven two-month old C57BL/6 mice underwent MR imaging on a 4.7T Varian INOVA system (Varian Associates, Palo Alto, CA) equipped with a gradient insert (60 G/cm, 10 cm inner diameter). An in-house built 2.5 cm surface coil was used for image acquisition. Animals were anesthetized with 1% isoflurane by nose cone and placed into the coil in prone position. Electrodes were attached to the front paws and right leg. Pre-amplified ECG signals were transferred through an optical fiber to a trigger unit for ECG gating and monitoring of the vital signs as previously described (12). The animals were kept warm by blowing hot air into the magnet using a blow dryer. The heat flow and the anesthesia level were manually adjusted to maintain the heart rate. The animal protocol was approved by the Animal Studies Committee of the Washington University Medical Center.

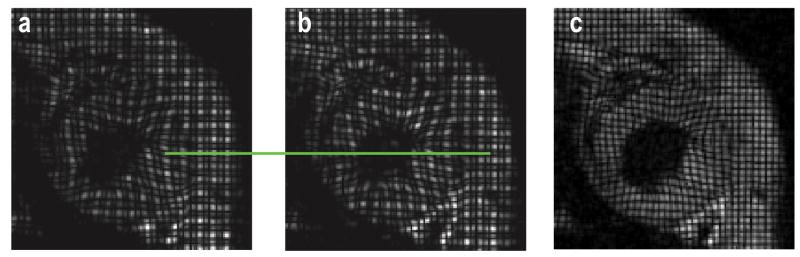
A series of scout images were acquired to obtain short-axis (SA) planes. After acquiring a horizontal long-axis (LA) image (four-chamber view), three contiguous SA images, parallel to the tricuspid and mitral valve plane, were prescribed at the midventricular level. Two sets of tagged images (0.6 mm tagging resolution) were acquired with either SPAMM11 or SPAMM11̄ sequence applied immediately after the detection of the R-wave, leading to a shift of the tagging grids by half a tagging voxel between the two data sets (Figure 1a&b). Such an approach yielded a final tagging resolution of 0.3 mm when the two data sets were combined (Figure 1c). The SPAMM sequence was followed by the acquisition of cine images using FLASH sequence with the following imaging parameters: TE, 3 ms; field of view, 4 cm×4 cm; matrix size, 256×128; slice thickness, 1 mm. TR was adjusted according to the heart rate such that a total of 15 frames were acquired per cardiac cycle.

Figure 1.

Tagging grids generated by SPAMM11 (a) and SPAMM11̄ (b), respectively. A shift of the taglines by half a tagging voxel can be seen at the green line between a and b. Combination of the two images yields a composite image with doubled tagging resolution (c).

Image Analysis

The SPAMM modulation of an MR image takes the form of a sinusoidal dependence of the longitudinal magnetization. For a SPAMM11 image, the resulting spatial modulation of an image can be described by (7)

$$I_1(\mathbf{\text{p}})=I_0(\mathbf{\text{p}})(c_0+c_{1}cos({\mathbf{\text{ω}}}^T\mathbf{\text{p}}))$$ (1)

where p is the spatial variable, I₀(p) is the image without tagging modulation, c₀ and c₁ are the coefficients determined by the flip angles, and ω is the spatial frequency determined by the tagging gradient. Similarly, a SPAMM11̄ sequence will shift the tagging grid by half a tagging voxel, leading to spatial modulation of the image described by

$$I_1(\mathbf{\text{p}})=I_0(\mathbf{\text{p}})(c_0+c_{1}sin({\mathbf{\text{ω}}}^T\mathbf{\text{p}}))$$ (2)

Thus, multiplication of the two images, I_H(p) = I₁(p)I₂(p), yields

$$I_H(\mathbf{\text{p}})=I_0^2(\mathbf{\text{p}})(c_0^2+c_0{c}_{1}cos({\mathbf{\text{ω}}}^T\mathbf{\text{p}})+c_0{c}_{1}sin({\mathbf{\text{ω}}}^T\mathbf{\text{p}})+\frac{1}{2}{c}_1^{2}sin(2{\mathbf{\text{ω}}}^T\mathbf{\text{p}}))$$ (3)

with the term sin(2ω^Tp) corresponding to the doubled tagging resolution.

Therefore, the Fourier transform of I_H generates harmonic peaks at 0, ω^T, and 2ω^T. The second-order harmonic peak at 2ω^T corresponds to the term sin(2ω^Tp) in the spatial domain, which gives rise to the doubled tagging resolution. The inverse Fourier transform of a harmonic peak has two parts. The magnitude image of a harmonic peak reflects the anatomy of the heart. HARP image refers to the phase image corresponding to a harmonic peak. The phase angle is a material property of the tagged tissue (6). It remains invariant throughout the cardiac cycle for a particular material point. Hence, by either tracing the isophase contours of a HARP image or calculating its spatial derivatives, HARP-based analysis allows automatic tracing of tag lines and direct quantification of the Lagrangian strain in myocardium (6-8).

However, directly extracting the second-order harmonic peak from the composite high-resolution image can lead to significant inaccuracy in tagline tracing or strain quantification due to the overlap with and the interference from the neighboring harmonic peaks. Alternatively, we can also extract the two first-order harmonic peaks separately from the two individual images with low tagging resolution, i.e., I₀(p)c₁cos(ω^Tp) and I₀(p)c₁sin(ω^Tp). Multiplication of these two harmonic peaks yielded the same second-order harmonic peak of I_H. The composite HARP image is virtually the addition of the two individual HARP images with low tagging resolution. Tagline deformation can then be tracked from the composite HARP images.

Myocardial strain can also be directly calculated from the spatial derivatives of these composite HARP images. Previously it has been shown that the displacement field is encoded in a HARP image (7), i.e.,

$$\frac{\partial \mathbf{\text{q}}}{\partial \mathbf{\text{y}}}={(W^{T}H)}^{-1}\frac{\partial \mathbf{\text{ϕ}}}{\partial \mathbf{\text{y}}}$$ (4)

where q is the position of a material point in the reference map at time t = 0, y(q,t) is the position of the same material point at time t, ϕ is a vector describing the harmonic phases in the two tagging directions, and W and H are the matrices associated with the tagging and imaging planes. The multiplication of the two first-order harmonic peaks from two low-resolution images yields the following relationship

$$\frac{\partial \mathbf{\text{q}}}{\partial \mathbf{\text{y}}}={(2W^{T}H)}^{-1}\frac{\partial ({\mathbf{\text{ϕ}}}_1+{\mathbf{\text{ϕ}}}_2)}{\partial \mathbf{\text{y}}}$$ (5)

where ϕ₁ and ϕ₂ are the harmonic phases corresponding to the two first-order harmonic peaks, and the coefficient 2 indicates the doubling of tagging resolution.

Image analysis employed an in-house developed MATLAB-based Cardiovascular MR Image Analysis Tool (CVMRI) as previously described (12-15). Epicardial and endocardial contours were traced interactively. The left-ventricle was segmented into anterior, lateral, posterior, and septal regions. Myocardial centerline was determined by connecting the mid-points of the radial cords intersecting the epicardial and endocardial contours. Sub-endorcardial and sub-epicardial regions were defined as the myocardium between the endocardial border and centerline, and that between the centerline and epicardial border, respectively.

Strain Computation

The 2D Lagrangian strain tensor was calculated from the relationship

$$\mathbf{\text{E}}=\frac{1}{2}({\mathbf{\text{F}}}^T\mathbf{\text{F}}-\mathbf{\text{I}})$$

where $\mathbf{\text{F}}=\frac{\partial \mathbf{\text{y}}}{\partial \mathbf{\text{q}}}={\left(\frac{\partial \mathbf{\text{q}}}{\partial \mathbf{\text{y}}}\right)}^{-1}$ is the 2D displacement field, and I is the identity matrix. The displacement field, F, was quantified directly from the spatial derivatives of the composite HARP images based on the method described previously (11). The Lagrangian strain tensor was further diagonalized to yield two principal strains (E₁ and E₂), with E₁ and E₂ being the maximal and minimal strains, respectively. The strain tensor was also transformed to a local myocardial coordinate system defined by the radial (r) and circumferential (c) directions, yielding radial (E_rr), circumferential (E_cc), and shear (E_rc) strains.

Statistics

All measurements are presented as mean±SD. Mean values of myocardial strains in sub-endocardial and sub-epicardial regions were compared by paired student's t-test. Mean values of peak systolic strains in septal, anterior, lateral, and posterior segments were compared separately by one-way ANOVA. If there were statistical differences, multiple pairwise comparisons were performed using Tukey's test. P values less than 0.05 were considered statistically significant.

Results

Global Functional Indexes

The animals had a mean heart rate of 412±62 bpm during the MRI study. LV volumes were 34.8±7.3 μl at end-diastole and 14.0±3.5 μl at end-systole. Mean ejection fraction was 59.9±4.3%.

HARP Analysis

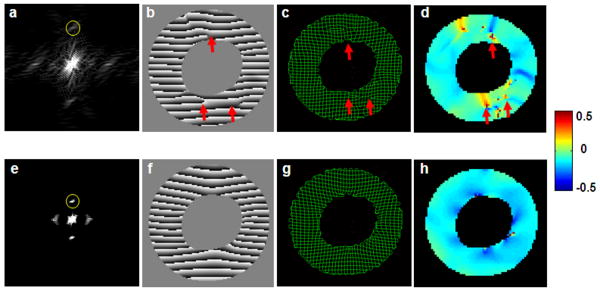
We first attempted to extract the second-order harmonic peaks directly from the composite images with high tagging resolution for strain quantification. The k-space image of such a composite image is shown in Figure 2a. The second-order harmonic peaks were of reduced intensity comparing with other peaks. In addition, there was severe interference from adjacent first-order harmonic peaks. As a result, there were obvious inaccuracies and artifacts in the corresponding HARP image and the synthetic taglines generated from the extracted second-order harmonic peaks, as well as in the calculated strain maps (Figure 2b-e).

Figure 2.

a&e. k-space images of a composite image with high tagging resolution and an original image with low tagging resolution, respectively. Yellow circles show the band-pass filter for harmonic peak extraction. b-d. representative HARP image, tag tracing, and E₂ strain map generated by extracting the second-order harmonic peak in a. f-h. representative composite HARP image, tag tracing, and E₂ strain map generated by extracting the first-order harmonic peaks from the original images of low tagging resolution. Arrows indicate artifacts and inaccuracies in tagline tracing and strain calculation.

Alternatively, we extracted individual first-order harmonic peaks from the original tagged images with low tagging resolution (Figure 2e). These harmonic peaks were subject to less interference from the adjacent DC peaks. Tagline tracing and strain quantification based on these composite HARP images yielded improved accuracy with less artifacts (Figure 2f-h).

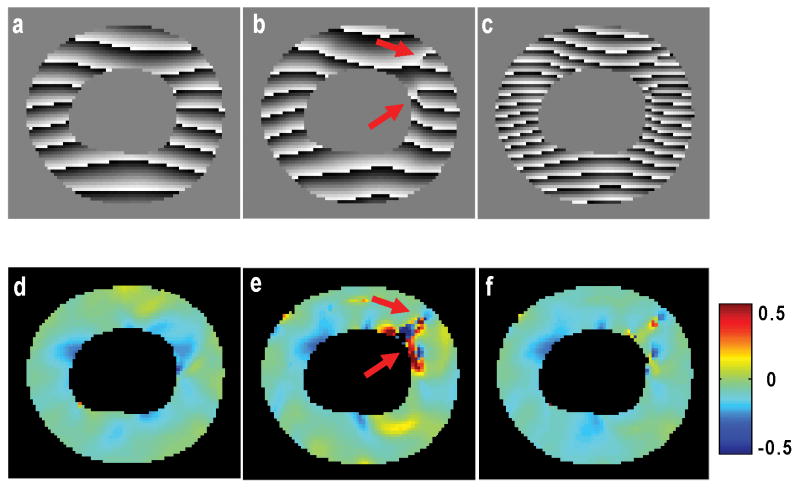
The proposed method also showed improved accuracy and robustness compared to results of HARP analysis using individual low-resolution images. As shown in Figure 3, one of the low-resolution images showed severe distortions in its HARP image and consequent artifacts in strain map (Figure 3b&e). These distortions typically occurred at the locations of phase wrapping. Since the other low-resolution image shifted the phase by π/2, the artifacts associated with phase disruption became less pronounced in the composite high-resolution image (Figure 3c&f).

Figure 3.

Comparison of HARP images and circumferential strain maps from low-resolution SPAMM11 tagging (a&d), SPAMM11̄ tagging (b&e), and composite high-resolution tagging (c&f) at peak systole. Arrows indicate phase discontinuity (b) and artifacts in strain map (e). The artifacts are attenuated in high-resolution strain map (f).

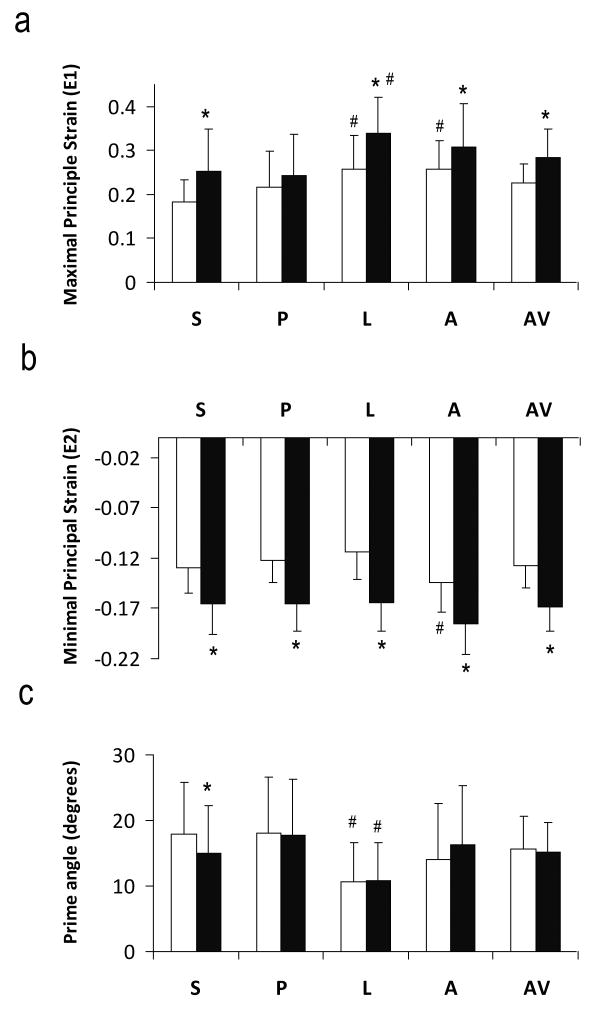
Principal Strains

Principal strains (E₁ and E₂) at peak systole are shown in Figure 4. E₁, an index of radial wall thickening, was positive, while E₂, an index of circumferential shortening, was of negative values. With the exception of posterior segment, sub-endocardial E₁ strain was significantly larger compared to that in the sub-epicardial region (P<0.05). Both sub-endocardial and sub-epicardial regions demonstrated significant regional heterogeneity with a larger E₁ strain at the anterior and lateral segments (P<0.05).

Figure 4.

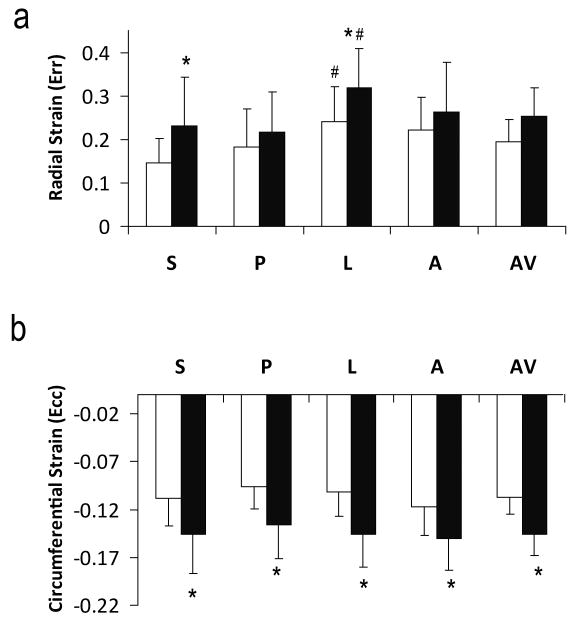
Maximal (a) and minimal (b) principal strains and the prime angle between the primary eigenvector and the radial direction (c). S, Septum; P, posterior; L, lateral; A, anterior; AV, slice average. White and black bars are sub-epicardium and sub-endocardium, respectively. *P<0.05 sub-epicardium versus sub-endocardium. ^#P<0.05 comparing with other segments.

E₂ strain in sub-endocardium was 27% to 45% larger in magnitude than that in sub-epicardium in all four segments (P<0.05). There was no significant regional difference in E₂ strain at sub-epicardium. Sub-epicardium exhibited more regional heterogeneity, with anterior E₂ strain being the largest in magnitude (P<0.05).

The prime angle, i.e., the angle between the primary eigenvector and the radial direction, was also calculated (Figure 4c). Average prime angles at sub-epicardial and sub-endocardial regions were 15.6±5.0° and 15.1±4.6°, respectively. Average prime angle was within 20° in all four segments. Smallest prime angle occurred in the lateral region (P<0.05). With the exception of septum, there was no significant difference between sub-endocardium and sub-epicardium.

Normal Strains

Radial and circumferential strains were calculated after transformation of strain tensor to the local myocardial coordinate system (Figure 5). Similar to E₁ and E₂ strains, radial strain was positive and heterogeneous (P<0.05), while circumferential strain was negative and more uniform. With the exception of radial strain in posterior wall, sub-endocardial radial and circumferential strains were all significantly larger in magnitude than those in sub-epicardial region (P<0.05). Lateral region exhibited the largest radial strain in both sub-endocardial and sub-epicardial regions (P<0.05).

Figure 5.

Radial (a) and circumferential (b) strains. S, Septum; P, posterior; L, lateral; A, anterior; AV, slice average. White and black bars are sub-epicardium and sub-endocardium, respectively. *P<0.05 sub-epicardium versus sub-endocardium. ^#P<0.05 comparing with other segments.

Discussion

The myocardial wall thickness of a mouse heart is only around 1 mm (12). Previous studies with a tagging resolution of around 0.6-1.2 mm can allow at most 3 taglines to be placed across the myocardial wall (16-20), frequently giving rise to only 1 tagging voxel in the ventricular wall. This limited tagging resolution is not sufficient to quantify the transmural strain in the heart. It also renders strain quantification susceptible to averaging and partial volume errors due to large tagging voxels. By acquiring two tagged image sets with shifted tagging grids, an effective tagging resolution of 0.3 mm was achieved in the current study. This resolution can consistently yield at least 4 tagging voxels across the myocardial wall of a mouse heart. With the improved resolution, it not only enables the quantification of transmural ventricular wall strain, but may also allow the characterization of myocardial wall deformation in right-ventricle with significantly reduced wall thickness, as well as the post-infarct zones in left-ventricle with significant wall thinning. Such characterization is not possible with low tagging resolution, as tagline spacing exceeds wall thickness in these regions.

While combing the two tagged images of shifted tagging grids can effectively double the tagging resolution, it also presents additional challenges to image analysis with doubled number of taglines. In the Fourier domain, a composite high-resolution tagged image consists of 9 harmonic peaks, with severe interference between the neighboring peaks. As a result, tag tracking and strain calculation by direct extraction of the second-order harmonic peaks suffered from artifacts and inaccuracies. On the contrary, the first-order harmonic peaks in the original tagged images of lower tagging resolution are better defined and subject to less interference from the only neighboring DC peak. The selection of appropriate band-pass filter to extract the first-order harmonic peaks has been shown to be robust and reproducible (7, 9, 11). In our current study, a composite high-resolution HARP image was generated from two first-order harmonic peaks of the original tagged images. Such a strategy can effectively reduce the inaccuracies and artifacts associated with direct extraction of the second-order harmonic peaks.

The current method used the multiplication of cosine- and sine-modulated images to achieve doubled tagging resolution. Theoretically, the multiplication of two cosine-modulated images also leads to doubled tagging resolution. However, as phase wrapping in two cosine-modulated images occurs at the same location, it is more likely that disruption from taking derivatives of incorrectly unwrapped phases will be duplicated, leading to inaccurate strain calculation. With the use of both cosine- and sine-modulated images, wrapped phase is spatially shifted by half a tagging grid. Such shift can effectively reduce the error associated with incorrect phase unwrapping, as is evident in Figure 3.

HARP method was first develop for semi-automated tracking of taglines (6). Subsequently, direct strain quantification methods was developed by calculating the pixel-wise spatial derivatives of a HARP image (9, 11). The method developed in the current study is equivalent to taking the average of the spatial derivatives of two HARP images with cosine- and sine-modulation respectively (Eq. 5). While it is possible that improving SNR of a single cosine-modulated image with doubled number of averages may improve the accuracy in strain quantification, such approach is less advantageous in handling errors in phase unwrapping for the same reason stated above. Also, the impact of prolonged acquisition on the quality of tagged image needs further investigation.

The transmural strain gradient has previously been examined in large animals by MRI tagging. It was shown in paced canine hearts that both the principal strain and the radial strain were about 50% greater in magnitude at the endocardium than those at the epicardium (21, 22). In a more recent human study using phase-contrast MRI, significantly larger endocardial radial strain was also observed in healthy humans (23). In our current study on normal C57BL/6 mice, we also observed significantly larger strain values in the sub-endocardial region. These observations suggest that while the magnitude of myocardial strain may vary among different species, transmural strain patterns are conserved from mouse to man.

The current method requires the acquisition of two tagged data sets to achieve doubled tagging resolution. It is important that heart rate is maintained constant during image acquisition, as changes in heart rate can affect image quality and strain quantification in several ways. First, the two data sets may not be acquired at the same time points during the cardiac cycle. Second, changes in heart rate are frequently accompanied by changes in contractility, rendering strain calculation inaccurate. However, as heart rate is affected by both temperature and anesthesia level, a relatively constant heart rate is achievable by carefully maintaining a physiological body temperature and appropriate anesthesia level during image acquisition.

Conclusion

In summary, a HARP-based method was developed for fast and accurate strain quantification of high-resolution tagged images using the method proposed by Stuber and colleagues (5). Previously, there has been limited application of this tagging technique due to the additional challenges of processing and integrating two separate data sets. By applying the technique to the functional characterization of mouse heart, an increased tagging resolution of 0.3 mm was achieved in the current study. Strain quantification using the current method showed significant transmural and regional differences in mouse myocardium.