Abstract
Contact activation of blood factor XII (FXII, Hageman factor) is moderated by the protein composition of the fluid phase in which FXII is dissolved. Solution yield of FXIIa arising from FXII contact with hydrophilic activating particles (fully-water-wettable glass) suspended in a protein cocktail is shown to be significantly greater than that obtained under corresponding activation conditions in buffer solutions containing only FXII. By contrast, solution yield of FXIIa arising from FXII contact with hydrophobic particles (silanized glass) suspended in protein cocktail is sharply lower than obtained in buffer. This confirms that contact activation is not specific to anionic hydrophilic surfaces as proposed by the accepted biochemistry of surface activation. Rather, contact activation in the presence of proteins unrelated to the plasma coagulation cascade leads to an apparent specificity for hydrophilic surfaces that is actually due to a relative diminution of activation at hydrophobic surfaces and an enhancement at hydrophilic surfaces. Furthermore, the rate of FXIIa accumulation in whole-plasma and buffer solution is found to decrease with time in the continuous presence of activating surfaces, leading to a steady-state FXIIa yield dependent on the initial FXII solution concentration for both hydrophilic and hydrophobic procoagulant particles suspended in either plasma, protein cocktail, or buffer. These results strongly suggest that activation competes with an autoinhibition reaction in which FXIIa itself inhibits FXII→FXIIa. Experimental results are modeled using a reaction scheme invoking FXII activation and autoinhibition linked to protein adsorption to procoagulant surfaces, where FXII activation is presumed to proceed by either autoactivation ( ) and autohydrolysis ( ) in buffer solution or autoactivation and reciprocal activation (kallikrein mediated hydrolysis) in plasma. FXII adsorption competition with other proteins in the fluid phase is proposed to affect the balance of activation and autoinhibition, leading to the observed moderation of FXIIa yield.
Keywords: Blood coagulation, FXII, Hageman factor, contact activation, autoactivation, protein adsorption
1. Introduction
Development of truly hemocompatible materials for a wide variety of cardiovascular devices remains a substantially unrealized objective of biomaterials science [1–3]. Even after decades of focused research, thrombosis remains the significant barrier to development and implementation of advanced blood-contacting medical devices [4, 5]. Clearly, an improved understanding of the events leading to thrombus formation on biomaterials is needed that will define new bioengineering routes to hemocompatibility. An approach we have taken has been to simplify the problem down to the minimum essential unit of study [6–12]. This strategy eliminates blood flow as it occurs in natural or synthetic blood conduits and further divides blood into cellular and humoral (plasma) categories.
Research into plasma-phase coagulation has focused on surface interactions with biomaterials that activate the so-called plasma coagulation cascade. This cascade is an interconnected series of self-amplifying, zymogen-enzyme conversions that penultimately produces thrombin (FIIa), a powerful serine protease. In the final step of the plasma coagulation cascade, FIIa hydrolyses fibrinogen into fibrin units that oligomerize into a fine mesh which causes plasma to gel or clot. The plasma-coagulation cascade is formally divided into two branches, the intrinsic and extrinsic pathways, that can be separately potentiated but merge into a common pathway leading to thrombin release. The extrinsic pathway is responsible for hemostatic control and response to vascular injury. The normal physiological function of the intrinsic pathway is not well understood [13, 14], but has been implicated as an important cause for poor hemocompatibility of cadiovascular biomaterials because it is triggered by contacting blood with artificial materials [15–20].
The initiating step of the intrinsic pathway is surface-contact activation of the blood zymogen FXII (Hageman factor) into an active enzyme form FXIIa ( , also termed autoactivation in the hematology literature [13]). FXII and FXIIa are central members of a self-amplifying activation complex involving the allosteric proteins prekallikrein (PK, Fletcher factor), high-molecular-weight kininogen (HMWK, Williams-Fitzgerald factor), and FXI (thromboplastin antecedent) [13]. FXII activation is thought to occur by contact or binding with material surfaces [13, 20]. The exact nature of the FXII contact/binding step is a matter of continued investigation in biomaterials surface science [7, 10], but the consensus opinion has long been that autoactivation occurs most efficiently when blood contacts “anionic” [21–23] or “hydrophilic” (water wettable) procoagulants [6–8, 10]. Specificity for anionic hydrophilic surfaces is presumed to be due to a chemically-specific binding event between FXII, HMWK, and surface-resident negative charges. A complex formed from PK, Factor XI, and surface-bound HMWK is thought to bring all factors and co-factors into reactive proximity [19, 24].
We have pursued studies of whole-plasma coagulation seeking to resolve detailed relationships among biomaterial surface chemistry, energy, and the propensity to activate the intact plasma coagulation cascade [6–12]. Results of these ‘holistic’ studies [11] have motivated us to serially simplify the focus of investigation from whole plasma, to a group of coagulation proteins, to finally purified enzymes of the cascade as a means of comparing activation of the pieces to activation of the whole [10, 11, 25]. In very brief summary, we found that potentiation of the intrinsic pathway in vitro leads to bolus release of thrombin (FIIa) in concentration proportion to the intensity of activation as measured by procoagulant surface area or surface energy (hydrophilicity, water wettability). Bolus production of FIIa suggests that the cascade somehow ‘turns off’ in the continuous presence of activating surfaces very soon after initial activation. Otherwise, continuous production of FIIa would be anticipated [10], not the punctuated release of a bolus inferred from experimental results. Autoactivation appears to be a likely point of control [21], leading us to further investigate how surface chemistry affects the reaction isolated from all other proteins. In so doing, we found the contrast between surface activation of whole plasma coagulation and FXII activation in pure-buffer solution nothing less than startling.
First, we were surprised to learn that FXII activation in neat-buffer solution (no proteins other than FXII) is not specific for anionic hydrophilic procoagulants as thought previously [25]. In fact, slightly greater FXIIa yield was measured at hydrophobic (poorly-water-wettable, silanized-glass) surfaces than at an equivalent surface area of hydrophilic (fully-water-wettable, clean glass) procoagulant surfaces. Second, we found that FXII activation in neat-buffer solution was effectively instantaneous upon contact with either hydrophilic or hydrophobic procoagulant type. Third, in sharp contrast to this second finding, we discovered that activation rate-and-yield were significantly attenuated at hydrophobic surfaces in the presence of plasma proteins, but not at hydrophilic surfaces. Finally, we found that autohydrolysis ( ) was a facile reaction in neat-buffer solution but insignificant in plasma [11, 26]. Needless to say perhaps, these new findings are quite contrary to expectations based on the traditional understanding of autoactivation biochemistry briefly outlined above.
Our collective interpretation of this new experimental evidence is that FXII activation in plasma leads to an apparent specificity for hydrophilic surfaces that is actually due to a relative diminution of the FXII→FXIIa reaction at hydrophobic surfaces, not to a real specificity for anionic/hydrophilic surfaces [25]. We speculated that depression of activation rate-and-yield at hydrophobic surfaces immersed in plasma results from a protein-adsorption competition between FXII and a host of other proteins that substantially reduced frequency of FXII-surface interactions which, in turn, reduced efficiency of activation at hydrophobic procoagulants. Presumably, little-or-no such protein-adsorption competition occurs at hydrophilic surfaces because fully-water-wettable surfaces adsorb little-or-no protein [7, 27–31]. This work confirms these speculations and elaborates our interpretation into a scheme that incorporates competitive-protein adsorption into a model of contact activation of blood coagulation.
2. Methods and Materials
2.1 Plasma and Coagulation Proteins
Citrated human platelet poor plasma (PPP) was prepared from outdated (within 2 days of expiration) lots obtained from the M.S. Hershey Medical Center Blood Bank. This work was performed with a single lot of pooled plasma aliquoted into 15 mL polypropylene tubes (Falcon, Becton Dickinson) and frozen at −20°C until use. We have observed consistent results with plasma prepared and stored in this manner over about 1 year of experimentation. Factor XII depleted plasma (12dPPP) with a dysfunctional contact activation system was used as received from George King Biomedical, Inc., Overland Park, KS (a negative control). Experience has shown that different lots of plasma yield quantitatively different but qualitatively similar results. Coagulation time of recalcified 12dPPP supplemented with 30 μg/mL FXII (physiologic concentration [32, 33]) exceeded 40 min., demonstrating that FXII used in this work was not contaminated with measurable quantities of FXIIa. Human FXII and αFXIIa were used as received from Haematologic Technologies, Inc. (Essex Junction, VT) and Enzyme Research Laboratories (South Bend, IN), respectively. αFXIIa activity was specified by the vendor in traditional units of Plasma-Equivalent-Units-per-milliliter (PEU/mL) [34]. Neat-buffer solutions of FXII and αFXIIa solutions were prepared in phosphate buffer saline (PBS, Sigma, pH=7.4).
2.2 Plasma Coagulation-Time Assay for FXIIa
Protocol for the coagulation-time assay for FXIIa applied in this work has been described in detail elsewhere [6–8, 10, 25]. Plasma coagulation time (CT) was used as the traditional hematology method [34] to quantify FXIIa in solution by appealing to an “αFXIIa titration” calibration curve that related CT to αFXIIa concentration (PEU/mL). αFXIIa titration curves in recalcified 12dPPP and PPP provided linear calibration curves when scaled on a logarithmic concentration axis [25]. αFXIIa titrations were carried out by equilibrating 0.5 mL of thawed plasma in 15×75 mm polystyrene tubes (VWR), mixing with increasing volumes of αFXIIa solution in PBS, and diluting with sufficient additional PBS to bring total volume to 900 μL. Coagulation was induced by recalcification with 100 μL of 0.1 M CaCl2 and contents were mixed on a slowly-turning hematology mixer (Roto-shake Genie, Scientific Industries, Inc.). CT after recalcification was noted by a distinct change in fluid-like rheology to gel formation, allowing determination of the end point of the coagulation process to within 10 seconds or so [6]. CT was observed to be exquisitely sensitive to αFXIIa with a minimum quantifiable concentration ~ 10−3 PEU/mL [25].
2.3 Procoagulant Surfaces
Test procoagulants applied in this work were 425–600 μm diameter glass beads (Sigma-Aldrich) in either cleaned or silanized form. Each contact-activation experiment used 100 or 30 mg of glass beads corresponding to approximately 500 or 150 mm2 surface area, respectively, based on a nominal diameter of 500 μm. Clean-glass procoagulants were prepared by 3X serial rinses in 18 MΩ water (obtained from a Millipore Simplicity unit), 2-propanol, and chloroform (reagent grade, VWR) followed by air-plasma treatment of a single layer of washed-glass beads held in a 15 mm Pyrex glass petri dish (10 min. at 100 watts plasma; Herrick, Whippany NY). Clean-glass beads were silanized by 1.5 hr. reaction with 5% v/v octadecyltrichlorosilane (OTS; United Chemical Technologies, Inc.) in chloroform. Silanized beads were 3X rinsed in chloroform and dried in a vacuum oven at 110°C for 24 hr. Contact angles of glass-slide witness samples measured by Wilhelmy balance tensiometry (CDCA-100, Camtel Ltd.) typically yielded advancing/receding contact angles 0°/0° and 110°/90° for clean and OTS-treated glass, respectively, with no more than about 10° variation among batches. Contact angles cannot be read directly on glass beads but optical microscopy of the shape of the liquid meniscus of beads partly immersed in water on a microscope slide qualitatively confirmed that the treated beads were not different from the witness samples. Test procoagulants prepared as above are referred to herein as either “hydrophilic” (clean glass) or “hydrophobic” (silanized glass) for simplicity, in full recognition of the vagaries associated with this terminology [35] for most biomedical applications [36]; as well as dispute in the literature regarding existence of hydrophilic/hydrophobic contrast in the biological response to materials [35, 37]. However, in the case of plasma coagulation in vitro, contact activation has been shown to scale very sharply with procoagulant surface energy [6, 10, 11], leading to a crisp discrimination between surface types that further justifies our choice of nomenclature.
2.4 Surface Activation of Activation of FXII in Buffer Solution and Plasma
The basic experimental strategy comparing FXII activation in neat-buffer solution (no proteins other than FXII and activation products therefrom) and PPP has been discussed in ref. [25] and was extended herein to measure FXII activation kinetics in PPP and steady-state FXII activation in buffer solutions. Putative FXIIa activity produced by timed contact with hydrophilic or hydrophobic procoagulant surfaces (“activation kinetics”) in PPP containing optional FXII spikes was quantified by measuring coagulation time of PPP directly by recalcification, using an αFXIIa titration curve to convert measured CT to apparent FXIIa activity (PEU/mL). FXII spikes were specified in multiples-of-nominal-physiologic-concentration (taken to be 30 μg/mL or 0.4 μM [13]; 1X means endogenous FXII, no exogenous spike; 1.25X means 25% exogenous spike prepared by addition of 7.5 μg/mL exogenous FXII, etc.; see column 1 of Table 1). The actual FXII concentration in the pooled human plasma used in this work was not measured. Putative FXIIa activity produced by 30 min. contact with hydrophilic or hydrophobic procoagulant surfaces (“steady-state activation”) in buffer solutions with optional protein supplement (protein cocktail) was quantified by measuring CT induced in 12dPPP, again with reference to an αFXIIa titration calibration curve. The protein cocktail was comprised of five proteins: human IgM (1000 kDa) and IgG (160 kDa) at 2 mg/mL each, human FAF and FV albumin (66 kDa) at 4 mg/mL each, bovine albumin at 4 mg/mL; yielding a total of 16 mg/mL protein added to FXII in buffer (cocktail proteins used as received from Sigma).
Table 1.
Rate Parameters Descriptive of FXII Autoactivation in Human Plasma
| Hydrophilic Procoagulant | Hydrophobic Procoagulant | |||||
|---|---|---|---|---|---|---|
| WF12o μg/mL | A ×10−3 PEU/mL·sec | B ×10−1 1/sec (%R2, N=8) | C PEU/mL×10−3 (N=4) | A ×10−3 PEU/mL·sec | B ×10−1 1/sec (%R2, N=8) | C PEU/mL×10−3 (N=4) |
| 30 (1X) (endogenous) | 1.07±0.22 | 1.43±0.29 (84.0) | 7.53±0.13 | 0 | 0 | 0.02±0.01 |
| 37.5 (1.25X) (endogenous +7.5 exogenous) | 2.63±0.42 | 2.35±0.37 (89.0) | 11.2±0.31 | 0.11±0.01 | 1.64±0.18 (92.2) | 0.66±0.05 |
| 45 (1.5X) (endogenous +15 exogenous) | 4.79±0.47 | 3.15±0.30 (94.7) | 15.2±0.28 | 0.56±0.08 | 3.00±0.39 (82.4) | 1.88±0.12 |
| 52.5 (1.75X) (endogenous +22.5 exogenous) | 4.90±0.44 | 2.94±0.24 (95.2) | 16.7±0.6 | 1.21±0.15 | 4.24±0.50 (82.5) | 2.85±0.12 |
| 60 (2X) (endogenous +30 exogenous) | 5.62±0.58 | 3.49±0.34 (93.4) | 16.1±0.6 | 1.57±0.21 | 4.54±0.60 (74.7) | 3.45±0.05 |
Notes: WF12o is the nominal FXII concentration assuming 30 μg/mL normal physiologic concentration. Procoagulants = 150 mm2 nominal surface area of water-wettable (hydrophilic) and silanized-glass (hydrophobic) particles (see Methods and Materials). Error in parameter A=B·C computed by propagation of error; error in parameter B is the standard error of the fit to Eq. 5 of Appendix I; error in parameter C the standard deviation of the mean of N=4 steady-state FXIIa concentrations (see Results).
3. Results
Figs. 1 and 2 compare contact activation of FXII dissolved in plasma and neat-buffer solutions optionally containing a protein cocktail, respectively. Activation by hydrophilic (fully-water-wettable glass particles) and hydrophobic (poorly-water wettable silanized glass particles) procoagulants were compared in these studies (see Methods and Materials for surface-preparation details and nomenclature). Experimental data was fit to a mathematical model of activation, resulting in smooth curves drawn through the data of Figs. 1 and 2. Rate parameters descriptive of FXII activation deduced from fitting the model to data are collected in Tables 1–4. The mathematical model was based on the reaction scheme of Fig. 3 that linked putative biochemical reactions involving FXII to adsorption/desorption (partitioning) of FXII and FXIIa. FXII activation in buffer solution was presumed to occur by autoactivation ( ) and autohydrolysis ( ) [25, 26] because proteins of the activation complex (PK, Factor XI, and HMWK) were purposely excluded from buffer solutions. FXII activation in plasma was presumed to occur by autoactivation and reciprocal activation [11, 38] (kallikrein mediated hydrolysis) in plasma because autohydrolysis has been shown to be inconsequential in plasma [11, 26]. All biochemical reactions were construed to occur within an “interphase” region supposed to surround procoagulant particles immersed in aqueous FXII solutions. Appendix I derives the mathematical model, identifies all important variables, and discusses assumptions employed to obtain analytic expressions that could be statistically fit to experimental data.
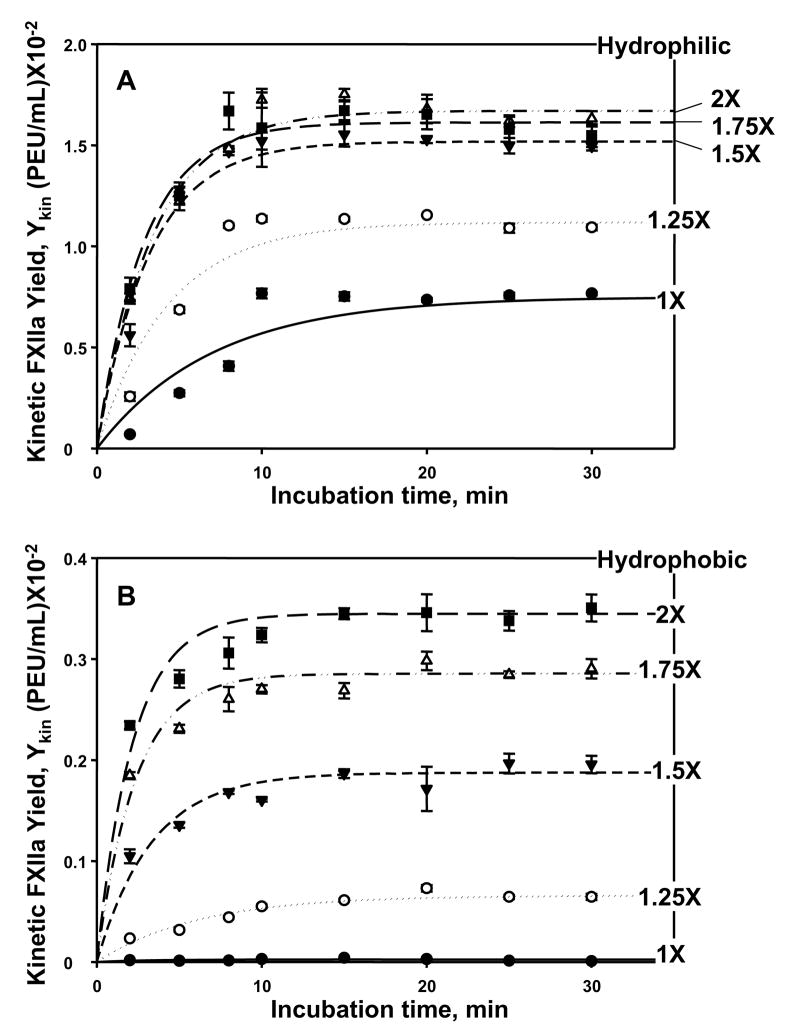
Figure 1.
FXII activation kinetics in citrated human platelet-poor plasma. Panel A, hydrophilic (fully water-wettable glass) procoagulant particles; Panel B, hydrophobic (poorly water wettable, silanized) procoagulant particles (each at 150 mm2 nominal surface area). Apparent FXIIa yield Ykin is expressed in plasma-equivalent-units-per-milliliter (PEU/mL) at varying contact (incubation) time with procoagulants, where error bars estimate uncertainty in Ykin arising from FXIIa-titration calibration curves (see Methods and Materials). Annotations express concentration of exogenous FXII spikes expressed in multiples-of-nominal physiologic concentration (taken to be 30 μg/mL; 1X means endogenous FXII, no exogenous spike; 1.25X means 25% exogenous spike prepared by addition of 7.5 μg/mL exogenous FXII, etc.; see column 1 of Table 1; filled circles = 1X, open circles = 2X, filled inverse triangles = 1.5X; open triangles = 1.75X, filled squares = 2X). Lines through the neat-buffer and protein-cocktail data represent the best fit to the mathematical model of FXII activation discussed in the text and derived in Appendix I. Note that FXIIa production rate asymptotically reaches a steady-state yield YSS at long incubation time that depends on initial FXII concentration.
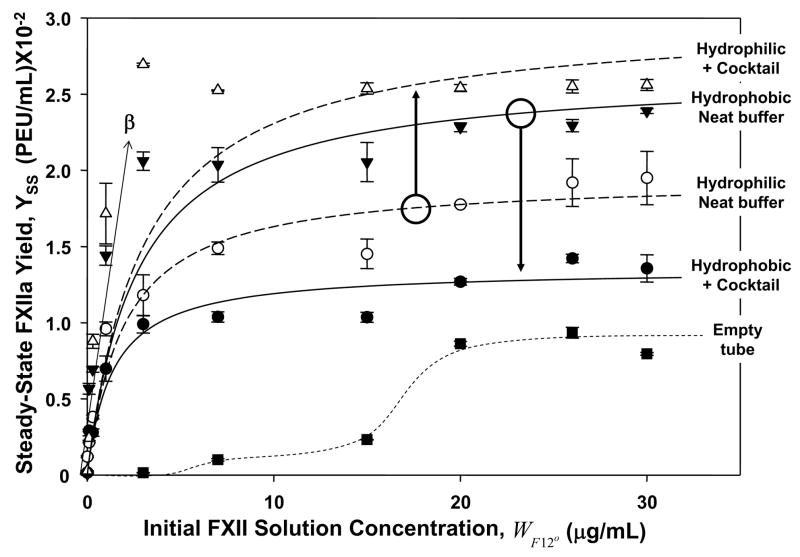
Figure 2.
Steady-state activation of FXII in neat-buffer and protein-cocktail solutions measuring FXIIa solution yield YSS (expressed in plasma-equivalent-units-per-milliliter, PEU/mL) after 30 min. contact with hydrophilic (fully water-wettable glass) procoagulant particles or hydrophobic (poorly water wettable, silanized) procoagulant particles (each at 500 mm2 nominal surface area). Annotations identify procoagulant surface type in either neat-buffer (open circles and filled inverse triangles) or protein-cocktail solution (+ cocktail; filled circles and open inverse triangles). Lines through the neat-buffer and protein-cocktail data represent the best fit to the mathematical model of FXII activation discussed in the text and derived in Appendix I. Curve marked “Empty tube” (filled squares) is a kind of negative control without procoagulant particles measuring FXII activation by contact with the polystyrene tubes used in the assay (dashed curve through the data is a guide to the eye). Initial, linear-like dependence of Yss with FXII solution concentration (μg/mL) provides a measure of the parameter β used to convert YSS in PEU/mL to FXIIa w/v solution concentration WF12a in mg/mL. Note that YSS produced by contact with hydrophilic procoagulants is significantly higher in protein-cocktail solution than neat buffer. In sharp contrast, YSS produced by contact with hydrophobic procoagulants is significantly lower in protein-cocktail solution than neat buffer.
Table 4.
Estimated Absolute and Ratio Rate Parameters Descriptive of FXII Autoactivation
| Hydrophilic | Hydrophobic | Hydrophilic/Hydrophobic Ratio | |||||||
|---|---|---|---|---|---|---|---|---|---|
| Parameter | Buffer | Cocktail | Plasma | Buffer | Cocktail | Plasma | Buffer | Cocktail | Plasma |
| ka (sec−1) | 15.2×10−3 | 5.6×10−3 | 2.7 | ||||||
| ki (mL/mgsec) | 6.3×10−3 | 15.6×10−5 | 40.4 | ||||||
| (mL/mg) | 5.1×10−1 | 3.3×10−1 | 4.1×10−1 | 3.8 ×10−3 | 7.4×10−3 | 2.7×10−2 | 134 | 44.6 | 15.2 |
| Buffer:cocktail Ratio | 1.6 | 0.5 | 3.2 | ||||||
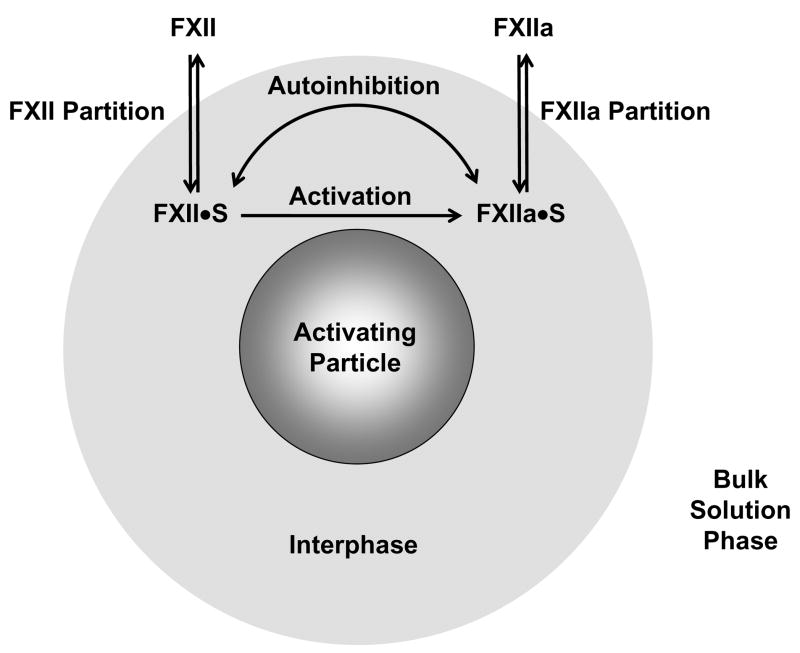
Figure 3.
Ad hoc model of FXII activation (FXII →FXIIa) at a procoagulant particle linked to FXII and FXIIa adsorption/desorption that serves as the basis for a mathematical model of activation derived in Appendix I. All biochemical reactions are proposed to occur within a vicinal “interphase” region that surrounds a procoagulant particle immersed in aqueous FXII solutions (grossly out of scale). Adsorption/desorption is a partitioning of species between interphase and bulk-solution phases indicated by the double-headed arrows labeled “FXII Partition” and “FXIIa Partition”. Partitioning establishes the interphase concentrations FXII·S and FXIIa·S that ultimately control rate and yield of FXIIa production in solution. FXII activation in buffer solution occurs by autoactivation ( ) and autohydrolysis ( ) whereas FXII activation in plasma occurs by autoactivation and reciprocal activation [11, 38] (kallikrein mediated hydrolysis). FXII activation competes with an autoinhibition reaction indicated by the double-headed curved arrow in which FXIIa itself inhibits FXII→FXIIa. Partitioning concentrates protein within the interphase of hydrophobic procoagulant particles but not within the interphase surrounding hydrophilic procoagulants. As a consequence, surface contact activation of FXII is moderated by the protein composition of the fluid phase in which FXII is dissolved (buffer, protein cocktail, or plasma).
Experimental and theoretical results are organized in this section as follows. First, FXII activation kinetics in plasma and steady-state activation in neat-buffer or protein-cocktail solutions are compared. Second, the FXII activation model used to interpret kinetic and steady-state autoactivation is described. Third, quantitative rate parameters obtained by applying this model to experimental data are compared and contrasted to derive insights into the dynamics that control FXIIa generation under various experimental conditions.
3.1 FXII Activation Kinetics in Plasma
Kinetics of FXIIa production and release into solution were slow enough in plasma to be measured using experimental methods of this work. Fig. 1 compares FXII activation induced by contact with hydrophilic (Panel A) and hydrophobic (Panel B) procoagulants (150 mm2 nominal surface area) in plasma supplemented with exogenous spikes of FXII. Annotations of Fig. 1A,B indicate different exogenous FXII concentrations used in kinetic experiments given in multiples of nominal physiologic concentration (see section 2.4). It is emphasized that activation-rate experiments reported in Fig. 1 reduced nominal procoagulant surface area from the 500 mm2 used in steady-state activation experiments (Fig. 2 and in the work reported in ref. [25]) to 150 mm2 in an attempt to slow activation rate, especially for hydrophilic procoagulants. Comparison of Fig. 1A data to that of Fig. 3B in ref. [25] revealed that this 3.3X reduction in procoagulant surface area caused ~4X decrease in initial rate (~5×10−3 PEU/mL in 10 min at 150 mm2 and 1X compared to ~ 20×10−3 PEU/mL in 10 min at 500 mm2 and 1X for hydrophilic procoagulants). Surface area reduction also caused ~3X decrease in the final FXIIa yield (7×10−3 PEU/mL at 150 mm2 and 1X compared to ~ 20×10−3 PEU/mL at 500 mm2 and 1X for hydrophilic procoagulants). A more detailed investigation would be required to be definitive about the relationship between procoagulant surface area and FXIIa activation rate/yield, but it appears from this very limited survey that rate-and-yield scale in rough proportion to procoagulant surface area.
Initial rate of FXIIa production and release into solution increased as a function of FXII solution concentration, WF12o (mg/mL), for both hydrophilic and hydrophobic procoagulants. This rate increase appeared to saturate between 1.5X and 2X exogenous FXII spikes for hydrophilic surfaces whereas the rate increase did not saturate at hydrophobic surfaces. Accumulation of FXIIa in solution asymptotically reached a plateau for all cases reported in Fig. 1, well within the 30 minutes used for steady-state activation experiments to be discussed subsequently. This maximal steady-state yield YSS (PEU/mL) was five-to-ten fold higher at the hydrophilic procoagulant surfaces than at hydrophobic procoagulants at comparable exogenous FXII spikes. Lines drawn through the data of Fig. 1 result from non-linear, least-squares statistical fitting of the Eq. (5) of Appendix I, as described further below.
3.2 Steady-State FXII Activation in Neat-Buffer and a Protein-Cocktail Solution
Kinetics of FXIIa production and release into neat-buffer or protein-cocktail solution were too rapid to be measured using experimental methods of this work [25]. Instead, the steady-state solution yield of FXIIa YSS was measured as a function of WF12o after FXII-containing solutions were continuously contacted with hydrophilic or hydrophobic procoagulants for 30 minutes. Fig. 2 compiles results of steady-state activation experiments in which FXII concentration was varied over the range 0 ≤WF12o ≤30 μg/mL. Note that YSS asymptotically increased with WF12o to a plateau near physiologic concentrations. A polystyrene (hydrophobic) test tube containing no added procoagulant particles served as a kind of negative control (see ‘Empty Tube’ in Fig. 2). Note that contact with test-tube walls was sufficient to activate FXII. Possibly, contact with tube surfaces contributes a measurable “background” to activation experiments, although it is not at all clear that activation in a tube with activator particles is a simple sum of contributions from particles and tube surfaces. Interestingly, in this latter regard, we note that the initial phase for this empty-tube control was more sigmoidal than observed in presence of activating particles (see guideline drawn through control data of Fig. 2); an outcome we tentatively attribute to poor mixing/contact of fluid contents with tube inner surface. Consequently, we are not inclined to treat the empty-tube results as a “blank” and results reported herein have not been corrected for this background activation nor was background activation specifically contemplated by the activation model of Fig. 3 and Appendix I. Lines drawn through the buffer and cocktail data of Fig. 2 result from non-linear, least-squares statistical fitting of the Eq. (8) of Appendix I, as described further below.
Experiments of Fig. 2 compared FXII activation at hydrophobic and hydrophilic procoagulants in neat-buffer solution to buffer solutions containing a protein supplement (protein cocktail; see section 2.4). Concentration of any one of these cocktail proteins was about 3 decades greater than FXII, roughly simulating the concentration differential that occurs in normal plasma [32, 33]. Otherwise, the somewhat arbitrary-selection criteria for these 5 proteins were (i) different protein types, (ii) spanning 3 decades of MW, and (iii) not being among proteins of the coagulation cascade [32]. Interestingly, YSS was significantly greater in protein-cocktail solutions than in corresponding experiments performed in neat buffer with hydrophilic procoagulant particles whereasYSS was significantly lower in protein cocktail than neat buffer for hydrophobic procoagulants (see arrow annotations of Fig. 2).
3.3 FXII Activation Model
Fig. 3 illustrates an ad hoc model used to accommodate experimental observations. The procoagulant particle (hydrophobic or hydrophilic) depicted in Fig. 3 (grossly out of scale) was construed to be surrounded by an aqueous “interphase” that separated bulk solution from the physical activating-particle surface. The interphase concept [30] has been discussed elsewhere in the context of protein adsorption [39–46]. The benefit accrued by use of an interphase model, as opposed to a more conventional 2D-surface adsorption model, was that adsorption/desorption of FXII and FXIIa could be interpreted in terms of partition coefficients (PF12 and PF12a) and surface concentrations (WF12·S and WF12a·S in mg/mL), as further discussed in Appendix I for readers interested in this level of detail.
Protein-interphase and protein-protein interactions occurring within the interphase contemplated by the model were:
FXII adsorption/desorption (partitioning between bulk phase and interphase regions).
FXII activation (FXII → FXIIa) within the interphase region.
FXIIa inhibition of FXII activation (autoainhibition) within the interphase region.
FXIIa adsorption/desorption (partitioning between bulk phase and interphase regions).
Steps (1) and (4) linked reactions (2) and (3) with protein adsorption and protein-adsorption competition. Adsorption was construed to be a partitioning of species between interphase and bulk-solution phases indicated by the double arrows labeled “FXII Partition” and “FXIIa Partition” in Fig. 3. Partitioning was assumed to be reversible within the timeframe of experimentation, achieving a microscopic equilibrium in both kinetic and steady-state activation experiments (see above and Methods and Materials).
The FXII activation step (2) was assumed to be chemically irreversible whether occurring by autoactivation, autohydrolysis, or reciprocal activation. Autoactivation was presumed to occur in proportion to procoagulant surface area [6, 8, 10, 11, 25] through an as-yet chemically-undefined reaction within the interphase. This surface-mediated reaction did not require proteolysis (as by kallikrein for example) to cleave the FXII Arg353-Val354 bond involved in FXII →FXIIa conversion [13]. At any time t, only a small fraction of FXII within the interphase (FXII·S in Fig. 3) was presumed to undergo the surface-catalyzed FXII →FXIIa that created FXIIa within the interphase region (FXIIa·S in Fig. 3; the “ ·S ” terminology is intended only to differentiate protein within the interphase from that in bulk solution and should not be interpreted as meaning “bound to the surface”). Autoinhibition of the FXII →FXIIa reaction (step 3 above) was also construed to occur only within the interphase region through an as-yet chemically-undefined interaction between FXII and FXIIa. Autoinhibition was further proposed to occur in proportion to FXIIa·S concentration (WF12a·S, mg/mL). WF12a·S included all sources of FXIIa, including amplification of autoactivation yield by autohydrolysis (buffer) or reciprocal activation (plasma). Separate consideration of individual sources of FXIIa (autoactivation, autohydrolysis, and reciprocal activation) was outside the scope of the model, which was intended only as a means of communicating the essential features of a paradigm that embraced protein adsorption and protein-adsorption competition effects in contact activation of FXII.
3.4 Mathematical Model of FXII Activation Kinetics
Appendix I derives rate equations based on the above model that were solved in terms of time-varying solution-phase yield of FXIIa Ykin (in PEU/mL, where the ‘kin’ subscript emphasizes kinetics). Parameters of the rate equations were t, WF12o, β, and the product KPF12. Time t (min) was the independent parameter in kinetic experiments (at serially-increasing initial FXII concentrations WF12o, mg/mL) whereas WF12o was the independent parameter in steady-state activation experiments (at fixed reaction time t = 30 min) discussed further below. The parameter β (in PEU/mg) was a proportionality constant that converted measured FXIIa yield in PEU/mL to FXIIa w/v solution concentrations (WF12a, mg/mL). A value for β was deduced from steady-state data as discussed below. KPF12 was the product of a rate ratio (mL/mg) and the FXII partition coefficient PF12 (dimensionless, see above and Appendix I); where ka (1/sec) was an activation rate constant and ki (mL/mg·sec) was an inhibition rate constant. Solution of the rate equation yielded an expression for Ykin that was exponentially-dampening with time. This equation was re-written in terms of grouped kinetic parameters A, B, and C. The parameter C = A/B measured Ykin at the steady-state plateau that evolved with time and was recovered from data of Fig. 1 by averaging the final four data points at t ≥ 15 min. Parameter B was recovered by non-linear least-squares fitting data to Ykin =C [1− e−Bt]. A was subsequently calculated from calculated from C and B. Table 1 compiles A, B, and C for hydrophilic and hydrophobic procoagulants. Quoted error in A resulted from propagation of error in B and C. Error in B was taken to be the standard error of the fit whereas error in C was the standard deviation of the mean. Quality of the one parameter (B) fit to the data was modest as measured by R2 (see columns 4 and 6) and error in estimated parameters was between 10–20%.
FXII-concentration-dependent kinetic parameters A, B, and C listed in Table 1 were used to calculate values for the rate parameters βka and KPF12. In agreement with Eq. (6) of Appendix I, a plot of against was found to be linear, yielding an estimate of βka from the slope. Column 2 of Table 2 collects βka with statistics of the fit (plot not shown; intercepts for hydrophilic procoagulant = (−3.0 ±1.3)×10−3 and for hydrophobic procoagulant = (−1.9 ±0.3) ×10−3 were statistically greater than zero). Similarly, as predicted by Eq. (8) of Appendix I, a plot of against was linear with a slope of kiPF12 and an intercept theoretically equal to ka. Column 3 of Table 2 collects kiPF12 with statistics of the fit (plot not shown). The intercept values were of no practical use in this work because the absolute endogenous FXII concentration in the pooled plasma used in this work was unknown, making accurate estimates of ka from the intercept where impossible to evaluate. Instead, ka was obtained from βka with β computed from steady-state activation modeling as described further below. Quality of the linear fits to the data was modest as measured by R2 (see columns 2 and 3) and error in estimated parameters was between 10–25%.
Table 2.
Rate Parameters Descriptive of FXII Autoactivation in Human Plasma
| Hydrophilic/Hydrophobic | ||||||
|---|---|---|---|---|---|---|
| Procoagulant | βka ×10−5 (%R2, N=5) | kiPF12 ×10−3 (%R2, N=5) | ||||
| Hydrophilic | 15.2±2.9 (90.3) | 6.3±1.5 (84.5) | 2.69 | 0.40 | ||
| Hydrophobic | 5.64±0.67 (95.9) | 15.6±1.9 (95.6) | ||||
Notes: Procoagulants = 150 mm2 nominal surface area of water-wettable (hydrophilic) and silanized-glass (hydrophobic) particles (see Methods and Materials). Listed error are standard errors of the fit to Eqs. 7, 8 of Appendix I.
3.5 Mathematical Model of Steady-State FXII Activation
Eq. (8) anticipated the experimental observation of Figs. 1, 2 that steady-state FXIIa yield at long reaction times was dependent on initial FXII concentration . Furthermore, Eq. (10) showed that the unknown proportionality constant β could be estimated from the initial, linear-like dependence of YSS on (see β annotation on Fig. 2). Analysis of low data (first 4 measurements within the range mg/mL for all experimental conditions of Fig. 2) led to the conclusion that β =(1.08 ±0.18) ×10−2 (R2 =73.0% with intercept (1.55 ±0.92) ×10−3). With this estimate for β in hand, YSS data of Fig. 2 was statistically fit to Eq. (8) of Appendix I using KPF12 as a single adjustable parameter. Table 3 collects KPF12 with statistics for hydrophilic and hydrophobic procoagulants under the experimental conditions listed in column 2. Quality of the one parameter fit to the data was modest as measured by R2 (see column 3) and error in KPF12 was between 5–10%.
Table 3.
Steady-State Parameters Descriptive of FXII Activation in Buffer and Protein Cocktail
| KPF12 Ratio | ||||
|---|---|---|---|---|
| Procoagulant | Experimental Condition | KPF12×10−1(%R2, N=10) | ||
| Hydrophilic | Neat Buffer | 5.13±0.24 (94.7) | 1.54 | |
| Protein Cocktail | 3.33±0.30 (83.0) | |||
| Hydrophobic | Neat Buffer | 3.78±0.33 (78.8) | 0.51 | |
| Protein Cocktail | 7.40±0.34 (94.0) | |||
Notes: Error in KPF12 is the standard error of a one parameter fit of data to Eq. 8 of Appendix I.
3.6 Interpretation of Rate Parameters for Kinetic and Steady-State Activation of FXII
Table 4 recalculates rate parameters from Tables 2 and 3 using the estimate β =0.01; further assuming PF12 =100 for hydrophobic procoagulants PF12 =1 for hydrophilic procoagulants. Assignment of PF12 =100 for hydrophobic procoagulants was based on measurements for similar-MW proteins discussed in ref. [47]. Assignment of PF12 =1 (no accumulation of protein within the interphase) for hydrophilic procoagulants was based on the observation that adsorption of blood proteins to hydrophilic surfaces used in this work cannot be detected by either tensiometry (contact angle and wettability) [27, 28, 30, 37] or the depletion method [31]. Row 7 and column 10 calculate ratios of parameters. It is important to emphasize that consideration of the data in Table 4 should bear in mind (i) that plasma results include the kallikrein-mediated (reciprocal) pathway of FXII activation that was not available in neat-buffer or protein-cocktail solutions of FXII and (ii) the activation rate constant ka includes all sources of FXIIa. Consequently, rate parameters should not be interpreted as characteristic of a single biochemical reaction.
4. Discussion
The primary experimental results of this work summarized in Figs. 1 and Fig. 2 demonstrate that:
Rate of FXIIa production induced by continuously contacting FXII in whole-plasma solution with either hydrophilic (water-wettable glass) or hydrophobic (poorly-water-wettable silanized glass) procoagulants is dependent on initial FXII concentration (Fig. 1).
Rate of FXIIa production in the continuous presence of either hydrophilic or hydrophobic procoagulants decreases with time to a steady-state FXIIa yield that scales with initial FXII concentration (Fig. 1).
FXII activation in buffer solution is not specific to anionic hydrophilic surfaces (Fig. 2).
Steady-state FXIIa yield in the continuous presence of either hydrophobic and hydrophilic procoagulants in neat-buffer and protein-cocktail solution is dependent on initial FXII concentration (Fig. 2).
Steady-state FXIIa yield in the continuous presence of either hydrophobic and hydrophilic procoagulants is dependent on the protein composition of the buffer solution in which activation is carried out (Fig. 2).
We collectively interpret these observations to be the outcome of FXII activation linked to protein-adsorption competition occurring within the surface region (interphase) surrounding procoagulant particles immersed in aqueous FXII solutions (Fig. 3). In both plasma and buffer, FXII activation is initiated by autoactivation ( ). FXIIa resulting from autoactivation is amplified by reciprocal (kallikrein mediated) activation of FXII in plasma or by autohydrolysis ( ) in buffer solution. In both plasma and buffer, autoinhibition caps the total yield of FXIIa. The ad hoc model depicted in Fig. 3 describes this overall process as an irreversible net activation reaction operating in competition with autoactivation. Mathematical solution of this model (Appendix I) quantifies parameters measuring activation and autoinhibition. Thus, the view of contact activation of FXII emerging from this work is that of a self-limiting set of interrelated physical and enzymic reactions that are not well described by coupled-enzyme reaction kinetics. Ordinary enzyme kinetics fail not only because FXII activation is inherently surface-catalyzed, but also because activation and autoinhibition are surface mediated by a protein-adsorption dynamic that moderates FXIIa rate-and-yield in a manner that is not true enzymatic inhibition or allosteric regulation. The following sections provide a more detailed interpretation of activation, autoinhibition, and the coupling with proteins adsorption at procoagulant surfaces.
4.1 Activation of FXII
Data of Fig. 2 confirms that FXII activation in buffer is not specific to anionic hydrophilic surfaces [25]. In light of the profound surface-chemical differences between anionic hydrophilic glass and hydrophobic silanized glass, similarity in FXIIa activation implies (but does not prove) that the sequence of chemical steps leading to (presumably) non-enzymatic cleavage of the FXII Arg353-Val354 bond involved zymogen activation [13] is a generic surface-mediated reaction unrelated to procoagulant surface chemistry. That is to say, FXII autoactivation readily occurs in contact with any artificial surface regardless of surface-chemistry type, where contact is meant here to mean adsorbed within the interphase region surrounding the procoagulant particle (i.e. not necessarily on the physical surface but rather in the interphase region). In this connection, it of interest to speculate that autoactivation involves surface-mediated covalent-bond breakage similar to that observed to occur in polymer-brush adsorption to various liquid and solid surfaces [48]. The model of Appendix I implements this generic surface-catalysis idea by proposing that the Arg353-Val354 bond happens to be labile only when FXII comes within close proximity of the physical surface. At any time t, only a small fraction of FXII within the interphase region (FXII ·S in Fig. 3) finds itself in such a proximity that is conducive to bond cleavage.
Before leaving the subject of autoactivation, it is important to stress that enzymatic (rather than physical) cleavage of the FXII Arg353-Val354 bond by ultra-trace FXIIa contamination of FXII stocks used in this work cannot be rigorously ruled out. That is to say, the hypothesis that autoactivation is really surface-catalyzed autohydrolysis due to the inevitable presence of vanishingly-small quantities FXIIa cannot be confidently eliminated (one cannot logically prove something does not exist) solely on the basis that FXII used in this work fails to induce coagulation of Factor XII-depleted plasma (see Methods and Materials and ref. [25]). Indeed, the lack of surface-chemical specificity observed in FXII activation in neat-buffer solutions would seem, on the face of it, to support a trace-FXIIa argument and autohydrolysis has been shown to be a facile reaction in buffer solutions (but not plasma) [26]. However, we are unable to rationalize all experimental observations by simply invoking FXIIa contamination; especially the added protein effect and kinetic saturation of FXIIa yield in both plasma and buffer solution. Rather, a minimum of two competing reactions, FXII activation and autohydrolysis, seem to be required to accommodate all experimental outcomes. Thus, the basic argument of this paper that two competing reactions control the extent of FXII contact activation would not be altered by the finding that autoactivation has enzymatic rather than physical origin. However activation of FXII is actually initiated, production of FXIIa is presumably amplified by reciprocal activation in plasma or autohydrolysis in buffer. The rate constant ka employed in the mathematical model of activation (Appendix I) measures the efficiency of the overall FXII →FXIIa reaction and embraces all factors involved in production of FXIIa, including autohydrolysis and reciprocal activation.
4.2 Autoinhibition
Self-limiting production of FXIIa in plasma and buffer, combined with the observation that FXII activation in neat-buffer solution nearly instantly produces a bolus concentration of FXIIa [25], strongly suggests that FXII→FXIIa in plasma and buffer solution is moderated by an autoinhibition reaction wherein FXIIa itself inhibits production of FXIIa. Otherwise, continuous FXIIa production in the continuous presence of activating particles would be anticipated, not the observed rise in FXIIa solution concentration with time to a steady-state level that is dependent on initial FXII concentration. Although an inhibitory role for antagonists such as C1, α-macroglobulin, ATIII cannot be ruled out in plasma, it is clear that FXII and derivatives thereof (FXIIa, FXIIf, etc.) are the only inhibitory alternatives in buffer solutions that purposely excludes all other proteins directly involved in plasma coagulation.
Degradation of FXIIa into forms with no coagulation activity does not explain results of Fig. 1 and 2. Although α-FXIIa is known to degrade into fragments such as FXIIf, these fragments retain coagulant activity [13, 14, 49] and would contribute to the apparent FXIIa activity measured by assays employed in this work. Further break down of FXIIa into fragments smaller than FXIIf without coagulant activity appears to require presence of proteases (such as kallikrein) [49], which are conspicuously absent in the simple FXII-buffer system.
We further argue that irreversible FXIIa adsorption to procoagulant surfaces cannot be solely responsible for inhibition of the FXII→FXIIa reaction on three basic counts. First and foremost, FXIIa is clearly not lost to either hydrophilic or hydrophobic procoagulant surfaces. Otherwise, no FXIIa activity would be observed in solutions containing procoagulants, especially procoagulants immersed in dilute FXII solutions (Fig. 2) that are well below surface-saturating protein concentrations (2–3 mg/mL; see also Appendix II). Second, it is experimentally observed that active FXIIa can be rinsed from both hydrophilic and hydrophobic procoagulant surfaces (although FXIIa appears to be more strongly adsorbed to hydrophobic surfaces) [25]. Third and finally, the FXII→FXIIa reaction appears to be similarly inhibited at both hydrophilic (not protein adsorbent) and hydrophobic (protein adsorbent) procoagulant surfaces (see refs. [39, 40, 43, 44] for adsorption properties of FXII and FXIIa and ref. [31] regarding protein adsorption as a function of surface energy). If irreversible FXIIa adsorption was indeed the moderating factor, then little-or-no inhibition would have been expected at hydrophilic surfaces, and data of Figs. 1 and 2 testify that this was not the case.
The model of Fig. 3 implements autoinhibition by asserting that increasing FXIIa·S concentration increasingly inhibits the FXII →FXIIa reaction occurring within the interphase region. The model of Appendix I incorporates autoinhibition by proposing that inhibition occurs in proportion to FXIIa concentration within the interphase, WF12a·S. As WF12a·S increases due to FXII activation so does autoinhibition, progressively leading to a cap on the amount of FXIIa that can be produced. The rate constant ki measures autoinhibition efficiency of and embraces all factors that affect inhibition.
4.3 Moderation by Competitive-Protein Adsorption
Experimental finding (v) above confirms an important role for proteins unrelated to the plasma coagulation cascade in moderating FXIIa yield in buffer solution and plasma. Using steady-state activation of FXII in pure-buffer solution as a standard of reference (Fig. 2), (v) demonstrates an ‘added-protein effect’ that increases FXIIa yield at hydrophilic procoagulant surfaces and decreases FXIIa yield at hydrophobic procoagulant surfaces. Clearly, cocktail proteins affect FXII activation in opposite directions for these two procoagulant surface types with effectively opposite water-wetting (surface energy) and protein-adsorption characteristics (see refs. [39, 40, 43, 44] for more discussion of protein adsorption).
Early studies reported inhibition of FXII binding to anionic surfaces by plasma proteins and that FXII activation was relatively inefficient in the presence of plasma [50]. However, these observations were not pursued using different procoagulant surface chemistries. Apparently, implications of these results were lost in the formulation of what has become the standard paradigm of contact activation. Inhibition of the FXII→FXIIa reaction by IgG and albumin has also been reported in the literature (see ref. [14] and citations therein), but no tangible explanation for such inhibition in molecular terms has been proffered. We observe opposite effects for hydrophilic and hydrophobic surfaces in protein cocktail, demonstrating that presence of IgG and albumin are not exclusively inhibitory. Thus, rather than attributing the added-protein effect to catalysis in the hydrophilic-procoagulant case and inhibition in the hydrophobic-procoagulant case, we propose that competitive-protein adsorption acts in opposite directions for these two different surface types, leading to an apparent specificity for hydrophilic surfaces that is actually due to a relative diminution of the FXII→FXIIa reaction at hydrophobic surfaces.
Fig. 3 proposes that the primary control points where protein adsorption affects FXIIa yield is protein partitioning between the interphase and bulk-solution phase. FXIIa yield is mediated by FXII partition because adsorption (partition into the interphase) feeds the FXII →FXIIa reaction and FXIIa desorption (partitioning out of the interphase region) produces detectable solution-phase FXIIa. Partitioning thus controls interphase concentrations WF12·S and WF12a·S which, in turn, mediate autoinhibition.
FXII and FXIIa adsorption is highly favored at hydrophobic surfaces over hydrophilic surfaces. The partition coefficients PF12 ≈ PF12a~100 at hydrophobic surfaces (interphase concentration is 100 fold larger that bulk concentration; WF12·S ~ 100WF12 and WF12a·S ~ 100WF12a). By contrast, PF12 ≈ PF12a~1 at hydrophilic surfaces (interphase and bulk-solution concentrations are approximately the same; WF12·S ~ WF12 and WF12a·S ~ WF12a). See refs. [39, 40, 43, 44] for more discussion of protein adsorption. According to the model of Fig. 3, increased FXII adsorption at hydrophobic procoagulants increases FXII-surface interactions and hence FXIIa yield. But this the same factor retards FXIIa desorption and reduces FXIIa release into solution, which increases WF12a·S thereby increasing efficiency of autoinhibition. By contrast, neither FXII adsorption nor FXIIa desorption is favored at hydrophilic surfaces (PF12≈ PF12a~1) and interphase concentrations approximate solution concentrations.
4.4 Qualitative Interpretation of FXII Activation
It is of interest at this juncture to use the model of Fig. 3 to qualitatively interpret the similar FXIIa yields obtained by activating FXII in neat-buffer-solution with equal surface area of hydrophilic or hydrophobic procoagulants (Fig. 2 and ref. [25]). According to the above, adsorption at hydrophobic surfaces increases WF12·S 100-fold over that at hydrophilic surfaces, which accelerates the FXII → FXIIa reaction. This enhancement is nearly counter balanced by the combined opposing effects of increased autoinhibition and the enhanced FXIIa adsorption affinity that resists FXIIa desorption into solution, leading to similar FXIIa yields at hydrophilic and hydrophobic procoagulant surfaces. It follows from this argument that FXII activation at hydrophobic surfaces would be much higher than at hydrophilic surfaces were it not for these latter compensating effects. Furthermore, any factor affecting FXII adsorption (or FXIIa desorption) would significantly affect FXIIa yield at hydrophobic procoagulants.
The model further explains that FXIIa yields are decreased at hydrophobic surfaces immersed in protein cocktail (relative to the neat-buffer solution, see Fig. 2) because these added proteins (at relatively high concentrations) effectively compete with FXII for adsorption to hydrophobic procoagulant surfaces. FXII adsorption to hydrophobic procoagulant surfaces is thus significantly blocked by competing proteins, efficiency of FXII contacts are sharply diminished, and FXIIa production is commensurately reduced. Increased FXIIa at yield hydrophilic procoagulants immersed in protein cocktail is interpreted to be due to the presence of “diluent” proteins that separate FXII ·S and FXIIa·S molecules and decrease efficiency of autoinhibition.
Thus the overall qualitative proposition is that total FXIIa yield at a particular procoagulant surface depends on a balance between activation and autoinhibition reactions that are, in turn, moderated by the total protein composition and concentration of the fluid phase in which FXII is dissolved. Quantitative resolution of these relationships is critically dependent on the availability of clear biochemical mechanisms for putative autoactivation/autoinhibition reactions and a complete understanding of protein adsorption from multi-component biological milieu. At this writing, autoactivation is a rather mysterious surface-mediated reaction and there is apparently no biochemical mechanism available for autoinhibition. Moreover, the physical chemistry of competitive-protein adsorption is as-yet understood only at a very rudimentary level (see refs. [41, 51] for more discussion). In lieu of this specialized knowledge, however, some quantitative insights into how activation and autoinhibition reactions are controlled by protein adsorption can be obtained from the mathematical model discussed below.
4.5 Mathematical Model of FXII Activation
Table 4 collects nominal estimated values for rate parameters descriptive of FXII activation in buffer, protein cocktail, and whole plasma. Accuracy of these parameters is critically dependent on the veracity of unverified assumptions used in calculation (see Results section) and the extent to which the highly-simplified activation model discussed above simulates the complex reality of FXII activation in buffer and plasma solution. Consequently, Table 4 should be considered only as a relative measure of the impact of different experimental conditions. Bearing this caveat in mind, inspection of row 4 reveals that the net activation rate constant ka for hydrophilic procoagulants in plasma was 2.7X larger than that for hydrophobic procoagulants, reflecting the substantially greater FXIIa yield obtained by activating plasma with hydrophilic surfaces. However, from row 5, it is apparent that ki for the hydrophilic procoagulant was 40X greater than for the hydrophobic procoagulant, indicating that autoinhibition at hydrophobic surfaces immersed in plasma was a substantially less important reaction than at hydrophilic surfaces. As qualitatively discussed above, we interpret these effects in terms of protein-adsorption at hydrophobic surfaces that is not significant at a hydrophilic surface. Protein crowding at the hydrophobic surface not only reduces efficiency of FXII-surface contacts (reduced ka relative to the hydrophilic case) but also separates adsorbed FXIIa molecules so that efficiency of autoinhibition is commensurately reduced (lower ki relative to the hydrophilic case).
Row 6 of Table 4 compares ratios obtained in neat-buffer, protein cocktails, and plasma. Within a class of procoagulant, values corresponding to buffer and cocktail were of similar magnitude. However, for hydrophilic procoagulants were 134X and 45X larger than for hydrophobic procoagulants (compare columns 8, 9 of row 6). Unfortunately, it is not possible to unambiguously interpret changes in ratios in terms of absolute values. However, in view of the plasma results above suggesting that ki is very sensitive to protein adsorption, we are inclined to suspect that reduced at hydrophobic surfaces is due to protein crowding at the hydrophobic surface that separates adsorbed FXIIa molecules and drastically reduces autoinhibition efficiency (sharply reduced ki). Similar conclusions can be drawn from plasma results, except that this effect is not as pronounced.
It is of further interest in the context of Table 4 to compare activation results in neat-buffer solution to the protein cocktail within a class of procoagulants. From row 7 it is evident that decreases upon addition of cocktail proteins at hydrophilic surface whereas increases at the hydrophobic surface, accounting for the increased FXIIa yield with added protein at hydrophilic surfaces and the decreased yield at hydrophobic surfaces (see Fig. 2). Again, it is not possible to unambiguously interpret ratios, but our interpretation here is that the relative values are predominately due to a decrease in ka at hydrophobic surfaces due to a crowding effect that reduces efficiency of FXII-surface contacts.
4.6 Implications for Contact Activation of Blood Coagulation
We conclude that contact activation of FXII occurs through a self-limiting set of interrelated physical and enzymic reactions that are moderated by protein adsorption to activating surfaces. In particular, we conclude that autoinhibition is responsible for capping the amount of FXIIa produced at procoagulant surfaces [10, 23]. Even so, autoinhibition cannot alone be responsible for the discontinuous activation of the blood-plasma coagulation cascade mentioned in the Introduction that leads to bolus production of thrombin [10]. For some as-yet unknown reason, the continuous presence of enzymatically-active FXIIa in plasma does not lead to continuous activation of subsequent steps of the plasma coagulation cascade. Apparently, other reactions of the plasma coagulation cascade downstream of autoactivation are subject to some form of inhibition that limits zymogen-enzyme conversion in a peculiar proportionality to activation stimulus.
5. Conclusions
Contact activation of blood factor XII (FXII) is not specific for anionic hydrophilic surfaces and is moderated by the protein composition of the fluid phase in which FXII is dissolved. FXII activation in the presence of proteins unrelated to the plasma coagulation cascade leads to an apparent specificity for hydrophilic surfaces that is actually due to a relative diminution of the FXII→FXIIa reaction at hydrophobic surfaces and an enhancement at hydrophilic surfaces. FXII activation in plasma or buffer solution in vitro produces a FXII-concentration-dependent, steady-state FXIIa yield through a competition between activation and autoinhibition. These results require a reassessment of how the intrinsic pathway of blood-plasma coagulation processes procoagulant stimulus and provokes a revision of the standard understanding of hemocompatibility.
Acknowledgments
This work was supported, in part, by the National Institute of Health PHS 2 R01 HL069965-05A1. Authors appreciate additional support from the Materials Research Institute and Departments of Bioengineering and Materials Science and Engineering, Penn State University.
Appendix I - Ad Hoc Model of Contact Activation of FXII
The reaction scheme diagrammed in Fig. 3 is phenomenological in that it attempts to account for experimental observations but does not provide specific chemical/biochemical reaction mechanisms accounting for surface-catalyzed conversion of FXII to FXIIa or mediation of the FXII→FXIIa reaction by autoinhibition. Protein-surface and protein-protein interactions embraced by the model are described in section 3.3. These interactions are construed to occur within an ‘interphase’ that surrounds a procoagulant particle, separating bulk solution from the physical adsorbent surface. This underlying concept is not itself new to surface science but has not been widely applied to the protein adsorption problem [30]. Thinking about protein adsorption in this way leads to a fresh perspective that helps interpret protein-adsorption effects in contact activation of coagulation.
The interphase has a finite volume VIi hypothetically consists of Mi integer slabs (layers) each with thickness δi, the characteristic size of the ith protein molecule under study (in cm); where the subscript “i” is carried to remind that these parameters are specific to a particular protein. The total interphase thickness (in cm) is Ωi = Miδi and volume VIi = AΩi = AMiδi (in cm3); where A is the adsorbent surface area (cm2) and Mi slabs may be fully or partially filled. Protein adsorbs from bulk solution into the interphase to an extent dictated by a partition coefficient Pi that measures adsorption avidity to the adsorbent under study; Pi ≡WIi/WBi (dimensionless); where WIi is protein w/v concentration within the interphase I and WBi is the corresponding bulk-solution concentration (both in mg/mL). The interphase is found to have a finite weight-concentration (not molar) capacity for protein (mg/mL) [40]. is characteristic of the adsorbent but not adsorbing protein or proteins because the energetics of interphase dehydration (displacement of water by adsorbing protein) caps the total amount of protein that can adsorb [40, 47]. This cap depends, in turn, on the energetics of water-adsorbent interactions as measured by adsorbent-surface water-wettability (for “ordinary” materials that do not bear specialized immobilization chemistries, specific biochemical ligands, or permanent ion-exchange charges; see ref. [52] for more discussion of surface types). Surface saturation occurs at the bulk-phase concentration . Increasing solution concentration above does not increase the amount of protein adsorbed because the interphase is saturated with adsorbate at .
Under experimental conditions employed herein, FXII (and thus FXIIa) is at least 3 decades below surface-saturating bulk-solution concentrations (see refs. [39, 40, 43, 44] for more discussion and adsorption properties of FXII and FXIIa). That is to say, at μg/mL, the procoagulant surface is not saturated with adsorbed protein (either FXII or FXIIa) and, as a consequence, FXII and FXIIa do not participate in adsorption competition for limiting space within the surface region [41] (i.e. FXII and FXIIa adsorb without positive or negative cooperativity [47]). Adsorption/desorption of FXII and FXIIa (interactions 1 and 4 of section 3.3) are therefore presumed to be governed by partition coefficients and ; where WF12·S and WF12a·S are the instantaneous w/v concentrations (mg/mL) within the interphase region sketched in Fig. 3, WF12 and WF12aare instantaneous bulk-solution concentrations (also mg/mL).
The focus of the autoactivation model is α, the fraction conversion of FXII ·S to FXIIa·S:
| (1) |
where the approximation of Eq. (1) incorporates the experimental observation that activation converts only a small amount of FXII to FXIIa [25], as further supported by mathematical modeling of plasma coagulation [11]. It is of further interest at this juncture to use partition coefficients to convert interphase concentrations to measurable bulk solution concentrations:
| (2) |
Here the approximation makes use of the experimental observations that interfacial energetics of FXII adsorption to hydrophobic surfaces are not measurably different from that of FXIIa [39, 40, 43, 44], implying that PF12 ≈ PF12a. We also note in this connection that partition coefficients vary only slightly among proteins of similar molecular weight [39, 43, 47]. Thus, according to Eq. (2), the weight-concentration ratio within the interphase is not too different from that in the bulk-solution phase.
The kinetic model proposes that α increases with time t in proportion to the fraction of FXII ·S that has not converted to FXIIa·S, (1 − α). At the same time, autoinhibition increases with increasing FXIIa·S concentration which, according to Eq. (2), is WF12a·S = αWF12·S. These two processes operating in opposition lead to the familiar supply-demand (source-sink) kinetics of Eq. (3):
| (3) |
where ka is an activation rate constant and ki is an inhibition rate constant. The approximation of Eq. (3) makes use of the fact that the depletion of FXII from solution by adsorption and activation is a small portion of the initial concentration so that (not much of the initial mass of FXII is consumed by adsorption/activation from plasma solutions so that WF12·S is effectively a constant at any given . This statement is further justified in Appendix II as it relates to adsorption and relies on the aforementioned experimental observation that autoactivation converts only a small amount of FXII to FXIIa. Solution of Eq. (3) with the boundary condition α(t → 0)=0 leads to a dampening exponential rise in α:
| (4) |
Eq. (4) is not experimentally useful in its current form because α is not directly measured by the coagulation assay for FXIIa and, furthermore, the measure yield Y is in units of enzyme activity, PEU/mL, not mg/mL. However, Eq. (2) can be used to convert α to mass ratio and, assuming that enzyme activity is directly proportional to FXIIa weight concentration such that Y = βWF12a, then Eq. (4) becomes:
| (5) |
where the grouped parameters A and B are adjustable parameters for non-linear, least-squares fitting to kinetic (Ykin vs. time) data. Eq. (5) can be used to derive expressions for the initial rate and steady-state FXIIa yield by taking short- and long-time limits, respectively:
| (6) |
| (7) |
| (8) |
where has been used to collect the unknown rate constants into a single adjustable parameter KPF12 for non-linear, least-squares fitting to steady-state data. It follows from Eq. (7) that the unknown factor βka can recovered from the slope of a plot of A as a function of . Likewise, the unknown parameter kiPF12 can be obtained from the slope of plotted as a function .
It is observed experimentally that YSS asymptotically reaches a constant maximum value at large (Fig. 2). This observation implies that under these conditions such that . Eq. (8) can be thus rewritten in terms of :
| (9) |
In turn, Eq. (9) can be solved for the unknown β factor:
| (10) |
from which it is evident that at low where . Thus, β is approximately proportional to YSS at low and can be estimated from the linear-like initial rise in YSS observed in steady-state activation of FXII (Fig. 2).
Appendix II – Solution Depletion of FXII by Adsorption
Mass balance equations for solution depletion of proteins by adsorption have been developed in ref. [47] and applied to adsorption competition among a mixture of proteins for the same adsorbent surface in ref. [51]. Mass balance insists that the depletion Di of any particular protein i adsorbed to an adsorbent immersed in purified solution is simply the loss of solution concentration such that ; where the interphase volume VIi is well defined in terms of the molecular dimensions protein i, VB is the volume of the bulk-solution phase from which protein i adsorbs and is the initial bulk-solution concentration. The depletion can be written explicitly in terms of interphase volumes and partition coefficients using the definition :
| (11) |
where the approximation corresponds to the situation when the bulk-solution volume greatly exceeds the product PiVIi, as will be seen to be the case for this work (VB =1 mL, see Methods and Materials).
The interphase volume for FXII can be roughly estimated from VIi = AΩ = AMδ; where A is the interfacial area (cm2) and M is an integer number of slabs that may be fully or partially occupied by adsorbed protein, and δ is the characteristic size of the protein molecule [40, 51]. Interpolating from experimental measurement of adsorbed-layer thicknesses [40, 51], it is anticipated that M =1for FXII. Globular protein molecules exhibit a core-protein radius rv =6.72×10−8MW1/3 (packing-volume radius in cm for MW expressed in kDa; see refs. [53–59] for basic information regarding spherical dimensions and molecular packing of proteins). Together with a hydration shell that causes proteins to pack with an effective (hydrodynamic) radius 1.3rv[40], the characteristic size (diameter) of a protein is δ = 2·1.3rv. Thus, using MW= 78 kDa for FXII, Therefore, the estimated interphase volume for 500 mm2 =5 cm2 activator surface area adsorbing a single layer of FXII is VIi =(7.5×10−7 cm)(5 cm2)=3.7×10−6 cm3 =3.7 nL, which is negligible relative to VB in Eq. (11). Taking Pi =100 for FXII (see ref. [47] for justification), an estimated from Eq. 9 that or about 0.04%, which is roughly consistent with estimates for albumin adsorbed to hydrophobic surfaces [39]. Thus, it is concluded that FXII is not significantly depleted by adsorption to low-surface-area activator surfaces, either from purified buffer solution or complex mixtures such as plasma, even when initial solution concentrations are very dilute. The reason is that the proportionality constant that relates depletion to is quite small.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Citations
- 1.Anderson RN, Minino AM, Hoyert DL, Rosenberg HM. In: National Vital Statistics Reports. Control CfD., editor. 2001. pp. 1–32. [PubMed] [Google Scholar]
- 2.Guzzo M. Medical Device Firms Focus on Cardiac, Respiratory Care. Pittsburgh Business Times. 2004 June;:4. [Google Scholar]
- 3.Lysaght MJ, O’Loughlin JA. Demographic Scope and Economic Magnitude of Contemporary Organ Replacement Therapies. ASAIO Journal. 2000 September/October;46(5):515–21. doi: 10.1097/00002480-200009000-00001. [DOI] [PubMed] [Google Scholar]
- 4.Rose EA, Gelijns AC, Moskowitz A, Heitjan DF, Stevenson LW, Dembitsky W, et al. Long-term Use of a Left Ventricular Assist Device for End-Stage Heart Failure. N Engl J Med. 2001;345(20):1435–43. doi: 10.1056/NEJMoa012175. [DOI] [PubMed] [Google Scholar]
- 5.Lavine M, Roberts M, Smith O. Bodybuilding: The Bionic Human. Science. 2002;295:995–1032. [Google Scholar]
- 6.Vogler EA, Graper JC, Harper GR, Lander LM, Brittain WJ. Contact Activation of the Plasma Coagulation Cascade.1. Procoagulant Surface Energy and Chemistry. J Biomed Mat Res. 1995;29:1005–16. doi: 10.1002/jbm.820290813. [DOI] [PubMed] [Google Scholar]
- 7.Vogler EA, Graper JC, Sugg HW, Lander LM, Brittain WJ. Contact Activation of the Plasma Coagulation Cascade.2. Protein Adsorption on Procoagulant Surfaces. J Biomed Mat Res. 1995;29:1017–28. doi: 10.1002/jbm.820290814. [DOI] [PubMed] [Google Scholar]
- 8.Vogler EA, Nadeau JG, Graper JC. Contact Activation of the Plasma Coagulation Cascade. 3. Biophysical Aspects of Thrombin Binding Anticoagulants. J Biomed Mat Res. 1997;40(1):92–103. doi: 10.1002/(sici)1097-4636(199804)40:1<92::aid-jbm11>3.0.co;2-m. [DOI] [PubMed] [Google Scholar]
- 9.Zhuo R, Colombo P, Pantano C, Vogler EA. Silicon Oxycarbide Glasses for Blood-Contact Applications. Acta Biomaterialia. 2005;1:583–9. doi: 10.1016/j.actbio.2005.05.005. [DOI] [PubMed] [Google Scholar]
- 10.Zhuo R, Miller R, Bussard KM, Siedlecki CA, Vogler EA. Procoagulant Stimulus Processing by the Intrinsic Pathway of Blood Plasma Coagulation. Biomaterials. 2005;26:2965–73. doi: 10.1016/j.biomaterials.2004.08.008. [DOI] [PubMed] [Google Scholar]
- 11.Guo Z, Bussard K, Vogler EA, Siedlecki CA. Mathematical Modeling of Material-Induced Blood Plasma Coagulation. Biomaterials. 2006;27:796–806. doi: 10.1016/j.biomaterials.2005.06.021. [DOI] [PubMed] [Google Scholar]
- 12.Miller R, Guo Z, Vogler EA, Siedlecki CA. Plasma Coagulation Response to Surfaces with Nanoscale Heterogeneity. Biomaterials. 2006;27:208–15. doi: 10.1016/j.biomaterials.2005.05.087. [DOI] [PubMed] [Google Scholar]
- 13.Colman RW, Schmaier AH. Contact System: A Vascular Biology Modulator With Anticoagulant, Profibrinolytic, Antiadhesive, and Proinflammatory Attributes. Blood. 1997;90(10):3819–43. [PubMed] [Google Scholar]
- 14.Fuhrer GGM, Heller W, Hoffmeister HE. FXII. Blut. 1990 Nov;61(5):258–66. doi: 10.1007/BF01732874. [DOI] [PubMed] [Google Scholar]
- 15.Colman RW, Scott CF, Schmaier AH, Wachtfogel TT, Pixley RA, Edmunds LH. Initiation of Blood Coagulation at Artificial Surfaces. Annals New York Academy of Sciences. 1987;516:253–67. doi: 10.1111/j.1749-6632.1987.tb33046.x. [DOI] [PubMed] [Google Scholar]
- 16.Cadena RAD, Wachtfogel YT, Coleman RW. Contact Activation Pathway: Inflammation and Coagulation. In: Colman RW, Hirsh J, Mardner BJ, Salzman EW, editors. Hemostasis and Thrombosis: Basic Principles and Clinical Practice. 3. Philadelphia: J. B. Lippincott; 1994. [Google Scholar]
- 17.Colman RW, Marder VJ, Salzman EW, Hirsh J. Overview of Hemostasis. In: Colman RW, Marder VJ, Salzman EW, Hirsh J, editors. Hemostasis and Thrombosis: Basic Principles and Clinical Practice. 3. Philadelphia: J.B. Lippincott Company; 1994. pp. 3–18. [Google Scholar]
- 18.Pokhilko AV, Ataullakhanov FI. Contact Activation of Blood Coagulation: Trigger Properties and Hysteresis Hypothesis Kinetic Recognition of Foreign Surfaces upon Contact Activation of Blood Coagulation: A Hypothesis. J Theor Biol. 1998;191:213–9. doi: 10.1006/jtbi.1997.0584. [DOI] [PubMed] [Google Scholar]
- 19.Colman RW. Contact Activation Pathway: Inflammatory Fibrinolytic, Anticoagulant, Antiadhesive, and Antiangiogenic Activities. In: Colman RW, Marder VJ, Hirsh J, Clowes AW, editors. Hemostasis and Thrombosis: Basic Principles and Clinical Practice. 4. Philadelphia: J.B. Lippincott Company; 2000. pp. 103–21. [Google Scholar]
- 20.Samuel M, Pixley R, Villanueva M, Colman R, Villanueva G. Human factor XII (Hageman factor) autoactivation by dextran sulfate. Circular dichroism, fluorescence, and ultraviolet difference spectroscopic studies. J Biol Chem. 1992 September 25;267(27):19691–7. [PubMed] [Google Scholar]
- 21.Mitropolos KA. High affinity binding of factor XIIa to an electronegative surface controls the rates of factor XII and prekallikrein activation in vitro. Thrombosis Research. 1999;94:117–29. doi: 10.1016/s0049-3848(98)00207-2. [DOI] [PubMed] [Google Scholar]
- 22.Mitropoulos KA. The Levels of FXIIa Generated in Hyman Plasma on an Electronegative Surface are Insensitive to Wide Variation in the Concentration of FXII, Prekallikrein, High Molecular Weight Kininogen or FXI. Thromb Haemost. 1999;82:1033–40. [PubMed] [Google Scholar]
- 23.Mitropoulos KA. High Affinity Binding of Factor FXIIa to an Electronegative Surface Controls the Rates of Factor XII and Prekallikrein Activation in vitro. Thrombosis Research. 1999;94:117–29. doi: 10.1016/s0049-3848(98)00207-2. [DOI] [PubMed] [Google Scholar]
- 24.Saito H, Kojima T. Factor XII, Prekallikrein, and High-Molecular-Weight Kininogen. In: High KA, Roberts HR, editors. Molecular Basis of Thrombosis and Hemostasis. New York: Marcel Dekker; 1995. pp. 269–85. [Google Scholar]
- 25.Zhuo R, Siedlecki CA, Vogler EA. Autoactivation of Blood Factor XII at Hydrophilic and Hydrophobic Surfaces. Biomaterials. 2006;27:4325–32. doi: 10.1016/j.biomaterials.2006.04.001. [DOI] [PubMed] [Google Scholar]
- 26.Zhuo R, Vogler EA. Practical Application of a Chromogenic FXIIa Assay. Biomaterials. 2006;27:4840–5. doi: 10.1016/j.biomaterials.2006.05.008. [DOI] [PubMed] [Google Scholar]
- 27.Vogler EA. Practical Use of Concentration-Dependent Contact Angles as a Measure of Solid-Liquid Adsorption II: Experimental Aspects. Langmuir. 1992;8:2013–20. [Google Scholar]
- 28.Vogler EA, Martin DA, Montgomery DB, Graper JC, Sugg HW. A Graphical Method for Predicting Protein and Surfactant Adsorption Properties. Langmuir. 1993;9:497–507. [Google Scholar]
- 29.Vogler EA. Interfacial Chemistry in Biomaterials Science. In: Berg J, editor. Wettability. New York: Marcel Dekker; 1993. pp. 184–250. [Google Scholar]
- 30.Vogler EA. Structure and Reactivity of Water at Biomaterial Surfaces. Adv Colloid and Interface Sci. 1998;74(1–3):69–117. doi: 10.1016/s0001-8686(97)00040-7. [DOI] [PubMed] [Google Scholar]
- 31.Noh H, Vogler EA. Volumetric Interpretation of Protein Adsorption: Mass and Energy Balance for Albumin Adsorption to Particulate Adsorbents with Incrementally-Increasing Hydrophilicity. Biomaterials. 2006;27:5801–12. doi: 10.1016/j.biomaterials.2006.08.005. [DOI] [PubMed] [Google Scholar]
- 32.Anderson NL, Anderson NG. The Human Plasma Proteome: History, Character, and Diagnostic Prospects. Molecular and Cellular Proteomics. 2002;1(11):845–67. doi: 10.1074/mcp.r200007-mcp200. [DOI] [PubMed] [Google Scholar]
- 33.Saito H, Ratnoff ODJP. Radioimmunoassay of human Hageman factor (factor XII) Journal of Laboratory and Clinical Medicine. 1976 Sep;88(3):506–14. [PubMed] [Google Scholar]
- 34.Friberger P. Synthetic Peptide Substrate Assays and Fibrinolysis and Their Application on Automates. Seminars in Thrombosis and Haemostasis. 1983;9(4):281–300. [PubMed] [Google Scholar]
- 35.Vogler EA. On the Origins of Water Wetting Terminology. In: Morra M, editor. Water in Biomaterials Surface Science. New York: John Wiley and Sons; 2001. pp. 150–82. [Google Scholar]
- 36.Hoffman AS. A General Classification Scheme for “Hydrophilic” and “Hydrophobic” Biomaterial Surfaces. J Biomed Mat Res. 1986;20:ix–xi. doi: 10.1002/jbm.820200903. [DOI] [PubMed] [Google Scholar]
- 37.Vogler EA. Water and the Acute Biological Response to Surfaces. J Biomat Sci Polym Edn. 1999;10(10):1015–45. doi: 10.1163/156856299x00667. [DOI] [PubMed] [Google Scholar]
- 38.Griffin JH. Role of surface in surface-dependent activation of Hageman factor (blood coagulation factor XII) Proc Natl Acad Sci U S A. 1978 Apr;75:1998–2002. doi: 10.1073/pnas.75.4.1998. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Krishnan A, Sturgeon J, Siedlecki CA, Vogler EA. Scaled Interfacial Activity of Proteins at the Liquid-Vapor Interface. J Biomed Mat Res. 2004;68A:544–57. doi: 10.1002/jbm.a.20104. [DOI] [PubMed] [Google Scholar]
- 40.Krishnan A, Siedlecki C, Vogler EA. Traube-Rule Interpretation of Protein Adsorption to the Liquid-Vapor Interface. Langmuir. 2003;19:10342–52. [Google Scholar]
- 41.Krishnan A, Siedlecki CA, Vogler EA. Mixology of Protein Solutions and the Vroman Effect. Langmuir. 2004;20(12):5071–8. doi: 10.1021/la036218r. [DOI] [PubMed] [Google Scholar]
- 42.Krishnan A, Wilson A, Sturgeon J, Siedlecki CA, Vogler EA. Liquid-Vapor Interfacial Tension of Blood Plasma, Serum and Purified Protein Constituents Thereof. Biomaterials. 2005;26:3445–53. doi: 10.1016/j.biomaterials.2004.09.016. [DOI] [PubMed] [Google Scholar]
- 43.Krishnan A, Liu Y-H, Cha P, Allara DL, Vogler EA. Interfacial Energetics of Globular-Blood Protein Adsorption to a Hydrophobic Surface from Aqueous-Buffer Solution. Journal of the Royal Society Interface. 2006;3:283–301. doi: 10.1098/rsif.2005.0087. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Krishnan A, Liu Y-H, Cha P, Allara DL, Vogler EA. Scaled Interfacial Activity of Proteins at a Hydrophobic Solid/Aqueous-Buffer Interface. J Biomed Mater Res. 2005;75A(2):445–57. doi: 10.1002/jbm.a.30444. [DOI] [PubMed] [Google Scholar]
- 45.Krishnan A, Liu Y-H, Cha P, Allara DL, Vogler EA. Interfacial Energetics of Blood Plasma and Serum Adsorption to a Hydrophobic Self-Assembled Monolayer Surface. Biomaterials. 2006;27:3187–94. doi: 10.1016/j.biomaterials.2005.12.032. [DOI] [PubMed] [Google Scholar]
- 46.Ariola F, Krishnan A, Vogler EA. Interfacial Rheology of Blood Proteins Adsorbed to the Aqueous-Buffer/Air Interface. Biomaterials. 2006;27:3404–12. doi: 10.1016/j.biomaterials.2006.02.005. [DOI] [PubMed] [Google Scholar]
- 47.Noh H, Vogler EA. Volumetric Interpretation of Protein Adsorption: Partition Coefficients, Interphase Volumes, and Free Energies of Adsorption to Hydrophobic Surfaces. Biomaterials. 2006;27:5780–93. doi: 10.1016/j.biomaterials.2006.07.038. [DOI] [PubMed] [Google Scholar]
- 48.Sheiko SS, Sun FC, Randall A, Shirvanyants D, Rubinstein M, Lee H-i, et al. Adsorption-induced scission of carbon–carbon bonds. Nature. 2006;440(7081):191–4. doi: 10.1038/nature04576. [DOI] [PubMed] [Google Scholar]
- 49.Dunn JT, Silverberg M, Kaplan AP. The Cleavage and Formation of Activated Human Hageman Factor by Autodigestion and by Kallikrein. J Biol Chem. 1982;257:1779–84. [PubMed] [Google Scholar]
- 50.Cochrane CG, Revak SD, Wuepper KD. Activation of Hageman Factor in Solid and Fluid Phases. J Exp Med. 1973;138:1564–83. doi: 10.1084/jem.138.6.1564. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 51.Noh H, Vogler EA. Volumetric Interpretation of Protein Adsorption: Competition from Mixtures and the Vroman Effect. Biomaterials. 2007;28:405–22. doi: 10.1016/j.biomaterials.2006.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Vogler EA. How Water Wets Biomaterials. In: Morra M, editor. Water in Biomaterials Surface Science. New York: John Wiley and Sons; 2001. pp. 269–90. [Google Scholar]
- 53.Richards FM. Areas, Volumes, Packing and Protein Structure. Ann Rev Biophys Bioeng. 1977;6:151–76. doi: 10.1146/annurev.bb.06.060177.001055. [DOI] [PubMed] [Google Scholar]
- 54.Chothia C. Structural Invariants in Protein Folding. Nature. 1975;254:304–8. doi: 10.1038/254304a0. [DOI] [PubMed] [Google Scholar]
- 55.Miller S, Lesk A, Janins J, Chothia C. The Accessible Surface Area and Stability of Oligomeric Proteins. Nature. 1987;328(27):834–6. doi: 10.1038/328834a0. [DOI] [PubMed] [Google Scholar]
- 56.Miller S, Janin J, Lesk A, Chothia C. Interior and Surface of Monomeric Proteins. J Mol Biol. 1987;196:641–56. doi: 10.1016/0022-2836(87)90038-6. [DOI] [PubMed] [Google Scholar]
- 57.Tsai J, Taylor R, Chothia C, Gerstin M. The Packing Density in Proteins: Standard Radii and Volumes. J Mol Bio. 1999;290:253–66. doi: 10.1006/jmbi.1999.2829. [DOI] [PubMed] [Google Scholar]
- 58.Gerstein M, Chothia C. Packing at the Protein-Water Interface. Proc Natl Acad Sci. 1996;93:10167–72. doi: 10.1073/pnas.93.19.10167. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Miller S, Janin J, Leak AM, Chothia C. Interior and Surface of Monomeric Proteins. J Mol Biol. 1987;196:641–56. doi: 10.1016/0022-2836(87)90038-6. [DOI] [PubMed] [Google Scholar]